Introduction

Better health outcomes management demands high quality assessment tools to evaluate the efficacy of specific pharmaceuticals and medical devices, or to monitor the outcome of a given treatment in terms of patients’ functioning and well being. There is a need for practical and user-friendly assessment systems that can capture health status data in real time and attain high precision without undue response burden for the patient. Item banks and Computerized Adaptive Testing (CAT) [1] have the potential to meet these needs.

In a CAT, the computer algorithm selects the items that are most informative for a particular respondent and scores the responses in a way that allows comparison with respondents answering a different set of items [1]. The psychometric theory that is utilized in solving these two tasks is called Item Response Theory (IRT) [2, 3, 4].

CAT and IRT methods have been used in educational assessment for decades, but the practical implementation in medical research is fairly new [5]. While medical research can use much of the methodology and approaches developed in educational testing, differences between the two fields necessitates some adaptation in the use of CAT and IRT within the framework of medical research. In this paper we will:

  1. 1.

    Discuss the IRT models that seem most relevant for patient reported outcomes (PRO) and their strengths and weaknesses for PRO research.

  2. 2.

    Discuss item banks, desirable attributes of a quality PRO item bank, and the steps to build an item bank. We illustrate these steps using a small item bank for mental health as an example.

  3. 3.

    Briefly illustrate the principles of CAT assessment.

  4. 4.

    Discuss differences between applications of CAT and IRT within educational testing and PRO assessment.

We will illustrate the steps in item bank development through a reanalysis of data on a well researched tool, the 34-item Mental Health Inventory (MHI) [6]. A more detailed empirical description of the psychometric analyses involved in item bank development can be found in a paper by Cook et al (this issue). IRT is further discussed by Orlando (this issue). A companion paper by Thissen et al. (this issue) discusses more general topics relating to the application of IRT and CAT methodology in PRO research.

IRT models

IRT models [2, 4] are statistical models of the relationship between a person’s score on the construct being measured and their probability of choosing each response on each item measuring that construct. IRT models can be used to evaluate how informative an item is for a specific range of scores and to estimate a person’s IRT score. Thus, IRT methods provide several advantages for computer-based assessment:

  1. 1.

    Test relevance and precision can be optimized for a given respondent burden.

  2. 2.

    Precision can be adapted to the needs of the specific application. If we do not require high precision for a given purpose the assessment can be stopped early to reduce respondent burden; if high precision is required, more items can be administered.

  3. 3.

    Scores are placed on the same metric regardless of which items in the bank are used.

  4. 4.

    Item banks can be expanded gradually by seeding and evaluating new items.

  5. 5.

    The response process can be monitored in real time to ensure assessment quality and that inconsistent response patterns are explored.

The mathematics of IRT models is discussed in detail in the psychometric literature (e.g. [2, 4]) and will only be reviewed briefly here. We will start our discussion with models assuming that all items are measuring the same latent construct (i.e., the unidimensional IRT models) and focus on two families of models that are the most frequently used in PRO research:

  1. 1.

    The Nominal Categories Model (NCM) [7] and special cases of this model such as the Generalized Partial Credit Model (GPCM) [8, 9], the Partial Credit Model (PCM) [10, 11] and the Rating Scale Model (RSM) [12],

  2. 2.

    The Graded Response Model (GRM) [13, 14].

For dichotomous items, these two families of models converges to the same model: the two-parameter logistic model (see Birnbaum in [15]). For a dichotomous (e.g. Yes = 1, No = 0) item, the two-parameter model can be written as a log odds (i.e. the logarithm to the ratio of two probabilities) in the following way:

$$ \log \left( {\frac{P\left( {X_{ij} =1\vert \theta _j } \right)}{P\left( {X_{ij} =0\vert \theta _j } \right)}} \right)=a_i \left( {\theta _j -b_i } \right), $$

where X ij is the response of person j to item i, θ j is the level of mental health (or whatever concept to be measured) for person j, and a i and b i are item parameters, describing characteristics of the particular item. b i is called the item difficulty or threshold parameter and is the value on the IRT scale where \({P(X_{ij}=0)=P(X_{ij} = 1)=.5}\) . a i is called the discrimination or slope parameter since it determines the amount of change in the log odds for one unit of change in the IRT score. The polytomous IRT models are described and compared in the most simple way through such log odds formulations (Table 1, also see [16, 17]). The models differ in the definition of the probabilities being compared and in the number of item parameters.

Table 1 The most frequently used IRT models for polytomous items
Full size table

In the NCM, each response category is compared to the baseline category (see Table 1). The model has a discrimination parameter a ic and an intercept parameter g ic for each response category (labeled c) except the first one (to identify the model, a i0 and g i0 can be set to zero). This model does not assume a rank order of the response categories and is therefore the most general of the described IRT models. However, the model still assumes a specific function for the log odds and thus may not fit all items (e.g. in case of multidimensionality or if a particular response option is favored a two very different level of health, but unlikely to be chosen in between, see [18]).

In the GPCM, each response category (c) is compared to the response category below and a common slope parameter is assumed for all response categories within one item. The model has a number of item category threshold parameters, b ic , (one less that the number of response categories). The GPCM is in fact a constrained version of the NCM (where a ic (in the NCM) = a i *c (in the GPCM) and g ic (in the NCM) = a i *c*b ic (in the GPCM)). This restriction reflects the assumption of rank ordered response categories made in the GPCM. If the model is further constrained by assuming a common slope parameter across all items, we achieve the PCM, which is part of the Rasch model family [2]. The slope parameter can either be constrained to 1 or have a common value different from 1 (see discussion later in this paper). If they fit the data, the Rasch models have unique advantages in terms of simplicity of interpretation and robust estimation techniques (see [2] for detailed discussion). However, many items will not fulfill the assumption of common discrimination.

The item category threshold parameter, b ic , of the PCM can be split into two terms \({(b_{ic}=l_{i}- d_{ic})}\) , where l i is termed a location parameter and d ic is called the item category parameter. If the item category parameters are constrained to be equal across items d ic  = d c , another Rasch family model, the RSM, is obtained. In statistical terms, the RSM is nested within the PCM, which is nested within the GPCM, which is nested within the NCM.

An alternative model is the GRM. As shown in Table 1 the GRM compares the probability of being in a certain response category or higher with the probability of being below that category. Except for this difference in the definition of the comparison of probabilities, the model is similar to the generalized partial model. Thus, the models have the same number of item parameters and both assume rank ordered response categories. An item that fits one of these models will usually also fit the other model well enough for practical use [19]. Finally, the GRM is very similar to the modern factor analytic models for analysis of categorical data [20, 21].

Figure 1 illustrates the GPCM [9] for three items concerning mental health (the three upper plots—full lines). In the upper plots, each full curved line (called item category response functions or option characteristic curves) represents the model’s prediction of the probability of choosing each of the item response categories for various levels of mental health (\({P(X_{ij}=c\vert \theta _{j})}\)). The horizontal (x-) axis is the mental health IRT score, “normed” so that the average adult in the USA has a score of 50 and a positive score indicates better mental health. At a score of 50, the most likely response on SF8MH (... how much have you been bothered by emotional problems...) is slightly (probability = .61), the most likely response on MHP01 (... how much of the time have you been a happy person) is most of the time (probability = .69) and the most likely response on MHC01 (... felt so down in the dumps that nothing could cheer you up) is none of the time (probability = .83). For the first item (SF8MH) we also estimated the GRM and plotted the item category response function for this model (broken lines). While not identical, the lines for the GRM are close to the lines for the GPCM.

Fig. 1
figure 1

Item category response functions and item information functions for three items on mental health. Full lines describe the GPCM, broken lines the GRM

Full size image

In the GPCM, the item category threshold parameters can be directly identified from these graphs as the point of intersection of adjacent category response functions. While the slope parameter cannot be directly identified from the graph, Fig. 1 conveys the sense that item 3 has higher slope than item 2, which has higher slope than item 1.

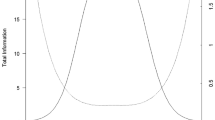
In contrast to classical psychometrics that typically assumes a constant measurement precision throughout the measurement range, IRT acknowledges that measurement precision depends on the score level. IRT allows for a calculation of a level-specific standard error of measurement for any combination of items. The contribution of each item to the overall measurement precision can be evaluated through item information functions. The item information functions shown in the lower part of Fig. 2 can be calculated from the IRT model [22]. Figure 1 shows that MHC01 is most informative for people with poor mental health and that MHP01 is the most informative items for people with good mental health. To evaluate the total information achieved from a combination of items, the item information functions are simply summed to achieve the test information function. The standard error of measurement is approximately equal to the inverse square root of the test information function.

Fig. 2
figure 2

Logic of computerized adaptive testing

Full size image

Use of IRT models in CAT item selection and score estimation

A typical CAT (Fig. 2, also see [1]) may begin with an initial global question that is asked of all respondents (Step 1). This question should be informative for a person with average health and have appropriate content for a first item. Alternatively, the first question could be selected based on previous information about the respondent such as their score on previous CAT-administrations or clinical data like disease stage. The response to the first item is used in Step 2 to estimate the person’s score and a respondent-specific confidence interval (CI). At Step 3, the computer algorithm determines whether any stopping rules have been fulfilled. If the stopping rule is not satisfied, Step 2 is repeated for the next most informative item. Often, the stopping rule is test-precision, in which case the computer evaluates whether the CI is within specified limits. Once the criterion is met, the algorithm ends the assessment of this construct. The required precision may vary according to score range or a maximum number of items may be specified. Thus, the CAT would stop if either a certain level of precision is achieved or if the maximum number of items has been used. Such safeguards may be useful to limit respondent burden. Other stopping rules may also be used, such as the probability of being below a certain cut point on the scale.

Figure 3 illustrates two possible sequences of score estimation and item selection in a CAT that uses SF8MH as the first global item. The scoring method used here, Expected a Posteriori (EAP) estimation [23], starts with a prior assumption about the distribution of mental health in the population (the normal distribution function in the first row). The mean (expected) IRT score is 50, but a wide range of values are possible (95% confidence interval 30–70). If the answer to SF8MH is extremely (second row, left column) the function for this response (bold black line) is multiplied with the prior distribution, which produces the “Posterior distribution 1” (row three). The IRT score estimate is the mean of this posterior distribution;

$${\hat{\theta}_j } ={\frac{\overset{+\infty}{\underset{-\infty }{\int}} {\; \overset{N}{\underset{i=1}{\prod}}{P(X_{ij} =c\vert \theta ) {\kern 1pt}\,\varphi \left( \theta \right){\kern 1pt}\,\theta \,{\kern 1pt}\hbox{d}\theta}}} {\overset{+\infty}{\underset{-\infty}{\int}}{\;\overset{N}{\underset{i=1}{\prod}}{P(X_{ij}} =c\vert\theta )\, \varphi \left(\theta \right){\kern1pt}\,\hbox{d}\theta}}}$$
Fig. 3
figure 3

Two possible CAT scenarios

Full size image

where N is the number of items and ϕ (θ) is the population distribution of θ. In practice, the equation is solved through numerical integration in a number of quadrature points (see e.g. [24]). The EAP estimate calculated from “Posterior distribution 1” is 30. The standard error of the EAP estimate is calculated as [24]:

$$\hbox{SE}\left( {\mathop {\hat{\theta}_j }} \right){\kern 1pt}\,=\sqrt {\frac{\overset{+\infty}{\underset{-\infty }{\int}} {\; \overset{N}{\underset{i=1}{\prod}} {P(X_{ij} =c\vert \theta ){\kern 1pt}\,\varphi \left( \theta \right){\kern 1pt}\,\left( {\mathop {\hat{\theta}_j}-\theta } \right)^2\,{\kern 1pt}\hbox{d}\theta }}}{\overset{+\infty}{\underset{-\infty }{\int}} {\; \overset{N}{\underset{i=1}{\prod}}{P(X_{ij} =c\vert \theta )\,\varphi \left( \theta \right){\kern 1pt}\,\hbox{d}\theta } } }} $$

The confidence interval can be calculated as \({\pm1.96*\hbox{SE} (\mathop{\hat{\theta}_j})}\) . For the IRT score estimate of 30, the confidence interval is 17–42 and thus considerably narrower than for the prior distribution.

At an IRT score of 30, MHC01 provides much more information than MHP01 (Fig. 1) and would thus be the logical choice for the next item. If the respondent answers a good bit of the time to this item (Fig. 3, row four) the function for this response is multiplied with posterior distribution 1 to produce posterior distribution 2 (row five). The IRT score estimate is now 29 with a 95% confidence interval of 21–36. If we had access to a large item bank and wanted more precision, we could continue to ask questions to continue to narrow the confidence interval.

If another respondent answers not at all to the first item, SF8MH, the CAT will take a different route (row two, right column). This response leads to an IRT score estimate of 58 with a 95% confidence interval of 44–74 (row three). In this score range, the MHP01 item provides more information and would be the logical choice. If the respondent answers most of the time to this item, the IRT score estimate after two items will be 57 with a 95% confidence interval of 46–70. Again, we can ask more questions to get more precision. However, the item MHC01 would be of little value or relevance here, since the respondent would be highly likely to select the response none of the time and the item would add very little information for this range of IRT scores (see Fig. 1). Although the two respondents answer different questions, their scores are on the same scale and can be compared no matter which or how many items from the item bank are answered.

While the sequence described above illustrates the principles of a CAT, further refinements to item selection techniques and stopping rules are possible (see e.g. [25]). For example, the item selection criteria of maximum information may be supplemented with selection criteria to ensure content balancing of the test (please see below). Also, other IRT scoring approaches than the EAP method may be used, e.g. weighted maximum likelihood estimation [26].

Initial steps in the development of an item bank for CAT

A good item bank should be content valid (cover all aspects of the construct to be measured) and have enough items to attain high measurement precision throughout the measurement range. The items should satisfy standard requirements for good items (e.g. simple, unequivocal, using common language, non-offensive) and should function the same way in different population subgroups. What constitutes sufficiently high measurement precision may vary and depend on the purpose of the assessment. For example, an assessment used in a clinical trial would likely demand high measurement precision throughout the measurement range to avoid floor and ceiling effects. However, an assessment used in the clinical care of individual patients might demand high precision at low health levels (where treatment and follow-up is necessary), but not for good levels of health (where intervention and follow-up is unnecessary).

For the analysis of the MHI, we used the baseline data (n = 2,786) from the Medical Outcomes Study [27, 28] for item bank development and US general population data from a 1998 survey (n = 5,038) [29] for norming the bank. The main steps in item bank development is outlined in Fig. 4 and described below (also see [30]):

Fig. 4
figure 4

Steps in the construction of an item bank

Full size image

Construct definition and item development

Meaningful assessments require clearly defined constructs and good items. Careful specification of the subdomains of the constructs and the domains that are not part of the constructs ensures that the item bank covers all relevant aspects of the constructs. Often this involves specifying hypotheses to be tested in later stages of validity testing, e.g. whether some domains can be seen as part of one overall construct (dimension) or whether they should be treated as separate constructs (dimensions). The MHI questionnaire builds on a conceptual model [6] for mental health that includes five subdomains: Anxiety, Depression, Behavioral/Emotional Control, Positive Well-being and Loneliness/Belonging. An important question for item bank development was whether these subdomains could be seen as part of one overall domain (see below).

Development of item banks often starts from established questionnaires [5]. The advantage of this approach is that content and construct validity and item quality have usually been evaluated previously. Also, the inclusion of established questionnaires in the bank enables the development of links that allows researchers to compare the results using the new scale with results from previous studies using the established questionnaire’s scores. However, several issues must be carefully considered, when building on established questionnaires:

  1. 1.

    Do all items measure the same construct? Different tools may use different names for the same construct or the same name for different constructs.

  2. 2.

    Are the time frames (recall period) from different questionnaires coherent and relevant for the current application?

  3. 3.

    Are some questions from different questionnaires practically identical, so only one of the set should be administered in any particular CAT?

  4. 4.

    Do the items use the same response choices? From a technical perspective, the IRT model can handle different response choices. However, difference in response choices may trigger different frames of reference. Further, while changes in response choices may keep the respondent more alert to the actual item content, multiple shifts in response choices may also be cognitively challenging for patients, particularly the elderly.

  5. 5.

    Are there issues of copyright and intellectual properties that need to be resolved?

If high measurement precision throughout the range of IRT scores is required, steps have to be taken to identify existing items or to develop new items that are relevant for the extremes of the scale. Such items often have poor performance on the indicators used in classical psychometrics (such as item-total correlations) and therefore they tend to be excluded from questionnaires developed using classical methods. The item information functions shown in Fig. 2 are fairly typical in the sense that the items provide most information for people with poorer than average health. It is often a challenge to develop items with high precision for people with better than average health.

Collecting data for item calibration and testing

The sample of respondents used for item bank development needs to be large and diverse enough to enable stable item parameter estimates and test of the various aspects of model fit. In the initial calibration stage of item bank development, representativity of the sample in terms of e.g. providing similar sociodemografic structures as the targeted population is less important for the analyses than having enough responses from people across the whole measurement range. To ensure good parameter estimates for items aimed at either very good or very poor health, respondents at these levels of heath may be oversampled to achieve responses in all item response categories. Since the ability to fit IRT models depends on the match between the items and the population (skewed items require larger sample sizes), no sample size guidelines will cover all situations. However, for IRT models like the GPCM and the GRM, sample sizes of 500–1,000 are probably sufficient [31, 32]. For smaller sample sizes, models with fewer parameters (e.g. the PCM or the RSM) may still work. The MOS sample used for item bank development in our example was large (n = 2,786) by these criteria and consisted of five disease groups (hypertension, diabetes, congestive heart failure, acute myocardial infarction, and depressive disorder). The inclusion of depressive disorder provided a fairly substantial proportion of people in poor mental health.

While a keyboard or a touch screen are the most common modes of administering a CAT, other modes are possible, e.g. automated phone interviews, computer assisted phone interview, or computer assisted personal interviews. For item bank development, paper-and-pencil administration is also a possible data collection mode. The item response distribution and thus the item parameters may depend on administration mode (see e.g. [33]). Within the PRO field, an interviewer effect has been well documented for phone interviews compared to paper-and-pencil self reports, causing more positive responses to items on mental health [34, 35]. Studies have found few mode differences between computerized assessment and paper-and-pencil administration [36, 37, 38], but no large studies have yet been performed within the PRO field for comparing these modes of data collection. In this demonstration, we used data collected by paper-and-pencil administration to develop an item bank, but ideally, the mode of administration for the item calibration sample should be the same as the mode in the final CAT.

Psychometric analyses: fitting an IRT model and testing model assumptions

Testing dimensionality and local independence

Standard unidimensional CAT requires that items provide information on the dimension of interest and that this dimension explains all co-variation between items (the assumption of local independence). Although a perfectly unidimensional item bank is probably not achievable for most theoretically interesting constructs, the bank needs to be sufficiently unidimensional to make a single score meaningful and to ensure that item parameter estimates (and in turn person IRT scores) are not unduly influenced by problems of multidimensionality or local dependence between items. Exploratory and confirmatory factor analytic methods for categorical data [39] represent strong and flexible approaches to testing dimensionality and local dependence [30], but many other methods exist (e.g. [40, 41, 42, 43]). If problems are identified, possible solutions include item exclusion, splitting the item pool into two or more unidimensional sub-pools, using a more general IRT model (e.g. a multidimensional model), or, in milder cases of multidimensionality, using special item selection rules to ensure content balance [25].

For the mental health item pool, dimensionality was evaluated using factor analysis for categorical data, comparing a unidimensional model with a five dimensional model (the five original subdomains) and with a second-order model where the five subdomains were seen as indicators of an overall mental health factor. Table 2 shows the factor correlations in a five-factor model run in the data set that combined the five disease groups in the MOS sample (similar results were found on separate analyses within each disease group). The factor correlations were high, except for the Loneliness/Belonging domain and for the correlation between Anxiety and Positive Well-being (Table 2). In the second-order model, loadings on the mental health factor are high for all subdomains and extremely high for depression and behavioral/emotional control (Table 2). In a simple one-factor model, loading of all items exceeded .7—except for one item from the Loneliness/Belonging domain (which had a loading of .65). Based on these and other results, a unidimensional IRT model for the items was seen as justified. Three items from the Loneliness/Belonging domain were excluded since they did not load strongly on the overall factor and had large residual correlations.

Table 2 Factor correlations and loadings on second-order factor for subdomains of Mental Health. N = 2,717
Full size table

Further, item selection rules were defined for CAT administration to ensure content balancing among the three main domains in the pool (Anxiety, Depression/Control, and Positive Well-being). This avoids the possibility of a respondent receiving only items concerning one of the attributes of mental health. While any selection of items from the bank should allow estimation of a mental health IRT score, we find that content balancing enhances the face and content validity of the CAT and provides for a more robust IRT-score estimate.

Initial analyses of item category response functions by non-parametric methods

Before fitting a parametric model, it is useful to examine non-parametric IRT models that allow visual inspection of the empirical item category response functions (option characteristic curves) [44]. This allows further identification of poor items and response choices. Items can be excluded, a more general IRT model can be used, or response choices that do not discriminate can be collapsed in the IRT analyses. The top graph in Fig. 5 illustrates a response option (1) that is not used by many respondents, but has the right rank order. This can be seen from the linear increase in the item category discrimination parameters, which were used to generate the functions (here, the NCM parameterization is used for illustration). On the other hand, for the item in the lower part of Fig. 5, response choice 1 and 2 does not have a clear rank order, as can also be seen from their item category discrimination parameters. These two response choices should be collapsed or an NCM model should be used for estimation.

Fig. 5
figure 5

Simulated data to illustrate item that do and do not fulfill the rank order requirements for models like the GPCM and GRM

Full size image

Fit an item-response model and test model fit

The choice of IRT model is sometimes hotly debated. One fundamental debate involves the choice between Rasch type model (such as the PCM and RSM models) and non-Rasch model (e.g. the NCM, GPCM, and GRM, see e.g. [45] for introduction to some of the issues). The Rasch type models, originating in the work of Georg Rasch [46, 47] were derived from theoretical requirements for valid measurements—partly relating to the use of the item sum score as the proxy measure for the latent trait (for an introduction see [48]). The second tradition, originating in the work of Thurstone, Lord, and Birnbaum (see [15, 24]) places greater emphasis on fitting a model for the data at hand (for an introduction see [3]). Since the Rasch type models generally incorporate fewer item parameters that the other models, robust parameter estimates may be achievable with smaller sample sizes. Also, special item parameter estimation methods (called conditional maximum likelihood estimation) are available for the Rasch type models only (see e.g. [49, 50]). Thus, few psychometricians would disagree that Rasch type models (being the most parsimonious models) should be used if they fit the data. However, often the Rasch models will not fit the data well, while other models do. In this situation, some psychometricians would achieve fit to Rasch type models by dropping items from the bank. This may be a good solution if it can be justified by other methods that the items do not conceptually belong to the scale. However, we would advocate against extensive deletion of items that satisfy requirements of unidimensionality, local independence, and lack of differential item functioning (see below) if such items can be fitted with a more general IRT model (such as the GPCM, GRM, and NCM).

If more general IRT models are pursued, a choice between the GRM and GPCM models has to be made. These models have the same number of item parameters and, as shown in the top plot of Fig. 1, the models often produce very similar item category response functions (see [19]). One advantage of the GPCM is that it is part of a series of nested models (see previous discussion). Working within a framework of nested models has some attraction because the significance of additional parameters can be evaluated through likelihood ratio tests and the interpretation of item category threshold parameters does not change when going from e.g. a PCM model to a GPCM model. One advantage of the GRM model is its similarity with modern factor analytic models for categorical items [21]. Also, implementation of IRT models for longitudinal data is currently easier for the GRM than for the GPCM (see [51], note that longitudinal models have also been implemented for the PCM and RSM [52]). In conclusion, no model can be recommended as generally superior to all other models for PRO data. The model choice can be informed by the considerations noted above and by information of model-data fit. All the described models can be used to calculate item information functions and estimate IRT scores. Technically, there is no problem in having different IRT models for different items in a CAT, as long as all items are calibrated to the same scale.

Several well researched fit tests are available for the Rasch type models (see [53, 54]). Fewer tests have been available for polytomous IRT models in general. A item-based G 2-test is available in the software program Parscale [9, 55]. In this test, the respondents are categorized in 10 groups based on their estimated IRT score. For each item, the predicted and observed item score distribution is compared for each of the 10 IRT score levels and summarized in a G 2-statistic [9]. A problem of this test is that the estimated IRT score is treated as if it was the true value. This can inflate the Type I error rates, flagging too many items as misfitting, particularly for short scales or small item banks [56]. Procedures that take this problem into account have been suggested by Stone [57, 58], Glas [59], and Orlando and Thissen [60]. For the current analyses, we used an extension of the Orlando and Thissen X 2-test appropriate for polytomous items. For both the GPCM and the GRM, we achieved satisfactory fit by statistical criteria for 23 items (22 of which were common for the two models). We chose the GPCM as the final model for this item bank. After inspecting plots of observed version predicted item score distribution for different levels of mental health, we decided that eight additional items could be used for this demonstration purpose since the deviations from the predicted values were minor and not systematic, the significance probably mostly being due to the fairly large sample size (2,786 respondents).

Test of differential item functioning (DIF)

One of the basic assumptions in outcomes measurement is that items function the same way in different disease and demographic groups. For a given scale or IRT score level, item responses should be independent of group membership. Although DIF is a general measurement problem, it is best conceptualized and detected using IRT or similar methods (for more discussion of DIF see Cook et al. (this issue) and Thissen et al. (this issue)). For the mental health item pool, DIF for gender was found for an item worded “How often have you felt like crying...”. For a given level of mental health, men were less likely to indicate feeling like crying. Such DIF can be corrected by using separate item parameters for males and females for this item, or by removing the item from the bank.

Setting the metric

After the item bank has been developed, the researcher has to decide how the metric (IRT score) should be defined. In Rasch type models, the metric is typically defined by the items, by setting the discriminating parameter to one and scaling the item category threshold parameters to sum to zero. This parameterization allows for easy comparison of item parameters estimated from different samples (in theory, these parameter estimates are sample invariant). For other IRT models, the metric is typically defined by the population in which the items were calibrated, by setting the mean to zero and the standard deviation to one. Item parameter estimates from two different samples can therefore not be directly compared, unless some kind of linking have been utilized (e.g. through common ‘anchor’ items). However, it is perfectly feasible to define the metric also for Rasch type models through the population mean and variance, or defining the metric of more general IRT models through restrictions on the item parameters (e.g. set the product of the item discrimination parameters to one and the sum of item category threshold parameters to zero. For generic health status measures it may be convenient to standardize the metric to a general population (e.g. the US population), setting the mean to 50 and the standard deviation to 10. For disease-specific domains, the metric could be based on a well-defined patient population. The population that defines the metric need not answer all the questions in the item bank—only enough questions to set the metric precisely. For the mental health item pool, a five-item subset of the mental health inventory (the MHI-5) was used to define the metric. These five items were administered to a representative sample of the US general adult population. The metric was then set so this population achieved a mean score of 50 and a standard deviation of 10. To evaluate whether the five items provided a sufficiently robust anchor for norming the item bank, we conducted five additional analyses using only four of the MHI-5 items. In these analyses, the variation in population mean was 49.8–50.0 and the variation in population standard deviation was 9.7–10.1. We concluded that the five polytomous items provide a robust anchor.

An alternative to norm based scoring is to anchor the assessment based on the items. For example, a score of 0 could be the lowest possible score (worst response on all items in the bank) and 100 could be the highest possible score. However, using such anchors would hinder the future expansion of the item bank as adding new items would change the anchoring of the scale.

Even when the metric is well defined, more work is still needed in order to make the score easy to interpret for the respondent, the clinician, and the fellow researcher. Tools to do this are “benchmarks” and cross calibration tables. Examples of benchmarks on a mental health scale would be the distribution of scores for people with major depression or the typical score where the patient is likely to have thoughts of committing suicide. Often a researcher also needs to compare his/her results with previous studies, which may have used other questionnaires—often scores by traditional sum score methods. Cross-calibration tables enable such comparisons by showing roughly equivalent values on the IRT score and the score on the traditional questionnaires (see [61]).

There may be times in health outcomes research when access to a computer is not possible. In these cases, a fixed short form can be created from the item bank and scored in the same metric (see e.g. [62]). The selection of such a short form should be based on both item information and content considerations. This emphasizes the need for item banks in PRO research to provide crucial flexibility in data collection methods.

Finalizing CAT specifications

To use the item bank in a CAT, item selection rules and stopping rules must be defined. Simulated CAT runs are effective in evaluating the impact of various rules on test length, precision, and validity. One approach is to run simulations of a CAT on the data already collected for the item bank development (so-called “real-data” or “post-hoc” simulations) [63]. These simulations can implement the steps shown in Fig. 2. The total set of responses used to develop the item bank is used as input, but during the simulation the computer only uses the responses that correspond to the questions that would have been asked during a real CAT. Another possibility is to simulate item responses based on the IRT model, and use these simulated responses as input to the CAT (“Monte Carlo” simulation); this is particularly useful when the item bank has been developed by linking items across several studies, so that no respondent has actually answered all items. Note that neither of these techniques are tests of the measurement model, they are simply ways of evaluating the precision and item use that are achieved by different stopping rules in a CAT based on the current item bank.

A “real-data” simulation of the Mental Health CAT based on the initial item bank using a item selection criteria based on maximum information (for the particular respondent) and a fixed stopping rule of five items resulted in excellent agreement between the CAT estimated score and the estimated score based on all 31 items (r = .985). For the final Mental Health CAT (which were scaled to a mean of 50 and standard of 10 in the US general population), higher precision was deemed necessary for people with poor mental health (e.g. those at high risk for having depression [64]). Therefore, the standard stopping rules were defined to be based on precision, but with requirements for precision (standard error of measurement; SEM), varying over the range: <42 (SEM < 3), 42–60 (SEM < 4), >60 (SEM < 6.6).

CAT in educational testing and in outcomes research

CAT was initially developed for the assessment of abilities (see e.g. [63]) and its applications in outcomes research builds heavily upon the methods developed in educational testing [1]. However, applications of CAT in outcomes research differ in four major areas: choice of IRT models, generation of items, response burden, and problems of item exposure.

IRT model

Educational tests most frequently use multiple-choice items that are scored right/wrong and analyzed by dichotomous IRT models. Such items are only informative over a narrow range of the scale and uninformative at other levels, which can increase the number of items needed to achieve a certain precision if the CAT is started at an inappropriate ability level [65]. As discussed below, such increase in respondent burden, may be unfortunate in outcomes research. However, outcomes research mostly uses items that are scored on an ordinal scale (e.g. 1–5) and analyzed by IRT models such as the GPCM model shown in Figs. 1 and 3. Such ‘polytomous’ response items provide more information over a broader range of scores. Therefore, the same level of precision can be obtained with fewer items and the choice of starting point is less crucial.

Item generation

To achieve precision over the full range of a scale, the item bank needs a large number of items with sufficient diversity. In an educational testing context, generation of new items is done routinely and the pool of potential items can be seen as unlimited for many topics. In contrast, the number of ways questions can be asked about patient-reported outcomes may be limited. Item banks based on pooling items from existing questionnaires may provide good measurement precision in some ranges, but insufficient precision at the extremes.

Item exposure

In educational testing, the assessment needs to take place in a controlled environment and item content needs to be kept secret to avoid cheating. Countering these problems necessitates special test sites, large item pools, and complex procedures for item exposure control [1]. For patient reported outcomes, items are not kept secret because item exposure is probably much less of a problem. However, it is not yet well researched whether very frequent exposure to particular items (e.g. through PRO diaries) could change the way they are interpreted. This could be evaluated through test of item drift using IRT models for repeated assessment [51] and anchoring on the items that are used less frequently.

The issue of faking better or worse health than actually experienced may also surface as a problem for PRO assessment, although probably not linked to item exposure the same way as in educational testing. Many different tests for response consistency have been developed within IRT (see e.g. [66]), but it is not yet tested whether they can detect attempts to faking PRO assessments.

Response burden

Health outcomes instruments are often used in research on the very ill, young children or the elderly who cannot tolerate prolonged assessment. In contrast, high-stakes educational testing can allow longer test lengths to ensure precise measurement. In our mental health example, a CAT score with five items had very good agreement with the total item bank score. Using such CAT specifications would produce instruments with a length similar to popular short forms like the SF-36 [67] (if a similar number of domains needs to be assessed), but having far better precision and much less floor and ceiling effects. Both shorter and longer CATs are also possible, although very brief assessments may not benefit much from CAT methodology. An important advantage of CAT is that the trade-off between response burden and test precision can be optimized for the particular purpose. Related to response burden is cost of assessment. In educational testing, assessment through CAT is more costly than paper-and-pencil assessment [1]. However, in the health field this may not be the case, if assessments are done through the Internet. For example, during the launch of one of the first CATs for a health outcome, the Headache Impact Test [68], almost 20,000 assessments could be performed at very low incremental costs once the test was developed [69].

Multidimensional CAT

For PROs, the researchers often want to measure several distinct yet related constructs and might want to gain measurement precision by utilizing information on the association among the different dimensions. It might also be more realistic to assume that some items measure more than one dimension. These tasks can be accomplished by multidimensional CAT, which builds on multidimensional IRT (MIRT) models and allows simultaneous measurement of multiple dimensions [70]. Some MIRT models can be estimated by factor analytic methods for categorical data (e.g. [39]) as has been done for a mental health instrument [71]. Multidimensional CAT is an exciting area for future development, but can also be very computer intensive and the interpretation of scores is even more complex.

Conclusion

The basic requirements for a good item bank for use in a CAT (such as a clearly defined construct, content validity, clear and unambiguous items) are no different than the requirements for developing any other PRO questionnaire. Item bank development requires careful attention to construct definition, to item selection and item development, to the selection of the developmental and norming samples, and to the psychometric analyses. Using IRT modeling, the psychometric analyses involves evaluation of unidimensionality and local independence, choosing an item response model and checking item fit, test of differential item functioning, and developing CAT specifications. Simulation studies presented in this article suggest that CAT assessment using as few as five polytomous items per domain achieves high precision and agreement with total score. Thus, CAT may considerably improve test precision and lower floor and ceiling effects as compared to those short form health surveys being used today.