Comparing maximum likelihood and PLS estimates for structural equation modeling with formative blocks

Abstract

A common misunderstanding found in the literature is that only PLS-PM allows the estimation of SEM including formative blocks. However, if certain model specification conditions are satisfied the model is identified, and it is possible to estimate a covariance-based SEM with formative blocks. Due to the complexity of both SEM estimation methods, we studied their relative performance in the framework of the same simulation design. The simulation results showed that the effect of measurement model misspecification is much larger on the ML-SEM parameter estimates. For a model that includes a correctly specified formative block, we found that the inter-correlation level among formative MVs and the magnitude of the variance of the disturbance in the formative block have evident effects on the bias and the variability of the estimates. For high inter-correlation levels among formative MVs, PLS-PM outperforms ML-SEM, regardless of the magnitude of the disturbance variance. For a low inter-correlation level among formative MVs the performance of the two methods depends also on the magnitude of the disturbance variance. For a small disturbance variance, PLS-PM performs slightly better compared to ML-SEM. On the contrary, as the disturbance variance increases ML-SEM outperforms PLS-PM.

1 Introduction

Structural equation modeling (SEM) is a statistical method aimed to model a network of relationships among variables that cannot be observed nor measured directly, i.e, the latent variables (LV). Each LV is measured by a number of observable indicators, usually defined as manifest variables (MV).

The estimation methods for SEM group into two different approaches: the covariance-based approach and the component-based approach. Maximum likelihood method (ML-SEM) is one of the most well-known estimation methods for covariance-based approach (Bollen 1989), whereas partial lelast squares path modeling (PLS-PM) is the most utilized method for Component-Based approach (Wold 1982). Both methods have distinctive statistical characteristics, and selecting a method to SEM depends on the particular research situation.

If the theoretical model is correct and the standard assumptions underlying SEM are satisfied, ML estimators are unbiased. PLS estimators lack the accuracy of ML estimators. However, PLS-PM is a powerful method because of the minimal demands on measurement scales, sample size, and data distributions. It is particularly applicable for predictive applications and theory building, but it can be also used appropriately for theory confirmation (Chin 1998; Falk and Miller 1992).

Even though there are situations in which MVs are more realistically thought of as causes of a LV (formative scheme), most researchers consider them as effects (reflective scheme) without even questioning their appropriateness for the specific LV at hand. This attitude may lead to misspecified models and there is growing evidence that measurement model misspecification has an impact into all SEM estimates (MacKenzie et al. 2005; Jarvis et al. 2003).

A common impression found in the literature is that only PLS-PM allows the estimation of formative blocks. The implication of formative MVs in Covariance-Based framework is a rather difficult task. However, if certain model specification conditions are satisfied, Covariance-Based methods are also capable of handling formative blocks (Bollen and Davis 2009; Williams et al. 2003).

We looked into this issue, and through a simulation study we investigated the effects of measurement model misspecification and the implications of formative MVs on both ML-SEM and PLS-PM parameter estimates.

2 Nature, direction and misspecification of relationships between latent variables and manifest variables

Relationships between MVs and LVs can be modeled in two different ways. Reflective MVs are considered as being caused by the related LV: variation in LV yields variation in MVs. On the contrary, formative MVs are viewed as causes of a LV: variation in MVs causes variation in LV¹ (see Fig. 1).

Fig. 1

Measurement models

The theoretical differences between the two schemes are not trivial. Reflective blocks should possess internal consistency (i.e., MVs in each block are supposed to be highly correlated among each other), while there is no reason to expect high correlation among formative MVs (Tenenhaus et al. 2005). This also implies that conventional measures used for evaluating the validity and reliability of a LV cannot be applied for formatively-measured LVs (Bollen and Lennox 1991; Diamantopoulos 2006). Confirmatory tetrad analysis (CTA) (Bollen and Ting 2000) is an example of an alternative way for testing construct validity. Reflective MVs are interchangeable: dropping an indicator from the measurement model should not alter the meaning of the LV (Bollen and Lennox 1991). This is not required when considering formative MVs. As for the nature of the error term in formative blocks, several definitions are found in the literature (Bollen and Lennox 1991; Edwards and Bagozzi 2000; Diamantopoulos 2006). The error term in formative blocks is not a measurement error and it is more properly called as “disturbance”.

In some particular situations determining the real nature of a LV is a difficult task (Edwards and Bagozzi 2000). Measurement model misspecification is fairly common among published research studies, and it is proven that it holds the potential for poor parameter estimates and misleading conclusions (MacKenzie et al. 2005; Jarvis et al. 2003). Its effects extend also to the estimates of the path coefficients connected to the misspecified block. This is due to the fact that a reflective treatment of a block that should instead be modeled as formative reduces the variance of the LV. The variance of a reflectively-measured LV equals the common variance of its MVs , whereas the variance of a formatively-measured LV encompasses the total variance of its indicators (Fornell et al. 1991).

Let us consider the common case of an exogenous formative block misspecified as reflective. If the level of the variance of the endogenous LVs is maintained, the estimates of the path coefficients connected to the misspecified exogenous LV is likely to be substantially inflated (Diamantopoulos et al. 2008).

3 Formative indicators in covariance-based SEM

Several alternative formulations have been proposed for SEM specification, but a very general formulation was given by Bentler and Weeks (1980). In the Bentler–Weeks approach any variable in the model (MVs, LVs, errors and so on) is either a dependent or an independent variable. The distinction between latent and manifest variables is secondary to the distinction between dependent and independent variables. The covariances among the independent variables can be part of the model parameters while the covariances among the dependent variables, or between the dependent variables and the independent variables, are explained by the model through the so-called free parameters. This model specification permits the inclusion of formative manifest variables in covariance-based SEM.

The general structural equation is written as

$$\begin{aligned} \varvec{\eta } = \mathbf{B}\varvec{\eta }+ \varvec{\Gamma }\varvec{\xi } \end{aligned}$$

(1)

The vector $\varvec{\eta } (m\times 1)$ contains all dependent variables, $\varvec{\eta }'=[\mathbf{y}',{\varvec{\uppi }}']$, where $\mathbf{y}$ is a vector of reflective MVs and ${\varvec{\uppi }}$ represents the endogenous LVs in the model. The vector $\varvec{\xi } (n\times 1)$ of all independent variables, $\varvec{\xi }^{'}=[\mathbf{x}',\varvec{\tau }{'},\varvec{\zeta }^{'},\varvec{\varepsilon }']$, contains the formative MVs $\mathbf{x}$, the exogenous LVs $\varvec{\tau }$, the disturbances $\varvec{\zeta }$, and measurement errors $\varvec{\varepsilon }$. $\mathbf{B} (m\times m)$ and $\varvec{\Gamma } (m\times n)$ contain coefficients capturing the effects of the independent variables on the dependent variables.

To simplify matters, let us consider $\varvec{\eta }, \varvec{\xi }, \mathbf{y}, \mathbf{x}$ as deviations from their means. Since some of the variables in $\varvec{\eta }$ are measured variables $\mathbf{y}$, we obtain them by means of a suitable selection matrix $\mathbf{G}$ with elements equal to 0 or 1 such that:

$$\begin{aligned} \mathbf{y} = \mathbf{G}_y\varvec{\eta } \end{aligned}$$

(2)

If we have formative MVes $\mathbf{x}$ in the vector $\varvec{\xi }$ we extract them by:

$$\begin{aligned} \mathbf{x} = \mathbf{G}_x\varvec{\xi } \end{aligned}$$

(3)

$\mathbf{G}_x$ and $\mathbf{G}_y$ are Boolean matrices with all zero entries except for a single element equal to 1 in each row to select $\mathbf{x}$ from $\varvec{\xi }$ and $\mathbf{y}$ from $\varvec{\eta }$ respectively.

From the “general structural equation” and the “selection models” follows the “implied covariance matrix”, given by the following matrix elements:

$$\begin{aligned} \varvec{\Sigma }_{yy}&= \mathbf{G}_y(\mathbb {\mathbf{I}}-\mathbf{B})^{-1}\varvec{\gamma }\varvec{\Phi } \varvec{\gamma }^{'}(\mathbb {\mathbf{I}}-\mathbf{B})^{-1}\mathbf{G}^{'}_{y} \nonumber \\ \varvec{\Sigma }_{yx}&= \mathbf{G}_y(\mathbb {\mathbf{I}}-\mathbf{B})^{-1}\varvec{\gamma }\varvec{\Phi }\mathbf{G}^{'}_{x} \nonumber \\ \varvec{\Sigma }_{xx}&= \mathbf{G}_x\varvec{\Phi }\mathbf{G}^{'}_{x} \end{aligned}$$

(4)

where $\varvec{\Phi }$ is the covariance matrix of the independent variables $\varvec{\xi }$, and it is not function of other parameters.

When no measured variable is included in $\varvec{\xi }$, there are no formative MVs, thus $\varvec{\Sigma }_{yx}$ and $\varvec{\Sigma }_{xx}$ are null, and $\varvec{\Sigma }_{yy} = \varvec{\Sigma }$.

Identification of formative measurement models still represents an open problem. Obviously, a necessary but not sufficient condition is the “t-rule” (i.e., the number of free parameters must not exceed the number of elements in the covariance matrix). Regarding the “scaling rule” (i.e. each LV needs to be scaled for the model to be identified), among other options, we can fix a weight from a formative MV to the LV at some non-zero value (MacCallum and Browne 1993).

To resolve the indeterminacy associated with the LV level error term, a necessary but not sufficient condition is the so-called “2+ Emitted Paths Rule”. Every LV with an unrestricted variance or unrestricted error variance must emit at least two directed paths to other variables, when these latter variables have unrestricted error variances (Bollen and Davis 2009). Another solution is to fix the variance of the disturbance term to zero. However, dropping the residual term implies the theoretical assumption that the formative MVs completely capture the underlying LV and no unexplained variance exists. The obtained variable becomes a “composite variable”, not a formatively-measured LV (MacCallum and Browne 1993).

Another strategy to identification is the so-called “piecewise identification”, based on breaking the model into smaller pieces and establishing the identification of one piece before moving on to the next piece (Bollen and Davis 2009).

Once a model is identified, we can estimate its parameters by standard estimation procedures (Bentler and Weeks 1980).

Another important issue that needs to be addressed when modeling formative blocks is what to do with the covariances among the exogenous MVs in the model (MacCallum and Browne 1993). Since formative MVs are simply exogenous variables, they may be correlated due to spurious causes not considered in the model, thus it would be more appropriate to free all covariances among them.

Finally, it must be stressed that in the recent SEM literature there is an interesting discussion on the meaning of the formatively-measured LV. Some researchers state that the known solutions for the matter of identification imply interpretation difficulties. A recent paper by Treiblmaier et al. (2011) clearly illustrates this issue. The authors state that a formatively-measured LV is actually a second-order factor that is predicted by some MVs and that explains the correlation of its consequent variables. Without this correlation the formatively-measured LV would disappear, and this is contrary to the idea that the LV is created solely by their exogenous MVs. This is a very interesting topic which needs further investigations.

4 Design of the simulation study

The aim of this study is to investigate, within the same simulation design, the performance of both PLS-PM and ML-SEM when a block is modeled as formative.

In order to satisfy the above mentioned identification rules, we considered a formative exogenous block with unrestricted disturbance variance, that emits at least two directed paths to other LVs, and the covariances between the measurement errors of the MVs related to the endogenous LVs were fixed to zero.

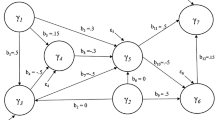
A model with this framework is particularly justified when dealing with customer satisfaction data. Indeed in the European Customer Satisfaction Index model (ECSI 1998) literature suggests that the LV Image may be formatively-measured. We considered the ECSI model consisting of one formatively-measured exogenous LV, Image (${\varvec{\uppi }}_1$), and five reflectively-measured endogenous LVs, from ${\varvec{\uppi }}_2$ to ${\varvec{\uppi }}_6$, that represent Customer Expectations, Perceived Quality, Perceived Value, Customer Satisfaction and Customer Loyalty, respectively.

The Monte Carlo simulation was conducted by EQS 6.1 for Windows. The data generation process is consistent with the procedure described by Paxton et al. (2001) for a Monte Carlo SEM study. We first pre-specified the relationships in the SEM and then simulated data for the given parameter values.

The true path coefficient values were chosen in order to be as similar as possible to those commonly encountered in the marketing literature (Vilares et al. 2010). The postulated structural model is:

$$\begin{aligned} {\varvec{\uppi }}_2&= 0.9{\varvec{\uppi }}_1 + \varvec{\zeta }_2 \nonumber \\ {\varvec{\uppi }}_3&= 0.8{\varvec{\uppi }}_2 + \varvec{\zeta }_3 \nonumber \\ {\varvec{\uppi }}_4&= 0.3{\varvec{\uppi }}_2 + 0.7{\varvec{\uppi }}_3 + \varvec{\zeta }_4 \nonumber \\ {\varvec{\uppi }}_5&= 0.3{\varvec{\uppi }}_1 + 0.1{\varvec{\uppi }}_2 + 0.4{\varvec{\uppi }}_3 + 0.3{\varvec{\uppi }}_4 + \varvec{\zeta }_5 \nonumber \\ {\varvec{\uppi }}_6&= 0.3{\varvec{\uppi }}_1 + 0.7{\varvec{\uppi }}_5 + \varvec{\zeta }_6 \end{aligned}$$

(5)

For the LV Image, we adopted the following formative model:

$$\begin{aligned} {\varvec{\uppi }}_1 = 0.4\mathbf{x}_1+0.25\mathbf{x}_2+0.15\mathbf{x}_3+0.1\mathbf{x}_4+0.1\mathbf{x}_5+\varvec{\zeta }_1 \end{aligned}$$

(6)

Afterwards, the outer weights were modified in order to obtain the variance of ${\varvec{\uppi }}_1$ equal to one, taking into account the variance of the disturbance $\sigma ^2_{\zeta _{1}}$ as well. In order to focus on the issue of formative blocks in SEM, the loadings between the reflective MVs and the related LVs were set all to 1.

We conducted the simulation setting different variance values of the disturbance $\varvec{\zeta }_{1}$ in the formative block. In particular, we set four different values of $\sigma ^2_{\zeta _{1}}$, from a small value of 0.05 (yielding a $R^2$ of 0.95) to a large value of .5 (yielding a $R^2$ of .5). The values of $\sigma ^2_{\zeta _{1}}$ were chosen to satisfy the equation:

$$\begin{aligned} R^2 = 1-\frac{Dev(\varvec{\zeta }_{1})}{Dev({\varvec{\uppi }}_1)} \end{aligned}$$

(7)

For the model considered in this simulation study, the 2+ emitted path rule and t rule are met. To satisfy the scaling rule a loading was fixed to 1 in each reflective block, and the first weight in the formative block was fixed to the given parameter value. Furthermore, to confirm the identification of the model we can use the piecewise identification strategy (Bollen and Davis 2009).

5 Data generation and simulation results

Once the population parameter values were set, we generated a total of 500 sets of data for three different sample sizes (100, 250, 500), four different disturbance variance values $\sigma ^2_{\zeta _{1}}$ (0.05, 0.2, 0.35, 0.5), three different numbers of MVs in the formative block (3, 5, 7), and three different levels of inter-correlation among MVs in the formative block (0.2, 0.4, 0.6). We did not take into account inter-correlation levels greater than 0.6 to avoid the issue of multicollinearity which might arise when estimating a formatively-measured LV. Given that very often the data do not follow multivariate normal distributions, we also generated data from non-symmetric distributions with different degrees of skewness and kurtosis (0.5, -0.8; 1.5, 2.5; 2.5, 9) following the Vale and Maurelli (1983) technique built in EQS 6.1.

In order to estimate the ML-SEM and PLS-PM parameters, we employed the “ML” Discrepancy function by means of EQS, and the “centroid scheme” by means of the package PLSPM in R, respectively.

Three commonly reported measures were used to assess how well the methods estimate the parameters: the Relative Bias ($RBias$), the Standard Deviation ($StD$) and the Root Mean Square Error ($RMSE$) of the estimates. $RBias$ is computed as,

$$\begin{aligned} RBias = \frac{1}{n}\sum _{i=1}^n\frac{(\hat{\theta }_i-\theta )}{\theta } \qquad i=1,2,\ldots ,500 \end{aligned}$$

(8)

where $n$ represents the number of replications in the simulation, $\hat{\theta _i}$ is the parameter estimate for each replication, and $\theta$ is the corresponding population parameter. $StD$ is computed as,

$$\begin{aligned} \sqrt{\frac{1}{n}\sum _{i=1}^n(\hat{\theta _i}-E(\hat{\theta )})^{2}} \qquad i=1,2,\ldots ,500 \end{aligned}$$

(9)

where $E(\hat{\theta })$ is the mean of the estimates across the 500 simulated datasets. $StD$ provides information on the efficiency of estimates.

Finally, $RMSE$ is computed as,

$$\begin{aligned} \sqrt{\frac{1}{n}\sum _{i=1}^n(\hat{\theta _i}-\theta )^2} \qquad i=1,2,\ldots ,500 \end{aligned}$$

(10)

Obviously, it holds that $MSE=bias(\hat{\theta })^2+Var(\hat{\theta })$. Thus $RMSE$ entails information on both bias and variability of the estimates.

In order to understand the effects of measurement model misspecification on the parameter estimates, we compared the performance of the two methods (PLS-PM and ML-SEM), applying both the correct measurement scheme for ${\varvec{\uppi }}_1$ (i.e., formative scheme) and the wrong measurement scheme (i.e., reflective scheme).

For the sake of simplicity, at this step we present only the mean of the $RMSE$ in the path coefficients connected to the exogenous LV ${\varvec{\uppi }}_1$.

Figure 2a reports the mean of $RMSE$ of the PLS-PM estimates for both the correctly specified measurement model and the misspecified measurement model, for each inter-correlation level among MVs (0.2, 0.4, 0.6).

Fig. 2

Mean of the $RMSE$ in the path coefficients connected to ${\varvec{\uppi }}_1$, for normal data scenario. a PLS-PM and b ML-SEM

The $RMSE$ of the PLS-PM estimates slightly increases when the measurement model is misspecified, but the inter-correlation level among MVs does not have any effect on the estimates. We found that the variability of the PLS-PM estimates is very low and almost equal for all these considered experimental conditions, thus different $RMSE$ values are due exclusively to the bias of the estimates. Confirming the expectation, PLS-PM tends to underestimate the path coefficients, and this bias slightly increases when the measurement model is misspecified.

This is not the case for the ML-SEM estimates (Fig. 2b). The $RMSE$ increases drastically when the measurement model is misspecified. This is due to the fact that ML-SEM overestimates the path coefficients connected to the exogenous misspecified block. As said above, reflective treatment of a block that should instead be modeled using the formative scheme reduces the variance of the LV.

In ML-SEM the MVs inter-correlation level influences the extent of the $RMSE$ in the path coefficients connected to the misspecified block. This is due to the fact that the greater the level of the MVs inter-correlation, the smaller the change in the variance of a LV produced by measurement model misspecification. High MVs inter-correlations yield a less severe misspecification effect.

As regards the variability of the estimates, we found that the $StD$ of the ML-SEM estimates increases when the measurement model is misspecified, for inter-correlation levels among MVs equal to 0.2 and 0.4. When the inter-correlation is on average equal to 0.6, the variability of the estimates is lower in the misspecified measurement model. Even though an inter-correlation level equal to 0.6—on average—is not extremely high, this result may be due to the issue of multicollinearity. High correlation among MVs of a formative block can be a significant problem for measurement model parameter estimates, while it is a virtue for reflective blocks. However, the $RMSE$ of the estimates is higher when the measurement model is misspecified, for all the inter-correlation levels among MVs.

In keeping with these results, we think that in the case of uncertainty on the real nature of a LV (i.e., the probability of erroneously selecting a measurement scheme is high), researchers should choose PLS-PM rather than ML-SEM, as the $RMSE$ of the ML estimates is much higher when the measurement model is misspecified.

Figure 3 reports the mean of the PLS-PM estimates $RMSE$ (3a) and the mean of the ML-SEM estimates $RMSE$ (3b) for both the correctly specified measurement model and misspecified measurement model, for the non-normal data scenario. It does this for each inter-correlation level among MVs (0.2, 0.4, 06). For the sake of simplicity we show only the results for data with the highest degrees of skewness and kurtosis, i.e., 2.5 and 9, respectively.

Fig. 3

Mean of the $RMSE$ in the path coefficients connected to ${\varvec{\uppi }}_1$, for non-normal data scenario. a PLS-PM and b ML-SEM

As we can see in Fig. 3, these results are not significantly different from those of the normal data scenario, for both the PLS-PM and the ML-SEM estimates. It is well known that PLS-PM is a powerful method because of the minimal demands on distributional assumptions of the variables (Chin 1998). However, ML-SEM is also generally robust against the violation of distributional assumptions (Satorra 1990). This may explain our simulation results for the non-normal data scenario.

We also compared the performance of the two methods for three different numbers of MVs in the formative block (3, 5, 7), and for three different sample sizes (100, 250, 500). The results were not unexpected and we obtained no interesting findings in the case of measurement model misspecification. On the whole, we found that ML-SEM estimates are sensitive to the sample size and the number of MVs in the formative block, while PLS-PM estimates are extremely robust.

For all the reasons above and for the sake of simplicity, we did not take into account these experimental conditions, which would also complicate the reading of the results. Following we show the results for the ECSI model presented above, with a sample size of 250 and five formative MVs.²

Table 1 shows $RBias, StD, RMSE$, and their absolute mean, $Mean(abs)$, for the formative block outer weights (except for the first weight that was fixed in the ML-SEM), for both the smallest value of $\sigma ^2_{\zeta _{1}}$ equal to 0.05 (left hand side) and the largest value equal to 0.5 (right hand side), for an inter-correlation level among the MVs equal to 0.6.

Table 1 Outer weights RBias, StD and RMSE, for two disturbance variance values ($\sigma _{\zeta _{1}} = \sqrt{0.05}$ and $\sigma _{\zeta _{1}} = \sqrt{0.5}$), and high inter-correlation level among the MVs ($\rho =0.6$)

When $\sigma ^2_{\zeta _{1}}$ is small, the outer weight estimates are nearly unbiased and with low variability in both methods. As the variance of $\varvec{\zeta }{1}$ increases (see the right-hand side of Table 1), we found that the bias of both PLS and ML estimates grows, but PLS-PM estimates are by far more biased compared to the ML’s. The variability of the estimates increases for both methods, but PL-PM still produces estimates with lower variability. In terms of the $RMSE$ we found that PLS-PM performs slightly better than ML-SEM, regardless of the magnitude of the disturbance variance.

Considering an inter-correlation level equal to 0.2 (see Table 2), we found that ML-SEM outperforms PLS-PM in terms of bias of the estimates, regardless of the disturbance variance magnitude. As $\sigma ^2_{\zeta _{1}}$ increases the bias of the PLS estimates grows drastically, while it slightly increases in the ML estimates. The variability of the estimates is almost similar for the two methods when the variance of $\varvec{\zeta }_{1}$ is small. As the variance of $\varvec{\zeta }_{1}$ increases the $StD$ of both methods estimates increases, but in this case ML-SEM outperforms PLS-PM also in terms of $StD$. In terms of the $RMSE$, when the variance of $\varvec{\zeta }_{1}$ is low the two methods perform almost similar. As the variance of $\varvec{\zeta }_{1}$ increases ML-SEM outperforms PLS-PM.

Table 2 Outer weights RBias, StD and RMSE, for two disturbance variance values ($\sigma _{\zeta _{1}} = \sqrt{0.05}$ and $\sigma _{\zeta _{1}} = \sqrt{0.5}$), and low inter-correlation level among the MVs ($\rho =0.2$)

Let us consider now the path coefficients connected to ${\varvec{\uppi }}_1$ when the inter-correlation level among MVs is equal to 0.6 (Table 3). On average, the PLS estimates are more biased compared to those of the ML-SEM, and the difference is more evident when $\sigma ^2_{\zeta _{1}}$ increases. In terms of $StD$, PLS-PM outperforms ML-SEM by far. As $\sigma ^2_{\zeta _{1}}$ increases the variability of the PLS estimates remains stable, while it increases in the ML estimates. In terms of $RMSE$, PLS-PM outperforms ML-SEM, regardless of the magnitude of $\sigma ^2_{\zeta _{1}}$.

Table 3 Inner paths coefficients RBias, StD and RMSE, for two disturbance variance values ($\sigma _{\zeta _{1}} = \sqrt{0.05}$ and $\sigma _{\zeta _{1}} = \sqrt{0.5}$), and high inter-correlation level among the MVs ($\rho =0.6$)

It must be noticed that ML-SEM method extremely overestimates the path coefficient between “Image”, (${\varvec{\uppi }}_1$), and “Customer Satisfaction”, (${\varvec{\uppi }}_5$), and it does this systematically. This result is unexpected and needs further investigations.

Considering a low inter-correlation level among MVs (see Table 4), we found that ML-SEM outperforms PLS-PM in terms of bias of the estimates, while PLS-PM outperforms ML-SEM in terms of $StD$, regardless of the magnitude of the disturbance variance. In terms of the $RMSE$, we found that PLS-PM performs slightly better than ML-SEM for a low variance of the disturbance. As the variance of $\varvec{\zeta }_{1}$ increases ML-SEM outperforms PLS-PM.

Table 4 Inner paths coefficients RBias, StD and RMSE, for two disturbance variance values ($\sigma _{\zeta _{1}} = \sqrt{0.05}$ and $\sigma _{\zeta _{1}} = \sqrt{0.5}$), and low inter-correlation level among the MVs ($\rho =.2$)

Overall, our simulation results confirm that PLS estimators lack the parameter accuracy of ML estimators, and this bias is manifested in overestimating the loadings and underestimating the path coefficients, and the larger the disturbance variance the bigger the bias. On the contrary, PLS generally produces estimates with lower variability compared to those obtained using ML estimation method.³

In order to provide researchers with some guidelines when having to choose between ML-SEM and PLS-PM to estimate formative blocks in SEM, we can take into account the $RMSE$ of the estimates. In keeping with the results we obtained, we think that for a quite high inter-correlation level among formative MVs ($\rho =$ 0.6), researchers should prefer PLS-PM rather than ML-SEM, regardless of the disturbance variance. For low inter-correlation levels among formative MVs the decision depends on the magnitude of the disturbance variance. When $\sigma ^2_{\zeta _{1}}$ is small, PLS-PM performs slightly better compared to ML-SEM. On the contrary, as the disturbance variance increases ML-SEM outperforms PLS-PM. Hence, in the latter case, researchers should prefer ML-SEM rather than PLS-PM.

6 Conclusion and future research

Measurement model misspecification may yield severe effects especially on the ML-SEM parameter estimates. Therefore, it is important to understand the effects of including formative blocks in SEM.

This study attempted to give some insight into this issue, comparing the bias and the variability of the ML-SEM estimates with those of the PLS-PM in the same simulation study.

For a model with a correctly specified formative block, we found that the inter-correlation level among formative MVs and the magnitude of the disturbance variance in the formative block have evident effects on the bias and the variability of the estimates.

In order to merge the information on the bias to the information on the variability of the estimates, we computed the $RMSE$ of the estimates. In terms of the Mean Square Error of the estimates, we found that for high inter-correlation levels among formative MVs, PLS-PM outperforms ML-SEM, regardless of the magnitude of disturbance variance. For low inter-correlation levels the performance of the two methods depends on the magnitude of the disturbance variance. When the disturbance variance is small, PLS-PM performs slightly better compared to ML-SEM. On the contrary, as the disturbance variance increases ML-SEM outperforms PLS-PM.

Different levels of complexity of the inner model were also included in this study. When the values of the population parameters were kept constant the complexity of the inner model did not have any effect on the estimates. On the contrary, the bias and the variability of the estimates were sensitive for different population parameter values. Since in a simulation study the value of the parameters should reflect values commonly encountered in applied research, we think that it would be interesting to run simulation studies considering other well-established models (like the ECSI model), where measurement model misspecification frequently occurs. Different model specifications can also be considered including an endogenous formatively-measured LV.

Besides the descriptive statistics that we used to summarize and present the simulation results, inferential statistics can be used as well. For example, the experimental conditions can be dummy or effect coded, and main effects and interactions among experimental conditions can be evaluated using standard regression procedures.

Finally, we think that it would also be interesting to look further into the issue of multicollinearity among formative MVs.