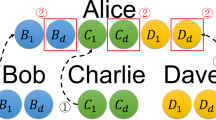1 Introduction

Classical cryptography can settle this problem [1], suppose a general manager Alice has a secret task assigned to two managers, Bob and Charlie. To ensure that the secret task is successfully completed, at least one of them is credible. Consequently, the general manager divided the secret message into two parts: one part to Bob and the other part to Charlie. Plainly, only when Bob and Charlie cooperate with each other can they get the secret message, which is not available to one participant. However, if this scheme is not combined with other technologies such as encryption, the security of classical cryptography cannot be guaranteed, and it is easy to eavesdrop and the eavesdropper cannot be detected. More precisely, if there is a malicious eavesdropper, Eve (including Bob or Charlie) can steal Alice’s information transmitted to Bob and Charlie through the communication channel, then the eavesdropper can obtain Alice’s secret message. Fortunately, quantum cryptography can solve secret sharing’s security problem, which we call quantum secret sharing.

In 1984, the first quantum key distribution protocol was proposed by Benett and Brassard [2]. After that, many exciting and valuable applications of quantum cryptography have been presented [3,4,5,6,7], such as quantum key distribution (QKD), quantum information science (QIS), quantum secure direct communication (QSDC), quantum dots (QDs), quantum secret sharing. Hence, Hillery et al. [8] proposed a QSS protocol based on Greenberger–Horne–Zeilinger (GHZ) state for the first time, which combines secret sharing and quantum technologies to achieve the purpose of eavesdropping detection. After the proposal of this protocol, the research on QSS has attracted extensive attention, and many scholars have studied it in a short period [9,10,11,12,13].

A neoteric notion of “semi-quantum” was first presented by Boyer et al. [14] in 2007. The definition of “semi-quantum” presents two kinds of participants: one participant with quantum capabilities and one participant with classical capabilities only. To be more precise, a participant who has the ability to do the following operations is called a quantum participant: (a) generating any quantum states; (b) performing any quantum measurements; (c) storing qubits in quantum memory. A participant who has the ability to do the following operations is called a classical participant: (a) generating qubits with the computational basis \(\{|0\rangle , |1\rangle \}\); (b) measuring qubits with the computational basis \(\{|0\rangle , |1\rangle \}\); (c) reflecting qubits without disturbance; (d) reordering qubits. Since the concept of “semi-quantum” only requires one participate has the quantum capability, it has been rapidly applied to traditional quantum cryptography [15,16,17,18,19], and the first semi-quantum secret sharing protocol [20] was proposed by Li et al. in 2010. They proposed two SQSS protocols, randomization-based SQSS protocol and measure–resend SQSS protocol, using maximally entangled GHZ-type states. Moreover, two protocols can resist eavesdroppers. Considering the realization of the protocol, Li et al. abandoned the entangled states and implements an SQSS scheme with the product states [21]. It is proved that if an eavesdropper tries to attack this protocol, it will introduce some errors and be detected. Xie et al. designed a new SQSS protocol which can share a specific message compared with the previous protocols [22]. An efficient SQSS protocol using Bell states [23] was presented by Yin et al. in 2017. Yin et al. proposed a novel SQSS protocol based on N different unspecific two-particle entangled state [24] and gave strong proof that it can resist eavesdropping attacks. Li et al. [25] proposed an SQSS protocol, including the following two innovations: Bob and Charlie do not need to measure, and Alice does not need quantum registers to improve the relative efficiency. In order to achieve scalable and more flexible secret sharing, Cao et al. proposed an SQSS protocol. Alice can adjust the number of users and user groups at any time [26]. Since there is no protocol using the W-state to compose SQSS, Tai et al. [27] used W-state to implement semi-quantum secret sharing and analyzed its security. To verify the identification of communication partners, a new semi-quantum secret sharing scheme where identity authentication is adopted base on GHZ-type states by Yin et al. [28].

In this paper, an SQSS protocol based on Bell states is presented. We give Alice enough rights to decide the content of the shared secret message and the number of detected particles. More precisely, the proposed scheme can share specific secret keys, and the efficiency of the protocol is controlled by Alice. For eavesdropping detection, using the decoy photons, Bob and Charlie choose to MEASURE (measure the qubits) or REFLECT (reflect the qubits without disturbed). For validity verification, using the test bits, Bob and Charlie take exclusive-OR operations and compare the results with Alice. The decoy photons are used to detect attacker Eve, while the test bits are used to verify the validity of the shared secrets. And then, we analyze the security of the protocol and prove that the protocol can resist common attacks, including intercept–resend attack, entangle–measure attack and Trojan horse attack. More meaningfully, compared with the previous schemes, our scheme is more flexible and practical.

The remaining parts of the paper are organized as follows. In Sect. 2, a novel SQSS protocol is detailed described. Next, the security and the comparison of the SQSS protocol are analyzed in Sect. 3. In Sect. 4, a conclusion is given.

2 Protocol

In this section, we present a three-party SQSS protocol based on Bell state. Alice, who has quantum capabilities, wants to share a secret with two classical participants, Bob and Charlie. The quantum capabilities include Alice can prepare arbitrary quantum state and perform measurement on an arbitrary basis. Compared with the quantum participant, the classical participant can only generate and measure qubits with Z basis. The three-party SQSS protocol is described as follows. The framework of the SQSS is given in Fig. 1, and the specification of the SQSS also is shown in Table 1.

Fig. 1
figure 1

Framework of SQSS protocol

Full size image
Table 1 Specification of SQSS protocol
Full size table
  1. (1)

    Alice prepares n entangled particle pairs, and each entangled state is randomly in \(|\Psi ^{-}\rangle \) and \(|\psi ^{+}\rangle \), where

    $$\begin{aligned} |\Psi ^{-}\rangle _{bc}= & {} (1/\sqrt{2})(|00\rangle -|11\rangle )_{bc},\end{aligned}$$
    (1)
    $$\begin{aligned} |\psi ^{+}\rangle _{bc}= & {} (1/\sqrt{2})(|01\rangle +|10\rangle )_{bc}. \end{aligned}$$
    (2)

    Suppose \(''0''\) is represented \(|\Psi ^{-}\rangle _{bc}\), \(''1''\) is used to represent \(|\psi ^{+}\rangle _{bc}\). According to what Alice prepared about the entangled states, she can obtain a random bit sequence \(K_A\). For each entangled state, Alice will transmit one to bob, and the other will be sent to Charlie. \(S_B = (p^1_b, p^2_b,\ldots , p^n_b)\) and \(S_C = (p^1_c, p^2_c,\ldots , p^n_c)\) are used to represent the two sequences of particles to be transmitted to Bob and Charlie, respectively, in which each \((p^i_b, p^i_c)\) is an entangled pair.

  2. (2)

    Alice prepares a set of decoy photons, where each decoy photon is randomly chosen from the four states \(\{|0\rangle , |1\rangle , |+\rangle , |-\rangle \}\). Then, Alice inserts decoy photons to \(S_B\) and \(S_C\) in random positions, respectively. Note that only Alice distinguishes the positions and states of these decoy photons. Alice obtains two new sequences which are represented by \(S^{'}_B\) and \(S^{'}_C\).

  3. (3)

    Alice transmits \(S^{'}_B\) and \(S^{'}_C\) to Bob and Charlie, respectively. After receiving the sequence \(S^{'}_B\), Bob announces he has received. Charlie takes similar operations to Bob.

  4. (4)

    Alice declares the positions of the decoy photons, which she inserted before.

  5. (5)

    Alice, Bob and Charlie perform the eavesdropping checking. According to the declaration from Alice, Bob (Charlie) selects decoy photons out and takes two operations at random. The first operation is MEASURE, and Bob (Charlie) measures the decoy photons with Z basis. The second operation is REFLECT, and Bob (Charlie) reflects the decoy photons without any disturbance. Then, Alice’s operations depend on Bob and Charlie’s choices.

    1. (a)

      If both Bob and Charlie choose to MEASURE, Alice will measure the received particles with Z basis and compare them with the measurements of Bob and Charlie. She can deduce whether there is an eavesdropper by the error rate. For example, Alice sends \(|0\rangle \) to Bob, and Bob measures the received qubit using Z basis and resends the measured qubit back to Alice. Alice measures the MEASURE qubit with Z basis. If there is no eavesdropper, the measurement result should be \(|0\rangle \) and the same as what Bob’s measurement. Once the measurement result is different from \(|0\rangle \) or Bob’s measurement, there exists an eavesdropper. If the error rate is higher than the predefined threshold, Alice will terminal this protocol. Otherwise, they continue to the next step.

    2. (b)

      If either Bob or Charlie takes REFLECT operation, Alice will compare the measurements of reflecting particles with the initial states she prepared. For example, Alice sends \(|+\rangle \) to Bob, and Bob returns the received qubit without any disturbance. Alice measures the REFLECT qubit with X basis. If there is no eavesdropper, the measurement result should be \(|+\rangle \). If there exists an eavesdropper, the measurement result is different from the initial qubit which she sent. If the error rate exceeds the threshold, they will abort this communication. Otherwise, they continue to the next step.

    After that, the sequences \(S_B\) and \(S_C\) are lifting in Bob and Charlie’s hands, respectively.

  6. (6)

    After the eavesdropping check, Bob and Charlie measure all qubits with Z basis in sequences \(S_B\) and \(S_C\). While Bob (Charlie) measured the qubit, Bob (Charlie) uses \(K_B\) (\(K_C\)) to record the measurement results. Note that the measurement result \(|0\rangle \) corresponds the classical bit \(''0''\) and the measurement result \(|1\rangle \) corresponds the classical bit \(''1''.\) The sequence \(K_B\) (\(K_C\)) contains the measurement results of qubits by Bob (Charlie) and is represented as the keys. To verify the validity of the shared secret, Bob and Charlie take out some bits as test bits from \(K_B\) and \(K_C\). Then, Bob and Charlie perform the exclusive-OR operation on test bits and compare them with the values of the corresponding bits of \(K_A\) in Alice’s hand. If the two values are equal, then the validity of the shared secret is verified. Finally, Bob and Charlie calculate Alice’s secret keys with the rest of \(K_B\) and \(K_C\) by

    $$\begin{aligned} \begin{aligned} K_A = {K_B \oplus K_C} \end{aligned} \end{aligned}$$
    (3)

    Only Bob and Charlie have cooperated, they can obtain the secret of Alice by performing the operation: exclusive-OR.

2.1 An example

Now, an example of this SQSS protocol will be given in this part. Quantum Alice prepares entangled pairs sequence \(\{|\Psi ^{-}\rangle ^1_{bc}, |\Psi ^{-}\rangle ^2_{bc}, |\psi ^{-}\rangle ^3_{bc}, |\Psi ^{-}\rangle ^4_{bc}, |\Psi ^{-}\rangle ^5_{bc}\), \(|\psi ^{-}\rangle ^6_{bc}, |\psi ^{-}\rangle ^7_{bc}, |\psi ^{-}\rangle ^8_{bc}\}\), which corresponds to classical bits sequence \(K^i_{A_1}=\{0^1, 0^2, 1^3, 0^4, 0^5, 1^6, 1^7, 1^8\}\). Then, Alice takes the first particle of entangled pairs out and constructs a new sequence \(S_B=\{|\Psi ^{-}\rangle ^1_{b}, |\Psi ^{-}\rangle ^2_{b}, |\psi ^{-}\rangle ^3_{b}, |\Psi ^{-}\rangle ^4_{b}, |\Psi ^{-}\rangle ^5_{b}, |\psi ^{-}\rangle ^6_{b}\), \(|\psi ^{-}\rangle ^7_{b}, |\psi ^{-}\rangle ^8_{b}\}\). The sequence \(S_C=\{|\Psi ^{-}\rangle ^1_{c}, |\Psi ^{-}\rangle ^2_{c}, |\psi ^{-}\rangle ^3_{c}, |\Psi ^{-}\rangle ^4_{c}, |\Psi ^{-}\rangle ^5_{c}, |\psi ^{-}\rangle ^6_{c}, |\psi ^{-}\rangle ^7_{c}, |\psi ^{-}\rangle ^8_{c}\}\) is comprised form the second particle of entangled pairs. Alice introduces the decoy photons to detect the eavesdroppers, and the \(S_B\) and \(S_C\) become the \(S'_B\) and \(S'_C\). Alice sends \(S'_B\) to Bob and \(S'_C\) to Charlie. After Bob and Charlie received the sequence, they announce they have received it to Alice, respectively. According to the information provided by Alice, Bob and Charlie select the decoy photons out and obtain the sequence \(S_B\) and \(S_C\). Hence, Alice can obtain her shared secret keys by \(K_A = \{0, 0, 1, 0, 0, 1, 1, 1\}\). Then, Bob and Charlie measure the qubits on Z basis, both of they obtain a sequence \(K_B=\{0^1,0^2,1^3,1^4,0^5,1^6,1^7,0^8\}\) and \(K_C=\{0^1,0^2,0^3,1^4,0^5,0^6,0^7,1^8\}\). Therefore, according to \(K_B\) and \(K_C\), Bob and Charlie can deduce Alice’s secret keys \(K_A = {K_B \oplus K_C} = \{0, 0, 1, 1, 0, 1, 1, 0\} \oplus \) \(\{0,0,0,1,0,0,0,1\} = \{0,0,1,0,0,1,1,1\}\).

3 Security analysis and comparison

In this section, we analyze the security of the proposed SQSS protocol and give a comparison with some similar SQSS protocols in detail. Suppose there is an eavesdropper, Eve, who is eager to steal the participants’ secret keys. In fact, for eavesdropping, the participant (Bob or Charlie) has more substantial eavesdropping capabilities than outside eavesdroppers Eve. As mentioned in, the security analysis of QSS should focus on preventing the dishonest participant from eavesdropping, the same as SQSS. Consequently, we will analyze the attack behaviors of the malicious participant in this protocol.

3.1 Intercept–resend attack

Without loss of generality, suppose Charlie is a dishonest participant who intends to acquire Alice’s secret key without the participation of the other. According to the known conditions, the malicious participate Charlie will take three eavesdropping strategies.

In the first eavesdropping strategy, Charlie intercepts the sequence \(S^{'}_B\) to measure \(S^{'}_B\) with computational basis and then sends the measured sequence to Bob. Considering one of the particles in the measured sequence, if Bob’s measurement basis is the same as that selected by Charlie, Charlie will acquire Bob’s measurement, which means that Charlie will get a secret key in \(K_B\). However, he cannot get the sequence \(K_B\) successfully. Charlie cannot distinguish the decoy photons from the entangled qubits in \(S^{'}_B\), because they are in the maximum mixing state \(\rho = (|0\rangle \langle 0| + |1\rangle \langle 1|)/2\). Therefore, for every decoy photon, the probability of error rate is 1/4 which will be introduced by Charlie.

In the second eavesdropping strategy, Charlie intercepted the sequence \(S^{'}_B\) and took Bell measurement on the qubits, which in the same position in \(S^{'}_B\) and \(S^{'}_C\). After measured, he sends \(S^{'}_B\) to Bob. What he did is to acquire Alice’s secret keys, i.e., the initial state of entangled pairs. Nevertheless, this strategy will not succeed. Alice inserted the decoy photons to disrupt the position of the sequence, which be sent to Bob (Charlie). Hence, Charlie cannot confirm which two qubits are initially entangled.

In the third eavesdropping strategy, Charlie intercepted sequence \(S^{'}_B\) and then sends a previously prepared fake particle sequence to Bob. Under this situation, Charlie gets Alice’s secret key completely, and he can take Bell measurement on \(S^{'}_B\) and \(S^{'}_C\) after Alice announced the position of decoy photons. Nevertheless, he does not know the positions and states of decoy photons when he sends the fake particle sequence. Therefore, no matter what kind of fake particle sequence Charlie prepares to send to Bob, the eavesdropping behavior will introduce errors when Alice and Bob detect eavesdropping, and thus, Charlie is found.

Stated thus, the proposed protocol can against intercept–resend attack.

Fig. 2
figure 2

Eavesdropper’s entangle–measure attacks with two operations \(U_F\) and \(U_R\)

Full size image

3.2 Entangle–measure attack

Suppose a malicious eavesdropper, Charlie, attempts to steal the secret key between Alice and Bob. Generally, the entangle–measure attack strategies including two unitary operations, \(U_F\) and \(U_R\). \(U_F\) represents the attacking qubit operation from Alice to Bob (Forward channel), and \(U_R\) acts as the attacking qubit operation from Bob to Alice (Reverse channel). Because this protocol only uses decoy photons to detect eavesdropping, we only consider the effect on decoy photons for entangle–measure attacks. The implementation of the entangle–measure attack is depicted in Fig. 2.

Theorem 1

Suppose that Charlie performs an attack (\(U_F, U_R\)) on the qubits sent from Alice to Bob. Then, for this attack inducing no error in eavesdropping detection, the final state of Charlie’s probe should be independent of Bob’s measurement result.

Proof

Denote the qubits sent from Alice to Bob by B, and denote eavesdropper Charlie’s probe by F. The evolution of the system will be B+F. \(\square \)

  1. 1.

    Before Charlie’s attack, the states are \(|0\rangle _{B}|0\rangle _{F}\), \(|1\rangle _{B}|0\rangle _{F}\), \(|+\rangle _{B}|0\rangle _{F}\) and \(|-\rangle _{B}|0\rangle _{F}\).

  2. 2.

    After Charlie has performed \(U_F\), the states evolves to

    $$\begin{aligned} |\varPhi _{1}\rangle= & {} U_F|0\rangle |F_n\rangle = |0\rangle |F_{00}\rangle + |1\rangle |F_{01}\rangle , \end{aligned}$$
    (4)
    $$\begin{aligned} |\varPhi _{2}\rangle= & {} U_F|1\rangle |F_n\rangle = |0\rangle |F_{10}\rangle + |1\rangle |F_{11}\rangle , \end{aligned}$$
    (5)
    $$\begin{aligned} |\varPhi _{3}\rangle= & {} U_F|+\rangle |F_n\rangle = |0\rangle |F_{00}\rangle + |0\rangle |F_{10}\rangle + |1\rangle |F_{01}\rangle + |1\rangle |F_{11}\rangle , \end{aligned}$$
    (6)
    $$\begin{aligned} |\varPhi _{4}\rangle= & {} U_F|-\rangle |F_n\rangle = |0\rangle |F_{00}\rangle - |0\rangle |F_{10}\rangle + |1\rangle |F_{01}\rangle - |1\rangle |F_{11}\rangle , \end{aligned}$$
    (7)

    where \(|F_{ij}\rangle \) represents the un-normalized state of Charlie’s probe.

  3. 3.

    When Bob receives the qubits sent from Alice, he takes operations MEASURE or REFLECT. After that, Charlie performs \(U_R\). We need to prove that the states of F after \(U_R\) having been performed are independent of Bob’s final states.

  4. 4.

    If Bob choose MEASURE, Charlie not being detectable in eavesdropping detection, \(U_R\) must satisfy the following conditions:

    $$\begin{aligned} \begin{aligned} U_R|x_{1}\rangle |F_{{x_{1}, x_{2}}}\rangle = |x_{1}\rangle |R_{{x_{1}, x_{2}}}\rangle , \end{aligned} \end{aligned}$$
    (8)

    where \(x_{1}, x_{2} \in \{0,1\}\), and the key of \(U_R\) operation is not change the state of B. Otherwise, Alice will detect this attack with nonzero probability. For example, for \(|0\rangle _{B}|0\rangle _{F}\), Bob measurement result is \(|0\rangle \), suppose that \(U_R\) changes \(|0\rangle |F_{00}\rangle \) to \(|0\rangle |R_{00}\rangle + |1\rangle |R_{01}\rangle \). The probability for Alice to detect the existence of errors is 1/2. For \(|+\rangle _{B}|0\rangle _{F}\), Bob measurement result is \(|0\rangle \), suppose that \(U_R\) changes \(|0\rangle |F_{00}\rangle \) to \(|0\rangle |R_{00}\rangle + |1\rangle |R_{01}\rangle \). Then, Bob have measured his qubit in \(|0\rangle \). The probability for Alice to detect the existence of errors is 1/2. Thus, some errors will be induced.

  5. 5.

    If Bob chooses REFLECT, Charlie not being detectable in eavesdropping detection, there is \(|R_{00}\rangle = |R_{11}\rangle \) must be satisfied. And the states of F after \(U_R\) are the same as those sent by Alice.

    $$\begin{aligned} |\varPhi '_{1}\rangle= & {} U_R|0\rangle |F_{n}\rangle = |0\rangle |R_{00}\rangle + |1\rangle |R_{01}\rangle , \end{aligned}$$
    (9)
    $$\begin{aligned} |\varPhi '_{2}\rangle= & {} U_R|1\rangle |F_{n}\rangle = |0\rangle |R_{10}\rangle + |1\rangle |R_{11}\rangle , \end{aligned}$$
    (10)
    $$\begin{aligned} |\varPhi '_{3}\rangle= & {} U_R|+\rangle |F_n\rangle = \frac{1}{2}[|+\rangle (|R_{00}\rangle + |R_{01}\rangle + |R_{10}\rangle + |R_{11}\rangle ) \nonumber \\&\quad + |-\rangle (|R_{00}\rangle - |R_{01}\rangle + |R_{10}\rangle - |R_{11}\rangle )], \end{aligned}$$
    (11)
    $$\begin{aligned} |\varPhi '_{4}\rangle= & {} U_R|-\rangle |F_n\rangle = \frac{1}{2}[|+\rangle (|R_{00}\rangle + |R_{01}\rangle - |R_{10}\rangle - |R_{11}\rangle )\nonumber \\&\quad + |-\rangle (|R_{00}\rangle - |R_{01}\rangle - |R_{10}\rangle + |R_{11}\rangle )]. \end{aligned}$$
    (12)

    Charlie not being detectable in eavesdropping detection, \(U_R\) must satisfy the following conditions:

    $$\begin{aligned}&|R_{01}\rangle = 0, \end{aligned}$$
    (13)
    $$\begin{aligned}&|R_{10}\rangle = 0, \end{aligned}$$
    (14)
    $$\begin{aligned}&|R_{00}\rangle - |R_{01}\rangle + |R_{10}\rangle - |R_{11}\rangle = 0, \end{aligned}$$
    (15)
    $$\begin{aligned}&|R_{00}\rangle + |R_{01}\rangle - |R_{10}\rangle - |R_{11}\rangle = 0. \end{aligned}$$
    (16)

    According to Eqs. (13)–(16), Eq. (17) can be deduced.

    $$\begin{aligned} \begin{aligned} |R_{00}\rangle = |R_{11}\rangle . \end{aligned} \end{aligned}$$
    (17)

    So Eqs. (9)–(12) can be written as:

    $$\begin{aligned} |\varPhi '_{1}\rangle= & {} |0\rangle |R_{00}\rangle , \end{aligned}$$
    (18)
    $$\begin{aligned} |\varPhi '_{2}\rangle= & {} |1\rangle |R_{11}\rangle = |1\rangle |R_{00}\rangle , \end{aligned}$$
    (19)
    $$\begin{aligned} |\varPhi '_{3}\rangle= & {} \frac{1}{2}|+\rangle (|R_{00}\rangle + |R_{01}\rangle + |R_{10}\rangle + |R_{11}\rangle ) = |+\rangle |R_{00}\rangle , \end{aligned}$$
    (20)
    $$\begin{aligned} |\varPhi '_{4}\rangle= & {} \frac{1}{2}|-\rangle (|R_{00}\rangle - |R_{01}\rangle - |R_{10}\rangle + |R_{11}\rangle ) = |-\rangle |R_{00}\rangle . \end{aligned}$$
    (21)

    From the above proof, to pass detect Alice’s eavesdropping, the final states of Charlie’s probes are always independent of Bob’s measurement results.

Therefore, we have proved Theorem 1, and the presented protocol can against entangle–measure attack.

3.3 Trojan horse attack

Here, Charlie plans to use Trojan horse attack. He intercepted \(S_B\) and attaches the invisible photons or the spy photons to \(S_B\); now, he gets \(S'_B\). Charlie will transmit the \(S'_B\) to Bob for Trojan horse attack. Nevertheless, the malicious operations can be easily resisted by applying the photon number splitter (PNS) and the wavelength filter devices (WF). Hence, the presented protocol can against Trojan horse attack.

3.4 Comparison

We will compare the proposed protocol with several SQSS protocols. In most previous protocols, few protocols can share the specific secret messages, whereas Alice can decide which secret messages to share in our protocol. She has wholly controlled the semi-quantum secret sharing all information. It includes the number of decoy photons for eavesdropping and the specific values of the shared secret messages. Therefore, when a master Alice needs to share secret messages, our protocol has more specific, detailed and convenient practical significance. Then, the comparisons with typical SQSS protocols are detailedly displayed in Table 2.

As shown in Table 2, the qubit efficiency of our protocol is higher than the most proposed protocols. Alice can decide the percentage of the detection qubits’ number by herself. Besides, the sharing secret messages can also determine by herself. Through the above comparison, the proposed protocol is more efficient and practical than others.

Table 2 Comparisons of the SQSS protocols
Full size table

4 Conclusion

A more practical and flexible SQSS scheme based on Bell states has been proposed in this paper. Different from the previous protocols, Alice can determine the specific message contents to share, and the detection intensity of eavesdropping can also be decided by herself. Next, we analyze the security of the proposed protocols which shows that our protocol can resist the intercept–resend attack, entangled attack and Trojan horse attack. In addition, we compare our scheme with the existing schemes, and the comparison shows that our scheme is more efficient and practical. The proposed protocol has a higher utilization rate of qubits than other protocols and can share specific secret messages. Further security analysis and extension to multi-level quantum systems are worthy of careful consideration in future work.