1 Introduction

Quantum correlation (QC) along with the superposition principle, triggered the advances in the field of quantum enabled science and technology. Right from its inception, quantum entanglement has exercised a pivotal role as a resource for manipulating the quantum information. In recent times, more general forms of non-classical correlations have been explored and are widely used as a resource for the successful implementation of various quantum information and computation protocols like dense coding, teleportation, key distribution, cryptography, parameter estimation, metrology [1,2,3,4,5,6,7,8,9], both theoretically and experimentally. Entanglement is an inevitable resource [10, 11] for achieving maximum possible success for a number of quantum information protocols (QIP), whereas it is considered as a non-critical resource in the realization of some of the aforementioned protocols. Nonzero fidelity for quantum remote state preparation [12] can be achieved using separable states, wherein quantum discord enables the process. Recently, it has been shown that PPT bound entangled states are useful for quantum parameter estimation in noisy environment [13].

The study on multipartite quantum teleportation reveals that maximum degree of entanglement is not necessary [14, 15] to attain optimum teleportation fidelity. All these cases of QC as a resource for QIP [16,17,18] invite wide attention for the exploration of more general forms of non-classical correlations in bipartite and multipartite quantum systems, and their dynamics under decoherence. Quantum decoherence is a phenomenon that occurs when quantum systems interact with their ambient environment, and is studied under the broader perspective of Open Quantum Systems [19, 20]. Open quantum systems have been applied extensively in recent times to various facets of quantum information, condensed matter systems [21], and relativistic as well as sub-atomic physics [22,23,24,25,26,27,28]. Coupling of the quantum system with the reservoir can be either weak or strong, leading to a wide range of dynamics. Quantum channels modeling these effects can be Markovian or non-Markovian, both unital as well as non-unital. The backflow of information from the reservoir to the system for a given non-Markovian quantum channel reveals many intriguing features of QC [29,30,31]. In general, investigating the dynamics of quantum correlations of open quantum system, both Markovian and non-Markovian, is pertinent, since the detailed study of coherence dynamics and correlations of quantum states is essential for the successful implementation of quantum information and computation protocols  [32,33,34,35,36,37,38].

The hierarchy of quantum correlations of states of composite systems is known; to begin with, the classifications of quantum correlations according to entanglement, steering and nonlocality were considered. The hierarchy of quantum correlations in the increasing order of their strength was identified as: entanglement, steerability and nonlocality [39,40,41]. For pure states, quantum states are either entangled or separable, and for mixed states, distinctive classification with respect to the aforementioned order of quantum correlations is more prominent. When correlated quantum states are used as a resource for teleportation, teleportation fidelity reveals two different aspects of nonclassicality or measures of correlations of quantum nature. If the teleportation fidelity is greater than \(\frac{2}{3}\) (classical limit), the state is non-classically correlated in the sense that it is useful for quantum teleportation. In addition to this, if the fidelity is greater than \(F_{lhv}\approx 0.87\) [39], then the state is nonlocal in the sense that its teleportation fidelity is incompatible with local hidden variable descriptions, and a state with fidelity greater than \(F_{lhv}\) satisfies all the measures of quantum correlations. In [42, 43], connection among the different measures of quantum correlations for achieving quantum teleportation fidelity, and the order of hierarchy of quantum correlations were discussed.

Decoherence of quantum states occurs due to the influence of noise, and it is known that the order of hierarchy of quantum correlations is preserved [40, 42, 44] under Markovian noisy channels for different class of pure and mixed states. The decay of quantum correlations happens in such a way that higher degree quantum correlations are lost for a lower value of noise, whereas lower degree QCs are lost for higher noise parameters [44].

The classification of quantum channels based on the divisibility properties is quite noteworthy in open system dynamics. According to the divisibility criterion, a quantum channel is Markovian if any intermediate map is completely positive (i.e., if the channel is CP-divisible) [45]. In [46, 47], a broader concept of memory is introduced, whereby CP-divisible quantum processes can occur in non-Markovian regimes as well. CP-divisibility of a quantum process always indicates the lack of information backflow. On the other hand, the absence of P-divisibility can manifest in the form of oscillations in correlation measures such as quantum mutual information, and trace distance, which are monotonic functions of time if the dynamics is P-divisible [34]. These oscillations indicate the backflow of information from the environment to the system. Here, we take into account Markovian as well as CP-divisible and P-indivisible non-Markovian channels, and their dynamics are investigated and compared

Quantum speed limit time \((\tau _{QSL})\) [48, 49], the minimal evolution time between two states, is another quantity that captures Markovianity of the quantum processes. The role of \(\tau _{QSL}\) as a witness of non-Markovianity associated with the non-unitary quantum evolution has been studied [50, 51]. We investigate the dynamics of \(\tau _{QSL}\), and avail its connection with the information backflow to analyze the behavior QC.

We consider entanglement, quantum steering, and Bell-CHSH nonlocality as a resource for quantum teleportation [52], and establish their connection with the teleportation fidelity for different class of pure and mixed states in the presence of unital and non-unital noisy channels. This points to the significance of considering the dynamics of two different aspects of nonclassicality/ measures of QC (\(F>\frac{2}{3}\) and \(F>F_{lhv}\)) associated with the teleportation fidelity along with the entanglement, steering and Bell-nonlocality. It is known that the effects of noise on a quantum system are not always detrimental in nature, and the revival of quantum correlations occurs due to the backflow of information from the environment to the system. We show that the decay and revival of quantum correlations under non-unitary evolution follow the order of hierarchy of QC. Also, we study the quantum speed limit time as a witness of the memory effects of quantum channels. It is shown that dynamics of quantum correlations can be described using \(\tau _{QSL}\). Markovian and non-Markovian noisy models of amplitude damping which are non-unital, as well as unital channels such as phase damping, depolarizing and random telegraph noise (RTN), are considered, and noise tolerance of QC in these cases is discussed.

The work is organized as follows. In Sect. 2, we briefly define different measures of quantum correlations, quantum speed limit time in noisy environment, and methods to quantify them. In Sect. 3, the effect of noisy channels on a quantum system taken to be in a pure entangled state is described, followed by the investigation of the dynamics of QC and \(\tau _{QSL}\) under the influence of various channels. We establish the connection among different measures of quantum correlations when they are used as a resource for quantum teleportation. A corresponding analysis for initial mixed states is made in Sec. IV. We show that quantum speed limit time can be availed to describe the dynamics of quantum correlations. Results and discussions in Sect. 5 are followed by the concluding section (Sect. 6).

2 Quantum correlations

Quantum correlations and quantum speed limit time, which can serve as indicators of quantumness in a system, are defined. Quantum correlations are used as a resource for quantum teleportation. The connections between quantum entanglement, steering and violation of Bell-CHSH inequality with two different aspects of nonclassicality associated with the teleportation fidelity are established. In this section, we discuss the methods to estimate different QC for a two-qubit state, \(\rho _{AB}\) and the derivation of \(\tau _{QSL}\) in open system dynamics.

2.1 Teleportation fidelity and Bell-CHSH inequality

In general, a two qubit state is given as:

$$\begin{aligned} \small \rho _{AB}=\frac{1}{4}(I_{2}\otimes I_{2}+\sum _{i=1}^{3}r_{i}\sigma _{i}\otimes I_{2}+\sum _{i=1}^{3}s_{i}I_{2}\otimes \sigma _{i} +\sum _{i,j=1}^{3}t_{i,j}(\sigma _{i}\otimes \sigma _{j})). \end{aligned}$$
(1)

We have \(\sum _{i=1}^{3}r_i=1\) and \(\sum _{i=1}^{3}s_i=1\). The correlation matrix is defined as \(T=\{t_{i,j}\}\) and the matrix elements \(t_{i,j}=Tr[\sigma _{i}\otimes \sigma _{j}\rho ]\). Two-qubit entangled states are used as a resource for quantum teleportation, and the teleportation fidelity [52] is calculated

$$\begin{aligned} F(\rho )=\frac{1}{2}\Bigg (1+\frac{N(\rho )}{3}\Bigg ), \end{aligned}$$
(2)

where \(N(\rho )=\sum _{i}^{3}u_{i}\); \(u_{i^{\prime s}}\) are the square root of the eigenvalues of \(T^{\dag }T\). The given state is useful for quantum teleportation iff \(N(\rho )> 1\), i.e., \(F(\rho )>\frac{2}{3}\) (classical limit).

The violation of Bell-CHSH inequality can be checked by estimating the expectation value of Bell observable B [52] for a given state \(\rho \), and \(B_{\max }=2 \sqrt{\max _{j>k}(u_{j}^{2}+u_{k}^{2})}\). The state \(\rho \) violates Bell-CHSH inequality for \(B(\rho )>2\).

2.2 Quantum steering

Quantum steering [53, 54] makes a reference to the fact that in the case of biseparable quantum systems, the state of a quantum system can be changed by the action of local measurements on the other system. The degree of steerability of a given quantum state is estimated by considering the amount by which a steering inequality is maximally violated [6]. The formula for two qubit-steering is:

$$\begin{aligned} S_{n}(\rho )=\max \left\{ 0,\frac{\Lambda _{n}-1}{\sqrt{n}-1 }\right\} , \end{aligned}$$
(3)

\(\Lambda _{2}=\sqrt{c^2-c_{\min }^2}\) and \(\Lambda _{3}=c\) are steering values in which measurements, \(n=2,3\) per party are involved, called two measurement and three measurement steering, respectively. Here, \(c = \sqrt{\mathbf {c}^2}\), \(c_{i^{\prime s}}\) are the eigenvalues of correlation matrix \(T=\{t_{i,j}\}\) (Eq. 1), and \(c_{\min } \equiv \min {\{|c_i|\}}\).

2.3 Quantum entanglement

We use concurrence [55, 56] as a measure to estimate the entanglement of a quantum state. The concurrence of a state \(\rho \) is defined

$$\begin{aligned} C(\rho )=\max \{0,\sqrt{\lambda _{1}}-\sqrt{\lambda _{2}}-\sqrt{\lambda _{3}}-\sqrt{\lambda _{4}}\}, \end{aligned}$$
(4)

where \(\lambda _{i^{\prime s}}\) are the eigenvalues of \(\rho \tilde{\rho }\) in the descending order and \(\tilde{\rho }=\sigma _{y}\otimes \sigma _{y}\rho ^{*}\sigma _{y}\otimes \sigma _{y}\), \(\rho ^{*}\) is the complex conjugate of the state \(\rho \). We have \(0<C(\rho )\le 1\) for entangled states and \(C=0\) for separable states.

2.4 Quantum speed limit time (\(\tau _{QSL}\))

Quantum speed limit time defines a bound on the minimum time required for a quantum system to evolve between two states [57,58,59]. The bound on the quantum speed limit time for open quantum systems [60, 61], whose evolution is governed by general quantum channels, is

$$\begin{aligned} \tau _{QSL}\ge \frac{2\theta ^2}{\pi ^2}\frac{\sqrt{tr\rho _{0}^{2}}}{\overline{\sum _{\alpha }{\vert \vert K_{\alpha }(t,0)\rho _{0}\dot{K}_{\alpha }^{\dag }(t,0)\vert \vert }}}, \end{aligned}$$
(5)

where \(\overline{X}=\tau ^{-1}\int _{0}^{\tau } X dt\). \(\rho _{0}\) is the initial state, \(K_{\alpha ^{\prime s}}\) are the Kraus operators characterizing the channel responsible for the evolution of the quantum state, \(\vert \vert A\vert \vert =\sqrt{tr(A^{\dag }A)}\) is the Hilbert–Schmidt norm of A, and \(\theta =\cos ^{-1}( Tr[\rho _{0} \rho _{t}]/Tr[\rho _{0}^2]\)). In this work, we investigate the dynamics of \(\tau _{QSL}\) for various noisy quantum channels, and the relationship between quantum correlations and speed limit time is demonstrated.

3 Action of noisy channels

The effect of noise on a system can be described using the operator-sum formalism. We consider various noisy models, both quantum and classical in nature, for example, the amplitude damping channel, phase damping, depolarizing and random telegraph noise (RTN). The evolution of a quantum system interacting with its environment is

$$\begin{aligned} \rho (t)=\sum _{i}E_{i}(t)\rho (0)E_{i}^{\dag }(t), \end{aligned}$$
(6)

where \(E_{i^{\prime s}}\) are the Kraus operators characterizing the noise. They satisfy the completeness relation \(\sum _{i}E_{i}^{\dag }E_{i}=1\). In general, local interactions of a two qubit system with noisy environments can be described as follows:

$$\begin{aligned} \rho (t)=\sum _{i,j}E_{i}(t)\otimes E_{j}(t)\rho (0)E_{i}^{\dag }(t)\otimes E_{j}^{\dag }(t). \end{aligned}$$
(7)

Here, we consider the scenario wherein the first qubit interacts with the noisy channel, whereas the second qubit evolves under the noise free condition. We consider the dynamics of quantum correlations under the influence of different noisy models, both Markovian and non-Markovian (unital as well as non-unital), and \(\tau _{QSL}\) is analyzed for both pure and mixed entangled initial states. A similar dynamics can be observed for the cases where both qubits evolve under noisy quantum channels.

3.1 Amplitude damping channel

The Kraus operators of non-Markovian dissipative quantum channel [62] are given as:

$$\begin{aligned} E_{0}=\vert 0\rangle \langle 0\vert +\sqrt{q}\vert 1\rangle \langle 1\vert , E_{1}=\sqrt{1-q}\vert 0\rangle \langle 1\vert , \end{aligned}$$
(8)

we have \(q=\exp (-\Gamma t)\{\cos (\frac{dt}{2})+\frac{\Gamma }{d}\sin (\frac{dt}{2})\}^{2}\), \(d=\sqrt{2\gamma \Gamma -\Gamma ^2}\). Where \(\Gamma \) is the line width that depends on the reservoir correlations time \((\tau _{r}\approx \Gamma ^{-1})\) and \(\gamma \) is the coupling strength related to qubit relaxation time \(\tau _{s}\approx \gamma ^{-1}\). The Kraus operators of the amplitude damping channel in the Markovian regime [63,64,65] can be obtained by assuming \(q=1-\nu \), where \(\nu \) is a Markovian exponential decay function .

Fig. 1
figure 1

Quantum correlations are plotted as a function of \(\gamma t\) \((\Gamma =0.01\gamma )\) in the case of non-Markovian amplitude damping quantum channel acting on maximally entangled bell state

Full size image
Fig. 2
figure 2

Quantum correlations of Bell state are plotted as a function of \(\gamma t\) for Markovian amplitude damping channel

Full size image

Let us consider the pure entangled state as initial state,

$$\begin{aligned} \vert \psi \rangle =\alpha \vert 00 \rangle +\beta \vert 11 \rangle , \end{aligned}$$
(9)

where \(\vert \alpha \vert ^{2}+\vert \beta \vert ^{2}=1\). Quantum correlations are calculated, and their dynamics are investigated for maximally entangled Bell state \((\alpha =\beta =\frac{1}{\sqrt{2}})\).

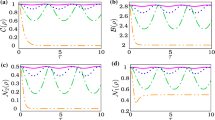
In Fig. 1, the behavior of quantum correlations of maximally entangled Bell state as a function of dimensionless quantity \(\gamma t\) under the influence of non-Markovian amplitude damping channel is depicted. We investigate the dynamics of two different aspects of nonclassicality associated with the quantum teleportation fidelity ( \(F(\rho )>\frac{2}{3}\) and \(F(\rho )>F_{lhv}(\rho )\approx 0.87\)) along with entanglement, quantum steering and the violation of Bell-CHSH inequality. QCs of Bell state evolving under the influence of the non-Markovian amplitude damping channel decay initially and revive back after all quantum correlations reach their minimum values, and this process continues. It is clear from Fig. 1 that the decay and revival of quantum correlations follow a particular order, and higher degree quantum correlations are lost for small values of channel parameter compared to the lower degree quantum correlations. The decay of QC, as a function of channel parameter, occurs in the following decreasing order: state’s teleportation fidelity less than \(F_{lhv}\approx 0.87\), non-violation of Bell-CHSH inequality, vanishing two and three measures of quantum steering, fidelity less than the classical limit and vanishing entanglement. Thus, \(q_{F_{lhv}}\le q_B \le q_{S_{2}}\le q_{S_{3}}\le q_{T}\le q_E\), where \(q_{F_{lhv}}\), \(q_{B}\), \(q_{S_{2}}\), \(q_{S_{3}}\), \(q_{T}\) and \(q_{E}\) are the channel parameter values at which, teleportation fidelity becomes less than 0.87, the states stop violating Bell-CHSH inequality, non-violation of two measure steering inequality, disappearance of three measure quantum steering, teleportation fidelity of states less than the classical limit (\(\frac{2}{3}\)) and vanishing entanglement (zero concurrence), respectively. Hereafter, we use \(q_{F_{lhv}}\), \(q_{B}\), \(q_{S_{2}}\), \(q_{S_{3}}\), \(q_{T}\) and \(q_{E}\) as the channel parameter values at which corresponding measure of quantum correlation fails to capture the quantumness of the state, i.e., \(q_{F_{lhv}}\),\(q_{B}\), \(q_{S_{2}}\), \(q_{S_{3}}\), \(q_{T}\) and \(q_{E}\) are the channel parameter values at which \(F(q)=0.87\), \(B(q)=2\), \(S_{2}(q)=0\), \(S_{3}(q)=0\), \(F(q)=\frac{2}{3}\) and \(C(q)=0\), respectively. This is considered for both the cases of decay and revival of QC interchangeably for all noisy models used in this work. The revival of the quantum correlations occurs in the reverse order, i.e., quantum correlations with lowest degree revive first, followed by the restoration of QC with increasing degree of their strength. The revival of quantum correlations follows the order: entanglement, teleportation fidelity greater than the classical limit, steerability of quantum states, violation of Bell-CHSH inequality and teleportation fidelity greater than \(F_{lhv}\) (\(q_E\le q_{T}\le q_{S_{3}}\le q_{S_{2}}\le q_B\le q_{F_{lhv}}\)). The dynamics of quantum correlations under the Markovian amplitude channel are shown in Fig. 2, and sudden death occurs for all quantum correlations except entanglement. The decay of quantum correlations follows the above discussed order of QC. Here, as expected, revival of QC is not observed. From Figs. 1 and 2, it is clear that the decay and revival of quantum correlations preserve the hierarchy of non-classical correlations.

Fig. 3
figure 3

Dynamics of quantum speed limit time of maximally entangled Bell state for non-Markovian amplitude damping channel (\(\Gamma =0.01\gamma \))

Full size image
Fig. 4
figure 4

Dynamics of quantum speed limit time of maximally entangled Bell state for Markovian amplitude damping channel

Full size image
Fig. 5
figure 5

Quantum correlations are plotted as a function of \(\gamma t\) for maximally entangled Bell state in the case of phase damping channel. a Non-Markovian (\(\Gamma =0.01\gamma \)) and b Markovian

Full size image
Fig. 6
figure 6

Dynamics of quantum speed limit of maximally entangled Bell states for a non-Markovian \((\Gamma =0.01\gamma )\) and b Markovian phase damping channels

Full size image

The dynamics of \(\tau _{QSL}\) has been considered as a signature of information backflow to the principle system from the reservoir [50]. From the dynamics of quantum speed limit time (Fig. 3) for non-Markovian amplitude damping channel, it is clear that \(\tau _{QSL}\) increases initially and starts decreasing after a certain time. The time at which a shift appears in the dynamics of \(\tau _{QSL}\) exactly matches with the time at which revival of lowest degree of quantum correlations starts (Fig. 1). This is interesting, since the investigation of \(\tau _{QSL}\) reveals the details of non-classical correlations’ evolution in the non-Markovian regime. The connection between the dynamics of quantum correlations and the speed limit time ascertain the importance of using the latter to analyze the behavior of QC in the case of non-Markovian quantum channels. For Markovian noise, the coupling between the system and reservoir is weak, and hence, there is no information backflow and no revival of QC occurs. This could be inferred from the dynamics of \(\tau _{QSL}\). The steady increase in \(\tau _{QSL}\) in Fig. 4 warrants the absence of both information backflow and the revival of quantum correlations for a Markovian approximation.

3.2 CP-divisible phase damping channel

We now discuss dephasing quantum channel and its influence on the evolution of quantum correlations. The Kraus operators for a dephasing channel that is historically taken to be non-Markovian [66] but is nevertheless P-divisible [47] are:

$$\begin{aligned} E_{0}=\vert 0\rangle \langle 0\vert +q\vert 1\rangle \langle 1\vert ,\, E_{1}=\sqrt{1-q^{2}}\vert 1\rangle \langle 1\vert . \end{aligned}$$
(10)

We have \( q=\exp [\frac{-\gamma }{2}\{t+\frac{1}{\Gamma }(\exp (-\Gamma t)-1)\}]\). \(\Gamma ^{-1}\approx \tau _{r}\) defines reservoir’s finite correlation time, and \(\gamma \) is the coupling strength related to qubit’s relaxation time. In the limit \(\Gamma \rightarrow \infty \), phase damping channel reduces to the Markov case, and \(q=\sqrt{1-\nu }\) identifies the Kraus operators for Markovian dephasing quantum channel.

The behavior of QC of maximally entangled Bell state as a function of \(\gamma t\) in the non-Markovian and Markovian regimes is given in Fig. 5. In both cases, revival of non-classical correlations does not occur, and the order of decay satisfies the same hierarchy as in the case of amplitude damping channel, i.e., we have \(q_{F_{lhv}}\le q_{B} \le q_{S_{2}}\le q_{S_{3}}\le q_{T}\le q_E\). Due to the memory effects of the non-Markovian phase damping channel, decay of QC occurs slowly as compared to their Markovian counterparts. The non-revival of QC for the non-Markovian regime here is due to the noise being CP-divisible and hence also P divisible [47], which indicates the absence of backflow. The dynamics of quantum speed limit time for non-Markovian and Markovian phase damping channels is given in Fig. 6, and in the absence of revival of QC, \(\tau _{QSL}\) increases steadily in both the cases.

3.3 Depolarizing quantum channel

The Kraus operators of non-Markovian depolarizing quantum channel [67] are

$$\begin{aligned} E_{i}=\sqrt{q_{i}}\sigma _{i}, \end{aligned}$$
(11)

where \(\sigma _{0}=I\), rest of the \(\sigma _{i^{\prime s}}\) are the three Pauli’s matrices. The complete positivity condition is ensured by identifying the values of \(q_{i^{\prime s}}\) as positive and are given as:

$$\begin{aligned} q_{0}= & {} \frac{1}{4}[1+\Omega _{1}+\Omega _{2}+\Omega _{3}],\nonumber \\ q_{1}= & {} \frac{1}{4}[1+\Omega _{1}-\Omega _{2}-\Omega _{3}],\nonumber \\ q_{2}= & {} \frac{1}{4}[1-\Omega _{1}+\Omega _{2}-\Omega _{3}],\nonumber \\ q_{3}= & {} \frac{1}{4}[1-\Omega _{1}-\Omega _{2}+\Omega _{3}]. \end{aligned}$$
(12)

Here, \(\Omega _{i}=\exp (-\frac{\Gamma t}{2})[\cos (\frac{\Gamma d_{i}t}{2})+\frac{1}{d_{i}}\sin (\frac{\Gamma d_{i}t}{2})]\), \(d_{i}=\sqrt{(\frac{4 \mu _{i}}{\Gamma _{i}})^2-1}\) with \(\mu _{i}^2=\gamma _{j}^2+\gamma _{k}^2\) for \(i\ne j\ne k\). Here, \(\gamma \) is the coupling strength of the system with the external environment, and \(\Gamma ^{-1}\) determines the most preferable frequency of the system. The function \(\Omega \) has two regimes—pure damping and damped oscillations. \(\frac{\mu }{\Gamma }\) determines the behavior of the dynamics. When \(0\le \frac{\mu }{\Gamma }\le 1/4\), the behavior is purely damping. In the regime \(\frac{\mu }{\Gamma }>1/4\), damped oscillations exist along with the pure damping. The parameters for which the depolarizing quantum channel is in the Markovian regime are \(\Omega _{i}=e^{-\nu _{i}t}\) and \(\nu _{i}=\frac{4}{\Gamma }(\gamma _{j}^{2}+\gamma _{k}^{2})\); here, the positivity condition in Eq. 12 is satisfied if and only if \(\nu _{i}\le \nu _{j}+\nu _{k}\). For an initial Bell state, the evolution of quantum correlations in the non-Markovian regime is depicted in Fig. 7. Differently from non-Markovian phase damping channel, both decay and revival of non-classical correlations happen for non-Markovian depolarizing noise.

Fig. 7
figure 7

Quantum correlations are plotted as a function of \(\Gamma t\) for damped oscillating non-Markovian depolarizing quantum channel. The values of coupling strengths are chosen as \(\gamma _{i}=0.2\Gamma _{i}\), \(i\in \{1,2\}\), \(\gamma _{3}=5\Gamma _{3}\) and \(\Gamma _{i}=\Gamma \)

Full size image
Fig. 8
figure 8

Dynamics of quantum speed limit time for depolarizing quantum channel in the fluctuating non-Markovian regime. The values of coupling strengths are chosen as \(\gamma _{i}=0.2\Gamma _{i}\), \(i\in \{1,2\}\), \(\gamma _{3}=5\Gamma _{3}\) and \(\Gamma _{i}=\Gamma \)

Full size image

The decay and revival dynamics of quantum correlations of an entangled initial state under the influence of depolarizing channel is seen to be consistent with the hierarchy of QC. The channel parameter values for which measures of QC fail to capture the quantumness of the state are in the order \(q_{F_{lhv}}\le q_B \le q_{S_{2}}\le q_{S_{3}}\le q_{T}\le q_E\). The restoration of quantum correlations occurs in the reverse order (\(q_E\le q_{T}\le q_{S_{3}}\le q_{S_{2}}\le q_B\le q_{F_{lhv}}\)). Initially, for a small value of noise parameter, the state become entangled, followed by the creation of other correlations in the increasing order of their strength. Figure 8 brings out the effect of non-Markovian depolarizing quantum channel on the evolution of quantum speed limit time for Bell state; the oscillatory nature of \(\tau _{QSL}\) is the signature of information backflow. In the case of unital non-Markovian depolarizing channel, we do not find a connection between \(\tau _{QSL}\) and QC as seen for the non-unital amplitude damping channel. The decay of QC and the behavior of \(\tau _{QSL}\) for depolarizing channel in the Markovian regime are given in Figs. 9 and 10, respectively. Purely damping behavior of QC and non-fluctuation of \(\tau _{QSL}\) are due to the lack of backflow of information.

Fig. 9
figure 9

Quantum correlations of Bell state are plotted as a function of \(\Gamma t\) for depolarizing quantum channel in the Markovian regime (\(\gamma _{i}=0.1\Gamma \))

Full size image
Fig. 10
figure 10

Dynamics of quantum speed limit time of Bell state for depolarizing quantum channel in the Markovian regime (\(\gamma _{i}=0.1\Gamma \))

Full size image

3.4 Random telegraph noise (RTN): P-indivisible phase damping

The quantum dephasing induced by random telegraph noise is now discussed. The Kraus operators representing random telegraph noise [34, 68,69,70], a P-indivisible phase damping channel, are

$$\begin{aligned} E_{0}= & {} \sqrt{\frac{1+q(t)}{2}}(|0\rangle \langle 0|+|1\rangle \langle 1\vert ),\nonumber \\ E_{1}= & {} \sqrt{\frac{1-q(t)}{2}}(|0\rangle \langle 0|-|1\rangle \langle 1\vert ). \end{aligned}$$
(13)
Fig. 11
figure 11

Dynamics of quantum correlations of maximally entangled Bell state under the influence of non-Markovian random telegraph noise (\(\frac{a}{\gamma }=40\))

Full size image

where q(t) is the noise parameter based on the damped harmonic oscillator model that accounts the effects of both Markovian and non-Markovian noise limits on quantum states,

$$\begin{aligned} q(t)=e^{-\gamma t}\Big [\cos \left( \sqrt{\big [\left( \frac{2a}{\gamma }\right) ^2-1}\big ]\gamma t\right) +\frac{\sin \left( \sqrt{\big [\left( \frac{2a}{\gamma }\right) ^2-1}\big ]\gamma t\right) }{\sqrt{\left( \frac{2a}{\gamma }\right) ^2-1}}\Big ]. \end{aligned}$$
(14)
Fig. 12
figure 12

Dynamics of quantum correlations of Bell state for Markovian random telegraph noise (\(\frac{a}{\gamma }=0.4\))

Full size image

The frequency of the harmonic oscillators is \(\sqrt{(\frac{2a}{\gamma })^2-1}\). The noise parameter describes two regimes of systems dynamics: For \(\frac{a}{\gamma }<0.5\), the channel corresponds to the Markovian dynamics, and the purely damping regime and damped oscillations for \(\frac{a}{\gamma }>0.5\) (damped oscillations) correspond to the non-Markovian evolution. The dynamics of quantum correlations in the non-Markovian regime of RTN channel is shown in Fig. 11. Initially, all QCs fluctuate and decay afterward. In the Markovian regime (Fig. 12), these non-classical correlations decay without fluctuating. The noise parameter values at which each measure of QC reaches its classical threshold limit obey the order \(q_{F_{lhv}}\le q_B \le q_{S_{2}}\le q_{S_{3}}\le q_{T}\le q_E\). The oscillatory behavior of \(\tau _{QSL}\) for non-Markovian RTN channel in Fig. 13 captures the presence of information backflow, whereas quantum speed limit time increases (Fig. 14) without fluctuation in the Markovian regime.

Fig. 13
figure 13

Dynamics of \(\tau _{QSL}\) of maximally entangled Bell state for non-Markovian random telegraph noise(\(\frac{a}{\gamma }=40\))

Full size image
Fig. 14
figure 14

Dynamics of \(\tau _{QSL}\) of maximally entangled Bell state for Markovian random telegraph noise(\(\frac{a}{\gamma }=0.4\))

Full size image

4 Mixed entangled states

The dynamics of quantum correlations and speed limit time for a class of initial mixed states under the influence of different quantum channels are investigated. The initial mixed state we consider is the Werner state, given as the convex sum of maximally entangled Bell state and maximally mixed separable state

$$\begin{aligned} \rho _{w}=\frac{1-p}{4}I_{4}+p\vert B\rangle \langle B\vert . \end{aligned}$$
(15)

Here, \(\vert B\rangle \) can be any one of the four maximally entangled Bell diagonal states. \(\rho _{w}\) is entangled for \(p>\frac{1}{3}\), and it violates Bell-CHSH inequality and \(ST_{2}\) steering for the values \(p>\frac{1}{\sqrt{2}}\). Here, we mainly focus on the decoherence effects of amplitude damping and RTN channels on \(\rho _{w}\), for a fixed value of mixedness.

Fig. 15
figure 15

Dynamics of quantum correlations of maximally entangled mixed Werner state for \(p=0.9\) \((\Gamma =0.01\gamma )\) under non-Markovian amplitude damping channel

Full size image
Fig. 16
figure 16

Dynamics of quantum correlations of maximally entangled mixed Werner state for \(p=0.9\) under the Markovian amplitude damping channel

Full size image

In Figs. 15 and 16, the effect of amplitude damping channel with and without memory on Werner state for a state parameter value \(p=0.9\) is depicted. As in the case of a pure state (Fig. 1), in the presence of memory, decay of QC takes place, followed by the revival (Fig. 15). Quantum correlations decay and do not revive (Fig. 16) in the Markovian regime. The deterioration of QC of mixed state under (non-) Markovian regimes upholds the hierarchy order. Similar to the pure state scenario, \(\tau _{QSL}\) (Fig. 17) can be used to analyze the dynamics of non-classical correlations for the non-Markovian amplitude damping channel. It can be seen that the shift in the nature of \(\tau _{QSL}\) matches exactly with the revival of lowest degree quantum correlation (quantum entanglement in the present case) (Fig. 15). In the absence of information backflow, \(\tau _{QSL}\) increases steadily for Markovian noise (Fig. 18). QC and \(\tau _{QSL}\) of Werner state for non-Markovian RTN channel are depicted in Figs. 19 and 20, respectively. It can be seen from Fig. 19 that the strength of QC initially decreases, but due to the system-reservoir coupling and the backflow of information, restoration of non-classical properties of states takes place. The dynamics of non-classical correlation of mixed states under non-Markovian channel is consistent with the order of hierarchy of QC.

Fig. 17
figure 17

Dynamics of quantum speed limit time of Werner state for \(p=0.9\) \((\Gamma =0.01\gamma )\) for non-Markovian amplitude damping channel

Full size image
Fig. 18
figure 18

Dynamics of quantum speed limit time of Werner state for \(p=0.9\) for Markovian amplitude damping channel

Full size image
Fig. 19
figure 19

Dynamics of quantum correlations of maximally entangled mixed Werner state for \(p=0.9\) for non-Markovian random telegraph noise (\(\frac{a}{\gamma }=40\))

Full size image
Fig. 20
figure 20

Quantum speed limit time of Werner state for \(p=0.9\) as a function of \(\gamma t\) for non-Markovian random telegraph noise (\(\frac{a}{\gamma }=40\))

Full size image
Table 1 The evolution of quantum correlations under the influence of various unital and non-unital Markovian and non-Markovian quantum channels
Full size table

5 Results and discussion

In this paper, we systematically investigated the dynamics of quantum correlations of two qubit states that are used as a resource for quantum teleportation in a noisy environment. We established the connection between quantum correlations and two different aspects of non-classicality associated with the teleportation fidelity. The dynamics of quantum speed limit time can be availed to demonstrate the decay and revival of quantum correlations in the case of memory and memory less quantum channels. We considered the case of QC in Markovian as well as CP-divisible and P-indivisible non-Markovian regimes. From the study of Markovian and non-Markovian channels, it can be inferred that the longevity of quantum correlations gets enhanced due to the memory effects of system-reservoir interaction. The dynamics of QC under the effect of various channels is tabulated in Table I. The revival of quantum correlations occurs for all considered non-Markovian channels in the case of both pure and mixed states, except for CP-divisible channels. The non-revival of QC in CP-divisible channels is due to the absence of backflow of information. In the case of non-unital non-Markovian amplitude damping channel, \(\tau _{QSL}\) exactly describes the decay and revival of quantum correlations. This is not true for unital non-Markovian quantum channels, and is consistent with [51]. For unital P-indivisible non-Markovian channels, fluctuating \(\tau _{QSL}\) and QC imply the existence of information backflow, whereas this is absent in CP-divisible non-Markovian regime. For a given Markovian quantum channel, quantum speed limit time increases as time increases, i.e., there occurs no oscillation of \(\tau _{QSL}\). This brings forth the marked differences in the behavior of \(\tau _{QSL}\) for Markovian, CP-divisible and P-indivisible non-Markovian dynamics [51]. This is highlighted by the shift in \(\tau _{QSL}\) coinciding with the revival of entanglement, for non-Markovian evolution that are P indivisible, exemplified by the non-Markovian amplitude damping channel.

6 Conclusions

We investigated the effects of reservoir memory on the dynamics of quantum correlations of two qubit quantum states. We considered quantum teleportation fidelity, Bell-CHSH function, quantum steering and entanglement as various measures that capture the non-classical aspects of quantum states. We discussed how these measures of QC are connected with each other under the influence of memory of quantum channels. We showed the existence of an order of hierarchy in the decay and revival of quantum correlations under both Markovian and non-Markovian noises, which is consistent with the previous works. The channel parameter values at which decay of non-classical correlations occur follow the order \(q_{F_{lhv}}\le q_B \le q_{S_{2}}\le q_{S_{3}}\le q_{T}\le q_E\), whereas the revival of quantum correlations occurs in the reverse order (\(q_E\le q_{T}\le q_{S_{3}}\le q_{S_{2}}\le q_B\le q_{F_{lhv}}\)), i.e., QC with lowest degree of strength revives first, followed by the revival of correlations in the increasing order of strength. QC revives under all non-Markovian noisy models (P-indivisible) considered except for the CP-divisible channels, which could be ascribed to the lack of backflow. Noise tolerance of QC under non-Markovian noise is seen to be high compared to that of their Markovian counterpart. We estimated the quantum speed limit time of states under different noises and showed that the study of \(\tau _{QSL}\) can be used to explain the characteristic dynamics of QC. Dynamics of QC and \(\tau _{QSL}\) were examined for both pure and mixed states in Markovian and non-Markovian regimes. Under Markovian noise, there exists no information backflow and this can be witnessed from the dynamics of quantum speed limit time, as it increases steadily as time increases without fluctuations. Among the non-Markovian noisy models studied here, except for the CP-divisible phase damping noise, fluctuation of \(\tau _{QSL}\) was observed for P-indivisible non-Markovian amplitude damping, depolarizing and RTN channels, which could be attributed to the (non-)existence of information backflow. It was seen that for a given non-Markovian non-unital amplitude damping channel, the dynamics of quantum speed limit time sheds light into the behavior of quantum correlations. We showed that for non-Markovian amplitude damping noise, the time at which the lowest degree QC decays exactly matches with the time at which a shift in the behavior of \(\tau _{QSL}\) occurs. The connection between QC and \(\tau _{QSL}\) as seen for non-unital channels cannot be easily established for unital quantum channels and requires further studies.