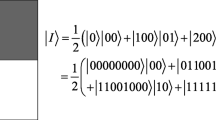Quantum circuit design for several morphological image processing methods

Abstract

Morphological image processing is a relatively mature image processing method in classical image processing. However, in quantum image processing, the related results are still quite scarce. In this paper, we first design the quantum circuits of the two basic operations of dilation and erosion for binary images and grayscale images. On this basis, for binary image, the quantum circuits of three morphological algorithms (noise removal, boundary extraction and skeleton extraction) are designed in detail. For grayscale image, the quantum circuits of three morphological algorithms (i.e., edge detection, image enhancement and texture segmentation) are also designed. In the design of these circuits, the parallelism of quantum computation is considered. The analysis of the circuits complexity shows that all the six morphological algorithms can speed up their classic counterparts.

1 Introduction

In 1982, Feynman had pointed out that there seemed to be essential difficulties in simulating quantum mechanical systems on the classical computers and suggested that building computers based on the principles of quantum mechanics would allow us to avoid those difficulties. Motivated by the suggestion, in 1985, Deutsch was naturally led to consider computing devices based upon the principles of quantum mechanics. These remarkable suggestions taken by Feynman and Deutsch were studied in the subsequent decade by many people, culminating in Peter Shor’s [1] demonstration that two enormously important problems—the problem of finding the prime factors of an integer and the so-called discrete logarithm problem—could be solved efficiently on the a quantum computer [1]. Further evidence for the power of quantum computers came in 1996 when Lov Grover showed that another important problem—the problem of conducting a search through some unstructured search space—could also be sped up on a quantum computer [2]. While Grover’s algorithm did not provide as spectacular a speedup as Shor’s algorithms, the widespread applicability of search-based methodologies has excited considerable interest in Grover’s algorithm. With the birth of these two famous algorithms, quantum computing and quantum informatics have quickly become an international research hot spot.

Quantum image processing is an emerging interdisciplinary subject based on quantum physics and integrated into computer science and classical image processing. Based on the principles of quantum mechanics, it studies the basic theory and method of image processing on quantum computer. In 2003, the concept of quantum image processing was first proposed in Ref. [3], marking the birth of this new discipline. The development of quantum image processing was described in detail in Ref. [4]. For quantum image processing, it is first necessary to convert a classic image into its quantum version, so quantum image description is the first step in quantum image processing. The qubit lattice representation [5] and the real ket representation [6] are two early models. Although these two models do not make full use of the superposition of quantum states, they lay the foundation for future development. The FRQI (flexible representation of quantum images) representation proposed in 2010 has led to the rapid development of quantum image processing, which used the quantum superposition state to store pixel positions for the first time [7]. Several subsequent models, such as SQR (simple quantum representation of infrared images) [8] and MCRQI (multichannel representation for quantum images) [9, 10], can be seen as modifications and extensions of the representation model. The NEQR (novel enhanced quantum representation) proposed in 2013 is a widely used quantum image description model [11]. In this model, the position and color of the pixels are represented by the quantum basis state, which overcomes the shortcoming that the color value of the pixels in FRQI model cannot be obtained accurately by performing a finite number of measurements.

Although the classical theory and technology of digital image processing have been perfected, quantum image processing is still in its infancy. Because of the essential difference between quantum computing and classical computing, all classical image processing algorithms cannot be simply transplanted into quantum image processing, but must be redesigned. At present, the content touched by quantum image processing mainly includes image scrambling [12,13,14,15,16,17], image encryption [18,19,20,21,22,23,24,25,26,27], image watermarking [28,29,30,31,32,33,34,35,36,37,38,39], image steganography [40,41,42,43,44,45,46,47,48], quantum movie [49], quantum audio [50], image matching [51], image location [52], geometric transformation [53], color processing [54], feature extraction [55] and image segmentation [56], morphological image processing [57,58,59], etc. Most of these studies have focused on quantum image encryption, watermarking, steganography, transformation, and so on, while the quantum morphology research is relatively rare. Reference [57] is the first reference to study image processing of quantum morphology, which focuses on the dilation and erosion of quantum binary images and grayscale images. Later, Zhou Rigui studied morphological dilation and erosion, and morphological gradient based on binary images [58] and grayscale images [59], respectively. So far, many other methods in classical morphological image processing such as opening, closing, top-hat transformation, bottom-hat transformation and skeleton extraction have no corresponding quantum version. Based on the above situation, in this work, we design the corresponding quantum circuits for several basic operations of morphological image processing, including dilation, erosion, opening, closing, top-hat transformation, bottom-hat transformation, morphological gradient, etc., and apply these circuits to noise removal, boundary extraction, skeleton extraction, edge detection, image enhancement and texture segmentation of quantum images. Different from the classical method, using the parallelism of quantum computing, these quantum methods designed can operate on a superposition of quantum states representing pixels in the input image, which can significantly accelerate their classical counterparts.

The remainder of this paper is organized as follows. Section 2 briefly introduces the NEQR model, and the morphology dilation and erosion of classical images. Section 3 presents the design method of quantum circuits for morphological dilation and erosion, and several quantum morphological processing methods are introduced in Sect. 4. Section 5 analyzes the complexity of the designed quantum circuits. Some simulations on classical computer are presented in Sect. 6. In Sect. 7, we offer a concluding remarks.

2 Preliminaries

2.1 NEQR model of representing quantum image

Considering that the morphological image processing involves a lot of grayscale value calculation, this paper represents the quantum image using NEQR model which is more suitable for grayscale value operation.

For a grayscale image, NEQR encodes q bits of binary grayscale values into q qubits. In NEQR, a grayscale image of size $2^n\times 2^n$ has representation,

$$\begin{aligned} |Q\rangle =\frac{1}{2^n}\sum \limits _{y=0}^{2^n-1}\sum \limits _{x=0}^{2^n-1}|f(y,x)\rangle |yx\rangle =\frac{1}{2^n}\sum \limits _{y=0}^{2^n-1}\sum \limits _{x=0}^{2^n-1}|c_{yx}^{q-1}c_{yx}^{q-2}\ldots c_{yx}^{0}\rangle |yx\rangle , \end{aligned}$$

(1)

where $c_{yx}^{q-1}, c_{yx}^{q-2},\ldots \,c_{yx}^{0}\in \{0,1\}$, and $f(y,x)\in \{0,1,\ldots , 2^{q}-1\}$.

It is clear from Eq. (1) that NEQR needs $q+2n$ qubits to represent a $2^n\times 2^n$ grayscale image. Taking $n=1$ and $q=8$ as an example, a $2\times 2$ grayscale image and its NEQR representation are shown in Fig. 1.

Fig. 1

A $2\times 2$ grayscale image and its NEQR representation

2.2 Morphological erosion and dilation for classical binary images

Erosion and dilation are fundamental to morphological processing. In fact, many of the morphological algorithms discussed in this paper are based on these two primitive operations. In general, let A denote a binary image and B denote a structuring element. In the binary image morphology operation, both the binary image and the structuring element are regarded as a set. The basic operation of binary image morphology is the operation defined on these two sets. Normally, the binary image morphology operation is performed on the pixel region having a value of 1 in the binary image A using the structuring element B. For ease of understanding, we first give the concept of structuring element.

Generally speaking, structuring elements are small sets or subimages used to probe an image under study for properties of interest. Figure 2 shows several examples of structuring elements where each shaded square denotes a member of the structuring element. In addition to a definition of which elements are members of the structuring element, the origin of a structuring element also must be specified. The origins of the various structuring elements in Fig. 2 are indicated by a black dot. (Although placing the center of an structuring element at its center of gravity is common, the choice of origin is problem dependent in general.) When the structuring element is symmetric and no dot is shown, the assumption is that the origin is at the center of symmetry.

It is worth noting that although the size and shape of the structuring elements are not unique, the square structuring elements with the size of $3\times 3$ are the most widely used. Therefore, unless otherwise specified, the square structuring elements of size $3\times 3$ are used in this paper.

Fig. 2

Examples of structuring. The dots denote the centers of the structuring elements

2.2.1 Erosion

With A and B as sets in $Z^2$, the erosion of A by B is defined as

$$\begin{aligned} A\ominus B=\{z|(B)_z\subseteq A\}. \end{aligned}$$

(2)

In other words, this equation indicates that the erosion of A by B is the set of all points z such that B, translated by z, is contained in A. In the following discussion, set B is assumed to be a structuring element. Because the statement that B has to be contained in A is equivalent to B not sharing any common elements with the background, we can express erosion in the following equivalent form:

$$\begin{aligned} A\ominus B=\{z|(B)_z\cap A^c=\emptyset \}, \end{aligned}$$

(3)

where $A^c$ is the complement of A and $\emptyset$ is the empty set.

2.2.2 Dilation

With A and B as sets in $Z^2$, the dilation of A by B is defined as

$$\begin{aligned} A\oplus B=\big \{z|\big (\hat{B}\big )_z\cap A\ne \emptyset \big \}. \end{aligned}$$

(4)

This equation is based on reflecting B about its origin, and shifting this reflection by z. The dilation of A by B then is the set of all displacements, z, such that $\hat{B}$ and A overlap by at least one element. Based on this interpretation, Eq. (4) can be written equivalently as

$$\begin{aligned} A\oplus B=\{z|[(\hat{B})_z\cap A]\subseteq A\}. \end{aligned}$$

(5)

As before, we assume that B is a structuring element and A is the set (image objects) to be dilated.

Equations (4, 5) are not the only definitions of dilation currently in use. However, the preceding definitions have a distinct advantage over other formulation in that they are more intuitive when the structuring element B is viewed as a convolution mask. The basic process of flipping (rotating) B about its origin and then successively displacing it so that it slides over set (image) A is analogous to spatial convolution. However, that dilation is based on set operations and therefore is a nonlinear operation, whereas convolution is a linear operation.

2.3 Morphological erosion and dilation for classical grayscale images

Morphological erosion and dilation operations of binary images can be extended to grayscale images. Structuring elements in grayscale morphology perform the same basic functions as their counterparts: They are used as “probes” to examine a given image for specific properties.

2.3.1 Erosion

The erosion of image f by a flat structuring element b at any location (x, y) is defined as the minimum value of the image in the region coincident with b when the origin of b is at (x, y). In equation form, the erosion at (x, y) of an image f by a structuring element b is given by

$$\begin{aligned}{}[f\ominus b](x,y)=\min \limits _{(s,t)\in b}\{f(x+s,y+t)\}, \end{aligned}$$

(6)

where x and y are incremented through all values required so that the origin of b visits every pixel in f. This is, to find the erosion of f by b, we place the origin of the structuring element at every pixel location in the image. The erosion at any location is determined by selecting the minimum value of f from all the values of f contained in the region coincident with b. For example, if b is a square structuring element of size of $3\times 3$, obtaining the erosion at a point requires finding the minimum of the nine values of f contained in the $3\times 3$ region defined by b when its origin is at that point.

Nonflat structuring elements have grayscale values that vary over their domain of definition. The erosion of image f by nonflat structuring element, $b_N$, is defined as

$$\begin{aligned}{}[f\ominus b_N](x,y)=\min \limits _{(s,t)\in b_N}\{f(x+s,y+t)-B_N(s,t)\}. \end{aligned}$$

(7)

Here, we actually subtract values from f to determine the erosion at any point. This means that, unlike Eq. (6), erosion using a nonflat structuring element is not bounded in general by the value of f, which can present problems in interpreting results. Nonflat structuring elements are seldom used in practice because of this, in addition to potential difficulties in selecting meaningful elements for $B_N$, computational burden was added when compared with Eq. (6).

2.3.2 Dilation

Similarly, the dilation of f by a flat structuring element b at any location (x, y) is defined as the maximum value of the image in the window outlined by $\hat{b}$ when the origin of $\hat{b}$ is at (x, y). That is,

$$\begin{aligned}{}[f\oplus b](x,y)=\max \limits _{(s,t)\in b}\{f(x-s,y-t)\}, \end{aligned}$$

(8)

where $\hat{b}$ is the reflection of b on its origin, i.e., $\hat{b}=b(-x,-y)$. The explanation of this equation is identical to the explanation in the morphological erosion of grayscale images, but using the maximum, rather than the minimum, operation and keeping in mind that the structuring element is reflected about its origin, which we take into account by using $(-s,-t)$ in the argument of the function. This is analogous to spatial convolution.

In a similar manner as erosion, dilation using a nonflat structuring element is defined as

$$\begin{aligned}{}[f\oplus b_N](x,y)=\max \limits _{(s,t)\in b_N}\{f(x-s,y-t)+b_N(s,t)\}. \end{aligned}$$

(9)

The same comments made in the previous grayscale erosion are applicable to dilation with nonflat structuring elements. When all the elements of $b_N$ are constant (i.e., the structuring element is flat), Eqs. (7) and (9) reduce to Eqs. (6) and (8), respectively, within a scalar constant equal to the amplitude of the structuring element.

3 Quantum circuits for morphological dilation and erosion

3.1 Quantum circuits for some auxiliary modules

Before giving the quantum circuits for dilation and erosion of binary images, several submodules of quantum circuits which will be used later are introduced, including Comparator, Copy, Modulo Plus 1 and Modulo Minus 1, Swap, Sort and Min–Max Calculation modules.

• 1. Comparator module

The Comparator module plays an important role in the design of quantum circuits for morphological image processing, and it is used to compare pixel positions between different images. Here, we use the quantum Comparator designed in [60], and its quantum circuit is shown in Fig. 3.

Fig. 3

(Figure adapted from [60])

Quantum circuit of Comparator

The Comparator compares x and y, where $x=x_{n-1}x_{n-2}\ldots x_0$, $y=y_{n-1}y_{n-2}\ldots y_0$, $x_i,y_i\in \{0,1\},i=n-1,n-2,\ldots ,0$. Qubits $e_1$ and $e_0$ are outputs. If $e_1e_0=10$, then $x>y$; if $e_1e_0=01$, then $x<y$; and if $e_1e_0=00$, then $x=y$.

• 2. Copy module

For a known n-bit quantum state, by using n controlled-NOT (CNOT) gates, it can be stored in another n-bit quantum register with an initial state of $|0\rangle ^{\otimes n}$. The specific quantum circuit is shown in Fig. 4. It is worth pointing out that this operation does not violate the conclusion that the quantum state cannot be accurately replicated, because the conclusion is for quantum states with unknown states. However, in the Copy module herein, the quantum state is fully known.

Fig. 4

Quantum circuit of Copy module

In the symbol of the Copy module, the side on which the control qubits are located is marked with solid bars.

• 3. Modulo Plus 1 and Modulo Minus 1 modules

These two modules used in this paper are derived from [55]. For an n-qubit unsigned integer x, these two modules can be used to, respectively, to implement $x+1$ and $x-1$ modulo $2^n$, and their quantum circuits are shown in Fig. 5.

Fig. 5

(Figure adapted from [55])

Quantum circuits of Modulo Plus 1 and Modulo Minus 1

• 4. Swap module

This module can be used to exchange the stored contents between two n-qubit quantum registers. In this module, the information carried by each pair of qubits in two quantum registers can be exchanged by three CNOT gates, and its quantum circuit is shown in Fig. 6.

Fig. 6

Quantum circuits of Swap module

• 5. Sort module

The module can achieve ascending order of two n-qubit numbers. For two n-qubit numbers x and y, first compare them with a quantum Comparator and then, when $a>b$, use the Swap module to exchange the two numbers. The specific quantum circuit is shown in Fig. 7.

Fig. 7

Quantum circuits of Sort module

• 6. Min–Max Calculation module

This module is used to calculate the minimum and maximum of nine q-qubit numbers. Firstly, nine numbers are sorted in ascending order by bubble sorting principle. For nine sorted numbers, the first is the minimum and the last is the maximum. The specific quantum circuit is shown in Fig. 8.

Fig. 8

Quantum circuits of Min–Max Calculation module

3.2 Quantum circuits of dilation and erosion for binary image

From the definition of binary image dilation in Sect. 2.2, it is known that the set generated by the dilation of the set A with the structuring element B is a set of origin positions of B when the flip and translation set of B and the set A have at least one nonzero element. For the convenience of design, this paper neglects the flip of structuring element and only considers the translation of structuring element. In fact, all the structuring elements used in this paper are symmetric, and there is no change after flipping, and so, this neglect is also feasible.

3.2.1 Quantum circuit of dilation

The dilation operation of binary image is similar to the spatial convolution using structuring element as convolution mask. In order to avoid the sliding of structuring element on binary image and make full use of the parallelism of quantum computation, this paper uses a method called “Translation, Stacking, logic AND, logic OR.” The method is specifically explained as follows.

The binary image is first translated by one unit or multiple units (depending on the size of the structuring element) in eight directions (i.e., top-left, top, top-right, left, right, bottom-left, bottom, bottom-right). Then, the translated images and the original image are stacked in a fixed order. In these stacked images, the pixels in the same position are those in the original image that are covered by the structuring element. Finally, in the stacked images, for those pixels with the same position, the logical “AND” operation is performed, respectively, with the corresponding pixels in the structure element, and then the logical “OR” operation is performed on the results of all the logical “AND” operations; thus, the dilation result of the binary image can be obtained. The advantage of this approach is that with the parallelism of quantum computing, all pixels in the same position in the stacked images can be processed simultaneously, and then, the classical computing can be accelerated.

Based on the above method, taking the $3\times 3$ structuring element with origin at the center as an example, the quantum circuit for binary image dilation designed in this paper is shown in Fig. 9. In this figure, the subfigure (a) represents the quantum circuit of the dilation operation, the subfigure (b) is the symbol of subfigure (a), for the sake of brevity, ignoring the auxiliary qubits, and subfigure (c) represents a $3\times 3$ structuring element with an origin at the center.

Fig. 9

Quantum circuits for morphological dilation of binary image

In Fig. 9, based on NEQR, the binary image A and the structuring element B can be, respectively, represented as

$$\begin{aligned} |A\rangle= & {} \frac{1}{2^n}\sum \limits _{y_{22}=0}^{2^n-1}\sum \limits _{x_{22}=0}^{2^n-1}|c_{22}\rangle |y_{22}\rangle |x_{22}\rangle , \end{aligned}$$

(10)

$$\begin{aligned} |B\rangle= & {} \frac{1}{3}\left( \begin{array}{l}|b_{11}\rangle |00\rangle +|b_{12}\rangle |01\rangle +|b_{13}\rangle |02\rangle \\ +|b_{21}\rangle |10\rangle +|b_{22}\rangle |11\rangle +|b_{23}\rangle |12\rangle \\ +|b_{31}\rangle |20\rangle +|b_{32}\rangle |21\rangle +|b_{33}\rangle |22\rangle \end{array}\right) . \end{aligned}$$

(11)

The quantum circuit shown in Fig. 9a consists of three parts. The first part is the circuit in the red dotted frame, and it is used to generate nine binary images as follows.

$$\begin{aligned} \left\{ \begin{array}{l} |I_{11}\rangle =\frac{1}{2^n}\sum \nolimits _{y_{11}=0}^{2^n-1}\sum \nolimits _{x_{11}=0}^{2^n-1}|c_{11}\rangle |y_{11}\rangle |x_{11}\rangle ,\\ |I_{12}\rangle =\frac{1}{2^n}\sum \nolimits _{y_{12}=0}^{2^n-1}\sum \nolimits _{x_{12}=0}^{2^n-1}|c_{12}\rangle |y_{12}\rangle |x_{12}\rangle ,\\ |I_{13}\rangle =\frac{1}{2^n}\sum \nolimits _{y_{13}=0}^{2^n-1}\sum \nolimits _{x_{13}=0}^{2^n-1}|c_{13}\rangle |y_{13}\rangle |x_{13}\rangle ,\\ |I_{21}\rangle =\frac{1}{2^n}\sum \nolimits _{y_{21}=0}^{2^n-1}\sum \nolimits _{x_{21}=0}^{2^n-1}|c_{21}\rangle |y_{21}\rangle |x_{21}\rangle ,\\ |I_{23}\rangle =\frac{1}{2^n}\sum \nolimits _{y_{23}=0}^{2^n-1}\sum \nolimits _{x_{23}=0}^{2^n-1}|c_{23}\rangle |y_{23}\rangle |x_{23}\rangle ,\\ |I_{31}\rangle =\frac{1}{2^n}\sum \nolimits _{y_{31}=0}^{2^n-1}\sum \nolimits _{x_{31}=0}^{2^n-1}|c_{31}\rangle |y_{31}\rangle |x_{31}\rangle ,\\ |I_{32}\rangle =\frac{1}{2^n}\sum \nolimits _{y_{32}=0}^{2^n-1}\sum \nolimits _{x_{32}=0}^{2^n-1}|c_{32}\rangle |y_{32}\rangle |x_{32}\rangle ,\\ |I_{33}\rangle =\frac{1}{2^n}\sum \nolimits _{y_{33}=0}^{2^n-1}\sum \nolimits _{x_{33}=0}^{2^n-1}|c_{33}\rangle |y_{33}\rangle |x_{33}\rangle ,\\ |\hat{I}\rangle =\frac{1}{2^n}\sum \nolimits _{\hat{y}=0}^{2^n-1}\sum \nolimits _{\hat{x}=0}^{2^n-1}|\hat{c}\rangle |\hat{y}\rangle |\hat{x}\rangle . \end{array} \right. \end{aligned}$$

(12)

where the first eight images (i.e., $|I_{11}\rangle , |I_{12}\rangle , |I_{13}\rangle , |I_{21}\rangle , |I_{23}\rangle , |I_{31}\rangle , |I_{32}\rangle , |I_{33}\rangle$) are identical to the binary image $|A\rangle$, and the last $|\hat{I}\rangle$ is a binary image with all the pixel values of 1.

The specific method is that, firstly, the position qubits and the grayscale value qubits of the nine images are initialized to $|0\rangle$, and then some Hadamard gates are used to convert the position qubits into equilibrium superposition states, and nine empty images can be obtained. Some Comparators and some Copy modules are used to assign the pixel values of the binary image $|A\rangle$ to the first eight empty images, making them the exact same image as $|A\rangle$. For the empty image $|\hat{I}\rangle$, a NOT gate acts on its pixel value qubit $|\hat{c}\rangle$ to make it a binary image with all the pixel values of 1.

The second part is the circuit in the middle blue dotted frame. It is used to translate the eight images (i.e., $|I_{11}\rangle , |I_{12}\rangle , |I_{13}\rangle , |I_{21}\rangle , |I_{23}\rangle , |I_{31}\rangle , |I_{32}\rangle , |I_{33}\rangle$) generated in the first part to eight directions, respectively, which is realized by changing the pixel position of eight images with Modulo Plus 1 and Modulo Minus 1 modules.

The third part is the circuit in the green dotted frame on the right side. It is used to stack the input image $|A\rangle$ and 8 shifted images generated in the second part, and further calculate the dilation result of binary image $|A\rangle$. Specifically, first, the 18 Comparators are used to determine those pixels in the same position in the ten images, and then, the nine Toffoli gates with a target qubit of $|0\rangle$ are used to implement a logical “AND” operation between the pixel value $|c_{ij},\rangle$ and the $|b_{ij}\rangle$ $(i,j=1, 2, 3)$ in the structuring element, respectively. A nine-controlled-NOT gate is used to perform logical “OR” operation on the results of the above nine “AND” operations, wherein the target qubit of each Toffoli gate is used as the control qubit, and the pixel value qubit $|\hat{c}\rangle$ of the binary image $|\hat{I}\rangle$ is used as the target qubit. At this time, the binary image $|\hat{I}\rangle$ is an dilation image of input image $|A\rangle$. Finally, a Swap module is used to exchange the pixel value qubit of $|A\rangle$ and $|\hat{I}\rangle$. At this time, the input image $|A\rangle$ becomes its own dilated image.

3.2.2 Quantum circuit of erosion

Erosion and dilation are duals of each other with respect to set complementation and reflection. This is,

$$\begin{aligned} (A\ominus B)^c=A^c\oplus \hat{B}^c, \end{aligned}$$

(13)

$$\begin{aligned} (A\oplus B)^c=A^c\ominus \hat{B}^c. \end{aligned}$$

(14)

Equation (13) indicates that erosion of A by B is the complement of the dilation of $A^c$ by $\hat{B}$, and vice versa. The duality property is useful particularly when the structuring element is symmetric with respect to its origin (as often is the case), so that $\hat{B}=B$. Then, we can obtain the erosion of an image by B simply by dilating its background (i.e., dilating $A^c$) with the same structuring element and complementing the result. Similar comments apply to Eq. (14).

We proceed to prove formally the validity of Eq. (13) in order to illustrate a typical approach for establishing the validity of morphological expressions. Starting with the definition of erosion, it follows that

$$\begin{aligned} (A\ominus B)^c=\{z|(B)_z\subseteq A\}^c. \end{aligned}$$

(15)

If set $(B)_z$ is contained in A, then $(B)_z\cap A^c=\emptyset$, in which case the proceeding expression becomes

$$\begin{aligned} (A\ominus B)^c=\{z|(B)_z\cap A^c=\emptyset \}^c. \end{aligned}$$

(16)

But the complement of the set of $z's$ that satisfy $(B)_z\cap A^c=\emptyset$ is the set of $z's$ such that $(B)_z\cap A^c\ne \emptyset$. Therefore,

$$\begin{aligned} (A\ominus B)^c=\{z|(B)_z\cap A^c\ne \emptyset \}=A^c\oplus \hat{B}, \end{aligned}$$

(17)

where the last step follows from Eq. (4).

According to the duality Eq. (13) of the erosion and dilation of the binary image, the quantum circuit for performing the binary image erosion operation is as shown in Fig. 10, in which the structuring elements are the same as those in dilation operation.

Fig. 10

Quantum circuits for morphological erosion of binary image

3.3 Quantum circuit of morphological dilation and erosion for grayscale image

Because nonflat structuring elements are seldom used in the morphological dilation and erosion operations of grayscale images, this paper only studies the design method of quantum circuits for dilation and erosion using flat structuring elements. For ease of description, we take a $3\times 3$ flat structuring element as an example to study the design method of quantum circuits for dilation and erosion.

From the definitions of the morphological erosion and dilation, Eqs. (6) and (8), for flat structuring elements, these two operations correspond to the maximum and minimum filtering, respectively, in which the flat structuring elements are used for the filter masks. In order to make full use of the parallelism of quantum computing, the quantum circuits of grayscale image dilation and erosion designed in this paper are shown in Figs. 11 and 12, respectively.

Fig. 11

Quantum circuits for morphological dilation of grayscale image

Fig. 12

Quantum circuits for morphological erosion of grayscale image

These two circuits are very similar, they are all made up of three parts and the first two parts are identical, only slightly different in the third part. Specific explanations are given below.

The first part is the circuit in the red dotted frame, and it is used to generate eight grayscale images (i.e., $|I_{11}\rangle , |I_{12}\rangle , |I_{13}\rangle , |I_{21}\rangle , |I_{23}\rangle , |I_{31}\rangle , |I_{32}\rangle , |I_{33}\rangle$) exactly the same as the input image $|I\rangle =\frac{1}{2^n}\sum \nolimits _{y=0}^{2^n-1}\sum \nolimits _{x=0}^{2^n-1}|c_{q-1}c_{q-2}\ldots c_{0}\rangle |y\rangle |x\rangle$. The method of generating these images can be seen from the explanation given in the dilation circuit of the binary image.

The second part is the circuit in the middle blue dotted frame. It is used to translate the eight images (i.e., $|I_{11}\rangle , |I_{12}\rangle , |I_{13}\rangle , |I_{21}\rangle , |I_{23}\rangle , |I_{31}\rangle , |I_{32}\rangle , |I_{33}\rangle$) generated in the first part to eight directions, respectively, which is realized by changing the pixel position of eight images with Modulo Plus 1 and Modulo Minus 1 modules.

The third part is the circuit in the green dotted frame on the right side. It is used to stack the input image $|I\rangle$ and eight shifted images generated in the second part, and further calculate the dilation or erosion result of input image $|I\rangle$. Specifically, first, the 16 Comparators are used to determine those pixels in the same position in the nine images, and then, a Min–Max Calculation module is used to compute the maximum (for dilation) or minimum (for erosion) of the pixel value $|c_{ij},\rangle , (i,j=1, 2, 3)$. At this time, the grayscale image $|I_{33}\rangle$ is an dilation image of input image $|I\rangle$, and the grayscale image $|I_{11}\rangle$ is an erosion image of input image $|I\rangle$. Finally, a Swap module is used to exchange the pixel value qubits of $|I\rangle$ and $|I_{33}\rangle$ (or the pixel value qubits of $|I\rangle$ and $|I_{11}\rangle$). At this time, the input image $|I\rangle$ becomes its own dilated or eroded image.

4 Quantum circuit design of several morphological image processing algorithms

4.1 Quantum circuits for some auxiliary modules

• 1. Adder module

As in classical computation, it is important to construct quantum circuits for performing elementary operations. Explicit constructions for several operations, including plain addition, modular addition and modular exponentiation, can be found in [61]. Here, we employ only the plain addition of two n-bit integers x and y (in binary representation, $x=x_{n-1}2^{n-1}+x_{n-2}2^{n-2}+\cdots +x_0\equiv x_{n-1}x_{n-2}\ldots x_0$ and analogously for $y\equiv y_{n-1}y_{n-2}\ldots y_0$). The quantum circuits implementing plain addition are shown in Fig. 13. If we reverse the action of the above Adder (i.e., if we apply each gate of the adder in the reversed order), we can get a quantum Subtractor. For a detailed explanation of these circuits, interested readers can refer to Ref. [61].

Fig. 13

(Figure adapted from [61])

Quantum circuits of quantum Adder

• 2. Image Adder and Image Subtractor modules

Considering that the addition and subtraction between two images are often involved in grayscale image morphological processing, the quantum circuits to realize the addition and subtraction of two grayscale images designed in this paper are shown in Fig. 14. The principle of the circuit is very simple. First, the positions of the pixels between two images are compared. When the positions are the same, the corresponding grayscale values of the pixels are added or subtracted.

Fig. 14

Quantum circuits of Image Adder and Image Subtractor

• 3. Image Copy module

In morphological processing of quantum image, a frequently encountered requirement is to generate another identical image from the current image. Therefore, this paper also specifically designed the quantum circuit to achieve image replication, as shown in Fig. 15. In this circuit, $|I\rangle =\frac{1}{2^n}\sum \nolimits _{y=0}^{2^n-1}\sum \nolimits _{x=0}^{2^n-1}|c\rangle |yx\rangle$ is the input image. Firstly, 2n Hadamard gates are used to change the quantum basis state $|\hat{y}\hat{x}=|0\rangle ^{\otimes n}$ into an equilibrium quantum superposition state. At this time, an empty image $|\hat{I}\rangle =\frac{1}{2^n}\sum \nolimits _{\hat{y}=0}^{2^n-1}\sum \nolimits _{\hat{x}=0}^{2^n-1}|\hat{c}\rangle |\hat{y}\hat{x}\rangle$ can be obtained (all grayscale values are 0), and then the comparator is used to compare the pixel positions between the two images $|I\rangle$ and $|\hat{I}\rangle$. When the position is the same, the Copy module is used to copy the grayscale value from $|c\rangle$ to $|\hat{c}\rangle$.

Fig. 15

Quantum circuits of Image Copy module

• 4. Opening and Closing modules

Opening and Closing are two basic operations in binary morphological image processing. The Opening operation is a cascade of erosion and dilation, which is denoted as $A\circ B$ and defined as $A\circ B=(A\ominus B)\oplus B$. While the Closing operation is a cascade of dilation and erosion, which is denoted as $A\bullet B$ and defined as $A\bullet B=(A\oplus B)\ominus B$. The specific quantum circuits are shown in Fig. 16.

Fig. 16

Quantum circuits of Opening and Closing modules

• 5. Login “AND” and logic “OR” modules

For two binary images of size $2^n\times 2^n$, $|I\rangle =\frac{1}{2^n}\sum \nolimits _{y=0}^{2^{n-1}}\sum \nolimits _{x=0}^{2^{n-1}}|c_{yx}\rangle |yx\rangle$, and $|\hat{I}\rangle =\frac{1}{2^n}\sum \nolimits _{\hat{y}=0}^{2^{n-1}}\sum \nolimits _{\hat{x}=0}^{2^{n-1}}|\hat{c}_{\hat{y}\hat{x}}\rangle |\hat{y}\hat{x}\rangle$, the quantum circuits implementing logical “AND” and “OR” are shown in Fig. 17.

Fig. 17

Quantum circuits of logic “AND” and logic “OR”

For the logical “AND” operation of two binary images, a $2^n\times 2^n$ empty image $|\tilde{I}\rangle =\frac{1}{2^n}\sum \nolimits _{\tilde{y}=0}^{2^{n-1}}\sum \nolimits _{\tilde{x}=0}^{2^{n-1}}|\tilde{c}_{\tilde{y}\tilde{x}}\rangle |\tilde{y}\tilde{x}\rangle$ is first generated by using 2n Hadamard gates. Then, two comparators are used to compare the pixel positions between the three images, $|I\rangle$, $|\hat{I}\rangle$ and $|\tilde{I}\rangle$. When the positions are the same, the Toffoli gate is used to implement the “AND” operations of $|c_{yx}\rangle$ and $|\hat{c}_{\hat{y}\hat{x}}\rangle$, and the results are stored in $|\tilde{c}_{\tilde{y}\tilde{x}}\rangle$. Finally, when the pixel positions of $|\hat{I}\rangle$ and $|\tilde{I}\rangle$ are the same, the values of $|\hat{c}_{\hat{y}\hat{x}}\rangle$ and $|\tilde{c}_{\tilde{y}\tilde{x}}\rangle$ are exchanged by the Swap module. At this time, $|\hat{I}\rangle$ is the result image of the logical “AND” operation of $|I\rangle$ and $|\hat{I}\rangle$.

According to the duality of logic “AND” and logic “OR” operation, the quantum circuit which performs logical “OR” operation between two binary images can be obtained by applying only three quantum NOT gates to the input and output ends of the logic “AND” module.

4.2 Quantum circuit of morphological algorithm for binary image

For binary image, this section introduces the design method of quantum circuits for three morphological processing algorithms, namely noise removal, boundary extraction and skeleton extraction. Without loss of generality, the structuring element of size $3\times 3$ is used in these methods.

4.2.1 Noise removal

The combination of opening and closing operations is a simple image denoising method. Let A denote a binary image and B denote a structuring element, and the denoising process generally performs an opening operation first and then performs a closing operation, which can be expressed as

$$\begin{aligned} \tilde{A}=(A\ominus B)\oplus B, \end{aligned}$$

(18)

where $\tilde{A}$ is the image after denoising.

The combination of opening and closing operations will affect the original boundary and shape of the target. Particularly, when the scale of the target itself is small, the denoising process can easily destroy the details of the boundary. Therefore, this method is not recommended for complex images. Quantum circuit for noise removal from binary image is shown in Fig. 18.

Fig. 18

Quantum circuits of noise removal from binary image

4.2.2 Boundary extraction

The erosion effect of structuring element B on set A is to shrink the target area. The difference set between set A and set $A\ominus B$ is the target boundary element removed by the erosion operation. These elements are just the boundary set of A. The process of boundary extraction can be expressed as

$$\begin{aligned} \beta (A)=A-(A\ominus B)=A\cap (A\ominus B)^c, \end{aligned}$$

(19)

where $\beta (A)$ represents the boundary set of A. The quantum circuit for boundary extraction from binary image is shown in Fig. 19.

Fig. 19

Quantum circuits of boundary extraction for binary image

In Fig. 19, $|I\rangle =\frac{1}{2^n}\sum \nolimits _{y=0}^{2^n-1}\sum \nolimits _{x=0}^{2^n-1}|c\rangle |yx\rangle$ is the input image. Firstly, a $2^n\times 2^n$ empty image $|I'\rangle =\frac{1}{2^n}\sum \nolimits _{y'=0}^{2^n-1}\sum \nolimits _{x'=0}^{2^n-1}|c'\rangle |y'x'\rangle$ is generated by using 2n Hadamard gates, and an image $|\hat{I}\rangle =\frac{1}{2^n}\sum \nolimits _{\hat{y}=0}^{2^n-1}\sum \nolimits _{\hat{x}=0}^{2^n-1}|\hat{c}\rangle |\hat{y}\hat{x}\rangle$ which is identical to the input image $|I\rangle$ is obtained by an Image Copy module. Then, an Erosion module and a quantum NOT-gate are applied on the input image $|I\rangle$ successively, and the complement of the $|I\rangle$’s eroded image is obtained. From Eq. (19), when the pixel positions of the three images, $|I\rangle$, $|\hat{I}\rangle$ and $|I'\rangle$ are the same, by employing $|c\rangle$ and $|\hat{c}\rangle$ as control qubits and $|c'\rangle$ as target qubit, the boundary of binary image $|I\rangle$ can be obtained by a Toffoli gate. At this point, the boundary image of $|I\rangle$ is stored in binary image $|I'\rangle$.

4.2.3 Skeleton extraction

Skeleton refers to the use of thin lines with a single pixel width to represent a target without changing its topological structure. Let A denote the target set and B denote the structuring element. A morphological skeleton calculation method is given in the following equation:

$$\begin{aligned} S(A)=\bigcup \limits _{k=0}^{K}S_k(A). \end{aligned}$$

(20)

The above equation shows that the skeleton S(A) of set A is the union of skeleton subset $S_k(A)$. The skeleton subset $S_k(A)$ is defined on the basis of the combination of erosion and opening operation, and its calculation formula is given by the following equation:

$$\begin{aligned} S_k(A)=(A\ominus kB)-(A\ominus kB)\circ B, k=0, 1, \ldots , K, \end{aligned}$$

(21)

where $A\ominus kB$ represents the continuous k-times erosion of structuring element B to set A, which can be expressed as

$$\begin{aligned} A\ominus kB=(A\ominus (k-1)B)\ominus B=(\cdots ((A\ominus B)\ominus )\ominus \cdots )\ominus B, \end{aligned}$$

(22)

where K is the calculation number of skeleton subsets, and its mathematical expression is

$$\begin{aligned} K=\max \{k|A\ominus kB\ne \emptyset \}. \end{aligned}$$

(23)

The above equation shows that K represents the maximum number of iterations before structuring element B erodes set A into an empty set. In other words, over K iterations, structuring element B erodes set A to an empty set.

The quantum circuit designed in this paper for skeleton extraction of binary image is shown in Fig. 20. The binary image $|I\rangle =\frac{1}{2^n}\sum \nolimits _{y=0}^{2^n-1}\sum \nolimits _{x=0}^{2^n-1}|c\rangle |yx\rangle$ is an input image, and the $|\hat{I}\rangle =\frac{1}{2^n}\sum \nolimits _{\hat{y}=0}^{2^n-1}\sum \nolimits _{\hat{x}=0}^{2^n-1}|\hat{c}\rangle |\hat{y}\hat{x}\rangle$ is a skeleton extraction result image, which is generated by some iterations, and its initial value is an empty image.

Fig. 20

Quantum circuits of skeleton extraction for binary image

From Eq. (21), when $k=0$, the skeleton subset $S_0=A-A\circ B=A\cap (A\circ B)^c$. The quantum circuit for skeleton subset $S_0$ is shown in the red dotted frame on the left side of Fig. 20c. The quantum circuit in the green dotted frame on the right side of Fig. 20c performs some continuous iteration. The number of iterations is determined by the pixel value qubit $|c\rangle$ of the input image $|I\rangle$. If there are 1-valued pixels in $|I\rangle$, the iteration will continue, otherwise the iteration will terminate. Each iteration produces a skeleton subset; for example, the k-th iteration produces the skeleton subset $S_k, k = 1, 2, \ldots ,K$, and the design method of the iterative circuit is shown in Fig. 20a and b.

4.3 Quantum circuit of morphological algorithm for grayscale image

4.3.1 Edge detection

In grayscale image morphological processing, edge detection algorithm is designed based on morphological gradient. Morphological gradient is defined as the difference between gray dilation image and gray erosion image, which can be expressed as

$$\begin{aligned} g=(f\oplus b)-(f\ominus b), \end{aligned}$$

(24)

where g represents the morphological gradient image, f represents the input image and b represents the structuring element.

The edge is between adjacent regions of different gray levels in the image, and image gradient is a measure to detect the change of local gray levels in the image. Grayscale dilation can expand the bright areas of the image, and grayscale erosion can shrink the bright areas of the image, and the difference between them highlights the edges in the image. As long as the size of the structuring element is appropriate, the uniform area will not be affected due to the offset of the subtraction operation. According to Eq. (24), the quantum circuit for grayscale image edge detection is shown in Fig. 21.

Fig. 21

Quantum circuits of edge detection for grayscale image

In this circuit, the Image Copy module is first used to generate an image $|\hat{I}\rangle$ identical to the input image $|I\rangle$, and then the Dilation and Erosion operations are performed on the $|I\rangle$ and $|\hat{I}\rangle$, respectively, and the morphological gradient is obtained using the Image Subtractor. Finally, the obtained image edge is stored in the image $|I\rangle$ by using the Swap module, and at this time, the input image becomes its own edge image.

4.3.2 Image enhancement

Grayscale image enhancement algorithm is designed with morphological top-hat and bottom-hat. The morphological top-hat and bottom-hat transformations are defined on the basis of grayscale opening and closing operations. The top-hat transformation of the structuring element b on the grayscale image f is defined as the difference between f and its grayscale opening operation $f\circ b$, which can be expressed as

$$\begin{aligned} h_{\mathrm{top}}=f-(f\circ b). \end{aligned}$$

(25)

The bottom-hat transformation of the structuring element b on the grayscale image f is defined as the difference between the grayscale closing operation $f\bullet b$ and f itself, which can be expressed as

$$\begin{aligned} h_{\mathrm{bot}}=(f\bullet b)-f. \end{aligned}$$

(26)

The top-hat transform retains the bright details in the image, while the bottom-hat transform retains the gray details in the image. Adding the top-hat to the original image while subtracting the bottom-hat can enhance the contrast of the original grayscale image. The quantum circuit for grayscale image enhancement is shown in Fig. 22.

Fig. 22

Quantum circuits of image enhancement for grayscale image

In Fig. 22, the circuit in the red dotted frame implements the top-hat transformation, and the circuit in the green dotted frame implements the bottom-hat transformation. The rightmost Image Adder and Image Subtractor implement the final enhancement.

4.3.3 Texture segmentation

The morphological texture segmentation of grayscale image mentioned in this paper is relatively simple. It is a kind of region segmentation, which is suitable for segmenting the region composed of different-size blobs. The quantum circuit is shown in Fig. 23.

Fig. 23

Quantum circuits of texture segmentation for grayscale image

In Fig. 23, the Image Copy module is first used to generate an image, $|\hat{I}\rangle$, identical to the input image $|I\rangle$, and then, on the image $|\hat{I}\rangle$, five operations of Dilation, Erosion, Erosion, Dilation and Morphological Gradient are performed successively. At this time, the image $|\hat{I}\rangle$ becomes the demarcation line of the two textures in the input image $|I\rangle$. Finally, an Image Adder is used to add this demarcation line to the input image $|I\rangle$, which can realize the segmentation of two texture regions in the input image.

5 Complexity analysis

5.1 Computational complexity of multibit-controlled-U gate

For ease of description, we begin by introducing some notation. For any single-qubit unitary operation U and $m\in \{0, 1, 2, \ldots \}$, define the $(m+1)$-bit ($2^{(m+1)}$-dimensional) gate $\wedge _m(U)$ as

$$\begin{aligned} \begin{array}{ll} &{}\wedge _m(U)(|x_1,\ldots ,x_m,y\rangle )\\ &{}\quad =\left\{ \begin{array}{ll}u_{y0}|x_1,\ldots ,x_m,0\rangle +u_{y1}|x_1,\ldots ,x_m,1\rangle &{} \quad \mathrm{if}\; \wedge _{k=1}^{m}x_k=1\\ |x_1,\ldots ,x_m,y\rangle &{}\quad \mathrm{if}\; \wedge _{k=1}^{m}x_k=0\end{array}\right. \end{array} \end{aligned}$$

for all $x_1,\ldots ,x_m,y\in \{0,1\}$. (In more ordinary language, $\wedge _{k=1}^{m}x_k$ denotes the AND of the Boolean variables $\{x_k\}$). Note that $\wedge _0(U)$ is equated with U [62].

Adriano Barenco [62] showed that a set of gates that consists of the $\wedge _0(U)$ gate and the $\wedge _1(U)$ gate (U is an arbitrary single-qubit unitary gate) is universal in the sense that all unitary operations on arbitrarily many qubits n can be expressed as compositions of these gates. In quantum computing, each reversible gate has a cost associated with it called quantum cost. For quantum implementation, the cost of $\wedge _1(U)$ gates far exceeds the cost of $\wedge _0(U)$ gates. Hence, the quantum cost of $\wedge _0(U)$ gates is usually ignored in the presence of $\wedge _1(U)$ implementations [63]. The quantum cost of all reversible $\wedge _1(U)$ gates is usually taken as unity, and so, the quantum cost of a quantum circuit is the number of $\wedge _1(U)$ gates required in designing it [64]. Next, we first give the complexity of $\wedge _2(U)$ and $\wedge _n(U)$. Let $V^2=U$. As can be seen from Ref. [62], the implementation of $\wedge _2(U)$ is shown in Fig. 24a. With $(n-2)$ auxiliary qubits $|0\rangle ^{\otimes (n-2)}$, the implementation of $\wedge _n(U) (n\ge 3)$ is shown in Fig. 24b. As can be seen from Fig. 23, the complexity of $\wedge _2(U)$ is O(5), and $\wedge _n(U)$ can be decomposed into $2(n-2)$ $\wedge _2(\sigma _x)$ and 1 $\wedge _2(U)$, here, $\sigma _x=\left( \begin{array}{lr}0~&{}~1\\ 1~&{}~0\end{array}\right)$. If $U=\sigma _x$, then $\wedge _n(\sigma _x)$ can be constructed from $(2n-3)$ $\wedge _2(\sigma _x)$. Hence, the complexity of $\wedge _n(U)$ is $O((2n-3)\times 5)=O(10n-15)$.

Fig. 24

(Figure adapted from [62])

Implementation of multiqubit-controlled-U gates

Next, we analyze the complexity of the quantum circuits designed in this paper. For ease of description, we first give the complexity of some basic modules, which are submodules for further design of complex circuits.

5.2 Complexity of some basic modules

• 1. Comparator and Copy modules

As can be seen from Fig. 3, the Comparator circuit consists of 4 $\wedge _2(\sigma _x)$, 4 $\wedge _4(\sigma _x)$, $\ldots$, 4 $\wedge _{2n}(\sigma _x)$. Since each $\wedge _{k}(\sigma _x)$ can be decomposed into $(2k-3)$ $\wedge _2(\sigma _x)$ and the complexity of the $\wedge _2(\sigma _x)$ is O(5), the complexity of the entire Comparator is $O(40n^2-20n)$. According to Fig. 4, the Copy module only includes n $\wedge _1(\sigma _x)$, and so, its complexity is O(n).

• 2. Modulo Plus 1 and Modulo Minus 1 modules

From Fig. 5, both modules are composed of $\wedge _0(\sigma _x)$, $\wedge _1(\sigma _x)$, $\ldots$, $\wedge _{n-1}(\sigma _x)$, and so, their complexity does not exceed $O(5n^2-20n+21)$.

• 3. Swap, Sort, and Min–Max Calculation modules

The Swap module consists of 3n $\wedge _1(\sigma _x)$, so its complexity is O(3n).

The Sort module is composed of Comparator and $\wedge _2(Swap)$. In fact, the $\wedge _2(Swap)$ is equivalent to 3n $\wedge _3(\sigma _x)$, and its complexity is O(45n). Hence, the complexity of Sort module is $O(40n^2+25n)$.

From Fig. 8, Min–Max Calculation modules consists of 36 Sort modules, each of which has a complexity of $O(40q^2+25q)$, so the complexity of the whole module is $O(1440q^2+900q)$.

• 4. Dilation and Erosion for binary images

The complexity of these two quantum circuits is the same. We only analyze the complexity of Dilation circuits. From Fig. 9, we can see that the module composition of the Dilation circuit is as shown in Eq. (27).

$$\begin{aligned} {\text {Dilation}}\; {\text {Circuit}}\Longleftrightarrow \left\{ \begin{array}{l}34~Comparators\\ 6\; Modulo\; Plus\; 1s\\ 6\; Modulo\; Minus\; 1s\\ 8\; \wedge _4(Copy)\Longleftrightarrow 8 \wedge _5(\sigma _x)\\ 9\; \wedge _2(\sigma _x)\\ 1\; \wedge _{45}(\sigma _x)\\ 1\; \wedge _{36}(Swap)\Longleftrightarrow 3 \wedge _{37}(\sigma _x).\end{array}\right. \end{aligned}$$

(27)

For binary images, the pixel values are described by only one qubit. Hence, 1 $\wedge _4(Copy)$ is equivalent to 1 $\wedge _5(\sigma _x)$, 1 $\wedge _{36}(Swap)$ is equivalent to 3 $\wedge _{37}(\sigma _x)$ and their complexity is O(35) and O(1065), respectively. The complexity of $\wedge _{45}(\sigma _x)$ is $((2\times 45-3)\times 5)=O(435)$. The complexity of the entire Dilation circuit is $O(34\times (40n^2-20n)+12\times (5n^2-20n+21)+8\times 35+9\times 5+435+1065)=O(1420n^2-920n+2077)$. By ignoring constant terms, the complexity is approximately $O(1420n^2-920n)$.

• 5. Dilation and Erosion for grayscale images

The complexity of these two quantum circuits is also the same. We only analyze the complexity of Dilation circuits. From Fig. 11, we can see that the module composition of the Dilation circuit is as shown in Eq. (28).

$$\begin{aligned} \begin{array}{l} {\text {Dilation}}\; {\text {circuit}}\Longleftrightarrow \\ \left\{ \begin{array}{l}32~ Comparators\\ 6\; Modulo\; Plus\; 1s\\ 6\; Modulo\; Minus\; 1s\\ 8\; \wedge _4(Copy)\Longleftrightarrow 8q \wedge _5(\sigma _x)\\ \begin{array}{lll}1\; \wedge _{32}(Min{-}Max~ Calculation)&{}\!\!\Longleftrightarrow \!\!&{}36 \wedge _{32}(Sort)\\ &{}\!\!\Longleftrightarrow \!\!&{}\left\{ \begin{array}{l}36\wedge _{32}(Comparator)\\ 36 \wedge _{34}(Swap)\!\!\Longleftrightarrow \!\!108q \wedge _{35}(\sigma _x)\end{array}\right. \end{array}\\ 1\; \wedge _{32}(Swap)\Longleftrightarrow 3q \wedge _{33}(\sigma _x).\end{array}\right. \end{array} \end{aligned}$$

(28)

For grayscale images, the pixel values are described by q qubits. Hence, 1 $\wedge _4(Copy)$ is equivalent to q $\wedge _5(\sigma _x)$, and 1 $\wedge _{32}(Swap)$ is equivalent to 3q $\wedge _{33}(\sigma _x)$. In addition, each $\wedge _{32}(Comparator)$ consists of $4 \wedge _{34}(\sigma _x), 4 \wedge _{36}(\sigma _x), \ldots , 4 \wedge _{2q+32}(\sigma _x)$, and so, its complexity is $O(40q^2+1260q)$. Hence, the complexity of the entire Dilation circuit is $O(32\times (40n^2-20n)+12\times (5n^2-20n+21)+8q\times 35+36\times (40q^2+1260q)+108q\times 335+3q\times 315)=O(1340n^2-880n+1440q^2+82765q+252)$. Considering that q is a constant independent of image size, the complexity is approximately equal to $O(1340n^2-880n)$.

• 6. Adder, Image Adder, Image Subtractor and Image Copy modules

From Fig. 13, the Adder consists of $(2n-1)$ Carry, n Sum and 1 $\wedge _1(\sigma _x)$. It is easy to know that the complexity of modules Carry and Sum is O(11) and O(2), respectively, and so, the complexity of Adder is $O(24n-1)$.

The Image Adder and the Image Subtractor have the same complexity. We only analyze the complexity of Image Adder circuits. From Fig. 14, we can see that the module composition of the Image Adder circuit is as shown in Eq. (29):

$$\begin{aligned} \begin{array}{l} \mathrm{Image}\; \mathrm{Adder}\; \mathrm{circuit}\Longleftrightarrow \\ \left\{ \begin{array}{l}2~ Comparators\\ 1\; \wedge _4(Adder)\Longleftrightarrow \left\{ \begin{array}{l}(2q-1)\wedge _4(Carry)\Longleftrightarrow \left\{ \begin{array}{l}(4q-2)\wedge _6(\sigma _x)\\ (2q-1)\wedge _5(\sigma _x)\end{array}\right. \\ q \;\wedge _{4}(Sum)\Longleftrightarrow 2q \wedge _{5}(\sigma _x)\\ 1\; \wedge _{5}(\sigma _x).\end{array}\right. \end{array}\right. \end{array} \end{aligned}$$

(29)

According to Eq. (29), the complexity of the Image Adder is $O(2(40n^2-20n)+(4q-2)((2\times 6-3)\times 5)+4q((2\times 5-3)\times 5))=O(80n^2-40n+320q-90)$.

From Fig. 15, the Image Copy module includes one Comparator and one $\wedge _2(Copy)$, and so, its complexity is equal to $O(40(2n)^2-20\times 2n+15q)=O(160n^2-40n+15q)$.

• 7. Opening and Closing modules

These two modules have the same complexity. We only analyze the complexity of Opening circuits. From Fig. 16a, the Opening operation is a cascade of Erosion and Dilation, and so, its complexity is no more than $O(2(1420n^2-920n+2077))=O(2840n^2-1840n+4154)$.

• 8. AND and OR modules

These two modules also have the same complexity. We only analyze the complexity of AND circuits. From Fig. 17a, the AND includes two Comparators, $1 \wedge _4(Toffoli)=1 \wedge _6(\sigma _x)$ and $1 \wedge _2(Swap)=3 \wedge _3(\sigma _x)$. Hence, the complexity of AND is $O(2(40*(2n)^2-20\times 2n)+(2\times 6-3)5+3(2\times 3-3)\times 5)=O(320n^2-80n+90)$.

5.3 Complexity of proposed morphological processing circuits

For the sake of simplicity, for the three binary image processing approaches, we only analyze the complexity of the skeleton extraction circuit, and for the three grayscale image processing approaches, we only analyze the complexity of the texture segmentation circuit.

The following discussions are based on a $(2^n\times 2^n)$-sized image with a total of $(2n+q)$ qubits, of which 2n qubits represent the position of the pixel and q qubit represents the grayscale value of the pixel, for binary images, $q = 1$.

5.3.1 Time complexity of skeleton extraction circuit

From Fig. 20, although this circuit is slightly complex, it contains Erosion, Image Copy, Opening, logic “AND,” logic “OR” modules. According to the complexity given in the previous introduction of each submodule, the complexity of skeleton extraction circuit is not more than $O((K+1)(1420n^2-920n+2077+160n^2-40n+15q+2840n^2-1840n+4154+2(320n^2-80n+90)))=O((K+1)(5060n^2-2960n+15q+6411))$. By ignoring constant terms, the complexity of skeleton extraction circuit is no more than $O((K+1)(5060n^2-2960n))$.

5.3.2 Time complexity of texture segmentation circuit

From Fig. 23, this circuit only contains five modules: Image Copy, Dilation, Erosion, Image Adder and Morphological Gradient. The complexity of the first four modules has been given before. The complexity of Morphological Gradient is discussed below. From Fig. 21, it consists of six modules: Image Copy, Dilation, Erosion, Image Subtractor, Comparator and $\wedge _2(Swap)$, and so, its complexity is $O(2960n^2-1860n+1440q^2+83145q+414)$. Finally, the complexity of texture segmentation circuit is $O((160n^2-40n+15q)+4(1340n^2-880n+1440q^2+82765q+252)$ $+(2960n^2-1860n+1440q^2+83145q+414)$ $+(80n^2-40n+320q-90))=O(8560n^2-5460n+7200q^2+166245q+1332)$. By ignoring constant terms, the complexity of texture segmentation circuit is no more than $O(8560n^2-5460n)$.

In summary, the time complexity of some basic modules and two morphological processing circuits is shown in Table 1, where $U=\sigma _x$.

Table 1 Time complexity of some basic modules and two morphological processing circuits

5.3.3 Comparison with the complexity of their classic counterparts

In summary, the computational complexity of the proposed schemes is only the second-order polynomial function of image size n. However, for the corresponding classic schemes, all morphological operations must be performed pixel by pixel, so the complexity must contain factor $2^{2n}$. In terms of this factor alone, the complexity of classical schemes is necessarily the exponential function of the image size n. Therefore, the proposed schemes can accelerate the classic counterparts, and the larger the image size n, the more obvious the acceleration effect.

5.3.4 Spatial complexity of proposed morphological processing circuits

The spatial complexity of quantum circuits mainly refers to the size of auxiliary qubits employed in the circuits. Firstly, the number of auxiliary qubits used by the basic modules is listed in Table 2, where “Au_qubits” denotes the “Auxiliary qubit.”

Table 2 Number of auxiliary qubits used by the basic modules

Table 2 shows that the number of auxiliary qubits in all basic modules is a linear function of image size n. Although $\wedge _n(\sigma _x)$ is widely used, it can be seen from Fig. 24b that all $(n-2)$ auxiliary qubits have been restored to their initial states at the output, so these auxiliary qubits can be reused. Therefore, the auxiliary qubits of six quantum circuits constructed by these basic modules for morphological processing must also be linear functions of image size n. That is, the spatial complexity of the quantum circuits designed in this paper is O(cn) by ignoring some constant terms, where the coefficient c is a constant.

6 Simulation on classical computer

Herein, we make several simulations of morphological processing methods on a classical computer due to the condition that the physical quantum computer is not in our grasp right now. The simulations are demonstrated with a classical computer with Intel(R) Core(TM) i5-3470 CPU @ 3.20 GHz, 4.00 GB RAM and 32-bit operating system. The realization of all quantum schemes in simulation is designed by linear algebra with complex vectors as quantum states and unitary matrices as unitary transforms with calculations performed using MATLAB 7.8.0(R2009a). All images used in the experiment are from following Web site: http://www.prenhall.com/gonzalezwoods.

6.1 Morphological processing of binary image

6.1.1 Noise removal

Figure 25a shows a binary image of a simple target with size $512\times 512$. There are isolated foreground noise in the background and holes in the target area. According to the shape and size of the target, the square structuring element with a size of $15\times 15$ and an origin at the center is selected as shown in Fig. 25b.

The opening operation is performed first, and then the closing operation is performed on the original image. Figure 25c is the result of opening operation, and Fig. 25d is the result of further closing operation in Fig. 25c. It can be seen from Fig. 25d that through this morphological denoising process, the isolated foreground noise is removed and the small holes in the target area are filled to obtain a clean binary image.

Fig. 25

Example of image denoising

6.1.2 Boundary extraction

Figure 26a is a binary image of a single target with a size of $512\times 512$, in which the white area represents the target and the black area represents the background.

This example uses a $(3\times 3)$-sized rhombic structuring element with an origin at the center shown in Fig. 26b to extract the eight-link boundary with a single pixel width for the target area of the original image. Figure 26c is the erosion image of the original image, and Fig. 26d is the extracted eight-link boundary with a single pixel width.

Fig. 26

Example of boundary extraction

6.1.3 Skeleton extraction

Figure 27a is a binary image of a maple leaf with a size of $256\times 256$ (denoted as set A). It has the characteristics of large target area and simple boundary. The skeleton of maple leaf image is extracted by using the rhombic structuring element with the center at the origin and the size of $3\times 3$ (denoted as set B) as shown in Fig. 27b. After 78 iterations, there are 5 1-value pixels in the set $(A\ominus 78B)$ and no 1-value pixel in the set $(A\ominus 79B)$ , so there are 79 skeleton subsets, which are $S_0, S_1, \ldots , S_{78}$, respectively. The number of 1-value pixels in the set $(A\ominus kB)$ varies with iteration step k as shown in Fig. 27c. The final extracted skeleton is shown in Fig. 27d.

Fig. 27

Example of morphological skeleton extraction

6.2 Morphological processing of grayscale image

6.2.1 Edge detection

Figure 28a is a grayscale image of size $1024\times 1024$, and Fig. 28b and c is the results of gray dilation and gray erosion of the image shown in Fig. 28a by using a $3\times 3$ square structuring element, respectively. The grayscale image shown in Fig. 28c is subtracted from the grayscale image shown in Fig. 28b, thereby producing a morphological gradient image as shown in Fig. 28d. As can be seen from Fig. 28d, the image edges are clearly represented as gradient images based on difference.

Fig. 28

Example of edge detection

6.2.2 Image enhancement

Figure 29a shows a $(512\times 512)$-sized grayscale image. In this example, the square structuring element of size $21\times 21$ is used to perform the opening operation, the closing operation, the top-cap transformation and the bottom-cap transformation on the image shown in Fig. 29a. The operation results are shown in Fig. 29b–e. The top-hat transform preserves the bright detail in the image, and the bottom-cap transform preserves the dark details in the image. In the original image, first add the top-hat transform and then subtract the bottom-cap transform; the resulting image is shown in Fig. 29f. Such processing enhances the contrast of the original image.

Fig. 29

Example of image enhancement

Fig. 30

Example of texture segmentation

6.2.3 Texture segmentation

Figure 30a shows a noisy image of dark blobs superimposed on a light background. The image has two textural regions: a region composed of large blobs on the right and a region on the left composed of smaller blobs. The objective is to find a boundary between the two regions based on their textural content.

If a closed operation is performed on the input image with a structuring element larger than the small blobs, these small blobs will be removed. The result in Fig. 30b, obtained by closing the input image using a square structuring element with a size of $55\times 55$, shows that indeed this is the case. (The radius of the blobs is approximately 25 pixels.) If we open this image in Fig. 30b using a structuring element that is large relative to the separation between these blobs, the net result should be an image in which the light patches between the blobs are removed, leaving the dark blobs and now equally dark patches between these blobs. Figure 30c shows the result obtained using a square structuring element with a size of $95\times 95$.

Performing a morphological gradient on this image with a $3\times 3$ structuring element of 1s will give us the boundary between the two regions as shown in Fig. 30d. Figure 30e shows the boundary obtained from the morphological gradient operation superimposed on the original image. All pixels to the left of this boundary are said to belong to the texture region characterized by large blobs, and conversely for the pixels on the left of the boundary.

7 Conclusions

The morphological concepts and techniques constitute a powerful set of tools for extracting features of interest in an image. One of the most appealing aspects of morphological image processing is the extensive set-theoretic foundation from which morphological techniques have evolved. A significant advantage in terms of implementation is the fact that dilation and erosion are primitive operations that are the basis for a broad class of morphological algorithm. Although various morphological algorithms are quite mature in classical image processing, the research on quantum version of them is just beginning. In this paper, we focus on several simple quantum versions of morphological processing operations and study their implementation methods based on quantum computing, including noise removal, edge extraction, skeleton extraction of binary images; and edge detection, image enhancement, texture segmentation of grayscale images. At the heart of these efforts is the design method of quantum circuits for the two basic morphological operations of dilation and erosion. The main contributions of this paper are as follows: Firstly, for binary image and grayscale image, the quantum circuits of dilation and erosion are designed, respectively; secondly, for binary image and grayscale image, three quantum versions of morphological methods are designed, respectively. Although these works are relatively simple, they can provide a valuable reference for the further development of quantum morphological image processing. The quantum implementation of more complex morphological processing methods, such as convex hulls, hole filling and connected component extraction, is the next issue we will continue to study in depth.