Entanglement property of the Werner state in accelerated frames

Abstract

We study the entanglement property of a free Dirac field in a Werner state as seen by two relatively accelerated parties. We study the concurrence, negativity, mutual information and $\pi$-tangle of the tripartite system. We show how these entanglement properties depend on both the free parameter F, which is a real parameter called fidelity, and the acceleration parameter r. The degree of entanglement is degraded by the Unruh effect, but we notice that the Werner state always remains entangled even in the acceleration limit, and thus, it can become a good candidate to quantum teleportation in uniform acceleration frame. We notice that the entropy $S(\rho _{A\, \mathrm{I}\, \mathrm{II}})$ decreases with the free parameter F, and also $S(\rho _{A\, \mathrm{I}\, \mathrm{II}})$, $S(\rho _{A})$ and $S(\rho _{\mathrm{I}\, \mathrm{II}})$ are independent of the acceleration parameter r. The von Neumann entropy is not a good entanglement measure any more for this mixed state. We verify that the Werner state in a noninertial frame obeys the Coffman–Kundu–Wootters (CKW) monogamous inequality and find that two useful relations for the concurrence and negativity.

1 Introduction

Over the past many years, stimulated from the original discoveries of Hawking radiation and the Unruh effect [1,2,3], a new field known as relativistic quantum information (RQI) which blends together concepts from gravitational physics and quantum computing has emerged. Its main aim is to understand the relationship between special and general relativity and quantum information. Such a combination has undergone significant revision in relativistic settings, and the new phenomena have been arisen [4,5,6,7,8,9,10]. For example, quantum teleportation fidelity can be affected between observers in uniform relative acceleration. The entanglement is an observer-dependent property that is degraded from the perspective of accelerated observers moving in flat spacetime. Up to now, the subject of RQI which pulls together concepts and ideas from special relativity, quantum optics, general relativity, quantum communication and quantum computation has attracted the attention of many authors [8, 11,12,13,14,15,16,17,18,19,20,21,22,23].

As we know, when an observer moves in uniform acceleration, he cannot access all information about the global spacetime. The appearance of the communication horizon will lead to the loss of information and a corresponding degradation of entanglement [24], which is called the Unruh effect. This will give us a quantitative understanding of such degradations in noninertial frames. It is known from the contributions mentioned above that the entanglement is observer dependent [5,6,7,8,9]. Among these contributions, the study by Alsing et al. analyzed the entanglement between two modes of a free Dirac field as seen by two relatively accelerated parties [11]. Wang et al. generalized Alsing’s study to three observers [13], which is revisited in our recent study [14]. After that, Smith and Mann first showed that tripartite nonlocality persists for fermionic systems in the infinite acceleration limit [15].

Generally speaking, it is assumed that Alice, Bob and Charlie initially share a Greenberger–Horne–Zeilinger (GHZ) state, which has the form $|{\mathrm{GHZ}}\rangle =(|000\rangle +|111\rangle )/\sqrt{2}$, and then, let Alice stay stationary, while Bob and Charlie move in a uniform acceleration. Except for the GHZ state, another popular study is concerned with the W-state, which has the explicit form $|\mathrm{W}\rangle =(|100\rangle +|010\rangle +|001\rangle )/\sqrt{3}$ and it is the special case of W-type state as studied by Weinstein [25]. It should be recognized that the pure GHZ and W-states are two different kinds of tripartite entangled states in quantum information. However, it should be pointed out that it is impossible to transform GHZ state into W-state, even with only a very small probability of success [12]. On the other hand, Qiang and his co-author have studied GHZ state in an accelerated frame and obtained some useful relations of entanglement [26]. Recently, we have studied the entanglement of the W-state and pseudo-pure state by using the concurrence measures [27,28,29], which is different from our present study since Werner state is a mixed state. We find that the W-state [27] is more complicated than GHZ state since its density matrix cannot be written as an X form, in which nonzero elements are arrayed in the diagonal or anti-diagonal when constructed in an orthonormal basis [30]. Particularly, we also noticed that the W-state is still entangled even in the infinite acceleration limit [27], which is unlike the GHZ state since the initially entangled GHZ state is not entangled any more in some acceleration r.

Recently, Moradi [31] has studied the Werner state [32], which is a mixed state of a Greenberger–Horne–Zeilinger (GHZ) state and the completely unpolarized state and involves a free parameter F, which determines the distillability of entanglement. Until now, precise quantitative knowledge on two-qubit Werner states has triggered important advances, e.g., regarding the relation between entanglement and nonlocality [32], entanglement purification, and noisy quantum channels [33], or mixed state entanglement under symmetries [34, 35]. Moradi studied its distillability of entanglement in accelerated frames only using a unique criterion whether there exists at least one negative eigenvalue of the partial transpose of density operator $\rho$, but such a study is simpler. His main motivation was to show how the states will change from distillable into separable for certain values of acceleration parameter r and free parameter F. Certainly, this aim can be achieved easily by this approach. Except for this criterion, in fact, some other crucial entanglement measures including the concurrence, negativity, mutual information and $\pi$-tangle can also be used to understand the entanglement property in accelerated frames. The different measures with its own advantages and disadvantages used to study the entangled system enable us to understand this state completely. Undoubtedly, these studies shall enrich and generalize the previous results [31]; and also they shall indicate how the degree of entanglement is affected by both the free parameter F and the acceleration parameter r from different measurement aspects. With the aid of the calculation skills used in our recent study about the W-state and pseudo-pure state as well as relevant concurrence [27,28,29], the purpose of this paper is focused on studying the entanglement properties of the Dirac field for the Werner state and their relevances with the parameters F and r. We attempt to see whether there also exist similar useful relations for the Werner state in accelerated frames as shown in [26].

The rest of this work is organized as follows. In Sect. 2, we present the concurrence and negativity of bipartite subsystems when the observer Bob is moving in a uniform acceleration. We calculate the threshold values of the free parameter F for both concurrence and negativity and also study their dependencies on the parameters F and r. We calculate the mutual information in Sect. 3 and show how it depends on the parameters F and r. In Sect. 4, we study the $\pi$-tangle of tripartite system in order to investigate the entanglement behavior of the global system. Some discussions are given in Sect. 5, and the conclusions are summarized in Sect. 6.

2 Concurrence and negativity of bipartite subsystem

As mentioned above, we are interested in how the acceleration parameter r of these observers except for the free parameter F will affect the degree of entanglement for bipartite and tripartite systems. Our setting consists of two observers: Alice and Bob. We first let Alice stay stationary, while Bob moves in uniform acceleration. Consider Bob to be accelerated uniformly in the (t, z) plane. Rindler coordinates $(\tau , \xi )$ are appropriate for describing the viewpoint of an observer moving in uniform acceleration. Two different sets of the Rindler coordinates, which differ from each other by an overall change in sign, are necessary for covering Minkowski space. These sets of coordinates define two Rindler regions that are disconnected from each other [11, 24]

$$\begin{aligned} t= & {} a^{-1}e^{a\xi }\sinh (a\tau ), ~z=a^{-1}e^{a\xi }\cosh (a\tau ), ~\text { Region I}\nonumber \\ t= & {} -a^{-1}e^{a\xi }\sinh (a\tau ), ~z=-a^{-1}e^{a\xi }\cosh (a\tau ), ~\text { Region II}. \end{aligned}$$

(1)

We denote the accelerating observer in regions I and II as Bob and anti-Bob, respectively, as shown in Fig. 1. A free Dirac field in $(3 + 1)$-dimensional Minkowski space satisfies the Dirac equation $i\gamma ^{\mu }\partial _{\mu }\psi -m\psi =0$. Here, m is the particle mass, $\gamma ^{\mu }$ are the Dirac gamma matrices, and $\psi$ is a spinor wave function, which is composed of the complete orthogonal set of fermion $\psi _{k}^{+}$, and antifermion $\psi _{k}^{-}$ modes and can be written as the following form

$$\begin{aligned} \psi =\int (a_{k}\psi _{k}^{+}+b_{k}^{\dagger }\psi _{k}^{-})\mathrm{d}k, \end{aligned}$$

(2)

where $a_{k}^{\dagger }(b_{k}^{\dagger })$ are the creation and annihilation operators for fermions (antifermions) of the momentum k, respectively. They satisfy the anticommutation relation $\{a_{i}, a_{j}^{\dagger }\}=\{b_{i}, b_{j}^{\dagger }\}=\delta _{ij}$. The quantum field theory for a Rindler observer can be constructed by expanding the spinor field in terms of a complete set of fermion and antifermion modes in regions I and II as

$$\begin{aligned} \psi =\int \sum _{\tau }(c_{k}^{\tau }\psi _{k}^{\tau +}+d_{k}^{\tau \dagger }\psi _{k}^{\tau -})\mathrm{d}k, ~~~~\tau \in \{\mathrm{I}, {\mathrm{II}}\}. \end{aligned}$$

(3)

Similarly, $c_{k}^{\tau \dagger }(d_{k}^{\tau \dagger })$ and $c_{k}^{\tau }(d_{k}^{\tau })$ are the creation and annihilation operators for fermion (antifermions), respectively, acting on region I (II) for $\tau ={\mathrm{I}}~({\mathrm{II}})$ and satisfying similar anticommutation relation as above. The relation between creation and annihilation operators in Minkowski and Rindler spacetimes can be found by using Bogoliubov transformation $a_{k}=\cos (r)\, c_{k}^{\mathrm{I}}-\sin (r)\, d_{-k}^{{\mathrm{II}}\dagger }, b_{k}=\cos (r)\, d_{k}^{\mathrm{I}}-\sin (r)\, c_{-k}^{{\mathrm{II}}\dagger }$, where $\cos (r)=1/\sqrt{1+e^{-2\pi \omega _{k} c/a}}$ with $\omega _{k}=\sqrt{|\mathbf{k}|^{\mathbf{2}}+\mathbf{m}^{\mathbf{2}}}$ and r is Bob’s acceleration parameter with the range $r\in [0, \pi /4]$ for $a\in [0, \infty )$. The detailed derivations can refer to Refs. [2, 11]. For example, Alsing et al. [11] have used single-mode approximation to show how the Unruh effect is arisen for Dirac particles through the Bogoliubov transformation and how the Bob’s states $|0_B\rangle$ and $|1_B\rangle$ are generated. Recently, Fuentes et al. discussed the Unruh effect beyond the single-mode approximation [2], in which two complex numbers $q_{R}$ and $q_{L}$ (the subindexes L and R corresponding to the left and right regions in Rindler diagram, i.e., regions I and II in Fig. 1) are used to construct the one-particle state, i.e., $|1\rangle =q_{R}|1_{R}0_{L}\rangle +q_{L}|0_{R}1_{L}\rangle$.

Fig. 1

(Color online) Rindler spacetime diagram: Lines of constant position $\xi$ are hyperbolas, and lines of constant proper time $\tau$ for the accelerated observer run through the origin. In the present work, we denote regions I and II as Bob and anti-Bob, respectively. The reader can refer to Ref. [24] for more information

In this work, we are only interested in the single-mode approximation for simplicity as previous study [11, 13, 15, 29]. That is to say, in our case one has $q_{R}=1, q_{L}=0$ to satisfy the normalization condition $|q_{R}|^2+|q_{L}|^2=1$. Using the single-mode approximation [11, 13, 15, 23, 27,28,29], Bob’s vacuum state $|0_B\rangle$ and one-particle state $|1_B\rangle$ in Minkowski space are transformed into Rindler space

$$\begin{aligned} \begin{aligned} |0_B\rangle =&\cos (r_b) |0_{B_{I}} 0_{B_{{II}}}\rangle +\sin (r_b) |1_{B_{I}} 1_{B_{{II}}}\rangle , \\ |1_B\rangle =&|1_{B_{I}} 0_{B_{{II}}}\rangle , \end{aligned} \end{aligned}$$

(4)

where $|n_{B_{I}}\rangle$ and $|n_{B_{{II}}}\rangle$ ($n=0, 1$) are the mode decomposition of $|n_B\rangle$ into two causally disconnected regions I and II in Rindler space. This implies that the vacuum state of a localized system defined by inertial observers is inequivalent to the vacuum state of a localized system undergoing uniform acceleration as seen by observers in accelerated frames (Rindler observers) as used in Refs. [9, 36, 37].

We assume that Alice and Bob share a bipartite state of Werner type [32] in inertial frames with the following form [31]

$$\begin{aligned} \rho _{AB}= & {} F |\Psi ^-\rangle \langle \Psi ^-|+\frac{1-F}{3}\left( |\Phi ^+\rangle \langle \Phi ^+|\right. \nonumber \\&+|\left. \Phi ^-\rangle \langle \Phi ^-|+|\Psi ^+\rangle \langle \Psi ^+|\right) , \end{aligned}$$

(5)

where $0\le F \le 1$ measures the overlap of the this state and the Bell state. In inertial system, for $0\le F\le 1/2$, the Werner state is unentangled, but entangled for $1/2<F\le 1$. Note that the Werner state has the simplest form $|\Psi ^{-}\rangle \langle \Psi ^{-}|$ for $F=1$, while it is the combination of other Bell states for $F=0$. The states $|\Phi ^{\pm }\rangle$ and $|\Psi ^{\pm }\rangle$ appeared in Eq. (5) are usual entangled Bell states

$$\begin{aligned} |\Phi ^{\pm }\rangle _{AB}= & {} \displaystyle \frac{1}{\sqrt{2}}(|0_{A}\rangle |0_{B}\rangle \pm |1_{A}\rangle |1_{B}), \end{aligned}$$

(6)

$$\begin{aligned} |\Psi ^{\pm }\rangle _{AB}= & {} \displaystyle \frac{1}{\sqrt{2}}(|0_{A}\rangle |1_{B}\rangle \pm |1_{A}\rangle |0_{B}), \end{aligned}$$

(7)

where $|0\rangle$ and $|1\rangle$ are the vacuum state and single-particle excitation state of the fermion mode, say k, in Minkowski space. All other modes of the field are in the vacuum state.

As what follows, we shall denote $|n_{B_{I}}\rangle (|n_{B_{{II}}}\rangle , \rho _{A\, B_I}, \rho _{A\, B_{II}}, \rho _{B_{I}\, B_{II}})$ as $|n_{I}\rangle (|n_{{II}}\rangle , \rho _{A\, I}, \rho _{A\, II}, \rho _{\mathrm{I}\, \mathrm{II}})$ for simplicity. Substituting $|\Phi ^{\pm }\rangle _{AB}$ and $|\Psi ^{\pm }\rangle _{AB}$ into Eq. (5), we obtain the density operator of the Werner state as follows

$$\begin{aligned} \rho _{A~{I}\, {II}}= & {} \frac{1}{3}(1-F)[\cos ^2(r)|0_{{I}}, 0_{{II}}, 0_A\rangle \langle 0_{{I}}, 0_{{II}}, 0_A|\nonumber \\&+\sin ^2(r)|1_{{I}}, 1_{{II}}, 0_A\rangle \langle 1_{{I}}, 1_{{II}}, 0_A|\nonumber \\&+\sin (r)\cos (r)(|1_{{I}}, 1_{{II}}, 0_A\rangle \langle 0_{{I}}, 0_{{II}}, 0_A| +|0_{{I}}, 0_{{II}}, 0_A\rangle \langle 1_{{I}}, 1_{{II}}, 0_A|)\nonumber \\&+ |1_{{I}}, 0_{{II}}, 1_A\rangle \langle 1_{{I}}, 0_{{II}}, 1_A|]\nonumber \\&+\frac{1}{6}(2 F+1)[\cos ^2(r)|0_{{I}}, 0_{{II}}, 1_A\rangle \langle 0_{{I}}, 0_{{II}}, 1_A| \nonumber \\&+\sin ^2(r)|1_{{I}}, 1_{{II}}, 1_A\rangle \langle 1_{{I}}, 1_{{II}}, 1_A|\nonumber \\&+\cos (r)\sin (r)(|1_{{I}}, 1_{{II}}, 1_A\rangle \langle 0_{{I}}, 0_{{II}}, 1_A| +|0_{{I}}, 0_{{II}}, 1_A\rangle \langle 1_{{I}}, 1_{{II}}, 1_A|)\nonumber \\&+|1_{{I}}, 0_{{II}}, 0_A\rangle \langle 1_{{I}}, 0_{{II}}, 0_A|]\nonumber \\&+\frac{1}{6}(1-4 F)[\cos (r)(|1_{{I}}, 0_{{II}}, 0_A\rangle \langle 0_{{I}}, 0_{{II}}, 1_A|\nonumber \\&+|0_{{I}}, 0_{{II}}, 1_A\rangle \langle 1_{{I}}, 0_{{II}}, 0_A|)\nonumber \\&+\sin (r)(|1_{{I}}, 1_{{II}}, 1_A\rangle \langle 1_{{I}}, 0_{{II}}, 0_A| +|1_{{I}}, 0_{{II}}, 0_A\rangle \langle 1_{{I}}, 1_{{II}}, 1_A|)]. \end{aligned}$$

(8)

In order to study the entanglement properties of bipartite systems, let us take the trace over the modes II, I and A, respectively, and obtain their density operators $\rho _{A\, {I}}, \rho _{A\, {II}}$ and $\rho _{{I}\, {II}}$ as follows:

$$\begin{aligned} \rho _{A\, {I}}= & {} \frac{1}{6}\{2(1-F)\cos ^2(r)|0_{{I}}, 0_A\rangle \langle 0_{{I}}, 0_A|\nonumber \\&+(2 F+1)\cos ^2(r)(|0_{{I}}, 1_A\rangle \langle 0_{{I}}, 1_A| \nonumber \\&+(1-4 F)\cos (r)(|1_{I}, 0_A \rangle \langle 0_{I}, 1_A|+|0_{I}, 1_A\rangle \langle 1_{I}, 0_A|) \nonumber \\&+[2 (1-F) \sin ^2(r)+(2 F+1)]|1_{{I}}, 0_A\rangle \langle 1_{{I}}, 0_A|\nonumber \\&+[(2 F+1) \sin ^2(r)+2 (1-F)]|1_{{I}}, 1_A\rangle \langle 1_{{I}}, 1_A|\}. \end{aligned}$$

(9)

$$\begin{aligned} \rho _{A\, {II}}= & {} \frac{1}{6}\{[2 (1-F) \cos ^2(r)+2 F+1]|0_{{II}}, 0_A\rangle \langle 0_{{II}}, 0_A|\nonumber \\&+(1-4 F)\sin (r)(|1_{{II}}, 1_A\rangle \langle 0_{{II}}, 0_A|\nonumber \\&+|0_{{II}}, 0_A\rangle \langle 1_{{II}}, 1_A|) \nonumber \\&+[(2 F+1) \cos ^2(r)+2 (1-F)]|0_{{II}}, 1_A\rangle \langle 0_{{II}}, 1_A|\nonumber \\&+2(1-F)\sin ^2(r)|1_{{II}}, 0_A\rangle \langle 1_{{II}}, 0_A|\nonumber \\&+(2 F+1)\sin ^2(r)|1_{{II}}, 1_A\rangle \langle 1_{{II}}, 1_A|\}. \end{aligned}$$

(10)

$$\begin{aligned} \rho _{{I}\, {II}}= & {} \frac{1}{2}[\cos ^2(r)|0_{{I}}, 0_{{II}}\rangle \langle 0_{{I}}, 0_{{II}}|+\sin ^2(r)|1_{{I}}, 1_{{II}}\rangle \langle 1_{{I}}, 1_{{II}}|\nonumber \\&+\cos (r)\sin (r)(|1_{{I}}, 1_{{II}}\rangle \langle 0_{{I}}, 0_{{II}}|\nonumber \\&+|0_{{I}}, 0_{{II}}\rangle \langle 1_{{I}}, 1_{{II}}|)+|1_{{I}}, 0_{{II}}\rangle \langle 1_{{I}}, 0_{{II}}|]. \end{aligned}$$

(11)

All of these density matrices have an X form,

$$\begin{aligned} \rho _x=\left( \begin{array}{cccc} a &{}\quad 0 &{}\quad 0 &{}\quad \omega \\ 0 &{}\quad b &{}\quad z &{}\quad 0 \\ 0 &{}\quad z^* &{}\quad c &{}\quad 0 \\ \omega ^* &{}\quad 0 &{}\quad 0 &{}\quad d \\ \end{array} \right) , \end{aligned}$$

(12)

from which we are able to calculate the concurrence in the following way [38, 39]

$$\begin{aligned} C(\rho _x)=2 \max [0, |z|-\sqrt{ad}, |\omega |-\sqrt{bc}]. \end{aligned}$$

(13)

Comparing the matrix forms of Eqs. (9), (10), (11) with Eq. (12), according to Eq. (13) we can easily obtain

$$\begin{aligned} C(\rho _{A\, {I}})= & {} \max [0, \frac{1}{3} \cos (r)(| 1-4 F|\nonumber \\&-\sqrt{2 (1-F)(3-(2 F+1) \cos ^2(r))}], \end{aligned}$$

(14)

$$\begin{aligned} C(\rho _{A\, {II}})= & {} \max [0, \frac{1}{3} \sin (r)(| 1-4 F|\nonumber \\&-\sqrt{2 (1-F)(3-(2 F+1) \sin ^2(r))})], \end{aligned}$$

(15)

$$\begin{aligned} C(\rho _{{I}\, {II}})= & {} \sin (r) \cos (r). \end{aligned}$$

(16)

We notice that replacing $\cos (r)$ by $\sin (r)$ in Eq. (14) allows us to obtain $C(\rho _{A\, {II}})$, and vice versa. On the other hand, we find that $C(\rho _{{I}~ {II}})$ only depends on the acceleration parameter r regardless of the free parameter F. We plot $C(\rho _{A\, {I}})$ and $C(\rho _{A\, {II}})$ as a function of the acceleration parameter r for various F in Figs. 2 and 3, respectively. We also plot the corresponding $C(\rho _{{I}\, {II}})$ in Fig. 4. It is shown that $C(\rho _{A\, {II}})$ and $C(\rho _{{I}\, {II}})$ increase with the acceleration parameter r, but $C(\rho _{A\, {I}})$ decreases with the increasing r. Moreover, both $C(\rho _{A\, {I}})$ and $C(\rho _{A\, {II}})$ increase with the free parameter F.

Fig. 2

(Color online) Plots of concurrence $C(\rho _{A\, {I}})$ as a function of the acceleration parameter r for $F=0.500$ (black), $F=0.625$ (dotted and blue), $F=0.750$ (dashed and purple), $F=0.875$ (dot-dashed and black), $F=1. 000$ (red)

Fig. 3

(Color online) Plots of concurrence $C(\rho _{A\, {II}})$ as a function of the acceleration parameter r for $F=0.500$ (black), $F=0.625$ (dotted and blue), $F=0.750$ (dashed and purple), $F=0.875$ (dot-dashed and black), $F=1. 000$ (red)

Fig. 4

(Color online) Plots of concurrence $C(\rho _{{I}\, {II}})$ (red) as a function of the acceleration parameter r

Apart from the concurrence, negativity as another important entanglement measure introduced by Vidal and Werner [40] can be calculated by the formula [41, 42] $N=\Vert \rho ^{T_A}_{AB}\Vert -1$, where $\Vert A\Vert =\text{ tr }(\sqrt{AA^\dag })$ is the trace norm of a matrix A, i.e., the sum of the singular values of A [43]. Alternatively, $\Vert A\Vert -1$ is equal to two times of the sum of absolute values of negative eigenvalues of A. For an X-type matrix (12), we are able to obtain the explicit negativities as follows:

$$\begin{aligned} N(\rho _x)= & {} \max \Big [0, \sqrt{(a-d)^2+4 | z|^2}-(a+d)\Big ] \nonumber \\&+ \max \Big [0, \sqrt{(b-c)^2+4 |\omega |^2}-(b+c)\Big ]. \end{aligned}$$

(17)

$$\begin{aligned} N(\rho _{A\, {I}})= & {} \max \Big [0, \frac{1}{6}\left( \sqrt{4 (1-4 F)^2 \cos ^2(r)+9 \sin ^4(r)}\right. \nonumber \\&\left. -(1-4 F) \cos ^2(r)-3\right) \Big ], \end{aligned}$$

(18)

$$\begin{aligned} N(\rho _{A\, {II}})= & {} \max \Big [0, \frac{1}{6}(\sqrt{4 (1-4 F)^2\sin ^2(r)+9 \cos ^4(r)} \nonumber \\&-(1-4 F) \sin ^2(r)-3)\Big ], \end{aligned}$$

(19)

$$\begin{aligned} N(\rho _{{I}\, {II}})= & {} \frac{1}{2}\left( \sqrt{\sin ^2(2 r)+1}-1\right) . \end{aligned}$$

(20)

Similar to the concurrence, by replacing $\cos (r)$ by $\sin (r)$ in Eq. (18), we get Eq. (19), and vice versa. We note that $N(\rho _{{I}\, {II}})$ only depends on the acceleration parameter r as the concurrence $C(\rho _{{I}\, {II}})$. After studying, we find that the negativities $N(\rho _{A\, {I}}), N(\rho _{A\, {II}})$ and $N(\rho _{{I}\, {II}})$ have similar behaviors to the concurrences $C(\rho _{A\, {I}}), C(\rho _{A\, {II}})$ and $C(\rho _{{I}\, {II}})$ with respect to the acceleration parameter r and the free parameter F. Therefore, we do not illustrate them for simplicity. In particular, we find that the negativity $N(\rho _{A\, I})$ asymptotically reaches a threshold value $R(r)=(\cos (2 r)-4)/(\cos (2 r)-7)=0.571429$ of the F in the acceleration limit $r=\pi /4$. This means that the Werner state always remains entangled even in the infinite acceleration limit. This could become a good candidate in quantum information tasks, such as teleportation, between parties in relative uniform acceleration.

3 Mutual information

We are now in the position to calculate the mutual information, which includes the information interaction $I_{0}$, the total information $I_{T}$ and dual information $I_{D}$. All these calculations which depend on the entanglement entropy $S(\rho )=-\sum _{i=1}^{4}\lambda _{i}\log _{2}\lambda _{i}$ are defined, respectively, as

$$\begin{aligned} I_{0}= & {} S(\rho _{A})+S(\rho _{I})+S(\rho _{II})\nonumber \\&-S(\rho _{A\, I})-S(\rho _{A\, II})-S(\rho _{\mathrm{I}\, \mathrm{II}})+S(\rho _{A\, \mathrm{I}\, \mathrm{II}}, \rho _{I}), \nonumber \\ I_{T}= & {} S(\rho _{A})+S(\rho _{I})+S(\rho _{II})-S(\rho _{A\, \mathrm{I}\, \mathrm{II}}), \nonumber \\ I_{D}= & {} S(\rho _{A\, I})+S(\rho _{A\, II})+S(\rho _{\mathrm{I}\, \mathrm{II}})-2S(\rho _{A\, \mathrm{I}\, \mathrm{II}}). \end{aligned}$$

(21)

As we know, the von Neumann entropy which can be regarded as an entanglement measure is only for pure state. For a mixed state, it is not a good entanglement measure any more. For the present problem, it is necessary to consider the mutual information. To calculate them, we have to calculate corresponding eigenvalues of the densities $\rho _{A}$, $\rho _{I}$, $\rho _{II}$, $\rho _{A\,I}$, $\rho _{A\,II}$, $\rho _{\mathrm{I\,II}}$, $\rho _{A\,\mathrm{I\,II}}$. For the case $\rho _{A}$, we have $\lambda _{A}^{1}=\lambda _{A}^{2}=1/2$. Its entropy $S(\rho _{A})=1$; for density matrix $\rho _{I}$, we have $\lambda _{I}^{1}=\cos ^2(r_b)/2, \lambda _{I}^{2}=(1+\sin ^2(r_b))/2$; for $\rho _{II}$, two eigenvalues can be obtained easily by interchanging $\cos (r_b)\leftrightarrow \sin (r_b)$. For the density matrix $\rho _{A\, I}$, however, their eigenvalues are given by

$$\begin{aligned} \lambda _{A\, I}^{1}= & {} -\frac{1}{3} (F-1) \cos ^2(r), ~\lambda _{A\, I}^{2}=\frac{1}{12} \left( -\tau +\alpha \right) , \nonumber \\ \lambda _{A\, I}^{3}= & {} \frac{1}{12} \left( \tau +\alpha \right) , ~\lambda _{A\, I}^{4}=\frac{1}{6} \left[ (2 F+1) \sin ^2(r)-2 F+2\right] , \end{aligned}$$

(22)

where

$$\begin{aligned} \tau= & {} \Big [-4 (1-4 F)^2 \sin ^2(r)+4 (1-4 F)^2+9 \sin ^4(r)\Big ]^{1/2}, \nonumber \\ \alpha= & {} (1-4 F) \sin ^2(r)+4 F+2. \end{aligned}$$

(23)

Based on the eigenvalues given in Eq. (22), we have

$$\begin{aligned} S(\rho _{A\, I})= & {} -\displaystyle \frac{1}{48 \ln (2)}\left\{ (\alpha -\tau ) \ln \left( \frac{\alpha -\tau }{48}\right) \right. \nonumber \\&+\displaystyle (\alpha +\tau ) \ln \left[ \frac{\alpha +\tau }{48}\right] -16 (F-1)\nonumber \\&\times \cos ^2(r) \ln \left[ -\frac{1}{3} (F-1) \cos ^2(r)\right] \nonumber \\&+8 \left[ (2 F+1) \sin ^2(r)-2 F+2\right] \nonumber \\&\left. \times \ln \left[ \frac{1}{6} \left( (2 F+1) \sin ^2(r)-2 F+2\right) \right] \right\} . \end{aligned}$$

(24)

It is shown in Fig. 5 that $S(\rho _{A\, I})$ first increases with the free parameter F and then decreases with it, but $S(\rho _{A\, I})$ increases with the acceleration parameter r.

As far as the case $\rho _{A\, II}$ is considered, the eigenvalues are calculated as

$$\begin{aligned} \begin{aligned} \lambda _{A\, II}^{1}=&-\frac{1}{3} (F-1) \sin ^2(r), ~\lambda _{A\, II}^{2}=\lambda _{A\, I}^{2}, \\ \lambda _{A\, II}^{3}=&\lambda _{A\, I}^{3}, ~\lambda _{A\, II}^{4}=\frac{1}{6} \left[ (2 F+1) \cos ^2(r)-2 F+2\right] . \end{aligned} \end{aligned}$$

(25)

We find that $\lambda _{A\, II}^{1}$ and $\lambda _{A\, II}^{4}$ can be obtained easily through replacing $\cos (r)$ in Eq. (22) by $\sin (r)$, and vice versa. With the same process of calculation as $S(\rho _{A\, I})$, we find that the $S(\rho _{A\, II})$ can be obtained from $S(\rho _{A\, I})$ through substituting $\cos (r)$ and $\sin (r)$ in $S(\rho _{A\, I})$ by $\sin (r)$ and $\cos (r)$, respectively. We plot $S(\rho _{A\, II})$ in Fig. 6 and find that $S(\rho _{A\, II})$ first increases with F and then decreases with it, but $S(\rho _{A\, II})$ does not always increase with the acceleration parameter r and depends on the interval of free parameter F. It is interesting to see that the $S(\rho _{A\, II})$ first increases with the parameter r and then decreases with it when the free parameter F arrives at the critical value $F=1$.

Now, we consider the case $\rho _{\mathrm{I}\, \mathrm{II}}$. In this case, the eigenvalues are given by $\lambda _{\mathrm{I}\, \mathrm{II}}^{1}=\lambda _{\mathrm{I}\, \mathrm{II}}^{2}=1/2$ and $\lambda _{\mathrm{I}\, \mathrm{II}}^{3}=\lambda _{\mathrm{I}\, \mathrm{II}}^{4}=0$, so its entropy $S(\rho _{\mathrm{I}\, \mathrm{II}})=1$. Hence, we have $S(\rho _{\mathrm{I}\, \mathrm{II}})=S(\rho _{A})=1$. Finally, let us study the entropy $S (\rho _{A\, \mathrm{I}\, \mathrm{II}})$ for tripartite case. The eigenvalues of the density $\rho _{A\,\mathrm{I\,II}}$ are given by $\lambda _{A\, \mathrm{I}\, \mathrm{II}}^{1, 2, 3}=(1-F)/3$ and $\lambda _{A\, \mathrm{I}\, \mathrm{II}}^{4}=F$. It is found that $S (\rho _{A\, \mathrm{I}\, \mathrm{II}})=(F-1) \log ((1-F)/3)-F \log (F)/\log (2)$, which is independent of the parameter r. The $S(\rho _{A\, \mathrm{I}\, \mathrm{II}})$ decreases with F as shown in Fig. 7.

Fig. 5

(Color online) Plot of entanglement entropy $S(\rho _{A\, I})$ as the functions of the free parameter F and the acceleration parameter r

Fig. 6

(Color online) Plot of entanglement entropy $S(\rho _{A\, II})$ as the functions of the free parameter F and the acceleration parameter r

Fig. 7

(Color online) Plot of $S(\rho _{A\, \mathrm{I}\, \mathrm{II}})$ as function of free parameter F

Fig. 8

(Color online) Plot of information interaction $I_{0}(\rho _{A\, \mathrm{I}\, \mathrm{II}})$ (in color yellow), total information $I_{T}$ (in color blue) and dual information $I_{D}$ (in color green) as the functions of the free parameter F and the acceleration parameter r

Fig. 9

(Color online) Plot of information interaction $I_{0}(\rho _{A\, \mathrm{I}\, \mathrm{II}})$ as the functions of the free parameter F and the acceleration parameter r

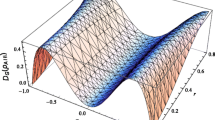
To illustrate the mutual information with respect to the parameters F and r, we show it in Figs. 8 and 9. It is found that the difference between $I_{T}$ and $I_{D}$ is almost zero. We note that the total information $I_{T}$ and dual information $I_{D}$ first decrease with the fidelity parameter F and then increase with it. They increase with the acceleration parameter r. However, the information interaction $I_{0}$ which is very small first increases with the fidelity $F\ge 1/2$ and the acceleration parameter r and then decreases with them.

4 $\pi$-tangle of three qubit system

In this section, we are going to investigate the entanglement property of the total system. Before starting, we notice that the negativity $N=0$ used in Section 2 becomes a unique necessary and sufficient condition to see whether the qubit–qubit ($\mathbf {2}\times \mathbf {2}$) or qubit-qutrit ($\mathbf {2}\times \mathbf {3}$) entangled system is separable or not.

When the dimensions of a quantum system in the Hilbert space exceed six, however, this condition becomes necessary but not sufficient [42, 44, 45]. To measure the degree of entanglement of the total system $\rho _{A\, {I}\, {II}}$, let us study the $\pi$-tangle [41]

$$\begin{aligned} \pi =\frac{\pi _A+\pi _B+\pi _C}{3}, \end{aligned}$$

(26)

where

$$\begin{aligned} \begin{aligned} \pi _A =&N_{A(BC)}^2- N_{AB}^2-N_{AC}^2, \\ \pi _B =&N_{B(AC)}^2- N_{BA}^2-N_{BC}^2, \\ \pi _C =&N_{C(AB)}^2- N_{CA}^2-N_{CB}^2 \end{aligned} \end{aligned}$$

(27)

with $N_{AB}=\Vert \rho _{AB}^{T_A}\Vert -1$ is $1-1$-tangle and $N_{A(BC)}=\Vert \rho _{A(BC)}^{T_A}\Vert -1$ is $1-2$-tangle. These definitions and Eqs. (9), (10), (11) enable us to easily calculate $N_{A({I}\, {II})}, N_{{I}(A\, {II})}$ and $N_{{II}(A\, {I})}$. After calculation, we find that

$$\begin{aligned} N_{A({I}\, {II})}=\Vert \rho ^{T_A}_{A({I}\, {II})}\Vert -1=\text{ max }[2 F-1, 0]. \end{aligned}$$

(28)

Similarly, we can also calculate $N_{{I}(A\, {II})}=\Vert \rho ^{T_{I}}_{{I}(A\, {II})}\Vert -1$ and $N_{{II}(A\, {I})}=\Vert \rho ^{T_{{II}}}_{{II}(A\, {I})}\Vert -1$, but the results are too complicated and we write them out in Appendix A. Based on the results $N(\rho _{A\, {I}}), N(\rho _{A{{II}}})$ and $N(\rho _{{I}~{{II}}})$ given above, it is not difficult to find $N_{A\, {I}}=N_{{I}A}=N(\rho _{A\, {I}})$, $N_{A\, {II}}=N_{{II}A}=N(\rho _{A\, {II}})$ and $N_{{I}\, {II}}=N_{{II}~{I}}=N(\rho _{{I}\, {II}})$. By substituting all $1-1$ tangles and $1-2$ tangles into Eq. (27) and considering Eq. (26), we can obtain $\pi (\rho _{\mathrm{A}(\mathrm{I}\, {\mathrm{II}})})$, $\pi (\rho _{\mathrm{I}(\mathrm{A}\, {\mathrm{II}})})$ and $\pi (\rho _{{\mathrm{II}}(\mathrm{A}\, \mathrm{I})})$-tangles directly. We plot the $\pi (\rho _{\mathrm{I}(\mathrm{A}\, \mathrm{I})})$ and $\pi (\rho _{{\mathrm{II}}(\mathrm{A}\, \mathrm{I})})$-tangles as a function of the acceleration parameter r for various values of the free parameter F in panels (a) and (b) of Fig. 10. We find that they increase with the increasing r and the free parameter F. The $\pi (\rho _{\mathrm{A}(\mathrm{I}\, {\mathrm{II}})})$-tangle has the similar variation to them and is not illustrated here for simplicity. The algebraic average $\pi$-tangle is displayed in Fig. 11.

Fig. 10

(Color online) Plot of $\pi (\rho _{\mathrm{I}(\mathrm{A}\, {\mathrm{II}})})$ and $\pi (\rho _{{\mathrm{II}}(\mathrm{A}\, \mathrm{I})})$-tangles as function of r for $F=0.500$ (black), $F=0.625$ (dotted and blue), $F=0.750$ (dashed and purple), $F=0.875$ (dot-dashed and black), $F=1. 000$ (red)

Fig. 11

(Color online) Plot of $\pi$-tangle as function of r. The parameter value of F is chosen as above

5 Discussions

After obtaining the expressions of concurrence, negativity, mutual information and calculating the $\pi$-tangle, let us discuss the whole properties of this Werner state in accelerated frame.

• 1. For the general case $1/2< F < 1$ and $0\le r \le \pi /4$. According to Eqs. (14), (18), we get the threshold value of the free parameter F for $C(\rho _{A\, {I}})$ and $N(\rho _{A\, {I}})$ as $R(r)=[2 \sin ^2(r)+3]/2[\sin ^2(r)+3]$, which is the same as that of Ref. [31]. Similarly, $C(\rho _{A\, {II}})$ and $N(\rho _{A\, {II}})$ also have a threshold value of the F as $S(r)=[5-2\sin ^2(r)]/2[4-\sin ^2(r)]$, which is also same as that given in [31], but $R(r)\ne S(r)$. We plot R(r) and S(r) as a function of the acceleration parameter r in Fig. 12. It is shown that R(r) increases from 0.5 when r increases, but S(r) decreases from $5/8=0.625$. Finally, they all tend to the same value $4/7\approx 0.5714$ in the acceleration limit $r=\pi /4$. How to interpret? Since an accelerated observer Bob in the Rindler region I has no access to the anti-Bob in the causally disconnected region II, then threshold value R(r) of subsystem ${A\, {I}}$ and that S(r) of subsystem ${A\, {II}}$ must tend to the same critical value 0.5714 in the infinite acceleration limit because they must be continuous at the boundary condition. Also, we might explain it in another way. As addressed as follows (see point 2), we notice that $C(\rho _{A\, I})=C(\rho _{A\, II})$ and negativity $N(\rho _{A\, I})=N(\rho _{A\, II})$ in this limit and both of them are equal to 0.5714. But this does not mean that both subsystem $\rho _{A\, {I}}$ and subsystem $\rho _{A\, {II}}$ generally are in the same entangled state.

  Now, let us give some useful remarks on these results. First, the concurrence $C(\rho _{A\, {I}})$, the negativity $N(\rho _{A\, {I}})$ and the negative eigenvalues of the partial transpose of the density operator $\rho _{A\, {I}}$ have the same threshold value R(r) of F; the $C(\rho _{A\, {II}}), N(\rho _{A\, {II}})$ and the negative eigenvalues of the partial transpose of the density operator $\rho _{A\, {II}}$ have the same threshold value S(r) of F. This means that any of these quantities for a qubit–qubit system can be used to judge the degree of entanglement. Second, we find that $R(r)\le S(r)$ is valid for any acceleration parameter r. Third, subsystem $\rho _{{I}\, {II}}$ is always entangled except for $r=0$. This means that the Werner state always remains entangled even in the infinite acceleration limit. Fourth, there are three different cases for the subsystem $\rho _{A\, {I}}$ and $\rho _{A\, {II}}$. When $F\le R(r)$, they are all separable; while $R(r)< F\le S(r)$, the subsystem $\rho _{A\, {I}}$ is entangled, but $\rho _{A\, {II}}$ is separable; they are both entangled for $F>S(r)$. We list $C(\rho _{A\, {I}}), C(\rho _{A\, {II}}), N(\rho _{A\, {I}})$ and $N(\rho _{A\, {II}})$ for some typical values of the acceleration parameter r and the free parameter F in Table 1.

• 2. When $r=0$ and $F>R(0)=1/2$, we have $C(\rho _{A\, {I}})=N(\rho _{A\, {I}})=2 F-1$ and find that they are nothing but those in inertial frame. This means that the values of concurrence and negativity of the Werner state in inertial frame are equal to each other even though they are different in noninertial frame. On the other hand, generally, one has $\rho _{A\, {I}}\ne \rho _{A\, {II}}, C(\rho _{A\, {I}})\ne C(\rho _{A\, {II}})$ and $N(\rho _{A\, {I}})\ne N(\rho _{A\, {II}})$, but in the infinite acceleration limit $r=\pi /4$, we find that $C(\rho _{A\, {I}})=C(\rho _{A\, {II}})=(4 F-1-\sqrt{(1-F) (5-2 F)})/(3 \sqrt{2})$ and $N(\rho _{A\, {I}})=N(\rho _{A\, {II}})=F-7+\sqrt{64 F (2 F-1)+17})/12$, both for $F>S(\pi /4)\approx 0.5714$. This implies that bipartite subsystems $\rho _{A\, {I}}$ and $\rho _{A\, {II}}$ equally share the entanglement of the system in the maximum acceleration.

• 3. We have calculated $\pi _A, \pi _{I}$ and $\pi _{{II}}$ numerically and found that $\pi _A, \pi _{I}$ and $\pi _{{II}}$ are nonnegative. This means that all $1-1$ tangles and $1-2$ tangles satisfy the Coffman–Kundu–Wootters (CKW) monogamy inequality [46], i.e., $\mathcal {Q}^2_{A|BC}\ge \mathcal {Q}^2_{AB}+ \mathcal {Q}^2_{AC}$, where the squares of one-entanglement and two-entanglement play the role of any measure of correlation Q. Therefore, we conclude that all tripartite subsystems considered here are monogamy.

• 4. Some useful relations of entanglement of the Dirac field in an accelerated frame for GHZ-like state were obtained [26]. We have also found some useful relations for this Werner state. For example, we have found a useful relation for the concurrence,

  $$\begin{aligned}&[3 \sec (r) C (\rho _{A\, {I}}) -| 1-4 F|]^2\nonumber \\&\quad + [3 \csc (r) C (\rho _{A {II}}) -| 1-4 F|]^2= 2 (1-F) (5-2 F). \end{aligned}$$

  (29)

Fig. 12

(Color online) Plot of threshold R(r) (red line) and S(r) (black line) for the entanglement of subsystems $\rho _{A\, {I}}$ and $\rho _{A {II}}$

Table 1 $C(\rho _{A\, {I}}), ~C(\rho _{A\, {II}}), ~~N(\rho _{A\, {I}}), ~~N(\rho _{A\, {II}})$ as the functions of the acceleration parameter r and free parameter F, where $0\le F=0.50<R(r)<F=0.55<S(r)<F=0.65$ for $r=\pi /6\approx 0.5236, \pi /8\approx 0.3927, \pi /12\approx 0.2618$

Similarly, we have obtained another useful relation for the negativity

$$\begin{aligned}&[6 N(\rho _{A\, {I}}) + 3 + (1 - 4 F) \cos ^2(r)]^2\nonumber \\&\quad +[6 N(\rho _{A\, {II}}) + 3 + (1 - 4 F) \sin ^2(r)]^2\nonumber \\&\quad +\frac{9}{2} [2 N(\rho _{{I}\, {II}}) + 1]^2 = \frac{35}{2} + 32 F (2 F-1). \end{aligned}$$

(30)

These two relations show that entanglement of bipartite subsystems depends on both acceleration parameter r and the free parameter F. As mentioned before, the Werner state is entangled for $F\in (1/2, 1]$, which has been verified by the results presented above. How to understand these two relations? The first relation (29) implies that the degree of entanglement reflected by the concurrence could be transferred between bipartites $\rho _{A\, I}$ and $\rho _{A\, II}$, but their sum associated with their accessories remains a quantity $2(1-F)(5-2F)$. Similarly, the relation (30) about the negativity can also be explained in the similar way to (29). That means the degree of entanglement reflected by the negativity could be transferred among the bipartite subsystems $\rho _{A\, I}$, $\rho _{A\, II}$ and $\rho _{\mathrm{I}\, \mathrm{II}}$.

6 Summary

In this work, we have studied the entanglement properties of the Dirac field initially entangled in a Werner state when one observer remains in inertial frame but another observer is moving in noninertial frame. The formulas of concurrence, negativity and mutual information for three bipartite subsystems $\rho _{A\, {I}}, ~\rho _{A\, {II}}$ and $\rho _{{I}\, {II}}$ are presented. The total system $\pi$-tangle is also calculated. It is found that the concurrence $C(\rho _{A\, {I}})$, $C(\rho _{A\, {II}})$, negativity $N(\rho _{A\, {I}})$, $N(\rho _{A\, {II}})$ and entanglement entropy $S(\rho _{A\, I})$, $S(\rho _{A\, II})$ and $S(\rho _{A\, \mathrm{I}\, \mathrm{II}})$ depend on the free parameter F, but the $C(\rho _{{I}\, {II}})$, $N(\rho _{{I}\, {II}})$ and $S(\rho _{\mathrm{I}\, \mathrm{II}})$ are regardless of the free parameter F. We have found that $S(\rho _{A\, \mathrm{I}\, \mathrm{II}})$ decreases with increasing free parameter F but it is independent of the acceleration parameter r. In particular, $S(\rho _{\mathrm{I}\, \mathrm{II}})=S(\rho _{A})$ is only a constant so that it is independent of both free parameter F and acceleration parameter r. We have found that the threshold values R(r) of the free parameter F with respect to the concurrence and negativity in the subsystem $\rho _{A\, {I}}$ are same, so is the S(r), which corresponds to $\rho _{A\, {II}}$. We have also verified that tripartite systems of the Werner state in an accelerated frame are monogamy and presented two useful relations (29) and (30).

Before ending this work, we give some useful remarks on this work. First, we find that many results obtained above are symmetric to Bob and anti-Bob distributed in region I and region II, respectively, through exchanging $\sin (r)$ with $\cos (r)$. This might be explained by the way that $\sin (r+\pi /2)=\cos (r)$ when Bob and anti-Bob $\bar{B}$ are exchanged. Moreover, as shown in Ref. [11] the Bogoliubov transformation that mixes a particle mode in region I of momentum k and an antiparticle mode in region II of momentum $-k$ is given by

$$\begin{aligned} \left[ \begin{array}{c} a_{k}\\ b_{-k}^{\dagger } \end{array} \right] =\left[ \begin{array}{cc} \cos (r)&{}-e^{-i\phi }\sin (r)\\ e^{i\phi }\sin (r)&{}\cos (r) \end{array} \right] \left[ \begin{array}{c} c_{k}^{\mathrm{I}}\\ d_{-k}^{{\mathrm{II}}\dagger } \end{array} \right] , \end{aligned}$$

(31)

where $\phi$ is an unimportant phase factor that can always be absorbed into the definition of the operators. When the phase factor $e^{\mp i\phi }=\pm 1$ for $\phi =n\pi , n=0, 1, 2, \ldots$, we find that the transformation between the creation and annihilation operators in regions I and II are connected by the irreducible representation of an SO(2) group. Second, we note that the degree of entanglement of this Werner state will become more robust when the free parameter $F\in (1/2, 1]$ increases, but it decreases with the increasing acceleration parameter r, which is related to acceleration a. Third, we find that the Werner state always remains entangled to a degree, and thus, it could be used in quantum information tasks, such as teleportation, between parties in relative uniform acceleration for bipartite subsystems. In particular, we have found that the bipartite subsystem $\rho _{{I}\, {II}}$ is always entangled and only depends on the acceleration parameter r regardless of the free parameter F. We can also perform such quantum information tasks by using the tripartite entanglement when some observers are falling into a black hole while others are hovering outside the event horizon, which is different from the entangled states in inertial frames. Fourth, it is possible to apply beyond the single-model approximation proposed by Fuentes et al. [2] to generalize the present study in the future. Finally, we might conclude that the degree of the entanglement will be degraded when the acceleration parameter r increases. Since the acceleration parameter r depends on the frequency of the field modes, then it is obviously relevant for the mass parameter of the field. For a wave vector $\mathbf{k}$ labeling the modes, one has the frequency $w_{k}=\sqrt{m^2+\mathbf {k}^2}$. Therefore, the degree of the entanglement will be increased with the increasing frequency $w_{k}$, which is proportional to mass of the particle.

Appendix A: Explicit expressions for \(1-2\) and \(1-1\) tangles

In this Appendix, we are going to write out explicitly the analytical expressions for these $1-1$ and $1-2$ tangles as follows:

$$\begin{aligned} N_{\mathrm{A}({\mathrm{I}})}= & {} \frac{1}{24} \left( 16 F \cos ^2(r)\right. \nonumber \\&\left. +\sqrt{8 (8 F-5) (8 F+1) \cos (2 r)+256 F (2 F-1)+18 \cos (4 r)+86}-2 (\cos (2 r)+7)\right) ,\nonumber \\ \end{aligned}$$

(A1)

$$\begin{aligned} N_{\mathrm{A}({\mathrm{II}})}= & {} \frac{1}{24} \left( (2-8 F) \cos (2 r)\right. \nonumber \\&\left. +\sqrt{-8 (8 F-5) (8 F+1) \cos (2 r)+256 F (2 F-1)+18 \cos (4 r)+86}+8 F-14\right) , \end{aligned}$$

(A2)

$$\begin{aligned} N_{{\mathrm{I}}({{\mathrm{II}}})}= & {} \frac{1}{4} \left( \sqrt{6-2 \cos (4 r)}-2\right) =\frac{1}{2}\left( \sqrt{\sin ^2(2 r)+1}-1\right) . \end{aligned}$$

(A3)

$$\begin{aligned} N_{\mathrm{A} ({\mathrm{I}}\, {{{\mathrm{II}}}})}= & {} -1 + 2 F, \end{aligned}$$

(A4)

$$ \begin{aligned} N_{{\mathrm{I}}(\mathrm{A}\, {{{\mathrm{II}}}})}= & {} \frac{1}{3} \Bigg \{-\text {Root}\Big [2 \#1^3+\#1^2 (2 F \cos (2 r)-6 F+\cos (2 r)-3)\nonumber \\&+\#1 \Big (-28 F^2 \sin ^2(r)-4 F^2 \sin ^2(r) \cos (2 r)\nonumber \\&+32 F \sin ^2(r)+8 F \sin ^2(r) \cos (2 r)-4 \sin ^2(r)-4 \sin ^2(r) \cos (2 r)\Big )\nonumber \\&+16 F^3 \sin ^4(r) \cos ^2(r)-24 F^2 \sin ^4(r) \cos ^2(r)\nonumber \\&+8 \sin ^4(r) \cos ^2(r) \& , 1\Big ]-\text {Root}\Big [2 \#1^3+\#1^2 (2 F \cos (2 r)\nonumber \\&+6 F-2 \cos (2 r)-6)+\#1 \Big (-28 F^2 \cos ^2(r)\nonumber \\&+4 F^2 \cos (2 r) \cos ^2(r)-4 F \cos ^2(r)+4 F \cos (2 r) \cos ^2(r)\nonumber \\&+\cos (2 r) \cos ^2(r)+5 \cos ^2(r)\Big )\nonumber \\&-16 F^3 \sin ^2(r) \cos ^4(r)+12 F \sin ^2(r) \cos ^4(r)+4 \sin ^2(r) \cos ^4(r) \& , 1\Big ]\Bigg \}, \end{aligned}$$

(A5)

$$ \begin{aligned} N_{{{{\mathrm{II}}}}(\mathrm{A}\, {\mathrm{I}})}= & {} \frac{1}{3} \Bigg \{-\text {Root}\Big [2 \#1^3+\#1^2 (-2 F \cos (2 r)+6 F+2 \cos (2 r)-6)\nonumber \\&+\#1 \Big (-28 F^2 \sin ^2(r)-4 F^2 \sin ^2(r) \cos (2 r)\nonumber \\&-4 F \sin ^2(r)-4 F \sin ^2(r) \cos (2 r)+5 \sin ^2(r)-\sin ^2(r) \cos (2 r)\Big )\nonumber \\&-16 F^3 \sin ^4(r) \cos ^2(r)+12 F \sin ^4(r) \cos ^2(r)\nonumber \\&+4 \sin ^4(r) \cos ^2(r) \& , 1\Big ]-\text {Root}\Big [2 \#1^3+\#1^2 (-2 F \cos (2 r)\nonumber \\&-6 F-\cos (2 r)-3)+\#1 \Big (-28 F^2 \cos ^2(r)\nonumber \\&+4 F^2 \cos (2 r) \cos ^2(r)+32 F \cos ^2(r)-8 F \cos (2 r) \cos ^2(r)\nonumber \\&+4 \cos (2 r) \cos ^2(r)-4 \cos ^2(r)\Big )\nonumber \\&+16 F^3 \sin ^2(r) \cos ^4(r)-24 F^2 \sin ^2(r) \cos ^4(r)+8 \sin ^2(r) \cos ^4(r) \& , 1\Big ]\Bigg \}. \end{aligned}$$

(A6)

It should be pointed out that those special symbols # and & that appeared in $N_{{\mathrm{I}}(\mathrm{A}\, {\mathrm{II}})}$ and $N_{{\mathrm{II}}(\mathrm{A}\, {\mathrm{I}})}$ are generated when we solve higher-order polynomial eigenvalue problems, but fortunately they do not affect the final results. On the other hand, we have reverified again why $F\ge 1/2$ based on the result $N_{\mathrm{A} ({\mathrm{I}}\, {\mathrm{II}})}=-1 + 2 F\ge 0$. However, in order to make the $\pi (\rho _{\mathrm{A}({\mathrm{I}}\, {\mathrm{II}})})$ not less than zero, the $F=0.5$ is excluded.