1 Introduction

Key agreement (KA) is an important branch of cryptography, which was first proposed by Diffie and Hellman [1]. In a KA protocol, each participant fairly contributes to the generation of a shared key and any nontrivial subset of the participants cannot decide a shared key. Ever since the concept of KA was put forward, many scholars focused on extending the two-party Diffie–Hellman protocol to a multiparty case and some efficient KA protocols [2,3,4,5] were proposed. As we know, the security of classical cryptosystems including KA protocols is mostly based on computation complexity. However, with the rapid development of quantum computation, classical cryptosystems are confronted with more and more austere challenges.

Fortunately, quantum cryptography, which is based on the principle of quantum mechanical (such as Heisenberg uncertainty principle and quantum no-cloning theorem), can provide unconditional security. In the past twenty years, many kinds of quantum cryptographic protocols, such as quantum key distribution (QKD) [6,7,8,9], quantum secret sharing (QSS) [10, 11], quantum secure direct communication (QSDC) [12,13,14,15,16,17], quantum private comparison (QPC) [18, 19], quantum private query (QPQ) [20,21,22,23,24] and quantum signature [25,26,27,28,29,30,31,32] have been proposed.

The first QKA protocol was proposed by Zhou et al. [33]. However, Tsai et al. [34] found that it is not a fair QKA protocol since one participant can fully determine a shared key alone without being detected by other participants. Chong et al. [35] proposed the first two-party QKA protocol, which has high qubit efficiency. Later, Shi et al. [36] presented a QKA protocol, which is based on EPR pairs and entanglement swapping. In Ref. [37], Liu et al. pointed out that Shi et al.’s protocol cannot resist the participant attack and they presented a multiparty quantum key agreement with single particles. Huang et al. [38] proposed a quantum key agreement which is based on EPR pairs and single-particle measurements. It is a pity that Huang et al’s protocol cannot be extended to multiparty case. In Ref. [39], the multiparty QKA protocols are divided into three categories. The authors pointed out that the second category [40,41,42,43,44] and the third category [45] are unfair. They also showed that the first category [37, 46, 47] is not efficient. Hence, how to design a fair, secure and efficient QKA protocol is an important research topic at present.

The local distinguishability of orthogonal product states is a hot topic in the field of quantum information. Many properties about the local distinguishability of orthogonal product states were proposed [48,49,50,51,52,53,54,55,56]. In a \(d\otimes d\) \((d\ge 3)\) quantum system, Yu et al. [51] gave \(2d-1\) orthogonal states that cannot be perfectly distinguished by local operations and classical communications (LOCC) and conjectured that any set of no more than \(2(d-1)\) product states can be perfectly distinguished by LOCC. Wang et al. [52] proved that \(3(m+n)-9\) orthogonal product states are locally indistinguishable in an \(m\otimes n\) quantum system, where \(m\ge 3\) and \(n\ge 3\). Recently, Zhang et al. [53] proved a smaller set with only \(2n-1\) orthogonal product states that are locally indistinguishable in \(m\otimes n\) (\(3\le m \le n\)). Xu et al. [54,55,56] gave different methods to construct a set of orthogonal product states that cannot be perfectly distinguished by LOCC both in a bipartite quantum system and a multipartite quantum system. However, there exist only a few results about the application of the local distinguishability of orthogonal product states at present. In Ref. [57], a novel QKD protocol based on locally indistinguishable orthogonal product states was proposed. This is the first time that the local indistinguishability is used to design a QKD protocol. Later, Zhao et al. [58] proposed a new QKD protocol based on locally distinguishable orthogonal product states, which is easier to carry out in practice. Yang et al. [59] presented a quantum secret sharing protocol, which is based on local indistinguishable orthogonal product states. In fact, the generation of an orthogonal product state is much easier than the generation of an entangled state. Moreover, the cryptographic protocols, which are designed based on orthogonal product states, have high efficiency [57,58,59]. Thus, it is an interesting thing to design a QKA protocol based on locally indistinguishable orthogonal product states since no one has ever done.

In this paper, we propose a novel QKA protocol that is based on local indistinguishable orthogonal product states. In the protocol, the two different particles of each product state are transmitted, respectively, which can ensure enough security under the condition of reducing the number of the detected particles. That is, the new protocol has high efficiency. The rest of the paper is organized as follows. In Sect. 2, some fundamental preliminaries are introduced. In Sect. 3, we propose our multiparty QKA protocol. In Sect. 4, the properties of our protocol such as security and efficiency are discussed. At last, a short conclusion is given in Sect. 5.

2 Preliminaries

In this section, we introduce some preliminaries that are used in what follows.

We say a set of orthogonal states is locally indistinguishable if it cannot be perfectly distinguished by LOCC [60].

Theorem 1

The following orthogonal product states in Eq. (1) cannot be perfectly distinguished by LOCC no matter who goes first.

$$\begin{aligned}&|\psi _{1,2}\rangle =\frac{1}{\sqrt{2}}(|0\rangle \pm |1\rangle )_{1}|1\rangle _{2}\nonumber \\&|\psi _{3,4}\rangle =\frac{1}{\sqrt{2}}(|0\rangle \pm |2\rangle )_{1}|2\rangle _{2}\nonumber \\&|\psi _{5,6}\rangle =\frac{1}{\sqrt{2}}|2\rangle _{1}(|0\rangle \pm |1\rangle )_{2}\nonumber \\&|\psi _{7,8}\rangle =\frac{1}{\sqrt{2}}|1\rangle _{1}(|0\rangle \pm |2\rangle )_{2} \end{aligned}$$
(1)

Here one party goes first [60] means that he is the first person to perform a nontrivial measurement upon the system. The proof of Theorem 1 is given in the “Appendix.”

3 Multiparty QKA protocol

Now, we introduce our n-party QKA protocol that is based on the eight local indistinguishable orthogonal product states. Suppose that the n participants are \(A_{1}, A_{2}, \ldots , A_{n}\). The detailed process of the protocol is as follows.

  1. (1)

    \(A_{i}\) generates a random 3l-bit string \(K_{i}\) as his secret key, where \(i=1,2,\ldots ,n\).

  2. (2)

    \(A_{i}\) successively divides his secret \(K_{i}\) into l groups (each group has 3 bits). For each group, \(A_{i}\) encodes it as a product state according the following rules:

    $$\begin{aligned}&000:\,\,\longmapsto |\psi _{1}\rangle =\frac{1}{\sqrt{2}}(|0\rangle +|1\rangle )_{1}|1\rangle _{2},\nonumber \\&001:\,\,\longmapsto |\psi _{2}\rangle =\frac{1}{\sqrt{2}}(|0\rangle -|1\rangle )_{1}|1\rangle _{2},\nonumber \\&010:\,\,\longmapsto |\psi _{3}\rangle =\frac{1}{\sqrt{2}}(|0\rangle +|2\rangle )_{1}|2\rangle _{2},\nonumber \\&011:\,\,\longmapsto |\psi _{4}\rangle =\frac{1}{\sqrt{2}}(|0\rangle -|2\rangle )_{1}|2\rangle _{2},\nonumber \\&100:\,\,\longmapsto |\psi _{5}\rangle =\frac{1}{\sqrt{2}}|2\rangle _{1}(|0\rangle +|1\rangle )_{2},\nonumber \\&101:\,\,\longmapsto |\psi _{6}\rangle =\frac{1}{\sqrt{2}}|2\rangle _{1}(|0\rangle -|1\rangle )_{2},\nonumber \\&110:\,\,\longmapsto |\psi _{7}\rangle =\frac{1}{\sqrt{2}}|1\rangle _{1}(|0\rangle +|2\rangle )_{2},\nonumber \\&111:\,\,\longmapsto |\psi _{8}\rangle =\frac{1}{\sqrt{2}}|1\rangle _{1}(|0\rangle -|2\rangle )_{2}. \end{aligned}$$
    (2)

    Thus, the Key \(K_{i}\) of \(A_{i}\) is encoded as a sequence of product states, \(S_{i}\).

  3. (3)

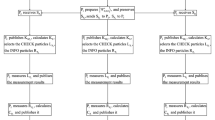
    \(A_{i}\) generates \(n-1\) same quantum sequences \(S_{i}\). For simplicity, we denote these sequences as \(S_{i1}\), \(S_{i2}\), \(\ldots \), \(S_{i,i-1}\), \(S_{i,i+1}\), \(\ldots \), \(S_{in}\) (See Fig. 1), where \(i=1,2,\ldots ,n.\)

  4. (4)

    For \(S_{ij}\), \(A_{i}\) picks out the first particle of each product state to form the sequence \(S_{ij}^{(1)}\) and the second one of each product state to form the sequence \(S_{ij}^{(2)}\). \(A_{i}\) generates rl decoy particles which are randomly in one of the four states \(\{|+y\rangle ,\,|-y\rangle ,\,|+\rangle ,\,|-\rangle \}\) and randomly inserts them into \(S_{ij}^{(1)}\) and \(S_{ij}^{(2)}\), where r is the detection rate, \(i=1,2,\ldots ,n\); \(j\in \{1,2,\ldots ,i-1,i+1,\ldots ,n\}\) and

    $$\begin{aligned} |+y\rangle= & {} \frac{1}{\sqrt{2}}(|0\rangle +i|1\rangle )\nonumber \\ |-y\rangle= & {} \frac{1}{\sqrt{2}}(|0\rangle -i|1\rangle )\nonumber \\ |+\rangle= & {} \frac{1}{\sqrt{2}}(|0\rangle +|1\rangle )\nonumber \\ |-\rangle= & {} \frac{1}{\sqrt{2}}(|0\rangle -|1\rangle ). \end{aligned}$$
    (3)

    It should be noted that the i of Eq. (3) is imaginary unit. Now, we denote the new sequences as

    $$\begin{aligned} \overline{S}_{i1}^{(1)},\overline{S}_{i1}^{(2)},\overline{S}_{i2}^{(1)}, \overline{S}_{i2}^{(2)},\ldots ,\overline{S}_{i,i-1}^{(1)},\overline{S}_{i,i-1}^{(2)}, \overline{S}_{i,i+1}^{(1)},\overline{S}_{i,i+1}^{(2)}, \ldots ,\overline{S}_{i,n}^{(1)},\overline{S}_{i,n}^{(2)}. \end{aligned}$$
  5. (5)

    \(A_{i}\) sends the sequence \(\overline{S}_{ij}^{(1)}\) to \(A_{j}\) (see Fig. 2), where \(i=1,2,\ldots ,n;\) and \(j=1,2,\ldots ,i-1,i+1,\ldots ,n.\)

  6. (6)

    After all the participants claim that they have received all the sequences that were sent to them, they begin to start the first eavesdropping detection. For the sequence \(\overline{S}_{ij}^{(1)}\), which was sent to \(A_{j}\) by \(A_{i}\), \(A_{i}\) announces the positions and the corresponding bases of the decoy particles. Then, \(A_{j}\) measures the decoy particles with the correct bases and randomly announces half of the measurement results. \(A_{i}\) publishes the initial states of the left half of the decoy particles. At last, they check whether or not the measurement results and the initial states are consistent. If there exists no error, they continue to carry out the protocol; otherwise, they abandon the protocol.

  7. (7)

    \(A_{i}\) sends the sequence \(\overline{S}_{ij}^{(2)}\) to \(A_{j}\) (Fig. 3), where \(i=1,2,\ldots ,n;\) \(j=1,2,\ldots ,i-1,i+1,\ldots ,n.\) After all the participants claim that they have received all the sequences that were sent to them, they make the second eavesdropping detection as they do in step (6). If there exists no error, they continue to carry out the protocol; otherwise, they abandon the protocol.

  8. (8)

    \(A_{j}\) recovers the sequence \(S_{ij}\) according to the remaining sequences \(S_{ij}^{(1)}\) and \(S_{ij}^{(2)}\), where \(i=1,2,\ldots ,j-1,j+1,\ldots ,n\) and \(j=1,2,\ldots ,n.\) Then \(A_{j}\) measures each product state of \(S_{ij}\) with the following basis

    $$\begin{aligned} \{|\psi _{1}\rangle ,|\psi _{2}\rangle ,|\psi _{3}\rangle ,|\psi _{4}\rangle ,|\psi _{5}\rangle , |\psi _{6}\rangle ,|\psi _{7}\rangle ,|\psi _{8}\rangle ,|\psi _{9}\rangle =|0\rangle |0\rangle \} \end{aligned}$$

    and recovers \(K_{i}\) according to the measurement results for \(i=1,2,\ldots ,j-1,j+1,\ldots ,n\).

  9. (9)

    \(A_{j}\) computes the final key \(K=K_{1}\oplus K_{2}\oplus \cdots \oplus K_{n},\) where \(j=1,2,\ldots ,n.\)

Fig. 1
figure 1

\(A_{i}\) encodes his key as the quantum sequences to be transmitted. Here \(S_{ij}\) is the quantum sequence of product states, and \(S_{ij}=S_{it}\) for \(j\ne t\). \(S_{ij}^{(k)}\) is the quantum sequence generated by the k-th particle of every product state of \(S_{ij}\) and \(\overline{S}_{ij}^{(k)}\) is generated by inserting decoy particles into \(S_{ij}^{(k)}\) for \(k=1,2\)

Full size image
Fig. 2
figure 2

\(A_{i}\) sends the first quantum sequence \(\overline{S}^{(1)}_{ij}\) to \(A_{j}\), where \(i=1,\ldots , n; j=1,\ldots ,i-1,i+1,\ldots ,n\)

Full size image
Fig. 3
figure 3

\(A_{i}\) sends the second quantum sequence \(\overline{S}^{(1)}_{ij}\) to \(A_{j}\), where \(i=1,\ldots , n; j=1,\ldots ,i-1,i+1,\ldots ,n\)

Full size image

Through the above steps, each participant can get the final key K.

4 Security and efficiency analysis of the proposed QKA protocol

In this section, we will give a detailed analysis of the security and efficiency of the new protocol. For the security analysis, we consider the outside attacks and the participants’ attacks.

4.1 Security analysis

Now, we prove that our QKA protocol is secure.

4.1.1 Outside attacks

Here we firstly consider the collective attack since the particles in the sequences are product states. In fact, the opportunity for an outside eavesdropper to obtain the information of the key is between step (5) and step (7). Because the positions and the bases of the decoy particles are unknown to the eavesdropper before the sender announces the corresponding information in step (6), an outside eavesdropper can perform the most general attack as follows. Firstly, he intercepts the transmitted sequences. Secondly, he performs a collective operation U on each intercepted particle and an additional particle \(|\theta \rangle \) which is prepared by him. Finally, he sends the operated particles to the receivers. Without loss of generality, suppose that the operation U holds:

$$\begin{aligned} U(|0\rangle |\theta \rangle )= & {} \lambda _{1}|s_{0}E_{0}\rangle +\lambda _{2}|s_{0}E_{1}\rangle +\lambda _{3}|s_{0}E_{2}\rangle \nonumber \\&+\,\lambda _{4}|s_{1}E_{0}\rangle +\lambda _{5}|s_{1}E_{1}\rangle +\lambda _{6}|s_{1}E_{2}\rangle \nonumber \\&+\,\lambda _{7}|s_{2}E_{0}\rangle +\lambda _{8}|s_{2}E_{1}\rangle +\lambda _{9}|s_{2}E_{2}\rangle \end{aligned}$$
(4)
$$\begin{aligned} U(|1\rangle |\theta \rangle )= & {} \mu _{1}|s'_{0}E'_{0}\rangle +\mu _{2}|s'_{0}E'_{1}\rangle +\mu _{3}|s'_{0}E'_{2}\rangle \nonumber \\&+\,\mu _{4}|s'_{1}E'_{0}\rangle +\mu _{5}|s'_{1}E'_{1}\rangle +\mu _{6}|s'_{1}E'_{2}\rangle \nonumber \\&+\,\mu _{7}|s'_{2}E'_{0}\rangle +\mu _{8}|s'_{2}E'_{1}\rangle +\mu _{9}|s'_{2}E'_{2}\rangle \end{aligned}$$
(5)
$$\begin{aligned} U(|2\rangle |\theta \rangle )= & {} \gamma _{1}|\overline{s}_{0}\overline{E}_{0}\rangle +\gamma _{2}|\overline{s}_{0}\overline{E}_{1}\rangle +\gamma _{3}|\overline{s}_{0}\overline{E}_{2}\rangle \nonumber \\&+\,\gamma _{4}|\overline{s}_{1}\overline{E}_{0}\rangle +\gamma _{5}|\overline{s}_{1}\overline{E}_{1}\rangle +\gamma _{6}|\overline{s}_{1}\overline{E}_{2}\rangle \nonumber \\&+\,\gamma _{7}|\overline{s}_{2}\overline{E}_{0}\rangle +\gamma _{8}|\overline{s}_{2}\overline{E}_{1}\rangle +\gamma _{9}|\overline{s}_{2}\overline{E}_{2}\rangle , \end{aligned}$$
(6)

where

$$\begin{aligned}&|\lambda _{1}|^{2}+|\lambda _{2}|^{2}+\cdots +|\lambda _{9}|^{2}= |\mu _{1}|^{2}+|\mu _{2}|^{2}+\cdots +|\mu _{9}|^{2}\\\nonumber&\quad = |\gamma _{1}|^{2}+|\gamma _{2}|^{2}+\cdots +|\gamma _{9}|^{2}=1,\\&\langle s_{0}|s_{1}\rangle =\langle s_{0}|s_{2}\rangle =\langle s_{1}|s_{2}\rangle =\langle E_{0}|E_{1}\rangle =\langle E_{0}|E_{2}\rangle =\langle E_{1}|E_{2}\rangle =0,\\&\langle s'_{0}|s'_{1}\rangle =\langle s'_{0}|s'_{2}\rangle =\langle s'_{1}|s'_{2}\rangle =\langle E'_{0}|E'_{1}\rangle =\langle E'_{0}|E'_{2}\rangle =\langle E'_{1}|E'_{2}\rangle =0,\\&\langle \overline{s}_{0}|\overline{s}_{1}\rangle =\langle \overline{s}_{0}|\overline{s}_{2}\rangle =\langle \overline{s}_{1}|\overline{s}_{2}\rangle =\langle \overline{E}_{0}|\overline{E}_{1}\rangle =\langle \overline{E}_{0}|\overline{E}_{2}\rangle =\langle \overline{E}_{1}|\overline{E}_{2}\rangle =0. \end{aligned}$$

If the eavesdropper wants to extract the encoded information precisely, the three reduced density matrices

$$\begin{aligned}&(|\lambda _{1}|^{2}+|\lambda _{4}|^{2}+|\lambda _{7}|^{2})|E_{0}\rangle \langle E_{0}| +(|\lambda _{2}|^{2}+|\lambda _{5}|^{2}+|\lambda _{8}|^{2})|E_{1}\rangle \langle E_{1}|\\&\quad +(|\lambda _{3}|^{2}+|\lambda _{6}|^{2}+|\lambda _{9}|^{2})|E_{2}\rangle \langle E_{2}|,\\&(|\mu _{1}|^{2}+|\mu _{4}|^{2}+|\mu _{7}|^{2})|E'_{0}\rangle \langle E'_{0}| +(|\mu _{2}|^{2}+|\mu _{5}|^{2}+|\mu _{8}|^{2})|E'_{1}\rangle \langle E'_{1}|\\&\quad +(|\mu _{3}|^{2}+|\mu _{6}|^{2}+|\mu _{9}|^{2})|E'_{2}\rangle \langle E'_{2}|,\\&(|\gamma _{1}|^{2}+|\gamma _{4}|^{2}+|\gamma _{7}|^{2})|\overline{E}_{0}\rangle \langle \overline{E}_{0}|+(|\gamma _{2}|^{2}+|\gamma _{5}|^{2}+|\gamma _{8}|^{2}) |\overline{E}_{1}\rangle \langle \overline{E}_{1}|+(|\gamma _{3}|^{2}+|\gamma _{6}|^{2}\\&\quad +|\gamma _{9}|^{2})|\overline{E}_{2}\rangle \langle \overline{E}_{2}| \end{aligned}$$

must be discriminated precisely, which means

$$\begin{aligned} \langle E_{i}|E'_{j}\rangle =\langle E_{i}|\overline{E}_{t}\rangle = \langle E'_{j}|\overline{E}_{t}\rangle =0 \end{aligned}$$

for \(i,j,t=0,1,2.\) Therefore, the unitary transformation U on the decoy particles and the additional particles has the universal form

$$\begin{aligned}&U\left( \frac{1}{\sqrt{2}}(|0\rangle +\tau |1\rangle )|\theta \rangle \right) \nonumber \\&\quad =\frac{1}{\sqrt{2}}(\lambda _{1}|s_{0}E_{0}\rangle +\lambda _{2}|s_{0}E_{1}\rangle +\lambda _{3}|s_{0}E_{2}\rangle +\lambda _{4}|s_{1}E_{0}\rangle +\lambda _{5}|s_{1}E_{1}\rangle +\lambda _{6}|s_{1}E_{2}\rangle \nonumber \\&\qquad +\,\lambda _{7}|s_{2}E_{0}\rangle +\lambda _{8}|s_{2}E_{1}\rangle +\lambda _{9}|s_{2}E_{2}\rangle +\mu _{1}\tau |s'_{0}E'_{0}\rangle +\mu _{2}\tau |s'_{0}E'_{1}\rangle +\mu _{3}\tau |s'_{0}E'_{2}\rangle \nonumber \\&\qquad +\,\mu _{4}\tau |s'_{1}E'_{0}\rangle +\mu _{5}\tau |s'_{1}E'_{1}\rangle {+}\mu _{6}\tau |s'_{1}E'_{2}\rangle {+}\mu _{7}\tau |s'_{2}E'_{0}\rangle {+}\mu _{8}\tau |s'_{2}E'_{1}\rangle {+}\mu _{9}\tau |s'_{2}E'_{2}\rangle )\nonumber \\ \end{aligned}$$
(7)

where \(\tau =1,-1,i,-i.\) So the reduced density matrix of the receiver’s system is

$$\begin{aligned}&\frac{1}{2}[(|\lambda _{1}|^{2}+|\lambda _{2}|^{2}+|\lambda _{3}|^{2})|s_{0}\rangle \langle s_{0}|+ (|\lambda _{4}|^{2}+|\lambda _{5}|^{2}+|\lambda _{6}|^{2})|s_{1}\rangle \langle s_{1}|\nonumber \\&\quad +\,(|\lambda _{7}|^{2}+|\lambda _{8}|^{2}+|\lambda _{9}|^{2})|s_{2}\rangle \langle s_{2}|+ (|\mu _{1}|^{2}+|\mu _{2}|^{2}+|\mu _{3}|^{2})|s'_{0}\rangle \langle s'_{0}|\nonumber \\&\quad +\,(|\mu _{4}|^{2}+|\mu _{5}|^{2}+|\mu _{6}|^{2})|s'_{1}\rangle \langle s'_{1}|+ (|\mu _{7}|^{2}+|\mu _{8}|^{2}+|\mu _{9}|^{2})|s'_{2}\rangle \langle s'_{2}|]. \end{aligned}$$
(8)

It is easy to see that the density matrix has nothing to do with the variable \(\tau \), which means the subsystems of the states on the decoy positions in the receiver’s hand are identical. Thus, the error rate in the detection stage is maximized. That means that an outside eavesdropper cannot steal the secret without introducing any error.

Finally, Eve may choose the delay-photon Trojan horse attack [61, 62] and the invisible particle eavesdropping Trojan horse attack [63]. We can use the photon number splitter find the multi-photon signals and the quantum filter to filter out the invisible particles [61,62,63]. Therefore, our protocol can resist these two kinds of Trojan horse attacks.

4.1.2 Participants’ attacks

Without loss of generality, suppose \(A_{1}\) is a dishonest participant. He has two different methods to cheat other participants. The first one is to extract the key information encoded in the sequences that he receives before he sends the sequences that he generates to other participants. The second one is that he announces different positions of the decoy particles in his favor.

For the first method, he cannot get any useful information before he sends the sequences that he generates to other participants. In fact, each participant encodes his own key information as a quantum sequence of product states. The quantum sequence is divided into two sequences. And the two sequences are sent to other participants separately after decoy particles are inserted. Only all the participants announce that they have received all the first sequences of other participants, they start to the first check eavesdropping. If there is no error, they send the second sequences to each of other participants. Thus, \(A_{1}\) cannot get any information according to the sequences that he receives before he sends the first sequence to all the other participants. This is because the key information is encoded as a sequence of product states that cannot be perfectly distinguished by LOCC and the two particles of each product state are transmitted separately.

For the second method, \(A_{1}\) publishes different positions of the decoy particles, i.e., some encoded particles become decoy particles and some decoy particles become encoded particles. For simplicity, we give an example to show our protocol is secure. Without loss of generality, suppose \(A_{1}\) chooses his key \(K_{1}=010\, \,101\, \,011\, \,110\). Thus he encodes \(K_{1}\) as the sequence of product states, S, according to Eq. (2), where \(S=\{|\psi _{3}\rangle ,\,|\psi _{6}\rangle ,\,|\psi _{4}\rangle ,\,|\psi _{7}\rangle \}\).

  1. (1)

    \(A_{1}\) generates the product sequence S and divides it into two sequences \(S_{1}\) and \(S_{2}\), where \(S_{1}=\{\frac{1}{\sqrt{2}}(|0\rangle +|2\rangle ),\,|2\rangle ,\,\frac{1}{\sqrt{2}} (|0\rangle -|2\rangle ),\,|1\rangle \}\) and \(S_{2}=\{|2\rangle ,\,\frac{1}{\sqrt{2}}(|0\rangle -|1\rangle ),\,|2\rangle ,\, \frac{1}{\sqrt{2}}(|0\rangle +|2\rangle )\}\).

  2. (2)

    \(A_{1}\) generates four decoy particles \(|-y\rangle ,\,|+\rangle ,\,|-\rangle ,\,|+y\rangle ,\,\) and inserts them into \(S_{1}\) and \(S_{2}\) to get \(S'_{1}\) and \(S'_{2}\), respectively, where \(S'_{1}=\{\frac{1}{\sqrt{2}}(|0\rangle +|2\rangle ),\,|-y\rangle ,\,|2\rangle ,\,|+\rangle ,\,\frac{1}{\sqrt{2}} (|0\rangle -|2\rangle ),\,|1\rangle \}\) and \(S'_{2}=\{|2\rangle ,\,|-\rangle ,\,\frac{1}{\sqrt{2}}(|0\rangle -|1\rangle ),\,|2\rangle ,\, \frac{1}{\sqrt{2}}(|0\rangle +|2\rangle ),\,|+y\rangle \,\}\).

  3. (3)

    \(A_{1}\) sends the sequence \(S'_{1}\) to an honest participant \(A_{i}\). Suppose that \(A_{1}\) announces the second particle and the fifth particle of \(S'_{1}\) are decoy particles, i.e., the fifth particle \(\frac{1}{\sqrt{2}}(|0\rangle -|2\rangle )\) is an encoded particle while it is announced a decoy particle.

Now, we consider the probability of the measurement outcomes of \(A_{i}\), when he measures the fifth particle with the basis \(\{|+y\rangle ,\,|-y\rangle \}\) or \(\{|+\rangle ,\,|-\rangle \}\). In fact,

$$\begin{aligned} \frac{1}{\sqrt{2}}(|0\rangle -|2\rangle )= & {} \frac{1}{2}|+y\rangle +\frac{1}{2}|-y\rangle -\frac{1}{\sqrt{2}}|2\rangle ,\\ \frac{1}{\sqrt{2}}(|0\rangle -|2\rangle )= & {} \frac{1}{2}|+\rangle +\frac{1}{2}|-\rangle -\frac{1}{\sqrt{2}}|2\rangle , \end{aligned}$$

thus, we have

$$\begin{aligned} p_{1}= & {} \frac{1}{\sqrt{2}}(\langle 0|-\langle 2|)|+y\rangle \langle +y| \left( \frac{1}{\sqrt{2}}(|0\rangle -|2\rangle )\right) \\= & {} \left( \frac{1}{2}\langle +y|+\frac{1}{2}\langle -y|-\frac{1}{\sqrt{2}}\langle 2|\right) |+y\rangle \langle +y|\left( \frac{1}{2}|+y\rangle +\frac{1}{2}|-y\rangle -\frac{1}{\sqrt{2}}|2\rangle \right) \\= & {} \frac{1}{4}\\ p_{2}= & {} \frac{1}{\sqrt{2}}(\langle 0|-\langle 2|)|-y\rangle \langle -y| \left( \frac{1}{\sqrt{2}}(|0\rangle -|2\rangle )\right) \\= & {} \left( \frac{1}{2}\langle +y|+\frac{1}{2}\langle -y|-\frac{1}{\sqrt{2}}\langle 2|\right) |-y\rangle \langle -y|\left( \frac{1}{2}|+y\rangle +\frac{1}{2}|-y\rangle -\frac{1}{\sqrt{2}}|2\rangle \right) \\= & {} \frac{1}{4}\\ p'_{1}= & {} \frac{1}{\sqrt{2}}(\langle 0|-\langle 2|)|+\rangle \langle +| \left( \frac{1}{\sqrt{2}}(|0\rangle -|2\rangle )\right) \\= & {} \left( \frac{1}{2}\langle +|+\frac{1}{2}\langle -|-\frac{1}{\sqrt{2}}\langle 2|\right) |+\rangle \langle +|\left( \frac{1}{2}|+\rangle +\frac{1}{2}|-\rangle -\frac{1}{\sqrt{2}}|2\rangle \right) \\= & {} \frac{1}{4}\\ p'_{2}= & {} \frac{1}{\sqrt{2}}(\langle 0|-\langle 2|)|-\rangle \langle -| \left( \frac{1}{\sqrt{2}}(|0\rangle -|2\rangle )\right) \\= & {} \left( \frac{1}{2}\langle +|+\frac{1}{2}\langle -|-\frac{1}{\sqrt{2}}\langle 2|\right) |-\rangle \langle -|\left( \frac{1}{2}|+\rangle +\frac{1}{2}|-\rangle -\frac{1}{\sqrt{2}}|2\rangle \right) \\= & {} \frac{1}{4}. \end{aligned}$$

That is, if \(A_{i}\) measures the fifth particle, \(\frac{1}{\sqrt{2}}(|0\rangle -|2\rangle )\), with the basis \(\{|+y\rangle ,\,|-y\rangle \}\), he will get \(|+y\rangle \) or \(|-y\rangle \) with the same probability \(\frac{1}{4}\); if he measures it with the basis \(\{|+\rangle ,\,|-\rangle \}\), he will get \(|+\rangle \) or \(|-\rangle \) with the same probability \(\frac{1}{4}\). Therefore, if \(A_{i}\) lets \(A_{1}\) publish the identity of the fifth particle, the error probability of \(A_{1}\) is \(\frac{3}{4}\). So if the decoy particles are enough, \(A_{i}\) can find \(A_{1}\)’s deception. This means that the second method cannot cheat an honest participant without being found.

According to the above analysis, the proposed QKA protocol is secure against both outside attacks and participants’ attacks.

4.2 Efficiency analysis

In Refs. [47, 64], quantum efficiency is introduced to judge the efficiency of QKA protocol. For QKA protocols with classical bits exchanged, quantum efficiency is

$$\begin{aligned} \eta =\frac{c}{q+b}, \end{aligned}$$
(9)

where c represents the total number of the agreement classic bits, q is the total number of the particles generated in the protocol and b represents the total number of classic bits exchanged for decoding of the message (classical bits utilized for eavesdropping check are not counted).

According to Eq. (9), we computer the efficiency of our QKA protocol. For comparison with the existing protocols, we take the three-party case as an example to calculate the efficiency of our protocol. If a 3l-bit agreement key is generated by our (three-party) protocol, every party needs to generated two quantum sequences to each of the other two parties. The two quantum sequences contain 2l particles (which come from l product states), \(2m_{1}\) decoy particles for detecting the delay-particle Trojan horse attack and \(2m_{2}\) decoy particles for detecting general eavesdropping attacks. Thus every party needs to send \(2\times (2l+2m_{1}+2m_{2})\) particles to the other two parties. Therefore \(c=3l\) and \(q=3\times 2\times (2l+2m_{1}+2m_{2})\). Since our protocol needs no classic bits exchanged for decoding the encoded information, the quantum efficiency of our protocol (three-party case) is

$$\begin{aligned} \eta =\frac{3l}{3\times 2\times (2l+2m_{1}+2m_{2})}. \end{aligned}$$
(10)

Suppose that \(4m_{1}=m_{2}=l\) (here the value is same as Ref. [47] for comparison), we have \(\eta =11.11\%\). According to Ref. [47], we can get the efficiencies of other existing protocol under a same standard.

Table 1 Comparison between the existing protocols and our protocol
Full size table

It should be noted that the data of Table 1 (except that of our protocol) come from Ref. [47].

From Table 1, it can be easily seen that the efficiency of our protocol is higher than that of other protocols (except XWGQ’s protocol. However, our new protocol is more secure than XWGQ’s protocol since the latter is an unfair QKA protocol [39]). That is, our new protocol is efficient.

5 Conclusions

The local distinguishability of orthogonal product states has got a lot of attention in the past two decades [51,52,53,54,55,56]. There exist only a few research results about the application of local indistinguishable orthogonal product states. In this paper, we proposed a QKA protocol based on local indistinguishable orthogonal product states. The new protocol can decrease the use of decoy particles without reducing the security since the different particles of each product states are transmitted separately. On the other hand, it can enhance the security with a same detection rate when compared with other QKA protocols [39].