1 Introduction

Quantum entanglement plays important roles in quantum information and quantum computation [1]. However, some quantum states without quantum entanglement can also perform quantum tasks [2, 3] such as quantum state discrimination [4, 5], remote state preparation [6], quantum state merging [7, 8], which have led to new definitions of quantum correlations such as quantum discord [9, 10], one-way quantum deficit [11–14], and various “discord-like” measures [15].

One-way quantum deficit was first proposed by Oppenheim et al. [11] for studying thermodynamical systems. They considered the amount of work which could be extracted from a heat bath by local operations. It quantifies the minimum distillable entanglement generated between the whole system and the measurement apparatus in measuring one subsystem of the whole system [16]. The analytical formulae of one-way quantum deficit are not known even for two-qubit states. With limited analytical results [17, 18], many discussions on quantum deficit only rely on numerical results, since it involves minimization of sum of local and conditional entropies.

Another famous measure of quantum correlations, the quantum discord [9, 10], is defined to be the difference of two classically equivalent expressions for the mutual information. There have been a lot of results on quantum discord for bipartite as well as multipartite mixed quantum states [15]. Nevertheless, due to the optimization problem involved, it has been recently shown that calculating quantum discord is an NP complexity problem [19].

It is meaningful to link directly one-way quantum deficit to quantum discord. The relationship between quantum discord and one-way quantum deficit was first discussed in Ref. [14]. Horodecki et al. show that the one-way quantum deficit is upper bounded by the quantum discord for any bipartite quantum states. In Ref. [20], a tradeoff relationship between one-way unlocalizable quantum discord and one-way unlocalizable quantum deficit has been presented. The tradeoff relationship between quantum discord and one-way quantum deficit is obtained [21].

Anyway, decisive results between quantum discord and one-way quantum deficit are not fully explored even for the two-qubit X states yet. Here, we revisit the relationship between one-way quantum deficit and quantum discord. We find that for special two-qubit X states the one-way quantum deficit can be derived from quantum discord exactly in some optimal measurement bases. Furthermore, we connect one-way quantum deficit to entanglement of formation directly.

To capture the non-classical correlations in bipartite systems, let us recall the following two popular measures of quantum correlations.

One-way quantum deficit Suppose Alice and Bob are allowed to perform only local operations. Consider a one-way classical communication, say, from Alice to Bob. The amount of information extractable from quantum system \(\varrho ^{AB}\) is given by \(\mathcal {I}_e=\log _2 \mathcal {D}-S(\varrho ^{AB})\), where \(\mathcal {D}\) is the dimension of the Hilbert space and \(S(\varrho )=-\mathrm{Tr}[\varrho \log _2 \varrho ]\) is the von Neumann entropy of a quantum state \(\varrho \).

The classical operations to extract the amount of information from the quantum state is \(\mathcal {I}_o=\log _2 \mathcal {D}-\min S((\varrho ^{AB})')\), where \((\varrho ^{AB})'=\sum _k M_k^A\varrho ^{AB} M_k^A\) is the quantum state after measurement \(M_k^{A}\) has been performed on A. The one-way quantum deficit [11–14] is given by the difference of \(\mathcal {I}_e\) and \(\mathcal {I}_o\) [16],

$$\begin{aligned} \overset{\rightharpoonup }{{\Delta }}= & {} \mathcal {I}_e-\mathcal {I}_o \nonumber \\= & {} \min S\left( \sum _k M_k^A\varrho ^{AB} M_k^A\right) -S\left( \varrho ^{AB}\right) . \end{aligned}$$
(1)

The minimum is taken over all local measurements \(M_k^{A}\). This quantity is equal to the thermal discord [22].

Quantum discord The quantum discord is defined as the minimal difference between quantum mutual information and classical correlation. The quantum mutual information is denoted by \(\mathcal {I}(\varrho ^{AB})=S(\varrho ^A)+S(\varrho ^B)-S(\varrho ^{AB})\), which is also identified as the total correlation of the bipartite quantum system \(\varrho ^{AB}\). The \(\varrho ^{A(B)}\) are the reduced density matrices \(\mathrm{Tr}_{B(A)}\varrho ^{AB}\), respectively. Let \(\{M_k^A\}\) be a measurement on subsystem A. Classical correlation is given as \(\mathcal {J}(\varrho ^{AB})=S(\varrho ^B)-\min \sum _k p_kS(\varrho _{M_k^A}^{B})\), where \(p_k=\mathrm{Tr}(M_k^A\otimes I_2 \varrho ^{AB})\) is the probability of kth measurement outcome and \(\varrho _{M_k^A}^{B}=\mathrm{Tr}_A[M_k^A\otimes I_2 \varrho ^{AB}]/p_k\) is the post-measurement state.

The quantum discord [9, 10] is defined by

$$\begin{aligned} \overset{\rightharpoonup }{{{\delta }}}= & {} \mathcal {I}\left( \varrho ^{AB}\right) -\mathcal {J}\left( \varrho ^{AB}\right) \nonumber \\= & {} S\left( \varrho ^A\right) +\min \sum _k p_k S\left( \varrho _{M_k^A}^{B}\right) -S\left( \varrho ^{AB}\right) . \end{aligned}$$
(2)

The superscript “\(\rightharpoonup \)” stands for that the measurement performed on subsystem A. The minimum is taken over all possible measurements \(\{M_k^A\}\) on the subsystem A.

2 Linking one-way quantum deficit to quantum discord

Let us consider bipartite systems in Hilbert space \(\mathbbm {C}^2\otimes \mathbbm {C}^2\). Generally, the quantum correlations are invariant under local unitary operations [15]. Hence, one can write the X states [23] in the form

$$\begin{aligned} \varrho ^{AB}=\frac{1}{4}\left( I_2\otimes I_2+a\sigma _z\otimes I_2+bI_2\otimes \sigma _z +\sum _{i\in \{x,y,z\}}c_i\sigma _i\otimes \sigma _i\right) , \end{aligned}$$
(3)

where \(\sigma _i \;(i\in \{x, y, z\})\) are Pauli matrices, \(I_2\) is the identity matrix, and the parameters \(\{a, b, c_x, c_y,c_z\}\in [-1, 1]\) are real numbers.

The optimal measurement with measurement operators satisfying \(M_k^A\geqslant 0\), \(\sum _kM_k^A=I\), is generally positive operator-valued measurement (POVM). For rank-two two-qubit systems, the optimal measurement is just projective ones [24]. It is also sufficient to consider projective measurement for rank three and four [25].

Let \(M_k^A=|k'\rangle \langle k'|\), \(k\in \{0, 1\}\), where

$$\begin{aligned} |0'\rangle= & {} \cos (\theta /2)|0\rangle -e^{-i\phi }\sin (\theta /2)|1\rangle , \end{aligned}$$
(4)
$$\begin{aligned} |1'\rangle= & {} e^{i\phi }\sin (\theta /2)|0\rangle +\cos (\theta /2)|1\rangle . \end{aligned}$$
(5)

For the given system (3), we obtain \(\overset{\rightharpoonup }{{\delta }}=S(\varrho ^{A})+\min \sum _k p_k S(\varrho _{M_k^A}^{B})-S(\varrho ^{AB})\), in which

$$\begin{aligned} p_{k\in \{0,1\}}=\frac{1}{2}(1\pm a\cos \theta ), \end{aligned}$$
(6)

\(S(\varrho ^{A})=h(\frac{1+a}{2})\) with \(h(x)=-x\log _2x-(1-x)\log _2(1-x)\),

$$\begin{aligned} \sum _k p_kS\left( \varrho _{M_k^A}^{B}\right)= & {} p_0S\left( \varrho _{M_0^A}^{B}\right) +p_1S\left( \varrho _{M_1^A}^{B}\right) \nonumber \\= & {} -\sum \limits _{k,j\in \{0,1\}}p_k w_{kj} \log w_{kj}, \end{aligned}$$
(7)

with \(w_{00}, w_{01}\) and \(w_{10}, w_{11}\) the eigenvalues of \(\varrho _{M_0^A}^{B}\) and \(\varrho _{M_1^A}^{B}\), respectively,

(8)

The corresponding quantity \(S(\sum _k M_k^A\varrho ^{AB} M_k^A)\) in the definition of one-way quantum deficit is given by

$$\begin{aligned} S\left( \sum _k M_k^A\varrho ^{AB} M_k^A\right)= & {} S\left( M_0^A\otimes p_0\varrho _{M_0^A}^{B}+M_1^A\otimes p_1\varrho _{M_1^A}^{B}\right) \nonumber \\= & {} S\left( p_0\varrho _{M_0^A}^{B}\right) +S\left( p_1\varrho _{M_1^A}^{B}\right) \nonumber \\= & {} -\sum \limits _{k,j\in \{0,1\}}p_k w_{kj} \log p_kw_{kj}\nonumber \\= & {} h(p_0)-\sum \limits _{k,j\in \{0,1\}}p_k w_{kj} \log w_{kj}. \end{aligned}$$
(9)

Substituting Eq. (7) into above equation, we have

$$\begin{aligned} S\left( \sum _k M_k^A\varrho ^{AB} M_k^A\right) =h(p_0)+\sum _k p_kS\left( \varrho _{M_k^A}^{B}\right) , \end{aligned}$$
(10)

which is joint entropy theorem [26].

Let us set

$$\begin{aligned} \mathcal {F}= & {} S(\varrho ^{A})+\sum _k p_k S\left( \varrho _{M_k^A}^{B}\right) -S\left( \varrho ^{AB}\right) , \end{aligned}$$
(11)
$$\begin{aligned} \mathcal {G}= & {} S\left( \sum _k M_k^A\varrho ^{AB}M_k^A\right) -S\left( \varrho ^{AB}\right) . \end{aligned}$$
(12)

Inserting Eqs. (7), (9) into Eqs. (11), (12), respectively, we have

$$\begin{aligned} \mathcal {F}= & {} S(\varrho ^{A})-\sum \limits _{k,j\in \{0,1\}}p_k w_{kj} \log w_{kj}-S(\varrho ^{AB}), \end{aligned}$$
(13)
$$\begin{aligned} \mathcal {G}= & {} h(p_0)-\sum \limits _{k,j\in \{0,1\}}p_k w_{kj} \log w_{kj}-S(\varrho ^{AB}). \end{aligned}$$
(14)

To search for the minimization involved in computing quantum discord and one-way quantum deficit is equivalent to seek for the minimal value of the function \(\mathcal {F}\) and \(\mathcal {G}\) with respect to the two parameters \(\theta \) and \(\phi \) in the measurement operators. According to the similar technique used in calculating the quantum discord which only need to minimize \(\mathcal {F}(\theta , 0)\) [27], here to minimize \(\mathcal {G}(\theta , \phi )\), we only need to minimize \(\mathcal {G}(\theta , 0)\) in calculating the one-way quantum deficit. We denote

$$\begin{aligned} G(\theta , \phi )=S\left( \sum _k M_k^A\varrho ^{AB} M_k^A\right) =-\sum \limits _{k,j\in \{0,1\}}p_k w_{kj} \log p_kw_{kj}=-\sum _{l=1}^4\lambda _l\log _2\lambda _l, \end{aligned}$$

where,

$$\begin{aligned} \lambda _{1,2}=\frac{1}{4} \left( p_{0}\pm \sqrt{R+T_0}\right) ,\quad \lambda _{3,4}=\frac{1}{4} \left( p_{1}\pm \sqrt{R+T_1}\right) , \end{aligned}$$

and \(p_{0}=1+ a \cos \theta \), \(p_{1}=1-a \cos \theta \), \(R=[c_x^2 \cos ^2\phi +c_y^2 \sin ^2\phi ]\sin ^2\theta \), \(T_{0}=\left( b+ c_z \cos \theta \right) {}^2\), \(T_{1}=\left( b-c_z \cos \theta \right) {}^2\). Since \(\lambda _l\geqslant 0\), one has \(p_{k}\geqslant \sqrt{R+T_{k}}\geqslant 0\).

Noting that \(G(\theta , \phi )=G(\pi -\theta , \phi )=G(\theta , 2\pi -\phi )\) and \(G(\theta , \phi )\) is symmetric with respect to \(\theta =\pi /2\) and \(\phi =\pi \), we only need to consider the case of \(\theta \in [0, \pi /2]\) and \(\phi \in [0,\pi )\). The extreme points of \(G(\theta , \phi )\) are determined by the first partial derivatives of G with respect to \(\theta \) and \(\phi \),

$$\begin{aligned} \frac{\partial G}{\partial \theta }=-\frac{\sin \theta }{4}H_{\theta }, \end{aligned}$$
(15)

with

$$\begin{aligned} H_{\theta }= & {} \frac{R\csc \theta \cot \theta -c_z \sqrt{T_0}}{\sqrt{R+T_0}}\log _2\frac{p_0 +\sqrt{R+T_0}}{p_0 -\sqrt{R+T_0}}+a\log _2\frac{p_1^2-(R+T_1)}{p_0^2-(R+T_0)}\nonumber \\&+\,\frac{R\csc \theta \cot \theta +c_z \sqrt{T_1}}{\sqrt{R+T_1 }}\log _2\frac{p_1 +\sqrt{R+T_1}}{p_1 -\sqrt{R+T_1}}, \end{aligned}$$
(16)

and

$$\begin{aligned} \frac{\partial G}{\partial \phi }=2\,ef\sin ^2\theta \,\sin 2\phi \, H_{\phi }, \end{aligned}$$
(17)

with

$$\begin{aligned} H_{\phi }=\frac{1}{\sqrt{R+T_0}}\log _2\frac{p_0 +\sqrt{R+T_0}}{p_0 -\sqrt{R+T_0}} +\frac{1}{\sqrt{R+T_1}}\log _2\frac{p_1 +\sqrt{R+T_1}}{p_1 -\sqrt{R+T_1}}, \end{aligned}$$
(18)

\(e=\frac{1}{4}|c_x+c_y|\) and \(f=\frac{1}{4}|c_x-c_y|\) where the absolute values have been taken since the phase for X states can be always removed by local unitary operation [15].

As \(H_{\phi }\) is always positive, \(\frac{\partial G}{\partial \phi }=0\) implies that either \(\phi =0, \pi /2\) for any \(\theta \), or \(\theta =0\) for any \(\phi \) which implies that Eq. (15) is zero and the minimization is independent on \(\phi \). If \(\theta \ne 0\), one gets the second derivative of G,

$$\begin{aligned} \left. \frac{\partial ^2G}{\partial \phi ^2}\right| _{(\theta ,0)}=4ef\sin ^2(\theta )H_{\phi =0}>0, \end{aligned}$$

and

$$\begin{aligned} \left. \frac{\partial ^2G}{\partial \phi ^2}\right| _{(\theta ,\pi /2)}=-4ef\sin ^2(\theta )H_{\phi =\pi /2}<0. \end{aligned}$$

Since for any \(\theta \) the second derivative \(\partial ^2 G/\partial \phi ^2\) is always negative for \(\phi =\pi /2\), we only need to deal with the minimization problem for the case of \(\phi =0\). To minimize \(G(\theta , \phi )\) becomes to minimize \(G(\theta , 0)\). Thus, we need only to find the minimal value of \(\mathcal {F}\) and \(\mathcal {G}\) by varying \(\theta \) only.

Denote \(\mathcal {F}(\theta )=\mathcal {F}|_{\phi =0}\), \(\mathcal {G}(\theta )=\mathcal {G}|_{\phi =0}\) and \(\mathcal {H}(\theta )=\mathcal {G}(\theta )-\mathcal {F}(\theta )\). The first derivative of \(\mathcal {H}(\theta )\) with respect to \(\theta \) is given by

$$\begin{aligned} \mathcal {H}(\theta )'=\frac{a}{2} \sin \theta \log _2 \frac{1+a \cos \theta }{1-a \cos \theta }. \end{aligned}$$
(19)

From \(\mathcal {H}(\theta )'=0\), we have either \(a=0\) or \(\theta =0,\pi /2\). Since these stationary points make \(\mathcal {F}(\theta )'=\mathcal {G}(\theta )'\), they are the sufficient conditions that both \(\mathcal {G}(\theta )\) and \(\mathcal {F}(\theta )\) reach the minimum with the same optimal measurement ensemble. Here a is a parameter of the X states and \(\theta \) is a parameter related to measurement. Substituting \(a=0\) or \(\theta =0,\pi /2\) into \(\mathcal {F}(\theta )\) and \(\mathcal {G}(\theta )\), we have the following results:

Theorem

For two-qubit X states, if the measurement is performed on the subsystem A (resp. B), then \(\overset{\rightharpoonup }{{{\Delta }}}=\overset{\rightharpoonup }{{{\delta }}}\) for \(a=0\) (resp. \(b=0\)). Depending on the parameters of the state, the optimum is either at \(\theta =0\) or at \(\theta =\pi /2\). If the optimum is at \(\theta =0\), then \(\overset{\rightharpoonup }{{{\Delta }}}=\overset{\rightharpoonup }{{{\delta }}}\). If the optimum is at \(\theta =\pi /2\), then \(\overset{\rightharpoonup }{{{\Delta }}}= \overset{\rightharpoonup }{{{\delta }}}-S(\varrho ^A)+1\).

Recently, we notice that in Ref. [28], the authors assumed that the quantum discord and one-way quantum deficit get their minimal values in the same measurement ensemble simultaneously. Thus similar to the quantum discord, the frozen quantum phenomenon under bit flip channels of one-way quantum deficit happens. Here, our Theorem gives the explicit conditions that both quantum discord and one-way quantum deficit have the same optimal measurement bases.

Corollary 1

The one-way quantum deficit is bounded by the quantum discord for two-qubit X states,

$$\begin{aligned} \overset{\rightharpoonup }{{\delta }} \leqslant \overset{\rightharpoonup }{{\Delta }} \leqslant S(\rho ^A). \end{aligned}$$
(20)

Proof

Since \(0\leqslant \mathcal {H}\leqslant 1\), we have \(\overset{\rightharpoonup }{{\delta }}\leqslant \overset{\rightharpoonup }{{\Delta }} \leqslant \overset{\rightharpoonup }{{\delta }}+1\) . By using the tight bound about one-way quantum deficit \(\Delta \leqslant S(\rho ^A)\) in Ref. [26], we obtain (20). \(\square \)

Corollary 2

One-way quantum deficit and the entanglement of formation satisfy the following relations for two-qubit X states,

$$\begin{aligned} \overset{\rightharpoonup }{{{\Delta }}}= & {} E_f(\varrho ^{BC})-S(\varrho ^{AB}) +\left\{ \begin{array}{ll} 1, &{} \hbox {a}=0\; \hbox {or}\;\theta =\pi /2; \\ h\left( \frac{1-a}{2}\right) , &{} \theta =0, \end{array}\right. \end{aligned}$$
(21)

where C is the assisted system to purify the state \(\varrho ^{AB}\), and \(E_f(\varrho ^{BC})\) is the entanglement of formation of \(\varrho ^{BC}\), while \(\varrho ^{BC}\) is the reduced state from a pure state \(|\psi \rangle _{ABC}\).

Proof

From the Koashi–Winter equality [29]

$$\begin{aligned} S(\varrho ^{B})=\mathcal {J}(\varrho ^{AB})+E_f(\varrho ^{BC}), \end{aligned}$$
(22)

and \(\mathcal {J}(\varrho ^{AB})=S(\varrho ^B)-\min \sum _k p_kS(\varrho _{M_k^A}^{B})\), one has \(E_f(\varrho ^{BC})=\min \sum _k p_kS(\varrho _{M_k^A}^{B})\). Consequently, quantum discord is rewritten as

$$\begin{aligned} \overset{\rightharpoonup }{{{\delta }}}=S(\varrho ^{A})+E_f(\varrho ^{BC})-S(\varrho ^{AB}). \end{aligned}$$
(23)

Thus, we have

$$\begin{aligned} \overset{\rightharpoonup }{{{\Delta }}}= \overset{\rightharpoonup }{{{\delta }}} =h\left( \frac{1-a}{2}\right) +E_f(\varrho ^{BC})-S(\varrho ^{AB}), \end{aligned}$$
(24)

where both of the optimal measurement bases are taken at \(\theta =0\). Hence for \(a=0\), we have \(\overset{\rightharpoonup }{{{\Delta }}}=E_f(\varrho ^{BC})-S(\varrho ^{AB})+1\) indeed. For \(\theta =\pi /2\), by using the relations in Theorem and Eq. (23) we also get \(\overset{\rightharpoonup }{{{\Delta }}}=E_f(\varrho ^{BC})-S(\varrho ^{AB})+1\). \(\square \)

Remark

Recently, in Ref. [21] by using measure of relative entropy of coherence,

$$\begin{aligned} C_{RE}(\varrho ^A)=\min _{\sigma \in \mathcal {I}} S(\varrho ^A||\sigma ), \end{aligned}$$
(25)

where \(\mathcal {I}\) stands for the set of decoherence states \(\sigma =\sum _i\mu _i|i\rangle \langle i|\) with \(\mu _i\in [0,1]\) and \(\sum _i\mu _i=1\), and the authors provided a tradeoff relationship between \(\overset{\rightharpoonup }{{\delta }}\) and \(\overset{\rightharpoonup }{{\Delta }}\), i. e., \(\overset{\rightharpoonup }{{{\delta }}}+C_{RE}(\varrho ^{A}) =\overset{\rightharpoonup }{{\Delta }}\).

In fact, one-way quantum deficit can be derived from quantum discord directly. We consider the exact relationship between quantum discord and one-way quantum deficit in the following examples.

Example 1

The Bell-diagonal state \(\varrho _{Bell}^{AB}=\frac{1}{4}(I_2\otimes I_2+\sum _{i\in \{x,y,z\}}c_i\sigma _i\otimes \sigma _i)\). In this case \(a=0\) and

$$\begin{aligned} \overset{\rightharpoonup }{{{\Delta }}} =\overset{\rightharpoonup }{{{\delta }}} =h\left( \frac{1-c}{2}\right) +\sum _{s\in \{jkl\}}A_s\log _2 A_s, \end{aligned}$$
(26)

where s is the set \( \{jkl\}=\{111,100,010,001\}\), \(A_{jkl}=\frac{1}{4}(1+(-1)^jc_x+(-1)^kc_y+(-1)^lc_z)\), and \(c\equiv \max \{|c_x|, |c_y|, |c_z|\}\). Therefore, from Theorem we get the analytical expression of one-way quantum deficit from quantum discord given in [30].

Example 2

Consider a class of X-state,

$$\begin{aligned} \varrho _q^{AB}=q|\psi ^-\rangle \langle \psi ^-|+(1-q)|00\rangle \langle 00|, \end{aligned}$$
(27)

where \(|\psi ^-\rangle =\frac{1}{\sqrt{2}}(|01\rangle -|10\rangle \)).

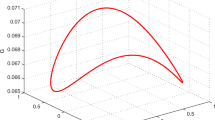
For this state, quantum discord is derived at \(\theta =\pi /2\) for \(q\in [0,1]\). The optimal basis of one-way quantum deficit for \(q\in [0.67,1]\) is also at \(\theta =\pi /2\). The value 0.67 is the solution of \(H_{\theta }'|_{\theta =\pi /2,\phi =0}=0\) in Eq. (16) for the state \(\varrho _q^{AB}\). According to the Theorem, we have

$$\begin{aligned} \overset{\rightharpoonup }{{{\Delta }}}= E_f(\varrho ^{BC})-S(\varrho ^{AB})+1, \end{aligned}$$
(28)

where the entanglement of formation

$$\begin{aligned} E_f(\varrho ^{BC})=h\left( \frac{1+\sqrt{1-\mathcal {C}^2}}{2}\right) \end{aligned}$$
(29)

with concurrence \(\mathcal {C}=\sqrt{2q(1-q)}\). So analytical one-way quantum deficit of state \(\varrho _q^{AB}\) is

$$\begin{aligned} \overset{\rightharpoonup }{{{\Delta }}} =h\left( \frac{1+\sqrt{1-\mathcal {C}^2}}{2}\right) -h(q)+1 \end{aligned}$$
(30)

for \(q\in [0.67, 1]\), see Fig. 1.

Fig. 1
figure 1

One-way quantum deficit (turquoise solid line) and quantum discord (blue dashed line) versus q. The interval \(q\in [0.67, 1]\) one-way quantum deficit and quantum discord both get their optimum at \(\theta =\pi /2\) (Color figure online)

Full size image

3 Quantum correlations under phase damping channel

A quantum system would be subject to interaction with environments. We consider now the evolution of one-way quantum deficit and quantum discord under noisy channels. Consider a class of initial two-qubit states,

$$\begin{aligned} \Omega =\frac{1}{4}\left( I_2\otimes I_2+bI_2\otimes \sigma _z +\sum _{i\in \{x,y,z\}}c_i\sigma _i\otimes \sigma _i\right) . \end{aligned}$$
(31)

If both two qubits independently go through a channel given by the Kraus operators \(\{K_i\}\), \(\sum _i K_i^\dagger K_i=I\). The state \(\Omega \) evolves into

$$\begin{aligned} \tilde{\Omega }=\sum _{i,j\in \{1,2\}}K_i^A\otimes K_j^B\cdot \Omega \cdot \left[ K_i^A\otimes K_j^B\right] ^\dagger . \end{aligned}$$
(32)

For phase damping channels [31], the Kraus operators are given by \(K_1^{A(B)}=|0\rangle \langle 0|+\sqrt{1-\gamma }|1\rangle \langle 1|\), and \(K_2^{A(B)}=\sqrt{\gamma }|1\rangle \langle 1|\) with the decoherence rate \(\gamma \in [0,1]\). Thus we have

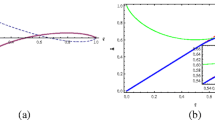
$$\begin{aligned} \tilde{\Omega }=\frac{1}{4}\left[ I_2\otimes I_2+bI_2\otimes \sigma _z +c_z\sigma _z\otimes \sigma _z+\sum _{i\in \{x,y\}}(1-\gamma )c_i\sigma _i\otimes \sigma _i\right] , \end{aligned}$$
(33)

which is a two-qubit X state with \(a=0\). From the Theorem, we obtain one-way quantum deficit and quantum discord performed on the subsystem A evolve coincidentally with each other all the time.

For example, we draw the quantum discord and one-way quantum deficit vs parameter \(\gamma \) in Fig. 2 for \(b=0.26\), \(c_x=0.13\), \(c_z=0.08\), and \(c_y=0.15, 0.25, 0.35, 0.45, 0.55\), respectively.

Fig. 2
figure 2

One-way quantum deficit and quantum discord evolve exactly in the same way under phase damping channel. The solid lines from bottom to top correspond \(c_y=0.15, 0.25, 0.35, 0.45, 0.55\), respectively, for fixed parameters \(b=0.26, c_x=0.13\), and \(c_z=0.08\)

Full size image

4 Conclusions

We have investigated the connections between one-way quantum deficit and quantum discord for two-qubit X states. Sufficient conditions are given that the one-way quantum deficit can be derived from quantum discord directly. The explicit relation between one-way quantum deficit and entanglement of formation is also presented. Moreover, we have shown that the one-way quantum deficit and quantum discord of a class of four parameters X states evolve coincidentally under phase damping channel. Our results may enlighten the understanding on the relations between one-way quantum deficit and quantum discord. It is also interesting to study the relationship between one-way quantum deficit and quantum discord for higher-dimensional and multipartite systems.