Schemes for remotely preparing an arbitrary four-qubit $\chi$-state

Abstract

Two schemes via different entangled resources as the quantum channel are proposed to realize remote preparation of an arbitrary four-particle $\chi$-state with high success probabilities. To design these protocols, some useful and general measurement bases are constructed, which have no restrictions on the coefficients of the prepared states. It is shown that through a four-particle projective measurement and two-step three-particle projective measurement under the novel sets of mutually orthogonal basis vectors, the original state can be prepared with the probability 50 and 100 %, respectively. And for the first scheme, the special cases of the prepared state that the success probability reaches up to 100 % are discussed by the permutation group. Furthermore, the present schemes are extended to the non-maximally entangled quantum channel, and the classical communication costs are calculated.

1 Introduction

One of the main tasks in quantum communication is transmitting a quantum state from one place to another as information is carried by a quantum state. Bennett et al. [1] first brought out a remarkable scheme called quantum teleportation to transmit an unknown qubit by utilizing a prior shared entanglement and some classical communication. Subsequently, Lo [2] proposed another interesting scheme called remote state preparation (RSP) to transmit a pure known quantum state. It has been shown that for some special ensembles of states, RSP protocols are more economical than quantum teleportation as the required quantum entanglement and classical communication cost (CCC) can be reduced in the case that the sender knows the state. For example, the RSP protocol proposed by Pati [3] requires only one classical bit from the sender to the receiver for a qubit chosen from equatorial or polar great circles on a Bloch sphere, while in standard teleportation two classical bits are needed. The trade-off between the classical communication cost and the required entanglement in RSP protocol has been studied distinctly by Bennett et al. [4]. So far, remote state preparation has received much attention both theoretically [5–21] and experimentally [22–28] due to its important application in quantum communication.

Quantum entanglement has been widely studied recently as it is the foundational resource of quantum information processing. One important work is that Yeo et al. [29] studied a genuine maximally entangled four-qubit $\chi$-state

$$\begin{aligned}&x_0|0000\rangle +x_1|0011\rangle +x_2|0101\rangle +x_3|0110\rangle \nonumber \\&\quad +x_4|1001\rangle +x_5|1010\rangle +x_6|1100\rangle +x_7|1111\rangle , \end{aligned}$$

(1)

where $x_0,\,x_1,\ldots ,x_7$ are complex and satisfy $\sum \nolimits _{i=0}^{7}|x_i|^2=1$. $\chi$-type entangled state is a special four-particle entangled state, which is different from a four-particle GHZ or W state under stochastic local operations and classical communication. It is known that the $\chi$-state has many interesting entanglement properties and is a very important entangled resource. For example, the $\chi$-state has been widely applied in teleportation, superdense coding [29], quantum secure direct communication [30] and quantum information splitting [31]. Recently, Qu et al. [32] investigated quantum steganography with large payload based on the entanglement swapping of $\chi$-states. Therefore, it is meaningful to investigate the preparation of $\chi$-state. Some schemes have been widely explored to prepare $\chi$-state in different systems [33–36], such as ion trap systems [33], cavity QED systems [34, 35] and linear optics elements [36]. However, few scheme [37] has been designed to prepare $\chi$-state at a remote site, which is very important for quantum network communication.

In this paper, we investigate the remote preparation of a four-particle $\chi$-state in Eq. (1). This general state includes more free coefficients comparing with the previous remote preparation of a four-particle GHZ state or cluster state with no more than four coefficients [10, 14–16]. Thus, the sender needs to construct a larger measurement basis. In fact, two schemes via maximally entangled states as the quantum channels are proposed to realize the remote preparation with high probabilities. In Sect. 2, we propose the first scheme using two EPR pairs and a four-particle GHZ state as the shared quantum resources, and construct a new set of measurement basis, which plays an important role in our scheme. It is shown that the $\chi$-state can be prepared with the success probability 50 % if the sender performs a four-particle projective measurement under this basis and the receiver adopts some appropriate unitary transformations. Also, some special cases that the success probability can reach up to 100 % are discussed by the permutation group. In Sect. 3, with the aid of two-step three-particle orthogonal basis projective measurement, a deterministic scheme is proposed. These schemes are extended to the non-maximally entangled quantum channel in Sect. 4. The classical communication costs of the two schemes are calculated in Sect. 5, while some discussions and conclusions are given in the last section.

2 Two EPR pairs and a four-qubit GHZ state as the quantum channel

The sender Alice wants to help the receiver Bob remotely prepare a four-qubit $\chi$-state in Eq. (1). Alice knows about $x_0,\ldots ,x_7$ completely, but Bob does not know them at all.

Assume that the sender Alice and the receiver Bob share two EPR pairs and a four-particle GHZ state

$$\begin{aligned} |\Phi \rangle _{1B_1}&= \frac{1}{\sqrt{2}}(|00\rangle +|11\rangle )_{1B_1}\nonumber \\ |\Phi \rangle _{2B_2}&= \frac{1}{\sqrt{2}}(|00\rangle +|11\rangle )_{2B_2}\\ |\Phi \rangle _{34B_3B_4}&= \frac{1}{\sqrt{2}}(|0000\rangle +|1111\rangle )_{34B_3B_4 }\nonumber \end{aligned}$$

(2)

as the quantum channel. The particles $(1,2,3,4)$ are held by Alice, while the particles $(B_1,B_2,B_3,B_4)$ belong to Bob. Hence, the initial state of the whole system can be written as

$$\begin{aligned} |\Psi \rangle _{1234B_1B_2B_3B_4}&= |\Phi \rangle _{1B_1}\otimes |\Phi \rangle _{2B_2}\otimes |\Phi \rangle _{34B_3B_4}\nonumber \\&= \frac{1}{2\sqrt{2}}(|00000000\rangle +|00110011\rangle +|01110111\rangle \nonumber \\&+|01000100\rangle +|10111011\rangle +|10001000\rangle +|11001100\rangle \nonumber \\&+|11111111\rangle )_{1234B_1B_2B_3B_4}. \end{aligned}$$

(3)

In order to realize the RSP with a high probability, we need to construct a set of useful measurement basis that relies on the parameters $x_0,\ldots ,x_7$ of the prepared $\chi$-state. Firstly, construct an $8\times 16$ matrix

$$\begin{aligned} M=(F\quad F^*), \end{aligned}$$

(4)

where

$$\begin{aligned} F=\frac{1}{\sqrt{2}}\left( \begin{array}{cccccccc} x_0 &{}\quad x_1 &{}\quad x_2 &{}\quad x_3 &{}\quad x_4 &{}\quad x_5 &{}\quad x_6 &{}\quad x_7\\ x_1 &{}\quad -x_0 &{}\quad x_3 &{}\quad -x_2 &{}\quad x_5 &{}\quad -x_4 &{}\quad -x_7 &{}\quad x_6\\ x_2 &{}\quad -x_3 &{}\quad -x_0 &{}\quad x_1 &{}\quad x_6 &{}\quad x_7 &{}\quad -x_4 &{}\quad -x_5\\ x_3 &{}\quad x_2 &{}\quad -x_1 &{}\quad -x_0 &{}\quad x_7 &{}\quad -x_6 &{}\quad x_5 &{}\quad -x_4\\ x_4 &{}\quad -x_5 &{}\quad -x_6 &{}\quad -x_7 &{}\quad -x_0 &{}\quad x_1 &{}\quad x_2 &{}\quad x_3\\ x_5 &{}\quad x_4 &{}\quad -x_7 &{}\quad x_6 &{}\quad -x_1 &{}\quad -x_0 &{}\quad -x_3 &{}\quad x_2\\ x_6 &{}\quad x_7 &{}\quad x_4 &{}\quad -x_5 &{}\quad -x_2 &{}\quad x_3 &{}\quad -x_0 &{}\quad -x_1\\ x_7 &{}\quad -x_6 &{}\quad x_5 &{}\quad x_4 &{}\quad -x_3 &{}\quad -x_2 &{}\quad x_1 &{}\quad -x_0 \end{array} \right) . \end{aligned}$$

(5)

It is noticed that all the row vectors in the matrix $M$ form unit orthogonal vector set. Thus, an $8\times 16$ matrix $N$ dependent on $x_0,\ldots ,x_7$ can always be found such that $\left( \begin{array}{c} M\\ N \end{array} \right)$ is a $16\times 16$ unitary matrix. For example, such a matrix $N$ can be found by performing the Gram-Schmidt orthogonal procedure on the linearly independent vector set which includes each row vector in the matrix $M$. In the following, we give an explicit expression of the matrix $N$. Notice that

$$\begin{aligned} FF^{\dagger }+F^*F^\mathrm{T}=E_8, \quad FF^\mathrm{T}=\lambda E_8, \end{aligned}$$

(6)

where $^\dagger$ denotes the conjugate transpose of a matrix, $^*$ denotes the conjugate of a matrix, $^\mathrm{T}$ denotes the transpose of a matrix, $E$ denotes the identity matrix, $\lambda =\frac{1}{2}\sum \nolimits _{i=0}^7x_i^2$. Then, we can take

$$\begin{aligned} N=\left( F^*, -\frac{\lambda ^*}{\lambda }F\right) , \end{aligned}$$

(7)

the constant $-\frac{\lambda ^*}{\lambda }$ is defined by 1 in the case that $\lambda =0$.

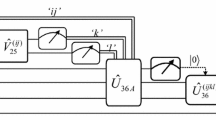
Alice performs a four-particle projective measurement on her particles $(1,2,3,4)$ under the basis $\{|\zeta _1\rangle ,\ldots ,|\zeta _{16}\rangle \}$, which has the following relationship to the computation basis $\{|0000\rangle ,\ldots ,|1111\rangle \}$:

$$\begin{aligned} \left( \begin{array}{ll} |\zeta _1\rangle \\ |\zeta _2\rangle \\ |\zeta _3\rangle \\ |\zeta _4\rangle \\ |\zeta _5\rangle \\ |\zeta _6\rangle \\ |\zeta _7\rangle \\ |\zeta _8\rangle \\ |\zeta _9\rangle \\ |\zeta _{10}\rangle \\ |\zeta _{11}\rangle \\ |\zeta _{12}\rangle \\ |\zeta _{13}\rangle \\ |\zeta _{14}\rangle \\ |\zeta _{15}\rangle \\ |\zeta _{16}\rangle \end{array} \right) = \left( \begin{array}{c} M\\ N \end{array} \right) ^{\dagger }\left( \begin{array}{l} |0000\rangle \\ |0011\rangle \\ |0111\rangle \\ |0100\rangle \\ |1011\rangle \\ |1000\rangle \\ |1100\rangle \\ |1111\rangle \\ |0001\rangle \\ |0010\rangle \\ |0101\rangle \\ |0110\rangle \\ |1001\rangle \\ |1010\rangle \\ |1101\rangle \\ |1110\rangle \end{array} \right) . \end{aligned}$$

(8)

By the way, the 16 states $|\zeta _1\rangle ,\ldots ,|\zeta _{16}\rangle$ form a complete orthogonal basis in 16-dimensional Hilbert space $\mathcal{C}^{16}$ since $\left( \begin{array}{cc} M\\ N \end{array} \right)$ is a $16\times 16$ unitary matrix. After the measurement, Alice tells Bob the measurement result through a classical channel.

To see how our protocol works, let us express the quantum channel in terms of the measurement basis. The state $|\Psi \rangle _{1234B_1B_2B_3B_4}$ in Eq. (3) can be expanded as

$$\begin{aligned} |\Psi \rangle _{1234B_1B_2B_3B_4}&= \frac{1}{4}[ |\zeta _1\rangle _{1234}(x_0|0\rangle +x_1|3\rangle +x_2|7\rangle +x_3|4\rangle \nonumber \\&+\,x_4|11\rangle +x_5|8\rangle +x_6|12\rangle +x_7|15\rangle )_{B_1B_2B_3B_4}\nonumber \\&+\,|\zeta _2\rangle _{1234}(x_1|0\rangle -x_0|3\rangle -x_3|7\rangle +x_2|4\rangle \nonumber \\&-\,x_5|11\rangle +x_4|8\rangle +x_7|12\rangle -x_6|15\rangle )_{B_1B_2B_3B_4}\nonumber \\&+\,|\zeta _3\rangle _{1234}(x_2|0\rangle +x_3|3\rangle -x_0|7\rangle -x_1|4\rangle \nonumber \\&-\,x_6|11\rangle -x_7|8\rangle +x_4|12\rangle +x_5|15\rangle )_{B_1B_2B_3B_4}\nonumber \\&+\,|\zeta _4\rangle _{1234}(x_3|0\rangle -x_2|3\rangle +x_1|7\rangle -x_0|4\rangle \nonumber \\&-\,x_7|11\rangle +x_6|8\rangle -x_5|12\rangle +x_4|15\rangle )_{B_1B_2B_3B_4}\nonumber \\&+\,|\zeta _5\rangle _{1234}(x_4|0\rangle +x_5|3\rangle +x_6|7\rangle +x_7|4\rangle \nonumber \\&-\,x_0|11\rangle -x_1|8\rangle -x_2|12\rangle -x_3|15\rangle )_{B_1B_2B_3B_4}\nonumber \\&+\,|\zeta _6\rangle _{1234}(x_5|0\rangle -x_4|3\rangle +x_7|7\rangle -x_6|4\rangle \nonumber \\&+\,x_1|11\rangle -x_0|8\rangle +x_3|12\rangle -x_2|15\rangle )_{B_1B_2B_3B_4}\nonumber \\&+\,|\zeta _7\rangle _{1234}(x_6|0\rangle -x_7|3\rangle -x_4|7\rangle +x_5|4\rangle \nonumber \\&+\,x_2|11\rangle -x_3|8\rangle -x_0|12\rangle +x_1|15\rangle )_{B_1B_2B_3B_4}\nonumber \\&+\,|\zeta _8\rangle _{1234}(x_7|0\rangle +x_6|3\rangle -x_5|7\rangle -x_4|4\rangle \nonumber \\&+\,x_3|11\rangle +x_2|8\rangle -x_1|12\rangle -x_0|15\rangle )_{B_1B_2B_3B_4}\nonumber \\&+\,|\zeta _9\rangle _{1234}(x_0^*|0\rangle +x_1^*|3\rangle +x_2^*|7\rangle +x_3^*|4\rangle \nonumber \\&+\,x_4^*|11\rangle +x_5^*|8\rangle +x_6^*|12\rangle +x_7^*|15\rangle )_{B_1B_2B_3B_4}\nonumber \\&+\,|\zeta _{10}\rangle _{1234}(x_1^*|0\rangle -x_0^*|3\rangle -x_3^*|7\rangle +x_2^*|4\rangle \nonumber \\&-\,x_5^*|11\rangle +x_4^*|8\rangle +x_7^*|12\rangle -x_6^*|15\rangle )_{B_1B_2B_3B_4}\nonumber \\&+\,|\zeta _{11}\rangle _{1234}(x_2^*|0\rangle +x_3^*|3\rangle -x_0^*|7\rangle -x_1^*|4\rangle \nonumber \\&-\,x_6^*|11\rangle -x_7^*|8\rangle +x_4^*|12\rangle +x_5^*|15\rangle )_{B_1B_2B_3B_4}\nonumber \\&+\,|\zeta _{12}\rangle _{1234}(x_3^*|0\rangle -x_2^*|3\rangle +x_1^*|7\rangle -x_0^*|4\rangle \nonumber \\&-\,x_7^*|11\rangle +x_6^*|8\rangle -x_5^*|12\rangle +x_4^*|15\rangle )_{B_1B_2B_3B_4}\nonumber \\&+\,|\zeta _{13}\rangle _{1234}(x_4^*|0\rangle +x_5^*|3\rangle +x_6^*|7\rangle +x_7^*|4\rangle \nonumber \\&-\,x_0^*|11\rangle -x_1^*|8\rangle -x_2^*|12\rangle -x_3^*|15\rangle )_{B_1B_2B_3B_4}\nonumber \\&+\,|\zeta _{14}\rangle _{1234}(x_5^*|0\rangle -x_4^*|3\rangle +x_7^*|7\rangle -x_6^*|4\rangle \nonumber \\&+\,x_1^*|11\rangle -x_0^*|8\rangle +x_3^*|12\rangle -x_2^*|15\rangle )_{B_1B_2B_3B_4}\nonumber \\&+\,|\zeta _{15}\rangle _{1234}(x_6^*|0\rangle -x_7^*|3\rangle -x_4^*|7\rangle +x_5^*|4\rangle \nonumber \\&+\,x_2^*|11\rangle -x_3^*|8\rangle -x_0^*|12\rangle +x_1^*|15\rangle )_{B_1B_2B_3B_4}\nonumber \\&+\,|\zeta _{16}\rangle _{1234}(x_7^*|0\rangle +x_6^*|3\rangle -x_5^*|7\rangle -x_4^*|4\rangle \nonumber \\&+\,x_3^*|11\rangle +x_2^*|8\rangle -x_1^*|12\rangle -x_0^*|15\rangle )_{B_1B_2B_3B_4}], \end{aligned}$$

(9)

where $|0\rangle =|0000\rangle ,\,|3\rangle =|0011\rangle ,\,|7\rangle =|0111\rangle ,\,|4\rangle =|0100\rangle ,\,|11\rangle =|1011\rangle ,\,|8\rangle =|1000\rangle ,\,|12\rangle =|1100\rangle ,\,|15\rangle =|1111\rangle$. It is transparent that only if Alice’s measurement outcome lies in $\{|\zeta _1\rangle ,\ldots ,|\zeta _8\rangle \}$, Bob can successfully recover the prepared state on his qubits $(B_1,B_2,B_3,B_4)$ by performing appropriate unitary operation. Bob first performs CNOT operations $C_{B_1B_3}C_{B_2B_3}$ on his qubits $(B_1,B_2,B_3)$ with $(B_1,B_2)$ being the controlled qubits, $B_3$ the target one. After the CNOT operations, Bob’s recovery operations conditioned on Alice’s measurement results are summarized in Table 1 ($X,Y,Z$ are Pauli operations).

Table 1 The relations among Alice’s measurement outcome (AMO), the transformed state (TS) after Bob performs CNOT operation $C_{B_1B_3}C_{B_2B_3}$ on the collapsed state and Bob’s appropriate unitary operation (BAUO) under the assumption that the $\chi$-state can be successfully prepared

Surely, it is also possible for Alice to get the measurement outcome $|\zeta _9\rangle , \cdots , |\zeta _{16}\rangle$. In contrast to the case of the former eight outcomes $|\zeta _1\rangle , \cdots , |\zeta _8\rangle$, for the latter eight outcomes, Bob is not able to convert the collapsed state into the $\chi$-state due to lack of $x_0,\ldots ,x_7$. Alice’s measurement outcome may be one of the sixteen states $\{|\zeta _j\rangle ,j=1,\ldots ,16\}$ and each one occurs with the equal probability $\frac{1}{16}$. Therefore, the total success probability is $8\times \frac{1}{16}=\frac{1}{2}$ in the general condition.

It naturally arises an intriguing question: if these coefficients of the prepared state are some special values, can the $\chi$-state be prepared with unit success probability? After extensive investigation, we give the following classification criterion.

Criterion   The $\chi$-state in Eq. (1) can be prepared under the scheme with unit success probability if and only if the coefficients $x_0,\ldots ,x_7$ satisfy

$$\begin{aligned} (x_0^*,x_1^*,x_2^*,x_3^*,x_4^*,x_5^*,x_6^*,x_7^*)=e^{i\tau _g} g(\pm x_0,\pm x_1, \pm x_2, \pm x_3, \pm x_4,\pm x_5, \pm x_6, \pm x_7), \end{aligned}$$

(10)

where $\tau _g$ is a real constant which depends on the permutation $g\in S_8$. Here, $S_8$ denotes the permutation group on the eight letters $\{a,b,c,d,e,f,g,h\}$ [38].

From Eq. (10) and the condition $\sum \nolimits _{i=0}^7|x_i|^2=1$, one can calculate the ensembles of coefficients that the $\chi$-state can be prepared with unit probability. In the following, an example is given to illustrate that for the special ensembles under the criterion, Bob can employ appropriate unitary operations to convert each collapsed state to the prepared state when Alice’s measurement outcome lies in $\{|\zeta _9\rangle _{1234},\ldots ,|\zeta _{16}\rangle _{1234}\}$. Suppose Alice’s measurement outcome is $|\zeta _9\rangle _{1234}$, she informs Bob of her outcome via a classical channel. For convenience, we use the following short notation:

$$\begin{aligned} |f(y_0,\ldots ,y_7)\rangle&= y_0|0\rangle \!+\!y_1|3\rangle \!+\!y_2|7\rangle +y_3|4\rangle \!+\!y_4|11\rangle \!+\!y_5|8\rangle \!+\!y_6|12\rangle +y_7|15\rangle .\nonumber \\ \end{aligned}$$

(11)

As a consequence, Bob knows his qubits $(B_1,B_2,B_3,B_4)$ are now in the state

$$\begin{aligned} |f(x_0^*,x_1^*,x_2^*,x_3^*,x_4^*,x_5^*,x_6^*,x_7^*)\rangle \end{aligned}$$

(12)

which can be rewritten as

$$\begin{aligned} |f(g(\pm x_0,\pm x_1, \pm x_2, \pm x_3, \pm x_4, \pm x_5, \pm x_6, \pm x_7))\rangle \end{aligned}$$

(13)

up to a global phase $e^{i\tau _g}$. Then, Bob can perform appropriate unitary operations on his particles $(B_1,B_2,B_3,B_4)$ and get the $\chi$-state.

3 Two three-qubit GHZ states and a four-qubit GHZ state as the quantum channel

In this section, we demonstrate the other deterministic scheme by performing two-step three-particle projective measurement and adding local operation.

Suppose the quantum channel shared between the sender Alice and the receiver Bob is two three-qubit GHZ states and a four-qubit GHZ state:

$$\begin{aligned} \begin{array}{ll} |\Phi \rangle _{14B_1}=\frac{1}{\sqrt{2}}(|000\rangle +|111\rangle )_{14B_1},\\ |\Phi \rangle _{25B_2}=\frac{1}{\sqrt{2}}(|000\rangle +|111\rangle )_{25B_2},\\ |\Phi \rangle _{36B_3B_4}=\frac{1}{\sqrt{2}}(|0000\rangle +|1111\rangle )_{36B_3B_4}. \end{array} \end{aligned}$$

(14)

The particles $(1,2,3,4,5,6)$ are held by Alice, while the particles $(B_1,B_2,B_3,B_4)$ by Bob. Obviously, the initial state of the combined system can be expressed as

$$\begin{aligned} \begin{array}{ll} |\Psi \rangle _{123456B_1B_2B_3B_4} &{}=|\Phi \rangle _{14B_1}\otimes |\Phi \rangle _{25B_2}\otimes |\Phi \rangle _{36B_3B_4}\\ &{}=\frac{1}{2\sqrt{2}}\sum \limits _{p,q,t=0}^1|pqtpqtpqtt\rangle _{123456B_1B_2B_3B_4}. \end{array} \end{aligned}$$

(15)

Notice that the four-qubit $\chi$-state in Eq. (1) can be rewritten as

$$\begin{aligned} |\chi \rangle&= r_0e^{i\theta _0}|0000\rangle +r_1e^{i\theta _1}|0011\rangle +r_2e^{i\theta _2}|0101\rangle +r_3e^{i\theta _3}|0110\rangle \nonumber \\&+\,r_4e^{i\theta _4}|1001\rangle +r_5e^{i\theta _5}|1010\rangle +r_6e^{i\theta _6}|1100\rangle +r_7e^{i\theta _7}|1111\rangle , \end{aligned}$$

(16)

where $r_je^{i\theta _j}=x_j,j=0,1,\ldots ,7$, real coefficients $r_j\ge 0$ with the normalization condition $\sum \nolimits _{j=0}^7r_j^2=1$, and $\theta _j \in [0,2\pi ),j=0,1,\ldots ,7$. Since Alice knows $x_j$, she knows $r_j,\,\theta _j$ completely. Alice first performs a three-particle projective measurement on the particle $(1,2,3)$ under the complete orthogonal basis $\{|\xi _0\rangle ,\ldots ,|\xi _7\rangle \}$, which are related to the computation basis $\{|000\rangle ,\ldots ,|111\rangle \}$ by the following relation:

$$\begin{aligned} \left( \begin{array}{ll} |\xi _{0}\rangle \\ |\xi _{1}\rangle \\ |\xi _{2}\rangle \\ |\xi _{3}\rangle \\ |\xi _{4}\rangle \\ |\xi _{5}\rangle \\ |\xi _{6}\rangle \\ |\xi _{7}\rangle \\ \end{array} \right) = \left( \begin{array}{cccccccc} r_0 &{}r_1 &{}r_2 &{}r_3 &{}r_4 &{}r_5 &{}r_6 &{}r_7\\ r_1 &{}-r_0 &{}r_3 &{}-r_2 &{}r_5 &{}-r_4 &{}r_7 &{}-r_6\\ r_2 &{}-r_3 &{}-r_0 &{}r_1 &{}-r_6 &{}r_7 &{}r_4 &{}-r_5\\ r_3 &{}r_2 &{}-r_1 &{}-r_0 &{}r_7 &{}r_6 &{}-r_5 &{}-r_4\\ r_4 &{}-r_5 &{}r_6 &{}-r_7 &{}-r_0 &{}r_1 &{}-r_2 &{}r_3\\ r_5 &{}r_4 &{}-r_7 &{}-r_6 &{}-r_1 &{}-r_0 &{}r_3 &{}r_2\\ r_6 &{}-r_7 &{}-r_4 &{}r_5 &{}r_2 &{}-r_3 &{}-r_0 &{}r_1\\ r_7 &{}r_6 &{}r_5 &{}r_4 &{}-r_3 &{}-r_2 &{}-r_1 &{}-r_0 \end{array} \right) \left( \begin{array}{l} |000\rangle \\ |001\rangle \\ |010\rangle \\ |011\rangle \\ |100\rangle \\ |101\rangle \\ |110\rangle \\ |111\rangle \\ \end{array} \right) . \end{aligned}$$

(17)

After the measurement, Alice does not perform the second-step measurement immediately but performs a unitary operation $U^k$ on her particles (4,5,6) conditioned on her first measurement result $|\xi _k\rangle _{123},\,k\in \{0,1,2,3,4,5,6,7\}$. Here,

$$\begin{aligned} \begin{array}{llll} U^{0}=I\otimes I\otimes I,&{}U^{1}=I\otimes I\otimes X, &{}U^{2}=I\otimes X \otimes I,&{}U^{3}=I\otimes X\otimes X,\\ U^{4}=X\otimes I\otimes I,&{}U^{5}=X\otimes I\otimes X, &{}U^{6}=X\otimes X \otimes I,&{}U^{7}=X\otimes X\otimes X, \end{array} \end{aligned}$$

(18)

with $I$ is the identity operation, and $X$ is the Pauli operation. Then, Alice performs a three-particle projective measurement on the particles $(4,5,6)$ under the complete orthogonal basis $\{|\eta _0\rangle ,\ldots ,|\eta _7\rangle \}$, which are defined by

$$\begin{aligned} \begin{array}{ll} (|\eta _0\rangle , |\eta _1\rangle , |\eta _2\rangle , |\eta _3\rangle , |\eta _4\rangle , |\eta _5\rangle , |\eta _6\rangle , |\eta _7\rangle )^\mathrm{T}\\ =\frac{1}{2\sqrt{2}}\left( \begin{array}{cccccccc} e^{-i\theta _0} &{}e^{-i\theta _1} &{}e^{-i\theta _2} &{}e^{-i\theta _3} &{}e^{-i\theta _4} &{}e^{-i\theta _5} &{}e^{-i\theta _6} &{}e^{-i\theta _7}\\ e^{-i\theta _0} &{}-e^{-i\theta _1} &{}e^{-i\theta _2} &{}-e^{-i\theta _3} &{}e^{-i\theta _4} &{}-e^{-i\theta _5} &{}e^{-i\theta _6} &{}-e^{-i\theta _7}\\ e^{-i\theta _0} &{}-e^{-i\theta _1} &{}-e^{-i\theta _2} &{}e^{-i\theta _3} &{}e^{-i\theta _4} &{}-e^{-i\theta _5} &{}-e^{-i\theta _6} &{}e^{-i\theta _7}\\ e^{-i\theta _0} &{}e^{-i\theta _1} &{}-e^{-i\theta _2} &{}-e^{-i\theta _3} &{}e^{-i\theta _4} &{}e^{-i\theta _5} &{}-e^{-i\theta _6} &{}-e^{-i\theta _7}\\ e^{-i\theta _0} &{}-e^{-i\theta _1} &{}e^{-i\theta _2} &{}-e^{-i\theta _3} &{}-e^{-i\theta _4} &{}e^{-i\theta _5} &{}-e^{-i\theta _6} &{}e^{-i\theta _7}\\ e^{-i\theta _0} &{}e^{-i\theta _1} &{}-e^{-i\theta _2} &{}-e^{-i\theta _3} &{}-e^{-i\theta _4} &{}-e^{-i\theta _5} &{}e^{-i\theta _6} &{}e^{-i\theta _7}\\ e^{-i\theta _0} &{}e^{-i\theta _1} &{}e^{-i\theta _2} &{}e^{-i\theta _3} &{}-e^{-i\theta _4} &{}-e^{-i\theta _5} &{}-e^{-i\theta _6} &{}-e^{-i\theta _7}\\ e^{-i\theta _0} &{}-e^{-i\theta _1} &{}-e^{-i\theta _2} &{}e^{-i\theta _3} &{}-e^{-i\theta _4} &{}e^{-i\theta _5} &{}e^{-i\theta _6} &{}-e^{-i\theta _7} \end{array} \right) \left( \begin{array}{l} |000\rangle \\ |001\rangle \\ |010\rangle \\ |011\rangle \\ |100\rangle \\ |101\rangle \\ |110\rangle \\ |111\rangle \end{array} \right) . \end{array}\nonumber \\ \end{aligned}$$

(19)

To see how our protocol works, without loss of generality, assume Alice’s first measurement result on her particles (1,2,3) is $|\xi _{1}\rangle _{123}$. Then, the particles collapse into

$$\begin{aligned}&(r_1|0000000\rangle -r_0|0010011\rangle +r_3|0100100\rangle -r_2|0110111\rangle \nonumber \\&\quad +\,r_5|1001000\rangle -r_4|1011011\rangle +r_7|1101100\rangle -r_6|1111111\rangle )_{456B_1B_2B_3B_4}.\nonumber \\ \end{aligned}$$

(20)

In this situation, Alice performs the unitary operation $U^{1}=I\otimes I\otimes X$ on her particles (4,5,6) and gets

$$\begin{aligned}&(-r_0|0000011\rangle +r_1|0010000\rangle -r_2|0100111\rangle +r_3|0110100\rangle \nonumber \\&\quad -\,r_4|1001011\rangle +r_5|1011000\rangle -r_6|1101111\rangle +r_7|1111100\rangle )_{456B_1B_2B_3B_4}.\nonumber \\ \end{aligned}$$

(21)

Then, Alice performs a three-particle projective measurement on her particles (4,5,6) under the basis $\{|\eta _0\rangle , \ldots ,|\eta _7\rangle \}$ defined by Eq. (19). Since the state in Eq. (21) can be rewritten as

$$\begin{aligned}&|\eta _0\rangle _{456}(-x_0|3\rangle +x_1|0\rangle -x_2|7\rangle +x_3|4\rangle \nonumber \\&\quad -\,x_4|11\rangle +x_5|8\rangle -x_6|15\rangle +x_7|12\rangle )_{B_1B_2B_3B_4}\nonumber \\&\quad +\,|\eta _1\rangle _{456}(-x_0|3\rangle -x_1|0\rangle -x_2|7\rangle -x_3|4\rangle \nonumber \\&\quad -\,x_4|11\rangle -x_5|8\rangle -x_6|15\rangle -x_7|12\rangle )_{B_1B_2B_3B_4}\nonumber \\&\quad +\,|\eta _2\rangle _{456}(-x_0|3\rangle -x_1|0\rangle +x_2|7\rangle +x_3|4\rangle \nonumber \\&\quad -\,x_4|11\rangle -x_5|8\rangle +x_6|15\rangle +x_7|12\rangle )_{B_1B_2B_3B_4}\nonumber \\&\quad +\,|\eta _3\rangle _{456}(-x_0|3\rangle +x_1|0\rangle +x_2|7\rangle -x_3|4\rangle \nonumber \\&\quad +\,x_4|11\rangle -x_5|8\rangle -x_6|15\rangle +x_7|12\rangle )_{B_1B_2B_3B_4}\nonumber \\&\quad +\,|\eta _4\rangle _{456}(-x_0|3\rangle -x_1|0\rangle -x_2|7\rangle -x_3|4\rangle \nonumber \\&\quad +\,x_4|11\rangle +x_5|8\rangle +x_6|15\rangle +x_7|12\rangle )_{B_1B_2B_3B_4}\nonumber \\&\quad +\,|\eta _5\rangle _{456}(-x_0|3\rangle +x_1|0\rangle -x_2|7\rangle +x_3|4\rangle \nonumber \\&\quad +\,x_4|11\rangle -x_5|8\rangle +x_6|15\rangle -x_7|12\rangle )_{B_1B_2B_3B_4}\nonumber \\&\quad +\,|\eta _6\rangle _{456}(-x_0|3\rangle +x_1|0\rangle +x_2|7\rangle -x_3|4\rangle \nonumber \\&\quad -\,x_4|11\rangle +x_5|8\rangle +x_6|15\rangle -x_7|12\rangle )_{B_1B_2B_3B_4}\nonumber \\&\quad +\,|\eta _7\rangle _{456}(-x_0|3\rangle -x_1|0\rangle +x_2|7\rangle +x_3|4\rangle \nonumber \\&\quad +\,x_4|11\rangle +x_5|8\rangle -x_6|15\rangle -x_7|12\rangle )_{B_1B_2B_3B_4}, \end{aligned}$$

(22)

where $|0\rangle =|0000\rangle ,\,|3\rangle =|0011\rangle ,\,|7\rangle =|0111\rangle ,\,|4\rangle =|0100\rangle ,\,|11\rangle =|1011\rangle ,\,|8\rangle =|1000\rangle ,\,|15\rangle =|1111\rangle ,\,|12\rangle =|1100\rangle$. From the above equation, one can see whatever Alice’s second measurement outcome is, Bob can get the prepared $\chi$-state by performing appropriate unitary operation on his collapsed particles. Firstly, Bob performs CNOT operations $C_{B_1B_4}C_{B_2B_4}$ on his qubits $(B_1,B_2,B_3,B_4)$ with $(B_1,B_2)$ being the controlled qubits, $B_4$ the target one. Then, Bob’s recovery operations conditioned on Alice’s second-step measurement results $|\eta _{j}\rangle _{456}\, (j=0,\ldots ,7)$ after the CNOT operations, are summarized into the Table 2 (X,Y,Z are Pauli operations).

As for the other seven cases corresponding to Alice’s first-step measurement results, similar analysis process can be made. Here, we do not depict them one by one anymore. Therefore, the total success probability for preparing the $\chi$-state is unit.

Table 2 For Alice’s first-step measurement outcome $|\xi _{1}\rangle _{123}$, the relation between Alice’s second-step measurement outcome $|\eta _{j}\rangle _{456}\,(j=0,\ldots ,7)$, and Bob’s appropriate unitary operation (BAUO) on the particles $(B_1,B_2,B_3,B_4)$ after the CNOT operations $C_{B_1B_4}C_{B_2B_4}$

4 Non-maximally entangled sates as the quantum channel

In real situations, however, it is most of the time not possible to have a maximally entangled state at one’s disposal. Because of the interaction with the environment, the quantum state of any system will become the mixed state after a certain period. This problem of decoherence can be mitigated but cannot be completely overcome. Also, it may happen that the source does not produce perfect maximally entangled states rather non-maximally entangled pairs. Therefore, it is important to investigate the RSP via non-maximally entangled quantum channel.

In this section, we extend the proposed schemes via the maximally entangled quantum channel to the case that non-maximally entangled states are taken as quantum channel. Take the scheme in Sect. 2 as an example.

Suppose the quantum channel is composed of two non-maximally entangled EPR pairs and a four-qubit GHZ state:

$$\begin{aligned} |\widetilde{\Phi }\rangle _{1B_1}&= (a|00\rangle +b|11\rangle )_{1B_1},\nonumber \\ |\widetilde{\Phi }\rangle _{2B_2}&= (c|00\rangle +d|11\rangle )_{2B_2},\\ |\widetilde{\Phi }\rangle _{34B_3B_4}&= (e|0000\rangle +f|1111\rangle )_{34B_3B_4},\nonumber \end{aligned}$$

(23)

where $a,b,c,d,e,f$ are real, $|a|\le |b|,\,|c|\le |d|,\,|e|\le |f|$ and $|a|^2+|b|^2=|c|^2+|d|^2=|e|^2+|f|^2=1$. The particles $(1,2,3,4)$ are held by Alice, while the particles $(B_1,B_2,B_3,B_4)$ by Bob. $a,b,c,d,e,f$ are known to both the sender Alice and the receiver Bob. Here, we give two equivalent schemes with the same success probability.

On the one hand, the sender Alice can perform normal local filtering [39] to convert the non-maximally entangled quantum channel to the maximally entangled quantum channel with a certain probability before the RSP and then follow the scheme in Sect. 2. In detail, Alice introduces an auxiliary two-level particle with initial state $|0\rangle _A$ into $|\widetilde{\Phi }\rangle _{1B_1}$, and makes a unitary transformation

$$\begin{aligned} \left( \begin{array}{cccc} 1 &{} 0 &{}0 &{}0\\ 0 &{}\frac{a}{b} &{}0 &{} \sqrt{1-(\frac{a}{b})^2}\\ 0 &{} 0 &{}-1&{}0\\ 0 &{}\sqrt{1-(\frac{a}{b})^2} &{}0 &{} -\frac{a}{b} \end{array} \right) \end{aligned}$$

(24)

under the basis $\{|00\rangle _{1A},|10\rangle _{1A},|01\rangle _{1A},|11\rangle _{1A}\}$, then Alice gets

$$\begin{aligned} a(|00\rangle +|11\rangle )_{1B_1}|0\rangle _{A}+b\sqrt{1-\left( \frac{a}{b}\right) ^2} |11\rangle _{1B_1}|1\rangle _A. \end{aligned}$$

(25)

Alice can obtain the maximally entangled state $\frac{1}{\sqrt{2}}(|00\rangle +|11\rangle )_{1B_1}$ with the probability $2a^2$ by measuring the auxiliary particle $A$ under the basis $\{|0\rangle _A,|1\rangle _A\}$. Similarly, Alice can get maximally entangled states $\frac{1}{\sqrt{2}}(|00\rangle +|11\rangle )_{2B_2}$ and $\frac{1}{\sqrt{2}}(|0000\rangle +|1111\rangle )_{34B_3B_4}$ from the non-maximally entangled states $(c|00\rangle +d|11\rangle )_{2B_2}$ and $(e|0000\rangle +f|1111\rangle )_{34B_3B_4}$ with the probability $2c^2$ and $2e^2$, respectively. It means that Alice can change the non-maximally entangled quantum channel in Eq. (23) into the maximally entangled quantum channel in Eq. (2) with the probability $8a^2c^2e^2$. Therefore, following the scheme in Sect. 2, the RSP can be successfully realized with the probability $(8a^2c^2e^2)\times \frac{1}{2}=4a^2c^2e^2$.

On the other hand, the local filtering can be completed in an equivalent form by the receiver Bob after the sender Alice’s measurement, i.e., Alice and Bob first follow the similar scheme as that in Sect. 2, and then, Bob performs the local filtering. The initial state of the combined system can be expressed as

$$\begin{aligned}&|\widetilde{\Phi }\rangle _{1B_1}\otimes |\widetilde{\Phi }\rangle _{2B_2}\otimes |\widetilde{\Phi }\rangle _{34B_3B_4}\nonumber \\&\quad =(ace|00000000\rangle +acf|00110011\rangle +adf|01110111\rangle +ade|01000100\rangle \nonumber \\&\qquad +\,bcf|10111011\rangle +bce|10001000\rangle +bde|11001100\rangle \nonumber \\&\qquad +\,bdf|11111111\rangle )_{1234B_1B_2B_3B_4}. \end{aligned}$$

(26)

Alice performs a four-qubit projective measurement on her particles $(1,2,3,4)$ under the basis $|\zeta _{1}\rangle ,\ldots ,|\zeta _{16}\rangle$ defined by Eq. (8). After the measurement, Alice sends the measurement outcome to Bob through a classical channel. If Alice’s measurement result is $|\zeta _1\rangle _{1234}$, by performing appropriate unitary operation as that in Sect. 2 on the collapsed particles $(B_1,B_2,B_3,B_4)$, Bob can get

$$\begin{aligned}&(acex_0|0000\rangle +acfx_1|0011\rangle +adfx_2|0101\rangle +adex_3|0110\rangle \nonumber \\&\quad +\,bcfx_4|1001\rangle +bcex_5|1010\rangle +bdex_6|1100\rangle +bdfx_7|1111\rangle )_{B_1B_2B_3B_4}.\nonumber \\ \end{aligned}$$

(27)

To obtain the prepared state, Bob introduces an auxiliary two-level particle $B$ with the initial state $|0\rangle _B$ and makes a unitary transformation

$$\begin{aligned} \left( \begin{array}{cc} D_1 &{}D_2\\ D_2 &{}-D_1 \end{array} \right) \end{aligned}$$

(28)

on the particles $(B_1,B_2,B_3,B)$ under the basis $\{|0000\rangle ,|0010\rangle ,|0100\rangle ,|0110\rangle$, $|1000\rangle ,|1010\rangle ,|1100\rangle ,|1110\rangle ,\,\{|0001\rangle ,|0011\rangle ,|0101\rangle ,|0111\rangle , |1001\rangle ,|1011\rangle ,|1101\rangle$, $|1111\rangle \}$. Here, $D_1,D_2$ are $8\times 8$ diagonal matrices defined as follows:

$$\begin{aligned} D_1&= \mathrm{diag}\{d_0,d_1,d_2,d_3,d_4,d_5,d_6,d_7\}, \nonumber \\ D_2&= \mathrm{diag}\left\{ \sqrt{1-d_0^2},\sqrt{1-d_1^2},\sqrt{1-d_2^2},\sqrt{1-d_3^2}, \sqrt{1-d_4^2},\sqrt{1-d_5^2}\right. , \nonumber \\&\quad \left. \sqrt{1-d_6^2},\sqrt{1-d_7^2}\right\} , \end{aligned}$$

(29)

with $d_0=1,\,d_1=\frac{e}{f},\,d_2=\frac{ce}{df},\,d_3=\frac{c}{d},\,d_4=\frac{ae}{bf},\,d_5=\frac{a}{b},\,d_6=\frac{ac}{bd},\,d_7=\frac{ace}{bdf}$.

Then, Bob can get

$$\begin{aligned}&ace|\chi \rangle _{B_1B_2B_3B_4}\otimes |0\rangle _B+ (acfx_1\sqrt{1-d_1^2}|0011\rangle +adfx_2\sqrt{1-d_2^2}|0101\rangle \nonumber \\&\quad +\,adex_3\sqrt{1-d_3^2}|0110\rangle +bcfx_4\sqrt{1-d_4^2}|1001\rangle +bcex_5\sqrt{1-d_5^2}|1010\rangle \nonumber \\&\quad +\,bdex_6\sqrt{1-d_6^2}|1100\rangle +bdfx_7\sqrt{1-d_7^2}|1111\rangle ) _{B_1B_2B_3B_4}\otimes |1\rangle _B. \end{aligned}$$

(30)

At last, Bob makes a measurement on the auxiliary particle $B$. If the measurement result is $|1\rangle _B$, the RSP fails as Bob cannot reconstruct the original state on his particles. While if the measurement result is $|0\rangle _B$, Bob can get the original state in his position. Similar discussion can be made when Alice’s measurement result is $|\zeta _j\rangle _{1234},j\in \{2,\ldots ,8\}$. Hence, the total success possibility is $8\times \frac{1}{16}\times 8a^2c^2e^2=4a^2c^2e^2$.

Consider the case that the quantum channel in Sect. 3 is non-maximally entangled. Assume that the quantum channel shared between the sender Alice and the receiver Bob is

$$\begin{aligned} |\widetilde{\Phi }\rangle _{14B_1}&= (a|000\rangle +b|111\rangle )_{14B_1},\nonumber \\ |\widetilde{\Phi }\rangle _{25B_2}&= (c|000\rangle +d|111\rangle )_{25B_2},\\ |\widetilde{\Phi }\rangle _{36B_3B_4}&= (e|0000\rangle +f|1111\rangle )_{36B_3B_4},\nonumber \end{aligned}$$

(31)

where $a,b,c,d,e,f$ are real, $|a|\le |b|,\,|c|\le |d|,\,|e|\le |f|$ and $|a|^2+|b|^2=|c|^2+|d|^2=|e|^2+|f|^2=1$. The particles $(1,2,3,4,5,6)$ are held by Alice, while the particles $(B_1,B_2,B_3,B_4)$ belong to Bob. By the similar discussion, we can construct two equivalent schemes with the success probability $8a^2c^2e^2$.

5 Classical communication cost

Classical communication plays an important role in quantum information. In this section, we calculate the classical communication cost to weigh the classical resources required.

Consider the RSP scheme via two EPR pairs and a four-particle GHZ state as the quantum channel in Sect. 2. Only 2.5 cbits are needed. In fact, only eight cases $\{|\zeta _1\rangle ,\ldots ,|\zeta _{8}\rangle \}$ out of 16 measurement results are useful for successful RSP, and each of the measurement results can be obtained with the probability $\frac{1}{16}$. Take other measurement outcomes leading to failed RSP as one type. Therefore, CCC for Alice is $8\times \frac{1}{16}\log _2 16+\frac{1}{2}\log _2 2=2.5$ cbits. As far as the deterministic scheme in Sect. 3, CCC for Alice is $8\times \frac{1}{8}\log _2 8+8\times \frac{1}{8}\log _2 8=6$ cbits.

6 Conclusions

In conclusion, two efficient schemes via various entanglement resources are proposed to remotely prepare a four-particle $\chi$-state with high success probabilities. In the first scheme, two EPR pairs and a four-particle GHZ state are used as the quantum channel. Through a four-particle measurement under a novel set of measurement basis, the original state can be successfully prepared with the probability 50 %. Moreover, by introducing the permutation group $S_8$, we have classified some special cases of the state that the success probability can reach 100 %. In the second scheme, two three-qubit GHZ states and a four-qubit GHZ state are used as the quantum channel. To design the deterministic scheme, we have constructed another useful measurement basis. Under the basis, the sender performs two-step three-particle projective measurement on her particles. After achieving the sender’s measurement results, the receiver can recover the prepared state deterministically. The classical communication costs in the proposed schemes are 2.5 and 6 cbits, respectively. Comparing with the previous schemes for remotely preparing the state with eight coefficients, the measurement basis we construct has no restriction on the coefficients, which means the proposed schemes are more applicable.

Furthermore, the two schemes are extended to the non-maximally entangled quantum channel. On the one hand, the sender can perform normal local filtering to convert the partially entangled quantum channel to the maximally entangled quantum channel before the beginning of RSP. On the other hand, the local filtering can be completed in an equivalent form at the site of the receiver after the sender performs projective measurement. It is shown that the receiver can reestablish the $\chi$-state with the success probabilities $4a^2c^2e^2$ and $8a^2c^2e^2$, respectively.

At last, we simply compare the proposed two schemes. On the one hand, three-particle projective measurement is more easily performed than four-particle projective measurement, and the success probability of the second scheme is twice as the first one. On the other hand, compared to the first scheme in Sect. 2, the second scheme also has unfavorable aspects. The sender Alice needs to use the information splitting and divide the complex coefficients $\{p + qi(= re^{i\theta })\}$ of the original state into $\{r\}$ and $\{\theta \}$ before constructing the measurement basis. Also, before performing the second-step three-particle projective measurement, the sender Alice needs to perform an additional unitary operation conditioned on her first-step projective measurement outcome.