Implementing a one-bit reversible full adder using quantum-dot cellular automata

Abstract

Quantum-dot cellular automata (QCA) technique is one of the emerging and promising nanotechnologies. It has considerable advantages versus CMOS technology in various aspects such as extremely low power dissipation, high operating frequency and small size. In this paper, designing of a one-bit full adder is investigated using a QCA implementation of Toffoli and Fredkin gates. Then, a full adder design with reversible QCA1 gates is proposed regarding to overhead and power savings. Our proposed full adder design is more preferable when considering both circuit area and speed. The proposed design uses only two QCA1 gates and maximizes the circuit density and focuses on a layout of the circuit which is minimal in using QCA cells.

1 Introduction

Nanotechnology has been the focus of extensive research in the recent years. Power dissipation of the circuit is one of the most important difficulties in the development of the modern computational systems [1]. A possible solution is reversible computations. Reversible computing considers the relation between information dissipation and energy dissipation at the logical level. Energy dissipation could be caused by information dissipation [2]. If a one-to-one mapping is established between the input and output vectors, reversible computation would be achieved at the logical level [3]. The one-to-one mapping is called bijective property. The bijective property investigated by Landauer. He proved heat dissipation for losing any bit of information would be KTln2 joules, where k is Boltzmann’s constant and T is the temperature at which computation is performed. Consequently, without losing any bit of information, no energy dissipation occurs [3].

The CMOS technology is accompanied by various problems such as high leakage currents, high power density levels and extremely high lithography costs [4]. One of the alternatives for CMOS technology is quantum-dot cellular automata (QCA). QCA has none of these problems and potentially has small feature size and ultra-low power consumption. An electron pair configuration within a quantum-dot cell specifies the logical states. The information is transferred by propagation of a polarization state in QCA technology [5]. QCA circuits can be constructed through molecular implementations by a self-assembly process [6]. QCA has a very high density, $10^{12}$ devices/cm$^{2}$, and operates at THZ frequencies [7].

Following paper presents a novel one-bit QCA full adder using QCA1 gates which uses the minimum number of QCA cells and clock zones. The proposed full adder is more efficient and less complex than previously reported designs. The structure of the paper is as follows. In Sect. 2, the background of QCA concept, reversible QCA gates and reversible full adders are presented. In Sect. 3, designing of a one-bit reversible full adder with reversible QCA1 gates is investigated. Our proposed QCA one-bit full adder is compared to available counterparts. In Sect. 4, simulation results verifying the proposed full adder are provided. We conclude in Sect. 5.

2 Background

2.1 Basic QCA devices

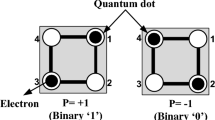
A QCA cell, which is a set of four quantum dots located at the corners and an electron pair, is used for constructing all components of circuits and wires [8]. If two electrons are placed in two quantum dots, they would be far from each other to possible space due to electron repulsion force. How electrons move in two quantum dots without getting away is simply justifiable by tunneling predicted by quantum physics. Three states can be occurred by providing tunneling junctions with potential barriers. The potential barriers are raised to prevent electron movement and lowered to permit electron movement. The mobile electrons can localize on any dot when barriers are low which is named as null state; two other states can occur when barriers are raised andthe cell is polarized. These two states representing logical “1” and “0” are shown in Fig. 1 as P = +1 and $\hbox {P} = -1$, respectively. Due to columbic interactions and depending on the polarization of a cell, the other cells next to the cell are forced into matching polarization. Hence, the polarization is propagated and information is transferred [9]. Majority gate is the fundamental logic gate in QCA implementations and is shown in Fig. 2a. Majority gate has three inputs and one output. The logic function of majority gate is as Eq. 1. Depending on the value of the inputs A, B and C, two mobile electrons in the other cells as well as output cell are forced into matching polarization and are located to the corner positions by columbic repulsion [8]. If the number of “1” states is more than “0” states in an input vector, the output of majority gate would be “1.” For instance, if inputs A = 1, C = 1 and B = 0, then the middle cell would be “1” because only two electrons are in the vicinity of each other in this case; Otherwise, If the middle cell is set to “0” state, four electrons would be in the vicinity of each other. Similarly, it is possible to obtain the outputs for other input vectors. The other basic gate is inverter gate and is shown in Fig. 2b. QCA cells are arranged in a way that the opposite polarization of the input-A is transmitted to the output-F in the inverter gate. Other logical functions such as AND and OR can be implemented by setting one input of the majority gate to “0” and “1,” respectively. The logic functions of AND and OR gates are as Eqs. 2a and 2b.

$$\begin{aligned} Majority(A,B,C)&= AB+BC+AC \end{aligned}$$

(1)

$$\begin{aligned} Majority(A,B,0)&= AB+B\times 0+A\times 0=AB=AND(A,B)\end{aligned}$$

(2a)

$$\begin{aligned} Majority(A,B,1)&= AB+B\times 1+A\times 1=AB+A+B=A(B+1)+B\nonumber \\&= A+B=OR(A,B) \end{aligned}$$

(2b)

AND and OR gates are shown in Fig. 2c, d. The binary wire and inverter chain are shown in Fig. 2e, f. The polarization of one QCA cell will be directly affected by the polarization of its neighbors. Hence, QCA cells are forced to synchronize their polarizations; the state of the input-A is transmitted to the output-F by columbic interactions in a QCA binary wire. For instance, if the input cell of a binary wire is set to “0,” since electrons tend to get to the farthest state, nearest neighbor of the input cell would set to “0” (two electrons would be consumedly approached to each other if the cell is set to “1”). This leads to getting the third cell to “0”; consequently, fourth and other cells would set to “0,” and the “0” state is propagated to the output cell (Fig. 2e). The polarization of 45$^\circ$-quantum cell is on the opposite state of its nearest neighbor in the inverter chain [5].

Fig. 1

Binary states

Fig. 2

a Majority gate, b inverter gate, c AND gate, d OR gate, e binary wire, f inverter chain

2.2 Clocking in QCA

Clock is a reference signal which controls timing in sequential CMOS circuits, whereas timing in QCA technology is performed by clocking in four periodic phases such as switch, hold, release and relax [6]. The four-phase clocking scheme is called Landauer clocking and is used to modulate the inter-dot tunneling barrier of QCA cells [8]. During the switch phase, in which actual computations are occurred, barriers are raised and a cell is affected by the polarization of its neighbors and a distinctive polarity is obtained. During the hold phase, barriers are high and the polarization of the cell is retained. During the release phase, barriers are lowered and the cell loses the polarity. In the relax phase, the cell is non-polarized. Four phases are shown in Fig. 3a in which a cell is controlled by a clock signal (clock0). A signal is latched and remained latched until the cells of the next clocking zone switches to the hold phase and acts as an input to the subsequent zone. Hence, inherent pipeline [10, 11] is possible in Landauer clocking scheme in which the cell is released after one clock cycle and it can participate in the next operation [12]. Inherent pipeline allows transferring multi-bit of information in QCA implementations [8]. Landauer clocking scheme uses four clocks to control QCA circuits. These four clocks are shown in Fig. 3b as clock0, clock1, clock2 and clock3. Each clock of Landauer clocking scheme is 90$^\circ$ out-of-phase from its previous clock [13]. To figure out how the clocking scheme operates, a binary wire is shown in Fig. 3b.

Fig. 3

a Four phases of Landauer clocking scheme, b a binary wire

A QCA circuit is partitioned into a number of clocking zones. QCA cells included in the same clocking zone are controlled by one clocking signal. The clocking signals are provided by CMOS wires which are located under the QCA circuit [12]. QCA cells of the binary wire are divided into four clocking zones as shown Fig. 3b. Each zone is controlled by a common clock signal. zone0 (input cell, cell1 and cell2) is controlled by clock0, zone1 (cell3 and cell4) by clock1, zone2 (cell5 and cell6) by clock2 and zone3 (cell7, cell8 and the output cell) by clock3. When QCA cells included in the zone0 are in the switch phase of clock0, QCA cells included in the zone1 would be in the relax phase of clock1, QCA cells in the zone2 in the release phase of clock2 and QCA cells in the zone3 in the hold phase of clock3. Three remained phases of each clock would be applied to these four zones, sequentially. After four phases of each clock applied to the four zones, one clock cycle is accomplished. During a clock cycle, all four clocks traverse four phases, however, with different starting phases [13].

During the switch phase of clock0, cell1 and cell2 are affected by the polarization of the input cell. During the switch phase of clock1, which clock0 is in the hold phase, cell3 and cell4 are polarized by cell2. When clock2 is in the switch phase and clock1 in the hold phase, cell5 and cell6 are polarized by cell4. When clock3 is in the switch phase and clock2 is in the hold phase, cell7, cell8, and finally the output cell are affected by the polarization of cell6. At the end, cell7, cell8 and the output cell switch to the hold phase and this cycle repeats [13]. In other words, a signal is latched when one clocking zone goes into the hold phase and acts as an input to the next zone. During a clock cycle, the polarization of the input cell is exactly propagated to the output cell and information propagation is performed in the binary wire.Clock0, clock1, clock2 and clock3 are shown with green, violet, blue and white colors, respectively, in QCA implementations.

2.3 Reversible QCA Fredkin and Toffoli gates

In this section, the QCA implementations of Toffoli and Fredkin gates are presented [14, 15]. There is neither energy loss nor information loss in reversible circuits. Reversible circuits are very attractive in nanotechnologies such as QCA where extremely low power consumption or heat dissipation is desirable.

2.3.1 Fredkin gate

The Fredkin gate is a $3\times 3$ universal gate. Using Fedkin gate, any logical reversible circuit can be implemented [15]. The truth table of this gate is shown in Table 1 [8].

Table 1 Truth table of Fredkin gate

Input $u$ acts as a control input. If the control input is $u=1$, then outputs $Y_{1}$ and $Y_{2}$ are exactly duplicates of the inputs $x_{1}$ and $x_{2}$; otherwise, if $u=0$, then two inputs $x_{1}$ and $x_{2}$ are swapped and transmitted to the outputs $Y_{1}$ and $Y_{2}$. The output functions of Fredkin gate are shown in Eq. 3 [8].

$$\begin{aligned} \begin{array}{l} V=u \\ Y1=\overline{u} .x_2 +u.x_1 \\ Y2=\overline{u.} x_1 +u.x_2 \\ \end{array} \end{aligned}$$

(3)

When two identical Fredkin gates are cascaded, the outputs of the second gate are same as the inputs of the first gate. Hence, Fredkin gate is named self-inverse. A QCA implementation of the gate is shown in Fig. 4 [8]. Inverter chains, which are usually used to implement wire crossings in the same layers, are used for crossing wires in the QCA implementation of Fredkin gate. The wire which is along the horizontal direction is a binary wire, and the other wire is an inverter chain located in the perpendicular direction.

Fig. 4

QCA implementation of Fredkin gate

The QCA implementation of Fredkin gate uses a two-level majority implementation with six majority gates; four of them are programmed as AND gates and two of them as OR gates [12].

2.3.2 Toffoli gate

The Toffoli gate is a reversible gate with three inputs and three outputs. It is also a universal and self-inverse gate [15]. The truth table of Toffoli gate is shown in Table 2 [8]. It passes inputs $x2$ and $x3$ to the outputs $Y2$ and $Y3$ without any changes but inverts input $x1$ when $x2=1$ and $x3=1$.

Table 2 Truth table of Toffoli gate

The output functions of Toffoli gate are shown in Eq. 4.

$$\begin{aligned} \begin{array}{l} Y1=x1\overline{x2} +x1\overline{x3} +\overline{x1} x2x3 \\ Y2=x2 \\ Y3=x3 \\ \end{array} \end{aligned}$$

(4)

The QCA implementation of Toffoli gate (Fig. 5) uses four majority gates which are implemented in two levels. Two numbers of majority gates are programmed as AND and OR gates [8].

Fig. 5

QCA implementation of Toffoli gate

2.3.3 Reversible QCA Feynman gate

Feynman gate is a reversible $2\times 2$ gate. The truth table of Feynman gate is shown in Table 3 [8]. The input $x1$ acts as a control input. If the control input $x1=0$, then the output $Y2$ is simply a duplicate of the input $x2$; otherwise, if the control input $x1=1$, then the output $Y2$ is inverse of the input $x2$.

Table 3 Truth table of Feynman gate

The output functions of Feynman gate are shown in Eq. 5.

$$\begin{aligned} \begin{array}{l} Y1=X1 \\ Y2=X1xorX2=x1\overline{x2} +\overline{x1} x2 \\ \end{array} \end{aligned}$$

(5)

As shown in Fig. 6, four clocking zones are used in the QCA implementation of Feynman gate. The rectangular area occupied by its entire layout is an area of $15\times 15$ cells [8].

Fig. 6

QCA implementation of Feynman gate

2.4 QCA1 and QCA2 gates

Two new reversible gates, called QCA1 and QCA2 were proposed for reversible QCA implementations in [12] and compared to QCA reversible Fredkin and Toffoli gates. QCA1 is a reversible gate and has three inputs and three outputs. The truth table of QCA1 gate is shown in Table 4 [8]. There is a one-to-one mapping between inputs and outputs.

Table 4 Truth table of QCA1

The output functions are expressed by Eq. 6.

$$\begin{aligned} \begin{array}{l} Y1=Majority(x1+x2+x3) \\ Y2=Majority(x1+x2+\overline{x3} ) \\ Y3=Majority(\overline{x1} +x2+x3) \\ \end{array} \end{aligned}$$

(6)

The QCA implementation of QCA1 gate is shown in Fig. 7 [8]. It requires only one level of majority gates [12]. QCA implementation of QCA1 has only a delay of two clocking zones and requires three majority gates [12].

Fig. 7

QCA implementation of QCA1 gate

QCA2 has similar properties to QCA1. The QCA implementation of QCA2 is shown in Fig. 8 [8]. The truth table of QCA2 gate is shown in Table 5. Three output functions of QCA2 gate are shown in Eq. 7 [8]:

Fig. 8

QCA implementation of QCA2 gate

Table 5 Truth table of QCA2 gate

$$\begin{aligned} \begin{array}{l} Y1=Majority(x1+x2+x3) \\ Y2=Majority(x1+x2+\overline{x3} ) \\ Y3=Majority(\overline{x1} +x2+\overline{x3} ) \\ \end{array} \end{aligned}$$

(7)

Figure 9 shows a schematic diagram of the reversible Fredkin, Toffoli, Feynman, QCA1 and QCA2 gates.

Fig. 9

a Toffoli gate, b Fredkin gate, c Feynman gate, d QCA1 gate and e QCA2 gate

A comparison was done among four QCA reversible Fredkin, Toffoli, QCA1 and QCA2 gates by [12]. The QCA1 and QCA2 gates have a one-level majority implementation and require only two clocking zones; therefore, their delays are less than Fredkin and Toffoli gates. QCA1 and QCA2 occupy a smaller area with a reduced number of QCA cells with no control cells. The thirteen standard combinational functions are implemented using each of the four reversible QCA gates by [12] and the number of required gates and clocking zones are obtained. The results are shown in Table 6. In comparison, QCA1 and QCA2 gates are more preferable than Fredkin and Toffoli gates for QCA implementation considering both circuit area and speed [12].

Table 6 Reversible implementation of thirteen standard functions

2.5 Reversible QCA full adder

In this section, designing of Full adder, which is a basic circuit in computing circuits, is investigated using reversible QCA Fredkin and Toffoli gates. To implement a reversible full adder, a reversible truth table is required. Hence, some extra don’t care inputs or outputs are usually added to the truth table of full adder to provide the bijective property and reversibility condition. Don’t cares (DCs) are some inputs whose corresponding outputs are not determined in the truth table of the function. These extra inputs and outputs are called constant inputs and garbage outputs. The value of a constant input is arbitrary [16]. It is proved that there is an optimum value for the number of constant inputs to obtain a circuit with minimum quantum cost (QC) [17]. The QC of a reversible logic circuit is the number of $1\times 1$ or $2\times 2$ reversible, and quantum logic gates are used to implement the circuit [18].The truth table of reversible full adder is depicted in Table 7 [16].

Table 7 Truth table of a reversible full adder

In [16], some heuristic methods are presented to use these DCs when an optimization algorithm such as the genetic algorithm is used as a synthesis tool. Figure 10 shows some optimal circuits of a Toffoli full adder using a genetic algorithm (optimized for quantum cost [18]).

Fig. 10

Different implementation of full adder using Toffoli gates

Toffoli full adder has four inputs and four outputs which one of the inputs is a constant input and two of the outputs are garbage outputs. Four gates are used to synthesize Toffoli full adder. QCA implementation of Toffoli and Feynman gates are investigated in Sects. 2.3.2 and 2.3.3, respectively. Each Toffoli gate consists of four majority gates, and Feynman gate has three majority gates; therefore, 14 majority gates are totally needed in the full adder design. Full adder with Toffoli gates totally uses 19 clocking zones, four clocking zones for each gate and three additional clocking zones [12] for interconnections. The QC is extensively used as a figure of merit in reversible and quantum designs. The QC of Toffoli full adder is 12 [19]. Toffolli full adder layout is complex because of using two-level majority implementations.

It is impossible to synthesize Fredkin full adder with four inputs and four outputs. One extra constant input and one garbage output are added to the truth table of the full adder to satisfy reversibility condition. The synthesis result of a Fredkin full adder using genetic algorithm is a circuit consists of five Fredkin gates and a five-to-five mapping with three garbage outputs. The QC of Fredkin full adder is 25. The results are shown in Fig. 11. The Fredkin gate uses a two-level majority implementation with 6 majority gates. Synthesized Fredkin full adder uses totally 30 majority gates, which is much more than Toffoli full adder. As a result, Toffoli full adder is more preferable than Fredkin full adder for reversible implementations. In the next section, a new reversible full adder with QCA1 gate is proposed which has significant improvements.

Fig. 11

Different implementation of full adder using Fredkin gates

3 Proposed full adder design using QCA1 gates

In this section, a one-bit full adder is proposed using only two QCA1 gates, whereas the conventional reversible Toffoli and Fredkin full adders use four and five gates, respectively. On the other hand, QCA1 is more preferable for QCA implementation compared to reversible QCA Toffoli and Fredkin gates considering circuit area and speed [12]. Two clocking zones are only used in QCA1 implementation in comparison with Toffoli gate which needs four clocking zones. As a result, occupied rectangular area by the entire layout of our proposed full adder is lower and the number of clocking zones is significantly reduced.

A one-bit full adder is defined as Eq. 8 [19]:

$$\begin{aligned} Sum&= abCin+\bar{{a}}\bar{{b}}Cin+\bar{{a}}b\bar{{C}}in+a\bar{{b}}\bar{{C}}in\end{aligned}$$

(8a)

$$\begin{aligned} Cout&= ab+aCin+bCin \end{aligned}$$

(8b)

where a, b and Cin are inputs; sum and Cout are the outputs of the full adder. Implementing a one-bit irreversible full adder requires five majority gates and three inverters to satisfy the set of equations sum and Cout, as shown in Fig. 12 [19].

Fig. 12

One-bit QCA full adder

An algorithm is proposed in [19] to reduce the number of required majority and inverter gates in a QCA circuit. The simplified majority expressions of the thirteen standard functions are presented in [20] using corresponding 3-cube structure. The algorithm enables us to convert any three-variable Boolean functions into the simplest majority expressions for QCA implementations. [20] proposes a procedure to build simplified majority expressions for a given Boolean function; then applies the proposed majority reduction method to QCA adders. The procedure uses a 4-step algorithm to generate a majority gate expression. For more information, refer to [20]. Sum and Cout equations are obtained as Eq. 9 using the reduction method [19]:

$$\begin{aligned} Cout&= Majority(a,b,Cin)\end{aligned}$$

(9a)

$$\begin{aligned} Sum&= Majority(\overline{Cout} ,Cin,M(a,b,\overline{Cin} )) \end{aligned}$$

(9b)

Proof

The proof of the Eq. 9b is as follows [19]:

Using the majority function (Eq. 1) and the Eq. 9a:

$$\begin{aligned} \overline{Cout} =\bar{{a}}\bar{{b}}+\bar{{a}}\bar{{C}}in+\bar{{b}}\bar{{C}}in=Majority(\bar{{a}},\bar{{b}},\bar{{C}}in) \end{aligned}$$

Then, the Eq. 9b can be rewritten as:

$$\begin{aligned} Sum&= (ab+\overline{a }\overline{ b })Cin+(\overline{ a b}\overline{Cin} +a\overline{b }\overline{Cin} )\\&= [(\overline{a }\overline{ b }+\overline{ a }\overline{Cin}+\overline{Cin} \overline{ b })+(ab+a\overline{Cin} +\overline{Cin}b)]Cin\\&+\,(\overline{a b}\overline{Cin} \!+\!a\overline{ b }\overline{Cin} ) \!=\!(\overline{ a }\overline{ b }\!+\!\overline{ a }\overline{Cin} \!+\!\overline{Cin} \overline{ b })Cin+(ab+a\overline{Cin} +\overline{Cin} b)Cin\\&+\,(\overline{ a b}\overline{Cin} \!+\!a\overline{ b }\overline{Cin} ) \!=\!(\overline{ a }\overline{ b }\!+\!\overline{ a }\overline{Cin} \!+\!\overline{Cin} \overline{ b })Cin+(ab+a\overline{Cin} +\overline{Cin} b)Cin\\&+\,(\overline{ a }\overline{Cin} +\overline{Cin} \overline{ b} )(a\overline{Cin} +b\overline{Cin} )\\&= (\overline{ a }\overline{ b }+\overline{ a }\overline{Cin} +\overline{Cin} \overline{ b })Cin+(ab+a\overline{Cin} +\overline{Cin} b)Cin\\&+\,(\overline{ a }\overline{ b }+\overline{ a }\overline{Cin} +\overline{Cin} \overline{ b })(ab+a\overline{Cin} +b\overline{Cin} ) \\&= Majority(\overline{ a },\overline{ b },\overline{Cin} )Cin+Majority(a,b,\overline{Cin} )Cin\\&+\,Majority(\overline{ a} ,\overline{ b },\overline{Cin} ).Majority(a,b,\overline{Cin} ) \\&= Majority(Majority(\overline{ a },\overline{ b },\overline{Cin} ),Cin,M(a,b,\overline{Cin} )) \\&= Majority(\overline{Cout} ,Cin,Majority(a,b,\overline{Cin} )) \end{aligned}$$

Based on the reduction method, Cout function involves one majority gate and sum function involves two majority gates. There is no inverter gates to get inversions and they can be directly obtained from interconnections of QCA cell lines ($\overline{Cout}$ and $\overline{Cin})$. The truth table of our proposed reversible full adder (Table 8) has the reversibility condition with $n\le m$, in which $n$ is the number of inputs and $m$ is the number of outputs. The inputs and outputs can be uniquely determined from each other and the full adder is reversible. Our proposed QCA1full adder is implemented regarding to the Eq. 9b. $\square$

We cascaded two reversible QCA1 gates to implement our proposed full adder design as shown in Fig. 13. Our proposed full adder design is reversible because it uses only reversible gates and its truth table has the reversibility condition.

Table 8 Truth table of the proposed reversible full adder

If we define inputs of the first QCA1 gate as x1 = a, x2 = b, and x3 = Cin, and Yij as $\hbox {i}_{\mathrm{th}}$ output of $\hbox {j}_{\mathrm{th}}$ QCA1 gate, then the outputs of the first QCA1 gate are as follows:

$$\begin{aligned} \begin{array}{l} Y11=Majority(X1,X2,X3)=Majority(a,b,Cin)=Cout \\ Y21=Majority(X1,X2,\overline{X3} )=Majority(a,b,\overline{Cin} ) \\ Y31=Majority(\overline{X1} ,X2,X3)=Majority(\overline{a} ,b,Cin)=Gar1 \\ \end{array} \end{aligned}$$

Therefore, Cout is directly obtained by $\hbox {Y}_{11}$. The output $\hbox {Y}_{31}$ is garbage output and is denoted as Gar1. Then, $\hbox {Y}_{11 }$ and $\hbox {Y}_{21}$ are applied to the first and second inputs of the next QCA1 gate as shown in Fig. 13. The outputs of the second QCA1 gate are obtained as follows:

$$\begin{aligned} \begin{array}{l} Y12=Majority(X1,X2,X3)=Majority(Cout,Majority(a,b,\overline{Cin} ),Cin)=Gar2 \\ Y22=Majority(X1,X2,\overline{X3} )=Majority(Cout,Majority(a,b.\overline{Cin} ),\overline{Cin} )=Gar3 \\ Y32=Majority(\overline{X1} ,X2,X3)=Majority(\overline{Cout} ,Majority(a,b,\overline{Cin} ),Cin)=sum \\ \end{array} \end{aligned}$$

The output $Y32$ satisfies the sum function of the full adder (Eq. 9a). As a result, sum and Cout functions of the one-bit full adder are obtained by cascading two reversible QCA1 gates. QCA implementation of the proposed full adder is shown in Fig. 14. To obtain the minimum delay in the proposed circuit, the second QCA1 gate is implemented in a way that inputs to the sum output delay is minimal. In other words, the second QCA1 gate is implemented reversely; the sum function is obtained in the first output of the second QCA1 gate. The rectangular area occupied by the entire layout as well as interconnections is only $35\times 31$, which in one QCA cell is considered as a unit area. Inverter chains are usually used to implement wire crossings in the same layers, but it is shown that binary wires can tolerate defects more than inverter chains [21]. Therefore, a multi-layer crossover scheme is used to decrease failure rate and wires are passed over each other to ensure that no interferences occur in the proposed design.

Fig. 13

Schematic diagram of the proposed full adder implementation with QCA1 gates

Fig. 14

QCA implementation of the proposed full adder design

The proposed full adder design implemented by reversible QCA1 gates requires only two gates, and it has a total delay of 6 clocking zones. [12] verifies an additional clocking zone that is required for interconnection between two reversible QCA gates. We, however, added two additional clocking zones for interconnection between QCA1 gates to ensure correct operation of our proposed full adder. The number of used clocking zones is lower than Toffoli full adder. The proposed design decreases QCA cell counts and input to output delays.

4 Simulation and verification results

QCA designer software which is a popular simulation tool for complex QCA circuits is used to simulate and verify the proposed full adder. The simulator tool uses an extensive set of CAD tools [22]. The simulator version is 2.0.3 and the following parameters are used: cell size = 18 nm, number of samples = 12,800, convergence tolerance = 0.001000, radius of effect = 65 nm, relative permittivity = 12.9, clock high = 9.8e$-$22, clock low = 3.8e$-23$, clock amplitude factor = 2.000, layer separation = 11.5000 nm and maximum iterations per sample = 100. Implementing a workable design with a compact layout is considered in our proposed QCA layout. It is considerable that the results are correct after one clock. Inputs a, b and Cin are marked with blue color, and the outputs sum and Cout are shown with yellow color in the simulation box (Fig. 15).

Fig. 15

Simulation results of the proposed full adder using QCA1 gates

Two reversible QCA full adders are compared and the results are shown in Table 9. In this paper, five figures of merit (FoM) are evaluated. Majority gates figure identifies the number of majority gates used in the QCA implementation. The number of constant inputs and the number of garbage outputs are provided. These two FoMs are used to evaluate reversible and quantum designs. The number of clocking zones is presented to quantify the delay between inputs and outputs. The number of control cells are also provided, which are the input cells with fixed polarization used for programming 2-input OR and AND gates.

Table 9 Comparison between two reversible QCA full adders

The obtained results by comparing designs indicate that our proposed full adder design has demonstrated significant improvements and is more preferable for reversible QCA implementation considering both circuit area and speed. Proposed implementation of the reversible full adder design uses the minimum number of clocking zones and gates, maximizes the circuit density and focuses on a layout of the circuit which is minimal in using QCA cells. Hence, the proposed design greatly reduces occupied area and decreases signal propagation delay from input to output. The design is also very simple to implement by QCA cells.

5 Conclusions

Recently, QCA has attracted a lot of researchers’ attention for implementing reversible computing. In this paper, designing a one-bit full adder investigated using reversible QCA gates. Reversible QCA gates compared and the results indicated that QCA1 and QCA2 gates are more preferable than Toffoli and Fredkin gates for reversible implementations. The conventional reversible full adders investigated using Toffoli and Fredkin gates and a new reversible full adder design proposed using only two QCA1 gates. Our proposed reversible full adder uses the minimum number of QCA cells, clocking zones and gates versus Toffoli full adder. Therefore, the proposed reversible QCA full adder is more efficient and less complex than its previous counterparts.