1 Introduction

It is well known that quantum entanglement, which is a strong nonclassical correlation between the bipartite quantum system, has been considered as a fundamental physical resource playing an important role in the practical application of quantum information processing, such as quantum dense coding, teleportation and so on [1–5]. Furthermore, in the past decades, the investigation into quantum entanglement has been promoted; however, the analytical results are actually known only for a few class of mixed bipartite state [6–10], so it is difficult to explicitly quantify the entanglement for an arbitrary two-qubit mixed state. What is more, this problem becomes much more knotty for the multipartite system, which has been thought to play a crucial function in many important physics phenomena including quantum phase transitions [11, 12] and quantum metrology [13].

As far as we know, some measures adopted in the previous studies of the multipartite quantum system are not always capture accurately the entanglement evolution [14–17], which is mainly due to the restricted forms of matrices and the lack of an analytical measure of multipartite entanglement. In order to settle this question, Rafsanjani etc. [18] have proposed a universal concurrence formula of an \(N\)-qubit X matrix where only nonzero elements are diagonal or antidiagonal when written in an orthonormal product basis; furthermore, they used the formula to investigate the dynamics of N qubits in generalized GHZ state. On the other hand, quantum system is inevitably subjected to the effect of its environment, in the case of some decoherence channels, the entanglement of the initial maximally entangled state will be weakened [19–28].

Due to that the X-state always remains X state under the most common noise influences [29, 30], and it is also conducive to quantify the entanglement of them [31–33]. In this paper, we mainly research the multipartite system under some conditions (i.e., phase damping, phase flip, bit flip and bit-phase flip [34]) in detail, where each qubit coupled with its own decoherence channel, respectively. Compared with the previous studies [15, 18], the most prominent superiority of our paper is that the concurrence just monotonously decreases and does not occur sudden death for the cases of \(k\ge 0\), when the system is coupled with the phase damping and phase flip channel. While Ref. [18] has shown that only one type (\(k>0\)) of GHZ state loses its entanglement in finite time and entanglement dies out asymptotically for the rest (\(k=0\)) when the system is interacted with the amplitude damping channel. In addition, we also find out that the initial entanglement monotonously decreases in company with an ESD for an arbitrary \(k\ge 0\) under the bit flip and bit-phase flip channel. It shows that the multi-particle concurrence under the phase damping and phase flip channel is more robust than that in the amplitude damping, bit flip and bit-phase flip channel. Meanwhile, the result further confirms that the time of ESD decreases with the number of qubit in the multipartite system.

This paper is organized as follows. In Sect. 2, we briefly review multipartite concurrence of \(N\)-qubit \(X\) matrices. In Sect. 3, we devote to investigate entanglement dynamic under the different decoherence. Finally, the discussions and conclusions are given in Sect. 4.

2 Multipartite concurrence of \(X\) matrices

The entanglement of a mixed state coupled with the noisy environments can be quantified conveniently by the concurrence, which is a monotonic function and invariant under the local unitary transformations for multipartite entanglement. Furthermore, if we choose the orthonormal basis for the matrix, and then the density matrix for an arbitrary \(X\) state can be written in the following form:

$$\begin{aligned} X=\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {a_1} &{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} {c_1} \\ 0&{} {a_2} &{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} {c_2} &{} 0 \\ 0&{} 0&{} .&{} 0&{} 0&{} 0&{} 0&{} .&{} 0&{} 0 \\ 0&{} 0&{} 0&{} .&{} 0&{} 0&{} .&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} 0&{} {a_n} &{} {c_n} &{} 0&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} 0&{} {c_n^*} &{} {b_n} &{} 0&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} .&{} 0&{} 0&{} .&{} 0&{} 0&{} 0 \\ 0&{} 0&{} .&{} 0&{} 0&{} 0&{} 0&{} .&{} 0&{} 0 \\ 0&{} {c_2^*} &{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} {b_2} &{} 0 \\ {c_1^*} &{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} {b_1} \\ \end{array}\right) \end{aligned}$$
(1)

where \(n=2^{N-1}\) and requiring \(\sum \nolimits _i^n {\left( {a_i +b_i}\right) } =1\) to ensure that the density matrix is positive and normalized. Then, the multipartite concurrence of \(N\)-qubit \(X\) matrix has been defined in Ref. [18], which is given by:

$$\begin{aligned} C=2\max \left\{ {0,\hbox {}\left| {c_i} \right| -w_i} \right\} , \quad i=0,1,\ldots ,n \end{aligned}$$
(2)

with \(w_i=\sum \nolimits _{j\ne i}^n {\sqrt{a_j b_j}}\). This formula quantitatively provides an opening measure to the concurrence of many-particle mixing system under the noisy scenarios as long as the initial density matrix is an \(X\) matrix. In the following, we will utilize this formula to study the dynamics of multiqubit system shared by GHZ states when each qubit is subjected to a local decoherence channel, respectively.

3 Dynamics of entanglement in decoherence

Now, we discuss the concurrence dynamics of \(N\)-qubit GHZ state.

$$\begin{aligned} \left| {\varphi _N^{\left( k \right) },\alpha } \right\rangle =\cos \alpha \left| {0^{\otimes N-k}1^{\otimes k}} \right\rangle +\sin \alpha \left| {1^{\otimes N-k}0^{\otimes k}} \right\rangle \end{aligned}$$
(3)

with \(N-k\) qubits either are primarily ground and the rest are in their excited state or \(k\) qubits are initially ground and the rest are in their excited state. In order to facilitate to study the variation in entanglement, we will present a detailed analysis only for the case of \(k=0\) and \(N=3\) in the following study, and the initially state is shown as:

$$\begin{aligned} \left| {\varphi _3^0,\alpha } \right\rangle =\cos \alpha \left| {000} \right\rangle +\sin \alpha \left| {111} \right\rangle \end{aligned}$$
(4)

and the density matrix is given as follows:

$$\begin{aligned} \rho (0)=\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {\cos ^{2}\alpha }&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} {\cos \alpha \sin \alpha } \\ 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0 \\ {\cos \alpha \sin \alpha }&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} {\sin ^{2}\alpha } \\ \end{array}\right) \end{aligned}$$
(5)

Subsequently, we put our attention on the multipartite system coupled with their noisy environments, which are the most usual channels for qubits, for instance, phase damping channel and various flip channels.

3.1 Phase damping channel

Now, we utilize Eq. (2) to study the dynamics of the \(N\)-qubit GHZ state when each qubit is subjected to a local phase damping channel, which describes a quantum noise process with loss of quantum information without losing energy. The dissipative interaction between the qubit and its environment can be given by [2]

$$\begin{aligned}&U\left( t \right) \left| 0 \right\rangle _S \left| 0 \right\rangle _E \rightarrow \left| 0 \right\rangle _S \left| 0 \right\rangle _E \nonumber \\&U\left( t \right) \left| 1 \right\rangle _S \left| 0 \right\rangle _E \rightarrow \sqrt{1-p}\left| 1 \right\rangle _S \left| 0 \right\rangle _E +\sqrt{p}\left| 1 \right\rangle _S \left| 1 \right\rangle _E \end{aligned}$$
(6)

where \(U(t)\) is the local propagator, and the relationship between the parameter \(p\) and time \(t\) is given by \(p=1-\mathrm{e}^{-\gamma t}\), where \(\gamma \) is the decay rate.

Then we can easily obtain the evolution density matrix according to the Eqs. (5) and (6); here, we are interested in the entanglement dynamics of the bipartite subsystems (especially the system–system dynamics), so the corresponding bipartite reduced matrixes should been considered, which can be obtained by taking the partial trace of over the degrees of freedom of the environment:

$$\begin{aligned} \rho \left( t \right) =\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {\cos ^{2}\alpha }&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} {\cos \alpha \sin \alpha \left( {1-p} \right) ^{\frac{3}{2}}} \\ 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0 \\ {\cos \alpha \sin \alpha \left( {1-p} \right) ^{\frac{3}{2}}}&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} {\sin ^{2}\alpha } \\ \end{array}\right) \end{aligned}$$

According to the formula given by Eq. (2), the multipartite concurrence of the initial state \(\left| {\varphi _3^0,\alpha } \right\rangle \) is given as:

$$\begin{aligned} C_3^0 =2\max \left\{ {0,\,\left| {z_1}\right| -w_1} \right\} =\hbox {max}\{0,Q_3^0\} =\max \left\{ {0,\,\sin 2\alpha \left( {1-p}\right) ^{\frac{3}{2}}} \right\} \end{aligned}$$

Simultaneously, we also calculate the cases of \(N=2, 4, 5\) and \(k>0\) in detail and the results are shown in Table 1:

Table 1 \(Q_N^k\) for various \(N\) with arbitrary integer \(k\) under phase damping channel
Full size table

Then, according to above results as shown in Table 1, we can conjecture the generic formula for multiqubit concurrence \(C_N^k\), which can be organized into the following form:

$$\begin{aligned} C_N^k =\left| {\sin 2\alpha } \right| \left( {1-p} \right) ^{\frac{N}{2}} \end{aligned}$$

In order to intuitively study the influence of noisy environment and the number of particles on the concurrence numerically, we choose the maximally entangled states \(\alpha =\pi /4\) and the variation of concurrence versus \(p\) and \(N\) has been displayed in Fig. 1.

Fig. 1
figure 1

The \(C_N^k\) versus \(p\) and \(N\) for the initial state \(\left| {\varphi _N^k, \frac{\pi }{4}}\right\rangle \) under phase damping channel

Full size image

As shown in Fig. 1, we can see that either the noisy environment or the number of particles has a great impact on the system entanglement, that is to say, the concurrence decreases monotonically as \(p\) and \(N\) increases. In addition, we can also find that the concurrence attenuated more quickly when \(N>2\).

Then, we study the effects of parameters \(\alpha \) and noisy environment \(p\) on the three-qubit system as follows:

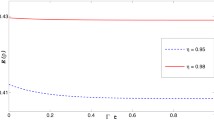
As shown in Fig. 2, we can clearly see that the concurrence monotonically increases as \(\alpha \) increases in company with reaching to the maximum value at the critical point \(\alpha =\pi /4\). Obviously, the concurrence decreases as \(p\) increases on the whole.

Fig. 2
figure 2

The \(C_3^k\) versus \(\alpha \) and \(p\) for the initial state \(\left| {\varphi _3^k, \alpha }\right\rangle \) under phase damping channel

Full size image

3.2 Various flip channels

Next, we discuss the evolution of entanglement dynamics when each qubit is subjected to a flip channel, the evolved state of such a quantum system under the local environments may be described as a completely positive trace preserving map, which, written in the operator-sum representation, is given by [28]:

$$\begin{aligned} \rho \left( t \right) =\sum \limits _{i,j,k} {\Gamma _i^{\left( a \right) }} \Gamma _j^{\left( b \right) } \Gamma _k^{\left( c \right) } \rho \left( 0 \right) \Gamma _k^{\left( c \right) ^{\tau }} \Gamma _j^{\left( b \right) ^{\tau }} \Gamma _i^{\left( a \right) ^{\tau }} \end{aligned}$$
(7)

where \(\Gamma _i^{\left( K \right) } \left( {K=a,b,c} \right) \) are the Kraus operators that describe the noise channels A, B and C.

In quantum computation, the set of Kraus operators for phase flip, bit flip and bit-phase flip channels are given by:

$$\begin{aligned} M_0 =\sqrt{1-p/2}I \quad M_1^i =\sqrt{p/2}\sigma _i \end{aligned}$$
(8)

with \(i=z\) is the phase flip, \(i=x\) gives the bit flip and \(i=y\) the bit-phase flip. These sets are easily interpreted as corresponding probability \(1-p/2\) of remaining in the same state, and a probability \(p/2\) of having an error.

3.2.1 Phase flip channel

There is a quantum noise process with loss of quantum information without loss of energy, and the Kraus operators are the following:

$$\begin{aligned} M_0 =\sqrt{1-p/2}I \quad M_1 =\sqrt{p/2}\sigma _z \end{aligned}$$
(9)

The phase flip channel has the same effects on the quantum system as the phase damping channel [2]; hence, we obtain the same results as phase damping channel. Simultaneously, the results showed that there is no phenomenon of entanglement sudden death apart from the critical condition \(p=1\).

3.2.2 Bit flip channel

From Ref. [2], we obtain the Kraus operators for the bit flip channel, which can be expressed as follows:

$$\begin{aligned} M_0 =\sqrt{1-p/2}I \quad M_1 =\sqrt{p/2}\sigma _x \end{aligned}$$
(10)

Then according to Eq. (7), it is convenient to obtain the reduced-density matrix of three qubits system:

$$\begin{aligned} \rho \left( t \right)&= \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {a_1}&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} {z_1} \\ 0&{} {a_2}&{} 0&{} 0&{} 0&{} 0&{} {z_2}&{} 0 \\ 0&{} 0&{} {a_2}&{} 0&{} 0&{} {z_2}&{} 0&{} 0 \\ 0&{} 0&{} 0&{} {b_2}&{} {z_2}&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} {z_2}&{} {a_2}&{} 0&{} 0&{} 0 \\ 0&{} 0&{} {z_2}&{} 0&{} 0&{} {b_2}&{} 0&{} 0 \\ 0&{} {z_2}&{} 0&{} 0&{} 0&{} 0&{} {b_2}&{} 0 \\ {z_1}&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} {b_1} \\ \end{array} \right) \\ a_1&= \left( {1-\frac{p}{2}} \right) ^{3}\cos ^{2}\alpha +\left( {\frac{p}{2}} \right) ^{3}\sin ^{2}\alpha \quad b_1 =\left( {\frac{p}{2}} \right) ^{3}\cos ^{2}\alpha +\left( {1-\frac{p}{2}} \right) ^{3}\sin ^{2}\alpha \\ a_2&= \left( {\frac{p}{2}} \right) \left( {1-\frac{p}{2}} \right) ^{2}\cos ^{2}\alpha +\left( {\frac{p}{2}} \right) ^{2}\left( {1-\frac{p}{2}} \right) \sin ^{2}\alpha \\ b_2&= \left( {\frac{p}{2}} \right) ^{2}\left( {1-\frac{p}{2}} \right) \cos ^{2}\alpha +\left( {\frac{p}{2}} \right) \left( {1-\frac{p}{2}} \right) ^{2}\sin ^{2}\alpha \\ z_1&= \left[ {\left( {1-\frac{p}{2}} \right) ^{3}+\left( {\frac{p}{2}} \right) ^{3}} \right] \cos \alpha \sin \alpha \\ z_2&= \left[ {\left( {\frac{p}{2}} \right) \left( {1-\frac{p}{2}} \right) ^{2}+\left( {\frac{p}{2}} \right) ^{2}\left( {1-\frac{p}{2}} \right) } \right] \cos \alpha \sin \alpha \end{aligned}$$

If we consider the initial maximally entangle state \(\left| {\varphi _3^0, \pi /4} \right\rangle \) and according to the formula given by Eq. (2), then the system concurrence can be written as

$$\begin{aligned} Q_3^0 =\left( {\frac{p}{2}} \right) ^{3}+\left( {1-\frac{p}{2}} \right) ^{3}-3\left( {\frac{p}{2}} \right) \left( {1-\frac{p}{2}} \right) \end{aligned}$$

Moreover, we calculate the case of \(N=2, 4, 5\) and \(k>0\) in detail, and then the results are shown as follows:

From the Table 2, we can conjecture the multiqubit concurrence and organize into the following form:

$$\begin{aligned} C_N^k =\max \left\{ {0,\hbox {}\left( {\frac{p}{2}} \right) ^{N}+\left( {1-\frac{p}{2}}\right) ^{N}-N\left( {\frac{p}{2}} \right) \left( {1-\frac{p}{2}}\right) }\right\} \end{aligned}$$

In order to reflect the variation in concurrence numerically, we display it in Fig. 3.

Fig. 3
figure 3

The \(C_N^k\) versus \(P\) and \(N\) for the initial state \(\left| {\varphi _N^k,\frac{\pi }{4}} \right\rangle \) under bit flip channel

Full size image
Table 2 \(Q_N^k\) for various \(N\) values with arbitrary integer \(k\) under bit flip channel
Full size table

As shown in Fig. 3, we plot the multiqubit concurrence as a function of the noisy environment and the number of particles under bit flip channel. One can clearly find out that the evolution of the entanglement is decreasing monotonically. Moreover, we can also find the concurrence attenuated more rapidly with a sudden death (ESD) at the critical point \(N>2\).

3.2.3 Bit-phase flip channel

The Kraus operators are the following:

$$\begin{aligned} M_0 =\sqrt{1-p/2}I \quad M_1 =\sqrt{p/2}\sigma _y \end{aligned}$$
(11)

When the system is coupled with this noise channel, we can obtain the density matrix:

$$\begin{aligned} \rho \left( t \right)&= \left( {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {a_1}&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} {z_1} \\ 0&{} {a_2}&{} 0&{} 0&{} 0&{} 0&{} {z_2}&{} 0 \\ 0&{} 0&{} {a_2}&{} 0&{} 0&{} {z_2}&{} 0&{} 0 \\ 0&{} 0&{} 0&{} {b_2}&{} {z_2}&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} {z_2}&{} {a_2}&{} 0&{} 0&{} 0 \\ 0&{} 0&{} {z_2}&{} 0&{} 0&{} {b_2}&{} 0&{} 0 \\ 0&{} {z_2}&{} 0&{} 0&{} 0&{} 0&{} {b_2}&{} 0 \\ {z_1}&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0&{} {b_1} \\ \end{array}}} \right) \\ a_1&= \left( {1-\frac{p}{2}} \right) ^{3}\cos ^{2}\alpha +\left( {\frac{p}{2}} \right) ^{3}\sin ^{2}\alpha \quad b_1 =\left( {\frac{p}{2}} \right) ^{3}\cos ^{2}\alpha +\left( {1-\frac{p}{2}} \right) ^{3}\sin ^{2}\alpha \\ a_2&= \left( {\frac{p}{2}} \right) \left( {1-\frac{p}{2}} \right) ^{2}\cos ^{2}\alpha +\left( {\frac{p}{2}} \right) ^{2}\left( {1-\frac{p}{2}} \right) \sin ^{2}\alpha \\ b_2&= \left( {\frac{p}{2}} \right) ^{2}\left( {1-\frac{p}{2}} \right) \cos ^{2}\alpha +\left( {\frac{p}{2}} \right) \left( {1-\frac{p}{2}} \right) ^{2}\sin ^{2}\alpha \\ z_1&= \left[ {\left( {1-\frac{p}{2}} \right) ^{3}-\left( {\frac{p}{2}} \right) ^{3}} \right] \cos \alpha \sin \alpha \\ z_2&= \left[ {\left( {\frac{p}{2}} \right) ^{2}\left( {1-\frac{p}{2}} \right) -\left( {\frac{p}{2}} \right) \left( {1-\frac{p}{2}} \right) ^{2}} \right] \cos \alpha \sin \alpha \end{aligned}$$

If we consider the maximally entangle state and according to Eq. (2), then the multipartite concurrence of the initial state can be written as:

$$\begin{aligned} Q_3^0 =\left( {\frac{p}{2}} \right) ^{3}-\left( {1-\frac{p}{2}} \right) ^{3}-3\left( {\frac{p}{2}} \right) \left( {1-\frac{p}{2}} \right) \end{aligned}$$

In addition, we can calculate the case of \(N=2, 4, 5\) and \(k>0\) in detail and obtain the following results:

Now, according to Table 3, we obtain the multiqubit concurrence\(C_N^k \)

$$\begin{aligned} C_N^k =\max \left\{ {0,\hbox {}\left( {\frac{p}{2}} \right) ^{N}+\left( {-1} \right) ^{N}\left( {1-\frac{p}{2}} \right) ^{N}-N\left( {\frac{p}{2}} \right) \left( {1-\frac{p}{2}} \right) } \right\} \end{aligned}$$

So for facilitating to compare the influence of different decoherence environment on the concurrence numerically, we consider the maximally entangled state and the variation of concurrence versus \(p\) for various \(N\)as shown in Fig. 4.

Fig. 4
figure 4

The \(C_N^k\) versus \(P\) for various qubits in the different decoherence channels for the initial state \(\alpha =\pi /4\), a Phase damping (flip) channel, b Bit flip channel, c Bit-Phase flip channel

Full size image
Table 3 \(Q_N^k\) for various \(N\) values with arbitrary integer \(k\) under bit-phase flip channel
Full size table

From Fig. 4, we can see that the behaviors of concurrence when the system is coupled with the different decoherence channels are analogous. It shows that the initial entanglement monotonous decreases faster (at smaller \(p\)) as the number of qubits increases. While the distinct difference between picture a and pictures b and c is that the entanglement under the phase damping or phase flip channel is always exists, and the system undergoes an ESD at the critical point only for the bit flip channel and bit-phase flip channels.

From the above results \(C_N^{k}\), we can see that the factor of \(Q_N^{k}\) determines the decay time of entanglement and the concurrence will undergo entanglement sudden death from Fig. 4. In order to study the relationship between the ESD time and number of particles, we adopt the numerical simulations and obtain the following approximate results as shown in Fig. 5. It confirms that the time of the entanglement sudden death decreases with the increases of the number \(N\), and the result can be applied to both the bit flip channel and bit-phase flip channels.

Fig. 5
figure 5

The time of ESD versus \(N\) for bit flip channel and bit flip phase channel

Full size image

4 Discussion and conclusion

In this paper, we investigate the dynamics of multiparticle entanglement for the remote qubits in generalized \(N\)-party GHZ state when each qubit interacts with a local decoherence channel. After a detailed calculation, we summarize some analogous algebraic formulas for the multiparticle concurrence under the different channels, such as phase damping, phase flip, bit flip and bit-phase flip channel. The results show that the concurrence just monotonously decreases and does not occur sudden death when the system is coupled with the phase damping and phase flip channel for the cases of \(k\ge 0\). In addition, we also find out that the initial entanglement monotonously decreases in company with an ESD for an arbitrary \(k\ge 0\) under the bit flip and bit-phase flip channel. It is shown that the multi-particle entanglement under the phase damping and phase flip channel is more robust than that in the amplitude damping, bit flip and bit-phase flip channel. Meanwhile, we confirm the conclusion shown in the previous studies about the time of ESD, that is, the time decreases with the number of qubit in the multipartite system.