Secret sharing based on quantum Fourier transform

Abstract

Secret sharing plays a fundamental role in both secure multi-party computation and modern cryptography. We present a new quantum secret sharing scheme based on quantum Fourier transform. This scheme enjoys the property that each share of a secret is disguised with true randomness, rather than classical pseudorandomness. Moreover, under the only assumption that a top priority for all participants (secret sharers and recovers) is to obtain the right result, our scheme is able to achieve provable security against a computationally unbounded attacker.

1 Introduction

Secret sharing plays a crucial role in cryptography, which enables a dealer to distribute his secret among a group of players. The dealer usually divide his secret message into $n$ pieces, where $n$ is the number of the intended secret sharers. A piece of a secret is customarily called a share (or a shadow). In a $(t,n)$ threshold scheme, any group of $t$ (for threshold) or more players is sufficient to recover the secret, while any number of less than $t$ shares contain no information about the secret (except for the length of the secret). In classical world, a popular technique to implement $(t,n)$ threshold scheme uses Lagrange interpolation method, which was presented by Shamir [1], and was often called Shamir’s secret sharing scheme (SSSS). At the same year, Blakley [2] independently introduced another threshold scheme for secret sharing.

However, classical secret sharing protocols have some limitations. For example, most of them make use of random bits. In order to distribute a one-bit secret among threshold $t$ players, $t{-}1$ random bits are necessary. On the other hand, classical secret sharing schemes generally do not involve the secure transmission of the shares, leaving this work to other cryptographic protocols [3]. With the boom in quantum information and computation, quantum secret sharing (QSS) is attracting more and more interest, and quantum state sharing (QSTS) is offering new perspectives. QSTS is QSS of quantum information, and it has no classical counterpart. From the point of view of information theory, QSS is the generalization of classical secret sharing.

The first QSS scheme was presented by Hillery et al. [4], which took advantage of multipartite entangled Greenberger– Horne–Zeilinger (GHZ) state to achieve both QSS and QSTS. After that, Cleve, Gottesman and Lo investigated quantum $(k,n)$ threshold scheme and showed that the threshold parameter $k$ should satisfy the condition that $k \le n < 2k-1$. They also considered the connection between QSS and quantum error-correction code. Soon Gottesman [5] generalized their results and showed that the size of each share in a QSS scheme must be at least as large as the size of the secret. From then on, a number of QSS and QSTS protocols were presented one after another. See, for example [3, 6–13].

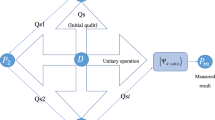
In 2003, a special and interesting QSS scheme was proposed by Hsu [9]. In Hsu’s work, through Grovers quantum searching algorithm, a $(2,2)$ threshold scheme was established. The basic idea that underlies the protocol in [9] remarkably differs from the ideas that underlie the protocols mentioned above. Then a natural question which arises is: can we design other special and interesting QSS schemes via different mechanisms? Bear this in mind and inspired by Dolev et al.’s [14] work, we propose a new QSS protocol based on quantum Fourier transform (QFT) in this paper. The scheme is an $(n,n)$ threshold one. Our QSS protocol enjoys the nice property that each share is protected by a random number. These numbers are generated totally randomly and uniformly, which is guaranteed by the principles of quantum mechanics. In contrast with traditional situation, classical random numbers are usually generated from a biasing resource and only offer pseudo randomness most of the time. Moreover, our new QSS scheme via QFT makes sense from the perspective of efficiency (or the number of qubits consumed in a scheme). The advantage of our QSS scheme is the efficiency gain due to using qudits rather than qubits to serve as the quantum channels. We will show that the new QSS protocol achieves a desirable speed-up compared with a kind of direct QSS using secure quantum key distribution. At last, our QSS scheme is proven to be secure based on a cryptographic simulator.

2 Assumptions and definitions

As stated by Katz and Lindell [15], exact definitions and precise assumptions are essential for a cryptographic protocol. The above two elements, together with rigorous proofs of security, constitute the basic principles of modern cryptography. We start with assumptions which are necessary in our QSS scheme. Note that each party may change his local input before executing the protocol. For example, if one party can recover the secret using his true input and the outcome of the joint computation running with his fake input and other parties’ true inputs, then he may obtain the secret exclusively. (Of course, it is the case that if two or more participants are not honest, then none will get the secret exactly.) However, this situation is unavoidable even when the parties utilize a trusted party. On the other side, noticing that other parties may take the same strategy to obtain the secret exclusively, the cheating party may reconsider the effectiveness of replacing his true input with a fake one. Therefore, if we assume that the first choice of a participant is to obtain the right secret and only when this situation is satisfied he may take all kinds of cheating strategies to prevent other participants from getting the secret rightly, then we can safely get rid of the possibility of a participant adopting the attack method of substituting his private input with a fake one. Formally, we have

Assumption 1

In a QSS scheme, suppose the first priority of each participant is to learn the secret exactly.

In fact, Assumption 1 can be replaced with a weaker one: suppose in the course of secret recovery the number of the cheating participants, whose strategy is to modify the true inputs, is not equal to 1. In other words, if the number of the cheating participants is 0, then all the participants will learn the right secret. In another case, if the number of the cheating parties is larger than 1, then none will get the secret rightly. However, this weaker assumption is somehow obscure and not straightforward, so we still adopt Assumption 1 as the only cryptographic assumption throughout our QSS protocol.

The following definitions are essential in the security proof of our QSS scheme. We use the same definitions as those in [16].

Definition 1

(View) Let $f$ be a functionality for cooperative computation and $\varPi$ be a multi-party protocol for computing $f$. The view of each party, during an execution of $\varPi$ on the inputs of all parties, is a tuple which includes the input of the party, the outcome of the party’s internal coin tosses, and the intermediate messages he has received.

It is worthwhile mentioning that the output of each party during an execution of $\varPi$ is implicit in the party’s view of the execution.

Definition 2

(Computational Indistinguishable) Two probability ensembles $\{X_n\}_{n \in N}$ and $\{Y_n\}_{n \in N}$ are computationally indistinguishable if they are indistinguishable by any probabilistic polynomial-time algorithm.

For example, we have two probability ensembles $\{X_n\}=r$ and $\{Y_n\}=10r$, where $r$ is distributed uniformly and randomly in real number field. Given that Alice outputs a sequence of values using one of $\{X_n\}$ and $\{Y_n\}$ as the resource, and Bob outputs another sequence using another probability ensemble. Then we cannot distinguish between these two sequences and thus cannot tell which is adopted by Alice, and vice verse. In this situation, we say that these two probability ensembles are computational indistinguishable.

3 QSS scheme

In our QSS protocol, each participant gets from the secret sharer his private shadow $s_i$. The goal to recover the right value of the secret can be expressed as a functionality $f(\cdot )$, where $f(\cdot )$ is defined as:

$$\begin{aligned} f(s_1,s_2,\ldots ,s_n)=\sum _{i=1}^{n}s_i \end{aligned}$$

(1)

Meanwhile, the value of each $s_i$ is protected. In order for $n$ participants to get a correct and privacy-preserving result, these participants can perform as follows.

Without loss of generality, we can assume that all $s_i (1 \le i \le n)$ are positive integers. Because the case that some $s_i$ s are not integers can be treated simply by multiplying a sufficiently large positive integer for all the input data. Let $N$ be a sufficiently large positive integer. Suppose that the $n$ parties share a priori an $n$-particle entangled states

$$\begin{aligned} |S\rangle =\frac{1}{\sqrt{N}}\sum _{j=0}^{N-1}|j\rangle _1 |j\rangle _2 \cdots |j\rangle _n, \end{aligned}$$

(2)

where each $|j\rangle$ is an $N$-dimensional basis state, and $|S\rangle$ is used to computing the summation. When the scheme begins, each participating party first applies an $N$-mode quantum discrete Fourier transform to his particle which comes form the composite quantum system $|S\rangle$. The quantum version of the discrete Fourier transform [17, 18] is a unitary transformation $\mathcal F$ which can be expressed in a chosen computational basis $\{|0\rangle ,|1\rangle ,\ldots ,|N-1\rangle \}$ as:

$$\begin{aligned} \mathcal F |j\rangle =\frac{1}{\sqrt{N}}\sum _{k=0}^{N-1}e^{2 \pi ijk/N}|k\rangle \end{aligned}$$

(3)

Then each participant performs a transformation $U^{i}$ on his particle, where $U^{i}$ is defined to be:

$$\begin{aligned} U^{i} |j\rangle =|j \oplus {s_i}\rangle , \end{aligned}$$

(4)

where $\oplus$ denotes addition modulo $N$. After these two transform operations, each participant makes a quantum measurement in computational basis, i.e. $\{|0\rangle ,|1\rangle ,\ldots ,|N-1\rangle \}$. Suppose their measurement results are $\hat{s}_1$, $\hat{s}_2$, $\ldots$, $\hat{s}_n$. Then they broadcast these numbers via a public classical channel. Now each participant can compute the summation by:

$$\begin{aligned} \sum _{i=1}^{n}s_i = \hat{s}_1 \oplus \hat{s}_2 \oplus \cdots \oplus \hat{s}_n \end{aligned}$$

(5)

The notation $\oplus$ in Eq. (5) represent addition modulo $N$ as well. Till now, each participant is able to get the secret.

4 Analysis and proofs

4.1 Correctness

We would like to analyse the correctness of the above scheme first. After the two transform operations by all participants, $|S\rangle$ is transformed into a new state $|\hat{S}\rangle$:

$$\begin{aligned} |\hat{S}\rangle&= (U^{1}\mathcal F ) \otimes (U^{2}\mathcal F ) \otimes \cdots \otimes (U^{n}\mathcal F ) |S\rangle \nonumber \\&= \frac{1}{\sqrt{N}}\sum _{j=0}^{N-1} (U^{1}\mathcal F )|j\rangle _{1} \otimes (U^{2}\mathcal F )|j\rangle _{2} \otimes \cdots \otimes (U^{n}\mathcal F )|j\rangle _{n} \nonumber \\&= \frac{1}{\sqrt{N}}\sum _{j=0}^{N-1} \left(U^{1} \frac{1}{\sqrt{N}}\sum _{k_1=0}^{N-1}e^{2 \pi ijk_1/N}|k_1\rangle \right) \otimes \nonumber \\&\quad \cdots \otimes \left(U^{n} \frac{1}{\sqrt{N}}\sum _{k_n=0}^{N-1}e^{2 \pi ijk_n/N}|k_n\rangle \right) \nonumber \\&= \frac{1}{\sqrt{N}}\sum _{j=0}^{N-1} N^{-\frac{n}{2}} \sum _{k_1,\ldots ,k_n} e^{\frac{2\pi ij}{N}(k_1+\cdots + k_n)} |k_1\oplus {s_1}\rangle \otimes \cdots \otimes |k_n \oplus {s_n}\rangle \end{aligned}$$

(6)

In the last step of Eq. (6), exchanging the order of summation, we get

$$\begin{aligned}&|\hat{S}\rangle = N^{-\frac{n+1}{2}}\sum _{k_1,\ldots ,k_n} \left(\sum _{j=0}^{N-1} e^{\frac{2\pi ij}{N}(k_1+\cdots + k_n)}\right)\nonumber \\&|k_1\oplus {s_1}\rangle \otimes \cdots \otimes |k_n \oplus {s_n}\rangle \end{aligned}$$

(7)

If we denote $\sum _{j=0}^{N-1} e^{\frac{2\pi ij}{N}(k_1+\cdots + k_n)}$ as $\zeta$, and denote $k_1+\cdots + k_n$ as $K$, then by calculation, we have

$$\begin{aligned} \zeta = \left\{ \begin{array}{l@{\quad }l} N&K=0 (\mathrm mod N)\\ 0&\mathrm otherwise \\ \end{array}\right. \end{aligned}$$

(8)

The second part of Eq. (8) is proven in “Appendix”. Combining Eqs. (7) and (8), we can get that

$$\begin{aligned} |\hat{S}\rangle = N^{-\frac{n+1}{2}}\sum _{K=0 (\mathrm mod N)} |k_1\oplus {s_1}\rangle \otimes \cdots \otimes |k_n \oplus {s_n}\rangle \end{aligned}$$

(9)

Let $\hat{s}_i$ be defined as in Sect. 3, then by Eq. (9) we know that

$$\begin{aligned}&\hat{s}_1 \oplus \hat{s}_2 \oplus \cdots \oplus \hat{s}_n\nonumber \\&\quad =k_1\oplus {s_1} \oplus k_2\oplus {s_2} \oplus \cdots \oplus k_n\oplus {s_n}\nonumber \\&\quad =(s_1+ s_2+ \cdots + s_n) \oplus K\nonumber \\&\quad =s_1+ s_2+ \cdots + s_n\nonumber \\&\quad =\sum _{i=1}^{n}s_i \end{aligned}$$

(10)

It goes to show that Eq. (5) is correct.

Now we can safely conclude that if all the participants execute the above scheme honestly, they will all learn the secret rightly.

4.2 Efficiency

In this subsection we discuss the efficiency of our QSS scheme. Intuitively, a simpler but not trivial $(n,n)$ threshold QSS can proceed as follows. In order to share a secret between $n$ players, the secret owner divides his secret into $n$ random shadows—each shadow for a player. He then sends the $i$th shadow to player $i$ respectively, using any of existing quantum key distribution (QKD) schemes. Obviously, this scheme does work, and its security is guaranteed by QKD, which has been proven to be unconditionally secure [19–22]. Therefore, a new QSS protocol should, at least, be as efficient as this one. For sake of concision, we call this kind of secret sharing scheme via QKD IQSS (Intuitive QSS) hereafter. We know that Holevo [23] proved an important theorem on the classical information capacity for a quantum channel. The Holevo theorem claims that, for any classical message, the cost of transmitting it from one party to another party using qubits is the same as the cost of sending it in terms of classical bits. If the mission requires $k$ bits on average, then it also requires $k$ qubits on average. Hence no matter what QKD protocol is invoked, the secret owner will communicate at least $m$ qubits to each player to transmitting a shadow, where $m$ is the length of each shadow. We now get that, to share a secret among $n$ participants, $nm$ qubits are essential for an IQSS.

To evaluate the efficiency (or the number of qubits consumed in a QSS scheme) of the above IQSS protocol, we would first like to introduce an important conclusion proved by Csirmaz [24].

Theorem 1

[24] In any $(n,n)$ threshold secret sharing scheme, if it is information-theoretically secure, then the size of each shadow is at least as large as the size of the secret.

Given the length of the secret is $M$, then by Theorem 1 we know that $m \ge M$. Thus we obtain that $nM$ qubits are necessary for an information-theoretically secure IQSS.

As for our QSS protocol based on QFT, in order to share and recover an $M$-bit secret within $n$ parties, we need only 1 qu $d$ it (with $d=M$) to create each $|j\rangle$ of the state $|S\rangle$ in Eq. (2). That is to say, $n$ qu$d$its (with $d=M$) are necessary in our QSS scheme. We know that $O (\log _2 M)$ qubits are sufficient to “simulate” any system of arbitrary $m$ level. This implies that our QSS scheme would about require $n\log _2 M$ qubits. Therefore it is evident that our scheme provides a desirable efficiency enhancement over IQSS.

Clearly, the advantage of our QSS scheme via QFT is the efficiency gain due to using qudits rather than qubits to serve as the quantum channels. If we weigh up this in terms of the number of qubits used in QSS schemes, then $n\log _2 M$ versus $nM$ gives us a definite result. This can also be deemed as a situation to embody the superiority of quantum entanglement.

4.3 Security

To accomplish the security proof, we will construct corresponding simulator for each participant who attempts to cheat in our QSS scheme. The general idea underlying the method of simulator is that if a simulator for a player can emulate the execution of a protocol with only the input this player’s private data and the intermediate messages he has received during the execution of the protocol, then we can safely conclude that this protocol is secure against this player and he is not able to obtain more information about other players’ private data. This is because the simulator itself has no knowledge about those private data. For more discussion of simulator, view and computational indistinguishable, we refer readers to Ref. [16].

Let us begin the security proof. We need to present a simulator for each party’s view. The simulator for participant $i$ is denoted as $E_i$. The view of party $i$ can be expressed as a tuple $(s_i,u_i,v_i,M_{-i})$, where $s_i$ represents the secret shadow of party $i$, $u_i$ is the state of his local particle (i.e., which in the state $|j\rangle _i$ in Eq. (2)), $v_i$ is his local output and $M_{-i}$ stands for the set of the values declared by all the participants other than party $i$. Taking this view as the input, the simulator $E_i$ selects uniformly and randomly a number on $[0,N-1]$ and outputs $v^{\prime }_i$. Similarly, $E_i$ uniformly and randomly chooses $n-1$ values on $[0,N-1]$ to output a set $M^{\prime }_{-i}$. The total output of $E_i$ can now be expressed as $(s_i,u_i,v^{\prime }_i,M^{\prime }_{-i})$. We show that this output and the view of participant $i$ are computational indistinguishable. Clearly, the first two elements are same, so we only need to consider the last two elements. i.e., $v_i$ versus $v^{\prime }_i$, and $M_{-i}$ versus $M^{\prime }_{-i}$. Note that although the QFT and unitary transformation $U^{i}$ of each party are determinate, the measurement outcome of the party is totally random and its value is taken from $[0,N-1]$ uniformly. Therefore, there is no method to distinguish from $v_i$ and $v^{\prime }_i$, even with a quantum computer. Similarly, $M^{\prime }_{-i}$ is distributed identically to $M_{-i}$. That is to say, the distribution of $E_i$’s total output is identical to the view of party $i$ in the real execution and the two tuples are computational indistinguishable. According to the basic idea of simulator, we are convinced that the QSS protocol is secure.

In addition, from the process of the above proof, we know that party $i$ does have the possibility of learn the secret exclusively by announce $v^{\prime }_i$ instead of $v_i$. However, as stated in Sect. 2, under Assumption 1, if his top priority is to obtain the right secret, he will follow the QSS protocol with an honest $v_i$.

Till now, we know that our QSS scheme based on QFT is secure against any computationally unbounded attacker.

5 Conclusion

In summary, we have shown that QFT can be utilized to construct secret sharing. Under the only cryptographic assumption that the first priority of each party is to learn the right secret, the QSS via QFT has been proven to be secure using a cryptographic simulator. Furthermore, a comparison of qubits consumed in QSS shows that our new protocol offers a desirable efficiency promotion over any IQSS scheme that reaches the upper bound of the efficiency ruled by the Holevo theorem.

Appendix: Proof of Equation (8)

The case that $\zeta =N$ if $K = 0$ mod $N$ is obvious, thus we only focus on the proof of $\zeta =0$ if $K \ne 0$ mod $N$. When $K \ne 0$ mod $N$, we know that

$$\begin{aligned} \zeta =\sum _{j=0}^{N-1} e^{\frac{2\pi ij}{N}K} \end{aligned}$$

(11)

Let $\frac{2\pi K}{N}=t$, then Eq. (11) can be rewritten as

$$\begin{aligned} \zeta =\sum _{j=0}^{N-1} e^{ijt}=\sum _{j=0}^{N-1} \cos {jt}+i\sum _{j=0}^{N-1} \sin {jt} \end{aligned}$$

(12)

It is not hard to verify and prove the following two Lagrange’s trigonometric identities [25]:

$$\begin{aligned} \sum _{n=0}^{N} \cos {n\theta }=-\frac{1}{2}+\frac{\sin {\left(N+\frac{1}{2}\right)\theta }}{2\sin {\frac{1}{2}\theta }} \end{aligned}$$

(13)

and

$$\begin{aligned} \sum _{n=0}^{N} \sin {n\theta }=\frac{\cos {\frac{1}{2}\theta }-\cos {\left(N+\frac{1}{2}\right)\theta }}{2\sin {\frac{1}{2}\theta }} \end{aligned}$$

(14)

Now we consider the first item of the right side of Eq. (12) using (13):

$$\begin{aligned} \sum _{j=0}^{N-1} \cos {jt}&= \sum _{j=1}^{N} \cos {jt}-\cos {Nt}+\cos {0}=\sum _{j=1}^{N} \cos {jt}\nonumber \\&= -\frac{1}{2}+\frac{\sin {\left(N+\frac{1}{2}\right)t}}{2\sin {\frac{1}{2}t}}\nonumber \\&= -\frac{1}{2}+\frac{\sin \left({2\pi K +\frac{\pi K}{N}}\right)}{2\sin {\frac{\pi K}{N}}}\nonumber \\&= -\frac{1}{2}+\frac{\sin {\frac{\pi K}{N}}}{2\sin {\frac{\pi K}{N}}}=0 \end{aligned}$$

(15)

The last step of (15) holds iff $K \ne 0$ mod $N$.

Similarly, we can get that $\sum _{j=0}^{N-1} \sin {jt}=0$ using (14) with $K \ne 0$ mod $N$.

So far, we can safely reach the conclusion that $\zeta =0$ iff $K \ne 0$ mod $N$ and thus Eq. (8) follows.