1 Introduction

The seminal paper of Farrell (1957) defined efficiency measures and suggested both non-parametric and parametric estimation methods, and Farrell and Fieldhouse (1962) used linear programming for the first time. Charnes et al. (1978) (CCR) coined the term data envelopment analysis (DEA) and generalised and put DEA into the linear programming format we use today.

After a decade of applications of DEA following the publication of CCR, it was recognised that results both concerning efficiency scores and shape of the frontier production function, on which Farrell efficiency measures are based, were not always adequate when confronted with expert knowledge of the units to which DEA was applied. Types of inadequacies discussed in the literature have been that too many efficient units may appear in some DEA models, a DEA model may show an inefficient unit from the point of view of experts as an efficient one, too many zeros appear as solutions for the multipliers (or shadow prices or weights) (variables appearing in the dual solution if the primal model is the envelopment model formulated in the space of inputs and outputs), and units are not ‘properly’ enveloped.

Already Farrell (1957, p. 256–257) restricted the estimation of the non-parametric frontier function and consequently some of the efficiency scores by introducing artificial observations of the zero-infinity type in order to secure convex isoquants. CCR criticised this approach and introduced a non-Archimedean number weighting the slacks in the objective function and restricting the shadow prices (multipliers) to be strictly positive “because all resources and outputs are assumed to have ‘some’ positive value” (Charnes et al. 1979).

Thompson et al. (1986) generalised the restriction on dual variables introduced by CCR restricting the multipliers (weights) in a more general way than using the non-Archimedean number as a lower constraint on the weights. The problem of Thompson et al. (1986) was that the number of units under investigation was so small (only six) that all but one of the units was rated efficient using conventional DEA. In order to increase the discrimination restrictions on the multipliers or shadow prices or weights were enforced.

Based on Thompson et al. (1986) an elegant and subtle approach was developed in the DEA literature to deal with the problems of inadequacies of the DEA models. This approach was based on incorporating domination cones (Yu 1974) in DEA models. A number of outstanding papers were devoted to substantiation, development and applications of domination cones to DEA models (Brockett et al. 1997; Thompson et al. 1990, 1997; Wei et al. 2008; Yu et al. 1996; Charnes et al. 1989, 1990). The two latter papers introduced the cone-ratio approach of basing the shape of the frontier on a few efficient units selected by experts by restricting the weights (multipliers) to be within cones in the dual space.

Building on an approach in Thanassoulis and Allen (1998) and Allen and Thanassoulis (2004) followed the idea of Farrell (without a reference) of dealing with the inadequacies of the DEA solution by introducing artificial observation termed anchor units in the case of constant returns to scale and a single input. This definition was generalised in Bougnol and Dulá (2009) to multiple inputs and outputs and variable returns to scale. An elaborate algorithm for finding anchor points was introduced. The empirical applications gave the somewhat surprising result that almost all extreme efficient units are in fact anchor points. The situation of some zeros for weights seems to be the normal situation for DEA applications. However, their algorithms may produce units that are just usual efficient units (vertices) in DEA models.

Thanassoulis et al. (2012) elaborated further the super-efficiency approach for finding anchor units in a general model exhibiting variable returns to scale. However, their approach does not reveal all efficient units that may be the point of departure for improving envelopment in the Banker et al. (1984) model of variable returns to scale.

Edvardsen et al. (2008) suggested an empirical witty method for discovering “suspicious” units, which is units that may cause inadequate results in the DEA models; they call them exterior units. However, their method cannot discover all suspicious units.

The purpose of this paper is to identify units that may unduly become efficient by making use of a new concept; a terminal unit. This concept is better suited as points of departure for introducing artificial observations than the definitions of anchor units or exterior units. The definition of terminal units is linked both to the Farrell approach of introducing artificial observations and to the approach of incorporating domination cones in DEA models.

Cones are usually determined in the dual space of multipliers. It is rather difficult, however, for a manager (the decision-maker) to determine cones in the multipliers space that is dual to the space of inputs and outputs where a production possibility set is constructed (Cooper et al. 2000). For this very reason only two particular DEA models with cones are widely used in practice at present: the assurance region model and the cone-ratio model (Cooper et al. 2000).

The plan of the paper is to go into the background in Sect. 2, using key elements from the cone-ratio approach developed in Charnes et al. (1990), based on the Banker et al. (1984) model of variable returns to scale, and establish necessary definitions. The main results are presented in Sect. 3, including the definition of a terminal unit and illustrating its difference from the term anchor unit and using domination cones to establish that terminal production units exist if some production units become inefficient if cones are inserted in the model. Some numerical experiments on data for Russian banks are carried out in Sect. 4, showing how to find a terminal unit and how to use experts to indicate an artificial efficient unit using a visual interactive graphical technique. Section 5 concludes and offer ideas for further research.

2 Background

It was shown in the DEA scientific literature (see Krivonozhko et al. 2009) that the model in Banker et al. (1984) exhibiting variable returns to scale (hereafter termed the BCC model) can approximate any DEA model from a large family of DEA models. For this reason, we consider the BCC model as a basic model in our exposition.

Consider a set of n observations of actual production units (X j , Y j ), j = 1, …, n, where the vector of outputs Y j  = (y 1j , …, y rj ) ≥ 0, j = 1, …, n, is produced from the vector of inputs X j  = (x 1j , …, x mj ) ≥ 0. The production possibility set T is the set {(X, Y) | the outputs Y ≥ 0 can be produced from the inputs X ≥ 0}. The primal input-oriented BCC model can be written in the form

$$\begin{aligned} & \hbox{min} \,\theta \\ & {\text{subject}}\,{\text{to}} \\ & \sum\limits_{j = 1}^{n} {X_{j} \lambda_{j} + S^{ - } = \theta X_{o} } , \\ & \sum\limits_{j = 1}^{n} {Y_{j} \lambda_{j} - S^{ + } = Y_{o} ,} \\ & \sum\limits_{j = 1}^{n} {\lambda_{j} = 1\,} , \\ & \lambda_{j} \ge 0,\quad j = 1, \ldots ,n, \\ & s_{k}^{ - } \ge 0,\quad k = 1, \ldots ,m, \\ & s_{i}^{ + } \ge 0,\quad i = 1, \ldots ,r, \\ \end{aligned}$$
(1a)

where X j  = (x 1j , …, x mj ) and Y j  = (y 1j , …, y rj ) represent the observed inputs and outputs of production units j = 1, …, n, \(S^{ - } = (s_{1}^{ - } , \ldots ,s_{m}^{ - } )\) and S + = (s +1 , …, s + r ) are vectors of slack variables. In this primal model the efficiency score θ of production unit (X o , Y o ) is found; (X o , Y o ) is any unit from the set of production units (X j , Y j ), j = 1, …, n.

Notice that we do not use an infinitesimal constant ɛ (a non-Archimedean quantity) explicitly in the DEA models, since we suppose that each model is solved in two stages in order to separate efficient and weakly efficient units.

The dual multiplier form of the BCC model (1a) is expressed as

$$\begin{aligned} & \hbox{max} \,\left( {u^{T} Y_{0} - u_{0} } \right) \\ & {\text{subject }}\,{\text{to}} \\ & u^{T} Y_{j} - v^{T} X_{j} - u_{0} \le 0,\quad j = 1, \ldots ,n \\ & v^{T} X_{0} = 1, \\ & v_{k} \ge 0,\quad k = 1, \ldots ,m,\quad u_{i} \ge 0,\quad i = 1, \ldots ,r \\ \end{aligned}$$
(1b)

where (v, u, u 0) is a vector of dual variables, v ∈ E m, u ∈ E r, u 0 is an unconstrained scalar variable associated with the convexity constraint.

The BCC primal output-oriented model can be written in the following form

$$\begin{aligned} & \hbox{max} \,\eta \\ & {\text{subject}}\,{\text{to}} \\ & \sum\limits_{j = 1}^{n} {X_{j} \lambda_{j} + S^{ - } = X_{0} } , \\ & \sum\limits_{j = 1}^{n} {Y_{j} \lambda_{j} - S^{ + } = \eta Y_{0} ,} \\ & \sum\limits_{j = 1}^{n} {\lambda_{j} = 1\,} , \\ & \lambda_{j} \ge 0\,\,,\quad j = 1, \ldots ,n, \\ & s_{k}^{ - } \ge 0,\quad k = 1, \ldots ,m, \\ & s_{i}^{ + } \ge 0,\quad i = 1, \ldots ,r. \\ \end{aligned}$$
(1c)

The dual multiplier form of the BCC output-oriented model (1c) is written in the form

$$\begin{aligned} & \hbox{min} \,\left( {v^{T} X_{0} + u_{0} } \right) \\ & {\text{subject}}\,{\text{to}} \\ & u^{T} Y_{j} - v^{T} X_{j} - u_{0} \le 0,\quad j = 1, \ldots ,n \\ & u^{T} Y_{0} = 1, \\ & v_{k} \ge 0,\quad k = 1, \ldots ,m,\quad u_{i} \ge 0,\quad i = 1, \ldots ,r, \\ \end{aligned}$$
(1d)

where (v, u, u 0) is a vector of dual variables, v ∈ E m, u ∈ E r, u 0 is a scalar variable associated with the convex constraint [the same symbols for dual variables are used as for models (1b)].

Definition 1

(Cooper et al. 2000). Unit (X o , Y o ) ∈ T is called efficient with respect to the input-oriented BCC model if and only if any optimal solution of (1a) satisfies: (a) θ * = 1, (b) all slacks s − k , s + i , k = 1, …, m, i = 1, …, r are zero.

If the first condition (a) in Definition 1 is satisfied, then unit (X o , Y o ) is called input weakly efficient with respect to the BCC input-oriented model. We denote the set of these weakly efficient points by WEff I T. In the DEA literature (Banker and Thrall 1992; Seiford and Thrall 1990) this set is also called the input boundary.

Definition 2

(Cooper et al. 2000). Unit (X o , Y o ) ∈ T is called efficient with respect to the output-oriented BCC model if and only if any optimal solution of (1c) satisfies: (a) η * = 1, (b) all slacks s − k , s + i , k = 1, …, m, i = 1, …, r are zero.

If the first condition in Definition 2 is satisfied, then unit (X o , Y o ) is called output weakly efficient with respect to the BCC model. We denote the set of these weakly efficient points by WEff O T. In the DEA literature (Banker and Thrall 1992; Seiford and Thrall 1990), this set is also called the output boundary.

Definition 3

(Cooper et al. 2000). Activity (X′, Y′) ∈ T is weakly Pareto efficient if and only if there is no (X, Y) ∈ T such that X < X′ and Y > Y′. We denote the set of weakly Pareto efficient activities by WEff P T.

We denote the set of efficient points of T with respect to the BCC model (1a–1d) by EffT. Krivonozhko et al. (2005) have proved that the following relations hold:

$$Eff\;T \subseteq WEff_{I} T \cap WEff_{O} T,\quad WEff_{I} T \cup WEff_{O} T \subseteq WEff_{P} T = Bound\;T,$$

where the boundary of T is designated as BoundT.

The production possibility set T B for the BCC model can be written in the form (Banker et al. 1984)

$$T_{B} = \left\{ {(X,Y)\;\left| {\,\sum\limits_{j = 1}^{n} {X_{j} \lambda_{j} \le X,\quad \sum\limits_{j = 1}^{n} {Y_{j} \lambda_{j} \ge Y,} \quad } } \right.} \right.\left. {\sum\limits_{j = 1}^{n} {\lambda_{j} = 1} ,\quad \lambda_{j} \ge 0,\quad j = 1, \ldots ,n} \right\}.$$
(2)

In this paper we will mainly consider production possibility sets of this type.

3 Main results

The use of cones will play a crucial role in our search for terminal units. The main idea of incorporating domination cones in DEA models is to reduce the domain of multipliers. For this purpose, additional constraints on multipliers are incorporated in the DEA models.

In the assurance region method, constraints on the multipliers are added to the CCR model in the following manner; see Charnes et al. (1990),

$$\begin{gathered} l_{1i} \le \frac{{v_{i} }}{{v_{1} }} \le k_{1i} ,\quad (i = 2, \ldots ,m), \\ L_{1s} \le \frac{{u_{s} }}{{u_{1} }} \le K_{1s} ,\quad (s = 2, \ldots ,r), \\ \end{gathered}$$
(3)

where l 1i , k 1i , L 1s , K 1s are given low and upper bounds on the ratios of multipliers.

Assertion 1

There exist polyhedral cones in multidimensional space E m+r that cannot be described by relations (3).

Thus, formulas (3) describe only some subset of possible polyhedral cones in multidimensional space E m+r. The next model enables one to use more general form of domination cones in the DEA models.

The dual multiplier form of the cone-ratio model is expressed as (Charnes et al. 1989, 1990; Yu et al. 1996)

$$\begin{aligned} & \hbox{max} \;\left( {uY_{o} - u_{o} } \right) \\ & {\text{subject}}\,{\text{to}} \\ & v^{T} X_{o} = 1, \\ & - v^{T} X_{j} + u^{T} Y_{j} - u_{o} \le 0,\quad j = 1, \ldots ,n, \\ & u \in U,\quad v \in V, \\ \end{aligned}$$
(4a)

where variables v ∈ E m, u ∈ E r, u o  ∈ E 1 and U ⊆ E r+ , V ⊆ E m+ are given polyhedral cones.

The primal problem of (4a) is written as

$$\begin{aligned} & \hbox{min} \,\theta \\ & {\text{subject}}\,{\text{to}} \\ & \sum\limits_{j = 1}^{n} {X_{j} \lambda_{j} - \theta X_{o} } \in V^{*} , \\ & Y_{o} - \sum\limits_{j = 1}^{n} {Y_{j} \lambda_{j} } \in U^{*} , \\ & \sum\limits_{j = 1}^{n} {\lambda_{j} = 1\,} , \\ & \lambda_{j} \ge 0,\quad j = 1, \ldots ,n, \\ \end{aligned}$$
(4b)

where V * and U * are negative polar cones of sets V and U, respectively.

In practice (Charnes et al. 1990; Cooper et al. 2000), polyhedral cones U and V are constructed as follows: (a) some excellent units are chosen from the point of view of experts; (b) averages of the optimal multipliers u * i , v * i are computed for every excellent unit i ∈ Ex, where Ex denotes the set of excellent units (a subset of Eff T). Vectors u * i , v * i , i ∈ Ex form polyhedral cones U and V.

Cones U and V reduce the feasible domain of multipliers, while the feasible domains of inputs, see Fig. 1, and outputs, see Fig. 2, are expanding.

Fig. 1
figure 1

Transformation of the frontier in the output subspace in the cone-ratio method

Full size image
Fig. 2
figure 2

Transformation of the frontier in the input subspace in the cone-ratio method

Full size image

Now, we make an attempt to reveal the causes of inadequacies in DEA models.

Assumption

Let the cone-ratio method allows one to reduce the number of “suspicious” production units, i.e. the units that are efficient, but should be inefficient from the point of view of experts.

Production possibility set T B (2) is a convex polyhedral set. According to the classical theorems of Goldman (1956) and Motzkin (1936) any convex polyhedral set can be represented as a vector sum of convex combination of vertices and the non-negative linear combination of vectors (rays).

Before going further, let us recall some notions from convex analysis. Faces are formed by an intersection of the supporting hyperplane and the polyhedral set. In the DEA models, the dimension of face may vary from 0 up to (m + r − 1), the maximal dimension. Faces of maximal dimension are called facets. Faces of 0-dimension are known as vertices, 1-dimension as edges.

Definition 4

We call an efficient (vertex) unit terminal unit if an infinite edge is going out from this unit.

According to the classification of Charnes et al. (1991) terminal units belong to the class E (extreme efficient).

We denote the set of terminal units with respect to the production possibility set (2) by T term .

Definition 5

We call a face Γ of set T B a terminal face if this face contains an infinite edge.

Then the following assertion can be proved.

Theorem 1

If some efficient production units in model (1a–1d) become inefficient in model (4a, 4b) as a result of inserting cones in the BCC model (1a–1d), then it is necessary that there exist terminal production units among such inefficient units.

Proof

See the proof of Theorem 12 in “Appendix 1” for a more general case.

Observe that the results of Theorem 1 was proved for the cone-ratio model at first, since this model was thoroughly elaborated from theoretical and practical points of view in the scientific literature on the DEA models, see Charnes et al. (1990), Brockett et al. (1997) and Cooper et al. (2000). However, the cone-ratio model cannot cover all possible cases where inadequate results may appear in the DEA models. Therefore, theorem 12 is proven in this paper for the generalized DEA model with domination cones.

Thus, Theorem 1 shows that terminal points are the first “suspicious” units which may cause inadequate results in the DEA models.

The following optimization models enable us to find terminal units or units belonging to terminal faces of the production possibility set. For this purpose two types of models are solved for every efficient unit (vertex) q that belongs to the class E according to the classification of Charnes et al. (1991).

Problem P k (q) (k = 1, …, m):

$$\begin{aligned} & \hbox{max} \,J_{1k} = \eta \\ & \sum\limits_{j = 1}^{n} {X_{j} \lambda_{j} } \le X_{q} + \tau \,d_{k} , \\ & \sum\limits_{j = 1}^{n} {Y_{j} \lambda_{j} } \ge \eta \,Y_{q} , \\ & \sum\limits_{j = 1}^{n} {\lambda_{j} } = 1, \\ & \lambda_{j} \ge 0,\quad \tau \ge 0, \\ \end{aligned}$$
(5)

where d k  = (0, …, 1, …, 0) ∈ E m, the unity is in kth position.

Variable τ provides that ray (X q  + τd k , Y q ) going out from unit (X q , Y q ) belongs to the feasible set of the model (5).

Theorem 2

If in problem (5) the optimal value J *1k  = 1, then unit (X q , Y q ) is a terminal one or belongs to a terminal face Γ ⊂ WEff O T.

Proof

Under any τ ≥ 0 ray (X q  + τd k , Y q ) is a feasible subset for production possibility set T B  (2) due to monotonicity of T B . As it follows from model (5), if J *1k  = 1, then this ray belongs to the set WEff O T B . Hence this ray is an unbounded edge or belongs to an unbounded face of set T B .

This completes the proof.

The following models determine infinite edges emanating along direction g i , where g i  = (0, …, 1, …, 0) ∈ E r (the unity is in ith position).

Problem R i (q) (i = 1, …, r)

$$\begin{aligned} & \hbox{min} \,J_{2i} = \theta \\ & \sum\limits_{j = 1}^{n} {X_{j} \lambda_{j} } \le \theta \,X_{q} , \\ & \sum\limits_{j = 1}^{n} {Y_{j} \lambda_{j} } \ge Y_{q} - \tau \,g_{i} , \\ & \sum\limits_{j = 1}^{n} {\lambda_{j} } = 1, \\ & \lambda_{j} \ge 0,\quad \tau \ge 0. \\ \end{aligned}$$
(6)

Theorem 3

If in problem (6) the optimal value J *2i  = 1, then unit (X q , Y q ) is a terminal one or belongs to a terminal face Γ ⊂ WEff I T.

The proof of Theorem 3 is very similar to the proof of the previous theorem and is therefore skipped.

Thus, models (5) and (6) enable us to reveal terminal units or efficient units belonging to unbounded faces and also directions of infinite edges going out from efficient units.

The following problems enable one to discover only terminal units among all units belonging to the class E.

Problem \(\bar{P}_{k} (q)\) (k = 1, …, m):

$$\begin{aligned} & \hbox{min} \,\bar{J}_{1k} = \lambda_{q} \\ & \sum\limits_{j = 1}^{n} {X_{j} \lambda_{j} } \le X_{q} + \tau d_{k} , \\ & \sum\limits_{j = 1}^{n} {Y_{j} \lambda_{j} } \ge Y_{q} , \\ & \sum\limits_{j = 1}^{n} {\lambda_{j} } = 1, \\ & \lambda_{j} \ge 0,\quad j = 1, \ldots ,n;\quad \tau \ge 0, \\ \end{aligned}$$
(7)

Theorem 4

Unit (X q , Y q ) from the class E is a terminal one if the optimal value of problem (7) \(\bar{J}_{1i}^{*} = \lambda_{q}^{*} = 1\).

Proof

Observe that solution λ j  = 0, j = 1, …, n, j ≠ q, λ q  = 1, τ = 0 is a feasible solution of problem (7). So, if λ * q  = 1, this implies that any interior point belonging to the ray (X q  + τd k , Y q ) cannot be represented as a convex combination of some other points of production possibility set T B . Hence this ray is an infinite edge and point (X q , Y q ) is a terminal unit.

However, if λ * q  < 1, this implies that some interior points of the ray (X q  + τd k , Y q ) can be represented as a convex combination of some other points of set T B .

This completes the proof.

The following problems allow one to find only terminal units and infinite edges emanating along directions g i , i = 1, …, r.

Problem \(\bar{R}_{i} (q)\) (i = 1, …, r)

$$\begin{aligned} & \hbox{min} \,\bar{J}_{2i} = \lambda_{q} \\ & \sum\limits_{j = 1}^{n} {X_{j} \lambda_{j} } \le X_{q} , \\ & \sum\limits_{j = 1}^{n} {Y_{j} \lambda_{j} } \ge Y_{q} - \tau g_{i} , \\ & \sum\limits_{j = 1}^{n} {\lambda_{j} } = 1, \\ & \lambda_{j} \ge 0,\quad j = 1, \ldots ,n;\quad \tau \ge 0, \\ \end{aligned}$$
(8)

Theorem 5

Unit (X q , Y q ) from the class E is a terminal one if the optimal value of problem (8) \(\bar{J}_{2i}^{*} = \lambda_{q}^{*} = 1\).

The proof of Theorem 5 is very similar to the proof of Theorem 4 and is therefore skipped.

Let us introduce the following designations \(\bar{d}_{k} = (d_{k},0) \in E^{m + r}\), k = 1, …, m, \(\bar{g}_{i} = (0,g_{i}) \in E^{m + r}\), i = 1, …, r.

Proposition

Only vectors of the following forms \(\bar{d}_{k} = (d_{k},0) \in E^{m + r}\), k = 1, …, m, \(\bar{g}_{i} = (0,g_{i}) \in E^{m + r}\), i = 1, …, r can be the direction vectors of infinite edges of set T B .

The assertion of the proposition follows from the structure of the polyhedral set T B (Goldman 1956; Nikaido 1968; Rockafellar 1970).

Based on assertions formulated above we can prove the following result.

Theorem 6

Unit (X q , Y q ) from the class E is a terminal one if and only if it turns out to be terminal at least in one of the problems \(\bar{P}_{k} (q)\), k = 1, …, m in (7) or \(\bar{R}_{i} (q)\), i = 1, …, r in (8).

Proof

Let unit (X q , Y q ) be a terminal one. Then an infinite edge with direction vector of the form \(\bar{d}_{k} = (d_{k},0) \in E^{m + r}\), k = 1, …, m, \(\bar{g}_{i} = (0,g_{i} ) \in E^{m + r}\), i = 1, …, r is going out from this unit according to Theorem 6. Let it be vector \(\bar{d}_{k}\), without loss of generality. Consider problem of type \(\bar{P}_{k} (q)\) (7), where direction vector d k is used. Since d k determines an infinite edge, then any interior point belonging to the ray (X q  + τd k , Y q ) cannot be represented as a convex combination of some other points of set T B . Hence \(\lambda_{q}^{*} = 1\), \(\lambda_{j}^{*} = 0\), j = 1, …, n, j ≠ q, τ * ≥ 0 is an optimal solution of problem (7).

Conversely, let unit (X q , Y q ) be a terminal one in one of the problems \(\bar{P}_{k} (q)\), k = 1, …, m in (7) or \(\bar{R}_{i} (q)\), i = 1, …, r in (8). Then according to Theorems 4 and 5, this unit is a terminal one.

This completes the proof.

Bougnol and Dulá (2009) determined an anchor point as an efficient vertex belonging to an unbounded face of set T B . They proposed algorithms for discovering anchor points.

Let us denote the set of anchor units in the BCC model (1a–1d) with respect to the definition of Bougnol and Dulá (2009) by T 1 anc .

Theorem 7

Unit (X q , Y q ) belongs to the set T 1 anc in the BCC model (1a–1d) if and only if the optimal value J *1k  = 1 and/or J *2i  = 1 at least in one of the problems P k (q), k = 1, …, m in (5) and R i (q), i = 1, …, r in (6).

Proof

The result follows from Theorems 2 and 3. Indeed, if J *1k  = 1 and/or J *2i  = 1 at least in one of the problems P k (q), k = 1, …, m (5) and R i (q), i = 1, …, r (6), then unit (X q , Y q ) belongs to an edge or to a terminal face of the production possibility set T B (2). Remember from the convex analysis that an edge of the polyhedral set represents also a face of 1-dimension. Hence unit (X q , Y q ) is an anchor point with respect to the definition of Bougnol and Dulá (2009).

Conversely, let vertex (X q , Y q ) belong to T 1 anc . Hence unit (X q , Y q ) belongs to an unbounded face. All unbounded directions of this face are determined by some of the vectors \(\bar{d}_{k}\), k = 1, …, m, \(\bar{g}_{i}\), i = 1, …, r. Take some of these vectors. Let it be vector \(\bar{d}_{k}\), without loss of generality. Consider problem of type P k (q) (5), where direction vector d k is used. The ray \((X_{q} + \tau {\kern 1pt} d_{k},Y_{q})\) belongs to the set \(WEff_{O} {\kern 1pt} T_{B}\), since (X q , Y q ) is an efficient unit (vertex) and vector (0, Y q ) is perpendicular to \(\bar{d}_{k}\). Hence solving (5), we obtain J *1k  = 1.

This completes the proof.

Thus Theorem 7 gives us a constructive way to reveal whether unit (X q , Y q ) from the class E belongs to the set T 1 anc or not. For this purpose one has to solve problems P k (q), k = 1, …, m (5) and/or R i (q), i = 1, …, r (6).

Now we can formulate the following result.

Corollary 1

The set of terminal units T term of the BCC model (1a–1d) belongs to the set of anchor points T 1 anc with respect to the definition of Bougnol and Dulá, i.e. T term  ⊆ T 1 anc .

This result immediately follows from Theorems 2, 3 and 7.

Edvardsen et al. (2008) suggested an empirical method for discovering “suspicious” units, they call them “exterior units”. Let T ext denote the set of exterior units in the BCC model (1a–1d). However, their method cannot discover all suspicious units. Indeed, consider the following illustrative example, Fig. 3, panel (a). The three dimensional BCC model is determined by units A, B, C, D. Inputs and outputs of these units are presented in Table 2, see “Appendix 2”. Again consider the BCC model with the same units, but now y is an input variable, x 1 and x 2 are output variables, see Fig. 3, panel (b), points E and F are projections of points B and C onto planes x 1 Oy and x 2 Oy, respectively. Point D is not efficient in this case. Hence this point is not exterior. At the same time this point is a “suspicious” unit, since it may cause inadequacy in the DEA model. Units, like point D, belonging to unbounded faces and not being terminal units are also “suspicious” points. These units may also cause inadequate results in the DEA models. However, our computational experience shows that the number of such units in real-life data sets is very small in comparison with the number of terminal units.

Fig. 3
figure 3

Point D is not an exterior unit in the 3-dimensional BCC model

Full size image

The next theorem establishes that the set of terminal units includes the set of exterior units.

Theorem 8

The set of terminal units T term of the BCC model contains the set of exterior units T ext , i.e. T ext  ⊆ T term .

Proof

See “Appendix 1”.

However, some terminal units may not belong to the set of exterior units. Indeed, consider the following illustrative example. Figure 4 depicts a 3-dimensional BCC model, points A–F (efficient units) determine the production possibility set T B . Inputs and outputs of these units are indicated in Table 3, see “Appendix 2”.

Fig. 4
figure 4

Three-dimensional BCC model, units D and E are not exterior ones

Full size image

Units D and E are terminal ones since these units belong to unbounded edges. However, these units are not exterior ones since these units will be inefficient after “reversing the inputs and outputs”.

The following assertion summarizes the results of Corollary 1 and Theorem 8.

Theorem 9

For BCC model (1a–1d) the following relations hold T ext  ⊆ T term  ⊆ T 1 anc .

Its proof is based on previously stated results.

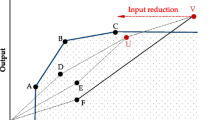
Thanassoulis et al. (2012, p. 178) proposed a new definition of anchor units for efficient units, “which with reference to the extreme-efficient DMUs [vertices] but excluding the evaluated DMU itself, can be rendered class F by contracting radially their output levels, while keeping their input level constant OR by increasing inputs and keeping their output levels constant”, where class F according to Charnes et al. (1991) contains inefficient DMUs that are on the PPS boundary. However, the set of anchor units with respect to definition of Thanassoulis et al. (2012, p. 178) does not coincide with the set of anchor units according to Bougnol and Dulá (2009). Indeed, consider the following illustrative example. In Fig. 5, a two-inputs/one-output BCC model is depicted. Units A, B, C, D, E are the observed efficient production units that determines set T B . Inputs and outputs of these units are indicated in Table 4, see “Appendix 2”.

Fig. 5
figure 5

Unit B is an anchor point, but not a terminal point

Full size image

Points M,A, B, C, L form the face of set T B . This face belongs to the orthant X 1 OY. However, unit B is just a common vertex of the BCC model. Let “unit B be rendered class F by increasing inputs and keeping their output levels constant”. As a result point B 1 will be obtained. This point belongs to segment AC, an efficient part of the frontier. Again, let “unit B be rendered class F by contracting radially their output levels, while keeping their input level constant”. As a result point B 2 will be obtained. Point B 2 belongs to an efficient part of the frontier, segment AC. Hence, unit B is not anchor unit according to Thanassoulis et al. (2012). However, unit B is an anchor unit according to Bougnol and Dulá (2009), since this unit belongs to an unbounded face.

Let us denote the set of anchor units in the BCC model (1a–1d) with respect to the definition of Thanassoulis et al. (2012, p. 178) by T 2 anc . Then the following assertion can be proved.

Theorem 10

For BCC model (1a–1d) the following relation holds T 2 anc  ⊆ T term .

Proof

See “Appendix 1”.

Theorem 10 shows that approach of Thanassoulis et al. (2012) does not reveal all efficient units that may be used for improving envelopment in BCC models.

Consider again an illustrative example in Fig. 4. Units D and E are not anchor units with respect to the definition of Thanassoulis et al. (2012). However, units D and E are terminal ones, since infinite edges start from this units. Figure 6 depicts an input isoquant for unit D. Unit G is inefficient. Its projection will be point G′ on some slack face. However, their approach cannot improve this part of the boundary, unit D is not identified as an anchor unit, since unit D can be moved to the efficient part of the frontier by contracting radially its output level while keeping its input levels constant or by increasing inputs and keeping its output levels constant. Figure 7 illustrates this fact. So, their approach is incomplete.

Fig. 6
figure 6

Input isoquants for units B and D

Full size image
Fig. 7
figure 7

Production function for unit D

Full size image

Summarizing all mentioned above, the following assertion can be formulated.

Theorem 11

For BCC model (1a–1d) the following relations hold T 2 anc  ⊆ T term  ⊆ T 1 anc .

So, the approach of Bougnol and Dulá (2009) generates excess number of anchor units and approach of Thanassoulis et al. (2012) may not generate sufficient number of units in order to improve the frontier.

The cone-ratio model (3) cannot help in every case where suspicious units appear in the DEA models. In Fig. 4, point B is a terminal unit. However, it is impossible to transform the frontier with the help of cones U and V in such a way that terminal point B would be inefficient, see Fig. 6.

Only simultaneous transformation of the frontier in the space of inputs and outputs enables one to make suspicious unit B inefficient, see Fig. 8.

Fig. 8
figure 8

Production function for unit B

Full size image

Yu et al. (1996) proposed the following generalized DEA (GDEA) model that unifies and extends most the well-known DEA models based on using domination cones (see, e.g. Yu 1974) in their constraint sets.

$$\begin{aligned} & \hbox{max} \;(u^{T} Y_{0} - \delta_{1} u_{0} ) \\ & {\text{subject}}\,{\text{ to}} \\ & v^{T} \overline{X} - u^{T} \overline{Y} + u_{0} \delta_{1} e^{T} \in K, \\ & v^{T} X_{0} = 1, \\ & \left( {\begin{array}{*{20}c} v \\ u \\ \end{array} } \right) \in W,\quad \delta_{1} \delta_{2} ( - 1)^{{\delta_{3} }} u_{0} \ge 0, \\ & v \in E^{m} ,\, u \in E^{r} ,\, u_{0} \in E^{1} . \\ \end{aligned}$$
(9a)

The optimization dual problem to (9a) is written in the form (Yu et al. 1996):

$$\begin{aligned} & \hbox{min} \;\theta \\ & {\text{subject}}\,{\text{to}} \\ & \left( {\begin{array}{*{20}c} {\overline{X} \lambda - \theta X_{0} } \\ { - \overline{Y} \lambda + Y_{0} } \\ \end{array} } \right) \in W^{*} , \\ & \delta_{1} e^{T} \lambda + \delta_{1} \delta_{2} ( - 1)^{{\delta_{3} }} \lambda_{n + 1} = \delta_{1} , \\ & \lambda \in - K^{*} ,\, \lambda_{n + 1} \ge 0,\, \theta \in E^{1} , \\ \end{aligned}$$
(9b)

where \(\overline{X} = (X_{1}, \ldots, X_{n})\) is an m × n matrix, X j  = (x 1j , …, x mj ) ≥ 0 is the input vector for the jth production unit j = 1, …, n; \(\overline{Y} = (Y_{1} , \ldots ,Y_{n} )\) is an r × n matrix, Y j  = (y 1j , …, y rj ) ≥ 0 is the output vector for the jth production unit j = 1, …, n. Parameters δ 1, δ 2, δ 3 are binary ones assuming only the values 0 and 1. Vector e is determined as e = (1, …, 1) ∈ E n. Sets W ⊆ E m+r and K ⊆ E n are the closed convex cones, where E m+r and E n are Euclidean spaces of the dimensions (m + r) and n, respectively. W * and K * are the negative polar cones (Charnes et al. 1989; Yu et al. 1996) of sets W and K, respectively. It is usually assumed in the DEA models that the polyhedral cones W ⊆ E m+r+ and K ⊆ E n+ and int W ≠ Ø and int K ≠ Ø, then we get W * ≠ Ø and K * ≠ Ø.

Theorem 12

If some efficient units in model (1a–1d) become inefficient in model (9a, 9b) as a result of inserting cones in the BCC model, then it is necessary that there exist terminal production units among such inefficient units.

Proof

See “Appendix 1”.

It is rather difficult for a manager (expert) to determine cones in the multipliers space that is dual to the space of inputs and outputs where a production possibility set is constructed.

For this very reason it is difficult to use the GDEA model in practice.

Krivonozhko et al. (2009) proposed a model that is more general than the GDEA model, on the one hand, as it covers situations that the GDEA model cannot describe. On the other hand, this model enables one to construct step-by-step any model from a large family of the DEA models by incorporating artificial units and rays in the space of inputs and outputs in the BCC model, which makes the process of model construction visible and more understandable.

The production possibility set of this model is written in the form

$$\begin{gathered} \hfill T_{G} = \left\{ {\,(X,Y)\;\,\left| {\;X \ge \sum\limits_{j = 1}^{n} {X_{j} \lambda_{j} } + \sum\limits_{i \in I} {D_{i} \mu_{i} } + \sum\limits_{k \in J} {A_{k} \rho_{k} } ,} \right.\quad \quad \quad \quad } \right. \\ \hfill Y \le \sum\limits_{j = 1}^{n} {Y_{j} \lambda_{j} } + \sum\limits_{i \in I} {G_{i} \mu_{i} } + \sum\limits_{k \in J} {B_{k} \rho_{k} } ,\,\,\sum\limits_{j = 1}^{n} {\lambda_{j} } + \sum\limits_{i \in I} {\mu_{i} } = 1,\quad \\ \hfill \left. {\lambda_{j} \ge 0,\,\;j = 1, \ldots ,n,\;\mu_{i} \ge 0,\;\;i \in I,\;\;\rho_{k} \ge 0,\;\;k \in J\mathop {}\limits_{{}} } \right\}. \\ \end{gathered}$$
(10)

where (D i , G i ), i ∈ I, I is a set of artificial production units, (A k , B k ), k ∈ J, J is a set of vectors (rays) added to the model.

Figure 9 shows the transformation of the frontier of the 2-dimensional BCC model with the help of artificial units and rays. In the figure, cone Q is formed by artificial rays, point B′ is an artificial unit.

Fig. 9
figure 9

Transformation of the frontier with the help of artificial units and rays

Full size image

In addition to problem (7) and (8), we can also discover terminal (suspicious) production units with the help of constructions of 2-dimensional and 3-dimensional sections of the frontier.

Define 3-dimensional affine subspace in space E m+r as

$${\text{Pl}}\,(\,X_{o} ,\,Y_{o} ,\,d_{1} ,\,d_{2} ,d_{3} )\, = \,(\,X_{o} ,\,Y_{o} )\, + \,\alpha \,d_{1} + \,\beta \,d_{2} + \gamma \,d_{3} ,$$
(11)

where (X o , Y o ) ∈ T B , α, β and γ are any real numbers, directions d 1, d 2, d 3 ∈ E m+r are not parallel to each other.

Next, define intersections of the frontier with 3-dimensional affine subspace

$$\begin{gathered} \hfill {\text{Sec}}\,(\,X_{o} ,\,Y_{o} ,\,d_{1} ,\,d_{2} ,d_{3} )\, = \{ \,(\,X,\,Y)\,\; |\,\;(\,X,\,Y) \in {\text{Pl}}\,(\,X_{o} ,\,Y_{o} ,\,d_{1} ,\,d_{2} ,d_{3} )\;\, \cap \quad \\ \hfill \cap \;WEff_{P} \,T(\,X,\,Y);\;\;d_{1} ,\,d_{2} ,d_{3} \in E^{m + r} \,\} , \\ \end{gathered}$$
(12)

where WEff P T is a set of weakly Pareto-efficient points. Krivonozhko et al. (2005) have proved that set WEff P T coincides with the boundary of T B  (2).

By choosing different directions d 1, d 2 and d 3 we can construct various 2-dimensional and 3-dimensional sections going through point (X o , Y o ) and cutting the frontier. Parametric optimization algorithms for construction of sections of the type (12) are described in detail by Krivonozhko et al. (2004) and Volodin et al. (2004).

Moreover, thanks to our package FrontierVision, one can add to the DEA model any artificial units and rays on the computer screen interactively.

Assertion 2

There always exists a section (12) that reveals any terminal unit and/or efficient units belonging to an unbounded face.

However, the specific section may not reveal some terminal units. In the 3-dimensional BCC model, see Fig. 4, unit B is a terminal one. In Fig. 6, unit B does not look like a terminal one. The section in Fig. 7 reveals this unit as a terminal point.

Generally speaking, a 2-dimensional section of the type (12) consists mainly of a number of segments and two rays. The first and the last vertices in the chain of segments are usually terminal units.

Next, a user (expert) can control the changes of efficiency scores of inefficient units as a result of inserting artificial rays and units with the help of our package FrontierVision. Indeed, the following assertion is valid.

Assertion 3

There always exists a vicinity for any terminal unit such that any change of this unit’s position within this vicinity will change only efficiency scores of some inefficient units within some small range.

So, if some changes in efficiency scores are unacceptable according to expert’s opinion, he/she can move artificial units closer to some small vicinity of a terminal unit just on the screen of the computer.

Now, we are ready to present our general Procedure for improving the adequacy of DEA models.

  1. 1.

    Solve BCC models (1a–1d) for all units DMU j , j = 1, …, n.

    If experts (decision making persons) agree with computational results, then STOP, else go to the next step.

  1. 2.

    Experts are requested to indicate units whose efficiency scores do not correspond to their opinions. For every such units several sections of the type (12) are constructed. Set T term of terminal units is determined. Experts are requested to indicate on the 2-dimensional or 3-dimensional sections artificial efficient units or rays in the some vicinity of every terminal unit.

  2. 3.

    Add the set of artificial units and rays to the current set of units.

    Solve BCC models (1a–1d) with modified set of production units.

    If computational results are acceptable, then STOP, else change vicinities of terminal units or/and positions of artificial units within vicinities of terminal units.

    Go to the beginning of step 3.

Observe that in the Procedure the process of frontier transformation is controllable from the very beginning up to the end. Our computational experiments showed that it is sufficient to make two or three steps of Procedure in order to adjust his/her model and obtain reliable computational results.

Notice that we present here only general Procedure for improving of the adequacy of the DEA models. This Procedure may be specified in dependence of the real-life problems. This is an interesting problem for future development.

4 Computational results

In order to illustrate consequences of letting experts choose one unit from the terminal units and change data to more reasonable values we used a dataset for 920 Russia banks’ financial accounts for January 1 of 2009. The following inputs and outputs for the BCC output-oriented model were used:

  • Inputs: working assets; time liabilities; demand liabilities.

  • Outputs: equity capital; liquid assets; fixed assets.

The data were financial accounts of Russian banks for the year 2008. Remember that this year was the first year of the world crisis. It was important at that time for financial experts to have reliable tools for forecasting the behavior of financial institutes and for warning about possible bankruptcies.

The number of efficient banks is very low; 42 units out of 920. The majority of banks have efficiency scores <50 %. This situation is different from the situation reported in Charnes et al. (1990).

However, financial experts expressed doubt about the result of full efficiency of some banks. For example, Fig. 10 presents a cut of the frontier in a 6-dimensional space by the 2-dimensional plane for bank A; certainly we use legends instead of real names of banks. The directions of the plane are determined by two inputs: demand liabilities and working assets. Small circles denote the projections of the actual observations of banks onto the 2-dimensional plane. The colors of circles are associated with the efficiency scores of appropriate units. The red color means that the corresponding unit is efficient. The green color designates units with low efficiency score; the yellow color denotes that a unit has an intermediate value of efficiency score.

Fig. 10
figure 10

Input isoquant for bank A

Full size image

The scale is such that point (1, 1) in the figure corresponds to bank A. According to the BCC model bank A is 100 % efficient. However, experts did not agree with this evaluation, and they were right, since bank A was bankrupted in 6 months. In fact point A is a typical terminal unit, since unbounded edges go out from this unit. However, Fig. 10 cannot help us to improve the frontier.

For this purpose we should use another section. Figure 11 shows a cut of the frontier in a 6-dimensional space by the 2-dimensional plane for bank A. The horizontal axis in the figure is determined by input vector X o and the vertical axis corresponds to output vector Y o of bank A, respectively. The scale is such that point (1, 1) corresponds to bank A. The solid line outlines the production function (the cut of the production possibility set) of the model. The balls in the figure denote projections of some other banks on the 2-dimensional plane. Again, according to the model, bank A is efficient, which contradicts experts’ opinion. However, Fig. 11 can help us to improve the frontier. Experts were asked to insert an artificial efficient unit on the screen by phrasing the question how much outputs should be expected from an efficient unit using the observed inputs of unit A (implicitly assuming a proportional increase of the outputs). This artificial unit is denoted by B. In the figure, the dotted line together with the solid line after it shows the frontier of the modified model.

Fig. 11
figure 11

Production function for bank A

Full size image

After the frontier transformation the efficiency score of bank A became 48.3 %. Some other banks also changed their efficiency scores after inserting artificial unit in the model. Table 1 shows efficiency scores of some banks, which were bankrupted during 6 months, in the BCC model before and after frontier transformation.

Table 1 Changes of efficiency scores after the frontier transformation
Full size table

After the second run of the model, the experts recognized the modelling results to be adequate and reliable.

We have presented an investigation for only one terminal unit, but demonstrated that the choice of terminal units as units that should be investigated using expert information worked out satisfactorily; reducing the efficient unit to an inefficient one and also reducing several other units’ scores and improving the realism of the results. However, the working out of a more formal procedure for eliciting expert help in providing more realistic efficient units based on terminal units is still to be done.

5 Conclusions

In this paper, we proposed tools for discovering units which may cause inadequate results in the DEA models. It was shown that terminal units constitute “suspicious” points in the first place. If the graph of intersection of the frontier with a 2-dimensional plane is constructed, then the first and the last vertices of the graph are usually terminal units. However, it is not necessarily the case that terminal units may cause inadequate results in the DEA models, such units may be quite normal efficient points. Only experts in the specific area can evaluate the adequacy of efficiency scores of terminal units.

Terminal units arise because a non-countable (continuous) production possibility set T is determined on the basis of a finite number of production units; some of these units turn out to be terminal ones. A gap between derivatives may take place at these points. For example, the left-hand side scale elasticity takes infinite value, and the right-hand side scale elasticity takes zero value at some terminal points, see Førsund et al. (2007).

Let us remember that Farrell (1957) introduced artificial units at infinity in order to smooth his model, see also Førsund et al. (2009).

We also propose how to deal with inadequacies in the DEA models with the help of incorporating artificial units and rays interactively on the screen of the computer by experts into some BCC model. This makes the DEA models more adequate and adjustable.

Only one case of eliciting information from experts suggesting artificial units that should be efficient based on terminal units has been shown. However, several other experiments were carried out. Carrying out systematic experiments on new real-life datasets will be attempted in a further research, together with developing more formal procedures for eliciting information from experts on the activities under investigation constructing artificial efficient units based on terminal units. The use of interactive graphical representation in a space of sufficiently reduced dimensions to be readily understandable and recognizable by experts seems a promising approach.