1 Introduction

The empirical estimation of X-efficiency has resulted in an extensive literature addressing both the econometric theory of efficiency estimation and the empirical application of the concepts in different situations. Of the approaches used to estimate frontiers and X-efficiency, the two most popular are stochastic frontier analysis (SFA) and data envelopment analysis (DEA). Both methods have their strengths and weaknesses and their own group of supporters/detractors. Despite a number of studies comparing the techniques, neither of the two methods has emerged as the preferred approach.

Generalized maximum entropy (GME) provides a potential alternative frontier estimation approach that combines the strengths of both SFA and DEA. An advantage GME shares with SFA is that it allows the researcher to explicitly estimate a stochastic frontier without requiring bootstrapping for statistical inference as with DEA. With maximum entropy estimation the researcher establishes a discrete set of support points for each parameter and then estimates the probability associated with each support point to arrive at the parameter estimate. For example, suppose a random variable, X, can take the values 1, 2, 3, or 4 with associated probabilities p 1, p 2, p 3, and p 4, respectively. GME is used, in combination with the prior information embedded in the support points, to estimate the associated probabilities and hence obtain a predicted value for X. Using the generalized maximum entropy methodology developed by Golan et al. (1996, Chap. 6), we specify a set of support points for the unknown parameters and then estimate the probabilities associated with these support points.

An advantage GME shares with DEA is that it does not require an ad hoc assumption about the distribution of the inefficiency component as is required with SFA. With GME the researcher also establishes a set of support points for the inefficiency component. These support points bound the estimated inefficiency and are based on theory or prior information. For example, we may have information that all firms within an industry are between 60% and 100% efficient. The range of support points for the inefficiency component would reflect this information. Due to the uncertainty regarding these support points, we examine the effects of using different sets of support points in our model. As expected, the estimated inefficiency is somewhat sensitive to the choice of support points, particularly the maximum and minimum points. However, the relative rankings of firms do not vary much with the choice of support points.

In this paper, we develop the GME frontier estimator. We compare GME estimation to SFA and DEA using a data set on 123 electric utilities in the US. This data set has been used extensively in econometric studies of efficiency estimation and provides an appropriate setting for the comparison of efficiency estimates across these models. The results suggest the GME formulation provides a link between the SFA and DEA estimators.

This paper is organized as follows: Sect. 2 provides a brief review of the efficiency literature including a few studies that use GME techniques. Section 3 presents the SFA and DEA cost frontier estimators and develops the GME approach. Section 4 compares cost efficiency estimates from SFA, DEA, and GME. Section 5 adds a production frontier example, allowing for a comparison with deterministic frontier results also. Concluding remarks are given in Sect. 6.

2 Review of the literature on efficiency estimation

The theoretical literature on productive efficiency originates with the work of Koopmans (1951), Debreu (1951), and Shephard (1953). The first attempt to estimate efficiency was found in Farrell (1957) who used linear programming (LP) techniques to estimate efficiency in US agriculture. Research on efficiency estimation continued with the development of SFA (Meeusen and van den Broeck 1977; Aigner et al. 1977; Battese and Corra 1977) and DEA (Charnes et al. 1978). Each of these techniques has subsequently been extended and developed further.Footnote 1

As these techniques matured, studies appeared that applied both SFA and DEA to the same data set and conducted an explicit comparison of results. Ferrier and Lovell (1990) use both approaches on a set of US banks, finding mixed results in terms of efficiency estimates. Hjalmarsson et al. (1996) compare SFA, DEA, and deterministic parametric models for a panel of 15 Colombian cement plants. Although each method finds similar trends in efficiency over time, the correlations between efficiency estimates are mixed. Sharma et al. (1997) estimate the technical efficiency of the swine industry in Hawaii using both SFA and three forms of DEA. They find that SFA leads to higher estimates of technical efficiency and that the correlation between rankings from the different approaches is positive. Bauer et al. (1998) also use both approaches and propose a set of conditions for comparing the two, finding mixed results using a set of US banks. Wadud and White (2000) estimate technical efficiency for rice farmers in Bangladesh using SFA and three forms of DEA and find some correlation between SFA and DEA estimates. Weill (2004) compares results from these approaches for banks from five European countries. The results are again mixed, although they are all generally consistent with standard measures of performance in the banking industry. These disparities across models are not unexpected given the differences in the statistical properties of the models used to develop the DEA and SFA estimators.Footnote 2

Due to mixed results from SFA and DEA, and in response to criticism of both approaches, we develop a GME frontier estimator. There has been very little research applying maximum entropy techniques to efficient frontier estimation, and even less of an emphasis on direct comparisons with other frontier estimation approaches. Sengupta (1992) applies maximum entropy to derive the distribution of the one-sided error term in a production frontier model. Given the error distribution, the productivity parameters are estimated using DEA. Miller (2002) also focuses on a production frontier model, proposing a procedure using a semiparametric specification of the production frontier and parametric specification of a one-sided efficiency component. He concentrates on the theoretical development of the model without an empirical application. Lansink et al. (2001) use GME to estimate intra- and inter-firm efficiency in an input–output model. They use GME to estimate a production frontier including an intra-firm efficiency component that is constrained to be between zero and one. GME estimates are presented but no comparison to other frontier techniques is provided. Rezek and Campbell (2007) use GME to estimate shadow prices for power plant emissions. They only include a two-sided error term and do not compare GME results to SFA or DEA results. The following is an attempt to extend the contributions of GME to efficiency estimation by performing a direct comparison with SFA and DEA results.

3 Data and methodology

This study uses SFA, DEA, and GME to estimate cost efficiency for a sample of 123 electric utilities in the US. This data set has been used in numerous studies on the estimation of cost functions/frontiers and efficiency (e.g. Christensen and Greene 1976; Greene 1990; Sengupta 1995). For each firm i, the data set includes a single output, y i , and three inputs: labor, capital, and fuel. Input quantities and prices are given by the column vectors x i  = (x il , x ik , x if ) and w i  = (w il , w ik , w if ). The total cost of production is given by \( C_{i} = w^{\prime}_{i} x_{i} \). Descriptive statistics are given in Table 1.

Table 1 Cost frontier data summary statistics (N = 123)
Full size table

3.1 Stochastic frontier analysis

Following Kumbhakar and Lovell (2000, pp. 136–142), in log form the cost frontier can be written as

$$ \ln \,C_{i} = \ln \,c(y,w_{i} ) + u_{i} + v_{i} $$

where u i is a non-negative inefficiency component and v i is a producer specific random disturbance. Cost efficiency is then \( {\text{CE}}_{i} = { \exp }\{ - u_{i} \} (0 \le {\text{CE}}_{i} \le 1,\;\forall \,i) .\) To allow for comparisons in this study, as well as with past research, the form of c(X) follows that used by Greene (1990). For firm i,

$$ \ln \,\left( {{C \mathord{\left/ {\vphantom {C {w_{f} }}} \right. \kern-\nulldelimiterspace} {w_{f} }}} \right) = \beta _{0} + \beta _{1} \ln \,y + \beta _{2} \ln ^{2} y + \beta _{3} \ln \left( {{{w_{l} } \mathord{\left/ {\vphantom {{w_{l} } {w_{f} }}} \right. \kern-\nulldelimiterspace} {w_{f} }}} \right) + \beta _{4} \ln \left( {{{w_{k} } \mathord{\left/ {\vphantom {{w_{k} } {w_{f} }}} \right. \kern-\nulldelimiterspace} {w_{f} }}} \right) + u + v $$
(1)

where total cost and the prices of labor and capital are divided by the price of fuel to ensure the cost frontier is linearly homogeneous in input prices. Maximum likelihood is use to estimate (1) assuming \( v_{i} \sim N\left[ {0,\,\sigma _{v}^{2} } \right] \) and the u i follow a one-sided distribution.

3.2 Data envelopment analysis

In contrast to SFA, the DEA approach is based on non-parametric linear programming techniques. Under certain assumptions, the non-parametric DEA estimator is shown to be a consistent, asymptotically Weibull distributed maximum likelihood estimator, with a known rate of convergence.Footnote 3 Following the approach outlined in Färe et al. (1985) and using the same notation as above, the linear programming problem for firm i is

$$ \begin{gathered} \begin{array}{*{20}c} {\mathop {{\text{Min}}}\limits_{{x_{i} }} C_{i} } & {} \\ {{\text{s}} . {\text{t}} .} & {y_{i} \le \sum\limits_{{i = 1}}^{N} {\mu _{i} y_{i} } ,} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {} & {x_{{il}} \ge \sum\limits_{{i = 1}}^{N} {\mu _{i} x_{{il}} } ,} \\ {} & {x_{{ik}} \ge \sum\limits_{{i = 1}}^{N} {\mu _{i} x_{{ik}} } ,} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {} & {x_{{if}} \ge \sum\limits_{{i = 1}}^{N} {\mu _{i} x_{{if}} ,} } \\ {} & {\mu _{i} \ge 0,\quad i = 1, \ldots ,N,} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {} & {\sum\limits_{{i = 1}}^{N} {\mu _{i} } = 1,} \\ \end{array} \hfill \\ \end{gathered} $$

where N is the number of firms and μ = (μ1,…,μ N ) is a vector of activity weights that forms convex combinations of the input and output vectors. The first four restrictions require each observation to be within the feasible production set, the fifth requires that the activity weights be non-negative. The final equation in the linear program above allows the underlying technology to exhibit variable returns to scale. Given the solution vector \( x_{s}^{*} \), cost efficiency for firm i is then the ratio \( w^{\prime}_{i} x_{i}^{*} /w^{\prime}_{i} x_{i} \).

3.3 Generalized maximum entropy

Finally, we estimate the cost frontier given by Eq. 1 by modifying the generalized maximum entropy methodology as described by Golan et al. (1996, Chap. 6). In GME, the parameter vector β, with K elements, is decomposed into a set of T support points (z k ) and probability weights (p k ) for each parameter, with 2 ≤ T < ∞. Intuitively, each parameter is equal to the product of a support point and its associated probability weight, summed over all support points. The supports are provided by the researcher based on prior information; the probability weights are estimated within the model and are restricted to sum to unity. The lower and upper bounds for the supports for β k are z k1 and z kT . The coefficient vector is then

$$ \beta = Zp = \left[ {\begin{array}{*{20}c} {z^{\prime}_{1} } & 0 & \cdots & 0 \\ 0 & {z^{\prime}_{2} } & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & {z^{\prime}_{K} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {p_{1} } \\ {p_{2} } \\ \vdots \\ {p_{K} } \\ \end{array} } \right] $$
(2)

where the z k ’s and p k ’s are both T × 1, so Z is K × KT and p is KT × 1. Similarly, for the random disturbances v i (i = 1,…,N), there is a set of L support points (r i ) and probability weights (ω i ) for each observation, with 2 ≤ L < ∞. The random disturbance vector is

$$ v = R\omega = \left[ {\begin{array}{*{20}c} {r^{\prime}_{1} } & 0 & \cdots & 0 \\ 0 & {r^{\prime}_{2} } & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & {r^{\prime}_{N} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\omega _{1} } \\ {\omega _{2} } \\ \vdots \\ {\omega _{N} } \\ \end{array} } \right] $$
(3)

where the r i ’s and ω i ’s are both L × 1, so v is N × NL and ω is NL × 1.

We extend the GME approach to include the one-sided inefficiency component u, which we define similarly to the two-sided error component. For each u i , there is a set of J support points (q i ) and probability weights (ϕ i ) for each observation, with 2 ≤ J < ∞. In contrast to the two-sided disturbances, the lower bound of the support points for the one-sided inefficiency component is zero for all observations. All other support points are positive:

$$ \begin{array}{*{20}c} {q_{{i1}} = 0} & {\forall \;i} \\ {q_{{ij}} > 0} & {\forall \;i\,{\rm and}\,j \ge 2} \\ \end{array} $$

In matrix form

$$ u = Q\phi = \left[ {\begin{array}{*{20}c} {q^{\prime}_{1} } & 0 & \cdots & 0 \\ 0 & {q^{\prime}_{2} } & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & {q^{\prime}_{N} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\phi _{1} } \\ {\phi _{2} } \\ \vdots \\ {\phi _{N} } \\ \end{array} } \right] $$
(4)

where the q i ’s and ϕ i ’s are both J × 1, so u is N × NJ and ϕ is NJ × 1.

Combining Eqs. 2–4, the general linear model to be estimated is

$$ C = XZp + Q\phi + R\omega . $$
(5)

The dependent variable C and the matrix of explanatory variables X come from observed data. The support points in the matrices Z, R, and Q are selected by the researcher using a priori information. The unknown vectors of probability weights p, ϕ, and ω, are estimated by maximizing the entropy function:

$$ \mathop {{ \max }}\limits_{{p,\phi ,\omega }} \;H(p,\phi ,\omega ) = - p^{\prime}\ln (p) - \phi ^{\prime}\ln (\phi ) - \omega ^{\prime}\ln (\omega ) $$

subject to:

$$ \begin{gathered} C = XZp + Q\phi + R\omega \hfill \\ \left( {I_{K} \otimes i_{{\text{T}}}^{\prime } } \right)p = i_{K} \hfill \\ \left( {I_{N} \otimes i_{{\text{J}}}^{\prime } } \right)\phi = i_{N} \hfill \\ \left( {I_{N} \otimes i_{{\text{L}}}^{\prime } } \right)\omega = i_{N} \hfill \\ \end{gathered} $$

where I is an identity matrix, i is a column of ones, and ⊗ is the Kronecker product. The first constraint imposes the linear cost function while the other constraints ensure that each set of probability weights sum to one. The GME solution selects the most uniform distribution consistent with the information provided in the constraints. Focusing on the inefficiency component of the model, the only a priori information needed is the set of support points. No assumptions are made about the distribution of the u.

4 Results

4.1 SFA and DEA results

For the SFA portion of the analysis, we estimate three versions of the model in Eq. 1 using different assumptions about the distribution of the inefficiency component u. We estimate the model using a half-normal, exponential, and a gamma distribution for u. Summary statistics for estimated efficiency are given in Table 2. For the half-normal model, average efficiency is 89%; that is, on average, costs are 11% higher than the efficient frontier would predict. Mean efficiency is slightly higher for the exponential and gamma versions at 91% and 92%, respectively. Standard deviations range from a low of 5% for the half-normal version to a high of 6% for the gamma version. All three sets of results are negatively skewed with most firms near the mean.

Table 2 Cost efficiency estimates summary statistics (N = 123)
Full size table

Efficiency measures from DEA are also described in Table 2. Average efficiency is lower at 71%, and the estimates show more dispersion with a standard deviation of 14%. In comparison to the SFA estimators, each firm is generally less efficient according to DEA.Footnote 4 This result is not surprising since the statistical foundations of the SFA and DEA estimators are quite different, as mentioned previously. The DEA result is obtained using linear programming techniques from a finite sample, thus the efficiency measures are sensitive to outliers. The DEA estimates are also negatively skewed, but are relatively less skewed than the SFA estimates.

4.2 GME results

In order to obtain GME estimates of Eq. 1, we must choose the support points in Z, R, and Q. We choose five support points for each of the regression coefficients, the two-sided random disturbance, and the one-sided inefficiency component.Footnote 5 Given the results of Greene (1990) using the same data and functional form, and the linear homogeneity assumption of the cost function, we expect the parameters, excluding the intercept, to be positive and less than one. Therefore, we choose supports of {−20, −10, 0, 10, 20} for the intercept and a narrower support of {−1, −0.5, 0, 0.5, 1} for all other parameters. Although we expect the slope parameters to be positive, we do not wish to impose this as a restriction so we allow the parameters to vary between −1 and 1. The supports for the two-sided random disturbance were chosen to be symmetric around zero since we expect the random errors to be mean zero. We follow the 3σ rule developed by Pukelsheim (1994) to choose the largest and smallest error support points. Since σ is unknown we use the consistent estimator \( \hat \sigma = 0.144 \) from OLS estimation of Eq. 1 to give us a guide for setting boundaries. Based on this result, we choose the two-sided error support vector to be {−0.5, −0.25, 0, 0.25, 0.5}.Footnote 6

For the inefficiency component, the lower bound for the supports is already chosen as zero due to the requirements of the frontier model as discussed above. However, the lower bound for efficiency of 0% is only obtained as the upper bound for the supports approaches infinity. Therefore, we vary this upper bound to examine the effects of changing the minimum efficiency and the prior mean of efficiency. The prior mean is the average of the support points or the efficiency that would be assigned to each firm without any data on costs, outputs, and inputs. We estimate five different GME models using different upper bounds. The model GME1 uses {0, 0.005, 0.01, 0.015, 1.67} as the support points for the inefficiency term. This gives a maximum efficiency of exp(0) = 100% and a minimum efficiency of exp(−1.67) = 18.8%, with a prior mean of exp(−0.340) = 71.2%. For the remaining four versions, GME2–GME5, we maintain the first four support points but use progressively smaller upper bounds of 1.27, 0.97, 0.67, and 0.37. In each case the minimum efficiency and prior mean increase slightly. For example, GME5 with the supports {0, 0.005, 0.01, 0.015, 0.37}, implies a minimum efficiency of exp(−0.37) = 69.1% and a prior mean of exp(−0.08) = 92.3%.Footnote 7

GME results for all five versions are given in Table 2. Mean efficiency ranges from 71% to 92% for the five versions with standard deviation of 2–7%. Across these five versions, as the range of u gets smaller, the mean efficiency rises and becomes closer to the SFA means. In addition, the distribution tightens as the range of u gets smaller as shown by the reduction in standard deviation from models 1 through 5. The degree of skewness also increases as the range of u shrinks. This trend reflects the tendency of GME estimation to choose the most uniform distribution consistent with the data, since the distribution becomes more uniform as the potential range is increased.

4.3 Comparison of GME with SFA and DEA

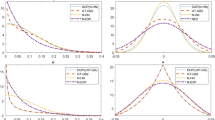
The GME estimates of mean efficiency span the same range as the SFA and DEA results, as expected given the prior means. Mean efficiency is the lowest for DEA at 71.2% and highest for SFA at 89–92.3%. The GME results range from 70.6% for the version with the largest range of support points for u, to 92.1% for the model with the smallest range. Looking beyond mean efficiency, and focusing on the distribution of estimates reveals that the GME results are more similar to DEA. All sets of estimates are negatively skewed, but the degree of skewness is much smaller for DEA and GME than for SFA. Another important observation this research highlights is that for the GME results, moving from GME1 to GME5, as the starting range of support points for u shrinks, the degree of skewness increases. To provide a view of the distribution of estimated efficiency across firms, a histogram was constructed for five of the models (Fig. 1).Footnote 8 The bar graph illustrates the high level of skewness found in the SFA estimates. The more restrictive version of GME (GME5) is the next closest to SFA, followed by the less restrictive GME3 and GME1 results. The DEA results show the least amount of skewness. Comparing means and the skewness of the estimates suggests that as the a priori range of the inefficiency component u shrinks, the mean estimated efficiency approaches SFA results. Conversely, as the a priori range of the inefficiency component u increases, the mean estimated efficiency approaches DEA results.

Fig. 1
figure 1

Histogram of cost efficiency estimates by estimator

Full size image

Another important feature of efficiency estimation is that the results allow for a numerical ranking of firms from most to least efficient. In this case it is possible that the different models used to estimate efficiency could lead to different rankings of firms. To examine this, rank correlations were computed for the nine models estimated (Table 3). Firm rankings from the three versions of SFA and the five GME models are all highly positively correlated with correlation coefficients near unity. The rankings from DEA are all positively correlated with the other eight models, but do not exhibit as high a degree of correlation (0.63–0.67). With regard to ranking firms according to efficiency, SFA and GME provide virtually the same results. Comparing rank correlations for DEA with the GME estimators, the similarity of the rankings declines slightly from GME1 to GME5. This downward trend in rank correlation provides weak confirmation of the relationship noted above that GME1 is relatively closer to DEA than the other versions of GME.

Table 3 Cost efficiency estimates rank correlations
Full size table

5 Production frontier example

In the empirical cost frontier application, even though GME can achieve mean efficiency results close to DEA, individual scores as reflected by the rank correlations can be quite different. In comparison, GME and SFA consistently have very similar rankings even when mean efficiency is not very close. As an example, GME1 results in mean efficiency that is 18% points lower than in the half-normal model, while the rankings of these two estimators have a correlation of 0.997. In contrast, the rank correlation between GME1 and DEA estimators is only 0.652 even though mean efficiency is very close.

The source of this similarity between SFA and GME and disparity with DEA may relate to the functional form used in the analysis. While SFA and GME use the same functional form for the cost frontier, DEA, as a non-parametric maximum likelihood estimator, makes no such assumption. What is needed is a parametric version of DEA that uses the same functional form as SFA and GME. By estimating a production frontier instead of cost, a deterministic parametric frontier (DFA) can be estimated, as in Hjalmarsson et al. (1996). DFA combines features of SFA and DEA estimators by including a parametric production function with a non-stochastic error. A measure of firm efficiency is constructed by solving a linear programming problem in which parameters are chosen subject to the constraint that all observations are on or below the estimated production frontier. Any differences between DFA, SFA, and GME estimators would then be due solely to the method employed to estimate u, rather than differences in the functional form.

Using the same data set described above, technical efficiency was estimated by constructing a simple Cobb–Douglas production frontier for SFA, GME, and DFA estimators.Footnote 9 Table 4 gives summary statistics of technical efficiency estimates of each. Table 5 gives the rank correlations and Fig. 2 gives a histogram of selected estimators. Although the magnitudes change, the technical efficiency results are similar to cost efficiency when compared across estimators. The GME models span the range of DFA and SFA results, approaching the SFA results as the range of the inefficiency component shrinks. Estimated skewness follows the same pattern as for cost efficiency, although here the degree of skewness for GME3–5 is very near that of the half-normal estimator. Rankings provided by SFA and GME estimators are also highly correlated as before.

Table 4 Technical efficiency estimates summary statistics (N = 123)
Full size table
Table 5 Technical efficiency estimates rank correlations
Full size table
Fig. 2
figure 2

Histogram of technical efficiency estimates by estimator

Full size image

The DFA results seem to follow the pattern of the DEA results for cost efficiency.Footnote 10 The DFA results in terms of efficiency and skewness are very close to the least restrictive GME estimator (GME1). The same pattern can be seen in Fig. 2. Turning to the rank correlations, the DFA rankings have virtually the same correlation with SFA and GME estimators as found in Table 3 for cost efficiency between DEA, SFA, and GME. This result suggests that the disparity between DEA and the SFA and GME approaches is due to the sensitivity of the linear programming approaches to outliers rather than the assumption about functional form.

In sum, although the numerical estimates of efficiency differ, the overall pattern of efficiency estimates is similar for both technical and cost efficiency. GME can achieve mean efficiency close to SFA, DEA, or DFA results, given the assumption of the appropriate prior mean. In terms of the distribution of efficiency estimates, GME yields results closer to DEA/DFA, but as the range of u gets smaller, the estimates become more negatively skewed like SFA estimates. When firms are ranked according to efficiency, then GME results are almost identical to SFA, regardless of the choice of the prior mean.

6 Conclusions

One of the notable features of GME is the ability of the researcher to impose a priori information on the estimated parameters. An application in which this feature is especially useful is the area of efficient frontier estimation. For these estimators, economic theory requires that the estimated inefficiency component is bounded by zero (100% efficiency) in one direction and can be bounded in the other direction as well assuming a reasonable minimum efficiency. In this paper, GME is used to estimate cost efficiency and compared to estimates using the two most common frontier estimators, SFA and DEA.

Mean efficiency as estimated by GME can approach either SFA or DEA results, depending on the choice of the prior mean. Turning to the distribution of efficiency estimates, GME results exhibit a smaller degree of skewness, much like DEA estimates. This outcome reflects the lack of a distributional assumption about the inefficiency component inherent to GME. However, when firms are compared according to efficiency ranks, GME and SFA are virtually the same. Rankings using these two methods are positively correlated with DEA rankings, but the correlation is much weaker.

These results are not dependent on the structure of the estimated frontier. By computing a DFA estimator with the same functional form as GME and SFA, differences in the error components of stochastic and LP-based estimators are isolated. The results are robust to this change. GME results are distributed more like the LP-based estimators, but give very similar firm rankings to the other stochastic approach.

Further examination of results from the three techniques suggests that GME efficiency estimates may provide a link between SFA and LP-based approaches like DEA and DFA. As the range provided for the inefficiency component is made smaller, GME results approach SFA. As the range for the inefficiency component is made larger, GME results move toward the DEA results. One possibility this suggests is a two-step estimation approach in which SFA or DEA is estimated first to guide selection of a prior mean. Then, using this prior mean to set bounds for the inefficiency component, GME can be used to compute final estimates of firm efficiency. However, examining the effectiveness of this approach using Monte Carlo analysis on generated data is left to future research. By including an explicit stochastic component and not requiring an ad hoc assumption about the distribution of inefficiency, GME effectively provides a combination of these two estimators, utilizing the best features of each.