Robustness in Nonsmooth Nonconvex Optimization Problems

Abstract

In this paper, the robust approach (the worst case approach) for nonsmooth nonconvex optimization problems with uncertainty data is studied. First various robust constraint qualifications are introduced based on the concept of tangential subdifferential. Further, robust necessary and sufficient optimality conditions are derived in the absence of the convexity of the uncertain sets and the concavity of the related functions with respect to the uncertain parameters. Finally, the results are applied to obtain the necessary and sufficient optimality conditions for robust weakly efficient solutions in multiobjective programming problems. In addition, several examples are provided to illustrate the advantages of the obtained outcomes.

1 Introduction

Optimization problems that arise in applications are often faced with uncertainty (that is, the input parameters are not known exactly). For example, we can mention to engineering and finance problems, management include energy management [51] and water management [4, 24], location planning [13], scheduling and delivering routing [16], allocation and network design problems [31], traveling salesman problem [14], transit network design [12], etc. Consequently, a great deal of attention has been focused on optimization problems with data uncertainty and try to study these problems from the theory and application aspects.

Robust optimization is an emerging area research and one of the computationally powerful deterministic approaches that deals with the optimization problems with data uncertainty. The goal of robust programming is to find a worst-case solution which simultaneously satisfies all possible realizations of the constraints to immunize an optimization problem against uncertain parameters in the problem, particularly when no probability distribution information on the uncertain parameters is given.

The concept of robust programming has been first introduced by Soyester [48] in 1973 in what now is called robust linear programming. Due to the importance of the theory and practical aspects many researchers have been widely studied the robust optimization over the past two decades (see, e.g., [3, 5,6,7,8,9,10, 18, 25, 26, 28, 30, 32, 33, 38, 47]). A successful treatment of the robust optimization approaches to convex optimization problems under data uncertainty was given in [7, 9, 49]. Recently, in [15] a nonsmooth and nonconvex multiobjective optimization problem with data uncertainty has been investigated by using a generalized alternative theorem within the framework of vector optimization.

In [27] the authors proved a Karush–Kuhn–Tucker (KKT) optimality condition for a robust programming with continuously differentiable functions. Optimality conditions for uncertain multiobjective programming with convex functions are studied in [29, 30]. In the continuation of the previous studies, in [33] the authors extended the optimality results to a robust multiobjective optimization problem for weakly and properly robust efficient solutions, where the involved functions are locally Lipschitz.

As seen in the robust optimization, the convexity of the uncertain sets and the concavity of the functions with respect to the uncertain parameters play a significant role in deriving the optimality conditions (see, e.g., [15, 30, 32, 33, 49]).

On the other hand, as we know in the optimization theory a feature of convex programming is that when Slater’s condition holds, the KKT optimality conditions are both necessary and sufficient. It is well known that this may fails without the convexity of the objective or constraint functions. Martínez-Legaz [40] used the notion of tangential subdifferential, a concept due to Pschenichnyi [46], for a class of nonconvex and nonsmooth functions. Very recently, in [41] optimality conditions for a nonsmooth and nonconvex constrained optimization problem have been established with the concept of tangential subdifferential in the absence of convexity of the feasible set.

Motivated and inspired by the previous studies, this paper is devoted to investigate a nonsmooth and nonconvex constrained optimization problem with data uncertainty both in objective and constraint functions. Our focus is to obtain the necessary and sufficient conditions for optimality by using a robust approach based on the tangential subdifferential. In spite of almost all of the previous studies, we drop the convexity assumption of the uncertain sets and the feasible set. Moreover, we do not need the concavity of the functions with respect to the uncertain parameters. We observe that the tangential subdifferential includes both convex subdifferential and Gâteaux derivative. Hence the robust optimality conditions in terms of tangential subdifferential give sharper results and can be employed for a large class of nonconvex and nondifferentiable robust optimization problems.

Further as far as we know, all the previous investigations obtained the optimality conditions under some strong constraint qualifications such as Mangasarian–Fromovitz or Slater constraint qualifications (see, e.g., [17, 29, 33, 49]). In this paper, some of the well known robust constraint qualifications such as generalized Abadie (ACQ), Cottle (CCQ), Mangasarian-Fromovitz (MFCQ), Robinson (RCQ), Kuhn–Tucker (KTCQ) and Zangwill (ZCQ) constraint qualifications are established in the framework of tangential subdifferential. Then the interrelations between these constraint qualifications are investigated. In particular, it is shown that (ACQ) is the weakest among all these constraint qualifications. In [17] the KKT optimality conditions for a nonsmooth and nonconvex robust multiobjective problem were established. These optimality results were presented in terms of the Mordukhovich subdifferential and obtained under a generalized Mangasarian–Fromovitz constraint qualification which is strictly stronger than the Abadie constraint qualification. Moreover in [19], the author extended the optimality results of [17] to infinite dimensional spaces by using advanced techniques of variational analysis.

We observe that our results include the results of ones which considered the convexity of the uncertain sets in addition to the concavity of the functions with respect to the uncertain parameters by using stronger constraint qualifications (see, e.g., [33, 49, 50]).

As an application of the robust tangentially convex programming, we provide necessary and sufficient conditions for weakly robust efficient solutions in multiobjective programming problems with data uncertainty which are less sensitive to small perturbations in variables than global optimum or global efficient solutions. We obtain these results by using the suitable robust constraint qualifications in terms of the tangential subdifferential.

An important feature is the structure of our constraint qualifications, which unlike most of the literature on multiobjective programming, in our setting the objective functions have no role in the definition of these constraint qualifications; (see, e.g., [22, 23, 37, 39]). Throughout the paper, several examples are given to clarify the results.

The paper is organized as follows: Sect. 2 is devoted to the basic definitions and preliminary results of convex and nonsmooth analysis. In Sect. 3, we establish some results in nonsmooth analysis that characterize the directional derivative of a certain function. A number of well known robust constraint qualifications are introduced based on the tangential subdifferential and their relationships are studied in Sect. 4. Then in Sect. 5, necessary and sufficient conditions for robust local optimality are proved. Finally, we show the viability of our results for robust weakly efficient solutions in multiobjective problems with uncertain data in Sect. 6. A number of examples are given through the paper to illustrate the obtained results.

2 Preliminaries

In this section, we recall some basic definitions and results from nonsmooth analysis needed in what follows (see, e.g., [2, 11, 20, 21]).

Our notation is basically standard. Throughout the paper, ${\mathbb {R}}^n$ signifies Euclidean space whose norm is denoted by ||.||. The inner product of two vectors $x,y\in {\mathbb {R}}^n$ is shown by $\langle x,y\rangle .$ The closed unit ball, the nonnegative reals and the nonnegative orthant of ${\mathbb {R}}^n$ are denoted by ${\mathbb {B}},$ ${\mathbb {R}}_+$ and ${\mathbb {R}}^n_+,$ respectively. For a given subset $S\subseteq {\mathbb {R}}^n, {\mathrm{cl}}\,S$ and ${\mathrm{co}}\,S$ stand for the closure and convex hull of S,  respectively.

Let $f:{\mathbb {R}}^n\rightarrow {\mathbb {R}}\cup \{+\infty \}$ and ${\bar{x}}\in \mathrm{dom}\,f:=\{x\in {\mathbb {R}}^n\ |\ f(x)<\infty \}.$ We say that f is upper semi continuous (u.s.c.) at ${\bar{x}}$ if $\limsup _{x\rightarrow {\bar{x}}}f(x)\le f({\bar{x}}).$

The lower and upper Dini derivatives of f at ${\bar{x}}$ in the direction $d\in {\mathbb {R}}^n$ are defined, respectively, by

$$\begin{aligned} \begin{array}{ll} f^-({\bar{x}};d):=\liminf _{t\downarrow 0}\dfrac{f({\bar{x}}+td)-f({\bar{x}})}{t},\\ f^+({\bar{x}};d):=\limsup _{t\downarrow 0}\dfrac{f({\bar{x}}+td)-f({\bar{x}})}{t}. \end{array} \end{aligned}$$

The directional derivative of f at ${\bar{x}}$ in the direction d is given by

$$\begin{aligned} f'({\bar{x}};d):=\lim _{t\downarrow 0}\frac{f({\bar{x}}+td)-f({\bar{x}})}{t}, \end{aligned}$$

(1)

when the limit in (1) exists.

In the following, we present the definition of a class of functions that was introduced by Pshenichnyi [46] and is called “tangentially convex” by Lemaréchal [36].

Definition 1

A function $f:{\mathbb {R}}^n\rightarrow {\mathbb {R}}\cup \{+\infty \}$ is said to be tangentially convex at ${\bar{x}} \in \mathrm{dom}\,f$ if for each $d\in {\mathbb {R}}^n$ the limit in (1) exists, is finite and the function $d\longmapsto f'({\bar{x}};d)$ is convex.

In fact in this case, $d\longmapsto f'({\bar{x}};d)$ is a sublinear function, since it is generally positively homogeneous.

It is worth mentioning that the class of tangentially convex functions contains convex functions with open domain and Gâteaux differentiable functions. This class is closed under addition and multiplication by scalars. Therefore, it contains a large class of nonconvex and nondifferentiable functions. The product of two nonnegative tangentially convex functions is also tangentially convex.

Corresponding to the concept of tangentially convex functions, the following notion of subdifferential is defined in [46].

Definition 2

The tangential subdifferential of $f:{\mathbb {R}}^n\rightarrow {\mathbb {R}}\cup \{+\infty \}$ at ${\bar{x}} \in \mathrm{dom}\,f$ is the set

$$\begin{aligned} \partial _Tf({\bar{x}}):=\{\xi \in {\mathbb {R}}^n\ |\ \langle \xi ,d\rangle \le f'({\bar{x}};d),\ \forall d\in {\mathbb {R}}^n\}. \end{aligned}$$

If f is tangentially convex at ${\bar{x}},$ then $\partial _Tf({\bar{x}})$ is a nonempty closed convex subset of ${\mathbb {R}}^n.$ It is also easy to show that $f'({\bar{x}};.)$ is the support function of $\partial _Tf({\bar{x}}),$ that is, for each $d\in {\mathbb {R}}^n$ one has

$$\begin{aligned} f'({\bar{x}};d)= \max _{\xi \in {\partial _Tf({\bar{x}})}}\langle \xi ,d\rangle . \end{aligned}$$

Obviously, if f is a convex function then $\partial _Tf({\bar{x}})$ reduces to the classical convex subdifferential $\partial f({\bar{x}})$ (see [11, p. 44]).

Following [40], we recall the notion of pseudoconvexity to the tangentially convex setting.

Definition 3

A function $f:{\mathbb {R}}^n\rightarrow {\mathbb {R}}\cup \{+\infty \}$ which is tangentially convex at ${\bar{x}} \in \mathrm{dom}\,f$ is said to be pseudoconvex at ${\bar{x}}$ if $f(x)\ge f({\bar{x}})$ for every $x\in {\mathbb {R}}^n$ such that $f'({\bar{x}};x-{\bar{x}})\ge 0.$

Finally in this section, let us recall from [2, 11, 21] the definitions of some tangent and normal cones to a closed set.

For a given nonempty closed subset S of ${\mathbb {R}}^n$ and ${\bar{x}}\in S,$

• The cone of feasible directions of S at ${\bar{x}}$ is

  $$\begin{aligned} D({\bar{x}};S):=\{d\in {\mathbb {R}}^n\ |\ \exists \delta >0,\ \text{ s.t. }\ {\bar{x}}+td\in S,\ \forall t\in (0,\delta )\}. \end{aligned}$$

• The cone of attainable directions of S at ${\bar{x}}$ is

  $$\begin{aligned}\begin{array}{ll} A({\bar{x}};S):=\{ d\in {\mathbb {R}}^n &{} | \exists \alpha :{\mathbb {R}}\rightarrow {\mathbb {R}}^n,\ \text{ s.t. }\ \alpha (0)={\bar{x}}\ \text{ and }\ \exists \delta >0,\ \text{ s.t. }\\ &{}\forall t\in (0,\delta ), \ \alpha (t)\in S\ \text{ and }\ \lim _{t\downarrow 0}\frac{\alpha (t)-\alpha (0)}{t}=d\}. \end{array} \end{aligned}$$

• The contingent cone of S at ${\bar{x}}$ is

  $$\begin{aligned}\begin{array}{ll} T({\bar{x}};S):=\{d\in {\mathbb {R}}^n|\ \exists t_k\downarrow 0,\ \exists d_k\rightarrow d,\ \text{ s.t. }\ {\bar{x}}+t_kd_k\in S, \ \forall k\}. \end{array} \end{aligned}$$

3 Max function

In this section, we try to prove some results in nonsmooth analysis that characterize the directional derivatives of a certain “max function” defined this way.

Let V be a nonempty compact subset of ${\mathbb {R}}^q$ and consider the function $g:{\mathbb {R}}^n\times V\rightarrow {\mathbb {R}}\cup \{+\infty \}.$ We define the function $\psi :{\mathbb {R}}^n\rightarrow {\mathbb {R}}\cup \{+\infty \}$ and the multifunction $V:{\mathbb {R}}^n\rightrightarrows {\mathbb {R}}^q$as follows:

$$\begin{aligned}&\psi (x):=\max _{v\in V}\ g(x,v), \end{aligned}$$

(2)

$$\begin{aligned}&V(x):=\{v\in V\ |\ \psi (x)=g(x,v)\}. \end{aligned}$$

(3)

We make the following assumptions in the remainder of this paper:

$(A_1)$:

The function $(x,v)\mapsto g(x,v)$ is u.s.c. at each $(x,v)\in {\mathbb {R}}^n\times V.$

$(A_2)$:

g is locally Lipschitz in x,  uniformly for $v\in V;$ i.e., for each $x\in {\mathbb {R}}^n,$ there exist an open neighbourhood N(x) of x and a positive number L such that for each $y,z\in N(x)$ and $v\in V,$ one has

$$\begin{aligned} |g(y,v)-g(z,v)|\le L||y-z||. \end{aligned}$$

$(A_3)$:

g is a tangentially convex function with respect to x;  i.e., $g'_x(x,v;d)$ which is the directional derivative of g with respect to x,  exists, is finite for every $(x,v)\in {\mathbb {R}}^n\times V,$ and is a convex function of $d\in {\mathbb {R}}^n.$

$(A_4)$:

The mapping $v\rightarrow g'_x(x,v;d)$ is u.s.c. at each $v\in V.$

A comparison between the above-mentioned assumptions and other related contexts shows that the assumptions $(A_1)$ and $(A_2)$ are common in robust optimization problems (see, e.g., [17, 19]). Assumptions $(A_3)$ and $(A_4)$ are related to the concept of the tangential subdifferential.

The following theorem, which is a nonsmooth version of Danskin’s theorem for max-functions [20], makes connection between the functions $\psi '(x;d)$ and $g'_x(x,v;d).$

Theorem 1

The directional derivative $\psi '(x;d)$ exists, and satisfies

$$\begin{aligned} \psi '(x;d)=\max _{v\in V(x)}g'_x(x,v;d),\ \forall d\in {\mathbb {R}}^n. \end{aligned}$$

(4)

Proof

We may suppose that $d(\ne 0)\in {\mathbb {R}}^n.$ Fix $(x,v)\in {\mathbb {R}}^n\times V$ and take an arbitrary sequence $t_i\downarrow 0$ such that

$$\begin{aligned} \psi ^+(x;d) =\lim _{i\rightarrow \infty }\dfrac{\psi (x+t_id)-\psi (x)}{t_i}. \end{aligned}$$

(5)

Thus for each i,  there exists some $v_i\in V(x+t_id)$ such that $\psi (x+t_id)=g(x+t_id,v_i).$ Due to the fact that $V(x+t_id)\subseteq V$ and the compactness of V,  one can find a subsequence $v_i$ converges to ${\bar{v}}\in V.$ Clearly for a fixed $v\in V$ and for each $i,\ g(x+t_id,v)\le g(x+t_id,v_i).$ Then passing to the limit, it follows that $g(x,v)\le \limsup _{i\rightarrow \infty }g(x+t_id,v_i).$ Now by assumption $(A_1),$ we get

$$\begin{aligned} g(x,v)\le \limsup _{i\rightarrow \infty }g(x+t_id,v_i)\le g(x,{\bar{v}}). \end{aligned}$$

This implies that ${\bar{v}}\in V(x),$ and hence $\psi (x)=g(x,{\bar{v}}).$

Further, it is clear that for each $t>0,$

$$\begin{aligned} \dfrac{\psi (x+td)-\psi (x)}{t}\ge \dfrac{g(x+td,{\bar{v}})-g(x,{\bar{v}})}{t}. \end{aligned}$$

Therefore passing to the limit as $t\downarrow 0,$ we get:

$$\begin{aligned} \psi ^-(x;d)\ge g'_x(x,{\bar{v}};d). \end{aligned}$$

(6)

Now consider the following double sequence:

$$\begin{aligned} \bigg \{\dfrac{g(x+t_jd,v_i)-g(x,v_i)}{t_j}\bigg \}_{(i,j)\in {\mathbb {N}}\times {\mathbb {N}}}. \end{aligned}$$

(7)

According to $(A_2),$ we obtain

$$\begin{aligned} \bigg |\dfrac{g(x+t_jd,v_i)-g(x,v_i)}{t_j}\bigg |\le L||d||, \end{aligned}$$

(8)

where L is a Lipschitz constant for g around x. Thus the sequence in (7) is bounded. Hence by [1, Theorem 8.39], we can find a subsequence (without relabeling) such that

$$\begin{aligned} \lim _{i,j\rightarrow \infty }\dfrac{g(x+t_jd,v_i)-g(x,v_i)}{t_j}=\alpha \in {\mathbb {R}}. \end{aligned}$$

On the other hand,

$$\begin{aligned} \lim _{i\rightarrow \infty } \lim _{j\rightarrow \infty }\dfrac{g(x+t_jd,v_i)-g(x,v_i)}{t_j}&= \lim _{i\rightarrow \infty }g'_x(x,v_i;d)\\&\le g'_x(x,{\bar{v}};d), \end{aligned}$$

where the last inequality is due to $(A_4).$ Thus using [1, Theorem 8.39], we get

$$\begin{aligned} \lim _{i,j\rightarrow \infty }\dfrac{g(x+t_jd,v_i)-g(x,v_i)}{t_j} \le g'_x(x,{\bar{v}};d). \end{aligned}$$

Then we construct a subsequence by taking $i=j=k,$ and get

$$\begin{aligned} \lim _{k\rightarrow \infty }\dfrac{g(x+t_kd,v_k)-g(x,v_k)}{t_k} \le g'_x(x,{\bar{v}};d). \end{aligned}$$

Thus by (5), we obtain

$$\begin{aligned} \psi ^+(x;d)&=\lim _{k\rightarrow \infty }\dfrac{\psi (x+t_kd)-\psi (x)}{t_k} \\&\le \lim _{k\rightarrow \infty }\frac{g(x+t_kd,v_k)-g(x,v_k)}{t_k}\\&\le g'_x(x,{\bar{v}};d). \end{aligned}$$

Using the above inequality together with (6), we get $\psi '(x;d)=g'_x(x,{\bar{v}};d).$ Moreover, for each $v\in V(x),$

$$\begin{aligned} g'_x(x,v;d)\le \psi '(x;d)= g'_x(x,{\bar{v}};d), \end{aligned}$$

which implies (4) and completes the proof of theorem. $\square$

The next two results provide some consequences needed in what follows.

Proposition 1

The following set

$$\begin{aligned} \varGamma :={\mathrm{co}}\,\bigcup _{v\in V(x)}\partial _T^xg(x,v) \end{aligned}$$

is closed.

Proof

Consider the sequence $\{\xi _i\}\subseteq \varGamma$ such that $\lim _{i\rightarrow \infty }\xi _i=\xi .$ Using Carathé-odory’s theorem [20] one has $\xi _i=\sum _{j=1}^{n+1}\lambda _{ij}\xi '_{ij},$

where $\xi '_{ij}\in \partial _T^xg(x,v_{ij})$ for some $v_{ij}\in V_j(x), \sum _{j=1}^{n+1}\lambda _{ij}=\lambda _i$ and $\lambda _{ij}\ge 0$ for all $j=1,\ldots ,n+1,\ i\in {\mathbb {N}}.$ Passing to subsequences if necessary, we can assume that for each fixed $j\in {\mathbb {N}},\ \lim _{i\rightarrow \infty }\lambda _{ij}=\lambda _j\ge 0,\ \sum _{j=1}^{n+1}\lambda _j=1,$ and also, there exists a subsequence $\{v_{ij}\}_{i\in {\mathbb {N}}}\subseteq V$ such that $\lim _{i\rightarrow \infty }v_{ij}=v_j\in V.$

It is clear that $(A_2)$ implies that for each $i,j\in {\mathbb {N}},\ ||\xi '_{ij}||\le L,$ where L is a Lipschitz constant of g around x. Thus for all $i,j\in {\mathbb {N}},$ we may assume that $\lim _{i\rightarrow \infty }\xi '_{ij}=\xi '_j.$ Further, for each $d\in {\mathbb {R}}^n,$ we have $\langle \xi '_{ij},d\rangle \le g'_x(x,v_{ij};d).$ Then passing to the limit as $i\rightarrow \infty ,$ we get $\langle \xi '_j,d\rangle \le g'_x(x,v_j;d),$ hence $\xi '_j\in \partial _T^xg(x,v_j).$ This implies that $\xi =\sum _{j=1}^{n+1}\lambda _j\xi '_j\in \varGamma$ and completes the proof. $\square$

The following proposition provides some properties of the max function $\psi (x).$

Proposition 2

Consider the max function $\psi (.)$ defined in (2). Then the following properties hold:

• (i) $\psi (.)$ is a tangentially convex function.

• (ii) $\partial _T\psi (x)$ is a compact set for each $x\in {\mathbb {R}}^n.$

Proof

• (i) The proof is straightforward of Theorem 1 and the tangential convexity of g with respect to x.

• (ii) According to (i) and [41, Lemma 3.1], the proof is simple.

$\square$

The next theorem investigates the relationships between the tangential subdifferentials of the functions $\psi$ and g.

Theorem 2

Consider the max function $\psi (.)$ defined in (2). Then the tangential subdifferential $\partial _T\psi (x)$ at each $x\in {\mathbb {R}}^n$ is given as follows:

$$\begin{aligned} \partial _T\psi (x)={\mathrm{co}}\,\bigcup _{v\in V(x)}\partial _T^xg(x,v). \end{aligned}$$

(9)

Proof

Define $\varGamma :={\mathrm{co}}\,\cup _{v\in V(x)}\partial _T^xg(x,v),$ we show that $\partial _T\psi (x)\subseteq \varGamma$. Assume by contradiction that there exists a point $\xi \in \partial _T\psi (x){\setminus }\varGamma$. Applying Proposition 1 together with the convex separation theorem, we get a nonzero vector $d_0\in {\mathbb {R}}^n$ and $\alpha \in {\mathbb {R}}$ such that

$$\begin{aligned} \langle \xi ,d_0\rangle >\alpha \ge \langle \xi ',d_0\rangle ,\ \forall \xi '\in \varGamma . \end{aligned}$$

Moreover, by the tangential convexity of the function $\psi ,$ and using Theorem 1, we get

$$\begin{aligned} \max _{v\in V(x)}g'_x(x,v;d_0)=\psi '(x;d_0)\ge \langle \xi ,d_0\rangle >\alpha \ge \langle \xi ',d_0\rangle , \end{aligned}$$

for all $\xi '\in \varGamma .$ On the other hand, there is some ${\hat{v}}\in V(x)$ such that $\psi '(x;d_0)=g'_x(x,{\hat{v}};d_0).$ Also there exists some ${\hat{\xi }}\in \partial _T^xg(x,{\hat{v}})$ such that $\langle {\hat{\xi }},d_0\rangle =g'_x(x,{\hat{v}};d_0).$ Now putting all above together, we get

$$\begin{aligned} g'_x(x,{\hat{v}};d_0)>\alpha \ge \langle {\hat{\xi }},d_0\rangle =g'_x(x,{\hat{v}};d_0), \end{aligned}$$

which is a contradiction.

Conversely, let $\xi \in \varGamma .$ Then $\xi =\sum _{j=1}^{n+1}\lambda _j\xi _j,\ \xi _j\in \partial _T^xg(x,v_j)$ for some $v_j\in V(x),\ \sum _{j=1}^{n+1}\lambda _j=1$ and $\lambda _j\ge 0$ for all $j=1,\ldots ,n+1.$ For fixed $d\in {\mathbb {R}}^n$ one has

$$\begin{aligned}\langle \xi ,d\rangle \le \sum _{j=1}^{n+1}\lambda _jg'_x(x,v_j;d)\le \max _{v\in V(x)}g'_x(x,v;d)=\psi '(x;d), \end{aligned}$$

which implies that $\xi \in \partial _T\psi (x),$ and completes the proof. $\square$

Corollary 1

Consider the functions $f_i:{\mathbb {R}}^n\rightarrow {\mathbb {R}}\cup \{+\infty \},\ i=1,\ldots ,r.$ Define $f(x):=\max _{1\le i\le r}f_i(x)$ for each $x\in {\mathbb {R}}^n.$ Suppose that each $f_i$ is tangentially convex and locally Lipschitz at ${\bar{x}}\in {\mathbb {R}}^n.$ Then f is tangentially convex at ${\bar{x}}$ and we have

$$\begin{aligned} \partial _Tf({\bar{x}})={\mathrm{co}}\,\bigcup _{i\in I({\bar{x}})}\partial _Tf_i({\bar{x}}),\ f'({\bar{x}};d)=\max _{i\in I({\bar{x}})}f'_i({\bar{x}};d), \end{aligned}$$

where $I({\bar{x}})$ denotes the set of indices i such that $f_i({\bar{x}})=f({\bar{x}}).$

Remark 1

In this work, we derive necessary and sufficient optimality results for robust optimization problems with uncertainly data based on the concept of tangential subdifferential. As it can be seen, we intensively use the nonsmooth calculus of the maximum functions of type (2) for our analysis. To this end, we prove an exact formula in (9) for the tangential subdifferential of the function $\psi$. A closer look reveals that the compactness has a critical role in the proof of the above formula. It is worth noting that some of the recent results in variational analysis offer various estimate subdifferential formulas for supremum functions without any compactness assumptions (see, e.g., [42,43,44,45]). Although this assumption seems to be restrictive for many applications, we impose the compactness of V for the following two reasons:

• 1. To guarantee that the maximum function $\psi$ is a tangentially convex function.

• 2. To state an exact formula for the tangential subdifferential of $\psi$ based on the tangential subdifferentials $\partial _T^xg(x,v)$, in order to obtain our sufficient optimality results.

In this regards, using some relatively strong concepts like compactness of the uncertain set V can be justifiable.

4 Constraint qualifications

In this section, we focus mainly on some nonsmooth constraint qualifications in the face of data uncertainty based on the tangential subdifferential. Let us consider the following robust constraint system:

$$\begin{aligned} S:=\{x\in {\mathbb {R}}^n\ |\ g_j(x,v_j)\le 0,\ \forall v_j\in V_j,\ j=1,\ldots ,m\}, \end{aligned}$$

where $g_j:{\mathbb {R}}^n\times V_j\rightarrow {\mathbb {R}}\cup \{\infty \},\ j=1,\ldots ,m,$ and $v_j\in V_j$ is an uncertain parameter for some nonempty compact subset $V_j\subseteq {\mathbb {R}}^{q_j},j=1,\ldots ,m, q_j\in {\mathbb {N}}:=\{1,2,...\}.$

From now on, we suppose that assumptions $(A_1)-(A_4)$ are satisfied for $g_j,\ j=1,\ldots ,m.$ Let the functions $\psi _j:{\mathbb {R}}^n\rightarrow {\mathbb {R}}\cup \{\infty \}$ be defined by

$$\begin{aligned} \psi _j(x):=\max _{v_j\in V_j}g_j(x,v_j),\quad j=1,\ldots ,m. \end{aligned}$$

(10)

Then it is clear that

$$\begin{aligned} S=\{x\in {\mathbb {R}}^n\ |\ \psi _j(x)\le 0,\ j=1,\ldots ,m\}. \end{aligned}$$

The index set of the active constraints at ${\bar{x}} \in S$ is denoted by $J({\bar{x}}),$ and given by

$$\begin{aligned} J({\bar{x}}):=\{j\in \{1,\ldots ,m\}\ |\ \psi _j({\bar{x}})=0\}. \end{aligned}$$

Moreover, for each $j\in J({\bar{x}}),$ we define

$$\begin{aligned} V_j({\bar{x}}):=\{v_j\in V_j\ |\ g_j({\bar{x}},v_j)=\psi _j({\bar{x}})\}. \end{aligned}$$

As usual in classical optimization, we require to use the following linearized cones at ${\bar{x}}:$

$$\begin{aligned} G_0({\bar{x}})&:=\{d\in {\mathbb {R}}^n\ |\ \psi '_j({\bar{x}};d)<0,\ \forall j\in J({\bar{x}})\},\\ G'({\bar{x}})&:=\{d\in {\mathbb {R}}^n\ |\ \psi '_j({\bar{x}};d)\le 0,\ \forall j\in J({\bar{x}})\}. \end{aligned}$$

It is easy to show that

$$\begin{aligned} {\mathrm{cl}}\,G_0({\bar{x}})\subseteq {\mathrm{cl}}\,D({\bar{x}};S)\subseteq {\mathrm{cl}}\,A({\bar{x}};S)\subseteq T({\bar{x}};S)\subseteq G'({\bar{x}}), \end{aligned}$$

(11)

while the converse inclusions do not hold in general (see [41]).

We now pay our main attention to define new constraint qualifications in terms of the tangential subdifferential. We say that the generalized

• Slater constraint qualification (SCQ) is satisfied at ${\bar{x}}$ if there exists $x_0\in S$ such that $\psi _j(x_0)<0$ for $j=1,\ldots ,m.$

• Cottle constraint qualification (CCQ) holds at ${\bar{x}}$ if $G'({\bar{x}})\subseteq {\mathrm{cl}}\,G_0({\bar{x}}).$

• Zangwill constraint qualification (ZCQ) holds at ${\bar{x}}$ if $G'({\bar{x}})\subseteq {\mathrm{cl}}\,D({\bar{x}};S).$

• Kuhn–Tucker constraint qualification (KTCQ) is satisfied at ${\bar{x}}$ if $G'({\bar{x}})\subseteq {\mathrm{cl}}\,A({\bar{x}};S).$

• Abadie constraint qualification (ACQ) holds at ${\bar{x}}$ if $G'({\bar{x}})\subseteq T({\bar{x}};S).$

• Robinson constraint qualification (RCQ) is satisfied at ${\bar{x}}$ if for some nonzero vector $d\in {\mathbb {R}}^n$ one has for each $j\in J({\bar{x}}),$ $\psi '_j({\bar{x}};d)<0.$

• Mangasarian-Fromovitz constraint qualification (MFCQ) holds at ${\bar{x}}$ if

  $$\begin{aligned} 0\in \sum _{j\in J({\bar{x}})}\lambda _j\partial _T\psi _j({\bar{x}}),\ \lambda _j\ge 0,\ \forall j\in J({\bar{x}}), \end{aligned}$$

  then

  $$\begin{aligned} \lambda _j=0,\ \forall j\in J({\bar{x}}). \end{aligned}$$

Obviously, all the above constraint qualifications reduce to their counterparts defined in [41].

The next proposition provides the relationships between the constraint qualifications defined above.

Proposition 3

The following assertions are satisfied.

• (i) (RCQ) is equivalent to $G_0({\bar{x}})\ne \emptyset .$

• (ii) (CCQ) is equivalent to (RCQ).

• (iii) (RCQ) is equivalent to (MFCQ).

• (iv) (RCQ) implies (ZCQ).

• (v) (SCQ) implies (CCQ) provided that for each $j\in J({\bar{x}}),\ \psi _j$ is pseudoconvex at ${\bar{x}}.$

Proof

The proof is straightforward and we refer the reader to [41, Section 3]. $\square$

The following diagram summarizes the results of Proposition 3:

We conclude this section with some examples that illustrate the relationships between the above constraint qualifications.

The first example presents a situation that all the constraint qualifications are satisfied.

Example 1

Consider the set S given by

$$\begin{aligned} S:=\{x=(x_1,x_2)\in {\mathbb {R}}^2|\ g_j(x,v_j)\le 0,\ \forall v_j=(v_{j1},v_{j2})\in V_j,\ j=1,2\}, \end{aligned}$$

where $g_1(x,v_{1}):=-x_1+2v_{11}v_{12}|x_2|,\ g_2(x,v_2):=-(v_{21}+1)^2x_1^2-(v_{22}+1)(x_2-1)^2+1,$ $V_1:=\{v_1=(v_{11},v_{12})\in {\mathbb {R}}^2\ |\ v_{11}^2+v_{12}^2\le 1,\quad v_{11}v_{12}\ge 0\}$ and $V_2:=[0,1]\times [0,1].$

It is clear that $V_1$ is a nonconvex set while $V_2$ is convex. Clearly,

$$\begin{aligned} S=\{x\in {\mathbb {R}}^2\ |\ \psi _j(x)\le 0,\ j=1,2\}, \end{aligned}$$

where

$$\begin{aligned} \psi _1(x):=\max _{v_1\in V_1}\ g_1(x,v_1)= \left\{ \begin{array}{ll} -x_1+|x_2|, &{}\ x_2\ne 0\\ -x_1, &{} \ x_2 = 0, \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} \psi _2(x):=\max _{v_2\in V_2}\ g_2(x,v_2)= \left\{ \begin{array}{ll} 1, &{} \ x_1=0,x_2=1\\ -(x_2-1)^2+1, &{} \ x_1 = 0,x_2\ne 1\\ -x_1^2+1, &{} \ x_1\ne 0,x_2=1\\ -x_1^2-(x_2-1)^2+1, &{} \ x_1\ne 0, x_2\ne 1. \end{array} \right. \end{aligned}$$

Moreover,

$$\begin{aligned} V_1(x)= \left\{ \begin{array}{ll} \{(\frac{-1}{\sqrt{2}},\frac{-1}{\sqrt{2}}),(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})\}, &{} \ x_2\ne 0\\ V_1, &{}\ x_2=0, \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} V_2(x)=V_{21}(x)\times V_{22}(x), \end{aligned}$$

where

$$\begin{aligned} V_{21}(x)= \left\{ \begin{array}{ll} [0,1], &{} \ x_1=0\\ \{0\}, &{}\ x_1\ne 0, \end{array} \right. \qquad V_{22}(x)= \left\{ \begin{array}{ll} [0,1], &{} \ x_2=1\\ \{0\}, &{}\ x_2\ne 1. \end{array} \right. \end{aligned}$$

It is easily seen that $g_1$ and $g_2$ satisfy assumptions $(A_1)-(A_4)$ at ${\bar{x}}=(0,0)\in S.$

Further, it follows immediately that (SCQ) holds at ${\bar{x}}$. A simple calculation shows that $\partial _T \psi _1({\bar{x}})=\{-1\}\times [-1,1],$ and $\partial _T \psi _2({\bar{x}})=\{(0,2)\}$ for all $d=(d_1,d_2)\in {\mathbb {R}}^2,\ \psi '_1({\bar{x}};d)=-d_1+|d_2|$ and $\psi '_2({\bar{x}};d)=2d_2.$ Taking $(d_1,d_2)=(2,-1)$, we get $G_0({\bar{x}})=\{(d_1,d_2)\in {\mathbb {R}}^2\ |\ -d_1+|d_2|<0,\ d_2<0\}\ne \emptyset .$ Therefore,

$$\begin{aligned}\begin{array}{ll} {\mathrm{cl}}\,G_0({\bar{x}})&{}= D({\bar{x}};S)=A({\bar{x}};S)=T({\bar{x}};S)=G'({\bar{x}})\\ &{}=\{(d_1,d_2)\in {\mathbb {R}}^2\ |\ -d_1+|d_2|\le 0,\ d_2\le 0\}. \end{array} \end{aligned}$$

Hence (CCQ), (MFCQ), (RCQ), (ZCQ), (KTCQ) and (ACQ) hold at ${\bar{x}}.$

The following examples illustrate that the above implications do not hold in the opposite directions in general. In the second example, we show that (ZCQ) does not generally imply (CCQ).

Example 2

Consider the following constrained system:

$$\begin{aligned} S:=\{x=(x_1,x_2)\in {\mathbb {R}}^2|\ g_j(x,v_j)\le 0,\ \forall v_j=(v_{j1},v_{j2})\in V_j,\ j=1,2,3\}, \end{aligned}$$

where $g_1(x,v_{1}):=-x_1+2v_{11}v_{12}|x_2|,\ g_2(x,v_2):=-(v_{21}+1)^2x_1^2-(v_{22}+1)(x_2-1)^2+1,\ g_3(x,v_3):=(v_{31}-1)^2x_1^2+(v_{32}-1)(x_2+1)^2+1,\ V_1:=\{v_1=(v_{11},v_{12})\in {\mathbb {R}}^2\ |\ v_{11}^2+v_{12}^2\le 1 , v_{11}\le 0\ \text{ or }\ v_{12}\le 0\},\ V_2:=[0,1]\times [0,1]$ and $V_3:=[-1,0]\times [-1,0].$

Obviously, $V_1$ is nonconvex and $V_2$ and $V_3$ are convex sets. Further, ${\bar{x}}=(0,0)\in S$ and $g_1,\ g_2$ and $g_3$ satisfy assumptions $(A_1)-(A_4).$ Clearly,

$$\begin{aligned} S=\{x\in {\mathbb {R}}^2\ |\ \psi _j(x)\le 0,\ j=1,2,3\}, \end{aligned}$$

where

$$\begin{aligned}&\psi _1(x):=\max _{v_1\in V_1}\ g_1(x,v_1)= \left\{ \begin{array}{ll} -x_1+|x_2|, &{}\ x_2\ne 0\\ -x_1, &{} \ x_2 = 0, \end{array} \right. \\&\psi _2(x):=\max _{v_2\in V_2}\ g_2(x,v_2)= \left\{ \begin{array}{ll} 1, &{} \ x_1=0,x_2=1\\ -(x_2-1)^2+1, &{} \ x_1 = 0,x_2\ne 1\\ -x_1^2+1, &{} \ x_1\ne 0,x_2=1\\ -x_1^2-(x_2-1)^2+1, &{} \ x_1\ne 0, x_2\ne 1, \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} \psi _3(x):=\max _{v_3\in V_3}\ g_3(x,v_3)= \left\{ \begin{array}{ll} 1, &{} \ x_1=0,x_2=-1\\ -(x_2+1)^2+1, &{} \ x_1 = 0,x_2\ne -1\\ -x_1^2+1, &{} \ x_1\ne 0,x_2=-1\\ -x_1^2-(x_2+1)^2+1, &{} \ x_1\ne 0, x_2\ne -1. \end{array} \right. \end{aligned}$$

Moreover,

$$\begin{aligned} V_1(x)= \left\{ \begin{array}{ll} \{(\frac{-1}{\sqrt{2}},\frac{-1}{\sqrt{2}})\}, &{} \ x_2\ne 0\\ V_1, &{}\ x_2=0, \end{array} \right. \\ V_2(x)=V_{21}(x)\times V_{22}(x), \end{aligned}$$

where

$$\begin{aligned} V_{21}(x)= \left\{ \begin{array}{ll} [0,1], &{} \ x_1=0\\ \{0\}, &{}\ x_1\ne 0, \end{array} \right. \qquad V_{22}(x)= \left\{ \begin{array}{ll} [0,1], &{} \ x_2=1\\ \{0\}, &{}\ x_2\ne 1, \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} V_3(x)=V_{31}(x)\times V_{32}(x), \end{aligned}$$

where

$$\begin{aligned} V_{31}(x)= \left\{ \begin{array}{ll} [-1,0], &{} \ x_1=0\\ \{0\}, &{}\ x_1\ne 0, \end{array} \right. \quad V_{32}(x)= \left\{ \begin{array}{ll} [-1,0], &{} \ x_2=-1\\ \{0\}, &{}\ x_2\ne -1. \end{array} \right. \end{aligned}$$

An easy computation shows that $\partial _T \psi _1({\bar{x}})=\{-1\}\times [-1,1],\$ $\partial _T \psi _2({\bar{x}})=\{(0,2)\}$ and $\partial _T \psi _3({\bar{x}})=\{(0,-2)\}.$ It is easy to observe that for all $d=(d_1,d_2)\in {\mathbb {R}}^2,\ \psi '_1({\bar{x}};d)=-d_1+|d_2|,\ \psi '_2({\bar{x}};d)=2d_2$ and $\psi '_3({\bar{x}};d)=-2d_2.$ Thus (MFCQ), (RCQ) and (CCQ) are not satisfied at ${\bar{x}}.$ While, one has clearly that $D({\bar{x}};S)=A({\bar{x}};S)=T({\bar{x}};S)=G'({\bar{x}})={\mathbb {R}}_+\times \{0\}$ which shows that (ZCQ), (KTCQ) and (ACQ) hold at ${\bar{x}}.$

Finally, the following example illustrates (KTCQ) does not imply (ZCQ) in general.

Example 3

Consider the set S given by

$$\begin{aligned} S:=\{x=(x_1,x_2)\in {\mathbb {R}}^2|\ g_j(x,v_j)\le 0,\ \forall v_j=(v_{j1},v_{j2})\in V_j,\ j=1,2\}, \end{aligned}$$

where $g_1(x,v_{1}):=2|v_{11}v_{12}x_1|^3-x_2,\ g_2(x,v_2):=-(v_{21}+1)x_1^2+v_{22}|x_2|,\ V_1:=\{v_1=(v_{11},v_{12})\in {\mathbb {R}}^2\ |\ v_{11}^2+v_{12}^2\le 1 , v_{11}v_{12}\ge 0\}$ and $V_2:=[0,1]\times [0,1].$ It is clear that $V_1$ is nonconvex set and $V_2$ is convex. Further, $g_1$ and $g_2$ satisfy assumptions $(A_1)-(A_4),$ and ${\bar{x}}=(0,0)$ is a feasible point. We observe that

$$\begin{aligned} S=\{x\in {\mathbb {R}}^2\ |\ \psi _j(x)\le 0,\ j=1,2\}, \end{aligned}$$

where

$$\begin{aligned}&\psi _1(x):=\max _{v_1\in V_1}\ g_1(x,v_1)= \left\{ \begin{array}{ll} |x_1|^3-x_2, &{}\ x_1\ne 0\\ -x_2, &{} \ x_1=0, \end{array} \right. \\&\psi _2(x):=\max _{v_2\in V_2}\ g_2(x,v_2)= \left\{ \begin{array}{ll} 0, &{} \ x_1=0,x_2=0\\ |x_2|, &{} \ x_1 = 0,x_2\ne 0\\ -x_1^2, &{} \ x_1\ne 0,x_2=0\\ -x_1^2+|x_2|, &{} \ x_1\ne 0, x_2\ne 0. \end{array} \right. \end{aligned}$$

Furthermore,

$$\begin{aligned} V_1(x)= \left\{ \begin{array}{ll} \left\{ \left( \frac{-1}{\sqrt{2}},\frac{-1}{\sqrt{2}}\right) ,\left( \frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right) \right\} , &{} \ x_1\ne 0\\ V_1, &{}\ x_1=0, \end{array} \right. \\ V_2(x)=V_{21}(x)\times V_{22}(x), \end{aligned}$$

where

$$\begin{aligned} V_{21}(x)= \left\{ \begin{array}{ll} [0,1], &{} \ x_1=0\\ \{0\}, &{}\ x_1\ne 0, \end{array} \right. \qquad V_{22}(x)= \left\{ \begin{array}{ll} [0,1], &{} \ x_2=0\\ \{1\}, &{}\ x_2\ne 0. \end{array} \right. \end{aligned}$$

For all $d=(d_1,d_2)\in {\mathbb {R}}^2,$ we have $\psi '_1({\bar{x}};d)=-d_2$ and $\psi '_2({\bar{x}};d)=|d_2|.$ Thus $\partial _T\psi _1({\bar{x}})=\{(0,-1)\}$ and $\partial _T\psi _2({\bar{x}})=\{0\}\times [-1,1].$ Clearly, (MFCQ) does not hold at ${\bar{x}}.$ Moreover, $A({\bar{x}};S)=T({\bar{x}};S)=G'({\bar{x}})={\mathbb {R}}\times \{0\},$ which implies that (KTCQ) and (ACQ) are satisfied at ${\bar{x}}.$ On the other hand, $D({\bar{x}};S)=\{(0,0)\},$ thus (ZCQ) does not hold at ${\bar{x}}$.

5 Optimality conditions for robust optimization problem

We start this section by introducing the concept of robust solution. Then we try to derive new necessary and sufficient optimality results for a robust optimization problem by using some suitable constraint qualifications defined in Sect. 4. For this purpose, we intend to study the following optimization programming problem in the face of data uncertainty in the constraints:

where $v_j\in V_j,\ j=1,\ldots ,m$ are uncertain parameters for some nonempty compact subset $V_j\subseteq {\mathbb {R}}^{q_j}.$ Moreover, $f:{\mathbb {R}}^n\rightarrow {\mathbb {R}}\cup \{+\infty \}$ is a tangentially convex function at a feasible point ${\bar{x}},$ and each $g_j:{\mathbb {R}}^n\times V_j\rightarrow {\mathbb {R}}\cup \{+\infty \}$ satisfies assumptions $(A_1)-(A_4).$ The problem ($UP_1$) is usually associated with its robust counterpart as follows:

where the uncertain constraints are enforced for every possible value of the parameters within their prescribed uncertainty sets $V_j,\ j=1,\ldots ,m.$ The problem ($RP_1$) can be considered as the robust case (the worst-case) of ($UP_1$).

Now we consider $S=\{x\in {\mathbb {R}}^n\ |\ g_j(x,v_j)\le 0,\ \forall v_j\in V_j,\ j=1,\ldots ,m\}$ as the feasible set of ($RP_1$) and make the following definitions.

Definition 4

Suppose that ${\bar{x}}$ is a feasible point of ($RP_1$). We say that ${\bar{x}}$ is

(i):

a robust local minimizer of ($RP_1$) if there exists a neighborhood $N({\bar{x}})$ of ${\bar{x}}$ such that for all $x\in S\cap N({\bar{x}}),$ one has $f(x)\ge f({\bar{x}}).$

(ii):

a robust B-stationary (Bouligand-stationarity) point of ($RP_1$) if for each $d\in T({\bar{x}};S),$ one has $f'({\bar{x}};d)\ge 0.$

The first main result of this section, provides necessary and sufficient optimality conditions for ($RP_1$).

Theorem 3

Let ${\bar{x}}$ be a feasible point of ($RP_1$). Then the following assertions hold:

• (i) If ${\bar{x}}$ is a robust local optimal point and f is Lipschitz near ${\bar{x}},$ then ${\bar{x}}$ is robust B-stationary.

• (ii) If ${\bar{x}}$ is robust B-stationary, f is Lipschitz near ${\bar{x}}$ and $f'({\bar{x}};d)>0$ for all $d\in T({\bar{x}};S){\setminus }\{0\},$ then ${\bar{x}}$ is a robust local optimal point.

• (iii) If (ACQ) holds at ${\bar{x}},$ then ${\bar{x}}$ is robust B-stationary if and only if

  $$\begin{aligned} 0\in \partial _Tf({\bar{x}})+{\mathrm{cl}}\,\big (\bigcup _{\begin{array}{l} \scriptstyle {\quad v_{jk}\in V_j({\bar{x}}) }\\ \scriptstyle {\lambda _{kj}\ge 0,\ j\in J({\bar{x}})}\\ \scriptstyle {\qquad l\in {\mathbb {N}}}\\ \end{array}} \sum _{k=1}^l \lambda _{kj}\partial _T^xg_j({\bar{x}},v_{jk})\big ). \end{aligned}$$

  (12)

• (iv) If (CCQ) holds at ${\bar{x}},$ then ${\bar{x}}$ is robust B-stationary if and only if

  $$\begin{aligned} 0\in \partial _Tf({\bar{x}})+ \sum _{ k=1}^l \lambda _{kj}\partial _T^xg_j({\bar{x}},v_{jk}), \end{aligned}$$

  (13)

  where $l\in {\mathbb {N}},\ \lambda _{kj}\ge 0,$ and $v_{jk}\in V_j({\bar{x}})$ for all $k=1,\ldots ,l,$ and $j\in J({\bar{x}}).$

Proof

• (i) , (ii) For the proof of parts (i) and (ii), we refer the reader to [41, Theorem 4.1(i,ii)].

• (iii) It is clear that the robust B-stationarity of ${\bar{x}}$ implies the B-stationarity of ${\bar{x}}$ as a feasible point of the following tangentially convex problem:

  

  where $\psi _j(x)$ is the same as defined in (10).

  It is easy to see that all the assumptions of [41, Theorem 4.1(iii)] are satisfied. Therefore there exists some positive real number ${\hat{\lambda }}_j,\ j\in J({\bar{x}})$ such that

  $$\begin{aligned} 0\in \partial _Tf({\bar{x}})+{\mathrm{cl}}\,(\bigcup _{{\hat{\lambda }}_j\ge 0}\sum _{j\in J({\bar{x}})} {\hat{\lambda }}_j\partial _T\psi _j({\bar{x}})). \end{aligned}$$

  (14)

  Now according to Theorem 2, we can rewrite (14) as follows:

  $$\begin{aligned} 0\in \partial _Tf({\bar{x}})+{\mathrm{cl}}\,(\bigcup _{{\hat{\lambda }}_j\ge 0}\sum _{j\in J({\bar{x}})} {\hat{\lambda }}_j{\mathrm{co}}\,\cup _{v_j\in V_j({\bar{x}})}\partial _T^xg_j({\bar{x}},v_j)). \end{aligned}$$

  (15)

  Then by using an argument similar to Proposition 1, we obtain (12).

• (iv) We proceed similarly to (iii) and by [41, Theorem 4.1(iv)], we get the result.

$\square$

In the following, we investigate the latter results in specific conditions.

Proposition 4

Consider the problem ($RP_1$). Suppose also that for each $j\in J({\bar{x}}),\ V_j$ is a convex set. Moreover, assume that for each $x\in S,\ g_j(x,.)$ is concave on $V_j,$ then

• (i) $V_j({\bar{x}})$ is a convex and compact set.

• (ii) $\partial _T\psi _j({\bar{x}})=\{\xi _j\ |\ \exists v_j\in V_j({\bar{x}})\ \text{ such } \text{ that } \ \xi _j\in \partial _T^xg_j({\bar{x}},v_j) \}.$

Proof

• (i) Let $v_j,w_j\in V_j({\bar{x}}),$ then

  $$\begin{aligned} \psi _j({\bar{x}})\ge g_j({\bar{x}},\lambda v_j+(1-\lambda )w_j)\ge \lambda g_j({\bar{x}},v_j)+(1-\lambda )g_j({\bar{x}},w_j)=\psi _j({\bar{x}}), \end{aligned}$$

  for each $\lambda \in [0,1].$ Thus $\lambda v_j+(1-\lambda )w_j\in V_j({\bar{x}})$ and $V_j({\bar{x}})$ is convex.

  To prove the compactness of $V_j({\bar{x}}),$ it is enough to show that $V_j({\bar{x}})$ is a closed set. To this end, consider a sequence $v_j^k\in V_j({\bar{x}})$ converging to $v_j.$ This implies that $\psi _j({\bar{x}})=g_j({\bar{x}},v_j^k).$ Now by assumption $(A_1)$, one can get

  $$\begin{aligned} \psi _j({\bar{x}})=\limsup _{k\rightarrow \infty }g_j({\bar{x}},v_j^k)\le g_j({\bar{x}},v_j)\le \psi _j({\bar{x}}), \end{aligned}$$

  and thus $\psi _j({\bar{x}})=g_j({\bar{x}},v_j).$ Therefore, $v_j\in V_j({\bar{x}})$ and the proof of (i) is complete.

• (ii) Define $\varLambda :=\{\xi _j\ |\ \exists v_j\in V_j({\bar{x}})\ \text{ such } \text{ that } \ \xi _j\in \partial _T^xg_j({\bar{x}},v_j) \}$ and assume that $\xi _j\in \varLambda .$ Thus one can find some $v_j\in V_j({\bar{x}})$ such that $\xi _j\in \partial _T^xg_j({\bar{x}},v_j).$ Obviously it follows that $\xi _j\in {\mathrm{co}}\,\cup _{v_j\in V_j({\bar{x}})}\partial _T^xg_j({\bar{x}},v_j)=\partial _T\psi _j({\bar{x}}).$

  Conversely, suppose that $\xi \in \partial _T\psi _j({\bar{x}}).$ Then according to Theorem 2, we can assume that $\xi =\sum _{i=1}^k\lambda _i\xi _i,$ where $\xi _i\in \partial _T^xg_j({\bar{x}},v_i)$ for some $v_i\in V_j({\bar{x}}),\ \lambda _i\ge 0$ for all $i=1,\ldots ,k$ and $\sum _{i=1}^k\lambda _i=1.$ Using an argument similar to the proof of part (i), we can get by the concavity of $g_j(x,.)$ on $V_j$ that $v=\sum _{i=1}^k\lambda _iv_i\in V_j({\bar{x}}).$ On the other hand, for a fixed $d\in {\mathbb {R}}^n$ and each $t>0$ one has

  $$\begin{aligned} \dfrac{{\sum _{i=1}^k\lambda _i(g_j({\bar{x}}+td,v_i)-g_j({\bar{x}},v_i))}}{t}&=\dfrac{{\sum _{i=1}^k\lambda _i(g_j({\bar{x}}+td,v_i)-\psi _j({\bar{x}}))}}{t} \\&\le \dfrac{{g_j({\bar{x}}+td,\sum _{i=1}^k\lambda _iv_i)-\psi _j({\bar{x}})}}{t}\\&=\dfrac{{g_j({\bar{x}}+td,v)-g_j({\bar{x}},v)}}{t}. \end{aligned}$$

  Thus we arrive at

  $$\begin{aligned} \langle \xi ,d\rangle \le \sum _{i=1}^k\lambda _ig_{jx}'({\bar{x}},v_i;d)\le g_{jx}'({\bar{x}},v;d), \end{aligned}$$

  which implies that $\xi \in \partial _T^xg_j({\bar{x}},v)$ and completes the proof of theorem.

$\square$

The following corollary is a direct consequence of Theorem 3 and Proposition 4.

Corollary 2

Under the assumptions of Proposition 4, the following assertions hold:

(i):

If (ACQ) holds at ${\bar{x}},$ then ${\bar{x}}$ is robust B-stationary if and only if

$$\begin{aligned} 0\in \partial _Tf({\bar{x}})+{\mathrm{cl}}\,(\bigcup _ {\lambda _j\ge 0}\sum _{\begin{array}{l} \scriptstyle { j\in J({\bar{x}})}\\ \scriptstyle { v_j\in V_j({\bar{x}})}\\ \end{array}} \lambda _j\partial _T^xg_j({\bar{x}},v_j)). \end{aligned}$$

(16)

(ii):

If (CCQ) holds at ${\bar{x}},$ then ${\bar{x}}$ is robust B-stationary if and only if there exist $v_j\in V_j({\bar{x}}),\ \lambda _j\ge 0$ such that

$$\begin{aligned} 0\in \partial _Tf({\bar{x}})+\sum _{j\in J({\bar{x}})} \lambda _j\partial _T^xg_j({\bar{x}},v_j). \end{aligned}$$

(17)

In the last part of this section, we extend the previous results for a robust optimization problem in the face of data uncertainty both in the objective and constraint functions. To this end, we consider the following problem:

where $u\in U$ and $v_j\in V_j,\ j=1,\ldots ,m$ are uncertain parameters for some nonempty compact subsets $U\subseteq {\mathbb {R}}^{p},$ and $V_j\subseteq {\mathbb {R}}^{q_j},$ respectively. Moreover, $f:{\mathbb {R}}^n\times U\rightarrow {\mathbb {R}}\cup \{+\infty \},$ and $g_j:{\mathbb {R}}^n\times V_j\rightarrow {\mathbb {R}}\cup \{+\infty \},\ j=1,\ldots ,m$ are functions that satisfy assumptions $(A_1)-(A_4).$ The robust optimization problem associated with the uncertain program ($UP_2$) is

We suppose that $S:=\{x\in {\mathbb {R}}^n\ |\ g_j(x,v_j)\le 0,\ \forall v_j\in V_j,\ j=1,\ldots ,m\}$ is the feasible set of ($RP_2$). We also consider the tangentially convex function $\phi :{\mathbb {R}}^n\rightarrow {\mathbb {R}}\cup \{+\infty \}$ given by $\phi (x):=\max _{u\in U}f(x,u),$ and define $U({\bar{x}}):=\{u\in U\ |\ \phi ({\bar{x}})=f({\bar{x}},u)\}.$

To prove the last main result of this section, we require the following optimality notions for $(RP_2.)$

Definition 5

Suppose that ${\bar{x}}$ is a feasible point of ($RP_2$). we say that ${\bar{x}}$ is

• (i) a robust local optimal solution of ($RP_2$) if there exists a neighborhood $N({\bar{x}})$ of ${\bar{x}}$ such that for all $x\in S\cap N({\bar{x}}),$ one has

  $$\begin{aligned} \phi (x)\ge \phi ({\bar{x}}). \end{aligned}$$

• (ii) a robust B-stationary solution of ($RP_2$) if for each $d\in T({\bar{x}};S),$ one has

  $$\begin{aligned} \phi '({\bar{x}};d)\ge 0. \end{aligned}$$

The following theorem presents the relationship between the above optimality notions.

Theorem 4

Let ${\bar{x}}$ be a feasible point of problem ($RP_2$). If ${\bar{x}}$ is a robust local optimal point, then ${\bar{x}}$ is robust B-stationary.

The converse is true provided that for all $d\in T({\bar{x}};S){\setminus }\{0\},$ one has $\phi '({\bar{x}};d)>0.$

Proof

The proof is simple and we left it to the reader. $\square$

The last result of this section, establishes necessary and sufficient optimality conditions for ($RP_2$).

Theorem 5

Consider the optimization problem ($RP_2$).

Then the following assertions hold true:

• (i) If (ACQ) holds at ${\bar{x}}\in S,$ then ${\bar{x}}$ is a robust B-stationary solution of ($RP_2$) if and only if there is some $s\in {\mathbb {N}},\ u_i\in U({\bar{x}})$ and $\eta _i\ge 0$ for all $i\in \{1,\ldots ,s\}$ with $\sum _{i=1}^s\eta _i=1$ such that

  $$\begin{aligned} 0\in \sum _{i=1}^s\eta _i\partial _T^xf({\bar{x}},u_i)+{\mathrm{cl}}\,\big (\bigcup _{\begin{array}{l} \scriptstyle {\quad v_{jk}\in V_j({\bar{x}}) }\\ \scriptstyle {\lambda _{kj}\ge 0,\ j\in J({\bar{x}})}\\ \scriptstyle {\qquad l\in {\mathbb {N}}}\\ \end{array}} \sum _{k=1}^l \lambda _{kj}\partial _T^xg_j({\bar{x}},v_{jk})). \end{aligned}$$

  (18)

• (ii) If (CCQ) holds at ${\bar{x}}\in S,$ then ${\bar{x}}$ is a robust B-stationary solution of ($RP_2$) if and only if

  $$\begin{aligned} 0\in \sum _{i=1} ^s\eta _i\partial _T^xf({\bar{x}},u_i)+ \sum _{k=1}^l \lambda _{kj}\partial _T^xg_j({\bar{x}},v_{jk}), \end{aligned}$$

  (19)

  where $s,l\in {\mathbb {N}},\ u_i\in U({\bar{x}})$ for all $i=1,\ldots ,s,\ \lambda _{kj}\ge 0,$ and $v_{jk}\in V_j({\bar{x}})$ for all $k=1,\ldots ,l,$ and $j\in J({\bar{x}}).$

Proof

• (i) It is clear that the robust B-stationarity of ${\bar{x}}$ for ($RP_2$) implies the B-stationarity of ${\bar{x}}$ as a feasible point of the following tangentially convex optimization problem:

  

  Obviously, the Abadie constraint qualification defined in [41] holds at ${\bar{x}}.$ Thus by using [41, Theorem 4.1(ii)],

  $$\begin{aligned} 0\in \partial _T\phi ({\bar{x}})+{\mathrm{cl}}\,(\bigcup _{{\hat{\lambda }}_j\ge 0}\sum _{j\in J({\bar{x}})}{\hat{\lambda }}_j\partial _T\psi _j({\bar{x}})). \end{aligned}$$

  Now using Theorem 2 we get

  $$\begin{aligned} 0\in {\mathrm{co}}\,\bigcup _{u\in U({\bar{x}})}\partial _T^xf({\bar{x}},u)+{\mathrm{cl}}\,(\bigcup _{{\hat{\lambda }}_j\ge 0}\sum _{j\in J({\bar{x}})}{\hat{\lambda }}_j{\mathrm{co}}\,\bigcup _{v_j\in V_j({\bar{x}})}\partial _T^xg_j({\bar{x}},v_j)). \end{aligned}$$

  Then by an argument similar to that of Proposition 1, we arrive at the inclusion in (18).

• (ii) Using an argument similar to Theorems 3 together with part (i), the proof is immediate.

$\square$

We conclude this section with the following example and we show that the closures in inclusions (12) and (18) cannot be omitted.

Example 4

Consider the following robust optimization problem:

$$\begin{aligned} \begin{array}{lr} \min \quad \displaystyle f(x,u)=(\cos u_1u_2)x_2^2-e^{\sin {x_1}},\ \forall u=(u_1,u_2)\in U \\ \ \text{ s.t. } \quad \displaystyle g(x,v)=||(v_1,v_2)||||(x_1,x_2)||-x_2\le 0,\ \forall v=(v_1,v_2)\in V\\ \quad \displaystyle x=(x_1,x_2)\in {\mathbb {R}}^2, \end{array} \end{aligned}$$

where $U:=\{u=(u_1,u_2)\in {\mathbb {R}}^2\ |\ u_1\in [0,\frac{\pi }{2}],\ u_2\in [0,\frac{\pi }{2}]\}$ and $V:=\{v=(v_1,v_2)\in {\mathbb {R}}^2\ |\ v_1^2+v_2^2\le 1,\ v_1v_2\ge 0\}.$ It is not difficult to check that the functions $f,\ g$ satisfy assumptions $(A_1)-(A_4),$ and ${\bar{x}}=(0,0)\in S$ is a robust local minimizer of the problem.

It is clear that the feasible set S can be presented as

$$\begin{aligned} S=\{x\in {\mathbb {R}}^2\ |\ \psi (x)\le 0\}. \end{aligned}$$

Obviously, S is a nonconvex set,

$$\begin{aligned} \psi (x):=\max _{v\in V}\ g(x,v)= \left\{ \begin{array}{ll} 0, &{}\ (x_1,x_2)=0\\ ||(x_1,x_2)||-x_2, &{} \ (x_1,x_2)\ne 0, \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} V(x)=\{(v_1,v_2)\in V\ |\ v_1^2+v_2^2=1,\ v_1v_2\ge 0\}. \end{aligned}$$

Thus one has $S=\{0\}\times {\mathbb {R}}_+.$ Further,

$$\begin{aligned} \phi (x):=\max _{u\in U}\ f(x,u)= \left\{ \begin{array}{ll} x_2^2-e^{\sin {x_1}}, &{}\ x_2\ne 0\\ -e^{\sin {x_1}}, &{} \ x_2=0, \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} U(x)=\left\{ \begin{array}{ll} \{(u_1,u_2)\in {\mathbb {R}}^2\ |\ u_1u_2=0\}, &{}\ x_2\ne 0\\ U, &{}\ x_2=0. \end{array} \right. \end{aligned}$$

A simple calculation gives us $\psi '({\bar{x}};d)=||(d_1,d_2)||-d_2$ and $G'({\bar{x}})=T({\bar{x}};S)=S.$ Therefore, (ACQ) holds at ${\bar{x}}.$ It is also easy to see that $\partial _T\phi ({\bar{x}})=\{(1,0)\},\ \partial _T\psi ({\bar{x}})={\mathbb {B}}+(0,-1)=\{x\ |\ x_1^2+(x_2+1)^2\le 1\},$ and

$$\begin{aligned} \bigcup _{\lambda \ge 0}\lambda \partial _T\psi ({\bar{x}})=\{x\ |\ x_2<0\}, \end{aligned}$$

which implies immediately that

$$\begin{aligned} 0\in \partial _T\phi ({\bar{x}})+{\mathrm{cl}}\,(\bigcup _{\lambda \ge 0}\lambda \partial _T\psi ({\bar{x}})). \end{aligned}$$

Further, for each $d\in T({\bar{x}};S),$ we have $\phi '({\bar{x}};d)=d_1=0,$ which means that ${\bar{x}}$ is a robust B-stationary point. However, it is clear that $G_0({\bar{x}})=\emptyset$ and (CCQ) does not hold at ${\bar{x}},$ and it is worth noting that $0\notin \partial _T\phi ({\bar{x}})+\bigcup _{\lambda \ge 0}\lambda \partial _T\psi ({\bar{x}}).$ Thus the closure in inclusion (18) cannot be omitted.

On the other hand a simple calculation gives us

$$\begin{aligned} f'_x({\bar{x}},u;d)=-d_1,\ \forall u\in U({\bar{x}})=U,\ \partial _T^xf({\bar{x}},u)=\{(-1,0)\}, \end{aligned}$$

and

$$\begin{aligned} g'_x({\bar{x}},v;d)=||(v_1,v_2)||||(d_1,d_2)||-d_2,\&\ \forall v\in V({\bar{x}})=V,\\ \partial _T^xg({\bar{x}},v)=||(v_1,v_2)||{\mathbb {B}}+\{(0,-1)\}. \end{aligned}$$

Taking $\eta _1=1,\ \eta _2=\eta _3=0,$ with $u^{(1)}=(1,0),u^{(2)}=(0,0)$ and $u^{(3)}=(0,1)$ together with $\lambda _1=1,\ \lambda _2=\lambda _3=0,\ v^{(1)}=(1,0),v^{(2)}=(0,\frac{1}{2})$ and $v^{(3)}=(0,0),$ we get

$$\begin{aligned} 0\in \sum _{i=1}^3\eta _i\partial _T^xf({\bar{x}},u^{(i)})+{\mathrm{cl}}\,\big (\bigcup _{\lambda _k\ge 0} \sum _{k=1}^3\lambda _k\partial _T^xg({\bar{x}},v^{(k)})\big ). \end{aligned}$$

Thus all assumptions of Theorem 5 are satisfied. It is worth mentioning that $V({\bar{x}})$ is not convex, thus part (i) of Proposition 4 is not satisfied. In other words, the concavity of g with respect to v is necessary for convexity of $V({\bar{x}}).$ Moreover, taking $v\in V({\bar{x}})$ with $||v||<1$ implies that

$$\begin{aligned} \partial _T\psi ({\bar{x}})\ne \{\xi \ |\ \exists v\in V({\bar{x}})\ \text{ such } \text{ that } \ \xi \in \partial _T^xg({\bar{x}},v) \}. \end{aligned}$$

This shows that part (ii) of Proposition 4 does not hold in general.

6 Application to multiobjective problems

The final section of this paper is devoted to the optimality conditions for a special class of optimization problems known as robust multiobjective programming problems.

For this purpose, we consider the following robust multiobjective programming problem:

where $f_i:{\mathbb {R}}^n\rightarrow {\mathbb {R}}\cup \{+\infty \},\ i=1,\ldots ,r,$ are tangentially convex functions at a feasible point ${\bar{x}}.$ Further, the assumptions $(A_1)-(A_4)$ are satisfied and S is the same as defined in the previous section.

To proceed, we recall the following optimality notions for ($RMOP_1$).

Definition 6

Suppose that ${\bar{x}}$ is a feasible point of ($RMOP_1$). We say that ${\bar{x}}$ is

• (i) a weakly robust efficient solution of ($RMOP_1$) if for all $x\in S,$ there exists some $i=1,\ldots ,r$ such that $f_i(x)\ge f_i({\bar{x}}).$ We call ${\bar{x}}$ a local weakly robust efficient solution if there exists a neighborhood $N({\bar{x}})$ such that for each $x\in N({\bar{x}})\cap S,\ {\bar{x}}$ is a weakly robust efficient solution.

• (ii) a weakly robust efficient B-stationary solution of ($RMOP_1$) if for every $d\in T({\bar{x}};S),$ there exists some $i=1,\ldots ,r$ such that $f'_i({\bar{x}};d)\ge 0.$

It is easy to check that the weakly robust efficiency of ${\bar{x}}$ as a feasible point of ($RMOP_1$) is equivalent to the weakly efficiency of ${\bar{x}}$ as a feasible point of the following problem:

where $\psi _j:{\mathbb {R}}^n\rightarrow {\mathbb {R}}\cup \{+\infty \},j=1,\ldots ,m$ is a function that defined in ($RP_1$).

The next theorem provides necessary and sufficient optimality conditions for ($RMOP_1$).

Theorem 6

Let ${\bar{x}}$ be a feasible point of ($RMOP_1$). Suppose that $f_i,i=1,\ldots ,r,$ are locally Lipschitz at ${\bar{x}}.$

Then the following statements are true:

• (i) If (ACQ) holds at ${\bar{x}},$ then ${\bar{x}}$ is a weakly robust efficient B-stationary solution of ($RMOP_1$) if and only if there exist some $\eta _i\ge 0,\ i=1,\ldots ,r$ with $\sum _{i=1}^r\eta _i=1$ such that

  $$\begin{aligned} 0\in \sum _{i=1}^r\eta _i\partial _Tf_i({\bar{x}})+{\mathrm{cl}}\,\big (\bigcup _{\begin{array}{l} \scriptstyle {\quad v_{jk}\in V_j({\bar{x}}) }\\ \scriptstyle {\lambda _{kj}\ge 0,\ j\in J({\bar{x}})}\\ \scriptstyle {\qquad l\in {\mathbb {N}}}\\ \end{array}} \sum _{k=1}^l \lambda _{kj}\partial _T^xg_j({\bar{x}},v_{jk})). \end{aligned}$$

  (20)

• (ii) If (CCQ) holds at ${\bar{x}},$ then ${\bar{x}}$ is a weakly robust efficient B-stationary solution of ($RMOP_1$) if and only if there exist some $\eta _i\ge 0,\ i=1,\ldots ,r,$ with $\sum _{i=1}^r\eta _i=1$ such that

  $$\begin{aligned} 0\in \sum _{i=1}^r\eta _i\partial _T^xf_i({\bar{x}})+\sum _{k=1}^l \lambda _{kj}\partial _T^xg_j({\bar{x}},v_{jk}), \end{aligned}$$

  (21)

  where $l\in {\mathbb {N}},\ \lambda _{kj}\ge 0$ and $v_{jk}\in V_j({\bar{x}})$ for all $k=1,\ldots ,l,$ and $j\in J({\bar{x}}).$

Proof

• (i) It is not difficult to show that the weakly robust efficient B-stationarity of ${\bar{x}}$ is equivalent to the B-stationarity of ${\bar{x}}$ as a feasible point of the following optimization problem:

  $$\begin{aligned} \min \quad&\quad \theta (x):=\max \{f_i(x)-f_i({\bar{x}}),\ i=1,\ldots ,r\} \\ \text{ s.t. }&\quad \psi _j(x)\le 0\ \forall j=1,\ldots ,m.{(P_\theta )} \end{aligned}$$

  Obviously, $(P_\theta )$ is a tangentially convex problem and all the assumptions of Theorem 3 (iii) are satisfied. Thus

  $$\begin{aligned} 0\in \partial _T\theta ({\bar{x}})+{\mathrm{cl}}\,\big (\bigcup _{\begin{array}{l} \scriptstyle {\quad v_{jk}\in V_j({\bar{x}}) }\\ \scriptstyle {\lambda _{kj}\ge 0,\ j\in J({\bar{x}})}\\ \scriptstyle {\qquad l\in {\mathbb {N}}}\\ \end{array}} \sum _{k=1}^l \lambda _{kj}\partial _T^xg_j({\bar{x}},v_{jk})). \end{aligned}$$

  (22)

  Then we observe that

  $$\begin{aligned} \partial _T\theta ({\bar{x}})={\mathrm{co}}\,\bigcup _{i=1}^r\partial _Tf_i({\bar{x}}). \end{aligned}$$

  Hence one can find some $\eta _i\ge 0$ with $\sum _{i=1}^r\eta _i=1$ such that (21) is satisfied.

• (ii) We proceed similarly to (i) and by Theorem 5 (ii), we get the result.

$\square$

In the following, we consider a more general case of robust multiobjective programming problem in the face of uncertainty both in the objective and the constraint functions as follows:

where $f_i:{\mathbb {R}}^n\times U_i\rightarrow {\mathbb {R}}\cup \{+\infty \},\ i=1,\ldots ,r,$ and $g_j:{\mathbb {R}}^n\times V_j\rightarrow {\mathbb {R}}\cup \{+\infty \},\ j=1,\ldots ,m$ are given functions. Furthermore, $u_i\in U_i,\ i=1,\ldots ,r$ and $v_j\in V_j,\ j=1,\ldots ,m$ are uncertain parameters for nonempty compact subsets of ${\mathbb {R}}^{p_i},\ p_i\in {\mathbb {N}}$ and ${\mathbb {R}}^{q_j}, q_j\in {\mathbb {N}},$ respectively. We also suppose that the assumptions $(A_1)-(A_4)$ are satisfied for all the functions $f_i,i=1,\ldots ,r$ and $g_j,j=1,\ldots ,m.$

The robust optimization problem associated with the uncertain program ($MOP_2$) is as follows

For each $i=1,\ldots ,r,$ we define the function $\phi _i:{\mathbb {R}}^n\rightarrow {\mathbb {R}}\cup \{+\infty \}$ by $\phi _i(x):=\max _{u_i\in U_i}\{f_i(x,u_i)\}$ and the set $U_i({\bar{x}}):=\{u_i\in U_i\ |\ \phi _i({\bar{x}})=f_i({\bar{x}},u_i)\}.$

To proceed, we require to define the following optimality concepts for ($RMOP_2$).

Definition 7

Suppose that ${\bar{x}}$ is a feasible point of ($RMOP_2$). We say that ${\bar{x}}$ is

• (i) a weakly robust efficient solution of ($RMOP_2$) if for all $x\in S,$ there exists some $i=1,\ldots ,r$ such that $\max _{u_i\in U_i}f_i(x,u_i)\ge \max _{u_i\in U_i}f_i({\bar{x}},u_i).$ We call ${\bar{x}}$ a local weakly robust efficient solution if there exists a neighborhood $N({\bar{x}})$ such that for each $x\in N({\bar{x}})\cap S,\ {\bar{x}}$ is a weakly robust efficient solution.

• (ii) a weakly robust efficient B-stationary solution of ($RMOP_2$) if for every $d\in T({\bar{x}};S),$ there exists some $i=1,\ldots ,r$ such that $\max _{u_i\in U_i({\bar{x}})}f'_i({\bar{x}},u_i)\ge 0.$

It is clear that the weakly robust efficiency of ${\bar{x}}$ is equivalent to the weakly efficiency of ${\bar{x}}$ as a feasible point of the following multiobjective tangentially convex problem:

$$\begin{aligned} \min \quad&\quad (\phi _1(x),\ldots ,\phi _r(x)) \\ \text{ s.t. } \quad&\quad \psi _j(x)\le 0,\ \forall j=1,\ldots ,m. \end{aligned}$$

The last result of this paper presents necessary and sufficient optimality conditions for ($RMOP_2$).

Theorem 7

Let ${\bar{x}}$ be a feasible point of ($RMOP_2$). The following assertions hold:

• (i) If (ACQ) holds at ${\bar{x}},$ then ${\bar{x}}$ is a weakly robust efficient B-stationary solution of ($RMOP_2$) if and only if there is some $u_{i}\in U_i({\bar{x}}),i=1,\ldots ,r,$ $\eta _{i}\ge 0$ with $\sum _{i=1}^r\eta _{i}=1$ such that

  $$\begin{aligned} 0\in \sum _{i=1}^r \eta _{i}\{{\mathrm{co}}\,\cup _{u_i\in U_i({\bar{x}})}\partial _T^xf_i({\bar{x}},u_{i})\}+{\mathrm{cl}}\,\big (\bigcup _{\begin{array}{l} \scriptstyle {\quad v_{jk}\in V_j({\bar{x}}) }\\ \scriptstyle {\lambda _{kj}\ge 0,\ j\in J({\bar{x}})}\\ \scriptstyle {\qquad l\in {\mathbb {N}}}\\ \end{array}} \sum _{k=1}^l \lambda _{kj}\partial _T^xg_j({\bar{x}},v_{jk})).\nonumber \\ \end{aligned}$$

  (23)

• (ii) If (CCQ) holds at ${\bar{x}},$ then ${\bar{x}}$ is a weakly robust efficient B-stationary solution of ($RMOP_1$) if and only if there is some $u_{i}\in U_i({\bar{x}}),i=1,\ldots ,r,$ $\eta _{i}\ge 0$ with $\sum _{i=1}^r\eta _{i}=1$ such that

  $$\begin{aligned} 0\in \sum _{i=1}^r \eta _{i}\{{\mathrm{co}}\,\cup _{u_i\in U_i({\bar{x}})}\partial _T^xf_i({\bar{x}},u_{i})\}+\sum _{k=1}^l \lambda _{kj}\partial _T^xg_j({\bar{x}},v_{jk}), \end{aligned}$$

  (24)

  where $l\in {\mathbb {N}},\ \lambda _{kj}\ge 0,$ and $v_{jk}\in V_j({\bar{x}})$ for all $k=1,\ldots ,l,$ and $j\in J({\bar{x}}).$

Proof

• (i) It is easy to check that the weakly robust efficient B-stationarity of ${\bar{x}}$ is equivalent to the B-stationarity of ${\bar{x}}$ as a feasible point of the following optimization problem:

  

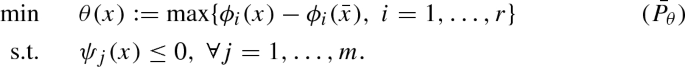
  Obviously, ($\bar{P_\theta }$) is a tangentially convex problem and all the assumptions of Theorem 3 (iii) are satisfied. Thus

  $$\begin{aligned} 0\in \partial _T\theta ({\bar{x}})+{\mathrm{cl}}\,\big (\bigcup _{\begin{array}{l} \scriptstyle {\quad v_{jk}\in V_j({\bar{x}}) }\\ \scriptstyle {\lambda _{kj}\ge 0,\ j\in J({\bar{x}})}\\ \scriptstyle {\qquad l\in {\mathbb {N}}}\\ \end{array}} \sum _{k=1}^l \lambda _{kj}\partial _T^xg_j({\bar{x}},v_{jk})). \end{aligned}$$

  (25)

  Applying Corollary 1 and Theorem 6 (i), we get the result.

• (ii) Using the similar arguments as used in part (i) and Theorem 6 (ii), the proof can be derived.

$\square$

We conclude the paper with an example illustrating Theorem 7.

Example 5

Consider the following robust multiobjective programming problem:

$$\begin{aligned} \begin{array}{lr} \min \displaystyle (f_1(x,u_1),f_2(x,u_2)),\ \forall u_i=(u_{i1},u_{i2})\in U_i,\ i=1,2 \\ \ \text{ s.t. }\displaystyle g_j(x,v_j)\le 0,\ \forall v_j=(v_{j1},v_{j2})\in V_j,\ j=1,2,3\\ \displaystyle x=(x_1,x_2)\in {\mathbb {R}}^2, \end{array} \end{aligned}$$

where $f_1(x,u_1):=u_{11}\max \{x_1,x_2\},\ f_2(x,u_2):=(u_{21}-u_{22})\min \{x_1,x_2\},$ and $U_i:=\{u_i\in {\mathbb {R}}^2\ |\ u_{i1}^2+u_{i2}^2\le 1,\ \}{\setminus }\{u_i\in {\mathbb {R}}^2\ |\ u_{i1}<0,\ u_{i2}<0\},\ i=1,2.$ Also we define the functions $g_j(x,v_j)$ as in Example 2.

It is easy to check that $f_i(i=1,2)$ and $g_j(j=1,2,3)$ satisfy the assumptions $(A_1)-(A_4).$ A simple calculation gives us

$$\begin{aligned} \phi _1(x):=\max _{u_1\in {U_1}} f_1(x,u_1)=|\max \{x_1,x_2\}|, \ \phi _2(x):=\max _{u_2\in {U_2}} f_2(x,u_2)=|\min \{x_1,x_2\}|, \end{aligned}$$

with

$$\begin{aligned} U_1(x)= \left\{ \begin{array}{ll} \{(1,0)\}, &{}\ \max \{x_1,x_2\}\ge 0\\ \{(-1,0)\}, &{}\ \max \{x_1,x_2\}<0, \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} U_2(x)= \left\{ \begin{array}{ll} \{(u_{21},u_{22})\in U_2 \ \text{ such } \text{ that }\ u_{22}=u_{21}-1\}, &{}\ \min \{x_1,x_2\}\ge 0\\ \{(u_{21},u_{22})\in U_2 \ \text{ such } \text{ that }\ u_{22}=u_{21}+1\}, &{}\ \min \{x_1,x_2\}<0. \end{array} \right. \end{aligned}$$

An easy calculation gives us for a feasible point ${\bar{x}}=(0,0):$

$$\begin{aligned} \phi '_1({\bar{x}};d):=|\max \{d_1,d_2\}|,\quad \phi '_2({\bar{x}};d):=|\min \{d_1,d_2\}|, \end{aligned}$$

for all $d=(d_1,d_2)\in {\mathbb {R}}^2,$ and

$$\begin{aligned} \partial _T\phi _1({\bar{x}})={\mathrm{co}}\,\{(\pm 1,0),(0,\pm 1)\},\quad \partial _T\phi _2({\bar{x}})={\mathrm{co}}\,\{(\pm 1,0),(0,\pm 1)\}. \end{aligned}$$

It is a simple matter to see that ${\bar{x}}$ is a weakly robust efficient solution of the problem and according to Example 2, (ACQ) holds at this point.

Taking $\eta _1=\eta _2=\frac{1}{2},$ and $\lambda _1=0,\lambda _2=\lambda _3=1,$ one has

$$\begin{aligned} 0\in \sum _{i=1}^2\eta _i\partial _T\phi _i({\bar{x}})+{\mathrm{cl}}\,\big (\bigcup _{\lambda _j\ge 0} \sum _{j=1}^3\lambda _j\partial _T\psi _j({\bar{x}})\big ). \end{aligned}$$

On the other hand, a simple calculation gives us

$$\begin{aligned} f'_{1x}({\bar{x}},u_1;d)=u_{11}\max \{d_1,d_2\},\ f'_{2x}({\bar{x}},u_2;d)=(u_{21}-u_{22})\min \{d_1,d_2\} \end{aligned}$$

with

$$\begin{aligned} \partial _T^xf_1({\bar{x}},u_1)={\mathrm{co}}\,\{(1,0),(0,1)\},\ \partial _T^xf_2({\bar{x}},u_2)={\mathrm{co}}\,\{(-1,0),(0,-1)\}, \end{aligned}$$

where

$$\begin{aligned} u_1\in U_1({\bar{x}})=\{(1,0)\},\ u_2\in U_2({\bar{x}})=\{(u_{21},u_{22})\in U_2\ |\ u_{22}=u_{21}-1\}. \end{aligned}$$

Further,

$$\begin{aligned} g'_{1x}({\bar{x}},v_1;d)=-d_1+2v_{11}v_{12}|d_2|,\ \partial _T^xg_1({\bar{x}},v_1)=\{-1\}\times [-2|v_{11}v_{12}|,2|v_{11}v_{12}|], \end{aligned}$$

for all $v_1=(v_{11},v_{12})\in V_1({\bar{x}})=V_1,$

$$\begin{aligned} g'_{2x}({\bar{x}},v_2;d)=2d_2(v_{22}+1)^2,\ \partial _T^xg_2({\bar{x}},v_2)=\{0,2(v_{22}+1)^2\}=\{(0,2)\}, \end{aligned}$$

for all $v_2=(v_{21},v_{22})\in V_2({\bar{x}})=[0,1]\times \{0\},$ and

$$\begin{aligned} g'_{3x}({\bar{x}},v_3;d)=2d_2(v_{32}-1)^2,\ \partial _T^xg_3({\bar{x}},v_3)=\{0,2(v_{32}-1)^2\}=\{(0,-2)\}, \end{aligned}$$

for all $v_3=(v_{31},v_{32})\in V_3({\bar{x}})=[-1,0]\times \{0\}.$ Taking $\eta _1=\eta _2=\frac{1}{2},$ $\lambda _{1i}=\frac{1}{3}$ with $v_{1i}=(v_{1i}^{(1)},v_{1i}^{(2)})=(\frac{-1}{\sqrt{2}},\frac{-1}{\sqrt{2}}),\ i=1,2,3,$ $\lambda _{21}=\frac{1}{2},\ v_{21}=(v_{21}^{(1)},v_{21}^{(2)})=(0,0),\ \lambda _{22}=\frac{1}{2},\ v_{22}=(v_{22}^{(1)},v_{22}^{(2)})=(1,0),\ \lambda _{23}=0$ with arbitrary $v_{23}=(v_{23}^{(1)},v_{23}^{(2)})\in V_2({\bar{x}}),$ and $\lambda _{31}=1,\ v_{31}=(v_{31}^{(1)},v_{31}^{(2)})=(-1,0),\ \lambda _{32}=\lambda _{33}=0$ with arbitrary $v_{32}=(v_{32}^{(1)},v_{32}^{(2)}),v_{33}=(v_{33}^{(1)},v_{33}^{(2)})\in V_3({\bar{x}}),$ the following condition is satisfied

$$\begin{aligned} 0\in \sum _{i=1}^2\eta _i\{{\mathrm{co}}\,\cup _{u_i\in U_i({\bar{x}})}\partial _T^xf_i({\bar{x}},u_{i})\} +{\mathrm{cl}}\,\big (\bigcup _{\begin{array}{l} \scriptstyle {v_{jk}\in V_j({\bar{x}})}\\ \scriptstyle { \lambda _{jk}\ge 0}\\ \end{array}} \sum _{k=1}^3\lambda _{jk}\partial _T^xg_j({\bar{x}},v_{jk})\big ). \end{aligned}$$

Thus all the assumptions of Theorem 7(i) are satisfied. It is worth mentioning that $V({\bar{x}})$ is not convex, thus part (i) of Proposition 4 is not satisfied. Hence, the concavity of $g_j$ with respect to $v_j$ is necessary for convexity of $V_j({\bar{x}}).$ Moreover, taking $v_j=(\frac{-1}{\sqrt{2}},\frac{-1}{\sqrt{2}})\in V_j({\bar{x}})$ implies that

$$\begin{aligned} \partial _T\psi _j({\bar{x}})=\{(-1,0)\}\subsetneqq \{\xi _j\ |\ \exists v_j\in V_j({\bar{x}})\ \text{ such } \text{ that } \ \xi _j\in \partial _T^xg_j({\bar{x}},v_j) \}, \end{aligned}$$

which shows that the equality in part (ii) of Proposition 4 does not hold.

7 Conclusion

In this work, a robust approach for nonsmooth and nonconvex optimization problems with the uncertainty data is studied. The robust optimality conditions are established in terms of tangential subdifferential. The results are obtained under data uncertainty in objective(s) and constraint functions by using the weakest constraint qualification (ACQ). Our results are obtained without requiring the convexity of the uncertain set and the concavity of the related functions with respect to the uncertain parameters. Moreover, the results are applied to present the necessary and sufficient optimality conditions for robust weakly efficient solutions in multiobjective programming problems. The obtained results provide sharper outcomes than the other related contexts; see for instance, [17, 33,34,35, 50].