Introduction

Traffic forecasts provide essential input for the appraisal of transport investment projects and public policies. In spite of significant improvements to transport demand models over the past few decades, there are still high levels of uncertainty in long-term forecasts. For instance, a recent study by Flyvbjerg et al. (2006) concludes that accuracy in forecasting traffic flow has not improved over time. Given that project profitability is highly dependent on predicted traffic flow, uncertainty has to be quantified and accounted for in project evaluation.

This article quantifies uncertainty in traffic forecasts for the tolled motorway network in Spain. We estimate a demand model using a panel data set covering 67 tolled motorway sections between 1980 and 2008. Uncertainty is quantified in the form of a confidence interval for the traffic forecast that takes account of both the variance of the traffic forecast related to the stochastic character of the model (model uncertainty) and the uncertainty that underlies the future values of the exogenous variables (input uncertainty). Furthermore, as an illustrative example we apply this methodology to a specific public policy consisting of suppressing the toll on a certain motorway sections before the concession expires. In this case, the government has to compensate the private motorway concessionaire for the revenue forgone up to the end of the concession period. We present a point estimate for the present value of the forgone revenue, as if the result were certain, and then a set of confidence intervals at different levels of significance that account for the variance of the forecasting error.

The predictions are based on an aggregate demand equation, where traffic flow depends on the following variables: Gross Domestic Product, toll per kilometre, petrol price and a set of dummy variables that account for major changes in the road network. However, if maximum infrastructure capacity is not allowed for in the model, it may well be that predictions lie above this maximum value. To avoid this problem we should, ideally, estimate an integrated demand–supply system. However, as is often the case, we are not able to model the supply side of the system due to lack of data. Our article contributes to this issue by proposing a new functional form for the demand equation that accounts for the fact that the rate of growth of traffic flow diminishes as the volume approaches full capacity. Specifically, as detailed in “The model” section, we suggest a modified partial adjustment model with variable adjustment speed. In our case, and in terms of forecasting capacity, this proposal is preferable to the traditional logistic functional form with a saturation level equal to maximum capacity, given that we avoid the assumption that traffic follows an S-shaped growth curve.

Literature review of uncertainty in traffic forecasting

Several recent studies confirm the inaccuracy of traffic predictions. Among them, the extensive work by Flyvbjerg et al. (2006) based on 210 transport infrastructure projects in 14 nations, 27 of which correspond to rail projects and the rest to road projects. They conclude that passenger forecasts for nine out of ten rail projects are overestimated, with an average overestimation of 106%. The authors suggest that there is a systematic positive bias in rail traffic forecasts. For road projects, forecasts are more accurate and balanced, although for 50% of the projects the difference between actual and forecasted traffic was more than ±20%.Footnote 1 For both road and rail projects, the estimated standard deviation of the forecasting error is high, showing a high level of uncertainty and risk.

Bain (2009) presents the results from a study that analyses the performance of traffic forecasts for toll road traffic from a database including over 100 international toll road projects. The research confirms a large range of error in traffic forecasting and the existence of systematic optimism bias. On average, toll road forecasts overestimated first-year traffic by 20–30%.

Using data on 14 toll motorway concessions in Spain, Vassallo and Baeza (2007) found that, on average, actual traffic during the first 3 years of operation was overestimated by approximately 35%. They conclude that there is a substantial optimism bias in the ramp-up period for toll motorway concessions in Spain.

The aforementioned studies suggest that the positive bias found for rail and toll motorways appears when there is a strong will for the approval of the project.

In spite of the significant errors present in traffic forecasting, uncertainty is often a neglected issue. Most of the predictions are presented as point estimates and the probability distribution of the outcome is forgotten about. The most common way to deal with uncertainty is to present alternative estimates based on different scenarios for the exogenous variables. However, this approach does not recognise all sources of uncertainty and, most importantly, does not provide the likelihood of each alternative forecast.

As stated by de Jong et al. (2007), the literature on quantifying uncertainty in traffic forecasting is fairly limited. The author reviews a considerable amount of the literature on that subject considering both the methodology employed and the results obtained. He distinguishes between input uncertainty, associated with the fact that future values of the exogenous variables are unknown, and model uncertainty, which includes random term uncertainty and coefficient uncertainty. Given that the 21 studies reviewed use different measures to express uncertainty and many of them do not present quantitative outcomes, providing an order of magnitude for uncertainty is difficult. De Jong suggests that input uncertainty is more important than model uncertainty; studies on input uncertainty or both input and model uncertainty obtain 95% confidence intervals for the mean value of traffic flow between ±18 and ±33%. The aforementioned paper also offers a methodology for quantifying uncertainty for a case study in The Netherlands.

The literature shows that quantifying forecast uncertainty and its causes is an area that deserves more attention. This article intends to contribute to this issue with new findings.

The model

Given that the demand equation is estimated in order to predict future traffic flow, when specifying the equation we should take into account that as the volume of traffic increases, costs related to congestion emerge and the rate of traffic growth diminishes as traffic volume approaches maximum capacity of a road section. Toll motorways were introduced in the early 1970s on the road network in Spain. Nowadays, some of these motorways are close to their maximum capacity. This problem mainly affects those toll roads near urban areas and the main corridor along the Mediterranean coast, where it is difficult and costly to expand capacity. In these cases capacity constraints need to be considered when forecasting in order to avoid excessively optimistic results.Footnote 2

Ideally, congestion costs and capacity constraints should be accounted for through a network assignment model, allowing a feedback between the various stages of the travel demand forecasting process.Footnote 3 However, frequently such a model is unavailable. As an alternative approach, we suggest a functional form that can be considered as an implicit reduced form for the demand function. Specifically, we estimate a modified partial adjustment model, where the speed of adjustment is variable. The proposed equation can be derived as follows:

The static equation of the partial adjustment model takes the standard form and shows the logarithm of the equilibrium value of traffic \( Y_{it}^{*} \) on road section i in period t as a function of a set of variables X it :

$$ \ln Y_{it}^{*} = \alpha_{i} + \beta \ln X_{it} $$
(1)

The dynamic of the adjustment is modified by introducing a variable adjustment parameter, λ it :

$$ \Updelta \ln Y_{it} = \ln Y_{it} - \ln Y_{it - 1} = \lambda_{it} \cdot (\ln Y_{it}^{*} - \ln Y_{it - 1} ) + \varepsilon_{it} $$
(2)

We assume that the speed of adjustment decreases as traffic flow increases in the following terms. Let us define the quality level of the motorway, τ, as a function of the traffic flow related to the maximum capacity of the infrastructure, Y max:

$$ \tau_{it} = {\frac{{Y_{i}^{\max } - Y_{it - 1} }}{{Y_{i}^{\max } }}} $$
(3)

Then, the adjustment parameter is assumed to be a function of τ it :

$$ \lambda_{it} = \theta \left( {{\frac{{Y_{i}^{\max } - Y_{it - 1} }}{{Y_{i}^{\max } }}}} \right) = \theta \cdot \tau_{it} $$
(4)

where θ is a parameter that links the speed of adjustment and the level of use of the motorway section.

This functional form accounts for the fact that the rate of traffic growth diminishes as traffic volume approaches the capacity limit. Its implications can be best observed in two extreme cases. When there is no traffic on the motorway, the speed of adjustment is maximum:

$$ Y_{it - 1} \to 0 \Rightarrow \tau_{it} \to 1 \Rightarrow \lambda_{it} \to \theta $$
(5)

In the opposite case, when traffic has reached capacity, the speed of adjustment is zero:

$$ Y_{it - 1} \to Y_{i}^{\max } \Rightarrow \tau_{it} \to 0 \Rightarrow \lambda_{it} \to 0 $$
(6)

By substituting \( Y_{it}^{*} \) from Eqs. 1 into 2, we get the first equation:

$$ \Updelta \ln Y_{it} = \lambda_{it} \cdot (\alpha_{i} + \beta \cdot \ln X_{it} - \ln Y_{it - 1} ) + \varepsilon_{it} $$
(7)

Next, substituting from λ it for Eq. 4 we get the final equation:

$$ {\frac{{\Updelta \ln Y_{it} }}{{\tau_{it} }}} = (\theta \cdot \alpha_{i} + \theta \cdot \beta \cdot \ln X_{it} - \theta \cdot \ln Y_{it - 1} ) + {\frac{{\varepsilon_{it} }}{{\tau_{it} }}} $$
(8)

This is a heteroskedastic model, so we have estimated using weighted least squares. This formulation does not need to be restricted to the partial adjustment model. It can be easily generalised to s lagged values, as shown in Appendix 1.

We estimate a standard demand equation where variables are expressed in logarithms.Footnote 4 The traffic volume in each section is a function of the level of economic activity (measured by Gross Domestic Product, GDP), the toll rate per kilometre, the price of gasoline and a set of dummy variables that capture major changes in the road network.Footnote 5 The full set of dummy variables is detailed in Appendix 2. The demand function can be expressed as follows:

$$ {\frac{{\Updelta \ln Y_{it} }}{{\tau_{it} }}} = (\theta \cdot \alpha_{i} + \theta \cdot \beta_{1i} \cdot \ln GDP_{t} + \theta \cdot \beta_{2i} \cdot \ln GP_{t} + \theta \cdot \beta_{3i} \cdot \ln T_{it} + \theta \cdot \gamma_{i} \cdot Z_{it} - \theta \cdot \ln Y_{it - 1} ) + {\frac{{\varepsilon_{it} }}{{\tau_{it} }}} $$
(9)

where Yit is the traffic volume on motorway section i in period t; GDPt is the real GDP in period t; GPt is the gasoline price in period t deflated by Consumer Price Index, CPI; Tit is the motorway toll in section i period t deflated by CPI; Zit is the dummy variables capturing major changes in the network; αi is the individual fixed effects; εit is the error term; (θ, α i , β1i , β2i , β3i , γ i ) are the coefficients to be estimated.

The individual fixed effects explain the differences between motorway sections (cross-section units) not captured by the variables included in the model. In our case, they may capture generation and attraction effects that determine the magnitude of traffic in each motorway section.

The data

To estimate the demand equation, we used a panel data set of 67 motorway sections observed between 1980 and 2008, although not all cross-section units were observed for this temporal span. The total number of observations was 1765. The cross-section observations correspond to the shortest motorway section allowed by the data collection processes, with an average length of 20 km.

The dependent variable is the annual average daily traffic volume in each section. The explanatory variables are: real GDP, gasoline price and toll per km. The last two deflated by CPI. GDP and gasoline price are defined at the national level and take the same value for all sections in the sample.Footnote 6 Finally, a set of 30 dummy variables captures the most important changes in the road network. For example, improvements on a parallel free road were captured by a dummy variable that takes value 1 since the opening year. The advantage of working with a panel data set is the high variability observed in the sample. See Table 1.

Table 1 Descriptive statistics
Full size table

It is interesting to note that there are substantial differences in traffic volume among the different sections of the motorway network. The daily average traffic flow ranges from 1689 vehicles in the section and year having the lowest volume to 90033 in the section and year with the highest. Furthermore, we found an extensive price range for toll rates. For the whole period, at 2006 prices, the lowest price paid per km was about 0.058 €, whereas the highest was about 0.34 €. The reasons for this wide variation are twofold. Firstly, each motorway has to cover its own construction costs, so the toll rates are higher on those motorways with larger construction costs or lower traffic volume. Secondly, the changes in toll policies during the last two decades have resulted in a wide variation of rates across the country and over time. For instance, on some motorway sections tolls decreased as much as 40% in one year.

The maximum capacity of each motorway section was calculated according to the number of lanes and types of vehicle.

Model estimation and results

Before estimating the model equation stated in (9), and in order to decide whether to estimate in levels or differences, we analyzed the existence of unit roots and cointegration of the series. The traffic volume and GDP variables were clearly non-stationary. So, both variables could be considered as integrated which means that the expected value and the variance are non constant. The evidence for motorway tolls and gasoline prices was more doubtful. In any case, to justify an estimation using levels for all the variables, it is necessary to guarantee that a cointegration relation exists among them. This means it is possible to find a linear combination of the series that is stationary. In our case, according to the Kao cointegration test for panel data, the null hypothesis of no cointegration was clearly rejected.Footnote 7 Therefore, we proceeded to estimate the equation in levels.

As specified in Eq. 9, the estimation of the demand equation would require to estimate 400 coefficients. Given that the number of total observations was 1765, it seemed advisable to introduce some constraints to the coefficients in order to allow for efficiency gains. Based on a previous work by Matas and Raymond (2003), we assumed that the demand elasticity of GDP and gasoline prices were the same across all motorway sections. Nonetheless, we maintained a specific toll coefficient for each motorway section.

Under these assumptions, we estimated Eq. 9 using weighted least squares. The random disturbance of the equation was modelled as a first order autoregressive process (rho) to control for autocorrelation. The coefficients for GDP, gasoline price, and the lagged value of the dependent variable take the expected sign and were estimated with a high degree of precision. In relation to the toll coefficients, a significant variation across motorway sections was observed. A Chi-square test allowed us to clearly reject the null hypothesis of equality of toll coefficients across all sections. However, the difference in the values of the toll coefficients could be explained by certain motorway characteristics: contiguous sections on the same motorway present very similar elasticities; the more inelastic sections are located on corridors with high traffic volumes, and demand is seen to be more elastic where a good alternative free road exists.

The observed results suggested the possibility of re-estimating the model by introducing the hypothesis of equality of toll coefficients across those motorway sections that showed similar coefficients in the initial model. Hence, we proceed by testing equality constraints among the toll coefficients for those motorways with similar coefficients in the original estimation. Based on the results of the Wald test, the motorway sections were classified into 3 groups as follows:

  • Low toll elasticity: sections with toll coefficient between 0 and −0.2.

  • Medium toll elasticity: sections with toll coefficient between −0.2 and −0.35

  • High toll elasticity: section with toll coefficients larger than −0.35.

The final estimation results are detailed in Table 2 and the coefficients for the dummy variables in Appendix 2. As can be observed, the toll coefficients are estimated with a high degree of precision. Given that the variables are log-transformed, the estimated coefficients can be interpreted as short term elasticities. Demand is sensitive to toll variations, although in the short term it is inelastic in all three groups.

Table 2 Summary of the estimation results
Full size table

To provide an additional insight into the accuracy of our model we compared its forecasting capacity to that of a logistic regression model. Using the same explanatory variables, we estimated a logistic regression with a saturation level equal to maximum capacity. According to the mean square error (MSE) for a dynamic forecast over the period 2000–2008, our approach was clearly preferable to the logistic approach.Footnote 8

An interesting property of the proposed functional form is that it makes it possible to avoid the often unrealistic assumption of constant elasticity. As shown in Appendix 3, demand elasticity with respect to an explanatory variable X k depends on the value of τ it , that is, it depends on the degree of motorway use. For τ it  = τ 0, the elasticity with respect to variable X k in period J is given by:

$$ \varepsilon_{J} = \beta_{k}^{*} \cdot {\frac{{(1 - \gamma^{*J + 1} )}}{{(1 - \gamma^{*} )}}} $$
(10)

where β * k  = τ 0 · β k , being β k the coefficient associated to X k , and γ * = (1 − τ 0 · θ)

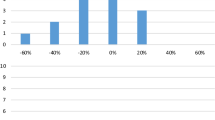
As an illustration, we compute the demand elasticity with respect to GDP for different values of τ 0 and for the first 6 years after the change in the exogenous variable. Elasticities are detailed in Table 3. For τ 0 = 1, when the level of traffic approaches 0, short-term elasticity is 0.8; after 5 years, the elasticity tends to the long-term value, 1.24. However, as traffic increases and τ 0 decreases, demand elasticity becomes less sensitive to GDP variations. For τ 0 = 0.1, when traffic flow approaches capacity, short-term elasticity is less than 0.1. The elasticity values computed for τ 0 = 0.7, which correspond to the average observed value our sample, are in line with those reported in the literature.

Table 3 Elasticities with respect to GDP
Full size table

Figure 1 displays the elasticity values for τ 0 ranging from 0.1 to 1.

Fig. 1
figure 1

Elasticities with respect to GDP for different tau values

Full size image

For the particular case where τ 0 = 1, the coefficients can be interpreted as those in the standard partial adjustment model. The short- and long-term elasticities for all the explanatory variables are reported in Table 4.

Table 4 Estimated demand elasticities
Full size table

Forecast results and uncertainty

From the estimated demand model, we proceeded to forecast traffic flow for the 2009–2025 period. The first step was to predict the explanatory variables in the model. GDP and gasoline price are predicted according to a time series model and motorway tolls are assumed to remain constant in real terms given that the toll revision formula is linked to CPI. We applied univariate distributions for the exogenous variables given that no correlations were observed among them.

Figure 2 displays the forecasted traffic flow for two representative motorway sections according to both a non-restricted model (standard partial adjustment model) and a capacity restricted model (modified partial adjustment model). In the first one, traffic flow is well below maximum capacity in the year 2025, whereas the second has reached capacity by approximately 2019. As can be observed, the effect of the capacity constraint is almost unnoticeable when traffic volume is below maximum capacity. However, the effect is clear for the second motorway section. The standard partial adjustment predicts an unrealistic level of traffic flow; whereas our suggested functional form forces traffic flow to remain below capacity.

Fig. 2
figure 2

Forecasted traffic flow for two motorway sections

Full size image

Finally, we proceeded to quantify uncertainty in the traffic forecasts. It is well known that there are three possible sources of error in traffic forecasting. The first one is input uncertainty, due to the fact that the future values of exogenous variables are unknown. The second one is random term uncertainty that accounts for the random disturbance in the demand equation. The third is coefficient uncertainty, due to using parameter estimates instead of true population values. The sum of the last two corresponds to model uncertainty.

To fix ideas, let us consider the following non-linear model:

$$ y = \Upphi (X,\beta ,\varepsilon ) $$
(11)

in which the dependent variable is, in general, a non-linear function of a set of explanatory variables, of a set of unknown β coefficients and of a random term ɛ. The forecasted values of the dependent variable are obtained by substituting the unknown terms by their respective estimates.

$$ \hat{y} = \Upphi (\hat{X},\hat{\beta },\hat{\varepsilon }) $$
(12)

In case we are dealing with a deterministic simulation, \( \hat{\varepsilon } \) is fixed in the expected value of ɛ, that is zero, \( \hat{\beta } \) is the estimated value of β, and \( \hat{X} \) is the assigned value of the explanatory variables.

In a stochastic simulation we assume that each of the elements of Eq. 11 follows a certain distribution. This is:

$$ \begin{gathered} X \sim Dist(\hat{X},\Upsigma_{{\hat{X}}} ) \hfill \\ \beta \sim Dist(\hat{\beta },\Upsigma_{{\hat{\beta }}} ) \hfill \\ \varepsilon \sim Dist(0,\Upsigma_{{\hat{\varepsilon}}} ) \hfill \\ \end{gathered} $$
(13)

M random realizations of such distributions are generated using a bootstrap methodology. The model is solved for each realization of those distributions. So, M forecasted values of the dependent variable are obtained. The empirical distribution of the forecasted values enables an expected value to be computed that is the arithmetical average. Using the empirical distribution, for a certain confidence level, it is also possible to compute upper and lower limits. The contribution to total uncertainty derived from the components could be calculated by subtraction. In this study all three types of uncertainty have been obtained through a stochastic simulation process.

To evaluate total forecast uncertainty we consider the distribution of \( \hat{y} \) after generating M realizations of X, β, ɛ.

To evaluate model forecast uncertainty we consider the distribution of \( \hat{y} \) after generating M realizations of β, ɛ; but holding the values of the explanatory variables X fixed at \( \hat{X} \).

Finally, input uncertainty can be computed from the difference between total forecast uncertainty and model forecast uncertainty.Footnote 9

Because the model is non-linear it should be noted that the empirical average of the stochastic simulations, in general, will not coincide with the deterministic simulation. Therefore, in non-linear models the deterministic simulation will offer a biased forecast.

In this study the model has been solved repeatedly for 1000 random draws of various components by using bootstraping method.

To illustrate the impact of uncertainty, we computed the 70% confidence interval for the traffic forecast of one of the motorway sections. As can be observed in Fig. 3, model uncertainty (dashed line) is relatively low and almost constant over time. However, once input uncertainty is added (solid line) the confidence interval widens and clearly increases over time. The second part of Fig. 3 shows the expected value of traffic for a deterministic forecast (dotted line), model uncertainty (solid line) and total uncertainty (dashed line). It can clearly be observed that the deterministic simulation will underpredict the average level of traffic flow.Footnote 10

Fig. 3
figure 3

Confidence intervals and expected traffic flow for one motorway section

Full size image

As previously mentioned and shown in Eq. 11, the model is non-linear and stochastic. Under these conditions, in general, the deterministic solution of a stochastic model will offer a biased estimate of the expected traffic value. Nonetheless, the expected value of the traffic forecast can be approximated by using the average of a set of stochastic simulations. Applying this approach to all the motorway sections in the sample, we found that the stochastic forecast for the year 2025 was on average 8.8% higher than the deterministic forecast.

Table 5 offers an order of magnitude of uncertainty for the same motorway section featured in Fig. 3. The coefficient of variation for total uncertainty ranges from 0.03 in the first forecasted year to 0.24 in the last. In the first few years, uncertainty is low and mainly explained by model uncertainty. However, as time goes by, total uncertainty increases due to lower precision in predicting the unknown values of exogenous variables.

Table 5 Coefficient of variation for total uncertainty and % explained by model and input
Full size table

Uncertainty effects on forecasting forgone revenue

An issue on the political agenda of the Spanish government is to remove tolls on certain motorways before the concession expires. In these cases, the government has had to compensate the private motorway concessionaire for the revenue forgone up to the end of the concession period. We selected one motorway section in the sample in order to compute the effect of uncertainty on the revenue to be forgone. The selected section was 20 kilometres in length with an average traffic value of around 12800 vehicles per day. We assumed that the concession period would expire in 2025.

The annual revenue was obtained by multiplying the predicted traffic by the average toll paid by 365 days a year.Footnote 11 This value is computed for each forecasted year from 2009 to 2025 and for each of the 1000 random draws. Next, we worked out the results by calculating the Net Present Value (NPV) of the revenue to be forgone along these 17 years at a discounting rate of 5%.

Finally, we analysed the empirical distribution of the NPV, which enabled us to calculate the mean and the confidence intervals for different significance levels. For the selected motorway section, the expected NPV of revenue is 123 million €. The minimum and maximum values for the confidence interval at 70% significance are 107 million € and 138 million €; when we compute the interval at 95% the figures are 94 million € and 155 million €. In the first case, the difference between the two extremes is 29%, whereas in the second it rises to 65%.

Figure 4 presents the empirical distribution of the NPV.

Fig. 4
figure 4

Distribution of the NPV of revenues foregone

Full size image

Quantifying uncertainty provides evidence that using point estimates to assess investments or public policies can lead to errors in the decision-making process. In this example, the negotiation process between government and concessionaire should include the probabilities associated with the different forecasted revenue values.

Conclusions

This article contributes to the literature on transport demand forecasting in three different ways: The proposal of a new methodology to account for capacity constraints in long term forecasting, the analysis of the role played by the different components of uncertainty, and the importance of using stochastic simulation techniques to avoid forecasting bias in non-linear models.

Firstly, the proposed functional allows handling existing restrictions on the capacity in those cases where it is not possible to jointly estimate the demand and supply side of the model. Our approach makes it possible to account for capacity constraints in long term forecasting without imposing an arbitrary functional form. This is achieved by specifying a dynamic model in which the speed of adjustment is related to the ratio between the actual traffic flow and the maximum capacity of the motorway. Furthermore, with this functional form, demand elasticity is not constant but depends on the degree of motorway use. As traffic increases, and approaches maximum capacity, demand becomes less sensitive to changes in the explanatory variables.

With respect to uncertainty, this article outlines the importance of developing stochastic simulations based on bootstrapping methodologies in order to obtain confidence intervals for the forecast. The results confirm that in the first few years model uncertainty explains most of the range of variation for the forecast traffic flow. However, as time goes by, whereas model uncertainty remains almost constant, input uncertainty steadily increases so that at the end of the forecasting period the last one accounts for almost 75% of total variability. Based on previous experiences and on the results of this article, it can be concluded that more effort must be made to improve model specification and to implement the necessary mechanisms to avoid bias in forecasting. Nevertheless, input uncertainty has proved to be the main factor for explaining uncertainty in the long run. Consequently, our study shows that forecasting explanatory variables deserves special attention. So it would be advisable to avoid introducing explanatory variables difficult to predict, although these variables might increase the level of adjustment of the model.

Finally, for non-linear models this article calls attention to the inadequacy of the deterministic simulation to forecast future traffic volumes. When dealing with non-linear models, the expected future traffic value can be approximated by averaging the different realizations of the variable using stochastic simulations. As an illustration, this article shows that the deterministic simulation at the end of the forecasting period underpredicts expected traffic flow across all motorway sections in the sample by on average 9% with a maximum difference of 12%.