Introduction

The development of processes for producing nanostructured polycrystalline materials has significantly increased interest in analyzing the sensitivity of the yield stress to the size of structural elements (grain diameter, microlayer thickness, etc.). Several features in the variation of mechanical properties in transfer from micro- to nanostructured state can be pointed out:

  1. 1)

    inverse Hall–Petch relation in the nanosized range resulting from sharp increase in the total surface area of interfaces and, thus, in the volume content of the ‘poor’ material associated with them [1,2,3,4,5,6, etc.];

  2. 2)

    transition, with decreasing grain size d, from hardening described by the Hall–Petch relation where ∆σ ~ d–1/2 to hardening where Δσ ~ d–1 even before transfer to nanostructured state [7,8,9,10,11];

  3. 3)

    potential for improving the quality of boundaries applying approaches proposed within interface engineering and, hence, producing extremely hardened state in the nanosized range (in fact, at the level of theoretical strength) [12, 13].

The objective of this paper is to consistently address the development of the above notions to obtain a generalized equation describing the yield stress versus gran sizes over a wide range (considering the state of grain boundaries and solid solution). The study individually focused on the hardening mechanisms for pure metals, lowdoped alloys, and multicomponent (Me–X) alloys, including high-entropy ones (HEAs). Additional options were analyzed for improving the properties of nanostructured materials through grain-boundary engineering (concentration of ‘useful’ impurities), which allows the strength to be brought to the level comparable with the maximum (theoretically) possible one (E/2π–E/30, where E is Young’s modulus).

Results and Discussion

Variation in Yield Stress in Transition from Micro- to Nanostructured State in Pure Metals and Low-Doped Alloys

Pure Metals. As indicated in the introduction, two grain-size ranges in which the effect of boundaries on strength can be described by different dependencies are usually distinguished. In the range of relatively large grains, the well-known Hall–Petch relation is obeyed [14, 15]:

$$ {\upsigma}_{\mathrm{y}}={\upsigma}_0+{k}_{\mathrm{y}}{d}^{-1/2}, $$
(1)

whose first term σ0 characterizes the averaged resistance to the slip of dislocations along the grains, and coefficient ky characterizes the resistance to the slip transfer through the grain boundary.

According to [16], the coefficient

$$ {k}_{\mathrm{y}}={\upsigma}_{\mathrm{s}}\sqrt{r} $$
(2)

accounts for the start stress σs of the dislocation source located at a certain distance r from the top of a flat dislocation pile-up in the neighboring grain.

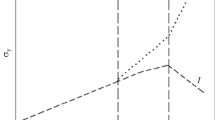
At grain sizes smaller than some critical value (~10 nm), there is a substantial deviation from Eq. (1), and the inverse Hall–Petch relation (Fig. 1) is often observed in the nanosized range when experimental data are plotted. To describe the inverse relation, a number of models have been proposed in which certain deformation mechanisms are predominant: grain-boundary plasticity (grain-boundary slip, diffusion plasticity at grain boundaries), twinning, and conventional slip of lattice dislocations [17,18,19,20,21,22,23,24,25,26,27,28,29, etc.]. Some of the models (for example, those provided in [25]) consider the competition of different deformation mechanisms since several mechanisms act simultaneously, as a rule, in actual materials. A potential change in the grain-size dependence of the yield stress (for example, in the transition from intracrystalline strain to intercrystalline strain) is shown in Fig. 2 [29].

Fig. 1.
figure 1

Grain-size dependence of copper yield stress [6]

Full size image
Fig. 2.
figure 2

Schematic transition from intracrystalline slip to intercrystalline slip with grain refinement [29]

Full size image

It should be noted that dislocation models assuming the presence of plastic flow carriers both as lattice and grain-boundary dislocations and as boundary intersection disclinations appear to be rather challenging. With such small grain sizes, stresses on the order of theoretical shear strength are required to activate dislocation sources; direct electron microscopy analyses indicate that there are no dislocations in the nanograins (see, for example, Fig. 3a). For this reason, models that are based on the representation of a nanocrystalline material as a two-phase composite consisting of intra- and intercrystalline phases (Fig. 3b) seem to be natural. The strength of such a composite can be calculated with the mixture rule [7, 19, 21, etc.].

Fig. 3.
figure 3

High-resolution electron-microscopy image of chromium deposited with magnetron sputtering [30] (a); composite nanomaterial structure (part of nanocrystals along the shear line) [21] (b)

Full size image

At the same time, it was noted in our papers [10, 11] that three rather than two grain-size ranges separated by two critical sizes (CS), dcr1 and dcr2, should be distinguished in analyzing the grain-size effect on the yield stress. In particular, the variation in the grain-boundary hardening mechanism should be considered in the submicron grain-size range before transfer to the nanosized range, which was noted in many studies [7,8,9, 33]. Hence, even Kocks noted in [7] that the following equation holds better than the Hall–Petch relation over a wide grain-size range:

$$ {\upsigma}_{\mathrm{y}}={\upsigma}_0+{k}_1{d}^{-1}. $$
(3)

Figure 4a shows very representative data obtained by Nokhrin et al. [34] for titanium grain refinement. An almost fivefold increase in ky was observed and the σ0 values were negative for the sharply ascending region of the σ(d) dependence, which seems to be incorrect. Figure 4b demonstrates the σ(d) dependence that we replotted according to Eqs. (1) and (3) for the experimental data provided in Fig. 4a. For convenient comparison with Fig. 4a, the dependence was plotted in the coordinates of Eq. (1). As is seen from Fig. 4b, the σ(d) dependence in the finegrain range (d ≤ 2.8 μm) plotted according to Eq. (3) agrees better with the experimental points.

Fig. 4.
figure 4

Grain-size dependence of the yield stress for titanium [34] (a) and dependence replotted by the authors according to Eqs. (1) and (3) (b)

Full size image

The change in the Hall–Petch parameter from d–1/2 to d–1 (i.e., compliance with Eq. (3)) is illustrated well by other numerous results: for example, for deformation-origin grains (deformation cells) [34]; for chromium coatings deposited by magnetron sputtering (0.1 μm ≤ d ≤ 5 μm grains) [30, 31]; and for the grain-size dependence of the fatigue limit determined by test [32].

In the above regard, besides the known critical grain size, dcr2, that was introduced previously and below which the Hall–Petch relation is inverse, we proposed [10, 11] critical grain size dcr1 for transition from Eq. (1) to Eq. (3). This transition is analyzed in detail in [11]. It is shown that critical grain size dcr1 can be determined by equating the right-hand sides of Eqs. (1) and (3):

$$ {d}_{\mathrm{cr}1}={\left({k}_1/{k}_{\mathrm{y}}\right)}^2. $$
(4)

This transition can be reached formally if we assume that the ky value is not a constant, but depends on the grain size according to the law

$$ {k}_{\mathrm{y}}={k}_1/{d}^{-1/2}. $$
(5)

Combining Eqs. (5) and (1), we can actually obtain Eq. (3).

In turn, Eq. (5) can be justified as follows. If ky is a constant in the Hall–Petch relation range (d ≥ dcr1), then it is obvious that the stress needed to activate the Frank–Reed source proportional to Gb/l (where G is the shear modulus, b is the Burgers vector, and l is the source length) becomes significantly dependent on the grain size at dcr1 ≤ d ≤ dcr1 since l cannot be larger than d. As r in Eq. (2) cannot exceed d either, Eq. (2) transforms to Eq. (5) with a fully logical assumption that l and r are proportional to d at d ≤ dcr1. Note that the grain-size dependence of ky is actually observed in the submicron grain-size range in accordance with Eq. (5) [32].

Therefore, there are at least three grain-size ranges separated by dcr1 and dcr2 in pure metals (singlecomponent materials), each range being characterized by its own σ(d) dependence. When the grains refine to dcr1, the σ1(d) dependence of the yield stress is described by the Hall–Petch relation (Eq. (1)); for the grain sizes varying from dcr1 to dcr2, the σ2(d) dependence is obeyed (Eq. (3)) (ky is not a constant here but depends on the grain size); and for the grain sizes smaller than dcr2, the yield stress (hardness) noticeably decreases, the inverse Hall–Petch relation described by the σ3(d) dependence being valid (Fig. 5).

Fig. 5.
figure 5

Three grain-size ranges divided by dcr1 and dcr2, each obeying its own σ(d) dependence

Full size image

To determine the σ3(d) dependence, we proposed the following equation in [10]:

$$ {\upsigma}_3=\left(1-{\left(\frac{d-t}{d}\right)}^2\right){\upsigma}_{\mathrm{b}}+{\left(\frac{d-t}{d}\right)}^2{\upsigma}_{\mathrm{CS}}, $$
(6)

where t is the grain-boundary thickness, σb is the grain-boundary strength, and σCS is the theoretical grain strength.

In deriving Eq. (6), we used the approach based on the mixture rule and considered that the volume content of the crystalline material was \( {\left(\frac{d-t}{d}\right)}^2 \) and the grain-boundary content was \( \left(1-{\left(\frac{d-t}{d}\right)}^2\right). \)

Since the strength of dislocation-free nanograins tends to the maximum possible (theoretical) value for a given material, it can be assumed that σCS corresponds to the theoretical strength, whose value ranges from E/2π to E/30 according to our paper [35]. It is reported in [18, 36], etc.] that the crystallite has some critical size at which conventional dislocation ductility and hardening mechanisms do not act and the grains acquire ideal strength. This grain critical size evaluated in [36] applying different approaches is smaller than 50 nm.

Equation (6) shows that the yield stress in the refinement of grains depends on the strength of their boundaries; in other words, the yield stress reduces with decreasing boundary strength, which is due to increase in the volume content of imperfect (so-called ‘poor’) material at grain boundaries and ternary intersections for singlecomponent materials.

In the paper [11], we combined Eqs. (1), (3), and (6) into one using the averaging integrals and obtained a generalized grain-size dependence of the yield stress accounting for change in the hardening mechanism in different grain-size ranges as follows:

$$ \upsigma (d)=\frac{1}{m_v}\underset{v1}{\overset{\infty }{\int }}{\upsigma}_1 Vf(V) dV+\frac{1}{m_v}\underset{v2}{\overset{\infty }{\int }}{\upsigma}_2 Vf(V) dV+\frac{1}{m_v}\underset{9}{\overset{v2}{\int }}{\upsigma}_3 Vf(V) dV, $$
(7)

where f(V) is the grain volume distribution function; \( {V}_1={d}_{\mathrm{cr}1}^3 \) and \( {V}_2={d}_{\mathrm{cr}2}^3 \) [33]. In doing so, we assumed that the f(V) function describing the grain volume distribution obeyed the lognormal law for polycrystalline materials. Hence, according to [25], the grain-size distribution function becomes

$$ f(d)=\frac{A}{s_{1,2}d\sqrt{2\uppi}}\exp \left(\frac{\ln (d)-\ln \left({d}_{\mathrm{cr}1,\mathrm{cr}2}\right)}{2{s}_{1,2}^2}\right), $$
(8)

where A = 1 = const and s1, 2 is the distribution dispersion for the first and second transitions. At \( {V}_1={d}_{\mathrm{cr}1}^3 \) and \( {V}_2={d}_{\mathrm{cr}2}^3 \), we have the grain volume distribution function, f(V).

According to Eq. (7), Hall–Petch relation (1) is obeyed if all grains that fit into this distribution are larger than dcr1, Eq. (3) holds for grain sizes ranging from dcr1 to dcr2, and Eq. (6) is met for grain sizes smaller than dcr2.

Note that the grain-size dependence of normalized hardness—hardness divided by Young’s modulus—should be obtained to analyze the level of hardening. This dependence is extremely convenient since the automated indentation (nanoindentation) technique allows hardness and Young’s modulus to be measured simultaneously at each experimental point. For transition from the H/E(d) dependence to the σ/E(d) dependence, the Marsh equation relating hardness HV to yield stress σ [37] can be used:

$$ \frac{HV}{\upsigma}=0.6\ln \frac{E}{\upsigma}+0.28+0.6\ln \frac{3}{4+\upnu}, $$
(9)

where E is Young’s modulus and σ is Poisson’s ratio.

The graphical H/E(d) dependences plotted in compliance with Eq. (7) using chromium as an example are provided in Fig. 6 (solid line). The following parameters were used to plot the dependence: σ0 = 0.22 GPa, σb = = 12 GPa, s = 0.3, ky = 1.6 · 10–2 GPa · mm1/2, t = 2 nm, dcr1 = 310 nm, and dcr2 = 67 nm. The experimental data points were obtained for chromium deposited by magnetron sputtering [12]. To describe the softening in singlecomponent materials, the grain-boundary strength σb at d < dcr2 was assumed to be lower than the grain strength and equal to E/50 and E/100, which is much lower than theoretical grain strength σCS (E/2π–E/30). When the grain size reduces to dcr2, the H/E(d) dependence is an ascending curve, which clearly shows the transition from the dependence described by Eq. (1) to Eq. (3) near dcr1 and good agreement with the experimental data points. In transition to the nanosized range (d < dcr1), a descending curve is inevitable for pure undoped metals, characterized by lower interface strength.

Fig. 6.
figure 6

Grain-size dependence of the hardness normalized to Young’s modulus for some strength values for the grain-boundary material: E/10 (a); E/30 (b); E/50 (c); E/100 (d) (point 1 corresponds to the values in films with 4.4 at.% O; PO2/PAr = 4.01 · 10–2) [38]

Full size image

At the same time, the transition from Eq. (1) to Eq. (3) may be unobservable on the experimental σ(d) dependence because of the rather narrow-scale X axis, insufficient number of the experimental data points, and great scatter of the data points. The incorrect choice of the resultant curve obtained by fitting the experimental data points to the σ(d) dependence is evidenced by increased ky, calculated from the Hall–Petch relation.

For example, ky calculated from the dependence (Fig. 7a) provided in [39] is 1750 MPa · nm1/2 for copper. If our generalized dependence, Eq. (7), is used to plot the curve with the same experimental data points considering two critical grain sizes (for contribution of ternary intersections at dcr1 = 20 nm and only for the Coble creep at dcr1 = 18 nm), then ky is equal to 1200 MPa · nm1/2 (Fig. 7b). Comparison of the dependences in Fig. 7a and Fig. 7b clearly shows that the experimental data points best agree with the resultant theoretical curves allowing for the existence of two critical grain sizes.

Fig. 7.
figure 7

Average grain-size dependence of the yield stress for pure copper: a) dependence from the paper [39] (the solid line considers diffusion at ternary intersections; the dashed line does not allowfor diffusion at ternary intersections; the straight dotted line is the classical Hall–Petch relation); b) dependence (a) replotted considering two critical grain sizes (curve 1 considers diffusion at ternary intersections; 2 does not allow for diffusion at ternary intersections)

Full size image

Low-Doped Alloys. It should be noted that Takeuchi [21] proposed a relation close to Eq. (6) to describe the σ3(d) dependence. However, Takeuchi considered only one option when the grain strength was, by definition, always higher than the grain-boundary strength and neglected the variant when the grain-boundary strength could be equal to or even higher than the grain strength. At the same time, unlike decrease in the yield stress (hardness) in the nanosized range for undoped pure metals, the composition and constitution of grain boundaries may change for commercial-purity materials and low-doped binary or multicomponent alloys; this change is accompanied by a substantial increase in the intergrain adhesion strength and, thus, in the yield stress.

We discussed this effect in the papers [12, 13], in which we proposed the concept of ‘useful’ impurities (the term was proven by Glikman back in 1972 [40]) for low-doped alloys. The main idea of the concept was that the intergrain adhesion strength might substantially increase through the segregation enrichment of the grain boundaries of metal M with impurity X so that the M–X bond energy became higher than the M–M bond energy. Doping elements possessing high heat of mixing with the solvent metal and substantially differing in atomic radii from the base metal can be regarded as such ‘useful’ impurities from this viewpoint. Small atoms can thus be displaced to the compressed regions at grain boundaries and large atoms to the elongated ones so that the weak places can be healed at grain boundaries. Oxygen in chromium and carbon in iron are examples of such ‘useful’ impurities.

According to Glikman, at the semiquantitative level, the tendency of an element to the enrichment of grain boundaries can be characterized by difference in the solid- and liquid-state solubility of doping elements, corresponding to the ratio of the first derivatives, ∂CL/∂c and ∂Cs/∂c (slopes of the liquidus and solidus curves), at the melting point of binary systems. This approach can be justified to some extent if the grain-boundary constitution is represented as a supercooled liquid model (Bilby model [41]).

In our papers [30, 31] focusing on chromium films deposited by magnetron sputtering, we also revealed sharp hardening in the same range (Fig. 8). The sharp increase in strength (hardness) of nanocrystalline chromium in accordance with our concept of ‘useful’ impurities [12, 13] results from the effect of interstitial oxygen atoms, which are ‘useful’ impurities for chromium as they have stronger chemical bonds with chromium atoms than the chemical bonds between the chromium atoms themselves. Oxygen segregation leads to a stronger (harder) shell from interfaces forming a cellular-like structure, softer plastic chromium grains being inside this structure (Fig. 3).

Fig. 8.
figure 8

Grain-size dependence of the yield stress for chromium deposited by magnetron sputtering [31, 32]

Full size image

Similar effects were found in [42] in hardening of the Fe–W condensates. The introduction of up to 0.3 wt.% W substantially refines the grains and increases the ky constant in the Hall–Petch relation as tungsten enriches the grain boundaries and does not dissolve in the grains. It is shown in [43] that severe shear deformation of surface layers of carbon steels leads to the ‘dissolution’ of cementite and carbon redistributes along the boundaries of emerging nanograins. The carbon enrichment of grain boundaries (carbon being a ‘useful’ impurity according to [40]) significantly increases the hardness, to 12 GPa and above; hence, the strength (hardness) increases almost threefold compared to pure iron with the same nanograin size [44].

Therefore, abrupt increase in the yield stress when the grain size becomes smaller than dcr2 is possible only in doped systems with an appropriate choice of components, allowing the grain-boundary strength to be increased. In single-component materials, grain refinement increases the volume content of imperfect material at the grain boundaries and ternary intersections and, thus, decreases the yield stress (hardness). Hence, the potential for hardening in grain refinement in single-component systems is limited. These both cases are well described by Eq. (7) and are clearly shown in Fig. 6. It is seen that the H/E ratio (or yield stress) may either increase or decrease depending on the grain-boundary strength at grain sizes smaller than dcr2.

Note also that the graphical H/E(d) dependence plotted in compliance with Eq. (7) can be used for tentative evaluation of the grain-boundary strength in the nanosized range. For example, comparison with the dependence shown in Fig. 6 and plotted with the data from [38] for magnetron-sputtered chromium films containing 4.4 at.% O and having 19.4 GPa hardness with 12 nm grains allowed us to evaluate the strength of grain-boundary material, being approximately equal to E/30 (respective point on curve b). These values approach the nanograin strength, which is close to the maximum possible (theoretical) strength for a given material in the absence of dislocations in nanograins.

At the same time, the σ(d) (H/E(d)) dependences plotted in accordance with Eq. (7) suggest that the state of the grain boundaries and solid solution remains unchanged; they actually correspond to constant σ0 and ky for each grain size, which is possible only for single-component materials of high purity. In the actual commercial-purity materials, the state of the grain boundaries and solid solution continuously varies and so do the ky and σ0 values with change in the grain size through heat treatment. In this regard, the construction of two bounding curves with limiting ky values seems to be more correct for plotting the generalized dependence and, in the case of potential change in the solid-solution state, two limiting σ0 values should be shown as well. All experimental data are located between the two curves, reflecting the difference in ky and σ0 for each grain size.

Figure 9 shows the grain-size dependences of hardness normalized to Young’s modulus in accordance with Eq. (7) using the bounding curves with E/30 and E/50 strength of the grain-boundary material for chromium and E/50 and E/500 for titanium. In the case of nanostructured magnetron-sputtered chromium films, the solubility of interstitial impurities in the solid solution is extremely low (for example, the maximum solubility of oxygen in chromium is only 0.04 at.% even at 1550°C [46]). Hence, the bounding curves should allow only for a potential change in the state of grain boundaries (i.e., ky). For titanium films, when not only ky but also σ0 changes, the bounding curves should also allow for change in σ0. The experimental limiting ky values (lower and upper curves) are 1.4 · 10–2 and 2.83 · 10–2 GPa · mm3/2 for chromium [30, 38] and 4 · 10–3 and 7.2 · 10–3 GPa · mm3/2 for titanium [46,47,48]. The σ0 values for titanium range from 0.2 to 0.47 GPa.

Fig. 9.
figure 9

Dependences of hardness normalized to Young’s modulus on the grain size of chromium and titanium at E/30 and E/50 strength of the grain-boundary material for chromium and E/50 and E/500 for titanium plotted using the bounding curves in accordance with Eq. (7); limiting ky values (lower and upper curves) are 1.4 · 10–2 GPa · mm3/2 and 2.83 · 10–2 GPa · mm3/2 [30, 38] for chromium and 4 · 10–3 GPa · mm3/2 and 7.2 · 10–3 GPa · mm3/2 [46,47,48] for titanium

Full size image

Hardening in Nanostructured Multicomponent Alloys

Solid-Solution Hardening in High-Entropy Single-Phase Alloys. In the last several years, multicomponent alloys containing at least five principle elements, content of each element varying from 5 to 35%, have been of great interest. These alloys are called high-entropy ones (HEAs) since they have high mixing entropy suppressing the formation of intermetallic phases and promoting the formation of a multicomponent solid solution with a simple crystalline structure (bcc, fcc, and bcc + fcc) in as-cast state. The high-entropy alloys feature high hardness, wear resistance, corrosion resistance, oxidation resistance, and high-temperature creep resistance [49,50,51,52,53,54,55,56].

The papers [52, 53] draw attention to abnormally high solid-solution hardening of HEAs, but the mechanisms of this hardening are not fully understood. For example, it is noted in [52] that the high hardness (5250 MPa) of the WNbMoTaV alloy with a bcc lattice can be due to a ‘nonobvious’ hardening mechanism. To evaluate the solid-solution hardening of the single-phase bcc TaNbHfZrTi alloy, Fleischer’s theory [57] (the alloy being regarded as a pseudobinary solid solution) is used in [53]. At the same time, we showed in [55, 56] that application of Fleischer’s theory was not possible to analyze the solid-solution hardening of the single-phase bcc AlTiVCrNbMo and fcc CrMnFeCoNi alloys.

The equiatomic bcc AlTiVCrNbMo alloy was used as an example in [55] to show that the HEA hardening is due to stronger temperature dependence of the critical shear strength and to abnormally high athermal hardening resulting from the Burgers vector component perpendicular to slip plane Δb = nb(Δa/a)av, where n ≈ 0.5, b is the Burgers vector, and (Δa/a)av = Σ[ci(ai–aexp)/aexp] is the averaged relative change in the HEA lattice parameter (ci and ai are the content and lattice parameter of an alloy element and aexp is the experimental lattice parameter of the alloy). The presence of this Burgers vector component leads to nonconservative elastic shear of dislocation regions.

To evaluate solid-solution hardening ∆H of high-entropy alloys, we proposed quite a simple equation allowing for the empirical (average) shear modulus and average lattice misfit parameter:

$$ \varDelta H={k}_{\mathrm{SSH}}\left.{\left(\varDelta a/a\right)}_{\mathrm{aV}}\right){G}_{\mathrm{aV}}, $$
(10)

where kSSH is the solid-solution hardening coefficient and Gav is the experimental (average) shear modulus.

Considering Eq. (10), hardness of the high-entropy alloy representing a single-phase substitutional solution is described in [55] as

$$ H={H}_{\mathrm{mix}}+\varDelta H={H}_{\mathrm{mix}}+{k}_{\mathrm{SSH}}\left(\varDelta a/a\right)\left.{}_{\mathrm{aV}}\right){G}_{\mathrm{aV}}, $$
(11)

where Hmix is the alloy hardness calculated with the mixture rule: Hmix = ΣciHi (ci and H are the content and hardness of an alloy element).

It is shown in [55, 56] that Eq. (10) holds well and kSSH is 1.5–1.6 for the bcc AlTiVCrNbMo alloy, fcc CrMnFeCoNi alloy, and several HEAs whose hardness was taken from the papers [53, 58].

Analysis of H0 and kH Parameters in Hall–Petch Relation for Single-Phase Multicomponent Alloys. To study the hardening of multicomponent solid solutions, including HEAs, it is of interest to analyze variation in the yield stress over a wide grain-size range. However, literature analysis has shown that research efforts are insufficient in this area and studies in the nanosized range are absent at all.

According to the paper [59], when the grain size varies from 3.9 to 26.2 μm, hardness of the single-phase high-entropy FeCrNiCoMn alloy corresponds to the classical Hall–Petch relation, though it has a relatively high kH coefficient:

$$ H={H}_0+{k}_H{d}^{-1/2}. $$
(12)

While the upper kH limit corresponds to ~600 MPa · μm–0.5 [60] for fcc metals, kH is 677 MPa · μm–0.5 for the above alloy. Therefore, the hardening of the grain boundaries in the FeCoNiCrMn alloy is apparently higher, which agrees with the idea of strong lattice distortion in HEAs. As a result, the dislocation line is not straight and dislocation slip is more complex than in conventional alloys.

Nevertheless, according to [61], just increase in the number of doping elements does not always makes the material harder. For example, addition of Co to pure Ni or FeNi insignificantly influences the hardening, while addition of Cr to NiCo and FeNiCo leads to great hardening. In other words, the nature of the added element is also important for hardening the equiatomic alloys. In general, there are the following factors that influence the solidsolution hardening: atomic size misfit and different elastic moduli of the alloy elements, change in the energy of stacking faults, and change in long-range or short-range ordering.

The paper [61] studied how microhardness HV of Ni and single-phase fcc NiCo, FeNi, NiCoCr, FeNiCo, and FeNiCoCr alloys changed with grain sizes varying from 150 to 25 μm. It is shown that Hall–Petch relation (1) is fully valid for this size range for the above alloys. The referenced paper also provides the H0 and kH values corresponding to Eq. (12) (Table 1).

Table 1. Values of the H0 and kH Parameters of Eq. (12), Shear Moduli Gexp [61], and Our Average Lattice Misfit Parameter Δa/aB for Ni and Some Binary and Multicomponent Alloys
Full size table

To process and analyze the results obtained in [61], we calculated the following characteristics: averaged lattice parameter of alloy aB = Σciai (ai is the fcc lattice parameter of an element) and averaged relative change in the alloy lattice parameters (Δa/aB)av = Δci(ai – aB)/aB. The fcc lattice parameter of chromium was determined with regard to transformation of its bcc lattice with a = 0.2885 to fcc lattice [62]. The correction factor was the bcc-to-fcc ratio for iron in its transition from the bcc to fcc lattice at 1183 K: \( {a}_{\mathrm{Fe}}^{\mathrm{BCC}}/{a}_{\mathrm{Fe}}^{\mathrm{FCC}} \) 2.8663/3.57 = 0.803 [53, 55]. The fcc lattice parameters for Cr and Fe, as well as for Ni and Co [62], are provided in Table 2.

Table 2. FCC Lattice Parameter a for FeNiCoCr Alloy Elements
Full size table

Our analysis shows that there is a linear dependence (Fig. 10) between the H0 and kH parameters obtained in [61] and the (Δa/a)av · G parameter included in Eq. (11) to evaluate solid-solution hardening ΔH for the singlephase fcc FeNi, NiCoCr, FeNiCo, and FeNiCoCr alloys (NiCo alloy was not considered as it is prone to twinning). Noteworthy is also that H0 increases by approximately a factor of two and kH by a factor of four when (Δa/a)av · G changes from ~0.2 to ~0.9. This allows us to assume that there is a specific hardening mechanism peculiar only to multicomponent solid solutions.

Fig. 10.
figure 10

Dependence of the H0 (a) and kH (b) [60] parameters included in Eq. (11) on Δa/aB · G

Full size image

Potential Changes in Yield Stress of Multicomponent Solid Solutions in Transition from Micro- to Nanostructured State. As is noted, the experimental data on variation in the yield stress in multicomponent solid solutions in transition from micro- to nanostructured state are still, unfortunately, missing in the literature. Hence, below is an assumption on potential features of this variation based on the above analysis of available data.

It is apparent that a somewhat different hardening mechanism may act in multicomponent systems (containing five or more doping elements) compared to low-doped alloys: even if grain boundaries are not rich in one predominant element, microscopic redistribution of different-size atoms forming the grain boundary may occur. For example, smaller atoms move to compressed regions and larger atoms to elongated ones, the boundary energy decreasing and density equalizing. Slip transfer through these boundaries is significantly hampered and will be accompanied by increase in kH.

It should also be noted that the H0 parameter significantly increases under the abnormal solid-solution hardening mechanism.

Generalized Schematic Dependence of Yield Stress on Grain Size for Pure Metals, Low-Doped Alloys, and Multicomponent Solid Solutions

According to the above analysis, a generalized schematic dependence is provided in Fig. 11 for pure metals, low-doped alloys, and multicomponent solid solutions to describe variation in the yield stress of polycrystals in transition from micro- to nanostructured state. The grain refinement in single-component materials (curve 1) to below dcr2 involves a noticeable decrease in the yield stress (hardness), i.e., leads to the inverse Hall–Petch effect. The σ0 and ky parameters (like H0 and kH) remain unchanged.

Fig. 11.
figure 11

Schematic grain-size dependence of yield stress σ: curve 1) for pure metals; lower bounding curve 2 and upper bounding curve 3) for low-doped alloys; and curve 4) for multicomponent solid solutions

Full size image

Significant hardening or, conversely, substantial softening can be observed in low-doped alloys, where the state of grain boundaries is largely determined by the segregation of the doping element along them, depending on whether the impurities are ‘useful’ or ‘poor’. Since the σ0 and ky parameters (like H0 and kH) may undergo changes, Fig. 11 shows two bounding curves (lower curve 2 and upper curve 3), corresponding to their minimum and maximum values.

Concerning multicomponent solid solutions (upper bounding curve 4), they show a specific hardening mechanism. The σ0 and ky parameters (like H0 and kH) may vary with grain refinement because of microscopic redistribution of different-size atoms forming the grain boundaries.

It should be noted that the maximum possible hardening of multicomponent solid solutions, ranging approximately from E/2π to E/30 according to our paper [35], will be ultimately determined (as is the case of lowdoped alloys) by their elastic modulus E.

Conclusions

According to the theoretical analysis, we have proposed a generalized schematic dependence of the yield stress of polycrystals on grain sizes, σ(d), over a wide range, with σ(d) variation for pure metals (1), low-doped alloys (2), and multicomponent solid solutions (3), including high-entropy alloys (HEAs).

The general shape of the σ(d) curves and the potential for options (1), (2), and (3) are determined by the state of the grain boundaries and the solid solution––actually by the σ0 and ky parameters (or H0 and kH) included in the Hall–Petch relation (or variant of Hall–Petch equation, H = H0 + kHd–1/2).

In transition from micro- to nanostructured state, at least three grain-size ranges separated by dcr1 and dcr2 critical sizes are observed, the grain-size dependence of the yield stress being qualitatively different in each range.

When grain sizes decrease below dcr1 (even before transfer to nanostructured state), the Hall–Petch parameter changes from –1/2 to –1, which is due to the absence of dislocation pile-up inside the grains. This transition can be reached formally if the ky coefficient in this equation becomes dependent on the grain size at dcr2 < d < dcr1.

The grain refinement in single-component materials to below dcr2 involves a noticeable decrease in the yield stress (hardness), i.e., the inverse Hall–Petch effect. The σ0 and ky parameters (or H0 and kH) remain unchanged.

The state of grain boundaries in low-doped alloys is largely determined by segregation of the doping element along them. Significant hardening or, conversely, substantial softening can be observed depending onwhether the impurity is ‘useful’ or ‘poor’ at grain sizes below dcr2. The σ0 and ky parameters (or H0 and kH) may undergo changes. The concept of ‘useful’ impurities has been proposed to bring the strength of nanostructured materials to the level comparable with the maximum (theoretically) possible one (E/2π–E/30).

A somewhat different hardening mechanism may act in multicomponent systems (containing five or more doping elements) compared to low-doped alloys: even if grain boundaries are not rich in one predominant element, microscopic redistribution of different-size atoms forming the grain boundary may occur, smaller atoms moving to compressed regions and larger atoms to elongated ones. The boundary energy decreases and density equalizes in the process. Slip transfer through these boundaries will be significantly hampered and accompanied by increase in ky (kH).

An important factor for multicomponent solid solutions is that the σ0 (H0) parameter significantly increases because of abnormal solid-solution hardening. Noteworthy is that the dependence of H0 on the (Δa/a)av · G parameter is linear. The dependence of kH on (Δa/a)av · G is even stronger: while the H0 parameter increases by approximately a factor of two when (Δa/a)av · G changes from ~0.2 to ~0.9, the kH parameter increases by a factor of four. We assume that this is due to a new specific mechanism peculiar to multicomponent solid solutions.