Introduction

Atmospheric pressure glow discharges are of interest as plasma sources for a number of technological applications, including plasma decontamination and sterilization, biomedical applications, material processing, modification of electromagnetic waves propagation, and plasma aerodynamics [1–3]. The glow discharge is normally obtained at low-gas pressures, but it can be maintained in a similar form if the pressure is increased up to and above the atmospheric value [2–11]. The experimental data show that both low and high-pressure glow discharges are characterized by a non-equilibrium distribution of energy among the different degrees of freedom of the plasma species [5–10]. Usually each energy distribution can be described by a characteristic temperature; such as the electron temperature (T e), vibrational temperature (T v), rotational temperature (T r), and translational (gas) temperature (T g). In non-equilibrium plasmas created by externally applied electric fields, typically Te > T v > T r = T g [6–8]. The non-equilibrium state allows for the creation of active species without generating excessive heat. However, at pressure levels of the order of the atmospheric value, a strong non-equilibrium plasma state is hardly to maintain due to the thermalization of the discharge, which leads to a sudden (or continuous [4]) transition from the glow to the arc phase [12–15]; being the final stage closer to the thermodynamic equilibrium. The transition is characterized by an increase in the current density and a considerable fall in the discharge voltage (due to the switching of secondary electron emission to thermionic emission of electrons from the cathode surface).

The discharge thermalization typically arises due to the so called thermal instability [12, 16], which results in a rapid increase in the gas temperature. Generally, the thermal instability can be prevented if the gas residence time in the discharge is small compared with the heating time (which is determined by the rate of energy transfer from the electrons to the translational degree of freedom of the heavy particles). In atomic gases the main mechanism of gas heating is by elastic collisions. For reduced electric fields E/N > 30 Td (where E is the electric field strength, N the gas number density and 1 Td ≡ 10−21 V m2), the fractional electron power transferred in elastic collisions to gas heating is less than a few times 10−3 [17]. In molecular gases, however, electrons can transfer energy to internal energy states of the molecule, such as the vibrational mode. Since for 30 < E/N < 50 Td the typical electron temperatures in molecular gases (of about 1 eV) are comparable to the characteristic vibrational energy values (0.2–0.5 eV) of the molecules, most of the electron energy (~80 to 98 %) is transferred to vibrational modes, and then partially to gas heating, mainly through the mechanism of vibrational–translational (V–T) relaxation [17, 18]. As inelastic losses are usually greater than elastic ones by one to two orders of magnitude [16], molecular gases typically have higher heating rates and are more susceptible to thermalization than atomic gases. This is due to the strong exponential dependence of the V–T relaxation rate coefficient on the gas temperature. Even small increases of the gas temperature lead to a significant increase of the V–T relaxation rate, intensification of heating, and then to a further growth of the gas temperature. This process takes typically a relatively long time (~100 µs) in nitrogen gas at atmospheric pressure [18].

In direct-current (dc) glow discharges at atmospheric pressure, high-speed gas flows have been used to provide sufficient cooling of discharges at high pressures [19, 20]. If the gas residence time in the discharge is small as compared with the V–T relaxation time, the gas heating is almost suppressed and the molecular gas is in a strongly non-equilibrium state. This state is characterized by a level of vibrational energy that considerable exceeds its equilibrium value. On the other hand, for discharge conditions such that the gas residence time in the discharge is larger than the V–T relaxation time (e.g., still discharges), the molecular gas changes to a state close to the thermodynamically equilibrium one, with a higher gas temperature as in an arc discharge.

In [21], experimental information on the properties of the atmospheric pressure constricted discharge in a longitudinal nitrogen flow was published. A steady-state pin-to-plane glow discharge was generated inside a tube where a flow of nitrogen was injected up to a velocity of 20 m/s. The inter-electrode gap was 15 mm. The results showed that the gas flow rate has a strong influence on the properties of the discharge.

In [22, 23], atmospheric pressure glow discharges in a fast longitudinal flow of air and nitrogen plasmas were investigated. The nitrogen gas was preheated up to 1800–2250 K and then was injected through a nozzle in the discharge region at a velocity of about 450 m/s. A glow discharge was ignited between two needle electrodes oriented along the axis of the gas stream, and separated a distance of 3.5 cm. The discharge current was I < 250 mA. Owing to the fast gas flow rate the gas temperature remained practically constant in the discharge region.

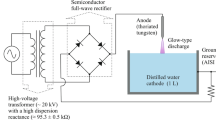
In [24], an atmospheric pressure glow discharge in a slow longitudinal flow of nitrogen plasma was investigated. Nitrogen was injected through a flow straightener and passed through the discharge region with a velocity of only 20 cm/s. The glow discharge was formed between a pair of platinum pins (separation 0.85 cm) that were vertically mounted along the axis of the gas stream. The discharge was maintained by a dc power supply (I < 250 mA) in a ballasted circuit. The radial profile of the N2 + concentration and the values of the gas rotational temperature were experimentally inferred for currents I = 52, 97, 142 and 187 mA. Peak (centerline) density values around 1018 m−3 and high-rotational temperature values (obtained from Boltzmann plots), ranging from 3100 to 4700 K, were measured in the given current range.

In contrast to the relatively large number of works devoted to the experimental characterization (mainly spectral and electrical characteristics of constricted discharges) of atmospheric pressure glow discharges in nitrogen (with flowing gas and with still gas) [2–11, 21–24], there are only few published investigations on the energy balance and charged particles kinetics relevant to the sustaining of the non-equilibrium state.

In [25], a one-dimensional model of a dc glow discharge with variable nitrogen flow rates (velocities up to 20 m/s) at atmospheric pressure for a low-current regime (I = 5 mA) and for a high-current regime (I = 40 mA); was presented. The results showed that the charged particle generation in both current regimes was mainly controlled by associative ionization involving molecular metastable states, although marked differences in the calculated plasma composition were found. For I = 5 mA the dominant ion was N3 + while for I = 40 mA was N+. Owing to the extremely low value of the recombination coefficient for atomic ions, the dynamic balance of the charged particles was non-local (with a large diffusion of the atomic ions) for the larger current value, while for the lower current value was local (volume electron-ion recombination). However, it should be noted that the calculated composition for I = 40 mA was not consistent with the measured results [24]; which indicated that the dominant ion under similar plasma conditions was the molecular one. In [26], another model for non-equilibrium nitrogen plasmas was presented. The rate constants of reactions involving electrons were obtained by averaging the corresponding cross sections with the Maxwellian electron energy distribution function (EEDF). The obtained results suggested that the vibrational temperature was well approximated by the gas temperature at low electron number densities and by the electron temperature at high electron number densities (thus indicating that the plasma switches from a regime where the vibrational levels are mainly equilibrated by collisions with heavy particles to another regime where they are equilibrated by collisions with electrons). In [27], a simplified chemical kinetic model of a slightly-ionized atmospheric pressure nitrogen discharge was given. No energy balance equation was used and the temperature of the species was imposed. The model was tested against calculations of Saha–Boltzmann equilibrium state, and a reasonable good agreement was achieved. It was found that in equilibrium conditions the electrons are produced by associative ionization involving atoms.

In this work, a model of an atmospheric pressure nitrogen glow discharge in high-gas temperature regimes (simulating the conditions of [24]) is proposed. The model includes a fairly complete set of chemical reactions and describes the processes of the energy balance and charged particles kinetic processes governing the discharge. The major difference between the model [25] and that used in this work is the inclusion of several processes with the participation of electronically exited nitrogen atoms. The results of calculations are compared with the available experimental data [24] and a good agreement is found.

The Model

The model includes the continuity equations for the most important neutral and charged species present in the nitrogen discharge together with the balance equations describing the mean-vibrational energy of the nitrogen molecules and the gas kinetic energy. The numerical calculations were done under the assumption that p = 1 atm, (where p is the gas pressure). The considered species for pure nitrogen are the vibrational manifold of ground state molecules N2(X 1∑ +g , v), the electronic excited states of nitrogen molecules N2(A 3∑ +u ), N2(B 3Πg), N2(a′1∑ −u ) and N2(C 3Πu), the electronic exited states of nitrogen atoms, N(2D) and N(2P), the atomic ground state N(4S), the positive ions N4 +, N3 +, N2 + and N+; and the electrons (e). The continuity equations for the active species were solved for the densities of N2(A 3∑ +u ), N2(B 3Πg), N2(a′1∑ −u ), N2(C 3Πu), N(2D), N(2P), N(4S), N4 +, N3 +, N+ and electrons. The density of the dominating sort of positive ions N2 +, was obtained from the condition of charge conservation (the electrodes sheaths were not included in the calculations) while the density of the dominant species N2(X 1∑ +g , v) was obtained from the constancy of the pressure. The continuity equations for the plasma particles were solved in a local approximation

$$ \frac{\partial }{\partial t}\left( {Y_{i} } \right) = \sum\limits_{j} {S_{ij} } , $$
(1)

where Y i is the number density and S ij is the rate of production of the ith species in the jth reaction (negative if the species is destroyed). In high-pressure plasmas this approximation is usually justified by the long time scale for diffusive losses (inversely proportional to the collision rate) compared with the relatively short time scale to achieve local equilibrium (proportional to the collision rate) [16]. The time scales for diffusive losses for charged and neutral particles may be estimated as R 2/D ea and R 2/D; where R is the radius of the discharge column, D ea is the coefficient of ambipolar diffusion of electrons in the presence of multiple ions, and D is the coefficient of diffusion of neutral species. The ambipolar diffusion D ea can be estimated in a simplified fashion in terms of the mobility μp of N2 + only, the dominating sort of positive ions in nitrogen under the considered conditions. According to [28], μp = 4.51 × 1021/N m2/V s. For T g ~ 4000 K and T e ~ 9000 K, it results D ea ~ 2.8 × 10−3 m2/s. The neutral diffusion coefficient D can be estimated for the N(2 P) atoms as D = 0.185 × 10−4 (T g/273)3/2 m2/s [18]. For the gas temperature T g ~ 4000 K D is about 1 × 10−3 m2/s. For the conditions of [24] the discharge radius is R ≈ 1.4 mm. It follows that the time scales of diffusive losses for charged and neutral species are about 7 × 10−4 and 2 × 10−3 s; respectively. Such a diffusion time values can be compared with the corresponding time scale to achieve local equilibrium. For instance, the time scale for loss of electrons by volume electron-ion recombination (estimated as (β Ne)−1, where β = 1.8 × 10−13 (300/T e)0.39 m3/s [29]) is about 1 × 10−5 s for an electron density Ne ~ 1018 m−3. The time scale for deactivation of N(2 P) by collisions with N2(X), whose rate coefficient is k(N(2 P) − N2) = 6.0 × 10−20 m3/s [30] may be estimated as (k(N(2 P) − N2) N2(X))−1. It results 8 × 10−6 s for the conditions of [24]. It follows that the diffusion losses plays only a minor role in the experimental conditions analyzed in this work and can be neglected. Also, for conditions as in [24], the motion of the gas has no appreciable effect on the discharge characteristics, since the influence of a longitudinal flow at velocities less than 50 cm s−1 is rather weak [31].

The model takes into consideration 52 elementary reactions that influence gas heating, excitation and de-excitation of vibrational and electronic states of nitrogen, dissociation due to electron and heavy particle impact, generation and loss of the charged particles due to direct, stepwise and Penning/associative ionization; and volume electron-ion recombination. The complete set of these processes is summarized in Table 1 (T g and T e units are in K). The rates for almost all processes are known in the literature and are widely used for nitrogen non-equilibrium discharge modelling (see, for instance, [25, 32]). However, the ionization reactions

$$ \begin{aligned} {\text{N}}_{2} \left( {A^{3} \sum {_{u}^{ + } } } \right) + {\text{N}}_{2} \left( {a^{\prime 1} \sum {_{u}^{ - } } } \right) & \to {\text{N}}_{4}^{ + } + {\text{e}} \\ & \to {\text{N}}_{2}^{ + } + {\text{N}}_{2} + {\text{e}} \\ \end{aligned} $$
(2)

and

$$ \begin{aligned} {\text{N}}_{2} \left( {a^{\prime 1} \sum {_{u}^{ - } } } \right) + {\text{N}}_{2} \left( {a^{\prime 1} \sum {_{u}^{ - } } } \right) & \to {\text{N}}_{4}^{ + } + {\text{e}} \\ & \to {\text{N}}_{2}^{ + } + {\text{N}}_{2} + {\text{e}} \\ \end{aligned} $$
(3)

according to reactions (R12)–(R15) in Table 1, have been considered as Penning [33] or associative [32] ionization (i.e., producing N2 + + N2 + e or N4 + + e, respectively) owing to the lack of experimental data. In the present calculation a branching ratio of 0.5 for each of the two possible products of ionization via (2) and (3) was assumed. The same assumption was taken in [34].

Table 1 Plasma processes (Ri) and their rate coefficients and applicable references
Full size table

The model approximation for the vibrational energy distribution function (VEDF) for N2(X 1∑ +g , v) was assumed as in [25]. The VEDF was divided into three groups. The first vibrational levels (v ≤ v 1) closely follow a Boltzmann distribution with temperature T v [17]. For the middle vibrational levels (v 1 < v ≤ v 2) it was assumed the existence of a ‘plateau’ where f(v) ∼ 1/(v + 1); where v 1 and v 2 are the left and right boundaries of the plateau. After the plateau (v > v 2) there is a sharp slope in the VEDF due to fast V–T relaxation from high-vibrational levels. This slope is characterized by a Boltzmann distribution with temperature T g. The width of the plateau decreases with an increase in the gas temperature [18]. The dependence of the right boundary of the plateau on the gas temperature was denoted as v 2 ∼ exp(−(T g − 300)/3000) [25]. Hence, the VEDF was finally written as:

$$ \left. {\begin{array}{*{20}l} {{\text{N}}_{2} \left( {X,v} \right) = {\text{N}}_{2} \left( {X,v = 0} \right)\exp \left( { - v\frac{\hbar \omega }{{kT_{\text{v}} }}} \right),\quad 0 < v \le v_{1} ;} \hfill \\ {{\text{N}}_{2} \left( {X,v} \right) = {\text{N}}_{2} \left( {X,v = v_{1} } \right)\frac{{v_{1} + 1}}{v + 1},\quad v_{1} < v \le v_{2} ;} \hfill \\ {{\text{N}}_{2} \left( {X,v} \right) = {\text{N}}_{2} \left( {X,v = v{}_{2}} \right)\exp \left( { - (v - v_{2} )\frac{\hbar \omega }{{kT_{\text{g}} }}} \right),\quad v > v_{2} ;} \hfill \\ {v_{1} = 9,\quad v_{2} = v_{1} + (35 - v_{1} )\exp \left( { - \frac{{T_{\text{g}} - 300}}{3000}} \right);} \hfill \\ \end{array} } \right\} $$
(4)

where k is the Boltzmann constant and \(\hbar \omega\) is the vibrational quantum (=0.29 eV) for the nitrogen molecule. Note that the harmonic oscillator model was employed in (4).

The calculation of the rate coefficients for electron-impact excitation (R1)–(R6), dissociation (R7) and ionization (R8); was based on finding the EEDF by means of a solution of the electron Boltzmann equation in the classical two-term approximation with the BOLSIG+ code [35]. The corresponding cross sections were taken from [36]. The effect of the superelastic collisions with vibrationally excited molecules on the processes with high energy threshold (electronic excitation, dissociation and ionization) was accounted for in the BOLSIG+ code by setting the excitation temperature as T v and the transition energy as the first vibrational threshold (0.29 eV) when solving the Boltzmann equation. Note that the BOLSIG+ code solves the electron Boltzmann equation in a homogeneous electric field within uniform and steady conditions. This assumption is valid as long as the relaxation time for achieving a steady state EEDF is short compared with the characteristic time of discharge development, and the length of the electron energy relaxation is much smaller than the effective discharge radius. Under the present conditions the EEDF relaxation time is ν −1u  ~ 10−9 s (e.g., [18], figure 4.1), which is much smaller than the integration time of (1) to achieve steady conditions (~10−3 s). Furthermore, the length of electron energy relaxation is much smaller than the effective discharge radius under conditions typical of molecular plasmas at atmospheric pressure (e.g., [31]). This means that the EEDF is governed by local values of the reduced electric field E/N, the mixture composition, and the vibrational temperature T v; which characterizes the first vibrational levels of the VEDF.

The conditions of vibrational excitation also facilitate the dissociation of the nitrogen. The dependence of the rate of the reaction (R51) (thermal dissociation of N2(X 1∑ +g , v)) on T v was taken into account through the Macheret–Fridman model [37–39]

$$ \begin{aligned} Z\left( {T_{\text{g}} ,T_{\text{v}} } \right) = \frac{{1 - \exp \left( { - \frac{3354}{{T_{\text{v}} }}} \right)}}{{1 - \exp \left( { - \frac{3354}{{T_{\text{g}} }}} \right)}}\left( {1 - L} \right)\exp \left( { - 113200\left( {\frac{1}{{T_{\text{v}} }} - \frac{1}{{T_{\text{g}} }}} \right)} \right) + L\,{ \exp }\left( { - 113200\left( {\frac{1}{{T_{\text{a}} }} - \frac{1}{{T_{\text{g}} }}} \right)} \right); \hfill \\ T_{\text{a}} = \alpha T_{\text{v}} + (1 - \alpha )T_{\text{g}} ;\quad L = \frac{2(1 - \alpha )}{{\pi^{2} \alpha^{3/4} }}\left( {\frac{{T_{\text{g}} }}{113200}} \right)^{3/2 - n} \left( {1 + \frac{{7\left( {1 - \alpha } \right)\left( {1 + \sqrt \alpha } \right)T_{\text{g}} }}{2 \times 113200}} \right) \hfill \\ \end{aligned} $$
(5)

where α = (mA/(mA + mB))2 (mA is the mass of an atom in the dissociating molecule and mB is the mass of an atom in the impinging molecule) (=0.25) for the reaction (R51) and n (=−1.5) is the exponent for the temperature T g in the pre-exponential factor of the Arrhenius form for the rate coefficient of the process (R51). Such a model was found to be the most accurate for nitrogen dissociation under non-equilibrium conditions in a recent study [40].

The rate coefficient of the three-body reaction (R52) (the inverse of the thermal dissociation process) was calculated by using the principle of detailed balance; being the corresponding equilibrium constant K 52(T g) ≡ [N2(X)]/([N(4 S)] [N(4 S)]). The partition function of the molecules for non-equilibrium conditions was calculated according to the method proposed in [41] using the molecular parameters taken from [42]. The atomic partition function was calculated by using the simplified approach presented in [43].

The rate coefficients for stepwise ionization from N2(A 3∑ +u ), N2(B 3Πg) and N2(a′1∑ −u ) (R9)–(R11) have been calculated from the cross section data reported in [44] by using the EEDF calculated with the help of BOLSIG+. The electronic excitation by electron impact was assumed to occur only from the vibrational ground state N2(X 1∑ +g , 0) (the rate coefficients for electronic excitation, dissociation and ionization from N2(X 1∑ +g , v) were assumed to be the same as those from N2(X 1∑ +g , 0)) [17].

The mean-vibrational energy ε v of the N2(X 1∑ +g , v) molecule was described by the energy balance equation

$$ \frac{\partial }{\partial t}\left( {{\text{N}}_{2} \left( X \right)\varepsilon_{\text{v}} } \right) = \eta_{\text{v}} \sigma E^{2} - {\text{N}}_{2} \left( X \right)\frac{{\varepsilon_{\text{v}} - \varepsilon_{\text{v}} \left( {T_{\text{g}} } \right)}}{{\tau_{\text{VT}} }} - 2 \times Q_{\text{D}} , $$
(6)

where η v is the fraction of the energy input transferred to the vibrational excitation of N2(X 1∑ +g , v) and σ is the electrical conductivity of the plasma. The mean vibrational energy of the nitrogen molecule was related to T v as εv = \(\hbar \omega\)/[exp(\(\hbar \omega\)/(kT v)) − 1]; being εv(T g) its equilibrium value. τVT is the time scale of the V–T energy relaxation by molecules and atoms collisions. At values of the reduced electric field E/N = 25–35 Td, realized in conditions similar to that of experiment [24], η v may be estimated with the help of the BOLSIG+ code as ~0.97 (e.g., [16], figure 5.11). A similar approach was used in [25, 45]. As the BOLSIG+ code only considers excitation reactions of the first vibrational levels (v ≤ 8), it might result in underestimated values of this parameter. However, under the conditions of [24] it is expected that the excitation reactions with v > 8 play only a minor role [17]. The term 2 Q D accounts for the rate of vibrational energy loss due to the loss of oscillators during strong vibrational non-equilibrium

$$ Q_{D} = \varepsilon_{D} \left( {Z\left( {T_{\text{g}} ,T_{\text{v}} } \right)k_{51} {\text{N}}_{2} \left( {X^{1} \sum {_{g}^{ + } } ,v} \right)^{2} - k_{52} {\text{N}}_{2} \left( {X^{1} \sum {_{g}^{ + } } ,v} \right){\text{N}}\left( {^{4} S} \right)^{2} } \right), $$
(7)

where ε D ~ 9.76 eV is the dissociation energy of the nitrogen molecule. Half of this energy relaxes into kinetic energy [38]. The calculation of τVT included collisions with vibrational ground state molecules as well as with dissociated ground state atoms, in according to the following processes

$$ {\text{N}}_{2} \left( {X^{1} \sum {_{g}^{ + } } ,0} \right) + {\text{N}}_{2} \left( {X^{1} \sum {_{g}^{ + } } ,1} \right) \to {\text{N}}_{2} \left( {X^{1} \sum {_{g}^{ + } } ,0} \right) + {\text{N}}_{2} \left( {X^{1} \sum {_{g}^{ + } } ,0} \right), $$
(8)
$$ {\text{N}}\left( {^{4} S} \right) + {\text{N}}_{2} \left( {X^{1} \sum {_{g}^{ + } } ,1} \right) \to {\text{N}}\left( {^{4} S} \right) + {\text{N}}_{2} \left( {X^{1} \sum {_{g}^{ + } } ,0} \right), $$
(9)

being the corresponding rate coefficients [18]

$$ k_{{N_{2} }}^{10} \left( {{\text{m}}^{3} / {\text{s}}} \right) = 7.8 \times 10^{ - 18} T_{\text{g}} \exp \left[ { - \frac{218}{{T_{g}^{1 /3} }} + \frac{690}{{T_{g} }}} \right]\left( {1 - \exp \left( { - \frac{\hbar \omega }{{kT_{g} }}} \right)} \right)^{ - 1} , $$
(10)

and

$$ k_{N}^{10} \left( {{\text{m}}^{3} / {\text{s}}} \right) = 2.3 \times 10^{ - 19} \exp \left[ { - \frac{1280}{{T_{g} }}} \right] + 2.7 \times 10^{ - 17} \exp \left[ { - \frac{10840}{{T_{g} }}} \right]. $$
(11)

The time scale of the V–T energy relaxation was calculated as [18]

$$ \tau_{\text{VT}} = \left[ {\left( {1 - \exp \left[ { - \frac{\hbar \omega }{{kT_{g} }}} \right]} \right)\left( {k_{{N_{2} }}^{10} {\text{N}}_{2} \left( {X,0} \right) + k_{N}^{10} {\text{N}}\left( {^{4} S} \right)} \right)} \right]^{ - 1} . $$
(12)

For the conditions of [24] the diffusion time of the nitrogen molecule is about 2 × 10−3 s; which is significantly larger than the V–T relaxation time (~100 μs) under the considered conditions. That is, all the vibrational-excited molecules transform energy into heat within the discharge zone. The translational temperature of the gas was described by the equation

$$ \frac{\partial }{\partial t}\left( {{\text{N}}_{2} \left( X \right)C_{\text{p}}^{*} T_{\text{g}} } \right) = Q{}_{\text{R}} + Q_{\text{D}} + {\text{N}}_{2} \left( X \right)\frac{{\varepsilon_{\text{v}} - \varepsilon_{\text{v}} \left( {T_{\text{g}} } \right)}}{{\tau_{\text{VT}} }} - \lambda^{*} \frac{{\left( {Tg - T_{\infty } } \right)}}{{R_{\text{th}}^{2} }}, $$
(13)

where \( C_{\text{p}}^{*} \) is the heat capacity at constant pressure per molecule, Q R is the ‘fast’ gas heating rate term, λ* is the gas thermal conductivity, T ∞ is the ambient gas temperature (=300 K) and R th is the radial length-scale for the variation of T g. The material quantities \( C_{\text{p}}^{*} \) and λ* were calculated by subtracting from the equilibrium values C p and λ values (taken form [46]), the contributions related to the vibrational excitation of the nitrogen molecules [31]

$$ C_{p}^{*} = C_{p} m_{{N_{2} }} - \frac{{d\varepsilon_{\text{v}} \left( {T_{\text{g}} } \right)}}{{dT_{\text{g}} }}, $$
(14)
$$ \lambda^{*} = \lambda - {\text{N}}_{2} \left( X \right)D_{\text{v}} \frac{{d\varepsilon_{\text{v}} \left( {T_{\text{g}} } \right)}}{{dT_{\text{g}} }}, $$
(15)

where m N2 is the mass of the nitrogen molecule and D v its diffusion coefficient. The radial length-scale for the T g variation was taken as R th ~ 2 R, since emission measurements in a similar experimental conditions [23] than those in [24], indicate that the rotational temperature profile is significantly wider than the charged species concentration profiles. The same result is shown in a 2-D model of an atmospheric pressure glow discharge [45].

The term Q R accounts for the heat released from chemical reactions in nitrogen gas, as was described in the model [47]. It included the dissociation reaction (R7) following pre-dissociation via electronically excited states [47–49]

$$ \begin{aligned} {\text{e}} + {\text{N}}_{2} \left( {X^{1} \sum {_{g}^{ + } } ,1} \right) & \to {\text{N}}_{2} \left( {E^{*} = 13\;{\text{eV}}} \right) \\ & \to {\text{N}}\left( {^{4} S} \right) + {\text{N}}\left( {^{2} D} \right) + 0.9\;{\text{eV}}, \end{aligned} $$
(16)

the quenching of the electronically excited N2(A 3∑ +u ) states in reaction (R35) [47–49]

$$ {\text{N}}_{2} \left( {A^{3} \sum {_{\text{u}}^{ + } } } \right) + {\text{N}}_{2} \left( {X^{1} \sum {_{g}^{ + } } ,v} \right) \to {\text{N}}_{2} \left( {X^{1} \sum {_{g}^{ + } } ,v = 2} \right) + {\text{N}}_{2} \left( {B^{3} \prod_{\text{g}} } \right) + 0.4\;{\text{eV}}, $$
(17)

and (R36) [47–49]

$$ {\text{N}}_{2} \left( {A^{3} \sum {_{\text{u}}^{ + } } } \right) + {\text{N}}_{2} \left( {X^{1} \sum {_{g}^{ + } } ,v} \right) \to {\text{N}}_{2} \left( {X^{1} \sum {_{g}^{ + } } ,v = 8} \right) + {\text{N}}_{2} \left( {C^{3} \prod_{\text{u}} } \right) + 2.0\;{\text{eV}}; $$
(18)

and during the electron-ion recombination processes (R19) [47–50]

$$ \begin{array}{*{20}l} \begin{aligned} {\text{e}} + {\text{N}}_{2}^{ + } & \to {\text{N}}\left( {^{4} S} \right) + {\text{N}}\left( {^{4} S} \right) + 5.82\;{\text{eV}} \\ & \to {\text{N}}\left( {^{4} S} \right) + {\text{N}}\left( {^{2} D} \right) + 3.44\;{\text{eV}} \\ & \to {\text{N}}\left( {^{4} S} \right) + {\text{N}}\left( {^{2} P} \right) + 2.25\;{\text{eV}} \\ \end{aligned} & \begin{aligned} 14.3\;\% \hfill \\ 77.1\;\% . \hfill \\ 8.6\;\% \hfill \\ \end{aligned} \\ \end{array} $$
(19)

Thus, the energy which goes to gas heating due to reactions (R19) results 3.7 eV. The fast gas heating term also included the heating at fast translational–translational T–T relaxation (due to the transfer of energy from electrons to molecules in elastic collisions) in according to the reaction (R1); as well as the rotational–translational R–T relaxation of the nitrogen molecule in according to (R2).

An estimation of an effective electron temperature T e as two-thirds of the mean-electron energy was obtained by means of the BOLSIG+ code. The electric field strength was obtained from the Ohm’s law [46] for a given value of the discharge current density J and the plasma composition

$$ J = \frac{{N_{e} e^{2} }}{{\sqrt {2\pi T_{e} m_{e} } NQ_{e - n} }}E, $$
(20)

where m e is the mass of electrons and Q en is the average momentum transfer cross-section for electron-nitrogen collisions. For T e ~ 9500 K, an average momentum transfer cross-section Q e−n = 1.08 ± 0.05 × 10−19 m2 was used [51]. Owing to the low-ionization degree of the discharge (~ 10−5) in the conditions of [24], the average collision frequency between electrons and heavy particles was dominated by collisions with neutrals. During the calculations the consistency of the approximate expression for the electron drift velocity employed in (20) was checked by replacing it by the calculated one on the basis of the EEDF by the BOLTSIG+ code. No large differences in the model results were obtained.

The input parameter of the model was the discharge current density J inferred from the experimental data of [24]. Initial conditions for all the plasma quantities were used to start the solution procedure (Ne = N2 + ~ 1017 m−3 ≫ N+, N3 +, N4 +; N2(X) = p/(k T g) ≫ N2(A), N2(B), N2(C), N2(a′), N(4 S), N(2 D), N(2 P); being T g = T v ~ 3000 K and T e ~ 9000 K). The specific values used for these initial conditions did not impact on the final converged results. From a given value of J and the initial plasma composition the electric field strength was calculated from de Ohm’s law. Once that the EEDF was found with the help of the BOLSIG+ (from the values of E/N and T v), the rate coefficients for the process involving electrons (and also the effective electron temperature) were obtained. Then, the continuity equations for atoms (N(2D), N(2P) and N(4S)) and the other different charged (N4 +, N3 +, N+ and electrons) and excited species (N2(A 3∑ +u ), N2(B 3Πg), N2(a′1∑ −u ) and N2(C 3Πu)) and the gas thermal and vibrational balance equations were solved to obtain new values of those quantities. Note that in these calculations the charged particle concentrations were constrained through the plasma quasi-neutrality condition. This calculation provided new values for the N2 + density. The new values for the N2(X 1∑ +g , v) density were obtained from the constancy of the pressure. The last obtained values of all the plasma quantities were then taken as new initial values for the next iteration. The iteration procedure continued until the equilibrium values were reached.

The continuity Eq. (1) for the plasma species are quite stiff, i.e., there is a wide range of time scales associated with the equations, which reduces the time step needed for accurate numerical integration. This arises because of the wide range of densities and corresponding source terms for the various species, typically amounting to ten orders of magnitude. The balance equations were solved numerically by a finite-difference explicit method with the second-order approximation in time [52]. Because of the stiffness of the equations, a short time-step for integration (=1.0 × 10−10 s) was used. The Eq. (1) were integrated for times of ~10−3 s, and it was sufficient for the density of each species to converge within an error of about 10−3 to its equilibrium value.

Results of Calculations and Discussion

The model calculations correspond to the experimental conditions of [24]; where as quoted previously, the radial profile of the N2 + concentration and the values of the gas rotational temperature were experimentally inferred for currents I = 52, 97, 142 and 187 mA. In order to make comparisons with the model results, the current density at the center J(r = 0), was determined by dividing the measured current by the effective discharge area A*; i.e., J(r = 0) ≡ I/A*; namely [23, 24]

$$ J\left( {r = 0} \right)A^{*} \equiv 2\pi \int\limits_{0}^{R} {J\left( r \right)rdr} , $$
(21)

being r the radial distance measured from the center of the discharge. As the rotational temperature profile is significantly wider than the charged species concentration profiles [23], the local current density J(r) is approximately proportional to the electron density profile [23, 24]. By assuming that the electron density is proportional to the measured N2 + at each radial position [24]; A* was calculated as

$$ A^{*} \equiv \frac{2\pi }{{{\text{N}}_{2}^{ + } \left( {r = 0} \right)}}\int\limits_{0}^{R} {{\text{N}}_{2}^{ + } \left( r \right)rdr} . $$
(22)

Thus Eq. (22) was employed to derive the current density at the center of the discharge column by using the measured radial profiles of N2 + ([24], figure 5) for each current value. The calculated values of J(r = 0) for I = 52, 97, 142 and 187 mA, were ~0.8, 1.6, 2.2 and 3 A/cm2; respectively. The electric field strength together with the plasma composition and the electron and gas temperature, as well as the vibrational temperature characterizing the first vibrational levels of the nitrogen ground state molecules were calculated from these values of current density. As a consequence, the model output gives estimations of the discharge variables evaluated at the center of the discharge under the experimental conditions of [24].

Figure 1 shows the values of the electric field and also the reduced electric field versus the discharge current. The electric field decreases when the current increases, resulting in a negative slope in the E–I characteristic of the discharge. A similar trend is observed for the reduced electric field. This behavior was observed in several works for this kind of discharge [4, 5, 7].

Fig. 1
figure 1

Electric field strength and reduced electric field versus the discharge current

Full size image

Figure 2 shows the values of the electron temperature, the gas temperature and the vibrational temperature of the nitrogen molecules versus the discharge current. As it can be seen, the vibrational temperature values are higher than the gas temperature in the given current range (thus indicating that the nitrogen molecules are in vibrational non-equilibrium state) being its difference smaller as the discharge current increases. This is expected since the rate of V–T energy transfer (12) and (13) increases exponentially with T g. A noticeable difference between the T e and T g values is also observed. The T e values (~9500 K) are typical of this kind of low-current discharges in molecular gases [31, 45]. As it can be seen, as the discharge current increases the electron temperature softly decreases while the gas temperature increases (with rather high values, above 3000 K); and consequently the plasma non-equilibrium degree decreases; but it is still maintained at a relatively high level T e/T g > 2. The calculated gas temperature values show good agreement with the experimental data [24] (within the experimental error of ±8 %) in the whole current range.

Fig. 2
figure 2

The electron, vibrational and gas temperatures versus the discharge current

Full size image

Figure 3 shows the densities of the electronic molecular and atomic metastable states and the electronic atomic ground state versus the discharge current. The rather high-gas temperature together with the vibrational non-equilibrium leads to the production of dissociation products as N(4 S), N(2 D) and N(2 P); mainly due to non-equilibrium thermal dissociation (see Fig. 4). The nitrogen dissociation degree varies in the range ~0.2 to 1.6 % in the whole current range. About 99 % of the atoms are in the ground state. The density of N(2 P) is higher than that of N(2 D) due to the production of the N(2 P) by the quenching of the N2(A 3∑ +u ) states through the reaction (R38) (see Fig. 5); thus producing a decrease in the density of the molecular metastable N2(A 3∑ +u ) and an increase in the density of N(2 P) as the discharge current increases. An increase in the density of the N(2 D) state for the larger values of the discharge current is also observed because the N(2 D) is mainly created by dissociative recombination (R19) in Table 1. The density of N2(a′1∑ −u ) is lower than that of N(2 D) almost in the whole current range (except for the smaller values of the discharge current).

Fig. 3
figure 3

Densities of the electronic molecular and atomic metastable states and the electronic atomic ground state versus the discharge current

Full size image
Fig. 4
figure 4

Dissociation contributions versus the discharge current

Full size image
Fig. 5
figure 5

Rates of the atomic metastable N(2 P) production and loss via different mechanisms versus the discharge current

Full size image

Figure 4 shows a comparison between the electron-impact dissociation (R7) in Table 1 with the thermal dissociation for vibrational excited molecules, accounted for by using the multiplicative non-equilibrium factor (5) in the rate coefficient of the reaction (R51) in Table 1. As it can be seen, several orders of magnitude exist between both dissociation rates; thus suggesting that the electron-impact dissociation process is not important under the considered low-electric field conditions; but the thermal dissociation of vibrationally excited molecules plays an essential role in the production of N(4 S) atoms. It should be noted that the used Macheret–Fridman model imposes no restriction onto the values of T g and T v, and does not depend on any semi-empirical parameter [37, 38].

Figure 5 shows the rates of the atomic metastable N(2 P) production and loss via different mechanisms versus the discharge current. It is observed that the dominant process of production of N(2 P) (marked with a dashed line in Fig. 5) within the whole current range is the quenching of the N2(A 3∑ +u ) state through the reaction (R38)

$$ {\text{N}}_{2} \left( {A^{3} \sum {_{\text{u}}^{ + } } } \right) + {\text{N}}\left( {^{4} S} \right) \to {\text{N}}_{2} \left( {X^{1} \sum {_{g}^{ + } } ,v} \right) + {\text{N}}\left( {^{2} P} \right), $$
(23)

while the loss is almost due to the quenching of N(2 P) in collisions with N2(X 1∑ +g , v) molecules through the reaction (R45) in Table 1; being both processes in a sort of detailed balance. The low difference between the rates of such processes for the larger current values is due to the increasing importance of the ionization associative process (R18). Under the analyzed conditions, the excitation rate of the N2(A 3∑ +u ) state due to mutual collisions of strongly vibrationally excited molecules in according to the reaction (R49), is much lower than the excitation rate due to collisions of energetic electrons with molecules in according to the reaction (R3). That is, the excitation rate of the N2(A 3∑ +u ) state is determined by the EEDF (calculated by the help of the BOLSIG+ code) and not by the approximation model of the VEDF.

Figure 6 shows the ion composition of the plasma versus the discharge current. As it can be seen, the dominant ion within the whole current range is the molecular N2 +, in according to experimental data [24]. Approximately 92, 88, 86 and 80 % of the ions are N2 +, the remainder is almost the atomic N+. The following inequality holds:

$$ {\text{N}}_{2}^{ + } + {\text{N}}^{ + } \gg {\text{N}}_{3}^{ + } + {\text{N}}_{4}^{ + } . $$
(24)
Fig. 6
figure 6

Ion composition of the plasma versus the discharge current

Full size image

The results on the plasma composition are quite different from those found in the model [25] for a current I = 40 mA, but the present results show good agreement (within the experimental error of ±10 %) with the peak values of the N2 + radial profiles measured in [24] in the whole current range. Note that it is quite irrelevant to consider reactions (R12)–(R15) as Penning or associative ionization processes, since the density of N4 + ions are quickly converted in N2 + due to the ion conversion reactions (R25)–(R34) in Table 1.

Figure 7 shows the rate of the electron production and loss via several mechanisms versus the discharge current. As it can be seen, the dominant process of production of electrons within the almost whole current range is the associative ionization in atomic collisions

$$ {\text{N}}\left( {^{2} P} \right) + {\text{N}}_{2} \left( {^{2} P} \right) \to {\text{N}}_{2}^{ + } + {\text{e}}, $$
(25)

in according to the process (R18) in Table 1. Only for low-current values ~50 mA or lower, the rate of the Penning/associative ionization process through reactions (R12) and (R13) in Table 1,

$$ \begin{aligned} {\text{N}}_{2} \left( {A^{3} \sum {_{u}^{ + } } } \right) + {\text{N}}_{2} \left( {a^{\prime 1} \sum {_{u}^{ - } } } \right) & \to {\text{N}}_{4}^{ + } + {\text{e}} \\ & \to {\text{N}}_{2}^{ + } + {\text{N}}_{2} + {\text{e}}, \end{aligned} $$
(26)

approaches to the rate of the process (R18). This is because the gas temperature is not high enough; however an increase in the current values (and thus in the gas temperature) leads to an exponential increase in the rate of the process (R18) until it is balanced with the dissociative recombination process (R19) (marked with a solid line in Fig. 7). For the larger current values, also the rate of ionization in according to the process (R17)

$$ {\text{N}}\left( {^{2} P} \right) + {\text{N}}_{2} \left( {^{2} D} \right) \to {\text{N}}_{2}^{ + } + {\text{e}}, $$
(27)

exceeds the rate of the processes (R12) and (R13) due to the strong increase in the density of the N(2 D) state (as is shown in Fig. 3). The processes of direct electron-impact ionization (R8) as well as the stepwise ionization from the metastables N2(A 3∑ +u ), and N2(a′1∑ −u ), in according to reactions (R9) and (R11) respectively; are not important under the present conditions.

Fig. 7
figure 7

Rates of the electron production and loss via several mechanisms versus the discharge current

Full size image

According to these results, the associative ionization in atomic collisions might plays a non-negligible role in the production of electrons under the conditions of [25], because the high-gas temperature (T g ~ 3600 K) predicted by that model at I = 40 mA for the nitrogen gas at rest.

Figure 8 shows the electron power and the fraction of it converted into heat versus de discharge current. As it can be seen, a very large fraction (up to ~94 %) of the electron power is converted into heat. The major source of gas heating is the V–T relaxation of nitrogen molecules owing to the rather high-gas temperature values of the discharge. The heat released from chemical reactions does not play any relevant role under these conditions because the fraction of the electron power transferred to the electronic excitation of the nitrogen is low (<2 %).

Fig. 8
figure 8

Electron power and the fraction of it converted into heat versus the discharge current

Full size image

Conclusions

A model describing an atmospheric pressure glow discharge in nitrogen gas to simulate the experimental conditions of [24], accounting for several processes with the participation of electronically excited atoms, was developed. The basic processes sustaining the discharge at a current range of 52–187 mA were identified. A good agreement between the calculated results and the experiment [24] was found. The model has shown that:

  1. 1.

    The thermal dissociation of vibrationally excited molecules plays an essential role in the production of N(4 S) atoms. The electron-impact dissociation process is not important under the considered low-electric field conditions.

  2. 2.

    The dominant ion within the investigated current range is the molecular N2 + with an increasing proportion of atomic N+ toward high-current values. The dominant process of production of electrons within the almost whole current range is the associative ionization in atomic collisions

    $$ {\text{N}}\left( {^{2} P} \right) + {\text{N}}_{2} \left( {^{2} P} \right) \to {\text{N}}_{2}^{ + } + {\text{e}}. $$
  3. 3.

    The dominant process of production of N(2 P) within the whole current range is the quenching of the N2(A 3∑ +u ) electronically excited molecules by nitrogen atoms

    $$ {\text{N}}_{2} \left( {A^{3} \sum {_{\text{u}}^{ + } } } \right) + {\text{N}}\left( {^{4} S} \right) \to {\text{N}}_{2} \left( {X^{1} \sum {_{g}^{ + } } ,v} \right) + {\text{N}}\left( {^{2} P} \right). $$
  4. 4.

    A very large fraction (up to ~94 %) of the electron power is converted into heat. The major source of gas heating is the V–T relaxation of nitrogen molecules owing to the rather high-gas temperature values of the discharge.