1 Introduction

Nonlinear partial differential equations are employed to examine the features of many physics models. One of these equations is the Schrödinger type equation. Such equation has a crucial role in fields such as mathematical physics, optic, plasma, and fiber-optic telecommunications engineering. Exact solutions of nonlinear Schrödinger’s equation have an important role in the applied mathematics Ali et al. (2020); Eslami et al. (2014); He (2020); Zhang et al. (2017); Gao et al. (2020a, 2020b). There are several techniques have been developed to extract exact solutions for nonlinear partial differential equations such as the bilinear neural network method Zhang and Bilige (2019); Zhang et al. (2021, 2020), the Kudryashov method Zafar et al. (2022); Alquran et al. (2021); Srivastava et al. (2020); Sulaiman et al. (2021), the extended rational sin-cos and sinh-cosh methods Cinar et al. (2021), the sine-Gordon expansion method Ali et al. (2020a, 2020b); Fahim et al. (2021); Abdul Kayum et al. (2020), the unified method and its generalized technique Abdel-Gawad and Osman (2015); Abdel-Gawad et al. (2016); Osman and Abdel-Gawad (2015), the extended simple equation method Khater et al. (2021), the \((G'/G)\)-expansion method Ismael et al. (2020); Durur (2020); Ekici et al. (2016), the Hirota bilinear method Abdulkadir Sulaiman and Yusuf (2021), the unified auxiliary equation method Zayed and Shohib (2019); Zayed et al. (2021), F-expansion method Biswas et al. (2019); Yıldırım (2021); Karaman (2021),the generalized exponential rational function method Khodadad et al. (2021), and other techniques Ali et al. (2020); Baskonus et al. (2018); Zhang et al. (2021a, 2021b); Ali et al. (2021); Rehman et al. (2020); Ali et al. (2020); Ozdemir et al. (2021). Additionally, many authors started up to employ the Jacobi elliptic function method Kurt (2019); Alquran and Jarrah (2019); Ali (2011); Ghanbari et al. (2021); Lü (2005); Zayed and Alurrfi (2015).

In this manuscript, we consider the perturbed Chen-Lee-Liu (CLL) model Ozdemir et al. (2021)

$$\begin{aligned} i\psi _{t}+\alpha \psi _{xx}+i \beta \vert \psi \vert ^{2}\psi _{x}=i[\gamma \psi _{x}+\mu ( \vert \psi \vert ^{2n}\psi )_{x}+\delta (\vert \psi \vert ^{2n})_{x}\psi ], \end{aligned}$$
(1)

where \( \gamma \) is the coefficient of inter-modal dispersion, \(\mu \) and \(\delta \) symbolize coefficients of self-steepening for short pulses and nonlinear dispersion, respectively. Additionally, the coefficients of the group velocity dispersion and the nonlinearity are refereed by \(\alpha \) and \(\beta \), respectively. We mention that n indicates the density for the complex wave function. The CLL equation drives solitons propagation dynamics in nonlinear optical fibers, and it also has applications in solitons cooling, optical couplers, meta-materials, and optoelectronic devices.

In this study, we investigate Eq. (1) at \(n=1\) which reads

$$\begin{aligned} i\psi _{t}+\alpha \psi _{xx}+i \beta \vert \psi \vert ^{2}\psi _{x}=i[\gamma \psi _{x}+\mu ( \vert \psi \vert ^{2}\psi )_{x}+\delta (\vert \psi \vert ^{2})_{x}\psi ]. \end{aligned}$$
(2)

We establish a variety of optical solutions with the help of the Jacobi elliptic function method to the perturbed Chen-Lee-Liu equation, which depicts the propagation of an optical pulse through plasma and optical fiber. In Yıldırım et al. (2020), the Riccati method has been employed. Sardar subequation method used to find solitary wave solutions Esen et al. (2021). Zhang et al. have investigated qualitative analysis and the bifurcation method in Zhang et al. (2011). Apart from these, many studies have been made and continue to be done for the Chen-Lee-Liu equation Biswas (2018); Biswas et al. (2018); Triki et al. (2018); Yıldırım (2019). Akbar and others studied the Chen-Lee-Liu model via using different solutions functions with the help of the Jacobi elliptic functions Akinyemi et al. (2021). Kudryashov found general solutions by using different methods with elliptic function approach Kudryashov (2019).

The main goal of this paper is implementing firstly the Jacobi elliptic function method to obtain new solutions with different wave structures for Eq. (2).

This study is organized as follows, introduction is given in Sect. 1. In Sect. 2, we devoted ourselves to presenting the Jacobi elliptic functions method. In Sect. 3, we studied the new exact solutions of the perturbed Chen-Lee-Liu equation by applying the described method. The figures of the constructed solutions are drawn by the degenerate states of the Jacobi elliptic functions for \(m\rightarrow 0\) and \(m\rightarrow 1\). The conclusion of this study is presented in Sect. 4.

2 Description of the Jacobi elliptic function method

The nonlinear partial differential equation is expressed as:

$$\begin{aligned} P(\psi ,\psi _{x},\psi _{t},\psi _{xx},\psi _{tt},\psi _{tx},\cdots )=0, \end{aligned}$$
(3)

where P is a polynomial function containing \(\psi (x,t)\) and its partial derivatives.

By taking the transformation

$$\begin{aligned} \psi (x,t)=U(v)\mathrm{e}^{i\phi (x,t)}, v=x-\rho t, \phi (x,t)=-kx+wt+\eta , \end{aligned}$$
(4)

Eq.(3) becomes a nonlinear ordinary differential equation (NODE) as follows

$$\begin{aligned} F(U^{'},U^{''},U^{'''},\cdots )=0. \end{aligned}$$
(5)

Here, U(v), \(\phi (x,t)\), \(\rho \), k, w and \(\eta \) stand for the amplitude competent, phase function, speed of the soliton, frequency, wave number, and phase, respectively. Then, The following steps are followed to construct the solutions:

  • Step 1 The solution of the NODE is as follows:

    $$\begin{aligned} U(v)=g_{0}+\sum _{i=1}^{D}(\frac{z(v)}{1+z(v)^{2}})^{i-1}\left( g_{i}\frac{z(v)}{1+z(v)^{2}}+f_{i}\frac{1-z(v)^{2}}{1+z(v)^{2}}\right) , \end{aligned}$$
    (6)

    where \(g_{i}\), and \(f_{i}\) are constants (\(g_{D}\ne 0\) or \(f_{D}\ne 0\)). The z(v) function is expressed as:

    $$\begin{aligned} z^{'}(v)=\sqrt{s+c z^{2}(v)+r z^{4}(v)}, \end{aligned}$$
    (7)

    where s, c and r are constants.

  • Step 2 The value of D is defined by the balance principle which depends on the comparison between the highest-order linear term and the non-linear term in Eq. (5).

  • Step 3 Substituting Eq. (6) along with Eq. (7) into Eq. (5), we get a polynomial in z(v) . Afterthat, we obtain a system of algabraic equations by setting the coefficients of \(z^{b}(v)\), \( {b=0,\cdots ,7} \) equal to zero. We solve the obtained system with the help of mathematica software to find the unknown parameters.

  • Step 4 The general solutions of Eq. (6) are as follows according to the conditions of s, c and r in Table 1:

    Table 1 Jacobi elliptic functions
    Full size table
    Table 2 Jacobi elliptic functions for \(m \rightarrow 0 \) and \(m \rightarrow 1\)
    Full size table

In Table 2, we express to change hyperbolic and trigonometric functions for \(m \rightarrow 0\) and \(m \rightarrow 1\) of the Jacobi elliptic functions. Thereby, solutions are structure of trigonometric and hyperbolic functions.

3 Applications

In this section, we apply the Jacobi elliptic function method to Eq.(2). Firstly, by inserting Eq. (4) into Eq.(2)

$$\begin{aligned} \begin{aligned}&-i \rho U^{'}-w U+\alpha U^{''}-2k\alpha i U^{'}-\alpha k^{2} U +i \beta U^{2}U^{'}\\&+\beta k U^{3}-i\gamma U^{'}-\gamma k U-3i \mu U^{2}U^{'}-\mu k U^{3}-2i \delta U^{2}U^{'}=0 , \end{aligned} \end{aligned}$$
(8)

is attain. We express the following parts of Eq.(8) as follows. The real part is

$$\begin{aligned} (-w-\alpha k^{2}-\gamma k ) U+\alpha U^{''}+k(\beta -\mu )U^{3}=0, \end{aligned}$$
(9)

and the imaginary part is

$$\begin{aligned} (-\rho -2k\alpha -\gamma ) U^{'}+ (\beta -3 \mu -2 \delta ) U^{2}U^{'}=0. \end{aligned}$$
(10)

Then, we set the coefficients of the components of the imaginary part equal to zero, we get \(\rho =-2k\alpha -\gamma \) and \(\beta =3\mu +2\delta \). Considering these two constraints in the real part, we get

$$\begin{aligned} (-w-\alpha k^{2}-\gamma k ) U+\alpha U^{''}+2k(\mu +\delta )U^{3}=0. \end{aligned}$$
(11)

By using the balance principle, we get \(D=1\). Considering Eq. (6), we may express the solution of Eq. (11) as below:

$$\begin{aligned} U(v)=g_{0}+g_{1}\frac{z(v)}{1+z(v)^{2}}+f_{1}\frac{1-z(v)^{2}}{1+z(v)^{2}}. \end{aligned}$$
(12)

If Eq. (12) is substituted in Eq. (11), we find the solutions by taking into account the equation system obtained for the following conditions by performing the necessary operations (Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9).

Result 1: Considering the case \(s= 1\), \(r=m^{2}\), \(c=-1-m^{2}\) and \(z(v)=sn(v,m) \).

When \(g_{0}=0\), \(g_{1}=\mp 2if_{1}\), \(f_{1}=f_{1}\), \(\mu =\frac{\alpha -k f^{2}_{1} \delta }{k f^{2}_{1}}\) and \(w=-2\alpha -k^{2}\alpha -k\gamma \). For \(m\rightarrow 1\), we have \(z(v)\rightarrow \tanh (v)\) and the general solution is given by

$$\begin{aligned} \psi _{1}(x,t)=(-if_{1}\tanh (2x-2\rho t)+f_{1} \text {sech}(2x-2\rho t))\mathrm{e}^{i(-kx+wt+\eta )}, \end{aligned}$$
(13)

which is a dark-bright solitary wave solution.

Fig. 1
figure 1

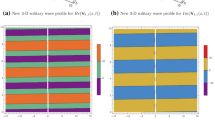
Dark-bright solitary wave solution of Eq. (13) for values of \(\alpha = -1\), \(k = 2\), \(\eta = 0.05\), \(\delta =0.01\),\(\gamma =-2\),\(f_{1}=2.3\), \(w=-2\alpha -k^{2}\alpha -k\gamma \), \(\mu =\frac{\alpha -k f^{2}_{1} \delta }{k f^{2}_{1}}\), \(\beta =3\mu +2\delta \), and \(\rho =-2k\alpha -\gamma \)

Full size image

Result 2: For \(s= 1-m^{2}\), \(r=-m^{2}\), \(c=-1+2m^{2}\) and \(z(v)=cn(v,m) \).

When \(g_{0}=\frac{f_{1}}{2}\), \(g_{1}=0\), \(f_{1}=f_{1}\), \(m=\frac{1}{2}\), \(\mu =\frac{\alpha -k f^{2}_{1} \delta }{k f^{2}_{1}}\), and \(w=\frac{1}{2}(5\alpha -2k^{2}\alpha -2k\gamma )\), we have

$$\begin{aligned} \psi _{2}(x,t)=\left( \frac{f_{1}}{2}+\frac{f_{1}(1- (cn(x-\rho t))^{2})}{(1+(cn(x-\rho t))^{2})}\right) \mathrm{e}^{i(-kx+wt+\eta )}. \end{aligned}$$
(14)

Result 3: Considering the case \(s= m^{2}\), \(r=1\), \(c=-1-m^{2}\) and \(z(v)=ns(v,m) \),

When \(g_{0}=0\), \(g_{1}=\mp \frac{4\sqrt{\alpha }}{\sqrt{-k\delta -k\mu }}\), \(f_{1}=0\), \(\mu =\frac{\alpha -k f^{2}_{1} \delta }{k f^{2}_{1}}\) and \(w=-8\alpha -k^{2}\alpha -k\gamma \). For \(m\rightarrow 1\), we have \(z(v)\rightarrow \coth (v)\) and the general solution is given by

$$\begin{aligned} \psi _{3}(x,t)=\left( \mp \frac{4\sqrt{\alpha }}{\sqrt{-k\delta -k\mu }}\frac{\coth (x-\rho t)}{(1+ (\coth (x-\rho t))^{2})}\right) \mathrm{e}^{i(-kx+wt+\eta )}, \end{aligned}$$
(15)

which represents a singular soliton solution under conditions \(\alpha k(\delta + \mu )<0\).

Fig. 2
figure 2

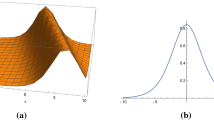
Singular soliton solution of Eq. (15)for values of \(\alpha = -0.25\), \(k = 0.7\), \(\eta = 0.9\),\(\mu =1.2\), \(\delta =0.02\), \(\gamma =3\), \(w=-8\alpha -k^{2}\alpha -k\gamma \), \(\beta =3\mu +2\delta \), and \(\rho =-2k\alpha -\gamma \)

Full size image

Result 4: For \(s=-m^{2}\), \(r=1-m^{2}\), \(c=-1+2m^{2}\) and \(z(v)=nc(v,m) \).

\(g_{0}=\frac{f_{1}}{2}\), \(g_{1}=0\), \(f_{1}=f_{1}\), \(m=\frac{\sqrt{3}}{2}\), \(\mu =\frac{\alpha -k f^{2}_{1} \delta }{k f^{2}_{1}}\) and \(w=\frac{1}{2}(-5\alpha -2k^{2}\alpha -2k\gamma )\), we have

$$\begin{aligned} \psi _{4}(x,t)=\left( \frac{f_{1}}{2}+\frac{f_{1}(1- (nc(x-\rho t))^{2})}{(1+(nc(x-\rho t))^{2})}\right) \mathrm{e}^{i(-kx+wt+\eta )}. \end{aligned}$$
(16)

Result 5: For \(s=\frac{1}{4}\), \(r=\frac{1}{4}\), \(c=\frac{1-2m^{2}}{2}\) and \(z(v)=ns(v,m)\mp cs(v,m)\).

When \(g_{0}=0\), \(g_{1}=g_{1}\), \(f_{1}=f_{1}\), \(\mu =-\delta \) and \(w=-\alpha -k^{2}\alpha -k\gamma \). For \(m\rightarrow 0\), we have \(z(v)\rightarrow \csc (v)\mp \cot (v)\). Thus, we get

$$\begin{aligned} \psi _{5}(x,t)=\left( g_{1}\frac{\cot (v)\mp \csc (v)}{1+(\cot (x-\rho t)\mp \csc (x-\rho t))^{2}}+f_{1}\frac{(1- (\cot (x-\rho t)\mp \csc (x-\rho t))^{2})}{(1+(\cot (x-\rho t) \mp \csc (x-\rho t))^{2})}\right) \mathrm{e}^{i(-kx+wt+\eta )}, \end{aligned}$$
(17)

which is a periodic solution.

Fig. 3
figure 3

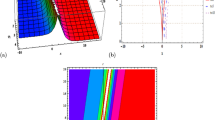
Periodic solution of Eq. (17) for values of \(\alpha = -0.6\), \(k = -1.7\), \(\eta = 1.9\), \(\mu =0.75\), \(\delta =-\mu \), \(\gamma =0.04\), \(g_{1}=0.3\), \(f_{1}=1.02 \), \(w=-\alpha -k^{2}\alpha -k\gamma \), \(\beta =3\mu +2\delta \), and \(\rho =-2k\alpha -\gamma \)

Full size image

Result 6: For \(s=\frac{1-m^{2}}{4}\), \(r=\frac{1-m^{2}}{4}\), \(c=\frac{1+m^{2}}{2}\) and \(z(v)=nc(v,m)\mp sc(v,m) \).

When \(g_{0}=0\), \(g_{1}=g_{1}\), \(f_{1}=f_{1}\), \(\mu =-\delta \) and \(w=-\alpha -k^{2}\alpha -k\gamma \). For \(m\rightarrow 0\), \(z(v)\rightarrow \sec (v) \mp \tan (v)\) and the solution is given by

$$\begin{aligned} \psi _{6}(x,t)=\left( g_{1}\frac{\sec (v)\mp \tan (v)}{1+(\sec (v)\mp \tan (v))^{2}}+f_{1}\frac{(1- (\sec (v)\mp \tan (v))^{2})}{(1+(\sec (v)\mp \tan (v))^{2})}\right) \mathrm{e}^{i(-kx+wt+\eta )}, \end{aligned}$$
(18)

which is a periodic solution.

Fig. 4
figure 4

Periodic solution of Eq. (18) for values of \(\alpha = -0.06\), \(k = -1.7\), \(\eta = 1.2\), \(\mu =0.75\), \(\delta =-\mu \), \(\gamma =0.4\), \(g_{1}=0.3\), \(f_{1}=0.5 \), \(w=-\alpha -k^{2}\alpha -k\gamma \), \(\beta =3\mu +2\delta \) and \(\rho =-2k\alpha -\gamma \)

Full size image

Result 7: For \(s=\frac{1}{4}\), \(r=\frac{m^{2}}{4}\), \(c=\frac{m^{2}-2}{2}\) and \(z(v)=\frac{sn(v,m)}{1\mp dn(v,m)}\).

When \(g_{0}=0\), \(g_{1}=\frac{\mp 2\sqrt{\alpha }}{\sqrt{-k \delta -k\mu }}\), \(f_{1}=0\), \(\mu =-\delta \) and \(w=-2\alpha -k^{2}\alpha -k\gamma \). For \(m\rightarrow 1\), \(z(v)\rightarrow \frac{\tanh (v)}{1\mp \text {sech}(v,m)}\), we have

$$\begin{aligned} \psi _{7}(x,t)=\left( \frac{\mp 2\sqrt{\alpha }}{\sqrt{k \delta -k\mu }}\frac{\sinh (x-\rho t)}{1\mp \sinh (x-\rho t)}\right) \mathrm{e}^{i(-kx+wt+\eta )}, \end{aligned}$$
(19)

which is a hyperbolic function solution under conditions \(\alpha k(\delta + \mu )<0\).

Fig. 5
figure 5

Hyperbolic function solutions of Eq. (19) for values of \(\alpha = 0.06\), \(k = -5.7\), \(\eta = 1.5\), \(\mu =1\), \(\delta =2.09\),\(\gamma =0.4\), \(w=-2\alpha -k^{2}\alpha -k\gamma \), \(\beta =3\mu +2\delta \), and \(\rho =-2k\alpha -\gamma \)

Full size image

Result 8: For \(s=1\), \(r=1-m^{2}\), \(c=2-m^{2}\) and \(z(v)=sc(v,m) \).

When \(g_{0}=0\), \(g_{1}=0\), \(f_{1}=f_{1}\), \(\mu =-\delta \) and \(w=-4\alpha -k^{2}\alpha -k\gamma \). For \(m\rightarrow 0\), \(z(v)=\rightarrow \tan (v)\) and we get

$$\begin{aligned} \psi _{8}(x,t)=\left( f_{1}\frac{1-(\tan (x-\rho t))^{2}}{1+(\tan (x-\rho t))^{2}}\right) \mathrm{e}^{i(-kx+wt+\eta )}, \end{aligned}$$
(20)

which is a periodic solution.

Fig. 6
figure 6

Periodic solution of Eq. (20) for values of \(\alpha = 2.06\), \(k = 0.1\), \(\eta = 5\), \(\mu =-\delta \), \(\delta =0.25\), \(\gamma =2.6\), \(f_{1}=0.3\), \(w=-2\alpha -k^{2}\alpha -k\gamma \), \(\beta =3\mu +2\delta \), and \(\rho =-2k\alpha -\gamma \)

Full size image

Result 9: For \(s=1-m^{2}\), \(r=1\), \(c=2-m^{2}\) and \(z(v)=cs(v,m) \).

\(g_{0}=0\), \(g_{1}=0\), \(f_{1}=f_{1}\), \(\mu =-\delta \) and \(w=-4\alpha -k^{2}\alpha -k\gamma \). For \(m\rightarrow 0\), \(z(v)\rightarrow \cot (v)\) and we get

$$\begin{aligned} \psi _{9}(x,t)=\left( f_{1}\frac{1-(\cot (x-\rho t))^{2}}{1+(\cot (x-\rho t))^{2}}\right) \mathrm{e}^{i(-kx+wt+\eta ),} \end{aligned}$$
(21)

which is a periodic solution.

Result 10: For \(s=m^{2}-1\), \(r=-1\), \(c=2-m^{2}\) and \(z(v)=dn(v,m) \).

When \(g_{0}=0\), \(g_{1}=\mp 2i f_{1}\), \(f_{1}=f_{1}\), \(\mu =\frac{-\alpha -k f^{2}_{1} \delta }{k f^{2}_{1}}\) and \(w=2\alpha -k^{2}\alpha -k\gamma \). For \(m\rightarrow 0\), \(z(v)\rightarrow 1\). Thus, we have

$$\begin{aligned} \psi _{10}(x,t)=(\mp if_{1})\mathrm{e}^{i(-kx+wt+\eta ),} \end{aligned}$$
(22)

which is an exponential function solution.

Fig. 7
figure 7

Exponential solution of Eq. (22) for values of \(\alpha =1.06\), \(k = 0.1\), \(\eta = 0.1\), \(\mu =\frac{-\alpha -k f^{2}_{1} \delta }{k f^{2}_{1}}\), \(\delta =1\), \(\gamma =2.6\), \(f_{1}=0.2\), \(w=2\alpha -k^{2}\alpha -k\gamma \), \(\beta =3\mu +2\delta \), and \(\rho =-2k\alpha -\gamma \)

Full size image

Result 11: For \(s=\frac{m^{4}}{4}\), \(r=\frac{1}{4}\), \(c=\frac{m^{2}-2}{2}\) and \(z(v)=ns(v,m)\mp ds(v,m) \).

When \(g_{0}=0\), \(g_{1}=\mp 2i f_{1}\), \(f_{1}=f_{1}\), \(\mu =\frac{\alpha -k f^{2}_{1} \delta }{k f^{2}_{1}}\) and \(w=\frac{1}{2}(-\alpha -2k^{2}\alpha -2k\gamma )\). For \(m\rightarrow 1\), \(z(v)=\coth (v)\mp \text {csch}(v)\). So, we have

$$\begin{aligned} \psi _{11}(x,t)=\left( \mp 2 if_{1}(\frac{\coth (x-\rho t)\mp \csc h(x-\rho t)}{1+(\coth (v)\mp \text {csch}(v))^{2}})+f_{1}\frac{1-(\coth (x-\rho t)\mp \text {csch}(x-\rho t))^{2}}{1+(\coth (c-\rho t)\mp \text {csch}(x-\rho t))^{2}}\right) \mathrm{e}^{i(-kx+wt+\eta )}, \end{aligned}$$
(23)

which represents a singular solitary wave solution.

Fig. 8
figure 8

Singular solitary wave solution of Eq. (23) for values of \(\alpha =1\), \(k =0.5\), \(\eta = 1.5\), \(\mu =\frac{\alpha -k f^{2}_{1} \delta }{k f^{2}_{1}}\), \(\delta =0.3\), \(\gamma =0.2\), \(f_{1}=3\), \(w=\frac{1}{2}(-\alpha -2k^{2}\alpha -2k\gamma )\), \(\beta =3\mu +2\delta \) and \(\rho =-2k\alpha -\gamma \)

Full size image

Result 12: For \(s=\frac{1}{4}\), \(r=\frac{(1-m^{2})^{2}}{4}\), \(c=\frac{1+m^{2}}{2}\) and \(z(v)=\frac{sn(v)}{dn(v)\mp cn(v)} \).

When \(g_{0}=0\), \(g_{1}=0\), \(f_{1}=f_{1}\), \(\mu =-\delta \) and \(w=-\alpha -k^{2}\alpha -k\gamma \). For \(m\rightarrow 1\), \(z(v)\rightarrow \frac{\sin (v)}{1\mp \cos (v)}\) and we have

$$\begin{aligned} \psi _{12}(x,t)=\left( f_{1}\frac{1-(\frac{\sin (x-\rho t)}{1\mp \cos (x- \rho t)})^{2}}{1+(\frac{\sin (x-\rho t)}{1\mp \cos (x-\rho t)})^{2}}\right) \mathrm{e}^{i(-kx+wt+\eta )}, \end{aligned}$$
(24)

which is a trigonometric function solution.

Fig. 9
figure 9

Trigonometric function solution of Eq. (24) for values of \(\alpha =6.02\), \(k = 0.1\), \(\eta = 1.05\), \(\mu =-\delta \), \(\delta =0.3\), \(\gamma =5.2\), \(f_{1}=1\), \(w=-\alpha -k^{2}\alpha -k\gamma \), \(\beta =3\mu +2\delta \), and \(\rho =-2k\alpha -\gamma \)

Full size image

4 Conclusions

In this article, we have found several novel solutions to the perturbed Chen-Lee-Liu equation by using the Jacobi elliptic function method. These solutions are Jacobi elliptic function, dark-bright, trigonometric, exponential, hyperbolic, periodic, and singular soliton solutions. The constraint conditions are determined to vouch the existence of valid solutions. For some values of free parameters, the 2D and 3D graphs to some of the obtained solutions are depicted. The obtained results can be effective in interpreting the physical meaning of this nonlinear system. The Jacobi elliptic function method is a powerful mathematical technique which can be utilized to acquire the analytical solutions to different complex nonlinear mathematical models.