1 Introduction

For a long time, many fields of science such as physics, chemistry and biology are concerned with the classical atomic diffusion problem (Risken 1989; Jung 1993; Ala-Nissila and Ying 1992). The permanent interest allocated to this topic resides on the large range of physical applications that are related to it. The study of thin film growth on such surfaces is very interesting. This interest stems from its important role in several areas that affect the daily lives of each us. We can cite as an example the photovoltaic cells and the electronic structures at low dimensions (micro and nano-capacitors). The diffusion surface has been observed in many experiments on different systems (Ehrlich 1991; Geisler et al. 2012; Liu et al. 2012). In the existing literature, the study of the diffusion of classical particles in a one-dimensional (1D) periodic potential has been developed by many different approaches: Klein-Kramers equation at high and low friction (Moro and Polimeno 1992; Ferrando et al. 1992), saw-tooth potentials (Magnasco 1993), fluctuation barriers (Reiman 1995; Hanggi et al. 1990), systems with time-dependent periodic perturbations (Jung 1993). Also, more efforts have been made to study the diffusion in two-dimensional periodic potential by several theoretical models (Zayzoune et al. 2009; Chhib et al. 2004; Asaklil et al. 2003; Lachtioui et al. 2009; Ferrando et al. 1999; Mazroui et al. 1997; Mazroui and Boughaleb 1996; Elkoraychy et al. 2014; Mazroui et al. 1998). However, the situation is not yet developed in the case of the deformable substrate. For this reason, we devote the present work to investigate the influence of the shape of the substrate potential on the diffusion process. We focus our attention on the Remoissenet–Peyrard potential, where its shape can vary continuously as a function of deformation parameter ξ.

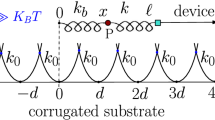
The diffusion phenomenon in a periodic potential is a transport mechanism at the microscopic scale. At this scale, the thermal energy \(k_{B} T\) (\(k_{B} {\kern 1pt}\) and T are the Boltzmann constant and the temperature respectively) is not negligible. In fact, the dynamic of such particle is influenced by its collisions with the heat bath. When a single adatom moves over a substrate, different mechanisms are possible, depending of the height barrier (compared with the thermal energy) and the coupling strength between the substrate and the adatom (the heat bath). For the present work, we assume that the diffusion only proceeds by jump mechanism. At low temperature \(k_{B} T < {\kern 1pt} E_{a}\) (E a is the activation barrier); the adatom spends most part of its time oscillating at the bottom of the adsorption sites. However, when the adatom receives enough energy from the substrate by the thermal fluctuations, it jump over the barrier from a potential well to another. If the adatom re-thermalize in a cell which is a nearest neighbor of the departure one, the diffusion process is called single jump; otherwise in a long jump, the adatom rethermalizes in a lattice cell which is not a nearest-neighbor of the departure cell. During the last few decades several theoretical works have been interest in how diffusion occurs on 2D periodic substrate for the real systems (Elkoraychy et al. 2015; Sbiaai et al. 2013, 2014; Montalenti and Ferrando 1999; Baletto et al. 2002; Han et al. 2014; Yildirim and Rahman 2009). They were shown that jump diffusion was favored energetically over other processes for several systems. Here we will investigate how diffusion of single adatom takes place on deformable substrate potential, what sort of atomic jumps occur and how information about these processes has been obtained?

The purpose of the present work is to investigate the dynamic properties of particle interacting with Remoissenet–Peyrard substrate potential within the strong collision model by molecular dynamics simulations. It tries to achieve two main goals: (1) to demonstrate the usefulness and versatility of the current theoretical method, and (2) to provide an up-to-date reference to theoretical results obtained for the diffusion adatom on deformable potential.

The rest of this paper is organized as follows. In Sect. 2 we give a detail description of our model together with the method of calculation and with the Remoissenet–Peyrard potential. In Sect. 3 the numerical results about the jump rate r j and the probability of the simple jump are presented and discussed. Finally, we present the conclusions in the Sect. 4.

2 Theoretical models and method

2.1 Theoretical model

Theoretically, the jump-diffusion of a classical particle in a periodic potential can be treated by various models. The Langevin model or the theory of Brownian motion in an external potential is one of the most popular models, both for theoreticians and experimentalists. In this approach, the moving particle is treated as a Brownian particle obedient to periodic potential and random forces due to the thermal vibrations of the crystal cage. This type of model is also suitable for other fields such as diffusion of adsorbed particles on plane or vicinal surfaces (Ala-Nissila et al. 2002; Ala-Nissila and Ying 1992). The simple approach based on the Langevin equation takes the following form:

$$m\frac{dv}{dt} = - m\eta v + F\left( r \right) + f\left( t \right){\kern 1pt} .$$
(1)

Where v is the velocity of the particle at r position, and \(F(r)\) the periodic force derived from periodic potential. In the case of white noise, the random force \(f(t)\) is connected to the friction force \(- \eta mv\) through the second fluctuation–dissipation theorem:

$${<}f\left( t \right)f\left( {t^{\prime } } \right){>} = 2{\kern 1pt} \eta mk_{B} {\kern 1pt} T{\kern 1pt} \delta \left( {t - t^{\prime } } \right).$$
(2)

With k B and T are respectively the Boltzmann’s constant and the temperature. At low friction, the particle will change its energy progressively, by suffering many weak collisions with the heat bath (the substrate in surface diffusion). Its velocity is slightly modified by a single collision, and the equilibration occurs because of the large number of those collisions. The Langevin approach with a white noise is valid when the characteristic vibrational times of the adparticle are slower than those of the substrate (Wahnström 1986). This will happen usually when the mass of the bath particles is smaller than that of the adsorbate. But in the opposite condition i.e., when the mass of the migrating particles is the same order with the substrate atoms or, in any case, for light adatoms, the diffusion can be modeled by a different approach which is based on the Boltzmann equation (Beenakker and Krylov 1998). However, the solution of this equation is very complicated and very expensive to solve numerically, even for dynamical systems possessing only a very modest numbers of degrees of freedom. For that it might to make a simple approximation of the velocity distribution of the particle after each collision. The Bhatnagar, Gross and Krook (BGK) equation is a well-known approximation (Bhatnagar et al. 1954), which assumes that after each collision the velocity of the particle is suddenly thermalized, i.e., after a collision the final velocity is extracted from the Maxwell distribution at the given temperature T. Within this model, the dynamics of a mobile particle subject to an external deterministic force \(F(x)\) which can describe mathematically by the following equation for the probability density in phase space \(f(x,v,t)\):

$$\frac{\partial f}{\partial t} + v\frac{\partial f}{\partial x} + \frac{F\left( x \right)}{m}\frac{\partial f}{\partial v} = \eta \left[ {M\left( v \right)\int_{ - \infty }^{ + \infty } {f\left( {x,v,t} \right)dv - f\left( {x,v,t} \right)} } \right],$$
(3)

where η is the collision frequency, \(F(x)\) is the periodic force coming from the potential \(V(x)\) , m is the mass of the particle, and \(M(v)\) is the Maxwell distribution:

$$M\left( v \right) = \left( {\frac{m}{{2{\kern 1pt} \pi {\kern 1pt} k_{B} T}}} \right)^{{\frac{1}{2}}} \exp \left( { - \frac{{mv^{2} }}{{2k_{B} T}}} \right).$$
(4)

As underlined in the introduction, in the case of the strong collision, the diffusion will be processed by an approach which is based on the BGK model. In this latter the diffusing particles collide with the environment at a given frequency η. After each collision, the particle’s velocity is suddenly thermalized and it is extracted from the Maxwell distribution at the given temperature. However, to solve numerically the BGK equation there are two methods in literature. The first one is based on the solution of the kinetic Eq. (3) by the Matrix-Continued-Fraction Method (Risken 1989), which is the effective method, because it gives very accurate numerical results and it is often used to investigate the limits of validity of analytical approaches, and it is also extremely precise and fast when dealing with one-dimensional problems with barriers below \(20K_{B} T\). By reason of that, in this work we have solved the BGK equation by used the direct simulation method. In this framework, the diffusing particle moves deterministically in the periodic field of force following the Newton equation of motion (Eq. 5) until it suffers a collision. But when the collision occurs, particle’s velocity is suddenly thermalized and it extracted from the Maxwell distribution. In fact, the BGK model can be numerically executed as follows: at each time step \(\delta t(\delta t \ll \eta^{ - 1} )\), the particle has a probability \(\eta \delta t\) to suffer a collision with the heat bath. At each step the quantity \(\eta \delta t \ll 1\) is calculated and a random number r is extracted with uniform probability in the interval [0,1]. If \(r < \eta \delta t\) the particle suffers a collision and its velocity is extracted from the Maxwell distribution at the desired temperature T. While, if \(r > \eta \partial t\) the particle continues its deterministic motion and the Newton equation is solved by using an algorithm of velocity Verlet (Ferrando et al. 2000, 2005; Allen and Tildesley 1987).

2.2 Remoissenet–Peyrard potential

In order to describe various systems in condensed matter physics, more complicated potentials than the cosine-like type potential may be required. In this work, we use a non-linear potential with a convenient shape of the on-site potential given by Remoissenet–Payrard to study the jump diffusion process of an adatom on a substrate. There are many versions of this potential, but we concentrate our analyses on the most general case defined in Ref. (Peyrard and Remoissenet 1982; Remoissenet and Peyrard 1984). Its analytical expression is given by:

$$V\left( x \right) = \frac{{V_{0} }}{2}\frac{{\left( {1 + \xi } \right)^{2} \left( {1 - \cos \left( {q_{0} x} \right)} \right)}}{{\left( {1 + \xi^{2} - 2\xi \cos \left( {q_{0} x} \right)} \right)}};\quad{\text{with}}\,q_{0} = \frac{2\pi }{a}.$$
(5)

Here, a is the separation between two nearest minima and the parameters V 0 and ξ represent the potential height and the deformation parameter, respectively. Which the latter parameter should be fulfills the following condition \(\left| \xi \right| < 1\). Likewise, the shape of our potential can be varying continuously as a function of the parameter ξ (see Fig. 1). As can be seen from Fig. 1, when ξ = 0, the potential (5) has a well-known form of a Sine–Gordon (SG), with energy barriers E a  = V 0. If ξ has positive values the potential lead to a shape with sharp wells separated by flat wide barriers. On the other hand, when ξ is negative the minimums become flat and separated by thin barriers (see again Fig. 1). Furthermore, the frequency of atomic vibrations at the minimum of the substrate potential is connected to the deformation parameter by the following formula:

$$\omega_{o} = q_{0} \left( {\frac{1 + \xi }{1 - \xi }} \right)\sqrt {\frac{{V_{0} }}{2m}} .$$
(6)
Fig. 1
figure 1

Representation of the RP potential for different values of the deformation parameter ξ. For \(\xi = - 0.9,0\,\,{\text{and}}\,\,0.9\)

Full size image

In the last two decades considerable effort has been made to use the Remoissenet–Peyrard (RP) potential for studying many problems of science like: to examine the influence of deformation of the substrate potential on the dissipative (over damped) dynamics in different commensurate structures of the Frenkel–Kontorova Model driven by dc and ac forces (Hu and Tekic 2007), to describe the disturbance of the sinusoidal shape of the substrate periodic potential of the Sine–Gordon equation (Braun and Kivshar 1998; Braun et al. 2000, 1990; Remoissenet 1999), to study the relationship between synchronization and the rate with which information is exchanged between nodes in a Spatio-temporal which describes the dynamics of classical particles under a substrate RP potential (Kakmeni and Baptista 2008), and so on (Peyrard and Remoissenet 1982; Remoissenet and Peyrard 1984; Kakmeni and Baptista 2008; Kofané and Dikandé 1993; Dikandé and Kofané 1994). In addition, it has also been used in many different domains such as deformable spin model Hamiltonian, discrete lattice systems (Nguenang et al. 2005), thermodynamically properties of kink-antikink at low temperatures (Alexander et al. 2008).

As discussed in the introduction, the main purpose of this work is to go beyond the restrictive assumption concerning the periodic sinusoidal potential (Ferrando et al. 1999; Elkoraychy et al. 2014; Ferrando et al. 2005), and to describe the diffusion phenomenon of a particle in the general case where the substrate potential is not sinusoidal, with particular reference to the effect of the shape parameter ξ. For this study we performed simulations of the molecular dynamics to solve the BGK equation in order to calculate the jump rate r j and the probability of single jump P 1 for different values of the parameter ξ and normalized collision γ.

3 Results and discussion

Very few works using deformable potential in the study of diffusion problems can be found in literature. In this section, we present the results of our simulation, studying the influence of substrate potential structure on the dynamics of classical particle, by using the Remoissenet–Peyrard substrate potential, which whose shape can be varied as a function of the deformation parameter. In order to investigate the diffusion phenomena of single adatom on RP potential, we consider a fixed barrier \(E_{a} = 6k_{B} T\) which is sufficient to ensure the jump diffusion regime, and varying the deformation parameter ξ and the normalized collision frequency \(\gamma\) which is defined by the following relation:

$$\gamma = \eta \frac{a}{2\pi }\sqrt {\frac{m}{{K_{B} T}}} {\kern 1pt} .$$
(7)

The simulation results are limited to jump-diffusion regime, this regime occurs when the activation barrier is sufficiently high compared to the thermal energy. For each value of the couple \((\xi ,\gamma )\), we calculate the jump rate r j and the probability distributions of the simple jump P 1.

The simulation results for the dependence of the jump rate on the deformation parameter ξ for a wide interval \(- 1 < \xi <1\) and different values of \(\gamma (\gamma = 0.1,\text{ }\gamma = 0.3\,{\text{and}}\,\gamma = 1)\) are summarized in Fig. 2. We note that the r j increases generally with the deformation parameter ξ, this increase becomes very important when the value of the parameter γ increases. This implies that the diffusion of the classical particle is very interesting in the case where the potential have the narrow wells separated by the thick barriers. In this specific case, the particle is well activated and makes a frequent jumps from a well to another, instead of spending the most part of the time by making small-amplitude oscillations around the well bottoms. When the particle has escaped a well, it may be retrapped in a nearest-neighbor one or it may make a flight after which is captured in a cell which is far away from the cell of departure: particle trajectories consist in ballistic flights. While in the opposite limit, when the potential has flat bottom separated by thin barriers, the diffusion process decreases quickly as well as the factor \(\xi\) tends towards −1.

Fig. 2
figure 2

Jump rate r j as a function of the deformability parameter ξ for three values of the normalized collision γ, at fixed barrier \(E_{a} = 6k_{B} T\)

Full size image

On the other hand, in order to study the collision frequency effects on the diffusion process, we have reported in Fig. 3, the behavior of the jump rate r j as a function of the normalized collision frequency γ for different values of the deformation parameter ξ \((\xi = - 0.9,{\kern 1pt} - 0.7,0,0.7\,\,{\text{and}}\,\,0.9)\). We recall that this physical quantity r j is obtained by dividing the total number of jumps by the simulation time.

Fig. 3
figure 3

Upper panel Jump rate r j as a function of the normalized collision frequency γ for three positive values of deformation parameter \(\xi (\xi = 0,0.7\,\,{\text{and}}\,\,0.9)\). Lower panel Jump rate r j as a function of the normalized collision frequency γ for three negative values of deformation parameter \(\xi (\xi = - 0.9,{\kern 1pt} \, - 0.7\,\,{\text{and}}\,\,0)\)

Full size image

As expected, this result shows that the usual turnover behavior that was already found in different works on 1D and 2D (Ferrando et al. 1999; Elkoraychy et al. 2014; Ferrando et al. 2005) systems, by using the Langevin and the BGK equation. For the upper panel (Fig. 3a), the r j has qualitatively the same behavior for the three values of the deformation parameter ξ. For the low values of γ, the r j increases for the three values of ξ until reaching a maximum value in the vicinity of γ = 1 and still tends to decrease to zero when the collision frequency γ tends to higher values. However, this increase is slightly more important when ξ is set to 0.9. This behavior is quite similar to that found in previous studies of 2D systems (Ferrando et al. 1999, 2000; Caratti et al. 1998). For the lower panel (Fig. 3b), we have obtained qualitatively the same behavior as for the left one, except for the deformation parameter ξ = −0.9. As can be seen from the figure for this value of ξ, the function r j is a monotonic decreasing function with the collision frequency. This behavior is essentially due to the structure of the periodic potential which seems to be rectangular for \(\xi = - 0.9\) (the width of its well increases). So, from this study the effects of the deformation parameter ξ and the normalized collision frequency γ on the jump rate are qualitatively well understood. However, from a quantitative point of view, the effects on the probability of making either simple jump are much stronger, as can be seen in Figs. 4 and 5. In Fig. 4, the probability of making single jumps P 1 is reported as a function of the deformation parameter \(\xi\) for three values of \(\gamma\) \((\gamma = 0.1,\text{ }\gamma = 0.3\,{\text{and}}\,\gamma = 1)\). The increase of ξ from −0.9 to 0.9 corresponds to a transformation of the shape potential from a narrowing barriers and wide wells to narrow wells separated by thick barriers. So, as can be seen from the figure, the diffusing particle has a high probability of jumping from one site to the neighboring one when the deformation parameter increases. This is understandable since the latter is the more stable configuration for an adsorbate due to the widening of the well. In this limit the particle spends the most of its time by making small-amplitude oscillations in the bottom of the wells. This behavior becomes more important when the collision frequency increases, (i.e., at fixed \(\xi\), \(P_{1} (\gamma = 1) > P_{1} (\gamma = 0.3) > P_{1} (\gamma = 0.1)\)).

Fig. 4
figure 4

Single-jump probability P 1 as a function of the deformation parameter ξ for γ = 0.1, γ = 0.3 and γ = 1

Full size image
Fig. 5
figure 5

Upper panel single-jump probability P 1 as a function of the normalized collision frequency γ for the three positive values of \(\xi (\xi = 0,{\kern 1pt} \,0.7\,{\text{and}}\,0.9)\). Lower panel single-jump probability P 1 as a function of the normalized collision frequency γ for three negative values of \(\xi (\xi = - 0.9,{\kern 1pt} \, - 0.7\,{\text{and}}\,0)\)

Full size image

In order to study in more details the effect of collision frequency γ, the probability of single jump P 1 is reported as a function of γ in the range 0 < γ < 1, for three different values of ξ (Fig. 5). In general, as expected, the probability of simple jump P 1 increases with increasing γ. We can compare the current results with those of Refs. (Ferrando et al. 1999; Elkoraychy et al. 2014; Ferrando et al. 2000), we found qualitatively the same behavior. For positive values of ξ, this increase of P 1 is slightly important compared to case corresponding to cosine-like potential as can be seen from Fig. 5a. While for negative values (see Fig. 5b), the increase of P 1 becomes weak and do not approaches to its asymptotic value. This finding shows that the diffusing of particle cannot proceed by simple jumps when the substrate potential presents a structure of flat bottoms separated by sharp peaks. In this limit, the diffusion mechanism is described by a liquid-like motion inside the unit cell.

Finally, in short, we study the effect of the normalized amplitude E a on the jump rate r j , to this we report in Fig. 6 the variation of the r j as a function of the deformation parameter ξ for two values of E a (\(E_{a} = 5k_{B} T\) and \(E_{a} = 6k_{B} T\)) and for γ = 0.3.

Fig. 6
figure 6

Jump rate r j as a function of the deformation parameter ξ for two values of the normalized amplitude E a at fixed γ = 0.3

Full size image

The analysis of this figure shows that, for the two values of the normalized amplitude E a we note that the r j has the same behavior, with a clear increase of the r j when the parameter ξ increases. Moreover, when the values of the normalized amplitude E a decreases, the r j tends to the important values. This behavior was already found by our group (Elkoraychy et al. 2014), in which the diffusion process was studied in the 2D triangular potential. The results have shown that, for the low values of the parameter γ the jump rate increases when the normalized amplitude decreases.

4 Conclusion

In this paper the jump rate and the simple-jump probability P 1 for a particle diffusing in 1D deformable periodic potential using a strong collision model (in which each collision with the thermal bath suddenly thermalizes the velocity) has been calculated by direct simulation of the BGK equation, our results have shown that the shape of the substrate potential plays a crucial role in the mobility of the particle. The jump rate r j is increased with the parameter ξ for the small γ (0.1 < γ < 1), the increase is interesting when the parameter ξ tends to high positive values; because the wells become narrow than the maxima. In contrast, for large γ (γ > 1), the decrease of the parameter ξ reduces the jump rate r j . Also, the parameter ξ has an effect on the single-jump probability P 1. As the values of the parameter ξ increases, P 1 reaches its maximums values more quickly. This effect is again due to the narrowing of the wells. The results presented here are almost entirely numerical. Although they were obtained with care, they need to be ultimately backed up by more analytical results. Work in this direction is in progress.