A two-stage optimization strategy for large-scale oil field development

Abstract

The optimization of the locations of a large number of wells in an oil or gas field represents a challenging computational problem. This is because the number of optimization variables scales with the maximum number of wells considered. In this work, we develop and test a new two-stage strategy for large-scale oil field optimization problems. In the first stage, wells are constrained to lie in repeated patterns, and the reduced set of optimization variables defines the pattern type and geometry (e.g., well spacing, orientation). For this component of the optimization, we introduce several important modifications, including optimization of the drilling sequence, to an existing well-pattern optimization procedure. The solutions obtained in the first stage are then used to initialize the second stage optimization. In this stage we apply comprehensive field development optimization, where the well location, type (injection or production well), drill/do not drill decision, completion interval for 3D models, and drilling time variables are determined for each well. Pattern geometry is no longer enforced in this stage. Specialized treatments (consistent with actual drilling practice) are introduced for cases where multiple geomodels, used to capture geological uncertainty, are considered. In both stages optimization is achieved using a particle swarm optimization-mesh adaptive direct search (PSO-MADS) method. The two-stage procedure is applied to 2D and 3D models corresponding to different geological scenarios. Both deterministic and geologically uncertain systems are considered. Optimization results using the new procedure are shown to clearly outperform those from the single-stage comprehensive field development optimization approach. Specifically, for the same number of function evaluations, the two-stage treatment provides net present values that exceed those of the single-stage approach by about 15–18% for the cases considered. This suggests that this optimization strategy may indeed lead to improved results in practical problems.

1 Introduction

Optimization of oil and gas field development decisions, such as the number, types, locations, drilling sequence and control of wells, represents a challenging mixed-integer nonlinear programming (MINLP) problem. MINLP problems are inherently difficult, and these optimizations typically require a very large number of function evaluations (flow simulations in this context). Problem difficulty in oil reservoir management settings generally scales with the number of decision variables, which in this case depends on the maximum number of wells considered. This renders the optimization computationally expensive, if not prohibitive, in large-scale systems where (potentially) hundreds of wells are involved. Large numbers of optimization variables may also lead to degradation in the performance of the optimization algorithm. Thus, it is evident that these problems would benefit from techniques that act to reduce the number of optimization variables. This can be achieved by decoupling the dependence between the number of decision variables and the (maximum) number of wells considered.

In an earlier study, Onwunalu and Durlofsky (2011) developed a well-pattern optimization (WPO) procedure for large-scale field development optimization. The parameterization in WPO defines the locations of wells constrained to lie in repeated patterns, and the optimization variables define the pattern type (e.g., a five-spot pattern, with four production wells surrounding an injection well) and pattern geometry (well spacing and orientation). Posing the optimization problem at the level of well patterns rather than individual wells significantly reduces the number of optimization variables. Our goal in this work is to develop and test a new two-stage technique for large-scale field development optimization. The two-stage procedure entails an enhanced version of the WPO procedure combined with comprehensive field development optimization. The resulting development plan includes well locations and types (with wells not constrained to be drilled in patterns), completion intervals (for 3D models), and drilling schedule.

As discussed by Khor et al. (2017), different techniques, with varying computational requirements, have been proposed to solve oil field development and production system optimization problems. To reduce the computational cost associated with these optimization problems, two general approaches have been introduced. The first set of techniques targets the flow problem. This generally entails replacing the high-fidelity flow simulation model with a lower-fidelity or reduced-order model, or with a model based on simplified flow physics. The second general approach involves reducing the dimension of the optimization problem itself; i.e., limiting the number of optimization variables. Methods based on the first approach include the use of reduced-order numerical models (Van Doren et al. 2006; Cardoso and Durlofsky 2010; He et al. 2011; Suwartadi et al. 2015; Jansen and Durlofsky 2017), machine-learning and deep-learning-based surrogates (e.g., Guo and Reynolds 2018; Nasir et al. 2020; Jin et al. 2020), reduced-physics simulations (e.g., Møyner et al. 2015; de Brito and Durlofsky 2020), or simpler analytical representations such as capacitance-resistance models (e.g., Albertoni and Lake 2003; Lasdon et al. 2017). Multilevel optimization approaches, in which a sequence of upscaled (coarsened) models are applied, have also been developed (Aliyev and Durlofsky 2017).

The second type of cost-reduction approach is applied in this work. There have been a significant number of previous studies along these lines, as we now discuss. Dimension reduction techniques have been proposed for both the production (well control) and field development optimization problems. As shown in previous studies (such as Oliveira and Reynolds 2015; Fonseca et al. 2017; Awasthi et al. 2019), clear benefit can be achieved by optimizing time-varying well settings (e.g., injection/production rates or wellbore pressures) for existing wells. In this problem, the number of decision variables increases as the number of well-control periods increases. The computational cost of such problems can become quite substantial when uncertainty in the geological model is considered (Jansen et al. 2005; Wang et al. 2009; Barros et al. 2020). Trigonometric (Awotunde 2014), polynomial approximation (Sorek et al. 2017), and principal component analysis (Fu and Wen 2018) parameterizations have been applied as dimension reduction techniques for the optimization of time-varying well settings. A review of several dimension reduction techniques for the well control optimization problem can be found in Awotunde (2019).

For field development optimization problems, well-pattern-based optimization has proven to be an effective technique to reduce the number of variables. Pan and Horne (1998) optimized the location of wells in an inverted five-spot pattern using the location of the injector and well-spacing parameters as optimization variables. Ozdogan et al. (2005) proposed a fixed pattern approach to determine the well count and well locations with a line-drive pattern. Volz et al. (2008) and Litvak and Angert (2009) considered the use of three different well patterns (inverted five-spot, inverted seven-spot, and staggered line drive) in optimizing giant oil fields. The well types, length of high-angle wells, and well spacing (from a predefined set) were optimized. More general well-pattern parameterizations (Onwunalu and Durlofsky 2011; Zhang et al. 2017; Fan et al. 2018) have also been introduced.

In this paper, we introduce a new two-stage field development optimization technique that takes advantage of the dimension-reduction capability of well-pattern-based optimization procedures. The optimization in the first stage is similar to the WPO procedure developed by Onwunalu and Durlofsky (2011), though several significant extensions are introduced. These include the incorporation of (pattern-based) drilling-sequence optimization, a reformulation of the problem to provide a further reduction in the number of optimization variables, and application to 3D models. The solutions obtained in the first stage are used to initialize the second-stage field development optimization, in which pattern geometry is not enforced. Optimization in both stages is performed using a derivative-free particle swarm optimization – mesh adaptive direct search (PSO-MADS) hybrid algorithm (Isebor et al. 2014a, b). We also introduce a realization-by-realization well completion technique, which is conceptually consistent with actual drilling practice, for cases where multiple 3D realizations are used to represent geological uncertainty.

This paper proceeds as follows. In Sect. 2, we introduce the comprehensive field development optimization problem, and then describe the enhanced well-pattern optimization procedure, including the drilling-scheduling technique. In Sect. 3, the full two-stage field development optimization approach is presented, along with the realization-by-realization well completion procedure. Computational results demonstrating the performance of the two-stage procedure, for both 2D and 3D problems, are presented in Sect. 4. An example involving geological uncertainty is also considered. We conclude in Sect. 5 with a summary and suggestions for future work.

2 Comprehensive field development and well-pattern optimization

In this section, we first present the comprehensive field development optimization problem. We then describe our implementation of the well-pattern optimization (WPO) procedure. This is similar to the method developed by Onwunalu and Durlofsky (2011), though we introduce several significant new features, including pattern-based drilling-sequence optimization.

2.1 Comprehensive field development optimization

Our goal in the field development optimization problem is to determine the number, types (producer or injector), locations, and drilling sequence for a set of wells. Additional optimization variables defining how the wells are controlled (e.g., time-varying rates or bottom-hole pressures) could also be included, though this is not done here. The comprehensive field development optimization problem, in the absence of well control variables, is written as follows:

$$\begin{aligned} \begin{array}{rrclcl} \displaystyle \max _{\mathbf{u} \in {\mathbb {U}},{\mathbf{v}} \in {\mathbb {V}},{\mathbf{w}} \in {\mathbb {W}}}&{J ({\mathbf{u}} ,{\mathbf{v}} ,{\mathbf{w}} )}, \ \ {\text {subject to }} {\mathbf{c}} ({\mathbf{u}} ,{\mathbf{v}} ,{\mathbf{w}} )\le {\mathbf{0}} , \end{array} \end{aligned}$$

(1)

where J is the objective function to be optimized, the decision vectors ${\mathbf{u}} \in {\mathbb {U}} \subseteq {\mathbb {Z}}^{2N_w}$ and ${\mathbf{v}} \in {\mathbb {V}} \subseteq {\mathbb {Z}}^{N_w}$ represent the discrete well location and drilling sequence variables, respectively, and the vector ${\mathbf{w}}$ (where for well i, $w_{i} \in \{-1,0,1 \}$) contains $N_w$ ternary categorical variables, where $-1$ represents the decision to drill a producer, 1 the decision to drill an injector, and 0 the decision to not drill the well. Here ${N_w}$ denotes the maximum number of wells that can be drilled. The spaces ${\mathbb {U}}$, ${\mathbb {V}}$, and ${\mathbb {W}}$ define the feasible regions for the optimization variables, including upper and lower bounds if applicable. The vector c defines optimization constraints such as minimum well-to-well distance, maximum number of wells to be drilled at a given drilling stage, and maximum production or injection limits.

The vector ${\mathbf{u}}$ contains the two areal location variables associated with each well (for now we assume that all wells are vertical and penetrate the entire formation). These integer coordinates, for well i, are represented by ($\xi _i$, $\eta _i$). The development plan is divided into several drilling stages, with variable $v_i$ defining the stage at which well i is drilled. A constraint is imposed so the number of wells drilled in each stage does not exceed the available number of drilling rigs. Although ${\mathbf{v}}$ and ${\mathbf{w}}$ each contain $N_w$ variables, only $N_w - 1$ components of each are optimized. This is because we assume that at least one producer is drilled in the first drilling stage.

The full set of optimization variables is represented as ${\mathbf{x}} = [{\mathbf{u}} ^T, {\mathbf{v}} ^T, {\mathbf{w}} ^T]^T$. The total number of optimization variables is $4N_w-2$. The number of optimization variables thus scales linearly with the maximum number of wells. Note that in this study, rather than optimize the well controls, we use a ‘reactive-control’ strategy, where wells are operated at fixed rates or bottom-hole pressures (bottom-hole pressure refers to the wellbore pressure at a particular depth) until a prescribed economic limit is reached. One such economic limit is the maximum water cut (fraction of water in the produced fluid) in a production well. This reactive treatment is suboptimal relative to optimizing the well settings, but it results in an optimization problem that is less demanding computationally.

In this work, we seek to obtain the decision variables that maximize net present value (NPV); i.e., we specify $J={NPV}$. Following Shirangi and Durlofsky (2015), we compute NPV as follows:

$$\begin{aligned} NPV({{\mathbf{x}}} )&=\sum \limits _{k = 1}^{N_t} \left[ \sum \limits _{i = 1}^{N_p} \left( p_{o} ~q^{i}_{o,k}-c_{pw}~q^{i}_{pw,k}\right) - \sum \limits _{i = 1}^{N_i} c_{iw}~q^{i}_{iw,k} \right] \frac{\varDelta t_k}{( 1+b )^{t_k/365}} \nonumber \\&\quad - \sum \limits _{i = 1}^{N_w} \frac{|w_i|~c_w}{(1+b)^{ t_i/365}}. \end{aligned}$$

(2)

Here $N_i$ and $N_p$ are the number of injectors and producers, respectively, $N_t$ is the number of time steps in the flow simulation, $t_k$ and $\varDelta t_k$ are the time and time step size at time step k, $t_i$ is the time at which well i is drilled, and $p_{o}$, $c_{pw}$, and $c_{iw}$ represent the oil price and the cost of produced and injected water. The variables $c_w$ and b represent the well drilling cost and annual discount rate. The rates of oil/water production and water injection, for well i at time step k are, respectively, $q^{i}_{o,k}$, $q^{i}_{pw,k}$, and $q^{i}_{iw,k}$. It should be noted that wells introduced by the optimizer (i.e., $w_{i} \in \{-1,1 \}$) that lack an active perforation due to placement in inactive cells, are not included in the drilling cost calculation.

For a given well configuration (potential solution) x, the evaluation of Eq. 2 requires a full flow simulation to be performed. This entails the solution, in time, of a discretized set of nonlinear partial differential equations. For oil-water problems, as are considered in this work, there are two equations and two unknowns for each grid block, which must be evaluated at each time step. Given that practical 3D models may contain $O(10^5{-}10^7)$ grid blocks, these simulations can be quite time consuming, and may require minutes to hours for a single run using a traditional (CPU-based) flow simulator. Thus these optimizations can be very expensive computationally, which provides a strong motivation to accelerate the overall procedure.

2.2 Well-pattern optimization overview

In well-pattern optimization (WPO), instead of optimizing decision variables associated with individual wells as described in the preceding section, the optimization variables describe a group of wells within a reference well pattern. A set of pattern operations is applied to geometrically transform the reference pattern in terms of its size, orientation and shape (skewness). A fixed reference well serves as the origin for each pattern operation, and its location does not change after the operation is performed. The reference well, which affects the pattern geometry and orientation, is an optimization variable associated with each of the pattern operations (the reference well may differ between operations). The patterns are replicated over the entire reservoir, with wells falling outside the reservoir boundary, or in inactive regions, eliminated.

Following Onwunalu and Durlofsky (2011), the three pattern operations considered in this work are illustrated in Fig. 1 for an inverted five-spot pattern. The gray lines indicate the initial well patterns, while the black lines show the resulting patterns after the operations. The scaling operator (Fig. 1a) increases the size of the reference well pattern in the $\xi$ and $\eta$ directions. Here well 3 (shown in green) is the reference well. By varying the size of the well pattern, this operator strongly impacts the number of wells drilled. Figure 1b illustrates the rotation operation, with well 2 as the reference well. Figure 1c depicts the shearing operation – here well 1 is the reference well. Following replication of this well pattern throughout the reservoir, we have the well configuration shown in Fig. 1d.

Fig. 1

Illustration of the scale, rotation and shearing operators for an inverted five-spot pattern. The black and red circles show the producers and injectors, respectively. The green-numbered wells show the reference well for that particular pattern operation (the reference well for each operation is also an optimization variable). (Color figure online)

WPO contains three groups of optimization variables: those associated with the well-pattern parameterization, the operator parameters, and (optionally) parameters that define the sequence of the application of the operators. Different well pattern types can be considered in WPO. The reference well pattern, ${\mathbf{w}} _{p}$, is defined as follows:

$$\begin{aligned} {\mathbf{w}_p} = \left[ {I}^{wp}, \ \xi _0, \ \eta _0, \ {a}, \ {b} \right] ^{T}, \end{aligned}$$

(3)

where $I^{wp} \in \{1,\ 2,\ 3 \}$ is a categorical variable that indicates the pattern type (five-spot, seven-spot and nine-spot are considered in this work), $\xi _0$ and $\eta _0$ are integer variables that define the areal location of the center of the pattern on the simulation grid, and a and b are user-defined well spacing parameters that specify the minimum size of the reference well pattern.

2.3 Well pattern operators

The manipulation of the reference pattern is achieved using the three geometric transformation operators described above along with a switch operator. The components of the corresponding geometric transformation matrices (including the reference well) are optimized in order to vary the size, shape, and orientation of the reference pattern. The geometric transformations can be described using:

$$\begin{aligned} {\mathbf{W}} _{out, j}^{T} = {{\mathbf{M}}} _{j}{} {\mathbf{W}} _{in, j}^{T}, \ \ j \in\{\text{scale, rot, shear} \}, \end{aligned}$$

(4)

where ${{\mathbf{M}}} _{scale}$, ${{\mathbf{M}}} _{rot}$, and ${\mathbf{M}} _{shear}$ $\in \mathbb {R}^{2\times 2}$ are geometric transformation matrices (discussed later) for the scaling, rotation and shearing operations. The matrix $\mathbf{W} _{in, j} \in \mathbb {R}^{N_{wp} \times 2}$ defines the well locations for the individual wells $(\xi _i, \ \eta _i; \ \ i = 1,\ldots , N_{wp})$, relative to the reference well location $(\xi ^{ref}_{j},~\eta ^{ref}_{j})$, prior to the transformation. Here $N_{wp}$ is the number of wells in the pattern. The matrix $\mathbf{W} _{out, j}$ defines the pattern after the transformation, with the new well locations $(\hat{\xi }_i,~\hat{\eta }_i)$ also defined relative to the reference well. The matrices $\mathbf{W} _{in, j}$ and $\mathbf{W} _{out, j}$ are given by:

$$\begin{aligned} \mathbf{W }_{in, j} = \begin{pmatrix} \xi _1 - \xi ^{ref}_{j} &{} \eta _1 - \eta ^{ref}_{j}\\ \xi _2 - \xi ^{ref}_{j} &{} \eta _2 - \eta ^{ref}_{j}\\ \vdots &{} \vdots \\ \xi _{N_{wp}} - \xi ^{ref}_{j} &{} \eta _{N_{wp}} - \eta ^{ref}_{j} \end{pmatrix}, \ \ \ \ \ \ \ \ \mathbf{W }_{out, j} = \begin{pmatrix} {{\hat{\xi }}}_1 - \xi ^{ref}_{j} &{} {{\hat{\eta }}}_1 - \eta ^{ref}_{j}\\ {{\hat{\xi }}}_2 - \xi ^{ref}_j &{} {{\hat{\eta }}}_2 - \eta ^{ref}_{j}\\ \vdots &{} \vdots \\ {{\hat{\xi }}}_{N_{wp}} - \xi ^{ref}_{j} &{} {{\hat{\eta }}}_{N_{wp}} - \eta ^{ref}_{j}\\ \end{pmatrix}. \end{aligned}$$

(5)

We now describe the various well pattern operators. The scale operator increases the size of the reference well pattern from its minimum size defined by the well spacing variables (a,  b). This is in contrast to the treatment in Onwunalu and Durlofsky (2011), where the scale operator decreases or increases the size of the reference well pattern, and a and b are additional decision variables.

The nonuniform scaling matrix, $\mathbf{M }_{scale}$, used to scale a well pattern in the $\xi$ and $\eta$ directions by (axis-aligned) scaling factors $S_{\xi }$ and $S_{\eta }$ (with $S_{\xi },~S_{\eta }\ge 1$), is given by:

$$\begin{aligned} \mathbf{M }_{scale} = \begin{pmatrix} S_{\xi } &{} 0\\ 0 &{} S_{\eta } \end{pmatrix}. \end{aligned}$$

(6)

The clockwise rotation matrix, ${\mathbf{M}} _{rot}$, is used to rotate a well pattern by an angle $\theta$ ($\theta > 0$ indicates clockwise rotation). This matrix is defined as:

$$\begin{aligned} \mathbf{M }_{rot} = \begin{pmatrix} \text {cos} \theta &{} \text {sin} \theta \\ -\text {sin} \theta &{} \text {cos} \theta \end{pmatrix}. \end{aligned}$$

(7)

The shear operator alters the shape of a well pattern by skewing the pattern in the $\xi$ and $\eta$ directions. The degree of shearing is dictated by the axis shearing factors $H_{\xi }$ and $H_{\eta }$. These quantities appear in the shear matrix $\mathbf{M }_{shear}$, given by:

$$\begin{aligned} \mathbf{M }_{shear} = \begin{pmatrix} 1 &{} H_{\xi }\\ H_{\eta } &{} 1 \end{pmatrix}. \end{aligned}$$

(8)

The rotation and shear operators are particularly important in optimizations involving channelized geomodels, as they give the optimizer more flexibility in terms of aligning wells with channels.

Finally, the switch operator is a non-geometric operator that converts the reference well pattern from inverted to normal. This is achieved by switching the well types in the reference pattern. The switching operation is dictated by a binary categorical variable $S_{p} \in \{0, 1\}$, where 1 represents the decision to switch the reference pattern from inverted to normal. Note that this procedure will, in general, affect the number of injection versus production wells, though it does not alter the total number of wells.

In our implementation of the WPO, we have a total of 12 optimization variables within the decision vector ${\mathbf{x}} _{w}$. These include two categorical variables (well pattern type and switch operator), two integer variables (these define the location of the reference well pattern), and eight continuous variables (components of the three geometric transformation matrices and their corresponding reference wells). Accordingly, ${\mathbf{x}} _{w}$ is given by:

$$\begin{aligned} {\mathbf{x}} _{w} = \Bigl [ \underbrace{{I}^{wp}, \ S_{p}}_{categorical}, \ \underbrace{\xi _0, \ \eta _0}_{integer}, \ \underbrace{S_{\xi }, \ S_{\eta }, \ \theta ,\ H_{\xi },\ H_{\eta }, \ R_{scale}, \ R_{rot}, \ R_{shear}}_{continuous} \Bigr ]^{T}, \end{aligned}$$

(9)

where $R_{scale}$, $R_{rot}$, and $R_{shear}$ $\in \mathbb {R}$ are scalar variables that define the reference wells for the scaling, rotation and shearing operators. These optimization variables are restricted to the range [0,  1], with the resulting value linearly mapped to the number of wells ($N_{wp}$) in the reference pattern to obtain the reference well (e.g., a value of 0.3 in a five-spot pattern would correspond to well 2).

The major advantage of this well pattern parameterization for the field development optimization problem is that the number of decision variables does not scale directly with the maximum number of wells considered. With the formulation described above, we found that the sequence in which the operators are applied does not have a noticeable effect on the well pattern and scheduling (described later) optimization problem. For this reason, in contrast to Onwunalu and Durlofsky (2011), we do not include sequence parameters in the full set of optimization variables.

Onwunalu and Durlofsky (2011) implemented an optional well-by-well perturbation (WWP) step that can be used to improve upon the repeated well pattern solution. This is achieved by optimizing well location perturbations, in the $\xi$ and $\eta$ directions, for each well in the repeated pattern solution. The perturbation step is illustrated in Fig. 2. The well pattern here corresponds to a standard five-spot (thus the pattern boundary is a square), and $\varDelta$ is a user-defined parameter that specifies the maximum perturbation for the central well. In this work we allow the perturbation to shift wells into adjacent patterns, though this was not permitted in the original WWP treatment. Optimization variables are $\varDelta \xi$ and $\varDelta \eta$ for each well, and the central well location after application of the perturbation is shown in the right image. WWP shares some similarities with the comprehensive field development optimization, where wells are optimized individually, though in WWP the well count and types are fixed and the search space is much smaller.

In this paper, we use ‘WPO’ to mean the pattern-based optimization method without the WWP step. We use the terminology ‘WPO-WWP’ to denote the case where WWP is applied after WPO.

Fig. 2

Illustration of the well-by-well perturbation (WWP) procedure for a standard five-spot pattern. The original position of the central well is shown as the red circle, and the perturbed position as the blue circle (right figure). (Color figure online)

2.4 Drilling sequence optimization for WPO

The WPO procedure described thus far provides optimized well patterns, but it does not define the sequence in which the well patterns are drilled. We now discuss our approach for optimizing the drilling sequence. We assume the wells are drilled in a maximum of $N_d$ discrete stages ($N_d$ is an input parameter), with all wells in a particular pattern drilled in the same stage. The optimized solution will in general entail fewer than $N_d$ stages. In practice, $N_d$ can be determined heuristically and/or based on well cost and the project budget. The WPO solution ${\mathbf{x}} _{w}$ is now taken to define the shape, size, orientation and location of the reference well pattern. This pattern is drilled in the first drilling stage, and is not yet replicated over the domain.

After the first well pattern is placed, we require that subsequent patterns be drilled adjacent to an existing pattern. This pattern-adjacency requirement could be relaxed though, consistent with many treatments at the WPO stage, it acts to reduce the complexity of the optimization problem. Complexity reduction is achieved because, by specifying pattern adjacency, the number of combinatorial options at each drilling stage are reduced, thus simplifying the overall optimization. This simplification of the drilling sequence component of WPO is thus compatible with our goal of emphasizing simplicity over generality at the first stage of the procedure. This requirement, along with the specification that wells be drilled in patterns, will be relaxed in the second stage. We note that pattern adjacency may, in some cases, be consistent with actual practice as it reduces rig movement.

Given the reference (initial) well pattern, the second-stage pattern can be drilled in four possible locations, adjacent to the reference well pattern. These potential locations are indicated by $p_1$, $p_2$, $p_3$ and $p_4$ in Fig. 3a for a five-spot reference well pattern (defined by the black lines). An additional null well pattern, $p_0$, is also considered by the optimizer at every drilling stage. If the optimizer selects $p_0$, no well pattern is drilled at that stage.

We introduce a vector $\mathbf{d} \in \mathbb {R}^{N_d-1}$ containing the decision variables that indicate which well pattern to drill in each of the $N_d - 1$ drilling stages (there is no decision variable for the first drilling stage). The values in $\mathbf{d}$ are bounded between 0 and 1. The corresponding drilling sequence decision variable for any drilling stage is then mapped, based on the number of patterns considered for drilling at that stage, to define the pattern to be drilled.

This treatment can be readily explained with reference to the five-spot patterns shown in Fig. 3. There are five options in the second stage ($p_0$ through $p_4$). If the decision variable for the second drilling stage ($d_1$) falls in the range $d_1 \le 0.2$, no well pattern (corresponding to $p_0$) is drilled in this stage. If $0.2 < d_1 \le 0.4$, then $p_1$ is drilled, if $0.4 < d_1 \le 0.6$, then $p_2$ is drilled, etc. The situation depicted corresponds to $p_3$ being drilled in stage 2 (meaning $0.6 < d_1 \le 0.8$). In the third drilling stage, shown in Fig. 3b, there are seven options for the next pattern. At this stage, for example, if $2/7 < d_2 \le 3/7$, then $p_2$ will be drilled. This process continues until all drilling stages are considered.

Fig. 3

Illustration of the drilling sequence procedure for a five-spot pattern at two different drilling stages. The black lines show the outer boundaries of patterns already drilled, while the gray lines indicate possible patterns that can be drilled at that stage. (Color figure online)

In order to impose a degree of ‘continuity’ on the drilling sequence optimization variable, at each drilling stage k, we reorder the well patterns under consideration based on their spatial location. With the new ordering, neighboring patterns have pattern-vector indices that are close to one another (e.g., pattern $p_3$ is near $p_4$). The reordered patterns are illustrated in Fig. 4. As a result of the reordering, small changes in $d_{k-1}$ generally correspond to small shifts in pattern location. We also introduce the concept of zones (see Fig. 4), which correspond to groups of patterns. Jumps in pattern index do not occur within a zone, but they may occur between zones (e.g., pattern $p_9$ is next to $p_1$, but they are in different zones). This reordering is useful when local search optimization algorithms such as MADS are applied, since these methods introduce small, systematic perturbations to the optimization variables. With this approach, large perturbations can be viewed as shifts between zones, while small perturbations correspond to shifts within a zone.

Fig. 4

Reordered well patterns and zones

The well pattern and drilling sequence optimization problem can now be expressed as follows:

$$\begin{aligned} \begin{array}{rrclcl} \displaystyle \max _{\mathbf{x}_{p} \in \mathbb {X}_{p}}&{J ({\mathbf{x}} _{p})}, \ \ \text {subject to } \mathbf{c} ({\mathbf{x}} _{p})\le \mathbf{0} , \end{array} \end{aligned}$$

(10)

where ${\mathbf{x}} _{p} = \left[ {\mathbf{x}} _{w}^{T}, \ \mathbf{d} ^{T} \right] ^{T}$ and J is taken to be NPV. The space $\mathbb {X}_{p}$ defines the allowable values of all decision variables. The total number of optimization variables for the well pattern and scheduling problem is $11+N_d$. Although this does depend on $N_d$, we reiterate that it is independent of the maximum number of wells considered.

3 Two-stage field development optimization and multiple realization treatment

In this section, we present the two-stage field development optimization procedure, followed by a brief description of the particle swarm optimization – mesh adaptive direct search (PSO-MADS) method (Isebor et al. 2014a, b) used in this work. Finally, the realization-by-realization well completion treatment, applicable for use in optimizations over multiple geomodels, is described.

3.1 Two-stage field development optimization technique

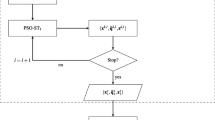
In fields that will be developed based on well patterns, the optimal development plan is defined by the ${\mathbf{x}} _{p}$ that maximizes the objective function J in Eq. 10. In cases where the goal is to solve the more general optimization problem represented by Eq. 1, however, this ${\mathbf{x}} _{p}$ will be suboptimal. As we will see, it nonetheless represents a reasonable initial guess for the general problem in Eq. 1. This is the motivation for the two-stage procedure, which we now describe.

In the first stage of this procedure, we solve the well pattern and scheduling optimization problem (Eq. 10) to provide ${\mathbf{x}} ^{opt}_{p}$. This optimization can be accomplished relatively efficiently since it involves only $11+N_d$ optimization variables. It should be noted that constraints on the minimum well-to-well distance, or on the maximum number of wells to drill within a given drilling stage, can be accommodated in this stage. The resulting ${\mathbf{x}} ^{opt}_{p}$ provides an estimate of the number of wells, the producer-to-injector ratio, well locations, and the drilling schedule for the comprehensive field development optimization.

Given ${\mathbf{x}} ^{opt}_{p}$ as an initial solution, we solve the comprehensive field development optimization problem in the second stage. We further enrich the quality of the initial PSO swarm/population in the second-stage optimization by including additional particles (potential solutions) from the final PSO swarm of the first-stage optimization. Specifically, particles corresponding to development plans with the same number of wells, or fewer wells, than ${\mathbf{x}} ^{opt}_{p}$ are included in the initial second-stage swarm. First-stage solutions are mapped to second-stage solutions by transforming the solutions represented by ${\mathbf{x}} _{p}$ to solutions represented by ${\mathbf{x}}$. This entails mapping from the WPO representation, which involves $11+N_d$ variables, to the comprehensive field development problem representation, involving $4N_w-2$ variables for 2D areal problems and $6N_w-2$ variables for multilayer problems (with $N_w$ determined from ${\mathbf{x}} ^{opt}_{p}$). The remaining initial particles in the second-stage optimization are initialized randomly.

If the optimization involves a multilayer reservoir model, the wells are completed in all layers during WPO. In the second stage, however, the completion interval for each well is optimized. This involves the determination of two additional optimization variables, which is why we have $6N_w-2$ variables in 3D. These variables correspond to the first and last layers at which each well is completed.

Although the same parameterization is used in the second stage of the two-stage procedure as in a comprehensive (single-stage) optimization, the two-stage approach has several advantages over the single-stage method. Specifically, in the second step of the two-stage approach, we have a reasonable estimate of the number of wells required for the field development, whereas in the single-stage approach a somewhat arbitrary (and relatively large) number of wells must be considered. This will typically result in more decision variables in the single-stage procedure. In addition, the use of ‘pre-optimized’ initial solutions in the second stage, which satisfy geometric and operational constraints, considerably reduces the computational cost of solving Eq. 1, as we will see later.

As noted earlier, optimization in both stages is accomplished using a derivative-free particle swarm optimization – mesh adaptive direct search (PSO-MADS) hybrid algorithm (Isebor et al. 2014a, b). PSO is a population-based stochastic search method that explores globally, though there is no guarantee of convergence to even a local optimum. Particles in the swarm/population move within the search space, from iteration to iteration, based on particle velocities. The search entails cooperative, explorative and exploitative aspects. MADS is a pattern-search algorithm that involves local search (polling), in randomly selected directions, around the best solution found thus far in the optimization. Under certain conditions MADS ensures convergence to a local optimum. In general, there is no practical way to determine how close this local optimum is to the (unknown) global optimum. However, the global search component provided by PSO, along with the fact that the overall PSO-MADS procedure is typically run multiple times, allows us to avoid converging to poor local optima in practice.

The hybrid PSO-MADS algorithm benefits from the global exploration accomplished by PSO in combination with the local search provided by MADS. The algorithm switches back and forth between PSO and MADS based on particular criteria and settings. This approach has been shown to be preferable to simply performing some number of MADS iterations after PSO has terminated (though this can also be effective). Interested readers are referred to Onwunalu and Durlofsky (2010) for the application of standalone PSO, and to Isebor et al. (2014a, b) for a detailed description of the PSO-MADS algorithm along with extensive computational results and performance comparisons. Other standalone and/or hybrid optimization procedures could also be considered for both WPO and the comprehensive field development optimization. Possible options include genetic algorithms, differential evolution and iterative Latin hypercube sampling.

Algorithm 1 below describes the treatments applied in both stages of the optimization.

3.2 Realization-by-realization well completion procedure

In cases where multiple realizations are used to capture geological uncertainty, the objective function is generally taken to be the expected NPV, defined as follows:

$$\begin{aligned} J({\mathbf{x}} )= \frac{1}{N_r} \sum \limits _{k = 1}^{N_r} \hbox {NPV}({\mathbf{x}} , {\mathbf{m}} _k). \end{aligned}$$

(11)

Here $N_r$ is the number of realizations considered, and ${\mathbf{m}} _k$, $k=1, \ldots , N_r$, represents the model parameters for realization k. For WPO, ${\mathbf{x}}$ is replaced by ${\mathbf{x}} _{p}$ in Eq. 11. As written, the same field development strategy proposed by the optimizer, ${\mathbf{x}}$ (or ${\mathbf{x}} _{p}$), is used to evaluate the NPV for all $N_r$ realizations in Eq. 11. This means, for example, that wells in all geomodels will have the same set of completions, even if real-time drilling data available to the operator suggest a different strategy.

To partially account for actual drilling and completion practice in our optimization, we introduce a realization-by-realization well completion treatment. With this approach, for each production well proposed by the optimizer, we apply a separate decision as to whether or not each intersected grid block, in each realization, should be perforated. This is meant to approximately mimic actual practice, where the well-completion strategy would be adjusted based on available data.

In this work, the perforate/do not perforate decision is based on a simple measure of local permeability. Specifically, for vertical wells in 3D geomodels (as are considered here), we compute an average permeability over a $3 \times 3$ region centered at the target well block. Inverse-distance-squared weighting is applied in this averaging procedure. If this average permeability exceeds a predefined threshold, the well is perforated in the block (otherwise it is not). A region beyond just the well block is considered because near-well (radial) ‘effective’ permeability is known to be impacted by permeability values outside the well block. In fact, effects extending a distance of $O(l_c)$ from the well, where $l_c$ is the permeability correlation length, were considered by Yeten et al. (2000) in their estimates of near-well effective permeability. Our treatment here is approximate, and more detailed measures of local permeability (such as that described by Yeten et al. 2000) could be readily incorporated. The perforations for injection wells are taken to be the same across all realizations.

The modified objective function for comprehensive field development under geological uncertainty is now given by:

$$\begin{aligned} J({\mathbf{x}} )= \frac{1}{N_r} \sum \limits _{k = 1}^{N_r} \hbox {NPV}({\mathbf{x}} _k, {\mathbf{m}} _k), \end{aligned}$$

(12)

where ${{\mathbf{x}}} _k$ is the field development solution with the ‘customized’ perforation strategy for realization k. The perforations associated with ${\mathbf{x}} _k$ always correspond to a subset of those defined by ${\mathbf{x}}$ (the latter represents the completion interval proposed by the optimizer). We note finally that the ability to perforate each realization differently leads to cost savings in two ways. First, there are direct cost savings due to fewer total perforations. Second, and perhaps more importantly, the optimizer has more flexibility in its proposals for ${\mathbf{x}}$, given that the ${\mathbf{x}} _k$ for each realization will, in general, be different.

4 Computational results

In this section, we apply the various field development optimization strategies to two example cases. The first case is a 2D system characterized by a Gaussian permeability field. This model, shown in Fig. 5a, contains $120 \times 120$ grid blocks (14,400 total cells). Porosity is constant and set to 0.2. The grid block dimensions are $\varDelta x = \varDelta y = \varDelta z = 50$ ft. The second case is based on the 3D Olympus model developed by Fonseca et al. (2018). The particular realization used in the deterministic optimization cases is shown in Fig. 5b. This model contains $118 \times 181 \times 16$ grid blocks (for a total of 341,728 cells, of which 192,750 are active), with each block of approximate size 164 ft $\times$ 164 ft $\times$ 10 ft. Porosity in this case varies spatially. An impermeable shale layer separates the model into two zones. The upper zone contains fluvial channel sands, and the lower zone is characterized by alternating layers of coarse, medium and fine sand. Different capillary and relative permeability curves, as provided in Fonseca et al. (2018), are specified for the four facies types (channel, coarse, medium, and fine sands).

Figure 6 shows the oil and water relative permeability curves for the medium sand in the Olympus model. These curves are also used in the 2D case. The simulation and optimization parameters for both cases are shown in Table 1. Many of these parameters are consistent with those given by Fonseca et al. (2018), though we increased the oil price to a value close to the average US spot price for 2019. Wells operate at prescribed bottom-hole pressures unless a maximum water cut (0.88) is reached in a production well, at which point the well is shut in (closed to flow).

Fig. 5

Log-permeability fields (with permeability in md) for the 2D Gaussian and 3D Olympus models

Fig. 6

Oil and water relative permeability curves for the medium sand facies of the Olympus model and the 2D Gaussian permeability case

For the 2D case, we assess the performance of a wide range of optimization strategies. These include the two-stage optimization approach, WPO with the additional WWP step (WPO-WWP), an aided single-stage comprehensive field development optimization procedure (by ‘aided’ we mean that we set the maximum number of wells, which defines the number of optimization variables in the comprehensive field development optimization, to the value determined by WPO), and single-stage comprehensive field development optimization with varying maximum number of wells. For the 3D Olympus case, which is more time consuming to run, we consider only the two-stage and aided comprehensive field development optimization strategies. We also evaluate the performance of the realization-by-realization well completion procedure, with eight realizations of the Olympus model. The abbreviations used for the different procedures, along with a brief description of each approach, are provided in Table 2.

A total of 12 drilling stages are considered in both cases. This means there are 23 optimization variables in WPO. For all WPO runs, we use 40 PSO particles and a 2n stencil in MADS, where n is the number of optimization variables. In all comprehensive field development and WWP optimization runs, where the decision variables are associated with individual wells, 100 PSO particles are used. Due to the stochastic nature of PSO-MADS, each optimization is run three times. Although this is not nearly enough runs to provide statistically converged results, it does reduce the chance of finding a poor local optimum (though this is not usually a major issue with PSO-MADS).

After the three WPO runs, the maximum number of wells in the optimal solutions, over all three runs, is specified to be the maximum number of wells in the second step of the two-stage optimization and in aided single-stage comprehensive field development optimization. In each second-step optimization, the initial solution is obtained from the corresponding WPO run. If the number of wells for that run is less than the maximum number of wells considered, additional wells are included in the set of optimization variables, though they are initialized with $w_i=0$ (which corresponds to do not drill). The maximum number of wells that can be drilled in a single drilling stage ($N_d$) is set to nine.

We now comment on the data that could be used to condition the geomodels considered in the optimizations. The models are assumed to be constructed such that they honor all available hard data and any measured production data. For a new field there will be very little production data, but in mature fields existing wells will provide some amount of production data, and these data can be used to condition the geomodels. Although not considered in this work, the models could be history matched at each step of the optimization procedure to ensure consistency with the production data from all previous drilling stages. A detailed procedure that accomplishes this, referred to as closed-loop field development (CLFD), was presented by Shirangi and Durlofsky (2015). This general approach could be employed with the optimization strategies considered here. Additional effects would need to be considered in WPO, however, as there will be existing wells (that are not in patterns) in all drilling stages after the first.

Table 1 Simulation and optimization parameters used in both cases

Table 2 Summary of the different optimization procedures considered

4.1 Example 1: 2D Gaussian permeability model

We now present optimization results for the 2D case. Oil-water flow is considered, and the simulations are performed using Stanford’s Automatic Differentiation-based General Purpose Research Simulator, AD-GPRS (Zhou 2012). The total simulation time frame is 2500 days, and each drilling stage is of length 200 days (with the simulation starting at the end of the first drilling stage). Thus, after all drilling is completed, there is a final production period of 300 days. The minimum well-to-well distance, which also defines the initial well pattern size, is set to 500 ft (corresponding to 10 grid blocks).

In these optimizations, as well as those for the 3D case, we assume there are sufficient rigs to drill all wells associated with a given drilling stage. In practice, if excess rigs are available during some periods, this could also be accomplished via pre-drilling, meaning some of the wells are drilled before the stage at which production or injection begins. In this work the only factor that affects capital cost is the number of wells drilled. Although not considered here, rig movement costs could be easily included in the NPV computation. If these costs are sufficiently high, they could impact the optimal field development plan as it will be beneficial to drill new wells near existing wells to reduce rig time.

The PSO runs are fully parallelized; i.e., 40 processors are used for the WPO runs, and 100 processors are used for all comprehensive field development optimization runs. The initial PSO particles for WPO and the single-stage comprehensive field development optimizations are randomly initialized, although user-defined solutions could also be incorporated. A maximum of 20,000 simulations is used as the termination criterion for the two-stage and comprehensive field development optimization procedures. In the two-stage procedure, the WPO stage is terminated after 1200 simulation runs. In some cases, NPV plateaus before these maximum values are reached, which suggests that the use of more sophisticated termination criteria would lead to efficiency improvements.

We first compare the two-stage approach to WPO with the well-by-well perturbation (WPO-WWP). Two different maximum perturbation sizes, $\varDelta = 5$ and $\varDelta = 10$ grid blocks, are considered in WWP. For $\varDelta = 10$, wells may be shifted into adjacent patterns. Figure 7 shows the evolution of NPV for the WPO procedure and Fig. 8 displays NPV evolution for the two-stage and WPO-WWP procedures. In these and subsequent figures, the solid curve depicts the mean, and the shaded region displays the range, for the three runs performed for each method. In Fig. 7, we see that the curve flattens after about 1000 simulations, though it is possible that some improvement could be achieved with additional iteration. It is evident in Fig. 8 that, following the WPO runs (green curves, extending out to 1200 simulations), WWP with either $\varDelta$ value (black and cyan curves) provides a slight improvement in NPV. There is, however, little increase in NPV after about 8000 simulations.

Fig. 7

Evolution of NPV for the 2D case using the WPO procedure. The shaded region indicates the range of NPV over the three runs, and the solid curve shows the mean. (Color figure online)

Fig. 8

Evolution of NPV for the 2D case, for the two-stage procedure (WPO-Comprehensive) and for WPO followed by WWP (WPO-WWP). Shaded regions indicate the range of NPV over the three runs, and curves indicate the mean. (Color figure online)

The two-stage approach (dark blue dashed curve) clearly leads to higher NPVs than WPO-WWP (even with $\varDelta = 10$) for this case. In fact, the optimal NPV continues to improve even up to the termination of the optimization at 20,000 simulations. This demonstrates the benefit of optimizing well count, well types, drilling sequence and well locations after WPO, rather than just perturbing the well locations as in WPO-WWP.

The performance of the two-stage approach is now compared to that of single-stage comprehensive field development optimization. Three different comprehensive (single-stage) cases are considered: aided comprehensive field development optimization, where we set the maximum number of wells to be that obtained from WPO (which in this case is 24 wells), a case with a maximum of 32 wells, and a case with a maximum of 40 wells. The latter two cases entail exploration of higher-dimensional search spaces than are considered in the aided comprehensive field development optimization, which has the same number of optimization variables as the second step of the two-stage approach. Results for all methods are presented in Fig. 9. It is apparent that the two-stage approach consistently outperforms aided comprehensive field development optimization. The average NPV obtained for the aided comprehensive field development optimization after 20,000 simulations is essentially that obtained by the two-stage approach after 2500 simulations (1200 WPO simulations followed by 1300 second-stage simulations). Interestingly, comprehensive field development optimization with a maximum of 32 wells slightly outperforms the same procedure with 40 wells. This is presumably because the latter case entails a more challenging optimization problem, and the optimum number of wells is (likely) less than 32. The mean results for these two cases are, however, quite close at the end of the runs.

Fig. 9

Evolution of NPV for the 2D case, for the two-stage procedure (WPO followed by comprehensive field development optimization), aided single-stage comprehensive field development optimization, and single-stage comprehensive field development optimization with a maximum of 32 and 40 wells. Shaded regions indicate the range of NPV over the three runs, and curves indicate the mean. (Color figure online)

Table 3 presents NPVs for the individual runs at different stages of the optimization. We see that WPO, after 1200 simulations, consistently provides better solutions than the aided single-stage comprehensive field development approach after 3000 simulations. In the best two-stage run (run 2), the optimal solution found using WPO has an NPV of $795.2 million. The second-stage optimization provides an NPV of $959.2 million, which represents a 20.6% increase over that of WPO. Compared to the best aided single-stage comprehensive field development optimization run (run 2, with an NPV of $814.0 million), the best solution from the two-stage approach yields an NPV that is 17.8% higher.

Table 3 NPV (in million USD) for two-stage and single-stage comprehensive (aided) optimization for the 2D case

The well configurations corresponding to the best solutions obtained using WPO, two-stage optimization, and aided single-stage comprehensive field development optimization, are displayed in Fig. 10. In the figure, the red circles denote production wells and the blue circles injection wells. The numbers inside the circles indicate the drilling stage. The reference well pattern (drilled in stage 1) of the best WPO solution is an inverted seven-spot. This WPO solution corresponds to a total of 24 wells (17 producers and seven injectors). In this solution, almost all producers are placed in high-permeability regions. The maximum number of wells in the aided single-stage comprehensive field development optimization, and in the second step of the two-stage optimization, is set to 24 (which corresponds to 94 optimization variables).

The optimal solution obtained using the two-stage approach, shown in Fig. 10b, has 12 producers and eight injectors. This is an increment of one injector and a decrease of five producers from the (initial) WPO solution. The solution from the aided single-stage comprehensive field development optimization approach corresponds to 12 producers and nine injectors, which is similar to the two-stage result (12 producers and eight injectors).

It is evident in Fig. 10 that wells drilled in the same drilling stage in the two-stage and aided single-stage comprehensive field development optimizations can be quite far apart. This is in contrast to the WPO solution shown in Fig. 10a. In that case, in order to simplify the optimization, new well patterns are constrained to be near existing patterns. The fact that wells in different portions of the field are drilled at the same time (in Fig. 10b and c) is consistent with our assumption that multiple rigs are available and that the cost of rig movement is small compared to drilling costs.

This assumption is reasonable in many onshore settings, such as those corresponding to the examples in this paper. Consider, for example, a case where we have three onshore ‘walking’ rigs that can move 33 ft per hour, with an interwell movement cost of $25,000 to $35,000 per day. In this case we estimate that, for the best two-stage solution (Fig. 10b), we would require total rig movement of approximately 34,000 ft (with nearby wells drilled using the same rig). This corresponds to $1.1 million to $1.5 million, which is significantly less than the cost ($300 million) required to drill the 20 wells in the two-stage solution. We note that, if rig movement costs are an important factor, they can be readily incorporated into any of the optimization procedures considered in this work.

The drilling sequences for the two-stage and aided optimization procedures are summarized in Fig. 11. The number of producers and injectors drilled in each stage are indicated, and these differ significantly between the two solutions. Specifically, all wells except for one injector in the two-stage solution are drilled by the end of drilling stage 7, while in the aided single-stage comprehensive field development solution, five wells are drilled at later stages.

Figure 12 presents the field-wide cumulative oil production, water production and water injection for the maximum NPV case for each of the three optimization strategies. As is evident in Fig. 12a, the best solution obtained using the two-stage approach results in the most cumulative oil production as well as the most water injection (Fig. 12c). Interestingly, this solution also corresponds to the latest water breakthrough time (Fig. 12b). This result is consistent with the better positioning and sequencing of wells in the two-stage solution.

Fig. 10

Best well configurations for WPO, two-stage, and aided single-stage comprehensive field development optimization procedures, for the 2D case. Red circles denote producers, blue circles denote injectors, and the numbers indicate the drilling stage. Black lines in (a) show the reference well pattern. (Color figure online)

Fig. 11

Drilling schedule showing the number of producers and injectors for the two-stage and aided single-stage comprehensive field development optimization procedures for the 2D case

Fig. 12

Field-wide cumulative oil production, water production and water injection for the best solutions obtained using WPO, two-stage, and aided single-stage comprehensive field development optimization approaches, for the 2D case

Figure 13 shows oil saturation maps at the beginning of different drilling stages for the best two-stage solution. The final oil saturation map, at 2500 days, is also presented. The heavier circles indicate wells drilled at that specific stage. We see that the overall development plan results in a fairly uniform sweep. Note the strategic drilling of wells in stages 6 and 12. The producer in stage 6 is clearly effective, as can be seen by the final saturation map. The injector drilled in stage 12, although very near a producer, is still beneficial considering the amount of oil left in that (low-permeability) region. This well does not lead to excessive water production, as there are only 300 days of production after the well is drilled.

Fig. 13

Oil saturation maps (including final saturation) at different drilling stages for the best solution obtained using the two-stage approach for the 2D case. Red circles denote producers, blue circles denote injectors, and heavy circles indicate wells drilled in the current drilling stage. Numbers indicate the drilling stage. (Color figure online)

4.2 Example 2: 3D Olympus model

We now present results for the two-stage and aided single-stage comprehensive field development optimization approaches using a single realization of the 3D Olympus model. Realization 1, used in this assessment, is shown in Fig. 5b. In this case, the oil-water flow simulations are performed using the Echelon GPU-based simulator (Echelon 2019). The total simulation time is 6500 days. Each drilling stage is of length 500 days, and there is a final production period of 1000 days. The simulations are performed on four GPUs. While this does not allow for full parallelization (as each iteration in the comprehensive field development procedure requires 100 simulations), it is still faster in terms of wall-clock time than running AD-GPRS on 100 CPU cores. Each Echelon simulation requires about 24 seconds on a Nvidia Tesla V100 GPU.

The wells in this case are all specified to be vertical. During WPO, wells are drilled (and perforated) in all layers. In the comprehensive field development optimization procedure, the completion interval (first and last layer in which the well is open to flow) for each well is also determined. This means we have two additional variables for each well, and the number of decision variables is now $6N_w - 2$. It should be noted that the number of decision variables in WPO is still $11 + N_d$. In addition to the base drilling cost per well, there is an additional within-reservoir drilling cost ($150,000 per model layer) and a perforation cost ($125,000 for each grid block in which the well is perforated). The minimum well-to-well distance (which also defines the initial pattern size) is set to 1640 ft. The WPO and comprehensive field development optimization runs are again terminated after 1200 and 20,000 total simulations.

Figure 14 shows the evolution of NPV for the two-stage and aided single-stage comprehensive field development optimization methods. The two-stage approach clearly outperforms the aided single-stage comprehensive field development procedure, consistent with our observations in the 2D case. In the second step of the two-stage method, and in the aided single-stage comprehensive field development optimization, there are a total of 112 decision variables (corresponding to $N_w = 19$, obtained with WPO). The average NPV obtained after 20,000 simulations by the aided single-stage comprehensive field development procedure is found by the two-stage approach after about 1800 simulations. In addition, as indicated by the red shaded region, the solutions obtained from the three runs of the aided single-stage comprehensive field development optimization are more variable in terms of NPV. This may be due to the challenges associated with optimizing this MINLP problem. Although the second step of the two-stage runs is terminated after 20,000 simulations, the results are seen to plateau earlier. The use of a termination criterion based on, e.g., a required degree of improvement over a prescribed number of iterations, would enable these runs to terminate before 20,000 simulations, thus leading to computational savings.

Fig. 14

Evolution of NPV for the 3D Olympus (single-realization) case, for the two-stage procedure (WPO followed by comprehensive field development) and aided single-stage comprehensive field development optimization. Shaded regions indicate the range of NPV over the three runs, and curves indicate the mean. (Color figure online)

Table 4 displays NPVs for the individual runs at different stages of the optimization. It is apparent that the WPO solutions after 1200 simulations correspond to considerably higher NPVs than the aided single-stage comprehensive field development optimization solutions after 3000 simulations. In the best two-stage run (run 2), the optimal solution found using WPO has an NPV of $1.113 billion. The second-stage optimization provides an NPV of $1.542 billion, which corresponds to a very substantial (38.5%) increase over the best WPO result. This best two-stage solution results in an NPV that is 15.1% higher than that from the best single-stage optimization run (NPV of $1.340 billion).

Table 4 NPV (in billion USD) for two-stage and aided single-stage comprehensive field development optimization for a single realization of the 3D Olympus model

Figure 15 presents the well configurations for the best solutions obtained using WPO, two-stage optimization, and aided single-stage comprehensive field development optimization. Areal displays for the latter two solutions appear in Fig. 16. The WPO arrangement in Fig. 15a corresponds to inverted five-spot patterns and involves a total of 19 wells (11 producers and eight injectors). The two-stage solution entails a development with a total of 13 wells (five injectors and eight producers), six wells fewer than the WPO solution. Aided single-stage comprehensive field development optimization also provides a solution with 13 wells, but in this case there are six injectors and seven producers. In the two-stage solution, six of the wells (three injectors and three producers) are completed in all layers. The areal plots in Fig. 16 illustrate the complex permeability ‘connectivity’ associated with this model. This connectivity is quite variable from layer to layer.

Fig. 15

Best well configurations for WPO, two-stage and aided single-stage comprehensive field development optimization procedures for a single realization of the 3D Olympus model. Red cylinders denote producers, and blue cylinders denote injectors. Note that, in addition to their areal locations, the completion intervals of the optimized wells also vary. (Color figure online)

Fig. 16

Areal views of best well configurations for two-stage and aided single-stage comprehensive field development optimization procedures for a single realization of the 3D Olympus model. Red circles denote producers, and blue circles denote injectors. Log-permeability scale and color bar shown in Fig. 5b. (Color figure online)

Results for field-wide cumulative oil and water production, and cumulative water injection, are shown in Fig. 17. The best solution obtained using the two-stage approach results in the most cumulative oil produced, along with more cumulative water produced and injected than either of the other solutions. The cost of this extra water is, however, more than compensated for by the additional oil recovered.

Fig. 17

Field-wide cumulative oil production, water production and water injection for the best solutions obtained using WPO, two-stage, and aided single-stage comprehensive field development optimization approaches, for a single realization of the 3D Olympus model

Finally, we present results for optimization over multiple realizations of the 3D Olympus model. Because computational cost scales with the number of realizations considered, we restrict ourselves here to $N_r=8$, though our procedures are applicable for larger values of $N_r$. The optimization problem in this case is different than that defined above for the single-realization case. Specifically, here we first apply comprehensive field development (single-stage) optimization, with the number of wells specified to be 15. In addition, in this multiple-realization optimization, we do not optimize drilling time, and instead treat all wells as being drilled at the start of the simulation. The simulation time frame is now 7200 days (as opposed to 6500 days in the single-realization case). In the first optimization step, wells are assumed to be completed in all layers in all realizations. There are thus 30 well location variables and 15 well type variables in this optimization. The economic and simulation parameters are the same as those used previously.

The optimal solution obtained using the eight realizations, with the setup described above, includes eight production wells and seven injection wells. The optimal expected NPV, computed using Eq. 11, is $898.7 million. This value is of the same order but differs from the NPVs for the single-realization case. This is reasonable given the somewhat different problem specifications and the fact that NPV is now an average over eight realizations.

We now assess the impact of the realization-by-realization perforation determination. Two approaches are considered. In the first treatment we optimize the completion intervals across all realizations for all wells, but for each realization perforations are only introduced for production wells if the near-well permeability (computed over the $3 \times 3$ region around the well-block) is greater than 10 md. Expected NPV is then computed using Eq. 12. In the second approach, all realizations have the same (optimized) completion intervals, and all wells are perforated over the full completion interval. Expected NPV in this case is computed using Eq. 11.

Fig. 18

Optimal perforated regions obtained using the realization-by-realization treatment for four of the eight Olympus realizations considered. Red, blue and black cylinders denote producers, injectors, and non-perforated regions, respectively. (Color figure online)

Figure 18 displays the optimal set of perforated regions obtained using the realization-by-realization treatment. Results are shown for four of the eight realizations. The black cylinders depict the portions of the completion intervals that are not perforated. It is evident from the figures that the perforated regions for the producers differ from realization to realization. The expected NPV achieved using the realization-by-realization treatment is $1.042 billion, while that obtained for the case in which the perforated regions are the same across models is $1.036 billion. We thus achieve a cost savings of $6 million in expected NPV using the realization-by-realization treatment. In the optimal solution, a total of 96 grid blocks comprise the completion intervals for the eight producers. In the realization with the fewest perforations, 68 of these blocks are perforated, while in the realization with the most perforations, 84 of these blocks are perforated. The average over the eight realizations is 77 blocks perforated.

A portion of the $6 million increase in expected NPV derives from the direct savings in perforation costs, and a portion derives from the fact that the optimizer finds different completion intervals under the realization-by-realization treatment. We note finally that, although the improvement in expected NPV is fairly small in this case (0.6%), in large-scale field development, where hundreds of production wells are considered, this treatment could lead to more significant cost savings. Additional savings could also be achieved in thicker reservoirs (since perforation cost scales with length) or when the per-foot perforation cost is higher.

5 Concluding remarks

In this work, we introduced a two-stage strategy for large-scale field development optimization, where we seek to determine the number of wells, their locations, types, drilling sequence and completion intervals (for multilayer models), such that an objective function (NPV) is maximized. In the first stage, an extended version of the well-pattern optimization procedure introduced by Onwunalu and Durlofsky (2011) is applied. Our implementation includes a new pattern-based drilling sequence optimization treatment and modifications that reduce the number of optimization variables. In the well-pattern optimization stage, the number of decision variables is relatively small and does not depend directly on the maximum number of wells considered. The solutions obtained in this stage are used to initialize the comprehensive field development optimization in the second stage. In this stage, decision variables are associated with individual wells, and pattern geometry is not enforced. A new realization-by-realization well perforation treatment was also developed for cases where multiple (multilayer) geomodels are used to represent geological uncertainty. This treatment, in which wells are only perforated in blocks with near-well permeability above a threshold value, allows for the effective incorporation of data available during drilling. A hybrid particle swarm optimization-mesh adaptive direct search (PSO-MADS) algorithm, introduced by Isebor et al. (2014a, b), was used for all of the optimizations in this study.

Two example cases, involving a 2D Gaussian permeability model and the 3D Olympus model (Fonseca et al. 2018), were used to investigate the performance of the two-stage optimization procedure. Optimization results clearly demonstrated the advantages of the two-stage approach over the single-stage optimization method. Specifically, for the 2D case, the best two-stage solution provided an NPV that was 17.8% higher than that obtained using the single-stage optimization procedure. The average NPV obtained by the single-stage optimization after 20,000 simulations was achieved by the two-stage approach after only about 2500 simulations. For the 3D case, the best two-stage solution resulted in an NPV 15.1% higher than that from the best single-stage optimization. In this case, the average NPV found after 20,000 simulations by the single-stage procedure was achieved after about 1800 simulations by the two-stage approach. The relative advantage of the two-stage optimization procedure over the single-stage approach can be expected to vary from case to case, and it will be important to assess performance for practical cases. The realization-by-realization treatment was shown to provide benefit in an optimization involving eight realizations of the 3D Olympus model.

In future work, it will be of interest to evaluate the two-stage optimization approach using different optimization procedures, including hybrid algorithms, with a range of termination and switching criteria. The joint optimization of well locations, types, drilling sequence and well operational settings should be considered. This will result in additional decision variables, so it will be useful to introduce dimension reduction techniques into the optimization. The inclusion of faster (surrogate) simulation models should additionally be considered. These capabilities could then be incorporated into a closed-loop field development framework (Shirangi and Durlofsky 2015), which would enable the full linkage of field development optimization and history matching procedures.

The methods introduced in this work should also be extended for use, and tested, in a range of practical problems. These could include both primary depletion problems involving new fields, and water or gas injection for new or mature fields. For primary depletion systems, the well patterns (viewed as well templates in this case) can be designed to include only sets of production wells. With parametric representations for these templates, our WPO procedure could be applied for, e.g., offshore systems with deviated or horizontal wells. The realization-by-realization well completion procedure could be extended for application to such systems. The existing methodology should also be tested for, e.g., $\hbox {CO}_2$ enhanced oil recovery, either involving patterns or general well configurations.