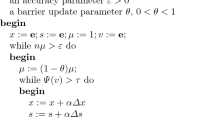An efficient twice parameterized trigonometric kernel function for linear optimization

Abstract

Recently, Bouafia et al. (J Optim Theory Appl 170:528–545, 2016) investigated a new efficient kernel function that differs from self-regular kernel functions. The kernel function has a trigonometric barrier term. This paper introduces a new efficient twice parametric kernel function that combines the parametric classic function with the parametric kernel function trigonometric barrier term given by Bouafia et al. (J Optim Theory Appl 170:528–545, 2016) to develop primal–dual interior-point algorithms for solving linear programming problems. In addition, we obtain the best complexity bound for large and small-update primal–dual interior point methods. This complexity estimate improves results obtained in Li and Zhang (Oper Res Lett 43(5):471–475, 2015), Peyghami and Hafshejani (Numer Algorithms 67:33–48, 2014) and matches the best bound obtained in Bai et al. (J Glob Optim 54:353–366) and Peng et al. (J Comput Technol 6:61–80, 2001). Finally, our numerical experiments on some test problems confirm that the new kernel function has promising applications compared to the kernel function given by Fathi-Hafshejani (Optimization 67(10):1605–1630, 2018).

1 Introduction

In this paper, we focus on the primal Linear Optimization ${\mathbf { LO}}$ problem as

$$\begin{aligned} (P)\ \min \{c^{t}x:Ax=b,x\ge 0\}, \end{aligned}$$

along with its dual problem as follows:

$$\begin{aligned} (D)\ \ \max \{b^{t}y:A^{t}y+s=c,s\ge 0\}. \end{aligned}$$

Where $A\in {{\mathbb {R}}} ^{m\times n}$, $rank(A)=m,b\in {{\mathbb {R}}} ^{m}$, and $c\in {{\mathbb {R}}} ^{n}$.

Karmarkar (1984) proposed a new polynomial-time method for solving linear programs. This method and its variants that followed are now called ${\mathbf {IPMs}}$. In our work, we refer to recent books on the subject as Peng et al. (2002), Bai and Roos (2002), Roos et al. (1997), Ye (1997).

Without loss of generality, we assume that (P) and (D) satisfy the interior-point condition ${\mathbf {IPC,}}$ i.e., there exist $(x^{0}$, $y^{0}$ , $s^{0})$ such that

$$\begin{aligned} \begin{array}{c} Ax^{0}=b,\ \ x^{0}>0,\quad A^{t}y^{0}+s^{0}=c, \quad s^{0}>0. \end{array} \end{aligned}$$

(1)

Kernel functions provide a characterization of the central path of the primal and dual problems by using its minima and derivatives. Furthermore, to compute the complexity bound, its derivatives, and the inverse functions of the kernel function with its derivatives.

Peng et al. (2001) and Peng et al. (2002) introduced and proposed new variants of ${\mathbf {IPMs}}$ based on a new nonlogarithmic kernel functions. They obtained the complexity results for large and small-update methods, which have ${\mathbf {O}}\left( \sqrt{n}\left( \log n\right) \log \frac{n}{\epsilon }\right)$ complexity for large-update and ${\mathbf {O}}\left( \sqrt{n} \log \frac{n}{\epsilon }\right)$ complexity for small-update methods.

Bai et al. (2005) proposed a new kernel function with an exponential barrier term. The same paper introduced the first new kernel function to have a trigonometric barrier term.

El Ghami et al. (2012) evaluated the first new kernel function with a trigonometric barrier term given by Bai et al. (2005). They obtained ${\mathbf {O}}\left( n^{\frac{3}{4}}\log \frac{n}{\epsilon }\right)$ iterations bound for large-update methods. Since then, research has focused on developing a new kernel function with a trigonometric barrier term to improve the complexity bound obtained by El Ghami et al. (2012).

Peyghami and Hafshejani (2014) proposed a new kernel function with an exponential trigonometric for ${\mathbf {LO}}$. They obtained ${\mathbf {O}}\left( \sqrt{n}\left( \log n\right) ^{2}\log \frac{n}{\epsilon }\right)$ iterations bound for large-update methods.

Li and Zhang (2015) presented another trigonometric barrier function, which has ${\mathbf {O}}\left( n^{\frac{2}{3}}\log \frac{n}{\epsilon }\right)$ complexity for large-update methods. These results improve the complexity bound obtained by El Ghami et al. (2012).

Bouafia et al. (2016a, b) proposed two parameterized kernel functions. The first has a trigonometric barrier term for interior point methods in $\mathbf {LO}$. We generalized and improved the complexity bound based on a new kernel function with trigonometric barrier terms obtained in Li and Zhang (2015), Peyghami and Hafshejani (2014), El Ghami et al. (2012) and Peyghami et al. (2014). We obtained the best known complexity results for large and small-update methods. The second function generalizes the kernel function given by Bai et al. (2005).

Bouafia et al. (2018) presented the first parameterized logarithmic kernel function. It is proven to efficiently give the best logarithmic complexity.

Fathi-Hafshejani et al. (2018) presented a large-update primal–dual interior-point algorithm for linear optimization problems based on a new kernel function with a trigonometric growth term. They obtained the best known complexity results for large which has ${\mathbf {O}}\left( \sqrt{n} \log n \log \frac{n}{\epsilon }\right)$ complexity for large-update method. This result improve the complexity bound obtained in Li and Zhang (2015), Peyghami and Hafshejani (2014), El Ghami et al. (2012) and Peyghami et al. (2014).

In this paper, we introduce a new twice parametric kernel function

$$\begin{aligned} \psi _{M}\left( t\right) =t^{2}+\frac{t^{1-q}}{q-1}-\frac{q}{q-1}+\frac{4}{ \pi p}\left[ \tan ^{p}h\left( t\right) -1\right] ,\ \left\{ \begin{array}{l} h\left( t\right) =\frac{\pi }{2t+2}, \\ p\ge 2,\ q>1. \end{array} \right. \end{aligned}$$

for the development of primal–dual interior-point algorithms for solving linear programming problems. We investigate the properties of the proposed kernel functions and corresponding parameters, improving the complexity bound obtained by Li and Zhang (2015) for ${\mathbf {LO}}$. More precisely, based on the proposed kernel function, we prove that the corresponding algorithm has ${\mathbf {O}}\left( pn^{\frac{\left( p+2\right) \left( q+1\right) }{2\left( p+1\right) q}}\log \frac{n}{\epsilon }\right)$ complexity bound for the large-update method and ${\mathbf {O}}\left( \left( p+q\right) ^{2}\sqrt{n}\log \frac{n}{\epsilon }\right)$ for the small-update method. In another interesting approach, where p and q is dependent on n, we take $p = q = logn$, and we obtain the known complexity bound for large-update methods namely ${\mathbf {O}}\left( \sqrt{n} \log n\log \frac{n}{\epsilon }\right)$. This bound improves the complexity results we have obtained so far for the large-update methods based on a trigonometric kernel function given by Li and Zhang (2015), Peyghami and Hafshejani (2014).

The paper is organized as follows. In Sect. 2, we recall the basic concepts of a central path, barrier function, and kernel function. A generic primal–dual $\mathbf {IPMs}$ based on kernel functions is described in Sect. 3. In Sect. 3, we present some properties of the new kernel function, as well as several properties and the growth behavior of the barrier function based on the kernel function, the estimate of the stepsize, and the decreasing behavior of the new barrier function decrease behavior of new barrier function. In Sect. 4, we derive the inner iteration bound and the total iteration bound of the algorithm. In Sect. 5, we compare our results to those of the algorithm given by Fathi-Hafshejani et al. (2018). Finally, we are finishing the paper with some remarks and a general conclusion showing the added value of our work. We use the following notations throughout the paper. ${{\mathbb {R}}} _{+}^{n}$ and ${{\mathbb {R}}} _{++}^{n}$denote the set of n-dimensional nonnegative vectors and positive vectors, respectively. For x, s$\in {{\mathbb {R}}} ^{n}$, $x_{\min }$ and xs denote the smallest component of the vector x and the componentwise product of the vector x and s, respectively. We denote $X = diag(x)$ by the n diagonal matrix with the components of the vector $x\in {{\mathbb {R}}} ^{n}$, the diagonal entries. Finally, e denotes the n-dimensional vector of ones. For $f\left( x\right) ,g\left( x\right)$  :  ${{\mathbb {R}}} _{++}^{n}\rightarrow {{\mathbb {R}}} _{++}^{n},$$f\left( x\right) ={\mathbf {O}}\left( g\left( x\right) \right)$ if $f\left( x\right) \le C_{1}g\left( x\right)$ for some positive constant $C_{1}$ and $f\left( x\right) =\varvec{\Theta }\left( g\left( x\right) \right)$ if $C_{2}g\left( x\right)$$\le f\left( x\right) \le C_{3}g\left( x\right)$ for some positive constant $C_{2}$ and $C_{3}$. And throughout the paper, || || denotes the 2-norm of a vector.

2 The generic primal–dual interior-point algorithm

In this section, we briefly describe the idea behind the interior point methods based on kernel functions. We also provide the structure of the generic primal–dual ${\mathbf {IPMs}}$ when the kernel functions are used to induce the proximity measure. One knows that for the feasible primal and dual linear optimization problems, i.e.problems (P) and (D), an optimal solution can be found by solving the following system:

$$\begin{aligned} \begin{array}{l} Ax=b,\ \ x\ge 0, \\ A^{t}y+s=c,\ \ s\ge 0, \\ xs=0. \end{array} \end{aligned}$$

(2)

The basic idea of primal–dual ${\mathbf {IPMs}}$ is to replace the third equation in (2), the so-called complementarity condition for (P) and (D) , by the parameterized equation $xs= \mu e,$ with $\mu >0$. Thus we consider the system

$$\begin{aligned} \begin{array}{l} Ax=b, x\ge 0, \\ A^{t}y+s=c, s\ge 0, \\ xs= \mu e. \end{array} \end{aligned}$$

(3)

It is shown that, under ${\mathbf {IPC}}$ condition and $rank(A) = m$, system (4) has a unique solution, for each$\mu >0$. This solution is denoted by $(x( \mu ),y( \mu ),s( \mu ))$, and we call $x( \mu )$ the $\mu$-center of (P) and $(y( \mu ),s( \mu ))$ the $\mu$-center of (D). The set of $\mu$-centers (with $\mu$ running through all positive real numbers) gives a homotype path, which is called the central path of (P) and (D). The relevance of the central path for linear optimization ${\mathbf {LO}}$ was recognized first by Sonnevend (1986) and Megiddo (1989). It is proved that as $\mu \rightarrow 0$, the limit of the central path exists and converges to an analytic center of the optimal solutions set of (P) and (D).

Let $\mu >0$ be fixed. A direct application of the Newton method on (4) provides the following system for $\varDelta x, \varDelta y \,\,{\text{and}}\,\, \varDelta s:$

$$\begin{aligned} \begin{array}{l} A\varDelta x=0, \\ A^{t}\varDelta y+\varDelta s=0, \\ s\varDelta x+x\varDelta s= \mu e-xs. \end{array} \end{aligned}$$

(4)

This system uniquely defines a search direction $(\varDelta x,\varDelta y,\varDelta s)$. By taking a step along the search direction, with the step size defined by some line search rules, we construct a new triple (x, y, s). If necessary, we repeat the procedure until we find iterates that are “close” to $(x( \mu ),y( \mu ),s( \mu ))$. Then $\mu$ is again reduced by the factor $1-\theta$, and we apply Newton’s method targeting the new $\mu$-centers, and so on. This process is repeated until $\mu$ is small enough, say until $n\mu \le \epsilon$; at this stage we have found an $\epsilon$-solution of problems (P) and (D).

The result of a Newton step with step size $\alpha$ is denoted as

$$\begin{aligned} \begin{array}{ccc} x_{+}=x+\alpha \varDelta x,&y_{+}=y+\alpha \varDelta y,&s_{+}=s+\alpha \varDelta s . \end{array} \end{aligned}$$

(5)

where, the step size $\alpha$ satisfies ($0<\alpha \le 1$).

Now we introduce the scaled vector v and the scaled search directions $d_{x}$ and $d_{s}$ as follows:

$$\begin{aligned} \begin{array}{ccc} v=\sqrt{\frac{xs}{\mu }},&d_{x}=\frac{v\varDelta x}{x},&d_{s}= \frac{v\varDelta s}{s}. \end{array} \end{aligned}$$

(6)

System (4) can be rewritten as follows:

$$\begin{aligned} \begin{array}{l} \overline{A}d_{x}=0, \\ \overline{A}^{t}\varDelta y+d_{s}=0, \\ d_{x}+d_{s}=v^{-1}-v. \end{array} \end{aligned}$$

(7)

where $\overline{A}=\frac{1}{\mu }AV^{-1}X,V=diag(v),X=diag(x)$. Note that $d_{x} = d_{s} = 0$ if and only $v^{-1}-v=0$ if and only $x=e$ if and only $x=x(\mu ), s=s(\mu )$. A crucial observation in (7) is that the right hand side of the third equation is the minus the negative gradient of the logarithmic barrier function $\varvec{\Phi }\left( v\right) ,$ i.e., $d_{x}+d_{s}=-\nabla \varvec{\Phi }\left( v\right)$, then system (7) can be rewritten as follows:

$$\begin{aligned} \begin{array}{l} \overline{A}d_{x}=0, \\ \overline{A}^{t}\varDelta y+d_{s}=0, \\ d_{x}+d_{s}=-\nabla \varvec{\Phi }\left( v\right) . \end{array} \end{aligned}$$

(8)

where the barrier function $\varvec{\Phi }\left( v\right)$$: {{\mathbb {R}}} _{++}^{n}\rightarrow {{\mathbb {R}}} _{+}$ is defined as follows:

$$\begin{aligned} \varvec{\Phi }\left( v\right)& = \varvec{\Phi }\left( x,s;\mu \right) = \sum _{i=1}^{n}\psi \left( v_{i}\right) , \end{aligned}$$

(9)

$$\begin{aligned} \psi \left( v_{i}\right)& = \frac{v_{i}^{2}-1}{2}-\log v_{i}. \end{aligned}$$

(10)

We use $\varvec{\Phi }\left( v\right)$ as the proximity function to measure the distance between the current iterate and the $\mu$-center for given $\mu >0$. We also define the norm-based proximity measure, $\delta (v)$$: {{\mathbb {R}}} _{++}^{n}\rightarrow {{\mathbb {R}}} _{+}$, as follows

$$\begin{aligned} \delta \left( v\right) =\frac{1}{2}\left\| \nabla \varvec{\Phi }\left( v\right) \right\| =\frac{1}{2}\left\| d_{x}+d_{s}\right\| . \end{aligned}$$

(11)

The new variant of primal–dual $\text{ IPMs }$ was developed by Peng et al. (2002) in which the proximity function $\varvec{\Phi }\left( v\right)$ is replaced by a new proximity function $\varvec{\Phi }_{M}\left( v\right) =\sum _{i=1}^{n}\psi _{M} \left( v_{i}\right) ,$ which will be defined in Sect. 3, where $\psi _{M} \left( t\right)$ is any strictly differentiable convex barrier function on ${\mathbb {R}}_{++}$ with $\psi _{M} \left( 1\right) =\psi ' _{M}(1)=0$.

Now, we describe one step of the $\text{ IPMs }$ based on the kernel function. Starting with the interior point $(x^{0}$, $y^{0}$, $s^{0})$, $\mu >0$, an accuracy $\epsilon >0$ and the proximity function $\varvec{\Phi }_{M}\left( v\right)$, let a good approximation of the $\mu$-center $(x(\mu ),y(\mu ),s(\mu ))$ be known for $\mu >0$. Then, the parameter $\mu$ is decreased by a factor $1-\theta$, for $0<\theta <1$, and we apply Newton’s method targeting the new $\mu$-centers, and so on. Indeed, we first solve system (8) for $d_{x} \,\,{\text{and}}\,\, d_{s}$ and then find the Newton directions $\left( \varDelta x,\varDelta y,\varDelta s\right)$. This procedure is repeated until we get to the point in which $x^{T}s<\epsilon$ In this case, we say that the current x and (y, s) are $\epsilon$-approximate solutions of the primal and dual problems, respectively. Now, we can outline the above procedure in the following primal–dual interior point scheme (Peng et al. 2002). The parameters $\tau ,\theta$ and the step size $\alpha$ should be chosen in such a way that the algorithm is optimized in the sense that the number of iterations required by the algorithm is as small as possible. The choice of the so-called barrier update parameter $\theta$ plays an important role in both theory and practice of $\text{ IPMs }$. Usually, if $\theta$ is a constant independent of the dimension n of the problem, for instance, $\theta = 1/2$, then we call the algorithm a large-update (or long-step) method. If $\theta$ depends on the dimension of the problem, such as $\theta =1/n$, then the algorithm is called a small-update (or short-step) method. The generic form of the algorithm is shown in Fig. 1.

Fig. 1

Generic algorithm

3 Properties of the new kernel function

Recently, Bouafia et al. (2016a), investigated a new efficient kernel function with trigonometric barrier for ${\text{LO}}$, which differs from the self-regular kernel functions. Motivated by their work, in this paper we introduce a new efficient twice parametric kernel function, which is a combination of the parametric classic function and the parametric kernel function trigonometric barrier term given by Bouafia et al. (2016a), for the development of primal–dual interior-point algorithms for solving linear programming problems, and we present a primal–dual interior-point algorithm for ${\text{LO}}$ based on this kernel function:

$$\begin{aligned} \psi _{M}\left( t\right) =t^{2}+\frac{t^{1-q}}{q-1}-\frac{q}{q-1}+\frac{4}{ \pi p}\left[ \tan ^{p}h\left( t\right) -1\right] ,\ \left\{ \begin{array}{l} h\left( t\right) =\frac{\pi }{2t+2}, \\ p\ge 2,\ q>1. \end{array} \right. \end{aligned}$$

(12)

3.1 Some technical results

In the analysis of the algorithm based on $\psi _{M} \left( t\right)$ we need its first three derivatives. These are given by

$$\begin{aligned} \psi _{M}^{\prime }(t)& = 2t-t^{-q}+\frac{4}{\pi }\left( 1+\tan ^{2}h\left( t\right) \right) \left( \tan ^{p-1}h\left( t\right) \right) \left[ -h^{\prime }\left( t\right) \right] . \end{aligned}$$

(13)

$$\begin{aligned} \psi _{M}^{\prime \prime }\left( t\right)& = 2+qt^{-q-1}+k\left( t\right) \left[ \begin{array}{c} \left[ \begin{array}{c} \left( p-1\right) \tan ^{p-2}h\left( t\right) + \\ \left( p+1\right) \tan ^{p}h\left( t\right) \end{array} \right] \left( h^{\prime }\left( t\right) \right) ^{2}+ \\ \left[ \tan ^{p-1}h\left( t\right) \right] \left( -h^{\prime \prime }\left( t\right) \right) \end{array} \right] , \end{aligned}$$

(14)

$$\begin{aligned} \psi _{M}^{\prime \prime \prime }\left( t\right)& = u\left( t\right) +k\left( t\right) \left[ \begin{array}{c} \left[ \begin{array}{c} \left( p-1\right) \left( p-2\right) \tan ^{p-3}h\left( t\right) + \\ 2p^{2}\tan ^{p-1}h\left( t\right) + \\ \left( p+1\right) \left( p+2\right) \tan ^{p+1}h\left( t\right) \end{array} \right] \left( -h^{\prime }\left( t\right) \right) ^{3}+ \\ \left[ \begin{array}{c} 3\left( p-1\right) \tan ^{p-2}h\left( t\right) + \\ 3\left( p+1\right) \tan ^{p}h\left( t\right) \end{array} \right] h^{\prime \prime }\left( t\right) h^{\prime }\left( t\right) + \\ \left[ \tan ^{p-1}h\left( t\right) \right] \left( -h^{\prime \prime \prime }\left( t\right) \right) \end{array} \right] . \end{aligned}$$

(15)

with

$$\begin{aligned} k\left( t\right)& = \frac{4}{\pi }\left( 1+\tan ^{2}h\left( t\right) \right) , \end{aligned}$$

(16)

$$\begin{aligned} u\left( t\right)& = -q\left( q+1\right) t^{-q-2}, \end{aligned}$$

(17)

and

$$\begin{aligned} h^{\prime }\left( t\right)& = \frac{\pi }{2\left( t+1\right) ^{2}}. \nonumber \\ h^{\prime \prime }\left( t\right)& = \frac{-\pi }{\left( t+1\right) ^{3}}.\nonumber \\ h^{\prime \prime \prime }\left( t\right)& = \frac{-3\pi }{\left( t+1\right) ^{4}}. \end{aligned}$$

(18)

We present some of the specificities of the function h that are given in Bouafia et al. (2016a), we need in the following proofs to present:

Lemma 3.1

(Lemma 3.1 in  Bouafia et al. (2016a)) For  $h\left( t\right)$ defined in (12) and $p\ge 2$, we have the following

$$\begin{aligned}&0<h\left( t\right) <\frac{\pi }{2},\ \ \ t>0. \end{aligned}$$

(19)

$$\begin{aligned}&\tan h\left( t\right)>0,\ \ \ t>0. \end{aligned}$$

(20)

$$\begin{aligned}&\tan h\left( t\right) -\frac{2}{\left( p+1\right) \pi t}>0,\ \ \ t>0. \end{aligned}$$

(21)

From (5–14,16,18), Lemma 3.1 and definition of kernel function (Bai et al. 2005), we can easy to check that

$$\begin{aligned} \psi _{M} ^{\prime }(1)=\psi (1)=0, \psi _{M} ^{\prime \prime }(t)>2, \lim \limits _{t\rightarrow 0^{+}} \psi _{M}\left( t\right) =\lim \limits _{t\rightarrow +\infty } \psi _{M}\left( t\right) =+\infty . \end{aligned}$$

which show that $\psi _{M}\left( t\right)$ is indeed a kernel function.

3.2 Eligibility of the new kernel function

The next lemma serves to prove that the new kernel function (18) is eligible.

Lemma 3.2

Let $\psi _{M}\left( t\right)$ be as defined in (12) and $t>0$. Then,

$$\begin{aligned}&\psi _{M}^{\prime \prime \prime }\left( t\right) <0. \end{aligned}$$

(22)

$$\begin{aligned}&t\psi _{M}^{\prime \prime }\left( t\right) -\psi _{M}^{\prime }\left( t\right) >0. \end{aligned}$$

(23)

$$\begin{aligned}&t\psi _{M}^{\prime \prime }\left( t\right) +\psi _{M}^{\prime }\left( t\right) >0. \end{aligned}$$

(24)

Proof

For (22), the sign of $\psi _{M}^{\prime \prime \prime }\left( t\right)$, using (15), (16) and (18), we have

$$\begin{aligned} \psi _{M}^{\prime \prime \prime }\left( t\right) <0,\ \text{ for } \text{ all } t>0, \end{aligned}$$

which implies that (22).

For (23), we again use (13) and (14),

$$\begin{aligned}&t\psi _{M}^{\prime \prime }\left( t\right) -\psi _{M}^{\prime }\left( t\right) \\&\quad =\left( q+1\right) t^{-q}+k\left( t\right) \left[ \begin{array}{c} \left( h^{\prime }\left( t\right) \right) ^{2}\left[ \begin{array}{c} \left( p-1\right) \tan ^{p-2}h\left( t\right) + \\ \left( p+1\right) \tan ^{p}h\left( t\right) \end{array} \right] t+ \\ \left( -h^{\prime \prime }\left( t\right) \right) \left( \tan ^{p-1}h\left( t\right) \right) t+\left( \tan ^{p-1}h\left( t\right) \right) h^{\prime }\left( t\right) \end{array} \right] . \end{aligned}$$

Form (16) and the positivity of $-h^{\prime \prime }\left( t\right)$, the right-hand side of the last equality is positive, which proves (23).

For (24), using (13) and (14), we have

$$\begin{aligned}&t\psi _{M}^{\prime \prime }\left( t\right) +\psi _{M}^{\prime }\left( t\right) \\&\quad =4t+\left( q-1\right) t^{-q}+k\left( t\right) \left[ \begin{array}{c} \left( h^{\prime }\left( t\right) \right) ^{2}\left[ \left( p-1\right) \tan ^{p-2}h\left( t\right) \right] t+ \\ \left( \tan ^{p-1}h\left( t\right) \right) \left[ \begin{array}{c} \left( \left( p+1\right) \left( h^{\prime }\left( t\right) \right) ^{2}\tan h\left( t\right) \right) t+ \\ -h^{\prime \prime }\left( t\right) t-h^{\prime }\left( t\right) \end{array} \right] \end{array} \right] . \end{aligned}$$

and

$$\begin{aligned}&\left[ \begin{array}{c} \left( \left( p+1\right) \left( h^{\prime }\left( t\right) \right) ^{2}\tan h\left( t\right) \right) t- \\ h^{\prime \prime }\left( t\right) t- \\ h^{\prime }\left( t\right) \end{array} \right] \\&\quad =\frac{\pi }{4\left( t+1\right) ^{4}}\left[ \begin{array}{c} 2t^{2}+ \\ \pi \left( p+1\right) t\left( \tan h\left( t\right) -\frac{2}{\left( p+1\right) \pi t}\right) \end{array} \right] \end{aligned}$$

using (20), the right-hand side of the above equality is positive, which proves (24).

The last property (24) in Lemma 3.2 is equivalent to convexity of composed functions $t\mapsto \psi _{M}\left( e^{t}\right)$ and this holds if only if $\psi _{M}\left( \sqrt{t_{1}t_{2}} \right) \le \frac{1}{2}\left( \psi _{M}\left( t_{1}\right) +\psi _{M}\left( t_{2}\right) \right)$ for any $t_{1}$, $t_{2}\ge 0$,this property is known in the literature, it was demonstrated by several researchers (see Peng et al. 2002; El Ghami et al. 2012; Bai et al. 2003).

As a preparation for later, we present the some technical results for the new of kernel function

Lemma 3.3

For $\psi _{M}\left( t\right)$, we have

$$\begin{aligned}&\left( t-1\right) ^{2}\le \psi _{M}\left( t\right) \le \frac{1}{4}\left[ \psi _{M}^{\prime }\left( t\right) \right] ^{2},\ \ \ t>0. \end{aligned}$$

(25)

$$\begin{aligned}&\psi _{M}\left( t\right) \le \left( \frac{3+q}{2}+\frac{\pi }{8}p\right) \left( t-1\right) ^{2},\ \ \ \ \ t>1. \end{aligned}$$

(26)

Proof

For (25), using (14), we have

$$\begin{aligned} \psi _{M}\left( t\right)& = \int _{1}^{t}\int _{1}^{x}\psi _{M}^{\prime \prime }\left( y\right) dydx\ge \int _{1}^{t}\int _{1}^{x}2dydx=\left( t-1\right) ^{2}\\ \psi _{M}\left( t\right)& = \int _{1}^{t}\int _{1}^{x}\psi _{M}^{\prime \prime }\left( y\right) dydx \\\le & \frac{1}{2}\int _{1}^{t}\int _{1}^{x}\psi _{M}^{\prime \prime }\left( y\right) \psi _{M}^{\prime \prime }\left( x\right) dydx \\\le & \frac{1}{2}\int _{1}^{t}\psi _{M}^{\prime \prime }\left( x\right) \psi _{M}^{\prime }\left( x\right) dx \\& = \frac{1}{2}\int _{1}^{t}\psi _{M}^{\prime }\left( x\right) d\psi _{M}^{\prime }\left( x\right) \\& = \frac{1}{4}\left[ \psi _{M}^{\prime }\left( t\right) \right] ^{2}. \end{aligned}$$

For (26), since $\psi _{M}\left( 1\right) =\psi _{M}^{\prime }\left( 1\right) =0,\psi _{M}^{\prime \prime \prime }\left( t\right) <0,$$\psi _{M}^{\prime \prime }\left( 1\right) =\left( 3+q+\frac{\pi }{4}p\right)$, and by using Taylor’s Theorem, we have

$$\begin{aligned} \psi _{M}\left( t\right)& = \psi _{M}\left( 1\right) +\psi _{M}^{\prime }\left( 1\right) \left( t-1\right) +\frac{1}{2}\psi _{M}^{\prime \prime }\left( 1\right) \left( t-1\right) ^{2}+\frac{1}{6}\psi _{M}^{\prime \prime \prime }\left( \xi \right) \left( t -1\right) ^{3} \\& = \frac{1}{2}\psi _{M}^{\prime \prime }\left( 1\right) \left( t-1\right) ^{2}+\frac{1}{6}\psi _{M}^{\prime \prime \prime }\left( \xi \right) \left( t -1\right) ^{3} \\\le & \frac{1}{2}\psi _{M}^{\prime \prime }\left( 1\right) \left( t-1\right) ^{2} \\& = \left( \frac{3+q}{2}+\frac{\pi }{8}p\right) \left( t-1\right) ^{2}. \end{aligned}$$

for some $\xi ,$$1\le \xi \le t.$ This completes the proof. $\square$

Let $\sigma :[ 0,+\infty [ \rightarrow [ 1,+\infty [$ be the inverse function of $\psi _{M}\left( t\right)$ for $t\ge 1$ and $\rho :[ 0,+\infty [ \rightarrow ] 0,1]$ be the inverse function of $\frac{-1}{2}\psi _{M}^{\prime }\left( t\right)$ for all $t\in ] 0,1]$. Then we have the following lemma.

Lemma 3.4

For $\psi _{M}\left( t\right)$, we have

$$\begin{aligned}&\sigma \left( s\right) \le 1+\sqrt{s}, \ \ s\ge 0. \end{aligned}$$

(27)

$$\begin{aligned}&\tan h\left( t\right) \le \left( 4z+2\right) ^{\frac{1}{p+1}}, \ \ \ \ z\ge 0. \end{aligned}$$

(28)

$$\begin{aligned}&t\ge \left[ \frac{1}{2z+2}\right] ^{\frac{1}{q}}, \ \ \ \ z\ge 0. \end{aligned}$$

(29)

Proof

For (27), let

$$\begin{aligned} s=\psi _{M}\left( t\right) ,t\ge 1,i.e.\ \sigma \left( s\right) =t, \ \ \ t\ge 1. \end{aligned}$$

By (25), we have

$$\begin{aligned} \psi _{M}\left( t\right) \ge \left( t-1\right) ^{2}. \end{aligned}$$

we have

$$\begin{aligned} s\ge \left( t-1\right) ^{2},t\ge 1. \end{aligned}$$

which implies that

$$\begin{aligned} t=\sigma \left( s\right) \le 1+\sqrt{s}. \end{aligned}$$

For (28), let

$$\begin{aligned} z=\frac{-1}{2}\psi _{M}^{\prime }\left( t\right) ,t\in ] 0,1] \Leftrightarrow 2z=-\psi _{M}^{\prime }\left( t\right) ,t\in ] 0,1 ] . \end{aligned}$$

By the definition of

$$\begin{aligned} \rho :\rho \left( z\right) =t,t\in ] 0,1] . \end{aligned}$$

By the definition of $\psi _{M}^{\prime }\left( t\right)$ and $h^{\prime }\left( t\right)$, we have

$$\begin{aligned} \begin{array}{ll} 2z&=-\left( 2t-t^{-q}+\frac{4}{\pi }\left( 1+\tan ^{2}h\left( t\right) \right) \left( \tan ^{p-1}h\left( t\right) \right) \left( -h^{\prime }\left( t\right) \right) \right) , \end{array} \end{aligned}$$

this implies

$$\begin{aligned} \left( 1+\tan ^{2}h\left( t\right) \right) \left( \tan ^{p-1}h\left( t\right) \right) =\left( 2z+2t-t^{-q}\right) \frac{\pi }{4h^{\prime }\left( t\right) }\le 2\left( 2z+1\right) \ for \ t\in ] 0,1] \end{aligned}$$

and

$$\begin{aligned} \tan ^{p+1}h\left( t\right) \le \left( 1+\tan ^{2}h\left( t\right) \right) \left( \tan ^{p-1}h\left( t\right) \right) \end{aligned}$$

which implies that

$$\begin{aligned} \tan h\left( t\right) \le \left( 4z+2\right) ^{\frac{1}{p+1}}, \ \ \ \ z\ge 0. \end{aligned}$$

For (29), we have

$$\begin{aligned} \left( 2z+2t-t^{-q}\right) \ge 0\ for\ t\in ] 0,1] . \end{aligned}$$

which implies that

$$\begin{aligned} t\ge & \left[ \frac{1}{2z+2t}\right] ^{\frac{1}{q}} \\\ge & \left[ \frac{1}{2z+2}\right] ^{\frac{1}{q}}. \end{aligned}$$

This completes the proof. $\square$

We offer important theorem which is valid for all kernel functions that satisfy (22) and (23) (Lemma 2.4 in Bai et al. 2005)

Theorem 3.1

(Bai et al. 2005) Let $\sigma :[ 0,+\infty [ \rightarrow [ 1,+\infty [$   be the inverse function of $\psi _{M}\left( t\right)$ for $t\ge 1$. Then we have

$$\begin{aligned} \varvec{\Phi }_{M}\left( \beta v\right) \le n\psi _{M}\left( \beta \sigma \left( \frac{\varvec{\Phi }_{M}\left( v\right) }{n}\right) \right) ,\quad v\in IR_{++},\ \beta \ge 1. \end{aligned}$$

Lemma 3.5

Let $0\le \theta <1$, $v_{+}=\frac{v}{\sqrt{1-\theta }},$ If $\ \varvec{\Phi }_{M}\left( v\right) \le \tau ,$ then we have

$$\begin{aligned} \varvec{\Phi }_{M}\left( v_{+}\right) \le \frac{\theta n+\tau +2 \sqrt{\tau n}}{1-\theta }. \end{aligned}$$

Proof

Since $\frac{1}{\sqrt{1-\theta }}\ge 1$ and $\sigma \left( \frac{\varvec{\Phi }_{M}\left( v\right) }{n}\right) \ge 1$, then $\frac{\sigma \left( \frac{\varvec{\Phi }_{M}\left( v\right) }{n}\right) }{\sqrt{1-\theta }}\ge 1$.

And for $t\ge 1,$ we have

$$\begin{aligned} \psi _{M}\left( t\right) \le t^{2}-1. \end{aligned}$$

Using Theorem 3.1 with $\beta =\frac{1}{\sqrt{1-\theta }}$, and (27) , for $\varvec{\Phi }_{M}\left( v\right) \le \tau$, we have

$$\begin{aligned} \varvec{\Phi }_{M}\left( v_{+}\right)\le & n\psi _{M}\left( \frac{1}{ \sqrt{1-\theta }}\sigma \left( \frac{\varvec{\Phi }_{M}\left( v\right) }{n} \right) \right) \\\le & n\left( \left[ \frac{1}{\sqrt{1-\theta }}\sigma \left( \frac{\mathbf { \Phi }_{M}\left( v\right) }{n}\right) \right] ^{2}-1\right) \\& = \frac{n}{1-\theta }\left( \left[ \sigma \left( \frac{ \varvec{\Phi }_{M}\left( v\right) }{n}\right) \right] ^{2}-(1-\theta ) \right) \\\le & \frac{n}{1-\theta }\left( \left[ 1+\sqrt{\frac{ \varvec{\Phi }_{M}\left( v\right) }{n}}\right] ^{2}+\theta -1\right) \\& = \frac{n}{1-\theta }\left( \left[ 1+\frac{\varvec{\Phi } _{M}\left( v\right) }{n}+2\sqrt{\frac{\varvec{\Phi }_{M}\left( v\right) }{n}} \right] +\theta -1\right) \\\le & \frac{n}{1-\theta }\left( \left( 1+\theta -1 \right) +\frac{\tau }{n}+2\sqrt{\frac{\tau }{n}}\right) \\& = \frac{\theta n+\tau +2\sqrt{\tau n}}{1-\theta }. \end{aligned}$$

This completes the proof. $\square$

Denote

$$\begin{aligned} \left( \varvec{\Phi }_{M}\right) _{0}=\frac{\theta n+2\tau +2\sqrt{ 2\tau n}}{1-\theta }=L\left( n,\theta ,\tau \right) ; \end{aligned}$$

(30)

then $\left( \varvec{\Phi }_{M}\right) _{0}$ is an upper bound for $\mathbf { \Phi }_{M}\left( v_{+}\right)$ during the process of the algorithm.

3.3 Determining a stepsize

In this section, we compute a default, stepsize $\alpha$ and the resulting decrease of the barrier function. After a damped step we have

$$\begin{aligned} x_{+}:& = x+\alpha \varDelta x; \\ s_{+}:& = s+\alpha \varDelta s; \\ y_{+}:& = y+\alpha \varDelta y; \end{aligned}$$

Using (6), we have

$$\begin{aligned} x_{+}:& = x\left( e+\alpha \frac{\varDelta x}{x}\right) =x\left( e+\alpha \frac{ d_{x}}{v}\right) =\frac{x}{v}\left( v+\alpha d_{x}\right) , \\ s_{+}:& = s\left( e+\alpha \frac{\varDelta s}{s}\right) =s\left( e+\alpha \frac{ d_{s}}{v}\right) =\frac{s}{v}\left( v+\alpha d_{s}\right) , \end{aligned}$$

So we have

$$\begin{aligned} v_{+}=\sqrt{\frac{x_{+}s_{+}}{\mu }}=\sqrt{\left( v+\alpha d_{x}\right) \left( v+\alpha d_{s}\right) }. \end{aligned}$$

Define, for $\alpha >0$,

$$\begin{aligned} f\left( \alpha \right) =\varvec{\Phi }_{M}\left( v_{+}\right) -\varvec{\Phi } _{M}\left( v\right) . \end{aligned}$$

Then $f\left( \alpha \right)$ is the difference of proximities between a new iterate and a current iterate for fixed $\mu$. By (24), we have

$$\begin{aligned} \varvec{\Phi }_{M}\left( v_{+}\right) =\varvec{\Phi }_{M}\left( \sqrt{\left( v+\alpha d_{x}\right) \left( v+\alpha d_{s}\right) }\right) \le \frac{1}{2} \left( \varvec{\Phi }_{M}\left( v+\alpha d_{x}\right) +\varvec{\Phi } _{M}\left( v+\alpha d_{s}\right) \right) . \end{aligned}$$

Therefore, we have $f\left( \alpha \right)$$\le$$f_{1}\left( \alpha \right)$, where

$$\begin{aligned} f_{1}\left( \alpha \right) =\frac{1}{2}\left( \varvec{\Phi }_{M}\left( v+\alpha d_{x}\right) +\varvec{\Phi }_{M}\left( v+\alpha d_{s}\right) \right) -\varvec{\Phi }_{M}\left( v\right) . \end{aligned}$$

(31)

Obviously, $f\left( 0\right) = f_{1}\left( 0\right) =0$. Taking the first two derivatives of $f_{1}\left( \alpha \right)$with respect to $\alpha$, we have

$$\begin{aligned} f_{1}^{\prime }\left( \alpha \right)& = \frac{1}{2}\sum _{i=1}^{n}\left( \psi _{M}^{\prime }\left( v_{i}+\alpha d_{xi}\right) d_{xi}+\psi _{M}^{\prime }\left( v_{i}+\alpha d_{si}\right) d_{si}\right) ,\\ f_{1}^{\prime \prime }\left( \alpha \right)& = \frac{1}{2}\sum _{i=1}^{n}\left( \psi _{M}^{\prime \prime }\left( v_{i}+\alpha d_{xi}\right) d_{xi}^{2}+\psi _{M}^{\prime \prime }\left( v_{i}+\alpha d_{si}\right) d_{si}^{2}\right) , \end{aligned}$$

Using (8) and (11), we have

$$\begin{aligned} f_{1}^{\prime }\left( 0\right) =\frac{1}{2}\nabla \varvec{\Phi }_{M}\left( v\right) ^{t}\left( d_{x}+d_{s}\right) =-\frac{1}{2}\nabla \varvec{\Phi } _{M}\left( v\right) ^{t}\nabla \varvec{\Phi }_{M}\left( v\right) =-2\delta (v)^{2}. \end{aligned}$$

For convenience, we denote

$$\begin{aligned} v_{1}=\min \left( v\right) ,\ \delta :=\delta (v),\ \ \varvec{\Phi }_{M}= \varvec{\Phi }_{M}\left( v\right) . \end{aligned}$$

Lemma 3.6

Let $\delta (v)$ be as defined in (11). Then we have

$$\begin{aligned} \delta (v)\ge \sqrt{\varvec{\Phi }_{M}\left( v\right) }. \end{aligned}$$

(32)

Proof

Using (25), we have

$$\begin{aligned} \varvec{\Phi }_{M}\left( v\right) =\sum _{i=1}^{n}\psi _{M}\left( v_{i}\right) \le \sum _{i=1}^{n}\frac{1}{4} \left( \psi _{M}^{\prime }\left( v_{i}\right) \right) ^{2}=\frac{1}{4} \left\| \nabla \varvec{\Phi }_{M}\left( v\right) \right\| ^{2}=\delta (v)^{2}, \end{aligned}$$

so

$$\begin{aligned} \delta (v)\ge \sqrt{\varvec{\Phi }_{M}\left( v\right) }. \end{aligned}$$

This completes the proof. $\square$

Remark 3.1

Throughout the paper, we assume that $\tau$$\ge 1$. Using Lemma 3.6 and the assumption that $\varvec{\Phi }_{M}\left( v\right)$$\ge$$\tau$, we have

$$\begin{aligned} \delta (v)\ge 1. \end{aligned}$$

From Lemmas 4.1–4.4 in Bai et al. (2005), we have the following Lemmas $\mathbf { 3.7-3.10}$.

Lemma 3.7

Let $f_{1}\left( \alpha \right)$ be as defined in (27) and $\delta (v)$ be as defined in (11). Then we have

$$\begin{aligned} f_{1}^{\prime \prime }\left( \alpha \right) \le 2\delta ^{2}\psi _{M}^{\prime \prime }\left( v_{\min }-2\alpha \delta \right) . \end{aligned}$$

Lemma 3.8

If the stepsize $\alpha$ satisfies the inequality

$$\begin{aligned} \psi _{M}^{\prime }\left( v_{\min }\right) -\psi _{M}^{\prime }\left( v_{\min }-2\alpha \delta \right) \le 2\delta , \end{aligned}$$

(33)

we have

$$\begin{aligned} f_{1}^{\prime }\left( \alpha \right) \le 0. \end{aligned}$$

Lemma 3.9

let $\rho :[ 0,+\infty [ \rightarrow ] 0,1]$   be the inverse function of $\frac{-1}{2}\psi _{M}^{\prime }\left( t\right)$ for all $t\in ] 0,1]$.  Then the largest stepsize $\overline{\alpha }$ satisfying (33) is given by

$$\begin{aligned} \overline{\alpha }=\frac{1}{2\delta }\left( \rho \left( \delta \right) -\rho \left( 2\delta \right) \right) . \end{aligned}$$

Lemma 3.10

Let $\overline{\alpha }$ be as defined in Lemma 3.9. Then

$$\begin{aligned} \overline{\alpha }\ge \frac{1}{\psi _{M}^{\prime \prime }\left( \rho \left( 2\delta \right) \right) }. \end{aligned}$$

Lemma 3.11

Let $\rho$ and $\overline{\alpha }$ be as defined in Lemma 3.10. If $\varvec{\Phi }_{M}\left( v\right) \ge$$\tau$$\ge$ 1, then we have

$$\begin{aligned} \overline{\alpha }\ge \frac{1}{\left( 4p\pi +11\right) \left( 8\delta +2\right) ^{\frac{\left( p+2\right) \left( q+1\right) }{\left( p+1\right) q}} }. \end{aligned}$$

Proof

Using Lemma 3.10, the definition of $\psi _{M}^{\prime \prime }\left( t\right)$, and (28) we have

$$\begin{aligned} \begin{array}{ll} \overline{\alpha }&\ge \frac{1}{\psi _{M}^{\prime \prime }\left( \rho \left( 2\delta \right) \right) } \end{array} \end{aligned}$$

And for $\rho \left( 2\delta \right) =t\in ] 0,1]$, we have

$$\begin{aligned} \left( h^{\prime }\left( t\right) \right) ^{2}& = \frac{\left( \pi \right) ^{2}}{\left( t+1\right) ^{4}}\le \left( \frac{\pi }{2}\right) ^{2} \\ -h^{\prime \prime }\left( t\right)& = \frac{\pi }{\left( t+1\right) ^{3}} \le \pi \\ \psi _{M}^{\prime \prime }\left( t\right)& = \frac{2+q\left( q+1\right) t^{-q-2}}{2-q}+\frac{4}{\pi }\left( 1+\tan ^{2}h\left( t\right) \right) \left[ \begin{array}{c} \left[ \begin{array}{c} \left( p-1\right) \tan ^{p-2}h\left( t\right) + \\ \left( p+1\right) \tan ^{p}h\left( t\right) \end{array} \right] \left( h^{\prime }\left( t\right) \right) ^{2}+ \\ \left[ \tan ^{p-1}h\left( t\right) \right] \left( -h^{\prime \prime }\left( t\right) \right) \end{array} \right] , \end{aligned}$$

for $z=2\delta$ we have $\tan h\left( t\right) \le \left( 4z+2\right) ^{ \frac{1}{p+1}}$, this implies

$$\begin{aligned} \tan ^{2}h\left( \rho \left( 2\delta \right) \right)\le & \left( 8\delta +2\right) ^{\frac{2}{p+1}} \\ \tan ^{p-2}h\left( \rho \left( 2\delta \right) \right)\le & \left( 8\delta +2\right) ^{\frac{p-2}{p+1}} \\ \tan ^{p-1}h\left( \rho \left( 2\delta \right) \right)\le & \left( 8\delta +2\right) ^{\frac{p-1}{p+1}} \\ \tan ^{p}h\left( \rho \left( 2\delta \right) \right)\le & \left( 8\delta +2\right) ^{\frac{p}{p+1}} \end{aligned}$$

using (29) and $\left( 8\delta +2\right) >1$, we have $t\ge \left[ \frac{1}{8\delta +2}\right] ^{\frac{1}{q}}$ this implies

$$\begin{aligned} \psi _{M}^{\prime \prime }\left( t\right)\le & 2+\left[ 8\delta +2\right] ^{\frac{q+1}{q}}+\left[ \frac{4}{\pi }\left( 2\right) \left( 2p\left( \frac{ \pi }{2}\right) ^{2}+\pi \right) \right] \left( 8\delta +2\right) ^{\frac{p+2 }{p+1}}. \\\le & \left( 4p\pi +11\right) \left( 8\delta +2\right) ^{\frac{\left( p+2\right) \left( q+1\right) }{\left( p+1\right) q}} \end{aligned}$$

we have

$$\begin{aligned} \overline{\alpha }\ge \frac{1}{\left( 4p\pi +11\right) \left( 8\delta +2\right) ^{\frac{\left( p+2\right) \left( q+1\right) }{\left( p+1\right) q}} }. \end{aligned}$$

This completes the proof. $\square$

Denoting

$$\begin{aligned} \widetilde{\alpha }=\frac{1}{\left( 4p\pi +11\right) \left( 8\delta +2\right) ^{\frac{\left( p+2\right) \left( q+2\right) }{\left( p+1\right) q }}}; \end{aligned}$$

(34)

we have that $\widetilde{\alpha }$ is the default stepsize and that $\widetilde{\alpha }\le \overline{\alpha }$.

Lemma 3.12

(4.5 in Bai et al. (2005)) If the stepsize $\alpha$ satisfies $\alpha$$\le \overline{\alpha }$, then

$$\begin{aligned} f\left( \alpha \right) \le -\alpha \delta ^{2}. \end{aligned}$$

Lemma 3.13

Let $\widetilde{\alpha }$ be the default stepsize as defined in (34) and let

$$\begin{aligned} \varvec{\Phi }_{M}\left( v\right) \ge 1. \end{aligned}$$

Then

$$\begin{aligned} f\left( \widetilde{\alpha }\right) \le -\frac{1}{1400\left( p+1\right) }\left[ \left( \varvec{\Phi }_{M}\right) _{0}\right] ^{\frac{pq-p-2}{2\left( p+1\right) q}}. \end{aligned}$$

(35)

Proof

Using Lemma 3.12 (4.5 in Bai et al. (2005)) with $\alpha =\widetilde{\alpha }$ and (34), we have

$$\begin{aligned} f\left( \widetilde{\alpha }\right)\le & -\widetilde{\alpha } \delta ^{2}\\& = -\frac{\delta ^{2}}{\left( 4p\pi +11\right) \left( 8\delta +2\right) ^{ \frac{\left( p+2\right) \left( q+1\right) }{\left( p+1\right) q}}} \\\le & -\frac{\delta ^{2}}{\left( 4p\pi +11\right) \left( 8\delta +2\delta \right) ^{\frac{\left( p+2\right) \left( q+1\right) }{\left( p+1\right) q}}} \\& = -\frac{\delta ^{2-\frac{\left( p+2\right) \left( q+1\right) }{\left( p+1\right) q}}}{100\left( 4p\pi +11\right) } \\\le & -\frac{\delta ^{\frac{pq-p-2}{\left( p+1\right) q}}}{100\left( 14p+11\right) }\le -\frac{1}{1400\left( p+1\right) }\left[ \varvec{\Phi } _{M}\left( v\right) \right] ^{\frac{pq-p-2}{2\left( p+1\right) q}} \\\le & -\frac{1}{1400\left( p+1\right) }\left[ \left( \varvec{\Phi } _{M}\right) _{0}\right] ^{\frac{pq-p-2}{2\left( p+1\right) q}} \end{aligned}$$

because

$$\begin{aligned} \delta \ge \sqrt{\varvec{\Phi }_{M}\left( v\right) }\ge 1. \end{aligned}$$

This completes the proof. $\square$

4 Iteration bounds of the algorithm

4.1 Inner iteration bound

After the update of $\mu$ to $\left( 1-\theta \right) \mu$, we have

$$\begin{aligned} \varvec{\Phi }_{M}\left( v_{+}\right) \le \left( \varvec{\Phi }_{M}\right) _{0}=\frac{\theta n+2\tau +2\sqrt{2\tau n}}{1-\theta }=L\left( n,\theta ,\tau \right) . \end{aligned}$$

We need to count how many inner iterations are required to return to the situation where $\varvec{\Phi }_{M}\left( v\right) \le \tau$ . We denote the value of $\varvec{\Phi }_{M}\left( v\right)$ after the $\mu$ update as $\left( \varvec{\Phi }_{M}\right) _{0}$; the subsequent values in the same outer iteration are denoted as $\left( \varvec{\Phi }_{M}\right) _{k}$, $k=1,2,...,K$, where K denotes the total number of inner iterations in the outer iteration. The decrease in each inner iteration is given by (35). In Bai et al. (2005) we can find the appropriate values of $\overline{\kappa }$ and $\gamma \in$ ]0, 1] :

$$\begin{aligned} \overline{\kappa }=\frac{1}{1400\left( p+1\right) }, \ \ \ \gamma =1-\frac{pq-p-2}{2\left( p+1\right) q}=\frac{\left( p+2\right) \left( q+1\right) }{2\left( p+1\right) q}. \end{aligned}$$

Lemma 4.1

Let K be the total number of inner iterations in the outer iteration. Then we have

$$\begin{aligned} K\le \left( \frac{2800\left( p+1\right) ^{2}q}{\left( p+2\right) \left( q+1\right) }\right) \left[ \left( \varvec{\Phi }_{M}\right) _{0}\right] ^{ \frac{\left( p+2\right) \left( q+1\right) }{2\left( p+1\right) q}}. \end{aligned}$$

Proof

By Lemma 1.3.2 in Peng et al. (2002), we have

$$\begin{aligned} K\le \frac{\left( \varvec{\Phi }_{M}\right) _{0}^{\gamma }}{\overline{ \kappa }\gamma }=\left( \frac{2800\left( p+1\right) ^{2}q}{\left( p+2\right) \left( q+1\right) }\right) \left[ \left( \varvec{\Phi }_{M}\right) _{0} \right] ^{\frac{\left( p+2\right) \left( q+1\right) }{2\left( p+1\right) q}}. \end{aligned}$$

This completes the proof. $\square$

4.2 Total iteration bound

The number of outer iterations is bounded above by $\frac{\log \frac{n}{ \epsilon }}{\theta }$ (see Roos et al. 1997, Lemma $\mathbf {II}$.$\mathbf {17}$, page $\mathbf {116}$). Through multiplying the number of outer iterations by the number of inner iterations, we get an upper bound for the total number of iterations, namely,

$$\begin{aligned} \left( \frac{2800\left( p+1\right) ^{2}q}{\left( p+2\right) \left( q+1\right) }\right) \left[ \left( \varvec{\Phi }_{M}\right) _{0}\right] ^{ \frac{\left( p+2\right) \left( q+1\right) }{2\left( p+1\right) q}}\frac{\log \frac{n}{\epsilon }}{\theta }. \end{aligned}$$

(36)

For large-update methods with $\tau ={\mathbf {O}}\left( n\right)$ and $\theta =\varvec{\Theta }\left( 1\right)$ we have

$$\begin{aligned} {\mathbf {O}}\left( pn^{\frac{\left( p+2\right) \left( q+1\right) }{2\left( p+1\right) q}}\log \frac{n}{\epsilon }\right) \textit{iterations complexity}. \end{aligned}$$

In case of a small-update methods, we have $\tau ={\mathbf {O}}\left( 1\right)$ and $\theta =\varvec{\Theta }\left( \frac{1}{\sqrt{n}}\right) .$ Substitution of these values into (36) does not give the best possible bound. A better bound is obtained as follows.

By (26), with

$$\begin{aligned} \psi _{M}\left( t\right) \le \left( \frac{3+q}{2}+\frac{\pi }{8}p\right) \left( t-1\right) ^{2},\ \ \ \ \ t>1, \end{aligned}$$

we have

$$\begin{aligned} \varvec{\Phi }_{M}\left( v_{+}\right)\le & n\psi _{M}\left( \frac{1}{ \sqrt{1-\theta }}\sigma \left( \frac{\varvec{\Phi }_{M}\left( v\right) }{n} \right) \right) \\\le & n\left( \frac{3+q}{2}+\frac{\pi }{8}p\right) \left( \frac{1}{\sqrt{ 1-\theta }}\sigma \left( \frac{\varvec{\Phi }_{M}\left( v\right) }{n}\right) -1\right) ^{2} \\& = \frac{n\left( \frac{3+q}{2}+\frac{\pi }{8}p\right) }{\left( 1-\theta \right) }\left( \sigma \left( \frac{\varvec{\Phi }_{M}\left( v\right) }{n} \right) -\sqrt{1-\theta }\right) ^{2} \\\le & \frac{n\left( \frac{3+q}{2}+\frac{\pi }{8}p\right) }{\left( 1-\theta \right) }\left( \left( 1+\sqrt{\frac{\varvec{\Phi }_{M}\left( v\right) }{n}} \right) -\sqrt{1-\theta }\right) ^{2} \\& = \frac{n\left( \frac{3+q}{2}+\frac{\pi }{8}p\right) }{\left( 1-\theta \right) }\left( \left( 1-\sqrt{1-\theta }\right) +\sqrt{\frac{\varvec{\Phi } _{M}\left( v\right) }{n}}\right) ^{2} \\\le & \frac{n\left( \frac{3+q}{2}+\frac{\pi }{8}p\right) }{\left( 1-\theta \right) }\left( \theta +\sqrt{\frac{\tau }{n}}\right) ^{2} \\& = \frac{\left( \frac{3+q}{2}+\frac{\pi }{8}p\right) }{\left( 1-\theta \right) }\left( \theta \sqrt{n}+\sqrt{\tau }\right) ^{2}=\left( \varvec{\Phi }_{M}\right) _{0}. \end{aligned}$$

where we also used that $1-\sqrt{1-\theta }=\frac{\theta }{1+\sqrt{1-\theta } }\le \theta$ and $\varvec{\Phi }_{M}\left( v\right) \le \tau$,using this upper bound for $\left( \varvec{\Phi }_{M}\right) _{0}$, we get the following iteration bound:

$$\begin{aligned} \left( \frac{2800\left( p+1\right) ^{2}q}{\left( p+2\right) \left( q+1\right) }\right) \left[ \left( \varvec{\Phi }_{M}\right) _{0}\right] ^{ \frac{\left( p+2\right) \left( q+1\right) }{2\left( p+1\right) q}}\frac{\log \frac{n}{\epsilon }}{\theta }. \end{aligned}$$

note the now $\left( \varvec{\Phi }_{M}\right) _{0}={\mathbf {O}}\left( p+q\right)$, and the iteration bound becomes

$$\begin{aligned} {\mathbf {O}}\left( \left( p+q\right) ^{2}\sqrt{n}\log \frac{n}{\epsilon }\right) \text{ iteration } \text{ complexity. } \end{aligned}$$

5 Comparison of algorithms

In this section we offer compared of their algorithm given by S. Fathi-Hafshejani et al. in Fathi-Hafshejani et al. (2018) and the result with ours. To prove the effectiveness of our new kernel function and evaluate its effect on the behavior of the algorithm, we offer a comparison between the results of algorithms of $\text{ IPMs }$, the following two kernel functions.

• 1. The first kernel function, given by S. Fathi-Hafshejani et al. in Fathi-Hafshejani et al. (2018), is noted kernel function F, defined by

  $$\begin{aligned} \psi _{F}\left( t\right) =2\pi \int _{1}^{t}(tan(v(x))-cot^{3p}(v(x)))dx, \ \ \ p>0, v(x)=\frac{\ x \pi }{2+2x}>0. \end{aligned}$$

• 2. Our new kernel function is noted kernel function M, defined in (12) by

  $$\begin{aligned} \psi _{M}\left( t\right) =t^{2}+\frac{t^{1-q}}{q-1}-\frac{q}{q-1}+\frac{4}{ \pi p}\left[ \tan ^{p}h\left( t\right) -1\right] ,\ \left\{ \begin{array}{c} h\left( t\right) =\frac{\pi }{2t+2}, \\ p\ge 2,\ q>1. \end{array} \right. \end{aligned}$$

  We summarize this results in the Table 1

Table 1 The default stepsize and the complexity results for large- and small-update methods

Comments For the same value of parameter p, for both functions:

• If $q>p$, the complexity results for large-update methods, of the algorithm based of our new kernel function best of the complexity results of the algorithm based of the kernel function given by Fathi-Hafshejani et al. (2018). While always the opposite of The complexity results for small-update methods.

• If $q=p=logn$, the complexity results for large-update methods, of the tow algorithms consolidate of the best known complexity bound for large-update methods namely ${\mathbf {O}}\left( \sqrt{n} \log n\log \frac{n}{\epsilon }\right)$.

5.1 Numerical tests

Recall that the considered problem is

$$\begin{aligned} n=2m,\ A\left( i,j\right) =\left\{ \begin{array}{lll} 0 & \text{ if } & i\ne j \ \ \,\,{\text{and}}\,\, \ \ j\ne i+m \\ 1 & \text{ if } & i=j \ \ \text{ or } \ \ j=i+m \end{array}\right. \end{aligned}$$

$c\left( i\right) =-1,$$c\left( i+m\right) =0,$$b\left( i\right) =2,$ and the interior-point condition $\mathbf {IPC}$, $x^{0}(i)=x^{0}(i+m)=1$, $y^{0}(i)=-2$, $s^{0}(i)=1, s^{0}(i+m)=2$ for $i\ =1, \ldots ,m$.

To prove the effectiveness of our new kernel function and evaluate its effect on the behavior of the algorithm, we conducted comparative numerical tests between the following two kernel functions previous.

To be solved, we used the Software Dev Pascal. We have taken $\epsilon =10^{-4}$, $\mu ^{0}=1$, $\theta =\frac{1}{2}$, $\tau =n$, $p\in \{4, logn\}$ and $q\in \{6, log n\}$ for the new kernel function.

We have the step size $\alpha$, satisfying $0<\alpha <\overline{\alpha }$ : we take respectively, $\alpha _{\textit{F}}$ and $\alpha _{\textit{M}}$, which match with the notation of precedent kernel functions; We choose $\alpha = min\{\alpha _{\textit{F}},\alpha _{\textit{M}}\}$.

In the table of results, (ex (m, n)): m is the number of constraints and n is the number of variables, $\left(\textit{Itr A} {\rm and} \textit{Med A}=\frac{{\rm total} {\rm iteration }}{{\rm outer} {\rm iteration}}\right)$ represents the number of outer iteration necessary to obtain the optimal solution and the median value of the number of internal iterations using the function A, Respectively. We summarize this numerical study in Tables 2, 3, 4 and 5.

Table 2 Comparison of examples for $p=4$ and $q=6$

Table 3 Comparison of examples for $p=4$ and $q=logn$

Table 4 Comparison of examples for $=logn$ and $q=6$

Table 5 Comparison of examples for $p=logn$ and $q=logn$

Comments These tables confirm the theoretical results obtained and show the reduction of the complexity results of the algorithm based of our new kernel function best of the complexity results of the algorithm based of the kernel function given by Fathi-Hafshejani et al. (2018).

6 Concluding remarks

In this work, we propose new efficient parameterized kernel functions with trigonometric barrier terms. We study the properties of the kernel functions and investigate the effects of parameters. Moreover, we improve the algorithmic complexity of the interior points method. We analyze large-update and small-update versions of the primal–dual interior algorithm described in Fig. 1, which is based on the new parameterized kernel functions (12). We prove that the iteration bound of the large-update interior-point method based on the kernel function considered in this paper is ${\mathbf {O}}\left( pn^{\frac{\left( p+2\right) \left( q+1\right) }{2\left( p+1\right) q}}\log \frac{n}{\epsilon }\right)$. Setting the bound to $p=q\ge 6$ improves the complexity results we obtained so far for large-update methods, the trigonometric kernel function given by Peyghami et al. (2014), i.e., ${\mathbf {O}}\left( n^{\frac{2}{3}}\log \frac{n}{\epsilon }\right)$. When p is dependent on n, it minimizes the iteration bound. In particular, if we take $p=q=\log n$, we obtain the best known complexity bound for large-update methods, namely ${\mathbf {O}}\left( \sqrt{n}\left( \log n\right) \log \frac{n}{\epsilon }\right)$. This bound improves the complexity results obtained so far for large-update methods, the trigonometric kernel function given by Peyghami and Hafshejani (2014), i.e.,${\mathbf {O}}\left( \sqrt{n}\left( \log n\right) ^{2}\log \frac{n}{\epsilon }\right)$. For small-update methods, we obtain the best know iteration bound, namely ${\mathbf {O}}\left( \sqrt{n}\log \frac{n}{\epsilon }\right)$, by taking $\left( p+q\right) ={\mathbf {O}}\left( 1\right)$. These results are an important contribution for improving the computational complexity of the problem under study.