1 Introduction

Renewable energy portfolio mandates and/or standards reduce emissions and the effects of climate change (International Energy Agency 2017). Governments within the United States have legislated their own standards, e.g., California plans to have 50% of its energy demands met using renewable energy technologies by 2030 (Clean Energy and Pollution Reduction Act (SB350)). However, as penetration of traditional variable generation sources, i.e., wind and photovoltaic solar, increases, so do challenges associated with grid stability and increased energy curtailment (Denholm and Hand 2011). Electric, thermal, and chemical energy storage mitigate this instability, thereby potentially increasing renewable energy share of the electricity market (Dunn et al. 2011).

Concentrating solar power (CSP) is a renewable energy technology that uses relatively inexpensive media such as high-temperature salt to store thermal energy for future power generation. CSP technologies capture solar thermal radiation by utilizing mirrors to concentrate the sun’s energy onto a receiver. There are four major CSP technologies: parabolic trough, linear Fresnel, dish Stirling, and power tower. Each of these technologies has its relative benefits and drawbacks. CSP power tower (also known as a “central receiver”) uses a field of thousands of mirrors, called heliostats, to focus the sun’s rays onto a receiver atop a tower. This CSP configuration can achieve high concentration ratios as defined by collectors-to-surface area, and, correspondingly, high operating temperatures, without the high cost, compared to those of any other CSP technology, thereby allowing the solar heat collection system to be paired with higher efficiency power cycles. CSP power tower technology presents a promising path forward for utility-scale energy production with the greatest potential for cost reduction and efficiency improvement (Mehos et al. 2017).

Wagner et al. (2018) provide an overview of CSP power tower technology advantages over those of other renewable and fossil alternatives. With the use of TES, CSP power tower plants decouple solar energy collection from electricity generation, allowing the technology to generate stable grid power through cloudy periods and throughout the night, shown in the case study of Rice, California. This decoupling of collection and generation also permits the power tower technology to be paired with any conventional thermodynamic conversion power cycles, e.g, a steam Rankine cycle. However, Turchi et al. (2013) and Dunham and Iverson (2014) present supercritical carbon dioxide power cycles as the most promising. The methodology presented in this paper can be adapted to supercritical carbon dioxide power cycles as the technology matures.

Photovoltaic (PV) solar energy uses panels comprised of an array of individual solar cells made of semi-conducting material that, when hit by a photon, generates a flow of electrons. Modules are connected in a variety of parallel and series configurations to provide voltage to a power inverter that transforms the direct current (DC) to alternating current (AC) at the grid’s regulated voltage and frequency. Photovoltaic panels can be mounted at a fixed orientation or can track the sun using a single- or double-axis system. PV can be coupled with electric energy storage, e.g., batteries, to provide some dispatchablity. However, battery technologies are still expensive and incapable of fully serving as a grid-scale storage method (Zakeri and Syri 2015). The cost of PV systems has dropped significantly in the last decade and, as a result, deployment has rapidly accelerated. Fu et al. (2017) reports that 2017 utility-scale PV systems are already below the Department of Energy’s 2020 SunShot target for levelized cost of energy. Basore and Cole (2018) argue that low-cost energy storage significantly increases PV generation capacity.

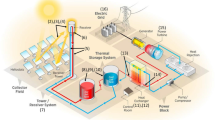
This paper demonstrates that hybridization of PV and batteries with CSP and TES reduces the cost of energy produced by the system while simultaneously providing reliable, dispatchable electricity. The proposed hybrid system exports low-cost PV generation during daytime hours while predominantly storing thermal energy collected by the CSP system. Stored energy can be dispatched for electricity generation at night or around disruptions in PV production, thereby achieving a high capacity factor and lower overall levelized energy cost. CSP-TES-PV-battery hybrid systems, shown in Fig. 1, are capable of replacing traditional fossil fuel baseload generation and are therefore gaining popularity in international markets, e.g., Morocco (New Energy Update: CSP 2018) and Chile (Meyers 2015) at the time of this writing. However, the design and simulation of CSP-TES-PV-battery hybrid systems presents significant challenges because the interaction of the two systems is not well understood.

Fig. 1
figure 1

CSP-TES-PV-battery hybrid system configuration (Graphic ©NREL/Al Hicks). On the left, the system consists of a molten salt power tower CSP plant, which consists of a heliostat field, molten salt receiver, thermal energy storage, and a Rankine power cycle. On the right, the system consists of a photovoltaic system with battery storage. The system depicted is not all-inclusive of components required for control or operation

Full size image

To analyze a CSP-TES-PV-battery hybrid design, we develop a mixed-integer linear programming (MILP) model that prescribes a dispatch strategy at a 10-min time fidelity. The strategy is implemented within an engineering simulation framework on a rolling time horizon to determine the performance of the system over a longer horizon—typically, one year. This approach makes use of existing methods and software tools both for the MILP characterizing CSP and for the engineering simulation of plant performance. The dispatch model determines an operating schedule that maximizes profits over the prescribed time horizon while accounting for solar resource and electricity price forecasts, sub-system sizing, operational limits, and performance characteristics.

The remainder of the paper is organized as follows: Section 2 provides a literature review of dispatch methodologies used for stand-alone CSP with TES, stand-alone PV with battery, and combined CSP-PV hybrids. Section 3 presents and discusses a mathematical formulation of the hybrid system dispatch optimization model. Section 4 describes the challenges of model complexity and corresponding solution techniques implemented to improve tractability and reduce solution time. Section 5 presents a case study that exercises the model with the CSP-TES-PV-battery hybrid system design evaluated for two locations and two corresponding markets. We present results regarding annual plant performance and solution time improvements, and contrast hybrid and stand-alone system performance. Section 6 concludes with a summary and extensions of our work.

2 Literature review

A system that combines PV with batteries is more commonly used in smaller residential markets, while CSP with TES is used only for larger commercial generation. However, with greater penetration of renewable energy sources in the electricity market, utility-scale battery storage is being considered to increase grid stability by providing ancillary services, shaving peak-load, and integrating renewables (Miller et al. 2010; Poullikkas 2013). The combination of PV and CSP has only in recent years gained traction. We review (1) PV with battery storage, and (2) CSP with TES separately and then (3) a combination of some subset of (1) and (2).

2.1 Photovoltaics with battery storage

In general, literature pertaining to PV-battery systems suggests that batteries should either “peak-shift” demand, store energy from lower-demand parts of the day for use during high demand, or smooth power output during variations in solar resource, e.g., Heymans et al. (2014). Utility companies provide price incentives to induce this behavior.

Combining PV and lithium-ion batteries can reduce residential electricity use on the grid. Tervo et al. (2018) demonstrate the cost effectiveness of these systems using bi-directional metering to sell energy back to the utility in each state in the United States of America. PV-plus-battery system sizing can be done at the residential scale for a single household (Weniger et al. 2014), or for a university campus (Borowy and Salameh 1996), and can include hybrid options such as wind or fuel cells, but does not employ mixed integer linear programs (MILPs) to determine the operations of the hybrid’s sub-systems such as we do. Gitizadeh and Fakharzadegan (2014) use a MILP to optimize the capacity of a battery for a grid-connected PV system and find that the resulting battery size is sensitive to the pricing structure.

Weather transients such as passing clouds significantly affect the performance of PV-plus-battery systems, though performance can be described using simplified models (Giraud and Salameh 1999); the authors compare results from an artificial neural network simulation model against experimental results during cloudy days. Shi et al. (2012) forecast PV based on simplified categorized weather conditions for the following day with a view towards maximizing energy output and profit. These models differ from ours because we use the System Advisor Model (SAM) to estimate the performance of renewable equipment (Blair et al. 2018).

Various researchers propose linear programs to determine a dispatch, rather than a design, strategy for a PV-plus-battery system in day-ahead and real-time markets (Nottrott et al. 2012, 2013), respectively; however, there is no consideration of the battery charge and discharge currents. Hassan et al. (2017) study a PV-plus-battery storage system with a feed-in-tariff incentive. Riffonneau et al. (2011) compare optimizing a PV-plus-battery grid-connected system using dynamic programming with a rule-based heuristic. Lu and Shahidehpour (2005) analyze the impact of scheduling short-term battery usage at hourly time fidelity on utility operations using a Lagrangian relaxation-based optimization algorithm. While these models use optimization, they do not simultaneously capture design and dispatch decisions, and, if a heuristic is used, optimality of the corresponding dispatch solutions cannot be guaranteed.

2.2 Concentrated solar power with thermal energy storage

CSP systems use heliostats to focus sunlight onto a central receiver located on top of a tower to heat molten salt. By using TES to store the heat of the molten salt for use in power production at a later time, a CSP system can participate more reliably in day-ahead markets. Vasallo and Bravo (2016) propose two models to optimize dispatch scheduling and apply the approach to a 50 MW CSP plant with TES to maximize profits in a day-ahead market. Algorithms exist to optimize the CSP plant’s market participation with scheduling and control decisions (Dowling et al. 2018); the authors show that incorporating detailed dynamics into multi-scale electricity markets can increase revenues by up to 50% for certain capacities of thermal energy storage. Optimally sizing CSP-TES systems is done with the System Advisor Model using a short-term control strategy or with a model developed by Casella et al. (2014). Usaola (2012) create a dispatch strategy based on day-ahead electricity market prices and examine the effects that incentives offer. Petrollese et al. (2017) discuss ways to handle weather uncertainty to mitigate its impact on revenue.

2.3 Hybrid systems

For the purposes of this analysis, a hybrid power generation system is one in which two or more technologies that are capable of independently producing and/or storing energy are deployed in a coordinated—and often co-located—design. As such, many hybrid concepts are possible and do not necessarily include CSP. For example, PV-battery systems might be used to support electrical generation for peak-load shaving and prevent peaking generators from turning on. Ashari and Nayar (1999) illustrate the use of a PV, battery, and diesel generator hybrid system to develop policies or dispatch rules to more efficiently meet load.

Previous work on migrogrids with generators demonstrates that hybrid systems can effectively support electrical demand. Scioletti et al. (2017) compare how integration of solar power and batteries into a diesel-powered microgrid reduces fuel consumption relative to a microgrid possessing only diesel generators, while Goodall et al. (2018) extend the work to capture fade and temperature effects of the batteries. Muselli et al. (1999) optimize equipment size in a microgrid consisting of PV, a battery, and gasoline or diesel generators, and show economic benefits over a PV stand-alone system. Marwali et al. (1998) optimize thermal unit commitment at hourly time fidelity for a day-long time horizon to demonstrate the benefits of the PV-battery system.

In the last half decade, the solar industry has shown increasing interest in the design and deployment of CSP-PV hybrid systems. Preliminary analysis suggests that the inclusion of photovoltaics can increase the capacity factor of a baseload CSP plant from 80% to roughly 90% in a cost-effective manner (Green et al. 2015). Determining optimal equipment sizes in the hybrid system is important for lowering the power purchase agreement price, which can be different between areas of variable and constant hourly demand (Starke et al. 2016). Denholm et al. (2013) explore the economic opportunities of solar energy systems for the United States grid. The optimal solar energy system design with storage for constant power output has a different CSP-to-PV size ratio in areas where there are significant changes in the length of day throughout the year (Petrollese and Cocco 2016).

Concentrating solar power systems with TES are dispatchable, increasing overall grid flexibility and allowing for greater penetration of other non-dispatchable renewable resources such as PV and wind (Denholm and Mehos 2011). Similarly, Cocco et al. (2016) improve power dispatchability, but instead use concentrated photovoltaics. Solar hybrids can generate baseload power at a lower levelized cost of electricity than CSP or PV systems could alone (Pan and Dinter 2017). An evaluation of a 50MW power plant for a mining operation in Chile shows how a PV, a CSP, and a hybrid PV-CSP system can effectively meet the mine’s electricity demand (Parrado et al. 2016); however, the study does not include a battery system. A similar analysis is performed on a desalination plant in northern Chile (Valenzuela et al. 2017), also without batteries.

2.4 Contribution

This paper presents a new hybrid system dispatch model that builds on existing work for optimizing dispatch for CSP (Wagner et al. 2017) and for PV with batteries (Husted et al. 2017). The results indicate that CSP with TES supplements the diurnal and variable PV generation profiles while the batteries provide rapid response to sudden changes in PV production or demand conditions. Furthermore, the model generates dispatch profiles at 10-min intervals for an annual time horizon determined in 48-h increments with a 24-h look-ahead policy, improving upon previous models with lower temporal fidelity. The approach both adapts existing and develops new techniques for this application; specifically: it (1) modifies a fix-and-relax heuristic in two ways (both with respect to system components and with respect to time); (2) linearizes nonlinear terms; and (3) develops valid inequalities to improve proof of optimality.

3 Dispatch optimization model

Designing CSP-PV hybrid systems possesses unique challenges, requiring simulation to couple both subsystems, which has historically been done using monthly average hourly PV production (Green et al. 2015). By taking an average of the monthly PV production, the variability of PV resource is not captured, thereby over-predicting the production of the CSP-PV hybrid system. We propose to replace a heuristic, which had been used for dispatch solely of a CSP system, with a detailed optimization model that contains PV and a battery and that determines decisions at a 10-min time fidelity, to determine an optimal schedule over a year-long time horizon.

Fig. 2
figure 2

System layout consisting of a CSP system (with TES), PV solar field generation, and battery storage

Full size image

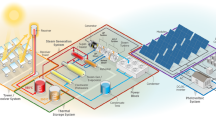
Figure 2 presents a block diagram of a solar hybrid system. On the left of the alternating current (AC) bus, there is the PV array with battery storage. To the right of the AC bus is a CSP field, a power cycle (for CSP generation), TES coupled to both of these, and a connection to and from the grid. The black arrows represent electricity flow while the red and blue arrows represent “hot” and “cold” TES molten salt flows, respectively. The hybrid system produces electricity that can be sold to the grid, and can also purchase electricity from the grid in the analyzed configuration. This configuration is one of several possible, and various constraints related to grid connection, intra-system connections, and design considerations may alter the system topology in practice.

This section describes the sets, parameters, variables, objective function, and constraining relationships comprising the optimization model. Parameters and variables that contain the subscript of time t indicate their time-varying nature. In general, upper-case letters denote parameters while lower-case letters are reserved for variables. We also use lower-case letters for indices and upper-case script letters for sets.

3.1 Notation

The following MILP, (\({\mathcal {H}}\)), requires the initial operational state of the system, the PV field and receiver energy generation forecasts, the expected cycle conversion efficiency profile as a function of ambient temperature and thermal input, and the energy price or tariff profile (Table 1).

Table 1 Hybrid dispatch model, (\({\mathcal {H}}\)), sets and parameters
Full size table

The variables (see Table 2) describe energy (thermal \(\hbox {kWh}{}_\textsf {t} \) or electric \(\hbox {kWh}{}_\textsf {e}\)) states and power flows (thermal \(\hbox {kW}{}_\textsf {t} \) or electric \(\hbox {kW}{}_\textsf {e}\)) in the system. Continuous variables “x,” “\({\dot{w}}\),” “u,” and “s” representing power and energy relate to the receiver, power cycle, PV field, battery, and TES. Binary variables “y” enforce operational modes and sequencing such that start-up must occur before normal operation, for example.

Table 2 Variables used in (\({\mathcal {H}}\))
Full size table

3.2 Objective function and constraints

We maximize the sale of electricity given as the revenue based on sales minus the cost of grid purchase throughout the time horizon in question. We decrement the revenue by penalties incurred for start-ups and shut-downs, changes in production between successive time periods, and operating costs related to the power cycle, the PV field, the receiver and the battery. Lesser penalties are introduced to enforce the logic associated with the receiver and power cycle shut down, and we also charge for battery lifecycles consumed during the time horizon.

$$\begin{aligned} ({\mathcal {H}})\;\; \text {maximize} \quad&\sum _{t \in {\mathcal {T}}} \Big [ {\varDelta }\cdot P_{t} ({\dot{w}}^{s}_{t}-{\dot{w}}^{p}_{t}) \nonumber \\&- \Big (\frac{1}{\gamma }\Big )^t ( C^{csu}y^{csup}_t + C^{chsp} y^{chsp}_t + \alpha y^{csd}_t + C^{\delta W} {\dot{w}}^{\delta }_t) \nonumber \\&- \Big (\frac{1}{\gamma }\Big )^t \big (C^{rsu} y^{rsup}_t + C^{rhsp} y^{rhsp}_t + \alpha y^{rsd}_t \big ) \nonumber \\&- \Big (\frac{1}{\gamma }\Big ) ^t {\varDelta }\big ( C^{pc} {\dot{w}}_t + C^{csb} Q^b y^{csb}_t + C^{pv} {\dot{w}}^{pv}_t + C^{bd} {\dot{w}}^{-}_t \nonumber \\&+ C^{bc} {\dot{w}}^{+}_t + C^{rec} x^{r}_t \big ) \Big ] - C^{bl}b^c \end{aligned}$$
(1)

3.2.1 Receiver operations

We include the following constraints that govern receiver operations:

Receiver Start-up

$$\begin{aligned}&u^{rsu}_t \le u^{rsu}_{t-1} + {\varDelta }x^{rsu}_t \ \ \forall \ t \in {\mathcal {T}}: t \ge 2 \end{aligned}$$
(2a)
$$\begin{aligned}&u^{rsu}_t \le E^r y^{rsu}_t \ \ \forall \ t \in {\mathcal {T}} \end{aligned}$$
(2b)
$$\begin{aligned}&y_t^r \le \frac{u^{rsu}_t}{E^r} + y^r_{t-1} + y^{rsb}_{t-1}\ \ \forall \ t \in {\mathcal {T}}: t \ge 2 \end{aligned}$$
(2c)
$$\begin{aligned}&y^{rsu}_t + y^r_{t-1} \le 1 \ \ \forall \ t \in {\mathcal {T}}: t \ge 2 \end{aligned}$$
(2d)
$$\begin{aligned}&x^{rsu}_t \le Q^{ru} y^{rsu}_t \ \ \forall \ t \in {\mathcal {T}} \end{aligned}$$
(2e)
$$\begin{aligned}&y^{rsu}_t \le \frac{Q^{in}_t}{Q^{rl}} \ \ \forall \ t \in {\mathcal {T}} \end{aligned}$$
(2f)

Receiver Supply and Demand

$$\begin{aligned}&x^{r}_t + x^{rsu}_t + Q^{rsd} y^{rsd}_t \le Q^{in}_t \ \ \forall \ t \in {\mathcal {T}} \end{aligned}$$
(3a)
$$\begin{aligned}&x^{r}_t \le Q^{in}_t y^r_t \ \ \forall \ t \in {\mathcal {T}} \end{aligned}$$
(3b)
$$\begin{aligned}&x^{r}_t \ge Q^{rl} y^r_t \ \ \forall \ t \in {\mathcal {T}} \end{aligned}$$
(3c)
$$\begin{aligned}&y^r_t \le \frac{Q^{in}_t}{Q^{rl}} \ \ \forall \ t \in {\mathcal {T}} \end{aligned}$$
(3d)

Logic Associated with Receiver Modes

$$\begin{aligned}&y^{rsu}_t + y^{rsb}_t \le 1 \ \ \forall \ t \in {\mathcal {T}} \end{aligned}$$
(4a)
$$\begin{aligned}&y^{r}_t + y^{rsb}_t \le 1 \ \ \forall \ t \in {\mathcal {T}} \end{aligned}$$
(4b)
$$\begin{aligned}&y^{rsb}_t \le y^{r}_{t-1} + y^{rsb}_{t-1} \ \ \forall \ t \in {\mathcal {T}}: t \ge 2 \end{aligned}$$
(4c)
$$\begin{aligned}&y^{rsup}_t \ge y^{rsu}_t - y^{rsu}_{t-1} \ \ \forall \ t \in {\mathcal {T}}: t \ge 2 \end{aligned}$$
(4d)
$$\begin{aligned}&y^{rhsp}_t \ge y^{r}_{t} - (1-y^{rsb}_{t-1}) \ \ \forall \ t \in {\mathcal {T}}: t \ge 2 \end{aligned}$$
(4e)
$$\begin{aligned}&y^{rsd}_{t} \ge (y^{r}_{t-1} - y^{r}_{t}) + (y^{rsb}_{t-1} - y^{rsb}_{t}) \ \ \forall \ t \in {\mathcal {T}}: t \ge 2 \end{aligned}$$
(4f)

In order for the system to generate power, we impose Constraint (2a) which accounts for receiver start-up energy “inventory”; we employ an inequality such that inventory can revert to a level of zero in time periods after which start-up has completed. Inventory is allowed to assume a positive value during time periods of receiver start-up (Constraint (2b)). Power production is positive only upon completion of a start-up or if the receiver also operates in the time period prior (Constraint (2c)). If the receiver is producing thermal power in time \(t-1\), it cannot be starting up in the following time period t (Constraint (2d)). Ramp-rate limits must be honored during the start-up procedure (Constraint (2e)). Trivial solar resource prevents receiver start-up (Constraint (2f)).

The parameter \(Q^{in}_t\) provides an upper bound on the thermal power produced by the receiver, from which any energy used for start-up or shutdown detracts (Constraint (3a)). Constraint (3b) permits the receiver to generate thermal power only while in power-producing mode. Receiver thermal power generation is subject to a lower bound by Constraint (3c) owing to the minimum turndown of molten salt pumps. In the absence of thermal power, the receiver is not able to operate (Constraint (3d)).

Standby mode allows molten salt to be circulated between the TES tanks and the receiver such that a restart can occur quickly; such a restart incurs a smaller financial penalty. Constraints (4a) and (4b) preclude (1) standby and start-up modes and (2) standby and power-producing modes from coinciding. Standby mode can only occur in time periods directly after which the receiver was either in standby or power-producing mode (Constraint (4c)). Specifically through the use of the start-up variables \(y_t^{rsup}\) and \(y^{rhsp}_t\) (as opposed to \(y_t^{rsu}\) which affords multiple time periods of start-up but therefore does not enforce penalty logic), Constraints (4d) and (4e) ensure that penalties for receiver start-up from an off or from a standby state are incurred, respectively. Constraint (4f) implements shut-down logic related to power-producing or standby states. Constraints (12a)–(12c) and (12e) enforce domain requirements on the variables except for \(x^{r}_t\) whose non-negativity is ensured via Constraints (3c).

3.2.2 Power cycle operations

Power cycle operation constraints are similar to those of receiver operations:

Cycle Start-up

$$\begin{aligned}&u^{csu}_t \le u^{csu}_{t-1} + {\varDelta }Q^c y^{csu}_t \ \ \forall \ t \in {\mathcal {T}}: t \ge 2 \end{aligned}$$
(5a)
$$\begin{aligned}&u^{csu}_t \le E^{c} y^{csu}_t \ \ \forall \ t \in {\mathcal {T}} \end{aligned}$$
(5b)
$$\begin{aligned}&y_t \le \frac{u^{csu}_{t-1}}{E^c} + y_{t-1} + y^{csb}_{t-1} \ \ \forall \ t \in {\mathcal {T}}: t \ge 2 \end{aligned}$$
(5c)
$$\begin{aligned}&x_t \le Q^u y_t \ \ \forall \ t \in {\mathcal {T}} \end{aligned}$$
(5d)
$$\begin{aligned}&x_t \ge Q^l y_t \ \ \forall \ t \in {\mathcal {T}} \end{aligned}$$
(5e)

Power Supply and Demand

$$\begin{aligned}&{\dot{w}}_t = \frac{\eta ^{amb}_t}{\eta ^{des}}[\eta ^p x_t + (W^u - \eta ^p Q^u)y_t] \ \ \forall \ t \in {\mathcal {T}} \end{aligned}$$
(6a)
$$\begin{aligned}&{\dot{w}}^{\delta }_t \ge {\dot{w}}_t - {\dot{w}}_{t-1} \ \ \forall \ t \in {\mathcal {T}} : t \ge 2 \end{aligned}$$
(6b)
$$\begin{aligned}&{\dot{w}}^{\delta }_t \ge {\dot{w}}_{t-1} - {\dot{w}}_{t} \ \ \forall \ t \in {\mathcal {T}} : t \ge 2 \end{aligned}$$
(6c)
$$\begin{aligned}&{\dot{w}}^{\delta }_t \le W^{\delta lim} \nonumber \\&+ \left( \frac{\eta ^{amb}_t}{\eta ^{des}}W^l - W^{\delta lim} \right) \left( y_t - y_{t-1} + 2y^{csb}_t + 2y^{csd}_t \right) \ \ \forall \ t \in {\mathcal {T}} : t \ge 2 \end{aligned}$$
(6d)
$$\begin{aligned}&{\dot{w}}^{s}_t \le W^{net}_t \ \ \forall \ t \in {\mathcal {T}} \end{aligned}$$
(6e)
$$\begin{aligned}&{\dot{w}}^{s}_t - {\dot{w}}^{p}_t = {\dot{w}}_t (1-\eta ^{c}_t) + \frac{{\dot{w}}^{-}_{t} - \alpha ^{-}y^{-}_t}{1 + \beta ^{-}}\nonumber \\&-\left[ (1 + \beta ^{+}) {\dot{w}}^{+}_t + \alpha ^+ y^{+}_t\right] + \frac{{\dot{w}}^{pv}_t - {\dot{w}}^{pv+}_t - \alpha ^{pv}y^{pv}_t}{1+ \beta ^{pv}} \nonumber \\&- L^r (x^{r}_t + x^{rsu}_t + Q^{rl} y^{rsb}_t) - L^c x_t - W^h y^{r}_t - W^b y^{csb}_t \nonumber \\&- W^{ht} y^{rsu}_t - \frac{E^{hs}}{{\varDelta }} \left( y^{rsu}_t + y^{rsb}_t + y^{rsd}_t \right) \ \ \ \ \ \ \forall \ t \in {\mathcal {T}} \end{aligned}$$
(6f)

Logic Governing Cycle Modes

$$\begin{aligned}&y^{csu}_t + y_{t-1} \le 1 \ \ \forall \ t \in {\mathcal {T}}: t \ge 2 \end{aligned}$$
(7a)
$$\begin{aligned}&y_{t} + y^{csu}_t \le 1 \ \ \forall \ t \in {\mathcal {T}} \end{aligned}$$
(7b)
$$\begin{aligned}&y^{csb}_t \le y_{t-1} + y^{csb}_{t-1} \ \ \forall \ t \in {\mathcal {T}}: t \ge 2 \end{aligned}$$
(7c)
$$\begin{aligned}&y^{csu}_t + y^{csb}_t \le 1 \ \ \forall \ t \in {\mathcal {T}} \end{aligned}$$
(7d)
$$\begin{aligned}&y_t + y^{csb}_t \le 1 \ \ \forall \ t \in {\mathcal {T}} \end{aligned}$$
(7e)
$$\begin{aligned}&y^{chsp}_t \ge y_t - (1 - y^{csb}_{t-1}) \ \ \forall \ t \in {\mathcal {T}}: t \ge 2 \end{aligned}$$
(7f)
$$\begin{aligned}&{y^{csd}_{t} \ge y_{t-1} - y_{t} + y^{csb}_{t-1} - y^{csb}_{t} \ \ \forall \ t \in {\mathcal {T}}: t \ge 2} \end{aligned}$$
(7g)
$$\begin{aligned}&y^{csup}_t \ge y^{csu}_t - y^{csu}_{t-1} \ \ \forall \ t \in {\mathcal {T}}: t \ge 2 \end{aligned}$$
(7h)

Constraint (5a) accounts for start-up energy “inventory,” which can only be positive during time periods in which the cycle is starting up (Constraint (5b)). Normal cycle operation can occur upon completion of start-up energy requirements, if the cycle is operating normally, or directly after stand-by mode (Constraint (5c)). Constraint (5d) and Constraint (5e) form the upper and lower bounds on the heat input to the power cycle, respectively. The relationship between electrical power and cycle heat input is modeled as a linear function with corrections for ambient temperature effects (Constraint (6a)). Constraints (6b) and (6c) measure the change in the production of electrical power over time. Constraint (6d) limits the ramp rate under cycle start up, stand by, and shut down to the minimum power output defined by Constraint (6a), with the appropriate transformation after substituting \(Q_l\) for \(x_t\) and 1 for \(y_t\); otherwise, it is restricted to the corresponding limit per time period. Constraint (6e) limits the grid transmission for net power production. Positive and negative power flow (corresponding to sold and purchased electricity, respectively) is determined by a power balance on the AC bus of the hybrid system (Constraint (6f)). The right-hand side of Constraint (6f) consists of the following terms, in the order in which they appear: (1) power cycle generation less condenser parasitic power, (2) battery discharge power accounting for DC-to-AC conversion losses, (3) battery charge power accounting for AC-to-DC conversion losses, (4) PV field generation less power used for battery charging directly from the field, accounting for inverter losses, (5) TES pumping power requirements for receiver operations, (6) TES pumping power requirements for cycle operation, (7) heliostat tracking power, (8) power cycle standby parasitic power, (9) tower piping heat trace for receiver start-up, and (10) heliostat field stow power for different receiver operations.

Constraint (7a) precludes power cycle start-up in consecutive time periods of power-producing operation. Constraint (7b) precludes power cycle start-up and operation from coinciding. The cycle-standby-mode constraint (Constraint (7c)) is analogous to that for the receiver. Standby and start-up modes cannot simultaneously occur (Constraint (7d)); this also holds for standby and power-producing modes (Constraint (7e)). Constraints (7f) and (7g) implement the following logic, respectively: (1) starting up after standby and (2) shutting down after producing power or standing by. Penalties incurred from a cycle cold start are incurred via Constraint (7h). Constraints (12a)–(12c) and (12f) enforce domain requirements on the variables except for \(x_t\) whose non-negativity is ensured via Constraint (5e).

3.2.3 TES energy balance

The system’s energetic state implies power terms that can assume either sign; the thermal storage charge state (\(s_t\)) reconciles their difference. We therefore impose some additional constraints with respect to TES state of charge:

TES State of Charge

$$\begin{aligned}&s_t - s_{t-1} = {\varDelta }[x^{r}_t - (Q^c y^{csu}_t + Q^b y^{csb}_t + x_t + Q^{rsb} y^{rsb}_t )] \ \ \ \forall \ t \in {\mathcal {T}}: t \ge 2 \end{aligned}$$
(8a)
$$\begin{aligned}&s_t \le E^u \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \qquad \qquad \qquad \quad \, \forall \ t \in {\mathcal {T}} \end{aligned}$$
(8b)
$$\begin{aligned}&s_{t-1} \ge {\varDelta }\cdot {\varDelta }^{rs}_t [{\mathbb {M}} (-3 + y^{rsu}_t + y_{t-1} + y_t + y^{csb}_{t-1} + y^{csb}_{t}) + x_t + Q^b y^{csb}_t] \nonumber \\&\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \qquad \qquad \qquad \quad \qquad \; \ \forall \ t \in {\mathcal {T}}: t \ge 2 \end{aligned}$$
(8c)

Constraint (8a) balances energy to and from TES with the charge; a time-scaling parameter \({\varDelta }\) reconcils power and energy. Constraint (8b) imposes the upper bound to TES charge state. If the power cycle is operating or standing by in time period \(t-1\) or t, and if the receiver is starting up in time t, then there must be a sufficient charge level in the TES in time \(t-1\) to ensure that the receiver can operate through its start-up period (Constraint (8c)). The expected fraction of a time period used for receiver start-up is given by (9), if applicable.

$$\begin{aligned} {\varDelta }^{rs}_t = \min \left\{ 1, \max \left\{ {\varDelta }^l, \frac{E^c}{ \max \left\{ \epsilon , Q^{in}_{t+1} {\varDelta }\right\} } \right\} \right\} \end{aligned}$$
(9)

Constraints (8a)–(8c) measure TES state of charge via energy flow. (Introducing energy quality as a function of the molten salt temperature yields a non-linearity that, at the time of this writing, is a level of detail not worth the extra computational effort.)

3.2.4 Battery and photovoltaic field operations

Lithium-ion and lead-acid batteries store energy. A lithium-ion battery outperforms a lead acid battery because, relative to a lead acid battery: (1) the lithium-ion battery commonly uses 80% of its available capacity, compared to 50% for a lead-acid battery; (2) throughout the life of the lithium-ion battery, it is expected to deliver twice the number of cycles; (3) the lithium-ion battery has a faster and more efficient charging process; (4) the round-trip DC-to-DC efficiency of a lithium-ion battery is 94–98%, compared to 76–82% for a lead-acid battery; (5) a lithium-ion battery is less susceptible to storage issues and leaks; (6) a lithium-ion battery is less affected by ambient temperature; (7) there are fewer maintenance requirements associated with a lithium-ion battery; and (8) a lithium-ion battery weighs less and is smaller than a lead-acid battery per unit capacity (O’Connor 2017; Mobbs 2016). A lithium-ion battery is rechargeable and uses lithium ions to store or release electrical energy. When charging a lithium-ion battery, lithium ions move from the cathode to the anode. These ions move in the other direction, from the anode to the cathode, to release the stored energy and produce electrical energy. We use a lithium-ion battery in our analysis because of the benefits mentioned above.

The addition of a PV and battery system to CSP enhances dispatch flexibility. The lithium-ion battery being used in this hybrid system is connected to PV and reacts quickly to changes in net demand, as is shown in the green box on the left-hand side of the connection layout in Fig. 2. The battery can either be charged directly from the PV system or through the rectifier connected to the AC bus; it discharges its energy through the inverter. We connect several 3.4 amp-hour lithium-ion cells to create the battery whose voltage is calculated for lithium-ion cells in series and should match that of the DC (direct current) system; buck-boost voltage converters adjust the battery’s voltage output. The capacity of the battery is determined by placing the lithium-ion cells in parallel. The battery is connected to an inverter to convert the current from DC to AC. The inverter is sized so as not to constitute the bottleneck such that power output is limited. Depending on the configuration of the overall CSP and PV hybrid system, multiple converters may be needed.

Battery Operations

$$\begin{aligned}&{{\dot{w}}^{+}_{t} + {\dot{w}}^{pv+}_{t} = v^{soc}_{t}i^{+}_{t} \ \ \forall \ t \in {\mathcal {T}} } \end{aligned}$$
(10a)
$$\begin{aligned}&{{\dot{w}}^{-}_{t} = v^{soc}_{t}i^{-}_{t} \ \ \forall \ t \in {\mathcal {T}} } \end{aligned}$$
(10b)
$$\begin{aligned}&{b^{soc}_{t} = b^{soc}_{t-1} + {\varDelta }\left( \frac{i^{+}_{t} - i^{-}_{t}}{C^{B}} \right) \ \ \forall \ t \in {\mathcal {T}}: t \ge 2 } \end{aligned}$$
(10c)
$$\begin{aligned}&{\underline{S}}^{B} \le b^{soc}_{t} \le {\bar{S}}^{B} \ \ \forall \ t \in {\mathcal {T}} \end{aligned}$$
(10d)
$$\begin{aligned}&v^{soc}_{t} = A^{V} b^{soc}_{t-1} + B^{V} \left( y^{+}_{t} + y^{-}_{t} \right) + I^{avg}R^{int} \left( y^{+}_{t} - y^{-}_{t} \right) \nonumber \\&\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \qquad \qquad \qquad \qquad \qquad \forall \ t \in {\mathcal {T}}: t \ge 2 \end{aligned}$$
(10e)
$$\begin{aligned}&{\underline{P}}^{B} y_{t}^{-} \le {\dot{w}}^{-}_{t} \le {\bar{P}}^{B} y_{t}^{-} \ \ \forall \ t \in {\mathcal {T}} \end{aligned}$$
(10f)
$$\begin{aligned}&{\underline{P}}^{B} y_{t}^{+} \le {\dot{w}}^{+}_{t} + {\dot{w}}^{pv+}_t \le {\bar{P}}^{B} y_{t}^{+} \ \ \forall \ t \in {\mathcal {T}} \end{aligned}$$
(10g)
$$\begin{aligned}&i^{-}_{t} \le I^{U-} b^{soc}_{t-1} \ \ \forall \ t \in {\mathcal {T}}: t \ge 2 \end{aligned}$$
(10h)
$$\begin{aligned}&i^{+}_{t} \le C^B \left( \frac{1- b^{soc}_{t-1}}{{\varDelta }} \right) \ \ \forall \ t \in {\mathcal {T}}: t \ge 2 \end{aligned}$$
(10i)
$$\begin{aligned}&{I^{L-} y_{t}^{-} \le i^{-}_{t} \le I^{U-} y_{t}^{-} \ \ \forall \ t \in {\mathcal {T}} } \end{aligned}$$
(10j)
$$\begin{aligned}&{I^{L+} y_{t}^{+} \le i^{+}_{t} \le I^{U+} y_{t}^{+} \ \ \forall \ t \in {\mathcal {T}} } \end{aligned}$$
(10k)
$$\begin{aligned}&{y_{t}^{+} + y_{t}^{-} \le 1 \ \ \forall \ t \in {\mathcal {T}} } \end{aligned}$$
(10l)
$$\begin{aligned}&b^{c} \ge \frac{{\varDelta }}{C^B} \sum _{t \in {\mathcal {T}}} \left[ \gamma ^{t} (i^+_t - i^+_tb^{soc}_{t-1})\right] \end{aligned}$$
(10m)

The nonlinear relationships between power, current, and voltage are represented by Constraints (10a) and (10b) for charging and discharging, respectively. (See Husted et al. (2017) for the associated linearization techniques.) Battery state-of-charge must be updated (Constraint (10c)), and this quantity is bounded both below and above (Constraint (10d)). Battery voltage is given by its current flow direction and previous state of charge (Constraint (10e)); the voltage is linear for a state of charge specified by Constraint (10d). Net power flow is bounded by Constraints (10f) and (10g). Constraints (10h) through (10k) restrict current flow. The battery cannot be charging and discharging simultaneously (Constraint (10l)) while Constraint (10m) measures battery cycle count similar to what is done in Scioletti et al. (2017).

Photovoltaic Field Operations

$$\begin{aligned}&{\dot{w}}^{pv}_t \le W^{DC}_t y^{pv}_t \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \forall \ t \in {\mathcal {T}} \end{aligned}$$
(11a)
$$\begin{aligned}&{\dot{w}}^{pv}_t - {\dot{w}}^{pv+}_t \le W^{I} y^{pv}_t \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \forall \ t \in {\mathcal {T}} \end{aligned}$$
(11b)
$$\begin{aligned}&{\dot{w}}^{pv+}_t \le {\dot{w}}^{pv}_t \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \forall \ t \in {\mathcal {T}} \end{aligned}$$
(11c)

PV curtailment is a process in which PV controls are purposefully set below the maximum power point of the PV modules. Constraint (11a) allows for curtailment by imposing only an upper limit on PV field generation. PV clipping is a process in which the rated power of the PV modules is larger than the inverter-rated power. When the difference between power produced by the PV field and power sent directly to the battery is greater than the inverter-rated power, the excess is lost or clipped (Constraint (11b)). Power sent to charge the battery directly from the PV field is limited by PV field generation (Constraint (11c)). Constraints (12b) and (12g) enforce domain requirements on the battery and PV field variables except for \(b^c\) whose non-negativity is ensured via Constraint (12d).

3.2.5 Variable bounds

Variable bounds are enforced in (12a)–(12g).

$$\begin{aligned}&u^{csu}_t, \; u^{rsu}_t, \; {\dot{w}}_{t}, \; {\dot{w}}^{p}_{t}, \; {\dot{w}}^{s}_{t}, \; x^{r}_t, \; x^{rsu}_t \ge 0 \ \ \forall \ t \in {\mathcal {T}} \end{aligned}$$
(12a)
$$\begin{aligned}&b^{soc}_{t}, \; i^{+}_{t}, \; i^{-}_{t}, \; v^{soc}_{t}, \; {\dot{w}}^{pv}_{t}, \; {\dot{w}}^{pv+}_{t}, \; {\dot{w}}_{t}^{+}, \; {\dot{w}}_{t}^{-} \ge 0 \ \ \forall \ t \in {\mathcal {T}} \end{aligned}$$
(12b)
$$\begin{aligned}&s_t, {\dot{w}}^{\delta }_t, x_t \ge 0 \ \ \forall \ t \in {\mathcal {T}} \end{aligned}$$
(12c)
$$\begin{aligned}&b^{c} \ge 0 \end{aligned}$$
(12d)
$$\begin{aligned}&y^r_t, \; y^{rhsp}_t, \; y^{rsb}_t, \; y^{rsd}_t, \; y^{rsu}_t, \; y^{rsup}_t \in \{ 0,1\} \ \ \forall \ t \in {\mathcal {T}} \end{aligned}$$
(12e)
$$\begin{aligned}&y_t, \; y^{chsp}_t, \; y^{csb}_t, \; y^{csd}_t, y^{csu}_t, \; y^{csup}_t \; \in \{ 0,1\} \ \ \forall \ t \in {\mathcal {T}} \end{aligned}$$
(12f)
$$\begin{aligned}&y^{+}_{t}, \; y^{-}_{t}, \; y^{pv}_{t} \in \{ 0,1\} \ \ \forall \ t \in {\mathcal {T}} \end{aligned}$$
(12g)

4 Solution techniques

The hybrid dispatch optimization model (\({\mathcal {H}}\)) is implemented within the SAM framework developed by the National Renewable Energy Laboratory in a manner shown in Fig. 3. A Python wrapper is used to specify system design inputs directly without use of the graphical interface and to invoke SAM’s simulation core for both photovoltaic and CSP power tower molten salt modules, enabling annual simulation of PV-CSP hybrids. The Python script contains decision logic that determines which processes are executed based on the program inputs. This decision logic adds flexibility of system designs to be explored. For example, if the hybrid plant includes some amount of PV, the script executes SAM’s detailed PV simulation module based on the user’s inputs. Upon completion, PV parameters used in (\({\mathcal {H}}\)) are stored in data files to be used during hybrid dispatch. If a battery exists in the system, the script calculates design parameters such as the number of cells and their configuration, operation limits, and performance curve fits, and stores them in a data file to be used during hybrid dispatch.

After the PV annual performance simulation has been run, the SAM simulation core generates estimates for the time-indexed parameters specified in Table 1; the dispatch model (\({\mathcal {H}}\)) yields an optimal schedule over the immediate 48-h planning horizon, which prescribes operational targets for the receiver and power cycle, yielding guidance for SAM’s simulation core over the next 24 h. After moving forward 24 h, the simulation core repeats the process and generates another look-ahead dispatch problem to be solved until an annual simulation, comprised of 365 dispatch problem instances, is complete. Wagner et al. (2017) provide a detailed description of the software architecture and rolling time horizon solution methodology for a CSP-only system. After the CSP simulation is complete, the annual time-series generation vector provided by SAM is consolidated to include CSP, PV, and battery operations.

Fig. 3
figure 3

Flow diagram of the software architecture implemented around the hybrid dispatch optimization model (\({\mathcal {H}}\))

Full size image

Due to the number of dispatch problem instances required for an annual simulation, individual (\({\mathcal {H}}\)) instances must solve quickly for a hybrid design to be evaluated in a timely manner. Solving the sub-hourly dispatch problem (\({\mathcal {H}}\)) in its original form, as described in Sect. 3, to a MILP gap of \(1\times 10^{-3}\) is computationally burdensome. To increase tractability, we implement three major solution techniques, the first of which is partly exact and partly inexact, the second of which does not compromise optimality, and the third of which constitutes a heuristic: (1) problem size reduction, (2) tighter LP relaxation, and (3) heuristic solution approach.

Fig. 4
figure 4

The original formulation has sub-hourly time periods throughout the problem’s time horizon. The reformulated model possesses sub-hourly time periods during the first 24 h and aggregates data to hourly fidelity for the second 24 h

Full size image

4.1 Problem size reduction

To reduce the overall problem instance size (i.e., number of variables and constraints), we reformulate (\({\mathcal {H}}\)) such that it consists of windows with two different time fidelities over the course of the horizon: (1) sub-hourly fidelity for the first 24 h that corresponds to that of the input weather file (i.e., 10-min); and (2) hourly time fidelity for the remainder of the horizon, which mimics the day-ahead energy market used to make future unit commitment decisions (see Fig. 4). To implement this reformulation, we introduce a new set, \({\mathcal {W}}\), defined as a set of time windows within the time horizon, i.e., \({\mathcal {W}} = \{1,2\}\). Each window, \(w\in {\mathcal {W}}\), contains a time step duration, \({\varDelta }_w\), and a set of time periods, \({\mathcal {T}}_w\). The union of the time period sets comprises the complete time horizon, i.e., \({\mathcal {T}}_1 \cup {\mathcal {T}}_2 = {\mathcal {T}}\). This reformulation improves tractability of the problem instances by reducing their size by 2280 continuous variables, 1800 binary variables, and 8640 constraints, which corresponds to a 41.6% decrease in each dimension.

For the hourly time fidelity window, \(w = 2\), we aggregate time-indexed parameters by taking a simple mean over the values for each time period within the hour; the lone exception is the parameter \({\varDelta }^{rs}_t\), which is recalculated using equation (9) and the updated aggregated value of \(Q^{in}_{t+1}\). The majority of formulation (\({\mathcal {H}}\)) is valid for both time windows. However, we modify Constraints (4f), (5c), (7b), and (6d) to reflect operational changes between modeling the system at hourly versus sub-hourly fidelity. The left-hand side of Constraint (4f) is adjusted to index the previous time period:

$$\begin{aligned} y^{rsd}_{t-1} \ge (y^{r}_{t-1} - y^{r}_{t}) + (y^{rsb}_{t-1} - y^{rsb}_{t}) \ \ \forall \ t \in {\mathcal {T}}_2 \end{aligned}$$
(13)

which results in receiver shutdown operations occurring during the same time period as the last production or standby operation. In Constraint (5c), the time index on the variable \(u^{csu}_{t-1}\) is adjusted to the current time period:

$$\begin{aligned} y_t \le \frac{u^{csu}_t}{E^c} + y_{t-1} + y^{csb}_{t-1} \ \ \forall \ t \in {\mathcal {T}}_2 \end{aligned}$$
(14)

which results in cycle start-up and operation occurring in the same time period. We add a constraint to ensure that the cycle input energy limit is not exceeded:

$$\begin{aligned} x_t + Q^c y^{csu}_t \le Q^u\ \ \forall \ t \in {\mathcal {T}}_2 \end{aligned}$$
(15)

which results in limited cycle energy production for the time period during which the cycle is starting up. Constraint (7b) must be removed to allow for cycle startup and energy production to occur during the same time period. Constraint (6d) is removed because we assume that the power cycle can ramp from minimum to maximum power output within an hour. The original forms of Constraints (4f), (5c), (7b), and (6d) still hold for the sub-hourly window, i.e., \(t \in {\mathcal {T}}_1\). The union of (\({\mathcal {H}}\)) and Constraints (13), (14), and (15) form the reduced hybrid dispatch problem, which is inexact relative to the problem with 10-min fidelity over a 48-h horizon but, as we show later, provides a fairly good approximation.

We also reduce the size of our problem by eliminating variables that could not assume values other than zero in any feasible solution during time periods with no solar resource (e.g., night time). For example, the decision to operate the CSP receiver, \(y^r_t\), can be preprocessed out during periods in which solar resource, \(Q^{in}_t\), is zero. This technique reduces the number of variables by about 12–16%, depending on the amount of daylight in a problem instance, and does not compromise optimality.

4.2 Tighter LP relaxation

Our formulation in Sect. 3 is weak owing to Constraints (5c), (6f), (7c)–(7g), (8a), and (8c), specifically, with respect to the binary variables for cycle start-up and standby. Cycle standby is an operational mode that allows the CSP power cycle to stay in a “hot” state by consuming TES but without generating electric power. From this operational state, the cycle can quickly come back on-line, generating power at a reduced start-up cost. Both cycle start-up and standby are indirectly related to the objective through the fixed-cost penalty.

To tighten the LP relaxation, thereby improving the guarantee of optimality, we introduce a binary variable, \(y^{o ff }_t\) that is defined as one if the power cycle is in an “off” state and zero otherwise, and reformulate the dispatch problem to include set partitioning Constraints (16) and (17):

$$\begin{aligned}&y^{csu}_t + y_t + y^{csb}_t + y^{o ff }_t = 1 \ \ \forall \ t \in {\mathcal {T}}_1 \end{aligned}$$
(16)
$$\begin{aligned}&y_t + y^{csb}_t + y^{o ff }_t = 1 \ \ \forall \ t \in {\mathcal {T}}_2 \end{aligned}$$
(17)

which results in a tighter LP relaxation because the cycle must be in exactly one of these operational states during any time period. We strengthen Constraint (6d) by substituting the binary variable \(y^{o ff }_t\) for \(y^{csd}_t\).

To further strengthen our formulation, we develop a cut that forces the cycle standby operation binary variable, \(y^{csb}_t\), to zero when the TES heat to the cycle, \(x_t\), is equal to its upper bound \(Q^u\), i.e., the power cycle is operating at full load:

$$\begin{aligned} y^{csb}_t \le 1 - \frac{x_t}{Q^u} \ \ \forall \ t \in {\mathcal {T}} \end{aligned}$$
(18)

The introduction of the binary variable, \(y^{o ff }_t\), the set partitioning constraints, and cycle standby cut reduce solution times of certain problem instances, as shown in Sect. 5, without compromising optimality.

4.3 Heuristic solution approach

To further reduce our solution times, we implement a two-phase heuristic solution technique, which we invoke after making the modifications described in Sects. 4.1 and 4.2 and call \(\hat{\mathbf{H }}\), shown in Fig. 5. In Phase 1, we set battery discharge power to zero, i.e., \({\dot{w}}^-_t = 0 \ \ \forall \ \ t \in {\mathcal {T}}\), effectively removing battery operation decisions, and solve the dispatch problem. The resulting solution represents operations of the CSP field, CSP power cycle, and PV field generation without accounting for battery interactions. This problem solves relatively quickly and can provide a lower bound on the objective function value of the monolith, (\({\mathcal {H}}\)). In Phase 2, we hold the power cycle standby decisions constant (i.e., \(y^{csb}_t\)), unfix battery discharge power, and re-solve the dispatch problem using the integer solution from the first solve as a warm start.

In practice, executing \(\hat{\mathbf{H }}\) allows for faster solve times because the two sub-problems are computationally less expensive than solving the whole problem at once. Despite being a heuristic, \(\hat{\mathbf{H }}\) produces near-optimal solutions because the interaction between cycle standby and battery operations is weak.

Fig. 5
figure 5

Flow diagram of the two-phase solution technique, using heuristic \(\hat{\mathbf{H }}\). The solution to Phase 1 is given to Phase 2 as an initial feasible solution

Full size image

5 Results

The dispatch model (\({\mathcal {H}}\)) is written in the AMPL modeling language version 20210630 (AMPL 2009) and solved using CPLEX version 12.8 (IBM 2016). Hardware architecture to generate solutions and solve times consists of a SuperServer 1028GR-TR with an Intel Xeon E5-2620 v4s at 2.1 GHz, running Ubuntu 16.04 with 128 GB of RAM, 1\(\times \)250 GB SSD, and 3\(\times \)500 GB SSDs hard dives.

5.1 Case study inputs

Designing a hybrid system for a specific location or market is beyond the scope of this work; therefore, we compare the dispatch of a fixed CSP-TES-PV-battery hybrid plant design in two locations and two electricity markets.

5.1.1 Hybrid system design

The hybrid system of study is grid-limited and requires the dispatch of individual sub-systems (i.e., power cycle and battery) to ensure that the transmission power limit of 310 \(\hbox {MW}_\text {e}\) is not exceeded. The CSP sub-system consists of two twin molten salt power tower CSP plants, each with a power cycle capable of 163 \(\hbox {MW}_\text {e}\) output with 12 h, or 4716 \(\hbox {MWh}_\text {t}\), of thermal storage and a receiver capable of 565 \(\hbox {MW}_\text {t}\) production. The PV sub-system consists of a single-axis tracking PV field capable of 325 \(\hbox {MW}_\text {dc}\) production with a maximum inverter power output of 270 \(\hbox {MW}_\text {ac}\). The battery sub-system has a capacity of 150 \(\hbox {MWh}_\text {e}\) with a maximum discharge rate of 1C, where we define the C-rate as the rate at which a battery is discharged relative to its maximum capacity; this is equal to the amount of current one is able to extract in one hour from a battery that is in a fully charged state. In our context, this equates to a maximum discharge power of 150 \(\hbox {MW}_\text {e}\). Table 3 summarizes design parameters and defines operational limits. Given solar resource and receiver-rated thermal power, SolarPILOT (Wagner and Wendelin 2018) generates the CSP heliostat field layout for the two locations.

Table 3 Case study plant design
Full size table

5.1.2 Operating costs

The system dispatch is determined by maximizing revenue at minimum operating cost. Due the nature of maximizing revenue, sub-system operating costs are required to enable decision making between the different energy generation technologies. Table 4 summarizes the operating cost of each sub-system. Receiver start-up cost is estimated at $10/\(\hbox {MW}_\text {t}\) of the receiver design thermal power. Receiver operating costs are estimated based on the heliostat field and receiver annual O&M costs and thermal energy generation, assuming daily start-ups. Power cycle operation, start-up, and change-in-production (ramping) costs are adapted from Kumar et al. (2012). Hot start-up costs of the receiver, \(C^{rhsp}\), and power cycle, \(C^{chsp}\), are assumed to be 10% of cold start-up costs. Battery life cycle costs penalize cycling during periods when there is excess generation capacity. There is uncertainty associated with all of these operating cost values. However, it is the relative magnitude of these costs that is important in deciding which technologies should be used to generate electricity at any given time period and, for days on which there is abundant solar resource, these costs determine which technology should be curtailed. For example, due to the low operating cost of PV systems, it is better to curtail CSP receiver generation and/or power cycle generation than PV field generation during abundant solar resource days. These operating costs also indicate that it is more economically advantageous to charge the battery system using the PV field rather than using the CSP power cycle.

Table 4 Estimated CSP-TES-PV-battery hybrid operating costs
Full size table

5.1.3 Battery specifications

We take parameter values used to model the lithium-ion battery from Husted et al. (2017), who addresses another type of hybrid system involving diesel generators, photovoltaics and a battery in a microgrid setting; see Table 5.

Table 5 Battery cell ratings
Full size table

5.2 Numerical experiment

The following analysis explores the performance and market outcomes for a fixed hybrid system design at two locations and in two markets. Although location (weather) and market are typically highly correlated, we evaluate all four market-location combinations to demonstrate the robustness of the solution techniques and to provide an understanding of how a single design might operate differently depending on its location and market conditions. The analysis is posed as a two-factor, two-level, numerical experiment.

5.2.1 Plant location

The location of the hybrid plant affects its performance and profitability. Geographic location determines the solar resource availability for electricity generation. For our case study, we choose northern Chile (N. Chile) and southern Nevada (S. Nevada) as the two levels for the location factor, the former location owing to its high solar resource and our industry partner’s interest in the development of hybrid plants within this region and the latter region owing to its solar resource and the availability of sub-hourly (i.e., 1-min time scale) solar data (Andreas and Stoffel 2006b).

The University of Nevada–Las Vegas (UNLV) weather station does not measure relative humidity or atmospheric pressure, two inputs required to model power cycle performance. However, Nevada Power Clark Station (Andreas and Stoffel 2006a), which is 5.2 miles, as measured by its straight-line distance from UNLV, reports relative humidity. Due to the low spatial variability, we can safely use the measurements of relative humidity from the Clark station with solar resource data from the UNLV station without introducing error into our calculations. For atmospheric pressure, we use an hourly typical meteorological year for Las Vegas and assume that atmospheric pressure remains constant at the sub-hourly level. The UNLV solar data reveals time periods in which the pyrheliometer instrument or the tracking system had faulted. Figure 6 shows an instance of the measurement fault in direct normal irradiance from the beginning of the solar day to approximately 13:40 PST, where the global horizontal irradiance measurements are close to clear-sky values with little-to-no measured direct normal irradiance. Therefore, we choose our data set to consist of twelve fault-free months, which span June 2012 to May 2013. These three data sources constitute an annual sub-hourly (i.e., 10-min) weather file for S. Nevada.

Fig. 6
figure 6

Example of UNLV data (taken from Andreas and Stoffel (2006b)) for which the pyroheliometer or tracking system had faulted

Full size image
Fig. 7
figure 7

Sorted histogram of the direct normal irradiance for N. Chile and S. Nevada

Full size image

The duration curve in Fig. 7 compares the direct normal irradiance for N. Chile and S. Nevada using a sorted histogram. The yearly totals for the three solar irradiance resources are given in Table 6. N. Chile has a higher solar resource than S. Nevada because the area has low atmospheric attenuation. S. Nevada has higher annual diffuse irradiance because there are more days with cloud cover than N. Chile. CSP systems can exploit direct normal irradiance, while PV systems generate electricity from both direct normal and diffuse horizontal irradiance.

Table 6 Solar global horizontal, direct normal, and diffuse horizontal irradiance year totals for N. Chile and S. Nevada
Full size table

5.2.2 Electricity markets

The electricity market into which the plant bids affects the dispatch strategy due to the time-of-use price of electricity. For our factorial experiment, we choose the N. Chile spot market (NC spot) and the 2016 Pacific Gas & Electric (PG&E) market as the two levels for the market factor, the former owing to our industry partner’s interest, and the latter owing to its simple design and the possibility that a plant in southern Nevada may be designed to dispatch against such a market.

Fig. 8
figure 8

Sorted histogram of the normalized prices for N. Chile spot (NC spot) and Pacific Gas & Electric (PG&E) full capacity deliverability markets

Full size image

Figure 8 compares the two markets using a sorted histogram of normalized electricity prices. Both markets follow a similar price trend. However, the PG&E market has more high-price and more highly priced hours relative to those in the NC spot market. Figure 9 depicts the time-of-use variation of the NC spot and PG&E markets. The NC spot market exhibits hourly, monthly, and week-versus-weekend variation in the electricity price, shown in Fig. 9a. Generally, high-price time periods occur at the end of the solar day during the winter and spring, e.g., July through December. During the fall (April through June), the NC spot market possesses relatively flat prices– either slightly above or below the annual average. The PG&E market has only hourly and seasonal variation, with the high-price time periods occurring between the hours of 4 and 9 p.m. The highest values occur during the months of July, August, and September.

Fig. 9
figure 9

Time-of-use variation of electricity prices for the Northern Chile spot (NC spot) and Pacific Gas & Electric (PG&E) market

Full size image

Due to the seasonal variation in both markets and plant locations being in both the northern and southern hemispheres, we shift the market by six months when evaluating the location-market combinations of N. Chile in a PG&E market and S. Nevada in a NC spot market. This seasonal shift is done by appending the first 181 days (i.e., first six months) of the year to the end of the last 184 days (i.e., last six months) of the year. This method does not preserve the monthly transitions present in the original price structure. However, it does allow for comparison between the original markets because this shift does not change the number of time periods that exhibit a particular price.

5.3 Solve times and solution quality

Each location-market combination in the numerical experiment requires 365 instances of the dispatch problem (\({\mathcal {H}}\)) to be solved to produce annual system performance results. We limit each instance (\({\mathcal {H}}\)) to 8 threads on the computing system to allow the four cases to be run in parallel, solving either to a relative optimality gap of \(1\times 10^{-3}\) or to a specified time limit, whichever occurs first.

To get a sense of the computational difficulty, we solve each location-market combination using the hybrid dispatch model (\({\mathcal {H}}\)) without applying any of the solution techniques described above and with a solve time limit of 120 s. Figure 10a shows the distributions of solution times for the 365 instances of (\({\mathcal {H}}\)) for each location-market combination in the numerical experiment.

From Fig. 10a, the S. Nevada location results in about three times the number of (\({\mathcal {H}}\)) solves that reach the time limit compared to the N. Chile location. With the exclusion of solves that reach the time limit, instances associated with the S. Nevada location solve faster, on average, than those associated with the N. Chile location. The annual solution times, i.e., solving all 365 instances of (\({\mathcal {H}}\)), range from 4 to 8 h, which is unacceptable for a single CSP-TES-PV-battery hybrid design evaluation. Furthermore, due to the large number of instances of (\({\mathcal {H}}\)) that reach the time limit, the dispatch solution quality is poor. Specifically, for the instances that reach the time limit, the average MILP gap ranges from 2 to 4% depending on the location-market combination, resulting in sub-optimal dispatch and lost revenue.

To discern the relative improvements each of the solution techniques described in Sect. 4 affords, we solve (\({\mathcal {H}}\)) with the problem-size reduction technique and note a 49–59% improvement in annual simulation solution time, relative to the original formulation; this corresponds to an average annual simulation time of 2.5 h. The combination of problem-size reduction and the tighter LP relaxation results in annual simulation solution times between 36 and 43 min, corresponding to an average solution time improvement of about 70% relative to that associated with (\({\mathcal {H}}\)) using only problem-size reduction. Finally, using \(\hat{\mathbf{H }}\) combined with problem-size reduction and tighter formulation results in an average annual simulation time of about 34 min, yielding an 85–93% overall solution time reduction.

Fig. 10
figure 10

Distribution of dispatch solution times from solving the 365 instances of (\({\mathcal {H}}\)) and \(\hat{\mathbf{H }}\) for each location-market combination of the numerical experiment

Full size image

Figure 10b shows the distribution of daily dispatch solution times using the heuristic approach, \(\hat{\mathbf{H }}\), and the other solution techniques described in Sect. 4. The distributions differentiate between the first and second phases of \(\hat{\mathbf{H }}\) and the total solution time (i.e., the sum of the two solves). Each execution of \(\hat{\mathbf{H }}\) is limited to 60 s. Solution times greater than 10 s are reported in the last bin of the distribution. Of the reported \(\hat{\mathbf{H }}\) solution times, one problem instance, corresponding to the first-phase solve of \(\hat{\mathbf{H }}\), reaches the time limit.

For the N. Chile location, on average, the first phase solves faster than the second phase (Fig. 10b). However, this differentiation disappears for the S. Nevada location, owing to the grid constraint being tight in more of the N. Chile instances, resulting in more difficulty scheduling the battery operations. In general, the S. Nevada instances’ total solve time is less than that of the N. Chile instances. However, the majority of total dispatch solution times, for all location-market combinations, is below 8 s.

5.3.1 Validation of the heuristic solution approach

To validate \(\hat{\mathbf{H }}\), we solve each dispatch problem: (1) using \(\hat{\mathbf{H }}\), and (2) invoking (\({\mathcal {H}}\)) directly, with the solution techniques from Sects. 4.1–4.3 applied, and compare corresponding objective function values. We use the heuristic solution from \(\hat{\mathbf{H }}\) as an initial feasible solution to (\({\mathcal {H}}\)) and impose no time limit on this problem. We observe the greatest difference between the objective function values of \(\hat{\mathbf{H }}\) and (\({\mathcal {H}}\)) to be $8935 for a two-day horizon, corresponding to a relative gap between \(\hat{\mathbf{H }}\) and (\({\mathcal {H}}\)) of about 0.83%. The difference between objectives averages less than $120 in revenue for a two-day horizon over all four combinations of the 365 48-h instances.

Fig. 11
figure 11

Annual solution responses from the numerical experiment: annual sales, solve time, annual generation, cycle starts, cycle ramping, and battery lifecycles

Full size image

5.3.2 Annual plant performance

Annual simulation of CSP-TES-PV-battery hybrid plants allows us to understand the performance of a particular system design in a given location and under certain market conditions. Figure 11 plots six annual simulation responses for the numerical experiment. We calculate annual sales as the sum, over all time periods within a year, of the product of energy generation, the normalized price multiplier, and an assumed PPA price of $0.1/kWh. This response plot shows that the PG&E market results in greater sales than the NC spot market owing to the higher price multiplier during high-price time periods in the former market relative to those in the latter market. However, the PG&E market has a greater effect on this plant design in S. Nevada than in N. Chile, owing to the lower solar resource in S. Nevada, illustrating the importance of dispatch optimization as solar resource decreases in a market structure similar to PG&E’s.

Figure 11 depicts annual solve time and generation responses; the former shows that N. Chile annual dispatch strategies require more computational time. Annual generation shows that there is little-to-no interaction between generation and market factor because the price at which electricity is sold should not have a significant impact on how much electricity the plant can generate throughout the year. However, the annual generation plot shows the impact of the location factor in this study. Due to the greater solar resource in N. Chile, this plant design produces about 700 GWh more electricity in N. Chile than in S. Nevada.

The responses cycle starts and cycle ramping demonstrate how the power cycles would be operated. Due to the abundant solar resource, the hybrid plant power cycle in N. Chile would only need to start up about 20 times in a given year. However, the same plant in S. Nevada would need to start the power cycle 50–100 times annually, depending on the market, which could cause more wear and tear on the cycle, resulting in an increase in maintenance costs. Cycle ramping is the daily average percentage of the rated power the cycle ramps up and down, e.g., 100% represents the power cycle ramping from zero to rated power and back down to zero every day. Interestingly, the PG&E market requires more cycle ramping than the NC spot market for the S. Nevada location, but less for the N. Chile location. In the lower solar resource location of S. Nevada, cycle start-up and ramping become more important to ensure electricity generation occurs during high-revenue times of the PG&E market.

The last response plotted is battery lifecycles, which determines if the battery must be replaced during the 25- to 30-year life of this project. The life of a lithium-ion battery ranges from 500 to 4000 cycles depending on the depth of discharge (Wang et al. 2011). Discharging more of a battery’s capacity at higher rates of power results in reduced expected lifecycle of the battery. Battery lifecycles are calculated based on the current throughput to-and-from the battery, \(i^-_t\) and \(i^+_t\), using the following equation:

$$\begin{aligned} b^{c} = \sum ^{|{\mathcal {T}|}}_{t=1} \frac{{\varDelta }(i^-_t + i^+_t)}{2 \cdot C^B} \end{aligned}$$

where \(C^B\) is the capacity of the battery. Of the four cases, S. Nevada within the NC spot market possesses the lowest number of battery lifecycles owing to the relatively flat price structure in the NC spot market and less abundant solar resource in S. Nevada. Therefore, battery storage operations become less desirable in this location-market combination. In N. Chile, battery storage captures excess solar energy that would otherwise be curtailed and discharged during high-price and/or less-solar-abundant periods. However, the hybrid system could be redesigned to include little-to-no solar curtailment. These design trade-offs are outside the scope of this paper.

5.3.3 Comparison to a CSP-only system

To demonstrate the value of a hybrid system, we compare performance metrics for both a CSP-PV and a CSP-PV-battery hybrid system to a stand-alone CSP system for the four location-market cases. These hybrid systems possess the design parameters given in the previous numerical experiments and are consistent with those produced by SAM and the corresponding dispatch optimization model (\({\mathcal {H}}\)). Table 7 provides metrics, i.e., capacity factor (CF), levelized cost of energy (LCOE), and power purchase agreement (PPA), normalized by the corresponding metric for a CSP-only system, where CF is defined as the quotient of annual energy generation and the maximum annual grid transmission, LCOE corresponds to the quotient of lifetime costs and electrical energy production, and PPA represents the minimum price to which a power producer can agree in order to meet a project’s desired internal rate of return (Blair et al. 2018). We use SAM default system costs for financial calculations, and assume that installed battery cost is $500/\(\hbox {kWh}_\text {e}\) with a lifespan of 2500 cycles and a replacement cost of $250/\(\hbox {kWh}_\text {e}\).

Table 7 Metrics for alternative power generation systems normalized by the corresponding metric for a CSP-only system
Full size table

Table 7 shows that both the CSP-PV-battery system and the corresponding system without battery storage result in a significant increase in CF for all location-market combinations we test; conversely, the value of LCOE for both types of hybrid systems and all location-market combinations is about three-quarters of that for the CSP-only system, and the corresponding PPA values are about 80–90%. These comparisons indicate that hybrid systems possess increased dispatchability at more competitive prices than their CSP-only counterparts; furthermore, while the addition of a battery increases the capacity factor slightly, it does so at the expense of the economic metrics. Overall, the battery is relatively insignificant in improving these metrics owing to its cost relative to that of the thermal energy storage with which the CSP is coupled.

6 Conclusions and future work

To analyze a CSP-TES-PV-battery hybrid system, we develop a dispatch optimization model (\({\mathcal {H}}\)) to schedule, at sub-hourly time fidelity, the different technologies for energy generation within a detailed simulation framework (SAM’s simulation core). The original formulation, (\({\mathcal {H}}\)), proves to be too computationally expensive for timely hybrid design evaluation. Therefore, we implement techniques to reduce solution times, resulting in annual instances (consisting of 365 48-h solves over progressive 24-h horizons) being executed in about 34 min, an 86–93% improvement compared to the solve times without the solution-time improvements. With manageable solution times, we are able to exercise the CSP-TES-PV-battery hybrid simulation tool with dispatch optimization using a two-factor, two-level numerical experiment based on plant location and pricing market. We compare solution times and present annual plant performance metrics for each of these cases. Also, we compare alternative hybrid systems to the CSP-only systems based on capacity factor, levelized cost of energy, and power purchase agreement. This analysis shows that hybrid systems dramatically outperform their CSP-only counterparts both from a capacity factor perspective and also economically.

An extension of this work uses our model (\({\mathcal {H}}\)) to inform the design of a hybrid system. At the opposite end of the planning spectrum, future research efforts might shorten the time fidelity of the model to 5 min to make dispatch decisions in the real-time electricity market using weather uncertainty, improving the return-on-investment for solar hybrid generation facilities and making them more competitive with conventional energy generation plants. Indeed, the presence of the battery in the hybrid system offers opportunity to participate in ancillary or real-time markets. However, such participation may only be of marginal value from a revenue standpoint for CSP-only systems (Jorgenson et al. 2018).