Abstract
This paper deals with bilevel programs with strictly convex lower level problems. We present the theoretical basis of a kind of necessary and sufficient optimality conditions that involve a single-level mathematical program satisfying the linear independence constraint qualification. These conditions are obtained by replacing the inner problem by their optimality conditions and relaxing their inequality constraints. An algorithm for the bilevel program, based on a well known technique for classical smooth constrained optimization, is also studied. The algorithm obtains a solution of this problem with an effort similar to that required by a classical well-behaved nonlinear constrained optimization problem. Several illustrative problems which include linear, quadratic and general nonlinear functions and constraints are solved, and very good results are obtained for all cases.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We consider the following bilevel programming problem (BLPP),

also called leader’s problem, where x∈ℝm; y∈ℝn; F,f:ℝm×ℝn→ℝ; G:ℝm×ℝn→ℝl and g:ℝm×ℝn→ℝp are continuous, twice differentiable functions. We also assume that G(x,y)≤0 defines a compact set. The problem (1.1) will be referred to as the lower level or the follower’s problem. The function F is called the upper level objective and the function G is the upper level constraint. Let the pair (x ∗,y ∗) be a solution of the BLPP. We suppose that at least one such pair exists.
The particular structure of bilevel programs facilitates the formulation of several practical problems that involve an hierarchical decision making process like engineering design, analysis of competitive economies, transport system planning, signal optimization, network design, strategic offensive and defensive force problems, government regulation, management, etc., see for example Ferris and Pang (1997), Shimizu et al. (1997), Vicente and Calamai (1994) and Dempe (2002).
We assume that the lower level problem is strictly convex in y for x fixed. Thus, it has a unique solution. Even if this assumption is strong, it is true for several engineering applications, where the lower level problem represents the mathematical model of a physical system. For instance, equilibrium of elastic structures can be obtained as the minimum of an energy functional under suitable constraints. Normally, designers seek for stable systems. Thus, the minimizer of the energy functional must be unique.
Convex bilevel programming presents difficulties normally not encountered in single-level mathematical programming. Since the implicit function y(x):ℝn→ℝm is not always a differentiable mapping, the objective function F and all the constraints are generally nonsmooth. If we substitute the lower level problem by its Karush-Kuhn-Tucker (KKT) conditions, see Bazaraa et al. (1993), we obtain a particular case of the so-called Mathematical Program with Equilibrium Constraints (MPEC), Luo et al. (1996), Anitescu et al. (2007). This is a problem that does not satisfy linear independence (LICQ) or Mangasarian Fromovitz (MFCQ) constraints qualifications, generally required for smooth nonlinear programs. In consequence, optimization methods based on KKT conditions cannot be directly applied to MPEC problem. However, several algorithms for MPEC and Mathematical Programs with Complementarity Constraints (MPCC) have been proposed (Leyffer et al. 2006; Fletcher and Leyffer 2004; Raghunathan and Biegler 2005). Anitescu (2000, 2005) studied the conditions for existence of multipliers for MPCC. Fletcher et al. (2006) proved local convergence of a SQP algorithm when applied to MPCC.
This paper presents the theoretical analysis of a bilevel programing technique introduced in Herskovits et al. (1997, 2000), applied to shape optimization of solids in contact, and in a Stackelberg-Cournot-Nash equilibrium problem, Leontiev and Herskovits (1997).
Various approaches have been developed in different branches of numerical optimization to solve bilevel programs, see Dempe (2003). We mention extreme point, branch and bound algorithms, cutting plane techniques, mixed integer programming, grid search, parametric complementary pivoting, and penalty function methods. A detailed list of references can be found in Shimizu et al. (1997) and Vicente and Calamai (1994).
Our technique is based on necessary and sufficient optimality conditions that involve an auxiliary single-level mathematical program. Under appropriate assumptions, the problem satisfies linear independence constraint qualifications. The auxiliary single level program is obtained by substituting the lower level problem by its KKT conditions and relaxing primal and dual feasibility constraints.
We prove that the set of nondegenerate solutions of the bilevel program is the same as the set of solutions of the auxiliary problem that are primal and dual feasible for the lower level problem.
The algorithm described here requires an initial point at the interior of the constraints of the first and second level problems. At each iteration, it computes a descent direction of the problem that is feasible with respect to both levels of constraints, by employing a formulation based on Herskovits’s interior point method for nonlinear optimization, Herskovits (1998). A line search procedure ensures that the new point is feasible and the upper objective function is lower. In this way, it is obtained an interior point sequence converging to a local solution of the bilevel program.
We give numerical results for a set of test problems having linear, quadratic and nonlinear objective functions and constraints. Also an example of Stackelberg-Cournot-Nash equilibrium problem is included. In all numerical experiments and applications the problems were solved in a very efficient way, without any change in the internal parameters of the algorithm.
We present and prove optimality conditions in the next section. In Sect. 3 we describe FDIPA, the Feasible Direction Interior Point Algorithm for nonlinear optimization. In the section that follows, we propose an algorithm for BLPP and analyze its convergence. Finally, a set of numerical tests is described and our conclusions are presented.
2 Optimality conditions for bilevel programming
Let \(\tilde{y}(x)\) be the global minimizer of the lower level problem (1.1) for a given x. The set
is the so called BLPP Constraint Region and Ω(x):={y∣g(x,y)≤0}, the Follower’s Feasible Region for x fixed. Finally, the BLPP Inducible Region:
represents the set of feasible points for the upper level objective function. We deduce that \(\tilde{y}(x)\) is a continuous closed point-to-point mapping. In consequence \(F(x,\tilde{y}(x))\) is continuous and, since G(x,y)≤0 defines a compact set, the inducible region IR is also compact. Thus, the leader minimizes a continuous function over a compact set, Edmunds and Bard (1991).
We assume that, for x fixed, a solution of the lower level problem satisfies linear independence regularity conditions, see Luenberger (1984). Replacing the lower level problem (1.1) by Karush-Kuhn-Tucker conditions, the following nonlinear single-level program is obtained:

where ξ∈ℝp is a vector of Kuhn-Tucker multipliers for the follower’s subproblem for x fixed. Since this equivalent problem is nonconvex, local minimum may exist. Note that ∇ represents the derivative with respect to (x,y,ξ) and that the derivative with respect a particular component is represented as ∇ x ,∇ y or ∇ ξ .
Theorem 1
If the follower’s objective function f is strictly convex and Ω(x) is a compact convex set for all allowable choices of the leader variables, then (x ∗,y ∗) is a solution of (1) if and only if (x ∗,y ∗,ξ ∗) is a solution of the problem (2). See Edmunds and Bard (1991).
A deep discussion of the previous theorem and of the equivalence of problems (1) and (2) can be found in a recent paper, Dempe and Dutta (2010).
Since the set of constraints
do not satisfy the linear independence constraint qualification, Bazaraa et al. (1993), problem (2) cannot be directly solved with classical algorithms exploiting KKT conditions. In fact, let (x,y,ξ) be a feasible point of problem (2). We have that

and denote I={i:g i (x,y)=0}. If i∈I, then ∇g i (x,y) and ∇(ξ i g i (x,y)) are linearly dependent. If i∉I, then ∇ξ i and ∇(ξ i g i (x,y)) are linearly dependent. Thus, the set of constraints of problem (2) do not satisfy the linear independence constraint qualification regardless of what function g(x,y) is taken and what assumptions about the properties of problem (1) are made, Scheel and Scholtes (2000). In Leyffer et al. (2006), an active set SQP method was proposed to overcome this problem.
We are going to show that the solutions of problem (1) can be found from the set of solutions to the problem

where L f (x,y,ξ) represents the Lagrangian function associated with the problem of the second level: L f (x,y,ξ)=f(x,y)+ξ t g(x,y).
We say that the solution \(\bar{y}\) of the problem (1.1) is nondegenerate if the strict complementary condition holds: \(\bar{\xi}_{i} > 0 \mbox{ when } g_{i}(\bar{x},\bar{y}) = 0\) for all i=1,…,p. A solution of the bilevel problem (1) is said to be nondegenerate if this is the case for the lower level problem. We will be looking only for nondegenerate solutions, even if degenerate solutions can exist.
Theorem 2
(Necessary optimality condition)
Let f and g be differentiable at (x ∗,y ∗) with respect to y, g is continuous at (x ∗,y ∗) with respect to x and a constraint qualification for problem (1.1) holds. If (x ∗,y ∗) is a nondegenerate solution of the problem (1), there exists ξ ∗∈ℝp,ξ ∗≥0 such that (x ∗,y ∗,ξ ∗) is a solution of (3).
Proof
Since (x
∗,y
∗) is a solution of (1), from Theorem 1 there exists ξ
∗ such that the triple (x
∗,y
∗,ξ
∗) solves (2). Since (x
∗,y
∗) is nondegenerate and the function g is continuous with respect to x and y at (x
∗,y
∗), there exists a neighborhood  of the point (x
∗,y
∗,ξ
∗) such that
of the point (x
∗,y
∗,ξ
∗) such that  the conditions ξ
i
g
i
(x,y)=0,i=1,…,p imply that g
i
(x,y)<0 and ξ
i
=0 or that ξ
i
>0 and g
i
(x,y)=0. This means that the set of constraints {ξ
i
g
i
(x,y)=0,i=1,…,p} is equivalent to {g(x,y)≤0,ξ≥0,ξ
i
g
i
(x,y)=0,i=1,…,p.} on
the conditions ξ
i
g
i
(x,y)=0,i=1,…,p imply that g
i
(x,y)<0 and ξ
i
=0 or that ξ
i
>0 and g
i
(x,y)=0. This means that the set of constraints {ξ
i
g
i
(x,y)=0,i=1,…,p} is equivalent to {g(x,y)≤0,ξ≥0,ξ
i
g
i
(x,y)=0,i=1,…,p.} on  . Then, the feasible sets of problem (2) and (3) on
. Then, the feasible sets of problem (2) and (3) on  are identical. Thus, (x
∗,y
∗,ξ
∗) gives a solution of the problem (3). Moreover we have g(x
∗,y
∗)≤0 and ξ
∗≥0. The proof is complete. □
are identical. Thus, (x
∗,y
∗,ξ
∗) gives a solution of the problem (3). Moreover we have g(x
∗,y
∗)≤0 and ξ
∗≥0. The proof is complete. □
Theorem 3
(Sufficient optimality condition)
If (x ∗,y ∗ ξ ∗) is a solution of the problem (3) such that
Then (x ∗,y ∗) is a solution of the BLPP (1).
The proof is trivial. Thus, (3)–(4) can be considered as an optimality condition for a nondegenerate solution of the BLPP (1). Now, it is possible to assume that the problem (3) verifies linear independence constraint qualification. This assumption is generically satisfied, even if counterexamples can be constructed. For example, the assumption is not true in the uncommon case when the set of derivatives of both levels constraints of problem (1) are not linearly independent. An interesting discussion about this assumption can be found in Scholtes and Stöhr (2001).
Our approach to find points that verify the present optimality conditions, consists in solving iteratively the nonlinear program (3) so that all the iterates verify (4).
3 The feasible direction interior point algorithm
This algorithm consists in Newton like iterations to solve the system of nonlinear equations, in the primal and the dual variables, given by the equalities included in KKT optimality conditions. To describe the basic ideas we consider the following optimization problem,

where z∈ℝnz, G:ℝnz→ℝmz and H:ℝnz→ℝpz.
Let ∇G∈ℝnz×mz and ∇H∈ℝnz×pz be the matrices of derivatives of G and H. We call λ∈ℝmz and μ∈ℝpz the vectors of dual variables corresponding to the inequality and equality constraints and define  , a diagonal matrix such that
, a diagonal matrix such that  , for a vector v in a finite dimensional space.
, for a vector v in a finite dimensional space.
The FDIPA requires the following assumptions about Problem (5):
Assumption 1
The functions F(z), G(z) and H(z) are continuously differentiable in Ω′≡{z∈ℝnz∣G(z)≤0 and H(z)≤0} and their derivatives satisfy a Lipschitz condition.
Assumption 2
Each \(z \in \operatorname{int}(\varOmega')\) satisfies G(z)<0, H(z)<0.
Assumption 3
(Regularity condition)
For all z∈Ω′, the vectors ∇G i (z), for i such that G i (z)=0, and ∇H j (z), for j=1,…,pz, are linearly independent.
Let z ∗ be a regular point of the problem (5), Herskovits (1998), then the corresponding Karush Kuhn Tucker first order necessary optimality conditions are expressed as: If z ∗ is a local minimum of (5) then there exists λ ∗∈ℝmz and μ ∗∈ℝpz such that



A quasi-Newton iteration for the solution of (6) to (8) in (z,λ,μ) can be stated as

where B represents a quasi-Newton approximation of the Hessian of the Lagrangian
(z,λ,μ) is the current point and (z α ,λ α ,μ α ) is a new estimate.
By denoting d 0=z α −z, λ 0=λ α and μ 0=μ α , then (9) becomes



which is independent of the current value of μ. In Herskovits (1998), it is proved that d 0 is a descent direction of the objective function F(z). However, d 0 cannot be employed as a search direction, since it is not necessarily a feasible direction.
An appropriate potential function is needed for the line search. We consider
where c i are positive constants. It can be shown that, if c i are large enough, then ϕ c (z) is an Exact Penalty Function of the equality constraints Luenberger (1984). On the other hand, ϕ c has no derivatives at points where there are active equality constraints. FDIPA uses ϕ c in the line search, but avoids the points where this function is nonsmooth. It generates a sequence with decreasing values of ϕ c at the interior of the inequality constraints and such that the equalities are negative. With this purpose, the system (10)–(12) is modified in a way to obtain a feasible direction of the inequalities that points to the negative side of the equalities and, at the same time, is a descent direction of ϕ c .
We define the linear system

where e=[1,1,…,1]t∈ℝpz.
Now, the search direction can be calculated by d=d 0+ρd 1, where we consider ρ as follows: If \(d^{t}_{1}\nabla\phi_{c}(z) > 0\), set
Otherwise, set \(\rho= \varphi\| d_{0} \|_{_{2}}^{^{2}}\).
The following assumptions about the algorithm are required:
Assumption 4
There exists positive numbers λ I, λ S and \(\overline{G}\) such that 0<λ i ≤λ S, i=1,…,mz and λ i ≥λ I for any i such that \(G_{i}(z) \geq-\overline{G}\), at every iterate of the algorithm.
Assumption 5
There exist positive numbers σ 1 and σ 2 such that
Assuming that the iterates given by the present algorithm are in a compact set, it was proved in Herskovits (1998) that the FDIPA is globally convergent to a Karush Kuhn Tucker point for any initial point at the interior of Ω′ and for any way of updating B and λ according to both the previous assumptions.
4 A numerical algorithm for bilevel programming
We present an algorithm that computes a solution of the problem

where H(x,y,ξ):=(∇ y L f (x,y,ξ),ξ 1 g 1(x,y),…,ξ p g p (x,y)). It follows from Theorem 3 that these are also solutions of the bilevel program. We assume that the computed solutions of problem (1) are nondegenerate.
We suppose that problem (14) verifies the assumptions required in Herskovits (1998) and satisfy the conditions in (4). Thus, we need to define the following sets:
and
In order to find solutions of (14) that verify (4), we take the initial point at the interior of Ω +≡Ω 1∩Ω 2.
Assumption 6
The set Ω + has an nonempty interior, \(\operatorname{int}(\varOmega^{+})\).
Assumption 7
Each \(( x,y,\xi)\in \operatorname{int}(\varOmega^{+})\) satisfies G(x,y,ξ)<0, H(x,y,ξ)<0.
Assumption 8
The functions F(x,y,ξ), G(x,y,ξ) and H(x,y,ξ) are continuously differentiable in Ω + and their derivatives satisfy a Lipschitz condition.
Assumption 9
(Regularity condition)
For all (x,y,ξ)∈Ω + the vectors ∇G i (x,y,ξ), for i such that G i (x,y,ξ)=0, and ∇H j (x,y,ξ), for j=1,…,n+p, are linearly independent.
Now, consider the function
where H:ℝm×ℝn×ℝp→ℝn+p is defined by
such that,
and c i are positive constants determined by the algorithm.
The present algorithm starts with an initial point \((x_{0},y_{0},\xi_{0})\in \operatorname{int}(\varOmega^{+})\). At each iteration we have that G(x,y,ξ)<0 and the equality constraints hold as negative inequalities, H(x,y,ξ)<0, being active only at the limit. For a given point (x,y,ξ), the algorithm finds a search direction d≡(d x ,d y ,d ξ ) that is a descent direction of Φ c (x,y,ξ) and points to the negative side of the equality and inequality constraints. A line search is then performed looking for a step length t such that \((x,y,\xi) + t d \in \operatorname{int}(\varOmega^{+})\) and a decrease of F(x,y,ξ) is obtained.
Then, the algorithm is stated as follows:
- Parameters.:
-
Let be ε>0, φ>0, γ∈(0,1) and ν∈(0,1).
- Data.:
-
Define initial values for \((x,y,\xi) \in \operatorname{int}(\varOmega^{+})\), B∈ℝ(m+n+p)×(m+n+p) symmetric and positive definite, λ∈ℝl, λ>0 and 0<c∈ℝn+p.
- Step 1.:
-
Computation of a search direction
-
(i)
Compute (d 0,λ 0,μ 0) by solving the linear system
 (15)
(15) (16)
(16) (17)
(17)If d 0≤ε, stop.
-
(ii)
Compute (d 1,λ 1,μ 1) by solving the linear system
 (18)
(18) (19)
(19) (20)
(20)where e=[1,…,1]t,e∈ℝn+p.
-
(iii)
If c i <−1.2μ 0i , then set c i =−2μ 0i ,for i=1,…,n+p.
-
(iv)
If \(d^{t}_{1} \nabla\varPhi_{c}(x,y,\xi) > 0\), set
$$\rho= \min \biggl\{ \varphi\| d_0 \|_{_2}^{^2} \;;\; (\gamma- 1) \dfrac{d^{t}_0 \nabla\varPhi_{c}(x,y,\xi)}{d^{t}_1 \nabla \varPhi_{c}(x,y,\xi)} \biggr\}. $$Otherwise, set \(\rho= \varphi\| d_{0} \|_{_{2}}^{^{2}}\).
-
(v)
Compute the search direction d=d 0+ρd 1 and also \(\bar{\lambda} = \lambda_{0}+\rho\lambda_{1}\).
-
(i)
- Step 2.:
-
Line search Compute t, the first number of the sequence {1,ν,ν 2,ν 3,…} satisfying
 (21)
(21) (22)
(22) (23)
(23)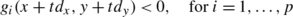 (24)
(24) (25)
(25) (26)
(26) - Step 3.:
-
Updates
-
(i)
Set (x,y,ξ):=(x,y,ξ)+td and define new values for λ>0 and B symmetric and positive definite.
-
(ii)
Go to Step 1.
-
(i)
In Herskovits (1998) was proved global convergence of the FDIPA. However, in the previous algorithm, the line search includes the conditions (23) and (24) to have the new iterate at the interior of Ω +. With this additional condition the result of Lemma 4.4 in Herskovits (1998) remains valid. In effect, by Assumption 8, there exist k i >0 such that
holds for any (x,y,ξ) and \((x,y,\xi)+td\in \operatorname{int}\varOmega^{+}\) such that \([(x,y,\xi),(x,y,\xi)+td]\subset \operatorname{int}\varOmega^{+}\).
By (17) and (20) we have that d t∇(ξ i g i (x,y))=−ξ i g i (x,y)−ρe. Then,
and we deduce that
if the following conditions are true:
Both inequality hold for any t∈[0,τ i ] such that
As in Herskovits (1998), we have that there exists \(\bar{\rho}_{i}>0\) such that \(\bar{\rho}_{i} < \rho /(k_{i} \Vert d\Vert _{2}^{2})\) for (x,y,ξ)∈Ω +. Then, \(\tau_{i} < \min\{ 1; \bar{\rho}_{i}\}\). In consequence, (28) is true for any t∈[0,τ i ] and we deduce that \((\xi_{i}+td_{\xi_{i}})> 0\) and g i (x+td x ,y+td y )<0 for any t∈[0,τ i ].
5 Tests examples
We carried out several numerical experiments with the proposed algorithm applied to the solution of benchmark problems. These problems are listed in Table 1. We note that all these problems have only nondegenerate solutions.
The numerical results are presented in Table 2. The abbreviation attached to the problem (column PROB.) describes the original source and the ordinal number in which the problem is given there. The column CLASS gives the classification of the problem. The characters denote the type of upper level objective function, upper level constraints, lower level objective function, and lower level constraints in the prescribed order, and are the following: L for linear, Q for quadratic, N for nonlinear in both x and y variables functions, and B for “box” constraints. We use the blank position “_” if constraints are absent. The following notation is also used: (x 0,y 0) for initial point of iterations; ITER for number of iterations; (x ∗,y ∗) for calculated solution; MIN for value of F(x ∗,y ∗).
Each iteration includes one computation of the search direction and the line search. In all examples our results correspond to the solution indicated in the original sources. We stop the algorithm when the norm of the gradient of the Lagrangian and the absolute value of the equality constraints are all less that ε=10 −6. All the iterates are strictly feasible with respect to the inequality constraints of both level problems.
The present technique was initially applied for shape optimization of nonlinear elastic solids in contact, Herskovits et al. (2000). This problem, that satisfies the assumptions required here, employs a finite element model and requires the solution of large bilevel programs. The results were obtained in about 10 iterations.
6 Conclusions
We have presented the theoretical basis of a class of optimality conditions for bilevel programming and of a numerical algorithm to solve them. This algorithm, that employs ideas of a feasible direction interior point technique for smooth optimization, solves two linear systems with the same matrix and performs an inexact line search at each iteration. We remark that the present approach is free of parameters to be adjusted and avoids bad conditioning produced by large penalty parameters or regularization techniques. The linear systems are in general well conditioned. If regularity conditions are not true at the solution, the linear systems conditioning can became worst in the final iterations.
Iterates are at the interior of both levels inequality constraints, being the objective function reduced at each iteration. Our algorithm is very simple to code. Since it works with linear systems, several numerical methods or techniques that take advantage of the structure can be employed.
The numerical results shown here and the large scale applications described in Herskovits et al. (2000, 1997) were all solved with a small number of iterations, employing the same set on parameters for line search and stopping criteria, suggesting that our technique is robust. We believe that the approach can be extended to mathematical programs with equilibrium constraints (MPEC) and generalized bilevel programming problems.
References
Aiyoshi E, Shimizu K (1984) A solution method for the static Stackelberg problem via penalty method. IEEE Trans Autom Control 29:1111–1114
Anitescu M (2000) On solving mathematical programs with complementarity as nonlinear programs. Tech rep, Argone National Laboratories, Illinois, 60439
Anitescu M (2005) Global convergence of an elastic mode approach for a class of mathematical programs with complementarity constraints. SIAM 16:120–145
Anitescu M, Tseng P, Wright SJ (2007) Elastic-mode algorithms for mathematical programs with constraints: global convergence and stationarity properties. Math Program 110:337–371
Bard J (1984) Optimality conditions for the bilevel programming problem. Nav Res Logist Q 31:13–24
Bazaraa M, Sherali H, Shetty C (1993) Nonlinear programming: theory and algorithms. Wiley, New York
Bi Z, Calamai P, Conn A (1989) An exact penalty function approach for the linear bilevel programming problem. Tech rep, University of Waterloo, Department of Systems Design Engineering
Calamai P, Vicente L (1994) Generating quadratic bilevel programming test problems. ACM Trans Math Softw 20:103–119
Chen Y, Florian M (1991) The nonlinear bilevel programming problem: a general formulation and optimality conditions. Tech rep, Centre de Recherche sur les Transports
Dempe S (2002) Foundations of bilevel programming. Kluwer Academic, Dordrecht
Dempe S (2003) Annotated bibliography on bilevel programming and mathematical programs with equilibrium constraints. Optimization 52:333–359
Dempe S, Dutta J (2010) Is bilevel programming a special case of a mathematical program with complementarity constraints? Math Program (Online), pp 1–12 (to appear)
Edmunds E, Bard J (1991) Algorithm for nonlinear bilevel mathematical programs. IEEE Trans Syst Man Cybern 21:83–89
Ferris MC, Pang JS (1997) Engineering and economic applications of complementary problems. SIAM Rev 39:669–713
Fletcher R, Leyffer S (2004) Solving mathematical program with complementarity constraints as nonlinear programs. Optim Methods Softw 19:15–40
Fletcher R, Leyffer S, Ralph D, Scholtes S (2006) Local convergence of SQP methods for mathematical programs with equilibrium constraints. SIAM J Optim 17:259–286
Friesz TL, Tobin RL, Cho HJ, Mehta NJ (1990) Sensitivity analysis based heuristic algorithms for mathematical programs with variational inequality constraints. Math Program 48:265–284
Herskovits J (1998) Feasible direction interior-point technique for nonlinear optimization. J Optim Theory Appl 99:121–146
Herskovits J, Leontiev A, Santos G (1997) A mathematical programming algorithm for optimal design of elastic solids in contact. In: Gutkowski W, Mroz Z (eds) 2nd world congress of structural and multidisciplinary optimization, WCSMO-2, Zakopane, Poland, vol 1, pp 67–72
Herskovits J, Leontiev A, Dias G, Santos G (2000) Contact shape optimization: a bilevel programming approach. Struct Multidiscip Optim 20:214–221
Leontiev A, Herskovits J (1997) New optimality conditions and algorithm for Stackelberg-Cournot-Nash equilibria. In: Proceedings of the “46° Seminário Brasileiro de Análise”, vol SBA-46, pp 801–809
Leyffer S, Lopez-Calva G, Nocedal J (2006) Interior methods for mathematical programs with complementarity constraints. SIAM J Optim 17:52–77
Luenberger DG (1984) Linear and nonlinear programming, 2nd edn. Addison-Wesley, Reading
Luo ZQ, Pang JS, Ralph D (1996) Mathematical programs with equilibrium constraints. Cambridge University Press, Cambridge
Raghunathan AU, Biegler L (2005) An interior point method for mathematical programs with complementarity constraints. SIAM J Optim 15(3):720–750
Savard G, Gauvin J (1994) The steepest descent method for the nonlinear bilevel programming problem. Oper Res Lett 15:275–282
Scheel H, Scholtes S (2000) Mathematical programs with equilibrium constraints: stationarity, optimality, and sensitivity. Math Oper Res 25:1–22
Scholtes S, Stöhr M (2001) How stringent is the linear independence assumption for mathematical programs with stationarity constraints? Math Oper Res 26:851–863
Shimizu K, Ishizuka Y, Bard JF (1997) Nondifferentiable and two-level mathematical programming. Kluwer Academic, Dordrecht
Tobin R (1992) Uniqueness results and algorithm for Stackelberg-Cournot-Nash equilibria. Ann Oper Res 34:21–36
Vicente L, Savard G, Júdice J (1994) Descent approaches for quadratic bilevel programming. J Optim Theory Appl 81:379–399
Vicente LN, Calamai PH (1994) Bilevel and multilevel programming: A bibliography review. J Glob Optim 5:291–306
Ye J, Zhu D (1993) Optimality conditions for bilevel programming problem. Tech rep, University of Victoria, Department of Mathematics and Statistics
Ye J, Zhu D, Zhu Q (1993) Generalized bilevel programming problems. Tech rep, University of Victoria, Department of Mathematics and Statistics
Acknowledgements
The authors thank to CNPq (Conselho Nacional de Desenvolvimento Científico e Tecnológico, Brazil) and FAPERJ (Fundação de Amparo à Pesquisa do Estado do Rio de Janeiro) for the support provided to this research.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Herskovits, J., Tanaka Filho, M. & Leontiev, A. An interior point technique for solving bilevel programming problems. Optim Eng 14, 381–394 (2013). https://doi.org/10.1007/s11081-012-9192-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11081-012-9192-4