A second-order fast compact scheme with unequal time-steps for subdiffusion problems

Abstract

In consideration of the initial singularity of the solution, a temporally second-order fast compact difference scheme with unequal time-steps is presented and analyzed for simulating the subdiffusion problems in several spatial dimensions. On the basis of sum-of-exponentials technique, a fast Alikhanov formula is derived on general nonuniform meshes to approximate the Caputo’s time derivative. Meanwhile, the spatial derivatives are approximated by the fourth-order compact difference operator, which can be implemented by a fast discrete sine transform via the FFT algorithm. So the proposed algorithm is computationally efficient with the computational cost about $O(MN\log M\log N)$ and the storage requirement $O(M\log N)$, where M and N are the total numbers of grids in space and time, respectively. With the aids of discrete fractional Grönwall inequality and global consistency analysis, the unconditional stability and sharp H¹-norm error estimate reflecting the regularity of solution are established rigorously by the discrete energy approach. Three numerical experiments are included to confirm the sharpness of our analysis and the effectiveness of our fast algorithm.

1 Introduction

In recent decades, fractional partial differential equations have attracted many attentions for its superiority in describing the phenomenon related to nonlocality and spatial heterogeneity. The time fractional differential equations are one of the important fractional models developed in various fields [1]. We consider the following reaction-subdiffusion problem

$$ \begin{array}{@{}rcl@{}} \partial^{\alpha}_{t}u-{\Delta} u&=&\kappa u+f(\mathbf{x},t)\qquad \text{ for } \mathbf{x} \in {\Omega} \text{ and } 0<t\leq T, \end{array} $$

(1.1)

$$ \begin{array}{@{}rcl@{}} u(\mathbf{x},t)&=&0\qquad\qquad\qquad\quad\text{ for } \mathbf{x} \in \partial {\Omega} \text{ and } 0<t\leq T, \end{array} $$

(1.2)

$$ \begin{array}{@{}rcl@{}} u(\mathbf{x},0)&=&u_{0}(\mathbf{x})\qquad\qquad\quad \text{ for } \mathbf{x}\in \bar{{\Omega}}, \end{array} $$

(1.3)

where ${\Omega }\subset \mathbb {R}^{d}$ is a bounded interval (d = 1), rectangle (d = 2), or cube (d = 3), and ∂Ω denotes its boundary. Δ be the d-dimensional Laplacian operator and the reaction coefficient κ is a positive constant. In (1.1), $\partial ^{\alpha }_{t}={}_{0}^{C}\mathcal {D}^{\alpha }_{t}$ represents the Caputo fractional derivative of order α with respect to t, defined by

$$ (\partial^{\alpha}_{t}v)(t):={{\int}_{0}^{t}}\omega_{1-\alpha}(t-s)v^{\prime}(s)\mathrm{d} s,\quad 0<\alpha<1, $$

(1.4)

where the weakly singular kernel ω_1−α(t − s) is defined by ω_μ(t) := t^μ− 1/Γ(μ) for t > 0.

Despite there are some theoretical methods to solve the fractional diffusion equations analytically, we may still have to explore numerical methods to obtain the solutions in general. In previous literatures, a large number of numerical methods are presented to approximate the Caputo derivative (1.4) availably. For instance, the well-known L1 formula [2, 3], which is constructed by using a piecewise linear interpolation on each subinterval and has the accuracy of order 2 − α. High-order approximations are constructed recently in [4,5,6,7] by using the piecewise quadratic polynomial interpolation. Most of discrete approximations for the Caputo derivative depend on the uniform time-steps and restrict the solutions to be sufficiently smooth. Nevertheless, studies in [8,9,10,11,12] show that the existence of the singular kernel makes the exact solution u always has an initial layer at t = 0, which is typically for fractional differential equations and has great influence on the convergence rate. In [10], the authors prove that the uniform L1 formula is accurate of orders $O(t_{n}^{\alpha -1}\tau )$ and $O(t_{n}^{-1}\tau )$ for smooth and nonsmooth initial data respectively, which are far from the desired goals. Recently, there appears several interesting works, including the specified mesh techniques [12,13,14,15,16] and the (generally) nonuniform mesh approaches [17,18,19,20], to fill this gap by resolving the initial regularity and restoring the optimal convergence rate.

However, due to the intrinsically nonlocal property and historical dependence of the fractional derivative, numerical applications of the aforementioned methods are always time-consuming, especially for the problems on two- or three-dimensional space domain. Therefore, it is imperative and necessary to develop efficient algorithms to reduce the huge storage and computational cost. Many efforts have been made in the literatures to develop fast time-stepping methods. Ke et al. [21] apply the fast Fourier transform for block triangular Toeplitz-like systems and propose a fast direct method for solving the time-fractional PDEs. Another idea is suggested by Baffet and Hesthaven [22], where the compression is carried out in the Laplace domain by solving the equivalent ODE with some one-step A-stable scheme. Recently, Jiang et al. [23] use the sum-of-exponentials (SOEs) technique to approximate the kernel and reduce the computational complexity significantly. The overall computational cost O(MN²) and storage O(MN) of the L1 formula are reduced to $O(MN\log N)$ and $O(M\log N)$, respectively, where M is the grid points in space and N is the total levels in time. Yan et al. [24] propose a second-order fast formula on uniform meshes to approximate the Caputo derivative. They also investigate the stability and convergence of the resulting second-order time-stepping scheme for the subdiffusion equations, corresponding to the case of κ = 0 of (1.1) by assuming that the solution is sufficiently smooth. Moreover, a fast L1 finite difference scheme on the graded mesh is reported in [25] for time-fractional diffusion equations by considering both the initial singularity and the long-time historical memory. Liao et al. [26] propose a two-level nonuniform L1 scheme for solving semilinear subdiffusion equations and prove that the fast linearized scheme is unconditionally stable on generally nonuniform meshes. To the best of our knowledge, no nonuniform fast algorithms for high-order numerical Caputo derivatives have been published yet.

The main contribution of this paper is to construct and analyze a computationally efficient difference algorithm on a general class of nonuniform time meshes for linear reaction-subdiffusion equations in multi-dimensions. More precisely, the nonuniform Alikhanov formula with the SOEs approximation is employed for the Caputo fractional derivative, and the fourth-order compact difference operator with a fast discrete sine transform (DST) is utilized for spatial discretization so that our algorithm is computationally efficient in both time direction and spatial dimensions. Consider the (possibly nonuniform) time levels 0 = t₀ < t₁ < ⋯ < t_k− 1 < t_k < ⋯ < t_N = T with the weighted time t_n−𝜃 := 𝜃t_n− 1 + (1 − 𝜃)t_n for an offset parameter 𝜃 ∈ [0,1). Denote the time-step sizes τ_k = t_k − t_k− 1 for 1 ≤ k ≤ N and the maximum time-step size $\tau :=\max \limits _{1\le k\le N }\tau _{k}$. Let the step size ratios ρ_k := τ_k/τ_k+ 1 for 1 ≤ k ≤ N − 1 and the maximum time-step ratio

$$ \rho:=\max\limits_{1\le k\le N -1}\rho_{k}. $$

Our accelerated discrete Caputo formula for the Caputo derivative (1.4) takes a form of

$$ (\partial_{a\tau}^{\alpha}v)^{n-\theta}:=\sum\limits_{k=1}^{n}\textsf{A}_{n-k}^{(n)}\triangledown_{\tau} v^{k}, $$

(1.5)

where $\triangledown _{\tau } v^{k}=v^{k}-v^{k-1}$ and the discrete convolution kernels $\textsf {A}_{n-k}^{(n)}$ are determined later. Let $\bar {{\Omega }}_{h}$ be the discrete spatial grid covered by $\bar {{\Omega }}$ with uniform spacings in each direction. For 0 ≤ n ≤ N, denote the numerical solution ${u_{h}^{n}}\approx u(\mathbf {x}_{h},t_{n})$, and $u_{h}^{n-\theta }:=\theta u_{h}^{n-1}+(1-\theta ){u_{h}^{n}}\approx u(\mathbf {x}_{h},t_{n-\theta })$ for $\mathbf {x}_{h} \in \bar {{\Omega }}_{h}$. We take 𝜃 = α/2 and have the following 𝜃-weighted compact difference scheme for the reaction-subdiffusion problem (1.1)–(1.3)

$$ \begin{array}{@{}rcl@{}} (\partial_{a\tau}^{\alpha}u_{h})^{n-\theta}-\mathfrak{D}_{h}u_{h}^{n-\theta}&=&\kappa u_{h}^{n-\theta}+f(\mathbf{x}_{h},t_{n-\theta})\qquad\text{ for } \mathbf{x}_{h} \in {\Omega}_{h} \text{ and } 1\leq n\leq N, \end{array} $$

(1.6)

$$ \begin{array}{@{}rcl@{}} {u_{h}^{n}}&=&0\qquad\qquad\qquad\qquad\qquad \text{ for } \mathbf{x}_{h} \in \partial {\Omega}_{h} \text{ and } 1\leq n\leq N, \end{array} $$

(1.7)

$$ \begin{array}{@{}rcl@{}} {u_{h}^{0}}&=&u_{0}(\mathbf{x}_{h})\qquad\qquad\quad\quad\quad \text{ for } \mathbf{x}_{h} \in \bar{{\Omega}}_{h}. \end{array} $$

(1.8)

Here, the compact difference operator $\mathfrak {D}_{h}$ will be defined in the next section, in which the numerical implementation of (1.6)–(1.8) is also described.

The stability and convergence analysis of (1.6)–(1.8) rely on the recently developed fractional Grönwall inequality in [18], which is applicable for any discrete fractional derivative having the discrete convolution form (1.5). For the completeness of presentation, we combine three previous results from [18, Lemma 2.2, Theorems 3.1, and 3.2] into the following lemma.

Lemma 1.1

Assume that discrete convolution kernels $\textsf {A}_{n-k}^{(n)}$ satisfy the following two criteria:

• A1. There is a constant π_A > 0 such that $\textsf {A}_{n-k}^{(n)}\geq \frac {1}{\pi _{A}}{\int \limits }_{t_{k-1}}^{t_{k}}\frac {\omega _{1-\alpha }(t_{n}-s)}{\tau _{k}}\mathrm {d} s$ for 1 ≤ k ≤ n ≤ N.

• A2. The discrete kernels are monotone, i.e., $\textsf {A}_{n-k-1}^{(n)}-\textsf {A}_{n-k}^{(n)}\geq 0$ for 1 ≤ k ≤ n − 1 ≤ N − 1.

Define also a sequence of complementary discrete convolution kernels $\textsf {P}^{(n)}_{n-k}$ by

$$ \textsf{P}_{0}^{(n)}:=\frac{1}{\textsf{A}_{0}^{(n)}},\quad \textsf{P}_{n-j}^{(n)}:= \frac{1}{\textsf{A}_{0}^{(j)}} \sum\limits_{k=j+1}^{n}\left( {\textsf{A}_{k-j-1}^{(k)}-\textsf{A}_{k-j}^{(k)}}\right)\textsf{P}_{n-k}^{(n)} \quad\text{ for } 1\leq j\leq n-1. $$

(1.9)

Then the complementary kernels $\textsf {P}^{(n)}_{n-k}\ge 0$ are well-defined and fulfill

$$ \begin{array}{@{}rcl@{}} &&\sum\limits_{j=k}^{n}\textsf{P}^{(n)}_{n-j}\textsf{A}^{(j)}_{j-k}= 1 \quad\text{ for } 1\le k\le n\le N. \end{array} $$

(1.10)

$$ \begin{array}{@{}rcl@{}} &&\sum\limits_{j=1}^{n}\textsf{P}^{(n)}_{n-j}\omega_{1+(m-1)\alpha}(t_{n})\leq \pi_{A}\omega_{1+m\alpha}(t_{n}) \quad\text{ for } m=0,1 \text{ and } 1\le n\le N. \end{array} $$

(1.11)

Suppose that the offset parameter 0 ≤ ν < 1, λ is a nonnegative constant independent of the time-steps and the maximum step size

$$ \tau\le1/\sqrt[\alpha]{2{\Gamma}(2-\alpha)\lambda\pi_{A}}. $$

If the nonnegative sequences $(v^{k})_{k=0}^{N}$ and $(\eta ^{k})_{k=1}^{N}$ satisfy

$$ \sum\limits_{k=1}^{n}\textsf{A}^{(n)}_{n-k}\triangledown_{\tau} v^{k}\le \lambda v^{n-\nu}+\eta^{n}\quad\text{ for }1\le n\le N, $$

(1.12)

or

$$ \sum\limits_{k=1}^{n}\textsf{A}^{(n)}_{n-k}\triangledown_{\tau} (v^{k})^{2}\le \lambda (v^{n-\nu})^{2}+v^{n-\nu}\eta^{n}\quad\text{ for } 1\le n\le N, $$

(1.13)

then it holds that for 1 ≤ n ≤ N,

$$ \begin{array}{@{}rcl@{}} v^{n}&\le&2E_{\alpha}\left( 2\max\{1,\rho\}\lambda\pi_{A} t_{n}^{\alpha}\right) \left( v^{0}+\max\limits_{1\le k\le n}\sum\limits_{j=1}^{k}\textsf{P}^{(k)}_{k-j}\eta^{j}\right)\\ &\le&2E_{\alpha}\left( 2\max\{1,\rho\}\lambda\pi_{A}t_{n}^{\alpha}\right) \left( v^{0}+\pi_{A}{\Gamma}(1-\alpha)\max\limits_{1\le k\le n}\{t_{k}^{\alpha}\eta^{k}\}\right), \end{array} $$

where $E_{\alpha }(z):={\sum }_{k=0}^{\infty }\frac {z^{k}}{{\Gamma }(1+k\alpha )}$ is the Mittag–Leffler function.

This fractional discrete Grönwall lemma suggests that these two criteria A1-A2 should be verified to guarantee the stability of the fully discrete scheme (1.6)–(1.8). In Section 3, we will prove some properties of the discrete convolution kernels $\textsf {A}^{(n)}_{n-k}$ by assuming

• M1. The maximum time-step ratio ρ = 3/2.

Then Lemma 1.1 leads to the unconditional stability, see Theorem 3.1. Note that, M1 is a mild mesh condition, but it implies that a sudden, drastic reduction of time-steps should be avoided to ensure the stability.

The present analysis is also built on a new concept named global consistency analysis, developed recently by Liao et al. in [19], where a sharp L²-norm error estimate of the nonuniform Alikhanov scheme for the problem (1.1)–(1.3) is established systematically. To make the analysis extendable (such as for distributed-order subdiffusion problems), we assume that the continuous solution u satisfies the regularity assumptions

$$ \|u\|_{H^{4}({\Omega})}\leq C_{u},\quad \|u^{(\nu)}(t)\|_{H^{2}({\Omega})}\leq C_{u}(1+t^{\sigma-\nu}), $$

(1.14)

where ν ∈{1,2,3} and 0 < t ≤ T, σ ∈ (0,1) ∪ (1,2) is a regularity parameter and C_u is a positive constant. For instance [9, 11, 12], this assumption holds with σ = α for the original problem (1.1) if f(x, t) = 0 and $u_{0}\in {H_{0}^{1}}({\Omega })\cap H^{2}({\Omega })$. Invoking to the new global consistency error analysis of the accelerated Alikhanov formula presented in Lemma 4.2 and the fractional discrete Grönwall lemma described earlier, we establish sharp H¹-norm error estimate by means of the time-space error splitting technique, see Theorem 4.1. This theorem implies that the convergence analysis is applicable to a general family of nonuniform time meshes satisfying M1. To resolve the initial singularity of solution and solve it efficiently, we choose the time-steps that satisfy the following condition:

AssG.:

There is a positive constant C_γ independent of k, such that $\tau _{k}\le C_{\gamma }\tau \min \limits \{1,t_{k}^{1-1/\gamma }\}$ for 1 ≤ k ≤ N, with t_k ≤ C_γt_k− 1 and τ_k/t_k ≤ C_γτ_k− 1/t_k− 1 for 2 ≤ k ≤ N.

Here, the parameter γ ≥ 1 controls the extent to which the time levels are concentrated near t = 0. If the mesh is quasi-uniform, then AssG holds with γ = 1. As γ increases, the initial step sizes become smaller compared with the later ones. A simple example satisfying AssG is the graded mesh t_k = T(k/N)^γ. Under the assumption of AssG, Theorem 4.1 shows the error estimate of the time-stepping scheme (1.6)–(1.8) as

$$ {\left|{u(t_{n})-{u_{h}^{n}}}\right|}_{1} \leq \frac{C_{u}}{\sigma(1-\alpha)}\left( \tau^{\min\{\gamma \sigma,2\}}+h^{4}+\epsilon\right)\quad\text{ for } 1\leq n\leq N, $$

and the second-order accuracy in time is achieved if γ ≥ 2/σ, see Corollary 4.1 and Remark 2. In the last section, three numerical examples are given to confirm the theoretical results and verify the accuracy and effectiveness of the fast scheme. Throughout the paper, any subscripted C, such as C_u, C_v, and C_Ω, denotes a general positive constant, which has different values in different circumstances, and always depends on the given data and the continuous solution but is independent of the time and spatial steps.

2 Accelerated Alikhanov formula and fully discrete scheme

In this section, based on the SOEs approximation, fast Alikhanov formula on generally nonuniform time meshes is considered at first. Then, we develop a fully discrete second-order compact scheme for the problem (1.1)–(1.3) combined with the compact difference operator. Furthermore, an efficient numerical implementation is given at the end of this section.

2.1 Fast Alikhanov formula on nonuniform grids

Denote π_1,kv and π_2,kv are the linear interpolation of a function v with respect to t_k− 1, t_k and the quadratic interpolation of v with respect to t_k− 1, t_k, and t_k+ 1, respectively. Recalling the definition $\triangledown _{\tau } v^{k}$, it is easy to check that for k ≥ 1,

$$ \begin{array}{@{}rcl@{}} ({\Pi}_{1,k}v)^{\prime}(t)&=&\frac{\triangledown_{\tau}v^{k}}{\tau_{k}},\quad\\ ({\Pi}_{2,k}v)^{\prime}&=&\frac{\triangledown_{\tau}v^{k}}{\tau_{k}} +\frac{2(t-t_{k-1/2})}{\tau_{k}(\tau_{k}+\tau_{k+1})} (\rho_{k}\triangledown_{\tau}v^{k+1}-\triangledown_{\tau}v^{k}). \end{array} $$

For simplicity of presentation, we always denote ϖ_n(ξ) := −ω_2−α(t_n−𝜃 − ξ) for 0 ≤ ξ ≤ t_n−𝜃 and $\varpi _{n}^{\prime }(\xi )=\omega _{1-\alpha }(t_{n-\theta }-\xi )$ for 0 ≤ ξ < t_n−𝜃. The nonuniform Alikhanov approximation to the Caputo fractional derivative (1.4) is defined as [19]

$$ \begin{array}{@{}rcl@{}} (\partial_{\tau}^{\alpha}v)^{n-\theta}&:=&\sum\limits_{k=1}^{n-1}{\int}_{t_{k-1}}^{t_{k}}\varpi_{n}^{\prime}(\xi)({\Pi}_{2,k}v)^{\prime}(\xi)\mathrm{d} \xi+{\int}_{t_{n-1}}^{t_{n-\theta}}\varpi_{n}^{\prime}(\xi)({\Pi}_{1,n}v)^{\prime}(\xi)\mathrm{d} \xi\\ &=\!&a_{0}^{(n)}\triangledown_{\tau}v^{n} + \sum\limits_{k=1}^{n-1}\left( a_{n-k}^{(n)}\triangledown_{\tau}v^{k} + \rho_{k}b_{n-k}^{(n)} \triangledown_{\tau}v^{k+1} - b_{n-k}^{(n)}\triangledown_{\tau}v^{k}\right), \end{array} $$

(2.1)

where the discrete coefficients $a_{n-k}^{(n)}$ and $b_{n-k}^{(n)}$ are defined by

$$ \begin{array}{@{}rcl@{}} a_{n-k}^{(n)}&:=&\frac{1}{\tau_{k}}{\int}_{t_{k-1}}^{\min\{t_{n-\theta},t_{k}\}}\varpi_{n}^{\prime}(\xi)\mathrm{d} \xi\quad\text{ for } 1\leq k\leq n, \end{array} $$

(2.2)

$$ \begin{array}{@{}rcl@{}} b_{n-k}^{(n)}&:=&\frac{2}{\tau_{k}(\tau_{k}+\tau_{k+1})}{\int}_{t_{k-1}}^{t_{k}}(\xi-t_{k-\frac{1}{2}})\varpi_{n}^{\prime}(\xi)\mathrm{d} \xi\quad\text{ for } 1\leq k\leq n-1 . \end{array} $$

(2.3)

Rearranging the terms in (2.1), we reformulate (2.1) in the following discrete convolution form

$$ (\partial_{\tau}^{\alpha}v)^{n-\theta}=\sum\limits_{k=1}^{n}A_{n-k}^{(n)}\triangledown_{\tau} v^{k}, $$

(2.4)

where the discrete convolution kernels $a_{n-k}^{(n)}$ are defined as: $A_{0}^{(1)}:=a_{0}^{(1)}$ if n = 1, and for n ≥ 2,

$$ A_{n-k}^{(n)}:=\left\{ \begin{array}{ll} &a_{0}^{(n)}+\rho_{n-1}b_{1}^{(n)}\quad \quad \quad \quad \quad \quad \quad \quad \text{for}\ k=n,\\ &a_{n-k}^{(n)}+\rho_{k-1}b_{n-k+1}^{(n)}-b_{n-k}^{(n)}\quad \quad \quad \text{for}\ 2\leq k\leq n-1,\\ &a_{n-1}^{(n)}-b_{n-1}^{(n)}\quad \quad \quad \quad \quad \quad \quad \quad \quad \ \text{for}\ k=1. \end{array} \right. $$

Due to the essentially nonlocal property of the fractional derivative, the formula mentioned above involves the solution information at all historical time-levels and it is time-consuming in practical calculations. Here, the SOEs technique is employed to deduce an accelerated Alikhanov formula to improve the efficiency. The key point of the SOEs approximation (see [23, Theorem 2.5] or [26, Lemma 2.2]) is as follows:

Lemma 2.1

Given α ∈ (0,1), an absolute tolerance error 𝜖 ≪ 1, a cut-off time Δt > 0, and a final time T, there exist a positive integer N_q, positive quadrature nodes s^ℓ, and positive weights 𝜗^ℓ (1 ≤ ℓ ≤ N_q) such that

$$ \left|{\omega_{1-\alpha}(t)-\sum\limits_{\ell=1}^{N_{q}}\vartheta^{\ell}e^{-s^{\ell}t}}\right|\leq \epsilon\quad \forall t\in [{\Delta} t,T], $$

where the quadrature nodes number N_q satisfies

$$ N_{q}=O\left( \log\frac{1}{\epsilon}\left( \log\log\frac{1}{\epsilon}+\log\frac{T}{{\Delta} t}\right)+\log\frac{1}{{\Delta} t}\left( \log\log\frac{1}{\epsilon}+\log\frac{1}{{\Delta} t}\right)\right). $$

In [24], the authors illustrate that $N_{q}=O(\log N)$ for T ≫ 1 and $N_{q}=O(\log ^{2}N)$ for T ≈ 1. Moreover, they also list a table to show the relationships between N_q and various parameters α, τ, and 𝜖, see Table 1 in [24]. These results indicate the SOEs strategy efficiently reduces the computational complexity and storage requirement. By virtue of this lemma, we divide (2.1) into a sum of a local part (an integral over [t_n− 1, t_n−𝜃]) and a historical part (an integral over [0,t_n− 1]). In the former part, linear interpolation is utilized to approximate $v^{\prime }(\xi ) (\xi \in (t_{n-1}, t_{n-\theta }))$ as before, and in the latter one, SOEs technique is applied to the convolution kernel $\varpi _{n}^{\prime }(\xi )$, i.e.,

$$ \begin{array}{@{}rcl@{}} (\partial_{\tau}^{\alpha}v)^{n-\theta}&\approx& {\int}_{t_{n-1}}^{t_{n-\theta}}\varpi_{n}^{\prime}(\xi) \frac{\triangledown_{\tau}v^{n}}{\tau_{n}}\mathrm{d} \xi+{\int}_{0}^{t_{n-1}}\sum\limits_{\ell=1}^{N_{q}}\vartheta^{\ell}e^{-s^{\ell}(t_{n-\theta}-\xi)}v^{\prime}(\xi)\mathrm{d} \xi\\ &=&a_{0}^{(n)}\triangledown_{\tau}v^{n}+\sum\limits_{\ell=1}^{N_{q}}\vartheta^{\ell}e^{-s^{\ell}(1-\theta)\tau_{n}} \mathcal{H}^{\ell}(t_{n-1})\quad\text{ for } n\geq 1, \end{array} $$

where

$$ \mathcal{H}^{\ell}(t_{k})={\int}_{0}^{t_{k}}e^{-s^{\ell}(t_{k}-\xi)}v^{\prime}(\xi)\mathrm{d} \xi\quad \text{with}\quad \mathcal{H}^{\ell}(t_{0})=0\quad\text{ for } 1\leq \ell \leq N_{q}. $$

To compute ${\mathcal{H}}^{\ell }(t_{k})$ efficiently, we attempt to obtain the recurrence formulation. Applying the quadratic interpolation to approximate $v^{\prime }(\xi )$ in each subinterval [t_k− 1, t_k] (1 ≤ k ≤ n − 1) yields

$$ \begin{array}{@{}rcl@{}} \mathcal{H}^{\ell}(t_{k}) &\approx& e^{-s^{\ell}\tau_{k}}\mathcal{H}^{\ell}(t_{k-1})+{\int}_{t_{k-1}}^{t_{k}}e^{-s^{\ell}(t_{k}-\xi)} ({\Pi}_{2,k}v)^{\prime}(\xi)\mathrm{d} \xi\\ &=& e^{-s^{\ell}\tau_{k}}\mathcal{H}^{\ell}(t_{k-1})+a^{(k,\ell)}\triangledown_{\tau}v^{k}+b^{(k,\ell)}(\rho_{k}\triangledown_{\tau}v^{k+1}- \triangledown_{\tau}v^{k}), \end{array} $$

where the coefficients are given by

$$ \begin{array}{@{}rcl@{}} a^{(k,\ell)}&=&\frac{1}{\tau_{k}}{\int}_{t_{k-1}}^{t_{k}}e^{-s^{\ell}(t_{k}-\xi)}\mathrm{d} \xi,\\ b^{(k,\ell)} &=&\frac{2}{\tau_{k}(\tau_{k}+\tau_{k+1})}{\int}_{t_{k-1}}^{t_{k}}(\xi-t_{k-\frac{1}{2}})e^{-s^{\ell}(t_{k}-\xi)}\mathrm{d} \xi. \end{array} $$

Note that these coefficients are calculated exactly based on the integral property of exponential functions. Overall, the accelerated nonuniform Alikhanov formula can be formulated as

$$ (\partial_{a\tau}^{\alpha}v)^{n-\theta}:=a_{0}^{(n)}\triangledown_{\tau}v^{n}+\sum\limits_{\ell=1}^{N_{q}}\vartheta^{\ell}e^{-s^{\ell}(1-\theta)\tau_{n}} \mathcal{H}^{\ell}(t_{n-1})\quad\text{ for }n\geq 1, $$

(2.5)

where ${\mathcal{H}}^{\ell }(t_{k})$ satisfies ${\mathcal{H}}^{\ell }(t_{0})=0$ and the recurrence relation

$$ \begin{array}{@{}rcl@{}} \mathcal{H}^{\ell}(t_{k})&=&e^{-s^{\ell}\tau_{k}}\mathcal{H}^{\ell}(t_{k-1})+a^{(k,\ell)}\triangledown_{\tau}v^{k}\\ &&+b^{(k,\ell)}(\rho_{k}\triangledown_{\tau}v^{k+1}- \triangledown_{\tau}v^{k})\quad\text{ for } k\geq 1,\ 1\leq \ell\leq N_{q}. \end{array} $$

Table 1 Temporal error of Example 1 for different α with σ = 0.8,γ = 1

2.2 Second-order compact scheme and implementation

We discretize the spatial domain ${\Omega } \in \mathbb {R}^{d}$ by equal spatial step sizes h_k = (x_{k, R} − x_{k, L})/M_k for the positive integers M_k (1 ≤ k ≤ d) and denote $h:=\max \limits _{1\leq k \leq d}h_{k}$ is the maximum spatial length. Let $x_{k,i_{k}}=x_{k,L}+i_{k}h_{k}$ for 0 ≤ i_k ≤ M_k, 1 ≤ k ≤ d, then the fully discrete grids in space can be defined as $\bar {{\Omega }}_{h}:=\{\mathbf {x}_{h}=(x_{1,i_{1}},x_{2,i_{2}},\cdots ,x_{d,i_{d}})|0\leq i_{k}\leq M_{k},1\leq k \leq d\}$. Set ${\Omega }_{h}=\bar {{\Omega }}_{h}\cap {\Omega }$ and the boundary $\partial {\Omega }_{h}=\bar {{\Omega }}_{h}\cap \partial {\Omega }$. Also, $M={\prod }_{k=1}^{d}(M_{k}+1)$ represents the total number of grid points in space. Denote an index vector h = (i₁, i₂, ⋯ ,i_d) and for any grid function v_h at the k th position (1 ≤ k ≤ d), we introduce the following difference operators:

$$ \delta_{k}v_{i_{k}+\frac{1}{2}}:=\frac{v_{i_{k}+1}-v_{i_{k}}}{h_{k}},\quad {\delta_{k}^{2}}v_{i_{k}}:=\frac{v_{i_{k}+1}-2v_{i_{k}}+v_{i_{k}-1}}{{h_{k}^{2}}},\quad \mathcal{I}_{k}v_{i_{k}}:=(\mathrm{I}+\frac{{h_{k}^{2}}}{12}{\delta_{k}^{2}})v_{i_{k}}, $$

and the compact difference operator is denoted as $\mathfrak {D}_{k}v_{i_{k}}:=\frac {{\delta _{k}^{2}}}{\mathcal {I}_{k}}v_{i_{k}}$. As a result, the second-order and fourth-order spatial approximations of Δv(x_h) for x_h ∈Ω_h can be denoted separately as ${\Delta }_{h}v_{h}:={\sum }_{k=1}^{d}{\delta _{k}^{2}}v_{h}$ and $\mathfrak {D}_{h}v_{h}:={\sum }_{k=1}^{d}\mathfrak {D}_{k}v_{h}$.

Let $\mathbb {V}_{h}=\{v=(v_{h})_{\mathbf {x}_{h} \in {\Omega }_{h}}|v_{h}=0\ \text {when}\ \mathbf {x}_{h} \in \partial {\Omega }_{h} \}$ be the space of grid functions. For any $v,w \in \mathbb {V}_{h}$, we define the discrete inner product $\langle v, w\rangle _{h}:=({\prod }_{k=1}^{d}h_{k}){\sum }_{\mathbf {x}_{h} \in {\Omega }_{h}}v_{h}w_{h}$ and the corresponding discrete L²-norm $\|v\|:=\sqrt {\langle v,v\rangle _{h}}$. Also, the discrete H¹ semi-norm is defined as $|{v}|_{1}:=\sqrt {{\sum }_{k=1}^{d}\|\delta _{k}v_{h}\|^{2}}$. Based on the embedding theorem, there exist a positive constant C_Ω dependent on the domain Ω such that

$$ \|v\| \leq C_{{\Omega}}|{v}|_{1}\quad\text{ for } v \in \mathbb{V}_{h}. $$

(2.6)

Combining with the fast Alikhanov formula derived earlier, one has a fully discrete second-order compact scheme (1.6)–(1.8) for the problem (1.1)–(1.3). To speed up the numerical computations, we introduce the fast discrete sine transform (DST) [27, 28] in spatial direction and bypass the direct calculations. Based on the DST and compact difference operator, for any grid function v_h at the k th position, fourth-order spatial approximation can be drawn:

$$ \begin{array}{@{}rcl@{}} &&\sum\limits_{j_{k}=1}^{M_{k}-1}\widehat{v^{\prime\prime}_{j_{k}}}\left[\sin\left( \frac{(i_{k}+1) j_{k}\pi}{M_{k}}\right)+10\sin\left( \frac{i_{k} j_{k}\pi}{M_{k}}\right)+\sin\left( \frac{(i_{k}-1) j_{k}\pi}{M_{k}}\right)\right]\\ &\approx&\frac{12}{{h_{k}^{2}}}\sum\limits_{j_{k}=1}^{M_{k}-1}\widehat{v_{j_{k}}}\left[\sin\left( \frac{(i_{k}+1) j_{k}\pi}{M_{k}}\right)-2\sin\left( \frac{i_{k} j_{k}\pi}{M_{k}}\right)+\sin\left( \frac{(i_{k}-1) j_{k}\pi}{M_{k}}\right)\right]. \end{array} $$

After simple calculations, for 1 ≤ j_k ≤ M_k − 1 and 1 ≤ k ≤ d, we have

$$ \widehat{v^{\prime\prime}_{j_{k}}}\approx\widehat{v_{j_{k}}}\frac{12}{{h_{k}^{2}}}\left( \cos\left( \frac{j_{k}\pi}{M_{k}}\right)-1\right) \left( \cos\left( \frac{j_{k}\pi}{M_{k}}\right)+5\right)^{-1}=\widehat{v_{j_{k}}}\hbar^{(j_{k},M_{k})}. $$

Denote an index set ν = {(j₁, j₂, ⋯ ,j_d)|1 ≤ j_k ≤ M_k − 1,1 ≤ k ≤ d}. Resorting to the fast Alikhanov formula in (2.5) and the fast DST mentioned above, numerical scheme (1.6) can be reformulated in the following way for implementation:

$$ \begin{array}{@{}rcl@{}} &&\left( \textsf{a}_{0}^{(n)}-(1-\theta)\kappa-(1-\theta)\sum\limits_{k=1}^{d}\hbar^{(j_{k},M_{k})}\right)\triangledown_{\tau}\widehat{u}_{\nu}^{n}= \left( \sum\limits_{k=1}^{d}\hbar^{(j_{k},M_{k})}+\kappa\right) \widehat{u}_{\nu}^{n-1}+\widehat{f}^{n-\theta}-\widehat{\mathcal{M}}^{n-1},\\ &&\widehat{\mathcal{M}}^{n-1}=\sum\limits_{\ell=1}^{N_{q}}\vartheta^{\ell}e^{-s^{\ell}(1-\theta)\tau_{n}}\widehat{\mathcal{H}}^{\ell}(t_{n-1})\\ &&=\sum\limits_{\ell=1}^{N_{q}}\vartheta^{\ell}e^{-s^{\ell}(1-\theta)\tau_{n}} \left[e^{-s^{\ell}\tau_{n}}\widehat{\mathcal{H}}^{\ell}(t_{n-2})+(a^{(n-1,\ell)}- b^{(n-1,\ell)})\triangledown_{\tau}\widehat{u}_{\nu}^{n-1}+b^{(n-1,\ell)} \rho_{n-1}\triangledown_{\tau}\widehat{u}_{\nu}^{n}\right], \end{array} $$

where $\widehat {{\mathcal{H}}}^{\ell }(t_{0})=0$. $\widehat {u}_{\nu }^{n-1}$ and $\widehat {f}^{n-\theta }$ are obtained from $u_{h}^{n-1}$ and f^n−𝜃 via the DST, respectively. The current solution ${u_{h}^{n}}$ is computed from $\widehat {u}_{\nu }^{n}$ via the inverse DST.

The fast DST is essentially implemented via the fast Fourier transform (FFT). In [29], the authors illustrate that FFT algorithm can reduce the numerical cost from O(M²) to $O(M\log M)$. Therefore, compared with traditional algorithms, the presented one reduces the overall computational cost from O(M²N²) to $O(MN\log M \log N)$ and the overall storage from O(MN) to $O(M\log N)$.

3 Properties of discrete convolution kernels and stability

To prepare for the subsequent analysis, in this section, we show that the discrete kernels $\textsf {A}_{n-k}^{(n)}$ of the fast approximation $(\partial _{a\tau }^{\alpha }v)^{n-\theta }$ satisfy A1-A2 in Lemma 1.1. Then, the stability in the H¹-norm can be verified rigorously via the fractional discrete Grönwall lemma.

3.1 Properties of discrete kernels

We eliminate the historical term ${\mathcal{H}}^{\ell }(t_{n-1})$ in (2.5) and reformulate the recursive relationship into the discrete convolution form. The recurrence relation in (2.5) leads to

$$ \mathcal{H}^{\ell}(t_{k})=\sum\limits_{j=1}^{k}e^{-s^{\ell}(t_{k}-t_{j})}\left( a^{(j,\ell)}\triangledown_{\tau}v^{j}+ \rho_{j}b^{(j,\ell)}\triangledown_{\tau}v^{j+1}-b^{(j,\ell)}\triangledown_{\tau}v^{j}\right). $$

(3.1)

Replacing k by n − 1 and plugging (3.1) into (2.5), we use the definitions (2.2)–(2.3) to obtain an alternative formula

$$ (\partial_{a\tau}^{\alpha}v)^{n-\theta} =\textsf{a}_{0}^{(n)}\triangledown_{\tau}v^{n}+\sum\limits_{k=1}^{n-1}\left( \textsf{a}_{n-k}^{(n)}\triangledown_{\tau}v^{k}+\rho_{k}\textsf{b}_{n-k}^{(n)} \triangledown_{\tau}v^{k+1}-\textsf{b}_{n-k}^{(n)}\triangledown_{\tau}v^{k}\right), $$

(3.2)

where the positive coefficients $\textsf {A}_{n-k}^{(n)}$ and $\textsf {b}_{n-k}^{(n)}$ are defined by

$$ \begin{array}{@{}rcl@{}} \textsf{a}_{0}^{(n)}&:=&a_{0}^{(n)}\quad\text{and}\quad \textsf{a}_{n-k}^{(n)}:=\frac{1}{\tau_{k}}{\int}_{t_{k-1}}^{t_{k}}\sum\limits_{\ell=1}^{N_{q}}\vartheta^{\ell}e^{-s^{\ell} (t_{n-\theta}-\xi)}\mathrm{d} \xi\quad\text{ for }1\leq k\leq n-1, \end{array} $$

(3.3)

$$ \begin{array}{@{}rcl@{}} \textsf{b}_{n-k}^{(n)}&:=&\frac{2}{\tau_{k}(\tau_{k}+\tau_{k+1})}{\int}_{t_{k-1}}^{t_{k}}\sum\limits_{\ell=1}^{N_{q}}\vartheta^{\ell}e^{-s^{\ell} (t_{n-\theta}-\xi)}(\xi-t_{k-\frac{1}{2}})\mathrm{d} \xi\quad\text{ for } 1\leq k\leq n-1. \end{array} $$

(3.4)

Correspondingly, we rearrange (3.2) and obtain the following discrete convolution form

$$ (\partial_{a\tau}^{\alpha}v)^{n-\theta}=\sum\limits_{k=1}^{n}\textsf{A}_{n-k}^{(n)}\triangledown_{\tau}v^{k}, $$

where the discrete convolution kernels $\textsf {A}_{n-k}^{(n)}$ are defined as: $\textsf {A}_{0}^{(1)}:=a_{0}^{(1)}$ if n = 1, and for n ≥ 2,

$$ \textsf{A}_{n-k}^{(n)}=\left\{ \begin{array}{ll} &\textsf{a}_{0}^{(n)}+\rho_{n-1}\textsf{b}_{1}^{(n)}\quad \quad \quad \quad \quad \quad \quad \quad \ \ \text{for}\ k=n,\\ &\textsf{a}_{n-k}^{(n)}+\rho_{k-1}\textsf{b}_{n-k+1}^{(n)}-\textsf{b}_{n-k}^{(n)}\quad \quad \quad \text{for}\ 2\leq k\leq n-1,\\ &\textsf{a}_{n-1}^{(n)}-\textsf{b}_{n-1}^{(n)}\quad \quad \quad \quad \quad \quad \quad \quad \quad \text{for}\ k=1. \end{array} \right. $$

Comparing the coefficients between (2.2)–(2.3) and (3.3)–(3.4), we see that the latter ones are obtained by replacing the SOEs approximations with the integral kernels in the formers. Then Lemma 2.1 gives

$$ \left|{\textsf{a}_{n-k}^{(n)}-a_{n-k}^{(n)}}\right|\leq \epsilon\quad\text{ for } 1\leq k \leq n-1, $$

(3.5)

and when M1 ($\rho _{k}\leq \rho =\frac {3}{2}$) holds, for 1 ≤ k ≤ n − 1,

$$ \left|{\textsf{b}_{n-k}^{(n)}-b_{n-k}^{(n)}}\right|\leq \frac{2\epsilon}{\tau_{k}(\tau_{k}+\tau_{k+1})}{\int}_{t_{k-1}}^{t_{k}} \left|{\xi-t_{k-\frac{1}{2}}}\right|\mathrm{d} \xi=\frac{{\tau_{k}^{2}}\epsilon}{2\tau_{k}(\tau_{k}+\tau_{k+1})}=\frac{\rho_{k}\epsilon}{2(1+\rho_{k})} \leq \frac{3\epsilon}{10}. $$

(3.6)

Next, we show that discrete convolution kernels $\textsf {A}_{n-k}^{(n)}$ satisfy the assumptions A1-A2. The following bounds which can be proved by the integral mean-value theorem will be utilized in several places,

$$ a_{n-k-1}^{(n)}>\omega_{1-\alpha}(t_{n-\theta}-t_{k})>a_{n-k}^{(n)}\quad\text{ for } 1\leq k\leq n-1. $$

(3.7)

Lemma 3.1

Let M1 holds. Denote $\epsilon ^{*}=\frac {\alpha }{2(1-\alpha )}\omega _{1-\alpha }(T)$ and $\epsilon ^{**}=\frac {1}{26}\omega _{1-\alpha }(T)$. If the tolerance error $\epsilon \leq \min \limits \{\epsilon ^{*},\epsilon ^{**}\}$, then the discrete convolutional kernels $\textsf {A}_{n-k}^{(n)}$ satisfy A1 with π_A = 2 for 1 ≤ k ≤ n. Furthermore, $\textsf {A}_{n-k}^{(n)}$ has an upper bound with $\textsf {A}_{n-k}^{(n)}\leq \frac {2}{\tau _{n}}\omega _{2-\alpha }(\tau _{n})$.

Proof

The definition of $\textsf {A}_{n-k}^{(n)}$ in (3.3) and the integral mean-value theorem yield

$$ \textsf{a}_{n-k-1}^{(n)}>\textsf{a}_{n-k}^{(n)}\quad\text{ for } 1\leq k\leq n-2, $$

where s^ℓ,𝜗^ℓ are positive in Lemma 2.1 and the monotonicity of exponential function was also used. For k = n − 1, the definition (2.2) and (3.7) yield

$$ a_{0}^{(n)}-a_{1}^{(n)}>\frac{1}{\tau_{n}}\omega_{2-\alpha}(t_{n-\theta}-t_{n-1})-\omega_{1-\alpha}(t_{n-\theta}-t_{n-1})= \frac{\alpha-\theta}{1-\alpha}(1-\theta)^{-\alpha}\omega_{1-\alpha}(\tau_{n}). $$

Since e^x > 1 + x for $x\in \mathbb {R}$ and $\ln (1-\frac {x}{2})<0$ for 0 < x < 1, one has

$$ a_{0}^{(n)}-a_{1}^{(n)}>\frac{\alpha}{2(1-\alpha)}e^{-\alpha\ln(1-\frac{\alpha}{2})}\omega_{1-\alpha}(\tau_{n}) >\frac{\alpha}{2(1-\alpha)}\omega_{1-\alpha}(\tau_{n})\geq \epsilon^{*}\geq \epsilon. $$

Therefore, we obtain $\textsf {a}_{0}^{(n)}=a_{0}^{(n)}> a_{1}^{(n)}+\epsilon \geq \textsf {a}_{1}^{(n)}$ by using the definitions in (3.3) and the inequality (3.5). It means that $\textsf {a}_{n-k-1}^{(n)}>\textsf {a}_{n-k}^{(n)}$ for 1 ≤ k ≤ n − 1.

In consideration of [19, Lemma 4.3] and $0<\theta <\frac {1}{2}$, it is easy to check

$$ b_{n-k}^{(n)}<\frac{\theta \tau_{k}}{2(t_{n-\theta}-t_{k})}\frac{\rho_{k}}{1+\rho_{k}}a_{n-k}^{(n)}\leq \frac{\theta \tau_{k}}{2(1-\theta)\tau_{k+1}}\frac{\rho_{k}}{1+\rho_{k}}a_{n-k}^{(n)}< \frac{{\rho_{k}^{2}}}{2(1+\rho_{k})}a_{n-k}^{(n)}. $$

(3.8)

For 1 ≤ k ≤ n − 1, the definition of $\textsf {A}_{n-k}^{(n)}$ and the inequalities (3.5)–(3.6) yield

$$ \textsf{A}_{n-k}^{(n)}\geq \textsf{a}_{n-k}^{(n)}-\textsf{b}_{n-k}^{(n)}>a_{n-k}^{(n)}-\epsilon-\frac{{\rho_{k}^{2}}}{2(1+\rho_{k})}a_{n-k}^{(n)}-\frac{3\epsilon}{10} =\frac{2+2\rho_{k}-{\rho_{k}^{2}}}{2(1+\rho_{k})}a_{n-k}^{(n)}-\frac{13\epsilon}{10}. $$

Note that $\frac {2+2x-x^{2}}{2(1+x)}$ is increasing for $x\in (0,\frac {3}{2}]$, and $\epsilon \leq \epsilon ^{**}\leq \frac {1}{26}w_{1-\alpha }(t_{n-\theta }-t_{k-1})<\frac {1}{26}a_{n-k}^{(n)}$, then we find

$$ \textsf{A}_{n-k}^{(n)}\geq \frac{11}{20}a_{n-k}^{(n)}-\frac{1}{20}a_{n-k}^{(n)}=\frac{1}{2}a_{n-k}^{(n)}> \frac{1}{2}{\int}_{t_{k-1}}^{t_{k}}\frac{\omega_{1-\alpha}(t_{n}-\xi)}{\tau_{k}}\mathrm{d} \xi\quad\text{ for } 1\leq k \leq n-1. $$

For the case of k = n, it is clear that $\textsf {A}_{0}^{(n)}\geq \textsf {a}_{0}^{(n)}=a_{0}^{(n)}>\frac {1}{2}{\int \limits }_{t_{k-1}}^{t_{k}}\frac {\omega _{1-\alpha }(t_{n}-\xi )}{\tau _{k}}\mathrm {d} \xi$. In summary, by choosing π_A = 2, the discrete convolution kernels $\textsf {A}_{n-k}^{(n)}$ satisfy A1 for 1 ≤ k ≤ n.

Now we derive an upper bound of $\textsf {A}_{n-k}^{(n)}$. From (3.6) and (3.8), one gets

$$ \textsf{A}_{0}^{(n)}=a_{0}^{(n)}+\rho_{n-1}\textsf{b}_{1}^{(n)}<a_{0}^{(n)}+ \frac{\rho_{n-1}^{3}}{2(1+\rho_{n-1})}{a_{1}^{n}}+\frac{3\epsilon}{10}\rho_{n-1}. $$

Note that $\frac {x^{3}}{2(1+x)}$ is increasing for $x\in (0,\frac {3}{2}]$, we apply (3.7) and M1 to get

$$ \textsf{A}_{0}^{(n)}< a_{0}^{(n)}+\frac{27}{40}a_{1}^{(n)}+\frac{9\epsilon}{20}< a_{0}^{(n)}+\frac{27}{40}a_{0}^{(n)}+\frac{9}{20}\times \frac{1}{26}a_{0}^{(n)}=\frac{22}{13} a_{0}^{(n)}<2 a_{0}^{(n)}. $$

Since $a_{0}^{(n)}=\frac {1}{\tau _{n}}(1-\theta )^{1-\alpha }{\int \limits }_{t_{n-1}}^{t_{n}}\omega _{1-\alpha }(t_{n}-\xi )\mathrm {d} \xi \leq \frac {1}{\tau _{n}}{\int \limits }_{t_{n-1}}^{t_{n}}\omega _{1-\alpha }(t_{n}-\xi )\mathrm {d} \xi$, we obtain an upper bound, i.e., $\textsf {A}_{n-k}^{(n)}\leq \frac {2}{\tau _{n}}{\int \limits }_{t_{n-1}}^{t_{n}}\omega _{1-\alpha }(t_{n}-\xi )\mathrm {d} \xi =\frac {2}{\tau _{n}}\omega _{2-\alpha }(\tau _{n})$. This completes the proof. □

Next, we establish the monotonicity of discrete kernels. For simplicity of presentation, two positive coefficients are introduced [19]

$$ I_{n-k}^{(n)}:=\frac{1}{\tau_{k}}{\int}_{t_{k-1}}^{t_{k}}(t_{k}-\xi)\varpi_{n}^{\prime\prime}(\xi)\mathrm{d} \xi,\ \ J_{n-k}^{(n)}:=\frac{1}{\tau_{k}}{\int}_{t_{k-1}}^{t_{k}}(\xi-t_{k-1})\varpi_{n}^{\prime\prime}(\xi)\mathrm{d} \xi\quad\text{ for } 1\leq k \leq n-1. $$

(3.9)

Some properties of the coefficients are also given as follows:

Lemma 3.2

The positive coefficients in (3.9) satisfy

$$ \begin{array}{@{}rcl@{}} && (i)\ I_{n-k}^{(n)}\geq \frac{1+\rho_{k}}{\rho_{k}}b_{n-k}^{(n)},\quad (ii)\ J_{n-k}^{(n)}\geq \frac{2(1+\rho_{k})}{\rho_{k}}b_{n-k}^{(n)}\quad\text{ for } 1\leq k \leq n-1.\\ && (iii)\ J_{n-k-1}^{(n)}\geq \frac{1}{\rho_{k}}J_{n-k}^{(n)}\quad\text{ for } 1\leq k \leq n-2. \end{array} $$

Proof

We refer to [19, Lemma 4.4] for (i)–(ii) and [19, Lemma 4.5] for (iii). □

Next, we are ready to prove the following monotonicity lemma.

Lemma 3.3

Let M1 holds. Denote $\epsilon _{k}=\frac {\alpha (1+5\rho _{k})\tau _{k}}{105T}\omega _{1-\alpha }(T)$ for 1 ≤ k ≤ n − 1. If the tolerance error $\epsilon \leq \min \limits _{1\leq k \leq n-1}\epsilon _{k}$, then the discrete convolutional kernels $\textsf {A}_{n-k}^{(n)}$ satisfy A2 for 1 ≤ k ≤ n.

Proof

Comparing the discrete convolution kernels between two formulas and invoking to the inequalities (3.5)–(3.6), one has $\textsf {A}_{0}^{(1)}=A_{0}^{(1)}$ if n = 1, and for n ≥ 2,

$$ \left|{\textsf{A}_{n-k}^{(n)}-A_{n-k}^{(n)}}\right| \leq \left\{ \begin{array}{ll} &\epsilon+\frac{3\epsilon}{10}\rho_{n-1} \leq \frac{29}{20}\epsilon\quad \quad \quad \quad \text{for}\ k=n,\\ &\epsilon+\frac{3\epsilon}{10}\rho_{k-1}+\frac{3\epsilon}{10} \leq \frac{7}{4}\epsilon\quad \quad \text{for}\ 2\leq k\leq n-1,\\ &\epsilon+\frac{3\epsilon}{10} \leq \frac{13}{10}\epsilon\quad \quad \quad \quad \quad \quad \text{for}\ k=1, \end{array} \right. $$

(3.10)

where M1 was also used. Also, we can derive a similar estimate of $\left |{\textsf {A}_{n-k-1}^{(n)}-A_{n-k-1}^{(n)}}\right |$. Combining these two inequalities, we have $A_{0}^{(1)}=\textsf {A}_{0}^{(1)}$ if n = 1. For n ≥ 2, $A_{0}^{(n)}\leq \textsf {A}_{0}^{(n)}+\frac {29\epsilon }{20}$ and

$$ A_{n-k-1}^{(n)}-A_{n-k}^{(n)}+\textsf{A}_{n-k}^{(n)}-\textsf{A}_{n-k-1}^{(n)} \leq \left\{ \begin{array}{ll} 16\epsilon/5\quad \quad \ \ &\text{for}\ k=n-1,\\ 7\epsilon/2\quad \quad \quad&\text{for}\ 2\leq k\leq n-2,\\ 61\epsilon/20\quad \quad&\text{for}\ k=1. \end{array} \right. $$

(3.11)

According to [19, Theorem 2.2 (II)] and Lemma 3.2 (i), it holds that

$$ A_{n-k-1}^{(n)}-A_{n-k}^{(n)}\geq (1+\rho_{k})b_{n-k}^{(n)}+\frac{1}{5}I_{n-k}^{(n)}\geq (1+\rho_{k})(\frac{1}{5\rho_{k}}+1)b_{n-k}^{(n)}\quad\text{ for } 1\leq k \leq n-1. $$

(3.12)

Recalling the definition of ϖ_n(ξ), we get the second derivative $\varpi _{n}^{\prime \prime }(\xi )=-\omega _{-\alpha }(t_{n-\theta }-\xi )>0$ and the third derivative $\varpi _{n}^{\prime \prime \prime }(\xi )=\omega _{-\alpha -1}(t_{n-\theta }-\xi )>0$ for 0 ≤ ξ < t_n−𝜃. By means of [19, Lemma 2.1], for 1 ≤ k ≤ n − 1, it is not difficult to check

$$ \begin{array}{@{}rcl@{}} b_{n-k}^{(n)}&=&{\int}_{t_{k-1}}^{t_{k}}\frac{(t_{k}-\xi)(\xi-t_{k-1})}{\tau_{k}(\tau_{k}+\tau_{k+1})}\varpi_{n}^{\prime\prime}(\xi)\mathrm{d} \xi \geq \frac{{\tau_{k}^{2}}}{6(\tau_{k}+\tau_{k+1})}\varpi_{n}^{\prime\prime}(t_{k-1})\\ &=&\frac{\rho_{k}\tau_{k}}{6(1+\rho_{k})}\varpi_{n}^{\prime\prime}(t_{k-1}). \end{array} $$

(3.13)

Substituting (3.13) into (3.12) and applying (3.11), one gets

$$ \textsf{A}_{n-k-1}^{(n)}-\textsf{A}_{n-k}^{(n)}\geq A_{n-k-1}^{(n)}-A_{n-k}^{(n)}-\frac{7\epsilon}{2}\geq \frac{(1+5\rho_{k})\tau_{k}}{30}\varpi_{n}^{\prime\prime}(t_{k-1})-\frac{7\epsilon}{2}. $$

When the hypothesis holds, i.e., $\epsilon \leq \min \limits _{1\leq k \leq n-1}\frac {\alpha (1+5\rho _{k})\tau _{k}}{105T}\omega _{1-\alpha }(T)$, we obtain

$$ \textsf{A}_{n-k-1}^{(n)}-\textsf{A}_{n-k}^{(n)}> -\frac{(1+5\rho_{k})\tau_{k}}{30}\omega_{-\alpha}(T)-\frac{7\epsilon}{2}= \frac{\alpha(1+5\rho_{k})\tau_{k}}{30T}\omega_{1-\alpha}(T)-\frac{7\epsilon}{2}\geq 0. $$

This completes the proof of Lemma 3.3. □

Remark 1

In numerical simulations, the SOEs tolerance error 𝜖 is always set to be small enough so that the convergence order should not be degraded. Hence, the condition of 𝜖 in Lemma 3.3 is allowed to guarantee the monotonicity of discrete convolutional kernels $\textsf {A}_{n-k}^{(n)}$.

In addition to the boundedness and monotonicity described above, the following auxiliary lemma is also indispensable in the subsequent analysis.

Lemma 3.4

Under the conditions of Lemma 3.3, it holds that

$$ \textsf{A}_{0}^{(n)}-\textsf{A}_{1}^{(n)}> \theta (2 \textsf{A}_{0}^{(n)}-\textsf{A}_{1}^{(n)})\quad\text{ for }n\geq 2. $$

Proof

The conclusion is equivalent to $\frac {1-2\theta }{1-\theta }\textsf {A}_{0}^{(n)}-\textsf {A}_{1}^{(n)}>0$. For n ≥ 2, (3.10) yields

$$ \frac{1 - 2\theta}{1\!-\theta}\textsf{A}_{0}^{(n)}-\textsf{A}_{1}^{(n)}\!\geq\! \frac{1-2\theta}{1-\theta}A_{0}^{(n)}-A_{1}^{(n)}-\frac{1-2\theta}{1-\theta}\cdot\frac{29\epsilon}{20}-\frac{7\epsilon}{4} \!>\!\frac{1 - 2\theta}{1\!-\theta}A_{0}^{(n)}-A_{1}^{(n)}-\frac{16\epsilon}{5}. $$

Resorting to the proof of [19, Theorem 2.2 (III)], we have

$$ \frac{1-2\theta}{1-\theta}A_{0}^{(n)}-A_{1}^{(n)} >\left\{ \begin{array}{lll} &J_{1}^{(n)}+b_{1}^{(n)}\quad \quad&\text{for}\ n=2,\\ &J_{1}^{(n)}-\rho_{n-2}b_{2}^{(n)}+b_{1}^{(n)}\quad \quad \quad&\text{for}\ n\geq 3. \end{array} \right. $$

By means of Lemma 3.2 (ii)–(iii) with k = n − 2, it is easy to check

$$ J_{1}^{(n)}=\frac{\rho_{n-2}^{3}}{2(1+\rho_{n-2})}J_{1}^{(n)}+\frac{2+2\rho_{n-2}-\rho_{n-2}^{3}}{2(1+\rho_{n-2})}J_{1}^{(n)} \geq \rho_{n-2}b_{2}^{(n)}+\frac{13}{40}J_{1}^{(n)}, $$

where M1 and $\frac {2+2x-x^{3}}{2(1+x)}\geq \frac {13}{40}$ for $x\in (0,\frac {3}{2}]$ were used. Then, it follows that

$$ \begin{array}{@{}rcl@{}} J_{1}^{(n)}-\rho_{n-2}b_{2}^{(n)}+b_{1}^{(n)}-\frac{16\epsilon}{5} &\geq& \frac{13 + 33\rho_{n-1}}{20\rho_{n-1}}b_{1}^{(n)}-\frac{16\epsilon}{5}\\ &\geq& \frac{(13 + 33\rho_{n-1})\tau_{n-1}}{120(1+\rho_{n-1})}\varpi_{n}^{\prime\prime}(t_{n-2})-\frac{16\epsilon}{5}, \end{array} $$

where Lemma 3.2 (ii) with k = n − 1 and (3.13) were used. Under the conditions of Lemma 3.3, one has $\epsilon \leq \epsilon _{n-1}=\frac {\alpha (1+5\rho _{n-1})\tau _{n-1}}{105T}\omega _{1-\alpha }(T)$. This together with M1 leads to

$$ J_{1}^{(n)}-\rho_{n-2}b_{2}^{(n)}+b_{1}^{(n)}-\frac{16\epsilon}{5} > \frac{\alpha (13 + 33\rho_{n-1})\tau_{n-1}}{120(1+\rho_{n-1})T}\omega_{1-\alpha}(T) -\frac{16\epsilon}{5}>0. $$

Overall, for n ≥ 2, we have $\frac {1-2\theta }{1-\theta }\textsf {A}_{0}^{(n)}-\textsf {A}_{1}^{(n)}>0$. This completes the proof of Lemma 3.4. □

If the tolerance error $\epsilon \leq \min \limits \{\epsilon ^{*}, \epsilon ^{**}, \min \limits _{1\leq k\leq n-1}\epsilon _{k}\}$ and M1 holds, Lemmas 3.1 and 3.3 state that the discrete convolution kernels $\textsf {A}_{n-k}^{(n)}$ satisfy the assumptions A1-A2 and have the property in Lemma 3.4. According to Lemmas 3.3 and 3.4, one has the following result.

Corollary 3.1

Under the conditions of Lemma 3.3, the fast Alikhanov formula (2.5) satisfies

$$ v^{n-\theta}(\partial_{a\tau}^{\alpha}v)^{n-\theta} \geq \frac{1}{2} \sum\limits_{k=1}^{n}\textsf{A}_{n-k}^{(n)}\triangledown_{\tau}\left( \left|{v^{k}}\right|^{2}\right)\quad\text{ for\ }1\leq n\leq N. $$

Proof

Lemma 3.3 implies that the discrete convolution kernels $\textsf {A}_{n-k}^{(n)}$ are monotone, and Lemma 3.4 shows that 𝜃⁽ⁿ⁾ ≥ 𝜃 for 1 ≤ n ≤ N, where

$$ \theta^{(1)}:=\frac{1}{2}\quad\text{and}\quad \theta^{(n)}:=\frac{\textsf{A}_{0}^{(n)}-\textsf{A}_{1}^{(n)}}{2\textsf{A}_{0}^{(n)}-\textsf{A}_{1}^{(n)}}\quad\text{ for }n\geq 2. $$

Then, the proof of [18, Lemma 4.1] leads to the claimed result. □

3.2 H ¹-norm stability

In the following analysis, we also need some results on the spatial approximation $\mathfrak {D}_{h}$. Recalling the compact difference operator, it is well-known that the matrix corresponding to $\mathcal {I}_{k}$ is a tridiagonal, real, symmetric, and positive definite matrix, and the eigenvalues are in the form of

$$ \lambda_{k,j_{k}}=\frac{5}{6}+\frac{1}{6}\cos(\frac{j_{k}\pi}{M_{k}})\quad\text{ for } 1\leq j_{k}\leq M_{k}-1,1\leq k \leq d. $$

Denote H_k is the matrix associated with the operator $\mathcal {I}_{k}^{-1}$ and $\lambda _{H_{k},j_{k}}$ represents the eigenvalues of H_k. For 1 ≤ k ≤ d, it is easy to check $1<\lambda _{H_{k},j_{k}}< \frac {3}{2}$ and

$$ \frac{3}{2}\langle{\Delta}_{h}v_{h}, v_{h}\rangle_{h}<\langle\mathfrak{D}_{h}v_{h}, v_{h}\rangle_{h}=\langle\sum\limits_{k=1}^{d}H_{k}{\delta_{k}^{2}}v_{h}, v_{h}\rangle_{h} < \langle {\Delta}_{h}v_{h}, v_{h}\rangle_{h}. $$

(3.14)

Now we establish the stability of the time-stepping scheme (1.6)–(1.8). Taking the discrete inner product of (1.6) with $2(\partial _{a\tau }^{\alpha }u_{h})^{n-\theta }$ and applying Cauchy-Schwarz inequality yield

$$ \begin{array}{@{}rcl@{}} 2\|(\partial_{a\tau}^{\alpha}u_{h})^{n-\theta}\|^{2}&=&2\langle \mathfrak{D}_{h}u_{h}^{n-\theta}, (\partial_{a\tau}^{\alpha}u_{h})^{n-\theta}\rangle_{h} +2\kappa\langle u_{h}^{n-\theta},(\partial_{a\tau}^{\alpha}u_{h})^{n-\theta} \rangle_{h}\\ &&+2\langle f^{n-\theta},(\partial_{a\tau}^{\alpha}u_{h})^{n-\theta}\rangle_{h}\\ &\leq& 2\langle \mathfrak{D}_{h}u_{h}^{n-\theta}, (\partial_{a\tau}^{\alpha}u_{h})^{n-\theta}\rangle_{h}+\kappa^{2} \|u_{h}^{n-\theta}\|^{2}\\ &&+\|f^{n-\theta}\|^{2}+2\|(\partial_{a\tau}^{\alpha}u_{h})^{n-\theta}\|^{2}. \end{array} $$

With the aids of (3.14) and embedding inequality (2.6), we apply Corollary 3.1 with $v:={\Delta }_{h}^{1/2}u_{h}$ and obtain

$$ \sum\limits_{k=1}^{n}\textsf{A}_{n-k}^{(n)}\triangledown_{\tau}({|{u_{h}^{k}}|}_{1}^{2})\leq \kappa^{2}C_{{\Omega}}{|u_{h}^{n-\theta}|}_{1}^{2}+\|f^{n-\theta}\|^{2}\quad\text{ for } 1\leq n\leq N, $$

which has the form of (1.12) with λ := κ²C_Ω, $v^{k}:=|{{u_{h}^{k}}}|_{1}^{2}$, and ηⁿ := ∥f^n−𝜃∥². Under the conditions of Lemmas 3.1 and 3.3, we see that Lemma 1.1 holds with π_A = 2. Consequently, Lemma 1.1 indicates the H¹-norm stability of the presented scheme in the following sense.

Theorem 3.1

Let the conditions of Lemmas 3.1 and 3.3 hold. If the restriction of maximum time-step $\tau \leq 1/\sqrt [\alpha ]{4\kappa ^{2}{\Gamma }(2-\alpha )C_{{\Omega }}}$, then the numerical solution ${u_{h}^{n}}$ of the scheme (1.6)–(1.8) is stable in the sense that

$$ \begin{array}{@{}rcl@{}} {\left|{u_{h}^{k}}\right|}_{1}^{2}&\le& 2E_{\alpha}\left( 6\kappa^{2}t_{n}^{\alpha} C_{{\Omega}}\right) \left( {\left|{u_{h}^{0}}\right|}_{1}^{2}+\max\limits_{1\le k\le n}\sum\limits_{j=1}^{k} \textsf{P}^{(k)}_{k-j}\|f^{j-\theta}\|^{2} \right)\\ &\le& 2E_{\alpha}\left( 6\kappa^{2}t_{n}^{\alpha} C_{{\Omega}}\right) \left( {\left|{u_{h}^{0}}\right|}_{1}^{2} + 2{\Gamma}(1 - \alpha)\max\limits_{1\le k\le n}\{t_{k}^{\alpha}\|f^{k-\theta}\|^{2}\} \right)\quad\text{ for }1\!\leq\! n\!\leq\! N. \end{array} $$

4 Global consistency analysis and convergence

4.1 Global consistency error analysis

We now proceed with the global consistency error analysis of the fast Alikhanov formula (2.5). First of all, the local consistency error of the standard Alikhanov formula on nonuniform girds in (2.1) is given (slightly simplified) from [19, Theorem 3.4].

Lemma 4.1

Let M1 holds. Assume that v ∈ C³(0,T], and there exists a positive constant C_v such that $|v^{\prime \prime \prime }(t)|\leq C_{v}(1+t^{\sigma -3})$ for 0 < t ≤ T, where σ ∈ (0,1) ∪ (1,2) is a regularity parameter. For the standard Alikhanov formula on nonuniform girds, there exist

$$ \left|{(\partial^{\alpha}_{t}v)(t_{n-\theta})-(\partial^{\alpha}_{\tau}v)^{n-\theta}}\right| \!\leq\! A_{0}^{(n)}G_{\text{loc}}^{n}+\sum\limits_{k=1}^{n-1}\left( A_{n-k-1}^{(n)} - A_{n-k}^{(n)}\right)G_{\text{his}}^{k}\quad\text{ for } 1\!\leq\! n\!\leq\! N, $$

where two quantities $G_{\text {loc}}^{n}$ and $G_{\text {his}}^{k}$ are defined as

$$ \begin{array}{@{}rcl@{}} G_{\text{loc}}^{n}&:=&\frac{3}{2}{\int}_{t_{n-1}}^{t_{n-1/2}}(\xi-t_{n-1})^{2}|v^{\prime\prime\prime}(\xi)|\mathrm{d} \xi+\frac{3\tau_{n}}{2}{\int}_{t_{n-1/2}}^{t_{n}}(t_{n}-\xi)|v^{\prime\prime\prime}(\xi)|\mathrm{d} \xi,\\ G_{\text{his}}^{k}&:=&\frac{5}{2}{\int}_{t_{k-1}}^{t_{k}}(\xi-t_{k-1})^{2}|v^{\prime\prime\prime}(\xi)|\mathrm{d} \xi+\frac{5}{2}{\int}_{t_{k}}^{t_{k+1}}(t_{k+1}-\xi)^{2}|v^{\prime\prime\prime}(\xi)|\mathrm{d} \xi. \end{array} $$

The main difference between the fast Alikhanov formula and the standard one is that the convolution kernels are approximated by SOEs with the tolerance error 𝜖. Denote $\hat {t}_{j}=\max \limits \{1,t_{j}\}$ for 1 ≤ j ≤ N. When j ≥ 2, the regularity assumptions (1.14) and (3.10) lead to

$$ \begin{array}{@{}rcl@{}} \left|{(\partial^{\alpha}_{a\tau}v)^{j-\theta}-(\partial^{\alpha}_{\tau}v)^{j-\theta}}\right| &\leq& \sum\limits_{k=1}^{j-1}|{\triangledown_{\tau}v^{k}}||{\textsf{A}_{j-k}^{(j)}-A_{j-k}^{(j)}}|\\ &\leq& \frac{7\epsilon}{4}\sum\limits_{k=1}^{j-1}{\int}_{t_{k-1}}^{t_{k}}|{v^{\prime}(\xi)}|\mathrm{d} \xi \leq \frac{C_{v}}{\sigma}t_{j-1}^{\sigma}\epsilon \leq \frac{C_{v}}{\sigma}\hat{t}_{j-1}^{2}\epsilon. \end{array} $$

From Lemma 4.1 and (3.11), we have $|{(\partial ^{\alpha }_{t}v)(t_{1-\theta })-(\partial _{\tau }^{\alpha }v)^{1-\theta }}|\leq \textsf {A}_{0}^{(1)}G_{\text {loc}}^{1}$ if j = 1, and for j ≥ 2,

$$ \begin{array}{@{}rcl@{}} \left|{(\partial^{\alpha}_{t}v)(t_{j-\theta})-(\partial_{\tau}^{\alpha}v)^{j-\theta}}\right|&\leq& \textsf{A}_{0}^{(j)}G_{\text{loc}}^{j}+\sum\limits_{k=1}^{j-1}\left( \textsf{A}_{j-k-1}^{(j)} -\textsf{A}_{j-k}^{(j)}\right)G_{\text{his}}^{k}\\ &&+ \frac{29\epsilon}{20}G_{\text{loc}}^{j}+\frac{7\epsilon}{2}\sum\limits_{k=1}^{j-1}G_{\text{his}}^{k}. \end{array} $$

In view of the regularity assumptions (1.14) and the definition of $G_{\text {loc}}^{n}$, it is not difficult to find $G_{\text {loc}}^{1}\leq C_{v}\sigma ^{-1}\tau _{1}^{\sigma }$ and $G_{\text {loc}}^{k}\leq C_{v}t_{k-1}^{\sigma -3}{\tau _{k}^{3}}$ for 2 ≤ k ≤ N. Accordingly, the regularity assumptions (1.14) and the definition of $G_{\text {his}}^{k}$ mentioned above imply that $G_{\text {his}}^{1}\leq C_{v}(\sigma ^{-1}\tau _{1}^{\sigma }+t_{1}^{\sigma -3}{\tau _{2}^{3}})$ and $G_{\text {his}}^{k}\leq C_{v}(t_{k-1}^{\sigma -3}{\tau _{k}^{3}}+t_{k}^{\sigma -3}\tau _{k+1}^{3})$ for 2 ≤ k ≤ N − 1. Hence, we have

$$ \begin{array}{@{}rcl@{}} \frac{29\epsilon}{20}G_{\text{loc}}^{j}+\frac{7\epsilon}{2}\sum\limits_{k=1}^{j-1}G_{\text{his}}^{k}&\leq& C_{h}\left( t_{j-1}^{\sigma}\epsilon+\frac{t_{1}^{\sigma}}{\sigma}\epsilon+\sum\limits_{k=2}^{j-1}(t_{k-1}^{\sigma}+ t_{k}^{\sigma})\epsilon\right)\\ &\leq& \frac{C_{v}}{\sigma}\hat{t}_{j-1}^{2}\epsilon\quad\text{ for } j\geq 2. \end{array} $$

Denote the local consistency error

$$ {\Upsilon}^{n-\theta}[v]:=(\partial^{\alpha}_{t}v)(t_{n-\theta})-(\partial^{\alpha}_{a\tau}v)^{n-\theta} $$

(4.1)

a triangle inequality leads to $|{{\Upsilon }^{1-\theta }[v]}|\leq \textsf {A}_{0}^{(1)}G_{\text {loc}}^{1}$ if j = 1, and for j ≥ 2,

$$ |{{\Upsilon}^{j-\theta}[v]}|\leq \textsf{A}_{0}^{(j)}G_{\text{loc}}^{j}+\sum\limits_{k=1}^{j-1}\left( \textsf{A}_{j-k-1}^{(j)} -\textsf{A}_{j-k}^{(j)}\right)G_{\text{his}}^{k}+\frac{C_{v}}{\sigma}\hat{t}_{j-1}^{2}\epsilon. $$

(4.2)

Multiplying the inequality (4.2) by $\textsf {P}_{n-j}^{(n)}$ and summing the index j from 1 to n, we exchange the order of summation and apply the definition (1.9) of $\textsf {P}_{n-j}^{(n)}$ to get

$$ \begin{array}{@{}rcl@{}} \sum\limits_{j=1}^{n}\textsf{P}_{n-j}^{(n)}|{{\Upsilon}^{j-\theta}[v]}|&\leq& \sum\limits_{j=1}^{n}\textsf{P}_{n-j}^{(n)} \textsf{A}_{0}^{(j)}G_{\text{loc}}^{j}+\sum\limits_{j=2}^{n}\textsf{P}_{n-j}^{(n)}\sum\limits_{k=1}^{j-1}\left( \textsf{A}_{j-k-1}^{(j)} -\textsf{A}_{j-k}^{(j)}\right)G_{\text{his}}^{k}+\frac{C_{v}\epsilon}{\sigma}\sum\limits_{j=2}^{n}\textsf{P}_{n-j}^{(n)}\hat{t}_{j-1}^{2}\\ &\leq& \sum\limits_{j=1}^{n}\textsf{P}_{n-j}^{(n)} \textsf{A}_{0}^{(j)}G_{\text{loc}}^{j}+ \sum\limits_{k=1}^{n-1}G_{\text{his}}^{k}\sum\limits_{j=k+1}^{n}\textsf{P}_{n-j}^{(n)}\left( \textsf{A}_{j-k-1}^{(j)} -\textsf{A}_{j-k}^{(j)}\right)+\frac{C_{v}\hat{t}_{n-1}^{2}\epsilon}{\sigma}\sum\limits_{j=2}^{n}\textsf{P}_{n-j}^{(n)}\\ &\leq& \sum\limits_{k=1}^{n}\textsf{P}_{n-k}^{(n)} \textsf{A}_{0}^{(k)}G_{\text{loc}}^{k}+ \sum\limits_{k=1}^{n-1}\textsf{P}_{n-k}^{(n)} \textsf{A}_{0}^{(k)}G_{\text{his}}^{k}+\frac{C_{v}}{\sigma}t_{n}^{\alpha}\hat{t}_{n-1}^{2}\epsilon. \end{array} $$

(4.3)

where (1.11) with m = 1 and π_A = 2 was used in the last step. Under the conditions of Lemma 3.1, the boundedness implies that $\textsf {A}_{0}^{(k)}\leq \frac {2}{\tau _{k}}\omega _{2-\alpha }(\tau _{k})$, $\textsf {A}_{k-2}^{(k)}\geq \frac {1}{2}\omega _{1-\alpha }(t_{k}-t_{1})$ and

$$ \frac{\textsf{A}_{0}^{(k)}}{\textsf{A}_{k-2}^{(k)}}\leq \frac{4\omega_{2-\alpha}(\tau_{k})}{\tau_{k}\omega_{1-\alpha}(t_{k}-t_{1})}\leq \frac{4}{1-\alpha}\frac{(t_{k}-t_{1})^{\alpha}}{\tau_{k}^{\alpha}}\leq \frac{C_{v}}{1-\alpha}t_{k}^{\alpha}\tau_{k}^{-\alpha}\quad\text{ for } 2\leq k\leq n\leq N. $$

Moreover, the identity (1.10) for the complementary discrete kernels $\textsf {P}_{n-j}^{(n)}$ gives

$$ \textsf{P}_{n-1}^{(n)}\textsf{A}_{0}^{(1)}\leq 1\quad\text{and}\quad \sum\limits_{k=2}^{n-1}\textsf{P}_{n-k}^{(n)}\textsf{A}_{k-2}^{(k)}\leq \sum\limits_{k=2}^{n}\textsf{P}_{n-k}^{(n)}\textsf{A}_{k-2}^{(k)}=1. $$

Then, it follows from (4.3) that

$$ \sum\limits_{j=1}^{n}\textsf{P}_{n-j}^{(n)}|{{\Upsilon}^{j-\theta}[v]}|\leq \textsf{P}_{n-1}^{(n)} \textsf{A}_{0}^{(1)}\left( G_{\text{loc}}^{1}+G_{\text{his}}^{1}\right)+\sum\limits_{k=2}^{n}\textsf{P}_{n-k}^{(n)} \textsf{A}_{0}^{(k)}G_{\text{loc}}^{k}+\sum\limits_{k=2}^{n-1}\textsf{P}_{n-k}^{(n)} \textsf{A}_{0}^{(k)}G_{\text{his}}^{k}+\frac{C_{v}}{\sigma}t_{n}^{\alpha}\hat{t}_{n-1}^{2}\epsilon. $$

The first term on the right-hand side is bounded by $C_{v}\left (\sigma ^{-1}\tau _{1}^{\sigma }+t_{1}^{\sigma -3}{\tau _{2}^{3}}\right )\leq C_{v}\frac {\tau _{1}^{\sigma }}{\sigma }$, and two terms in the middle can be bounded by

$$ \begin{array}{@{}rcl@{}} &&\frac{C_{v}}{1-\alpha}\left( \sum\limits_{k=2}^{n}\textsf{P}_{n-k}^{(n)} \textsf{A}_{k-2}^{(k)}t_{k}^{\alpha}\tau_{k}^{-\alpha}G_{\text{loc}}^{k}+\sum\limits_{k=2}^{n-1}\textsf{P}_{n-k}^{(n)} \textsf{A}_{k-2}^{(k)}t_{k}^{\alpha}\tau_{k}^{-\alpha}G_{\text{his}}^{k}\right)\\ &\leq& \frac{C_{v}}{1-\alpha}\left( \max\limits_{2\leq k\leq n}t_{k}^{\alpha}t_{k-1}^{\sigma-3}\tau_{k}^{3-\alpha}+ \max\limits_{2\leq k\leq n-1}t_{k}^{\alpha}(t_{k-1}^{\sigma-3}\tau_{k}^{3-\alpha}+t_{k}^{\sigma-3}\tau_{k+1}^{3}\tau_{k}^{-\alpha})\right)\\ &\leq& \frac{C_{v}}{1-\alpha}\max\limits_{2\leq k\leq n}t_{k}^{\alpha}t_{k-1}^{\sigma-3}{\tau_{k}^{3}}\tau_{k-1}^{-\alpha}(\rho_{k-1}^{\alpha}+1) \leq \frac{C_{v}}{1-\alpha}\max\limits_{2\leq k\leq n}t_{k}^{\alpha}t_{k-1}^{\sigma-3}{\tau_{k}^{3}}\tau_{k-1}^{-\alpha}\quad\text{ for } 2\leq n\leq N. \end{array} $$

Combining these inequalities together, one has

$$ \sum\limits_{j=1}^{n}\textsf{P}_{n-j}^{(n)}|{{\Upsilon}^{j-\theta}[v]}|\leq C_{v}\left( \frac{\tau_{1}^{\sigma}}{ \sigma}+\frac{1}{1-\alpha}\max\limits_{2\leq k\leq n}t_{k}^{\alpha}t_{k-1}^{\sigma-3}{\tau_{k}^{3}}\tau_{k-1}^{-\alpha}+ \frac{\epsilon}{\sigma}t_{n}^{\alpha}\hat{t}_{n-1}^{2}\right). $$

In conclusion, by taking the initial singularity into account, we have the following global consistency error analysis of the fast Alikhanov approximation on nonuniform meshes.

Lemma 4.2

Assume that v ∈ C³(0,T] and there exist C_v > 0 such that $|v^{\prime }(t)|\leq C_{v}(1+t^{\sigma -1})$ and $|v^{\prime \prime \prime }(t)|\leq C_{v}(1+t^{\sigma -3})$ for 0 < t ≤ T, where σ ∈ (0,1) ∪ (1,2) is a regularity parameter. Denote $\hat {t}_{n}=\max \limits \{1,t_{n}\}$. Under the conditions of Lemma 3.1, the global consistency error of the fast Alikhanov approximation (2.5) satisfies

$$ \sum\limits_{j=1}^{n}\textsf{P}_{n-j}^{(n)}|{{\Upsilon}^{j-\theta}[v]}|\leq C_{v}\left( \frac{\tau_{1}^{\sigma}}{ \sigma}+\frac{1}{1-\alpha} \max\limits_{2\leq k\leq n}t_{k}^{\alpha}t_{k-1}^{\sigma-3}{\tau_{k}^{3}}\tau_{k-1}^{-\alpha}+\frac{\epsilon}{ \sigma}t_{n}^{\alpha}\hat{t}_{n-1}^{2}\right)\quad \text{ for } 1\leq n\leq N. $$

4.2 Sharp H ¹-norm error analysis

As described in section 3.1 of [20], under the assumption of AssG, the traditional H¹-norm analysis together with the discrete Grönwall inequality in Lemma 1.1 shows the error estimate of the time-stepping scheme (1.6)–(1.8) as

$$ |{u(t_{n})-{u_{h}^{n}}}|_{1} \leq \frac{C_{u}}{\sigma(1-\alpha)}\left( \tau^{\min\{2-\alpha, \gamma(\sigma-\alpha/2)\}}+h^{4}+\epsilon\right)\quad\text{ for } 1\leq n\leq N. $$

It is obvious that a loss of theoretical accuracy $O(\tau ^{\gamma \frac {\alpha }{2}})$ exists in time under the regularity assumption (1.14), which leads to a suboptimal error estimate due to the initial singularity and the discrete convolution form. The authors utilize the time-space error splitting technique to overcome this problem (see [20] for more details). In the following analysis, an alternative two-stage error analysis is applied to establish sharp H¹-norm error estimate for the fully discrete scheme (1.6)–(1.8) under the realistic assumption of solution.

Define the continuous inner product $(v,w):={\int \limits }_{{\Omega }}v(\mathbf {x})w(\mathbf {x})\mathrm {d} \mathbf {x}$ with the associated L²-norm $\|v\|_{L^{2}}:=\sqrt {(v,v)}$. Also, the H¹ semi-norm is defined as $|{v}|_{{H}^{1}}:=\sqrt {(-{\Delta } v, v)}$. It is easy to check $\|v\|_{L^{2}}\leq C_{{\Omega }}|{v}|_{H^{1}}$ via the embedding inequality. Additionally, we have $|{v}|_{1}\leq C_{{\Omega }}|{v}|_{H^{1}}$ by using the Cauchy-Schwarz inequality.

Stage 1: Temporal error analysis for time-discrete system We apply the fast Alikhanov formula (3.2) to approximate the problem (1.1)–(1.3) and obtain the time-discrete system

$$ \begin{array}{@{}rcl@{}} (D^{\alpha}_{\tau}u)^{n-\theta}&=&{\Delta} u^{n-\theta}+\kappa u^{n-\theta}+f(\mathbf{x},t_{n-\theta})\quad\text{ for } \mathbf{x} \in {\Omega} \text{ and } 1\leq n\leq N, \end{array} $$

(4.4)

$$ \begin{array}{@{}rcl@{}} u^{n}(\mathbf{x})&=&0\qquad\qquad\qquad\qquad\qquad\quad\quad \text{ for } \mathbf{x} \in \partial {\Omega} \text{ and } 1\!\leq\! n\!\leq\! N, \end{array} $$

(4.5)

$$ \begin{array}{@{}rcl@{}} u^{0}(\mathbf{x})&=&u_{0}(\mathbf{x})\qquad\qquad\qquad\qquad\quad\quad \text{ for } \mathbf{x}\in \bar{{\Omega}}. \end{array} $$

(4.6)

The existence and uniqueness of the solution uⁿ can be proved straightforward since it is a linear elliptic problem. Denote the solution error eⁿ(x) := u(x, t_n) − uⁿ for x ∈Ω, then the governing equation reads

$$ (D^{\alpha}_{\tau}e)^{n-\theta}={\Delta} e^{n-\theta}+\kappa e^{n-\theta}+{\Upsilon}^{n-\theta}[u]+R_{\tau}^{n-\theta}, $$

(4.7)

where Υ^n−𝜃[u] is the local consistency error described in (4.1), and

$$ R_{\tau}^{n-\theta}:=(\kappa+{\Delta})[u^{n-\theta}(\mathbf{x})-u(\mathbf{x},t_{n-\theta})]\quad\text{ for } \mathbf{x} \in {\Omega}. $$

(4.8)

Taking the continuous inner product of (4.7) with −Δe^n−𝜃, we have

$$ ((D^{\alpha}_{\tau}e)^{n-\theta} ,-{\Delta} e^{n-\theta})+\|{\Delta} e^{n-\theta}\|_{L^{2}}^{2}=(\kappa e^{n-\theta},-{\Delta} e^{n-\theta})-({\Upsilon}^{n-\theta}[u],{\Delta} e^{n-\theta})-(R_{\tau}^{n-\theta},{\Delta} e^{n-\theta}). $$

In terms of the first Green formula and Cauchy-Schwarz inequality, we apply Corollary 3.1 with v := Δ^1/2e and obtain

$$ \sum\limits_{k=1}^{n}\textsf{A}_{n-k}^{(n)}\triangledown_{\tau}\left( |{e^{k}}|_{H^{1}}^{2}\right)\leq 2\kappa |{e^{n-\theta}}|_{H^{1}}^{2}+2|{e^{n-\theta}}|_{H^{1}}\left( |{{\Upsilon}^{n-\theta}[u]}|_{H^{1}} +|{R_{\tau}^{n-\theta}}|_{H^{1}}\right), $$

which takes the form of (1.13) with λ := 2κ, $v^{k}:=|{e^{k}}|_{H^{1}}$, and $\eta ^{n}:=2\left (|{{\Upsilon }^{n-\theta }[u]}|_{H^{1}}+|{R_{\tau }^{n-\theta }}|_{H^{1}}\right )$. By virtue of Lemmas 3.1 and 3.3, we see that Lemma 1.1 is satisfied with π_A = 2. Thus, under the restriction of maximum time-step size $\tau \le 1/\sqrt [\alpha ]{8\kappa {\Gamma }(2-\alpha )}$, Lemma 1.1 gives

$$ |{e^{n}}|_{H^{1}}\leq 2E_{\alpha}\left( 12\kappa t_{n}^{\alpha}\right) \max\limits_{1\le k\le n}\sum\limits_{j=1}^{k} \textsf{P}^{(k)}_{k-j}\left( |{{\Upsilon}^{j-\theta}[u]}|_{H^{1}}+|{R_{\tau}^{j-\theta}}|_{H^{1}}\right). $$

Similar to the proof of [19, Lemma 3.8], it is easy to find

$$ \sum\limits_{j=1}^{n}\textsf{P}^{(n)}_{n-j}|{R_{\tau}^{j-\theta}}|\leq C_{u}\left( \frac{\tau_{1}^{\sigma+\alpha}}{ \sigma}+t_{n}^{\alpha}\max\limits_{2\leq k\leq n}t_{k-1}^{\sigma-2}{\tau_{k}^{2}}\right)\quad\text{ for } 1\leq n\leq N. $$

(4.9)

Therefore, Lemma 4.2 and (4.9) show that

$$ |{e^{n}}|_{H^{1}}\leq C_{u}\left( \frac{\tau_{1}^{\sigma}}{\sigma}+\frac{1}{1-\alpha} \max\limits_{2\leq k\leq n}t_{k}^{\alpha}t_{k-1}^{\sigma-3}{\tau_{k}^{3}}\tau_{k-1}^{-\alpha}+t_{n}^{\alpha}\max\limits_{2\leq k\leq n}t_{k-1}^{\sigma-2}{\tau_{k}^{2}}+\frac{\epsilon}{\sigma}t_{n}^{\alpha}\hat{t}_{n-1}^{2}\right). $$

(4.10)

Stage 2: Spatial error analysis for fully discrete system Now return to the fully discrete system, which can be viewed as the spatial approximation of time-discrete system (4.4)–(4.6). Under the priori assumptions in (1.14), this system has a unique solution uⁿ ∈ H⁴(Ω) for 1 ≤ n ≤ N. Denote the solution error ${e_{h}^{n}}:=u^{n}-{u_{h}^{n}}$ for x_h ∈Ω_h, the governing equation reads

$$ (\partial_{a\tau}^{\alpha}e_{h})^{n-\theta}=\mathfrak{D}_{h}e_{h}^{n-\theta}+\kappa e_{h}^{n-\theta}+R_{s}^{n-\theta}, $$

(4.11)

where $R_{s}^{n-\theta }=(\mathfrak {D}_{h}-{\Delta })u^{n-\theta }$. By means of Taylor’s expansion with integral reminder, it is easy to check that $\|R_{s}^{n-\theta }\|\leq C_{u}h^{4}$.

Taking the discrete inner product of (4.11) with 2$(\partial _{a\tau }^{\alpha }e_{h})^{n-\theta }$, one has

$$ 2\|(\partial_{a\tau}^{\alpha}e_{h})^{n-\theta}\|^{2} -2\langle\mathfrak{D}_{h}e_{h}^{n-\theta},(\partial_{\tau}^{\alpha}e_{h})^{n-\theta}\rangle_{h} =2\langle\kappa e_{h}^{n-\theta},(\partial_{a\tau}^{\alpha}e_{h})^{n-\theta}\rangle_{h} +2\langle R_{s}^{n-\theta},(\partial_{a\tau}^{\alpha}e_{h})^{n-\theta}\rangle_{h}. $$

By means of (3.14) and the embedding inequality (2.6), we apply Corollary 3.1 with $v:={\Delta }_{h}^{1/2}e_{h}$ and obtain

$$ \sum\limits_{k=1}^{n}\textsf{A}_{n-k}^{(n)}\triangledown_{\tau}\left( |{{e_{h}^{k}}}|_{1}^{2}\right) \leq \kappa^{2}\|{e_{h}^{n-\theta}}\|^{2}+\|R_{s}^{n-\theta}\|^{2} \leq \kappa^{2}C_{{\Omega}} |{e_{h}^{n-\theta}}|_{1}^{2}+\|R_{s}^{n-\theta}\|^{2}, $$

which has the form of (1.12) with λ := κ²C_Ω, $v^{k}:=|{{e_{h}^{k}}}|_{1}^{2}$, and $\eta ^{n}=\|R_{s}^{n-\theta }\|^{2}$. Under the conditions of Lemmas 3.1 and 3.3, we see that Lemma 1.1 holds with π_A = 2. If the maximum time-step size $\tau \le 1/\sqrt [\alpha ]{4\kappa ^{2}{\Gamma }(2-\alpha )C_{{\Omega }}}$, Lemma 1.1 yields

$$ |{{e_{h}^{n}}}|_{1}\leq \sqrt{2E_{\alpha}(6\kappa^{2}C_{{\Omega}} t_{n}^{\alpha}){\Gamma}(1-\alpha)}\max\limits_{1\le k\le n}\{t_{k}^{\alpha/2}\|R_{s}^{k-\theta}\|\}\leq C_{u}t_{n}^{\alpha/2}h^{4}. $$

(4.12)

Combining (4.10) with (4.12), we utilize the triangle inequality

$$ \begin{array}{@{}rcl@{}} |{u(t_{n})-{u_{h}^{n}}}|_{1}&\leq& |{e^{n}}|_{1}+|{{e_{h}^{n}}}|_{1}\leq C_{{\Omega}}|{e^{n}}|_{H^{1}}+|{{e_{h}^{n}}}|_{1}\\ &\leq& C_{u}\left( \frac{\tau_{1}^{\sigma}}{\sigma}+\frac{1}{1-\alpha} \max\limits_{2\leq k\leq n}t_{k}^{\alpha}t_{k-1}^{\sigma-3}{\tau_{k}^{3}}\tau_{k-1}^{-\alpha}+t_{n}^{\alpha}\max\limits_{2\leq k\leq n}t_{k-1}^{\sigma-2}{\tau_{k}^{2}}+t_{n}^{\alpha/2}h^{4}+\frac{\epsilon}{\sigma}t_{n}^{\alpha}\hat{t}_{n-1}^{2}\right). \end{array} $$

Overall, we establish the convergence of the numerical solution.

Theorem 4.1

Assume that the exact solution u satisfies the regularity property in (1.14) with the parameter σ ∈ (0,1) ∪ (1,2). Let M1 holds and $\hat {t}_{n}=\max \limits \{1,t_{n}\}$ for 1 ≤ n ≤ N. Under the restriction of maximum time-step $\tau \le 1/\sqrt [\alpha ]{4\kappa \max \limits \{2, \kappa C_{{\Omega }}\}{\Gamma }(2-\alpha )}$ and the SOEs tolerance error $\epsilon \leq \min \limits \{\epsilon ^{*}, \epsilon ^{**}, \min \limits _{1\leq k\leq n-1}\epsilon _{k}\}$, the numerical solution ${u_{h}^{n}}$ is convergent with respect to the discrete H¹-norm,

$$ |{u(t_{n})-{u_{h}^{n}}}|_{1} \leq C_{u}\left( \frac{\tau_{1}^{\sigma}}{\sigma}+\frac{1}{1-\alpha}\max\limits_{2\leq k\leq n}t_{k}^{\alpha}t_{k-1}^{\sigma-3}{\tau_{k}^{3}}\tau_{k-1}^{-\alpha}+t_{n}^{\alpha}\max\limits_{2\leq k\leq n}t_{k-1}^{ \sigma-2}{\tau_{k}^{2}}+t_{n}^{\alpha/2}h^{4}+\frac{\epsilon}{\sigma}t_{n}^{\alpha}\hat{t}_{n-1}^{2}\right). $$

As mentioned in Section 1, the aforesaid analysis is applicable to a wider class of unequal time-steps satisfying M1. On the other hand, if AssG holds, one has

$$ \begin{array}{@{}rcl@{}} t_{k}^{\alpha}t_{k-1}^{\sigma-3}{\tau_{k}^{3}}\tau_{k-1}^{-\alpha}&\leq& C_{\gamma} t_{k}^{\alpha+\sigma-3}\tau_{k}^{3-\alpha} \leq C_{\gamma}t_{k}^{\alpha+\sigma-3}\tau_{k}^{3-\alpha-\beta}(\tau\min\{1,t_{k}^{1-1/\gamma}\})^{\beta}\\ &\leq& C_{\gamma}t_{k}^{\sigma-\beta/\gamma}\left( {\tau_{k}/t_{k}}\right)^{3-\alpha-\beta}\tau^{\beta} \leq C_{\gamma}t_{k}^{\max\{0,\sigma-(3-\alpha)/\gamma\}}\tau^{\beta}\quad\text{ for } 2\leq k\leq n, \end{array} $$

(4.13)

where $\beta :=\min \limits \{2,\gamma \sigma \}$. Obviously, $\tau _{1}^{\sigma }\leq C_{\gamma }\tau ^{\gamma \sigma }\leq C_{\gamma }\tau ^{\beta }$. Moreover, it is easy to check

$$ \begin{array}{@{}rcl@{}} t_{k-1}^{\sigma-2}{\tau_{k}^{2}} &\leq& C_{\gamma}t_{k}^{\sigma-2}\tau_{k}^{2-\beta}(\tau\min\{1,t_{k}^{1-1/\gamma}\})^{\beta}\\ &\leq& C_{\gamma}t_{k}^{\sigma-\beta/\gamma}\left( {\tau_{k}/t_{k}}\right)^{2-\beta}\tau^{\beta} \leq C_{\gamma}t_{k}^{\max\{0,\sigma-2/\gamma\}}\tau^{\beta}\quad\text{ for } 2\leq k\leq n. \end{array} $$

(4.14)

Then, Theorem 4.1 gives the following corollary.

Corollary 4.1

Let the conditions of Theorem 4.1 hold. If the time mesh satisfies AssG, the discrete solution ${u_{h}^{n}}$ is convergent in the sense that

$$ |{u(t_{n})-{u_{h}^{n}}}|_{1} \leq \frac{C_{u}}{\sigma(1-\alpha)}\left( \tau^{\min\{\gamma \sigma,2\}}+h^{4}+\epsilon\right)\quad\text{ for } 1\leq n\leq N. $$

It says that the optimal grading parameter γ_opt = 2/σ.

Remark 2

Actually, an alternative estimate of (4.13) can be obtained similarly

$$ t_{k}^{\alpha}t_{k-1}^{\sigma-3}{\tau_{k}^{3}}\tau_{k-1}^{-\alpha} \leq C_{\gamma} t_{k}^{\alpha+\sigma-3}\tau_{k}^{3-\alpha} \leq C_{\gamma}t_{k}^{\alpha+\sigma-3}(\tau\min\{1,t_{k}^{1-1/\gamma}\})^{3-\alpha} \leq C_{\gamma}t_{k}^{\sigma-(3-\alpha)/\gamma}\tau^{3-\alpha}. $$

This means that the fast nonuniform Alikhanov formula $(\partial _{a\tau }^{\alpha }v)^{n-\theta }$ approximates $(\partial _{t}^{\alpha }v)(t_{n-\theta })$ to order $O(\tau ^{\min \limits \{\gamma \sigma , 3-\alpha \}})$, and the optimal grading parameter γ_opt = (3 − α)/σ. However, restricted by the term (4.14) arising from $R_{\tau }^{n-\theta }$ in (4.8), the temporal convergence rate of the new scheme is to order O(τ²) if γ ≥ 2/σ.

5 Numerical examples

In this section, three examples are presented to verify the effectiveness and accuracy of the new scheme. For comparisons, we denote the numerical scheme using the standard Alikhanov (Alikhanov) approximation (2.4) as Scheme 1 in the tables, while the fully discrete scheme (1.6)–(1.8) using the accelerated Alikhanov (AccA) formula is called Scheme 2 for simplicity. To illustrate superiority of the fast algorithm, comparisons of computational cost between Scheme 1 and Scheme 2 are also indicated.

Example 1

To test the validity and accuracy of the fast Alikhanov approximation, we begin by considering a fractional ordinary differential equation $\mathcal {D}^{\alpha }_{t}u=\omega _{1+\sigma -\alpha }(t)$. The time interval is (0,1) and the exact solution is u = ω_1+σ(t) which satisfies the regularity assumptions (1.14). To trade off the accuracy and efficiency, here and in what follows, we choose 𝜖 = 10^− 12 in the simulations for the fast algorithm.

Tables 1 and 2 display the temporal error and convergence order in uniform mesh (γ = 1). Due to the lack of smoothness near the initial time, we find that all convergence orders are hard to achieve O(τ^3−α). Orders in two tables can be described as O(τ^σ) which supports the sharp error estimate in Remark 2. By comparison test, we observe that the convergence rate is improved with the increase of the regularity parameter σ. It is also in agreement with the theoretical analysis. Additionally, computational errors in two tables indicate that the accelerated formula has the same accuracy as well as the standard one.

The graded grids are employed to improve the convergence order. Tables 3, 4, and 5 list the temporal error and convergence order for σ = 0.8 in nonuniform partitions with different parameters α and γ. The effectiveness of the fast Alikhanov formula is still held in this situation due to the same temporal error between two formulas. Comparing with Table 1, it is not difficult to find that the convergence rate is increased with different γ. Numerical results in Tables 3, 4, and 5 witness the predicted time accuracy in Remark 2. Moreover, invoking to the data in three tables, one gets the optimal mesh parameter γ_opt = (3 − α)/σ which is also coincide with our analysis. All these results substantiate the validity of nonuniform meshes in resolving the initial singularity and the sharpness of error estimate in Remark 2. Also, we see that the fast Alikhanov approximation is effective no matter in uniform grid or nonuniform ones.

Table 2 Temporal error of Example 1 for different α with σ = 1.6,γ = 1

Table 3 Temporal error of Example 1 for different γ with α = 0.2,σ = 0.8

Table 4 Temporal error of Example 1 for different γ with α = 0.5,σ = 0.8

Table 5 Temporal error of Example 1 for different γ with α = 0.8,σ = 0.8

Example 2

We consider the problem (1.1)–(1.3) in Ω = (0,π)² to witness the effectiveness and accuracy of Scheme 2. Let T = 1, κ = 2, and $f=\omega _{1+\sigma -\alpha }(t){\sin \limits } x {\sin \limits } y$. The continuous problem has an exact solution $u=\omega _{1+\sigma }(t){\sin \limits } x {\sin \limits } y$ which satisfies the regularity assumptions (1.14).

Define the $L_{\infty }(H^{1})$ semi-norm solution error $e(N,h)=\max \limits _{1\leq k\leq N}|{u^{k}-{u_{h}^{k}}}|_{1}$. In numerical tests, temporal order and spatial order are investigated by supposing that e(N, h) ≈ C(τ^p + h^q) and evaluating the convergence rates $p\approx \log [e(N,h)/e(2N,h)]$ and $q\approx \log [e(N,h)/e(N,h/2)]$. To check the spatial accuracy, we choose the parameters α = 0.4,σ = 1.6 and set N = 1000 to avoid contamination of the temporal error. Spatial errors and convergence rates for both uniform partition and nonuniform ones are recorded in Table 6. We see that the spatial errors of Schemes 1 and 2 are equal and both two schemes preserve the fourth-order accuracy well. This is consistent with our predicted space accuracy in Corollary 4.1. Table 7 displays the errors and orders in time for different parameters γ with α = 0.4,σ = 1.6 and a fine mesh size h = π/200. Temporal errors of Schemes 1 and 2 remain the same which confirms the effectiveness and accuracy of the fully discrete scheme. Unfortunately, numerical results in the third part of Table 7 are different from the first two cases. The convergence rates in this part are higher than 2, maybe can reach γσ. This amusing phenomenon shows that there are certain differences between theory and experiment. It seems that the truncation error of u(t_n−𝜃) − u^n−𝜃 in (4.9) can be further enhanced at least for the coarse meshes.

Table 6 Spatial error of Example 2 for different γ with α = 0.4,σ = 1.6,N = 1000

Table 7 Temporal error of Example 2 for different γ with α = 0.4,σ = 1.6,h = π/200

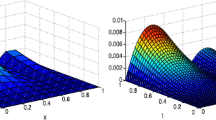
The left panel of Fig. 1 shows the errors with the parameters α = 0.5,σ = 0.5,h = π/10 at T = 1 for different γ. We can conclude that the performance of nonuniform grids is better than the uniform one. Error curves on different nonuniform partitions are indicated in the right panel. These curves illustrate that the fully discrete scheme is unconditionally stable.

Fig. 1

Error curves of the fully discrete scheme (1.6)–(1.8) for different γ in Example 2 (left); Error curves of the fully discrete scheme (1.6)–(1.8) on nonuniform meshes for different γ and h in Example 2 (right)

Since the computational cost in space had been proved in [29], we just examine the computational cost in time. Taking the parameters α = 0.6,σ = 1.6,γ = 1.5,h = π/10, and T = 1, we consider the relationship between CPU time and the time-step size N. The left panel of Fig. 2 reports the CPU time in seconds for Schemes 1 and 2 versus N. We find that the CPU time increase via the number of N is linear with the slopes of one and two in the logarithm for Scheme 2 and Scheme 1, respectively. It verifies that the new scheme is much faster than the normal one.

Fig. 2

Comparisons of computational cost between two schemes for 2D problem in Example 2 (left) and 3D problem in Example 3 (right)

Example 3

Consider the three-dimensional problems (1.1)–(1.3) in Ω = (0,π)³ and the time interval is (0,1]. Let κ = 3 and $f=\omega _{1+\sigma -\alpha }(t){\sin \limits } x {\sin \limits } y {\sin \limits } z$, so that the reaction-subdiffusion problem has an exact solution $u=\omega _{1+\sigma }(t){\sin \limits } x {\sin \limits } y {\sin \limits } z$. This solution still satisfies the regularity assumptions (1.14).

We choose the paremeters α = 0.8,σ = 0.8 and still test the temporal error and spatial error separately. For spatial accuracy, N = 1000 is taken as Example 2 to ignore the temporal error. Errors and convergence orders are reported in Table 8 by varying mesh sizes from h = π/5 to π/40. For the case of uniform partition, we observe that the errors are almost invariable when the mesh size is refined to h = π/10. This problem might be caused by too small regularity parameter σ, so that the temporal error contaminates the final data. On the contrary, numerical results of nonuniform partitions are close to the fourth-order accuracy which agrees well with our theoretical prediction. In general, the nonuniform grids outperform the uniform one for the problem with singularity solutions. Always, the same parameters are selected to check the temporal convergence rates in Table 9. We choose h = π/200 enable to avoid the errors in space and double increase the number of N. Numerical results in the first two cases maintain the theoretical analysis in Corollary 4.1 for both uniform partition and nonuniform ones. However, the third part in this table arises an interesting phenomenon similar to Example 2, namely, the convergence rate is higher than 2, approaches 3 − α.

Table 8 Spatial error of Example 3 for different γ with α = 0.8,σ = 0.8,N = 1000

Table 9 Temporal error of Example 3 for different γ with α = 0.8,σ = 0.8,h = π/200

Analogously, comparisons of error curves between two types of meshes and unconditional stability of the proposed scheme are listed in Fig. 3. In the left panel, error curve of the uniform grid is still higher than the other nonuniform ones. On the other side, the performances of error curves on different nonuniform grids illustrate the unconditionally stability of the new scheme.

Fig. 3

Error curves of the fully discrete scheme (1.6)–(1.8) for different γ in Example 3 (left); Error curves of the fully discrete scheme (1.6)–(1.8) on nonuniform meshes for different γ and h in Example 3 (right)

Comparisons of computational complexity are also reported for 3D case. CPU times with the parameters α = 0.6,σ = 1.6,h = π/10 at T = 1 and different numbers of time steps N are shown in the right panel of Fig. 2. The fast scheme has almost linear complexity in N and is much more efficient than the normal one.

In conclusion, compared with Scheme 1, the fully discrete scheme (Scheme 2) not only has the same accuracy but also reduces the computational cost and storage requirement significantly for long time calculation and spatial multi-dimensional cases.

6 Concluding remarks

By taking the intrinsically initial singularity of solution into account, an accelerated nonuniform version of Alikhanov formula is presented for approximating the Caputo fractional derivative. In the finite difference framework, we utilize the discrete sine transform and develop a second-order fast compact scheme for solving the subdiffusion problems. Unconditional stability and sharp H¹-norm error estimate are established by employing the discrete fractional Grönwall inequality and global consistency analysis. Some numerical examples are presented to support the effectiveness of this scheme and the sharpness of our analysis. The theoretical results in time approximation together with their proofs here would be also valid for some other spatial discretizations such as finite element method and spectral method.