1 Introduction

Ultra-low-power wireless sensors have a wide range of applications in mobile communication, the Internet of Things, and wearable devices. The question of obtaining a steady and sustainable green energy supply has become an important development direction for energy management. Piezoelectric vibration energy harvesting (VEH) technologies [1,2,3] have been widely investigated for their advantages of a stable output voltage, high power density, simple structure, long life expectancy, avoidance of environmental pollution, and lack of electromagnetic interference.

Conventional linear VEHs are easy to design and manufacture. However, their narrow operating band makes it difficult to match the vibration frequency of the external medium, which significantly reduces the vibration collection efficiency and the conversion efficiency of these devices. To solve this problem and to achieve an effective increase in energy harvesting efficiency, scientists will need insight into the energy harvesting mechanism of the VEH device and optimize the energy harvesting mechanisms so that the mechanical system’s linear or nonlinear structure becomes perfect [4, 5]. With the continuous deepening of research, researchers have proposed many nonlinear VEH systems with improved structures and investigated their energy harvesting mechanisms [6,7,8,9,10]. Based on these results, many structurally complex nonlinear VEH systems have been designed to improve the energy harvesting performance, such as U-shaped [11, 12], M-shaped [13], T-shaped [14], S-shaped [15], X-shaped [16] and Star-shaped [17] structures. The nonlinear bistable structure has aroused many concerns because it has characteristics and so on nonlinearity, bistability and wider frequency bandwidth, versus nonlinear monostable energy capture system. Furthermore, the researchers found through experiments that such systems can generate high-energy inter-well oscillations [18, 19], which can cause an increase in the output voltage, even under noisy excitation, and still achieve high output power [20]. However, the amplitude of a bistable VEH system can easily be trapped within a single potential well, resulting in a significant decrease in the system’s energy harvesting efficiency. Aimed at such problems, based on the nonlinear bistable VEH system, the system can achieve a stable and efficient energy output by introducing a vibro-impact mechanism [21,22,23].

Vibro-impact is a ubiquitous phenomenon in natural systems, especially in the field of mechanical vibration, and is now receiving increasing attention from experts [24, 25]. We know that vibro-impact processes between mechanical components inevitably cause local strain and energy dissipation. In order to better characterize the local deformation and energy dissipation that occurs during vibro-impact, a Hertzian-damped model [26] that differs from the conventional vibro-impact model [27, 28] has been proposed and applied to several practical problems [29,30,31,32]. Furthermore, the random environmental excitation inevitably affects the dynamic behavior of the mechanical vibration system, which inevitably affects the energy harvesting efficiency of the VEH system [33,34,35,36,37,38]. At the same time, some analysis methods combining non-smooth transforms are proposed to theoretically study the energy harvesting performance of the nonlinear VEH systems under random excitation [39,40,41,42,43,44,45,46]. Recently, several improved stochastic averaging techniques have been developed and ultimately applied to nonlinear VEH systems with non-Gaussian white noise excitation [47,48,49,50], and good results have been obtained. However, there are few studies on inelastic vibro-impact VEH systems, especially how to understand the evolution of the energy harvesting efficiency of bistable VEH systems under the combined effects of stochastic excitation and inelastic vibro-impact. Therefore, it is necessary to theoretically analyse the dynamical behavior and energy acquisition mechanism of the inelastic vibro-impact bistable VEH system under stochastic excitation to design an optimal vibro-impact bistable VEH system and apply it to engineering practice.

The manuscript studied the probabilistic response and the evolution law of the energy harvesting performance of a bistable VEH system with bilateral Hertz-damp impact constraints under colored noise excitation. In Sect. 2, a nonlinear bistable VEH model with symmetric bilateral stoppers is proposed, in which the Hertz-damp model is used to describe the inelastic impact process of the system. In Sect. 3, combining the relationship between the system’s total energy and the potential energy of the obstacle position, the analytical expressions of the probability density function (PDF), the mean square output voltage, the root mean square (RMS) voltage and the mean output power of the system are determined by the quasi-conservative averaging method, and the steady-state power conversion efficiency (PCE) of the system is derived. In Sect. 4, an example is presented to discuss the effects of the physics parameters in the model on the probabilistic response and energy harvesting performance of the system, and the validity of the proposed method is verified using Monte Carlo (MC) numerical simulations, and an optimal noise intensity is given to maximize the PCE. Conclusions follow in Sect. 5.

2 Mathematical modeling

The vibro-impact mechanism can cause the stochastic VEH system to produce a wider frequency band. This section explains the model’s stochastic control equations and the inelastic vibro-impact mechanism. By relating the potential energy at the location of the obstacle to the system’s total energy to determine whether the vibro-impact phenomenon is occurring, the period and frequency of the vibro-impact bistable VEH system are also obtained.

Fig. 1
figure 1

Simplified representation of bistable VEH model with symmetric inelastic stoppers

Full size image

2.1 Stochastic bistable system with bilateral constraints

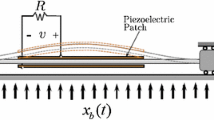
The bistable or vibro-impact energy harvesting devices can capture low-frequency energy from different external excitations. To fully exploit this advantage, a bistable magnetic repulsion harvester [18, 22, 47] with a symmetric inelastic baffle [51, 52] will be considered below, whose model can be described by a nonlinear bistable piezoelectric VEH model with symmetric inelastic stoppers. As shown in Fig. 1, the coupled motion equation is

$$\begin{aligned}{} & {} M\ddot{\bar{X}} + C\dot{\bar{X}} - {K_{1}}{\bar{X}} + {K_{2}}{{\bar{X}}^{3}} \nonumber \\ {}{} & {} \quad + f(\bar{X},\dot{\bar{X}}) I \left( |\bar{X}| - \bar{\delta _{r}} \right) +\theta \bar{V}=-M{\ddot{\bar{X}}_{b}}, \end{aligned}$$
(1a)
$$\begin{aligned}{} & {} {C_{p}}\dot{\bar{V}}+\frac{1}{R}\bar{V}=\theta \dot{\bar{X}}, \end{aligned}$$
(1b)

where \({\bar{X}}\) represents the displacement of the mass M and the dot is the differentiation with respect to time \({\bar{t}}\). C, \(K_{1}\) and \(K_{2}\) are the linear viscous damping coefficient, linear stiffness coefficient and nonlinear stiffness coefficient, respectively. \(\bar{\delta _r}\) is a position parameter that describes the equilibrium position and the fixed distance between one of the two inelastic stoppers. \(\theta \) is the linear electromechanical coupling coefficient. \(\bar{V}\) represents the output voltage across equivalent resistive load R. \({C_p}\) is the piezoelectric capacitance. \({\ddot{\bar{X}}_{b}}\) denotes the stochastic base acceleration. The function \(f (\bar{X},\dot{\bar{X}})\) represents the inelastic impact force, which describes the collision process of the bistable VEH system with either of the two inelastic baffles. \(I \left( |\bar{X}| - \bar{\delta _{r}} \right) \) is indicator function, which is applied to describe the vibro-impact effects and it can be defined as

$$\begin{aligned} I \left( |\bar{X}| - \bar{\delta _{r}} \right) = {\left\{ \begin{array}{ll} 0, &{} |\bar{X}| \le \bar{\delta _{r}}, \\ 1, &{} |\bar{X}| > \bar{\delta _{r}}. \end{array}\right. } \end{aligned}$$
(2)

We introduce now the following non-dimensional variables

$$\begin{aligned}{} & {} t=\omega _0 \bar{t},\ \ X=\frac{\bar{X}}{l_L},\ \ V=\frac{{C_p}\bar{V}}{\theta l_L},\ \ c=\frac{C}{M},\ \ \nonumber \\{} & {} {\omega _{0}}^{2}=\frac{K_{1}}{M},\ \ \kappa =\frac{K_{2}{l_L}^2}{M},\ \ \nonumber \\{} & {} \beta =\frac{\theta ^{2}}{M{C_p}},\ \ \lambda =\frac{1}{R{C_p}},\ \ f(X,\dot{X})=\frac{f(\bar{X},\dot{\bar{X}})}{M{l_{L}}},\ \ \nonumber \\{} & {} \eta (t)=-\frac{\ddot{\bar{X}}_{b}}{{l}_{L}}, \end{aligned}$$
(3)

in which \(l_L \) represents a length scale chosen to be the ratio between the area of the equivalent piezoelectric capacitor and the distance between its parallel plates. Substituting Eq. (3) into Eq. (1), we get

$$\begin{aligned}&\ddot{X}+c\dot{X}-{\omega _{0}}^{2}X+\kappa {X^{3}}+f(X, \dot{X}) I \left( |X| - \delta _{r} \right) \nonumber \\ {}&\quad + \beta V= \eta (t), \end{aligned}$$
(4a)
$$\begin{aligned}&\dot{V}+\lambda V=\dot{X}, \end{aligned}$$
(4b)

where the Hertz-damp impact constraint model [26] \(f(X, \dot{X})\) is

$$\begin{aligned} f(X,\dot{X})= K{\left( |X| - \delta _{r} \right) }^{\frac{3}{2}}\left[ 1+\frac{3\left( 1 - e^{2} \right) }{4{\dot{\delta }_{r}}^{(-1)}}\dot{X} \right] , \end{aligned}$$
(5)

in which e is restitution coefficient. K is the contact stiffness at the time of the vibro-impact, which depends on the geometry and material properties of the object composed of the vibrator and the inelastic stopper. \(\dot{\delta _{r}}^{(-1)}\) indicates the instantaneous velocity at the beginning of the contact and can be determined by \({\dot{\delta }_{r}}^{(-1)}=\sqrt{2H-2U(\delta _{r})}\). \(\eta (t) \) is the Gaussian colored noise with zero mean, and its statistical characteristics of autocorrelation function \(R(\tau ) \) and power spectral density \(S(\omega ) \) are

$$\begin{aligned} R\left( \tau \right)&=E\left[ \eta \left( t\right) \eta \left( t+\tau \right) \right] =\frac{D}{\tau _{1}}\exp \left( -\frac{\left| \tau \right| }{\tau _{1}} \right) , \end{aligned}$$
(6a)
$$\begin{aligned} S\left( \omega \right)&=\frac{1}{2\pi }\int _{-\infty }^{\infty }E\left[ \eta \left( t\right) \eta \left( t+u\right) \right] \cdot {e^{-j\omega u}}du\nonumber \\ {}&=\frac{D}{\pi \left( 1+{\omega ^{2}}\tau _{1}^{2} \right) }, \end{aligned}$$
(6b)

in which \(E\left[ \cdot \right] \) is the expectation operator. \( \tau _{1} \) is the correlation time of the noise, and D is the noise intensity. For numerical simulations, the numerical values of the physical parameters of the various components of the system listed in Table 1.

Table 1 Characteristics of the reference main structure
Full size table

Introduction of variable transformation based on the stable equilibrium points of the system [47, 53]

$$\begin{aligned} \begin{aligned}&\mathrm{{sgn}} (X- X_H^{*})\sqrt{U(X)}=\sqrt{U(X)}\cos \theta , \\&\dot{X}=-\sqrt{2H}\sin \theta , \end{aligned} \end{aligned}$$
(7)

where \(X_H^{*}\) is any stable equilibrium point of the bistable VEH system. It should be noted that the bistable VEH system has two stable equilibrium points \(X_H^{*} = \pm \tilde{X}_H \) and an unstable equilibrium point \(X_H^{*} = 0\). H(t) and U(X) are the total energy and the potential energy function of the system respectively. This transformation plays an important role in finding the relationship between the voltage and the mechanical system displacement and velocity, and their specific forms are described in Sect. 2.2. Then we introduce the total phase \(\theta \left( t\right) \) as

$$\begin{aligned} \begin{aligned} \theta \left( t\right) =\int _{0}^{t}\omega \left( H\right) ds+\phi \left( t\right) , \end{aligned} \end{aligned}$$
(8)

here \(\omega \left( H\right) \) is the system frequency dependent on energy, and \(\phi \left( t\right) \) is the residual phase. Since the second term of the total phase changes much more slowly than the first term, we can obtain the following approximation expression

$$\begin{aligned} \theta \left( t-\tau \right)&=\int _{0}^{t-\tau }{\omega _{H}}d\tau +\phi \left( t-\tau \right) \nonumber \\ {}&\approx \int _{0}^{t}{\omega _{H}}d\tau +\phi \left( t\right) -\omega \left( t\right) \tau \approx {\theta _{t}}-{\omega _H}\tau , \end{aligned}$$
(9a)
$$\begin{aligned} \dot{X}\left( t-\tau \right)&=-\sqrt{2 H}\sin \theta \left( t-\tau \right) \nonumber \\ {}&\approx {\dot{X}_{t}}\cos \left( {\omega _H}\tau \right) +\mathrm{{sgn}} \left( {X_{t}-X_H^*}\right) \nonumber \\ {}&\quad \sqrt{2{U}\left( X_{t}\right) }\sin \left( {\omega _H}\tau \right) . \end{aligned}$$
(9b)

Then using Eq. (9b) to solve Eq. (4b), one obtains

$$\begin{aligned} \begin{aligned} V\left( t\right)&=\frac{\omega \left( H\right) }{\lambda ^{2}+\omega ^{2}\left( H\right) }\mathrm{{sgn}} (X-X_H^*) \sqrt{2 U\left( X\right) }\\ {}&\quad +\frac{\lambda }{\lambda ^{2}+\omega ^{2}\left( H \right) }\dot{X}\\&=\frac{\omega ^{2}\left( H\right) }{\lambda ^{2}+\omega ^{2}\left( H\right) } (X-X_H^*)+\frac{\lambda }{\lambda ^{2}+\omega ^{2}\left( H\right) }\dot{X}. \end{aligned} \end{aligned}$$
(10)

Then substitute Eq. (5) and Eq. (10) into Eq. (4), and mark \(N_{1}(H)=\beta \lambda / (\lambda ^{2}+\omega ^{2}\left( H\right) )\), \(N_{2}(H)=\beta \omega ^{2}\left( H\right) / (\lambda ^{2}+\omega ^{2}\left( H\right) )\). The system Eq. (4) can be rewritten as follows

$$\begin{aligned} \begin{aligned} \ddot{X}+C(X)\dot{X}-{N_{2}}(H)X_{H}^{*}+u(X)=\eta (t), \end{aligned} \end{aligned}$$
(11)

where

$$\begin{aligned} C\left( X\right){} & {} = c + N_{1}(H) \nonumber \\ {}{} & {} \quad + \frac{3 K \left( 1- e^{2} \right) }{4{\dot{\delta }_{r}}^{(-1)}}{{\left( |X| - {\delta _{r}} \right) }^{\frac{3}{2}}} I\left( |X| - {\delta _{r}}\right) , \nonumber \\ u\left( X\right){} & {} = -\left( \omega _0^2 -N_2(H)\right) X \nonumber \\ {}{} & {} \quad + \kappa X^{3} {+} K \left( |X|{-}{\delta _{r}} \right) ^{\frac{3}{2}} I\left( |X| {-} \delta _{r}\right) , \end{aligned}$$
(12)

2.2 Undisturbed system

To understand the physical properties of the nonlinear bistable vibro-impact VEH system defined in Eq. (4), we will now show how to use the relation between the potential energy at the location of the obstacle and the total energy of the system to obtain the period and frequency of the system. The undamped free vibration equation of the system Eq. (11) can be written as

$$\begin{aligned} \begin{aligned} \ddot{X}+u(X)=0. \end{aligned} \end{aligned}$$
(13)

The total energy  H(t) and the potential energy function  U(X) corresponding to the system Eq. (13) are expressed as follows

$$\begin{aligned}&H(t)=\frac{1}{2}{\dot{X}^{2}}+U(X), \end{aligned}$$
(14)
$$\begin{aligned}&U(X)=\frac{1}{4}\beta {\left( X^{2}-\frac{{\omega _{0}}^{2}-{N_{2}}(H)}{\beta }\right) ^{2}}\nonumber \\ {}&\quad \quad \quad \quad +I\left( \left| X \right| -{\delta _{r}}\right) \frac{2}{5}K(\left| X \right| -{\delta _{r}})^{\frac{5}{2}}. \end{aligned}$$
(15)
Fig. 2
figure 2

The diagrams of physical characteristics for the undisturbed vibro-impact bistable system. a The relation graph of the total energy H for the system versus displacement and velocity. b The relation graph of the frequency \(\omega \) for the undisturbed system versus displacement and velocity

Full size image

It’s not hard to see that the system (13) have a unstable equilibrium point \(\left( X = 0 \right) \) and two stable equilibrium points \(\left( {\tilde{X}_{H}}= \pm \sqrt{(\omega _{0}^{2}-{N_{2}}(H))/\beta } \right) \) for an arbitrary given the total energy H. From this, the maximum displacement of the system (13) also will be determined by solving the polynomial \(U\left( X\right) - H = 0\), denoted as \(\left| {A_{H_{i}}} \right| (i=1,2)\) as the maximum displacement. By analyzing the dynamic properties of bistable system (13), there are two possible cases. The first is the vibration of system trapped in one of the single potential well, then \(H \le U\left( 0\right) \) and \(\left| {A_{H_{1}}} \right| <\left| {A_{H_{2}}} \right| \); the second is \(H > U\left( 0\right) \), then the vibration of system will cross the potential barrier and satisfy the condition \(\left| {A_{H_{1}}} \right| =\left| {A_{H_{2}}} \right| \). In addition, the existence of a collision stop leads to two possible appeals in both cases, which inevitably leads to the change of the whole period and frequency, so the period \(T_H\) of the undisturbed system (13) is determined as

$$\begin{aligned} T_{H}= {\left\{ \begin{array}{ll} 2\int _{|A_{H_{1}}|}^{|A_{H_{2}}|}{\frac{dX}{\sqrt{2H-2U(X)}}}, &{} H\leqslant U\left( 0\right) \ \mathrm{{and}} \ H< U\left( \delta _{r}\right) , \\ 2\left( \int _{|A_{H_{1}}|}^{\delta _{r}}{\frac{dX}{\sqrt{2H-2U(X)}}} +\int _{\delta _{r}}^{|A_{H_{2}}|}{\frac{dX}{\sqrt{2H-2U(X)}}}\right) , &{} H\leqslant U\left( 0\right) \ \mathrm{{and}} \ H> U\left( \delta _{r}\right) , \\ 4\int _{0}^{|A_{H_{2}}|}{\frac{dX}{\sqrt{2H-2U(X)}}}, &{} H>U\left( 0\right) \ \mathrm{{and}} \ H < U\left( \delta _{r}\right) , \\ 4\left( \int _{0}^{\delta _{r}}{\frac{dX}{\sqrt{2H-2U(X)}}}+\int _{\delta _{r}}^{|A_{H_{2}}|}{\frac{dX}{\sqrt{2H-2U(X)}}}\right) , &{} H>U\left( 0\right) \ \mathrm{{and}} \ H > U\left( \delta _{r}\right) . \end{array}\right. } \end{aligned}$$
(16)

The frequency of bistable VEH system can be obtained by

$$\begin{aligned} \begin{aligned} \omega =\frac{2\pi }{T_{H}}. \end{aligned} \end{aligned}$$
(17)

Finally, to express the variation of energy H(t) and system frequency \(\omega _H\) for displacement X and velocity \(\dot{X}\) in the undisturbed bistable system Eq. (13) more clearly, the dependencies and relationship between energy or frequency and state variables are shown Fig. 2. In addition, Fig. 3 shows the change of energy harvesting scopes of frequency and voltage response of the unperturbed conservative system Eq. (13) for the situations of collision \(K \ne 0\) and non-collision \(K \equiv 0\).

3 The analysis of probabilistic response and PCE of vibro-impact bistable VEH

In this section, the quasi-conservative stochastic averaging method is developed and apply it to the proposed stochastic nonlinear bistable vibro-impact VEH system, so as to determine the response statistics and the PCE.

3.1 Q uasi-conservative stochastic averaging method

In this study, we assume that the correlation time of the stochastic excitation (colored noise) is much smaller than the relaxation time of the VEH system, and the system have been affected by small damping and weak stochastic excitation. Substituting transformation Eq. (7) into system Eq. (11), and it can be rewritten as

$$\begin{aligned} \dot{H}={} & {} -2 H C\left( H, \theta \right) \sin ^{2}\theta -\sqrt{2H}{N_{2}}(H)X_{H}^{*}\sin \theta \nonumber \\ {}{} & {} + g_{1} \left( H,\theta \right) \eta \left( t\right) ,\nonumber \\ \dot{\phi }={} & {} -C\left( H, \theta \right) \sin \theta \cos \theta -\frac{1}{\sqrt{2H}}{N_{2}}(H)X_{H}^{*}\cos \theta \nonumber \\ {}{} & {} + g_{2} \left( H,\theta \right) \eta \left( t\right) , \end{aligned}$$
(18)

where

$$\begin{aligned} g_{1}\left( H,\theta \right) {=} {-}\sqrt{2 H}\sin \theta ,\quad g_{2}\left( H,\theta \right) {=} -\frac{1}{\sqrt{2H}}\cos \theta . \nonumber \\ \end{aligned}$$
(19)
Fig. 3
figure 3

The effects of the presence or absence of inelastic impact on the frequency response of the output voltage are shown, where the regions enclosed by the black dashed and solid red lines indicate the results in the absence and presence of the impact mechanism, respectively. (Color figure online)

Full size image

Based on the above assumptions, the total energy H is slow-varying processes and can be approximated to the Markov process, so it is efficient to use the quasi-conservative stochastic averaging method [53,54,55,56] to investigate the probabilistic response of the proposed nonlinear bistable VEH system. Applying this technology, the following averaged It\(\mathrm {\hat{o}}\) stochastic differential equation can be obtained

$$\begin{aligned} dH=m_{\tau _{1}}(t,H)dt+\sigma _{\tau _{1}}(t,H)dB(t), \end{aligned}$$
(20)

in which B(t) is the standard Brownian motion. \({m}_{\tau _{1}}(t,H)\) and \(\sigma _{\tau _{1}}(t,H)\) are the averaged drift and averaged diffusion coefficients, they can be expressed by

$$\begin{aligned} m_{\tau _{1}}\left( t,H\right){} & {} = - \left\langle 2H C\left( H, \theta \right) \sin ^{2} \theta \right\rangle _{t} \nonumber \\ {}{} & {} -\left\langle \sqrt{2H}{N_{2}}(H)X_{H}^{*}\sin \theta \right\rangle _t\nonumber \\ {}{} & {} \quad + \int _{-\infty }^{0} \left\langle g_{1}\left( t+\tau \right) \frac{\partial g_{1}\left( t\right) }{\partial H} + g_{2}\left( t+\tau \right) \frac{\partial g_{1}\left( t\right) }{\partial \phi } \right\rangle _{t}\nonumber \\ {}{} & {} \quad \quad R\left( \tau \right) d\tau \nonumber \\ {}{} & {} = - \left[ c + N_{1}(H) \right] \left\langle \dot{X}^{2} \right\rangle _{t} + N_{2}(H)X_{H}^{*}\left\langle \dot{X} \right\rangle _{t}+\pi S(\omega ) \nonumber \\ {}{} & {} \quad - \frac{3 K \left( 1- e^{2} \right) }{4{\dot{\delta }_{r}}^{(-1)}} \left\langle {\left( |X| - {\delta _{r}} \right) }^{\frac{3}{2}} \dot{X}^{2} I\left( |X| - {\delta _{r}}\right) \right\rangle _{t},\nonumber \\ \end{aligned}$$
(21)
$$\begin{aligned} \sigma _{\tau _{1}}^{2}\left( t,H\right){} & {} =\int _{-\infty }^{\infty } \left\langle g_{1} \left( t+\tau \right) g_{1}\left( t\right) \right\rangle _{t} R \left( \tau \right) d\tau \nonumber \\{} & {} = 2\pi S(\omega ) \left\langle \dot{X}^{2} \right\rangle _{t}, \end{aligned}$$
(22)

where \(\left\langle \left[ \cdot \right] \right\rangle _{t} = \int _{0}^{T_{H}} \left[ \cdot \right] dt / T_{H}\) is the time averaging of function \( \left[ \cdot \right] \) over a quasi-period \(T_{H}\). The procedure described in Eqs. (21) and (22) is called quasi-conservative stochastic averaging. According to the analysis in Sect. 2.2, the system period is associated with both the potential energy at instable point and potential energy at the collision position under the H(t) given, which will inevitable lead to \({m}_{\tau _{1}}(t,H)\) and \(\sigma _{\tau _{1}}(t,H)\) relay on the \(U\left( 0\right) \) and \(U\left( \delta _{r}\right) \). So the \(\left\langle \dot{X}^{2} \right\rangle _{t}\) and \(\left\langle {\left( |X| - {\delta _{r}} \right) }^{\frac{3}{2}} \dot{X}^{2} I\left( |X| - {\delta _{r}}\right) \right\rangle _{t}\) can be given by the following case

$$\begin{aligned}{} & {} \left\langle \dot{X}^2 \right\rangle _{t}= \frac{2}{T_H} \times {\left\{ \begin{array}{ll} \int _{A_{H_{1}}}^{A_{H_{2}}}{\sqrt{2H-2U(X)}}dX, &{} H\leqslant U(0)\ \mathrm{{and}}\ \left| {A_{H_{2}}} \right|<\delta _{r}, \\ \left( \int _{A_{H_{1}}}^{\delta _{r}}{\sqrt{2H-2U(X)}}dX +\int _{\delta _{r}}^{A_{H_{2}}}{\sqrt{2H-2U(X)}}dX\right) , &{} H\leqslant U(0)\ \mathrm{{and}}\ \left| {A_{H_{2}}} \right|>\delta _{r}, \\ 2\int _{0}^{A_{H_{2}}}{\sqrt{2H-2U(X)}}dX, &{} H>U(0)\ \mathrm{{and}}\ \left| {A_{H_{2}}} \right| <\delta _{r}, \\ 2\left( \int _{0}^{\delta _{r}}{\sqrt{2H-2U(X)}}dX+\int _{\delta _{r}}^{A_{H_{2}}}{\sqrt{2H-2U(X)}}dX\right) , &{} H>U(0)\ \mathrm{{and}}\ \left| {A_{H_{2}}} \right| >\delta _{r}. \\ \end{array}\right. }\end{aligned}$$
(23)
$$\begin{aligned}{} & {} \left\langle {\left( |X| - {\delta _{r}} \right) }^{\frac{3}{2}} \dot{X}^{2} I\left( |X| - {\delta _{r}}\right) \right\rangle _{t} \nonumber \\{} & {} \quad = \frac{2}{T_{H}} \times {\left\{ \begin{array}{ll} 0, &{} \left| {A_{H_{2}}} \right| \le {\delta _{r}},\\ \int _{\delta _r} ^{A_{H_{2}}} {\left( |X| - {\delta _{r}} \right) }^{\frac{3}{2}} \sqrt{2 \left[ H - U\left( X\right) \right] } dX, &{} H \leqslant U(0) \ and \ \left| {A_{H_{2}}} \right|>\delta _{r}, \\ 2 \int _{\delta _r} ^{A_{H_{2}}} {\left( |X| - {\delta _{r}} \right) }^{\frac{3}{2}} \sqrt{2 \left[ H - U\left( X\right) \right] } dX, &{} H>U(0) \ and \ \left| {A_{H_{2}}} \right| >\delta _{r}. \end{array}\right. } \end{aligned}$$
(24)

Finally, substituting Eqs. (23) and (24) into Eqs. (21) and (22), the averaged drift and averaged diffusion coefficients can be determined of an arbitrary given total energy H.

Fig. 4
figure 4

The effects of the different inelastic stopper constraint parameters on the stationary PDF of the system displacement responses are compared, where solid lines result from analytical solutions in Sect. 3 and symbols result from MC simulation. a The position parameter \(\delta _{r}\) are 1.0 and 1.2; b The restitution coefficient e are 0.5 and 0.9; c The contact stiffness K are 5.0 and 13.0

Full size image

3.2 The probability response statistics and PCE

The following subsection will give the analytical expressions for the probability response, mean square output voltage, RMS voltage, mean output power, and PCE of the proposed vibro-impact VEH system. Firstly, by solving the Fokker–Planck–Kolmogorov (FPK) equation corresponding to It\(\mathrm {\hat{o}}\) equation Eq. (20), one can obtain the stationary PDF \( p_{\tau _{1}}\left( H\right) \) of the energy H(t) of the system Eq. (11) [50]:

$$\begin{aligned} p_{\tau _{1}}\left( H\right) =\frac{C_{0}}{\sigma _{\tau _{1}}^{2}\left( H\right) }\exp \left[ 2\int _{0}^{H}\frac{m_{\tau _{1}}\left( \tau _{1},u \right) }{\sigma _{\tau _{1}}^{2}\left( u\right) } du \right] , \end{aligned}$$
(25)

where \(C_0\) is a normalized constant. The joint PDF of the displacement X and velocity \(\dot{X}\) is

$$\begin{aligned} p_{\tau _{1}}\left( X,\dot{X}\right) =\left. \frac{p_{\tau _{1}}\left( H\right) }{T_{H}} \right| _{H=\frac{\dot{X}^{2}}{2}+U\left( X\right) }. \end{aligned}$$
(26)

Then the marginal PDF of the displacement X and velocity \(\dot{X}\) can be written as

$$\begin{aligned} p_{\tau _{1}}\left( X\right)= & {} \int _{-\infty }^{\infty } p_{\tau _{1}} \left( X,\dot{X}\right) d\dot{X}, \nonumber \\ p_{\tau _{1}}\left( \dot{X}\right)= & {} \int _{-\infty }^{\infty } p_{\tau _{1}}\left( X,\dot{X}\right) dX. \end{aligned}$$
(27)

On the basis of Eq. (10), the expression of mean square output voltage \(E\left[ V_{\tau _{1}}^{2} \right] \) is

$$\begin{aligned} E\left[ V_{\tau _{1}}^{2}\right]{} & {} =E\left[ \left( \frac{\omega ^{2}\left( H\right) }{\lambda ^{2}{+}\omega ^{2}\left( H\right) }(X-X_H^*) {+} \frac{\lambda }{\lambda ^{2}{+}\omega ^{2}\left( H\right) }\dot{X} \right) ^{2} \right] \nonumber \\{} & {} =\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\left( \frac{\omega ^{2}\left( H\right) }{\lambda ^{2}{+}\omega ^{2}\left( H\right) }(X-X_H^*)\right. \nonumber \\{} & {} \quad \left. {+}\frac{\lambda }{\lambda ^{2}{+}\omega ^{2}\left( H\right) }\dot{X} \right) ^{2}p_{\tau _{1}}\left( X,\dot{X}\right) dX d\dot{X}, \end{aligned}$$
(28)

and the RMS voltage \(V_{\mathrm{{rms}}}\) can be obtained by

$$\begin{aligned} V_{\mathrm{{rms}}} = \sqrt{E \left[ V^{2}_{\tau _{1}}\right] }. \end{aligned}$$
(29)

Applying the linear relationship between the square voltage and power, the mean output power \( E\left[ P_{\tau _{1}}\right] \) can be written as

$$\begin{aligned} E\left[ P_{\tau _{1}}\right] = \beta \lambda E\left[ V_{\tau _{1}}^{2} \right] = \beta \lambda V_{\mathrm{{rms}}}^{2} . \end{aligned}$$
(30)

In addition, the PCE \( \eta _{\mathrm{{eff}}} \left( \%\right) \) as another physical quantity to evaluate the energy harvesting performance of a harvesting device is also used for examining the conversion of mechanical to electrical energy [57]. In order to realize theoretical analysis the PCE of the vibro-impact bistable VEH system, we first rewrite Eq. (4a) as follows:

$$\begin{aligned} \ddot{X}+\tilde{C}(X)\dot{X}+\tilde{u}(X)+\beta V=\eta (t) \end{aligned}$$
(31)

where

$$\begin{aligned}{} & {} \tilde{C}(X)=c+\frac{3K\left( 1-{e^2}\right) }{4{\dot{\delta }_r}^{(-1)}}{\left( |X|-{\delta _r} \right) ^{\frac{3}{2}}}I\left( |X|-{\delta _r} \right) \nonumber \\ \end{aligned}$$
(32a)
$$\begin{aligned}{} & {} \tilde{u}(X)=-{\omega _0}^{2}X+\kappa {X^3}+K{\left( |X|-{\delta _r} \right) ^{\frac{3}{2}}}I\left( |X|-{\delta _r} \right) \nonumber \\ \end{aligned}$$
(32b)

Multiplying Eq. (31) by the velocity \(\dot{X}\) and integrating with respect to time variable t yields

$$\begin{aligned} \int {\eta }(t)\dot{X}dt{} & {} =\,\frac{1}{2}{\dot{X}^{2}} +\int {\tilde{C}(X){\dot{X}^{2}}}dt\nonumber \\ {}{} & {} \quad +\int \tilde{u}(X)\dot{X}dt+\int {\beta }V\dot{X}dt, \end{aligned}$$
(33)

here \( \int \beta V\dot{X}dt \) represents the transferred energy of the VEH system, which corresponds to the part of mechanical energy that is converted into electrical energy. \( \int {\eta }(t)\dot{X}dt \) denotes the externally provided energy. Subsequently, multiplying both sides of Eq. (4b) by \(\beta V\) and integrating over t, the externally provided energy in steady-state operation can be rewritten as

$$\begin{aligned} \int {\eta }(t)\dot{X}dt=\int {\tilde{C}(X){\dot{X}^{2}}}dt+\int {\beta }\lambda {V^2}dt. \end{aligned}$$
(34)

Finally, the steady-state PCE of the system is

$$\begin{aligned} {\eta _{eff}}\left( \% \right)&= \frac{\int {\beta }\lambda {V^2}dt}{\int {\eta }(t)\dot{X}dt} = \frac{\int {\beta }\lambda {V^2}dt}{\int {\tilde{C}(X){\dot{X}^{2}}}dt+\int {\beta }\lambda {V^2}dt}\nonumber \\&\quad \times 100=\frac{E\left[ {W_e} \right] }{E\left[ {W_m} \right] }\times 100, \end{aligned}$$
(35)

where \( W_e \) and \( W_m \) are of the following specific form:

$$\begin{aligned} W_{e}{} & {} = \beta \lambda V^{2}_{\tau _{1}},\nonumber \\ W_{m}{} & {} = \left[ c + I\left( |X|-\delta _{r} \right) K\left( |X|-\delta _{r} \right) ^{\frac{3}{2}} \frac{3\left( 1 -e^{2}\right) }{4\dot{\delta }_{r}^{(-1)}} \right] \nonumber \\{} & {} \quad \times \dot{X}^{2}+\beta \lambda V_{\tau _{1}}^{2}. \end{aligned}$$
(36)

Substituting Eqs. (27), (28) and (36) into Eq. (35), the \( \eta _{\mathrm{{eff}}}\) will be derived. Meanwhile, by looking for the extremum condition of Eq. (35), the maximum PCE is obtained on the theory, the noise intensity D should meet the following condition

$$\begin{aligned}{} & {} \left[ c+I(\left| X \right| -{\delta _{r}})K(\left| X \right| -{\delta _{r}})^{\frac{3}{2}}\frac{3(1-{e^{2}})}{4{\dot{\delta }_{r}}^{(-1)}} \right] {\dot{X}^{2}}\cdot \frac{\partial \left( \beta \lambda {V^{2}} \right) }{\partial D}\nonumber \\{} & {} \quad =\beta \lambda {{V}^{2}}\cdot \frac{\partial \left( \left[ c+I(\left| X \right| -{{\delta }_{r}}) K{{(\left| X \right| -{{\delta }_{r}})}^{\frac{3}{2}}}\frac{3(1-{{e}^{2}})}{4{{{\dot{\delta }}}_{r}}^{(-1)}} \right] {{{\dot{X}}}^{2}} \right) }{\partial D}.\nonumber \\ \end{aligned}$$
(37)

4 Probabilistic response and harvesting performance of bistable VEH system

This section will verify the validity of the abovementioned methods with an example. The effects of the physical parameters of the VEH instance models on the probabilistic response and energy acquisition performance were analysed, and the corresponding analysis results were verified using MC simulation. Unless otherwise stated, the values of the parameters of the model have been listed in Table 1. The parameters of the colored noise are \(D=0.02\), \(\tau _{1}=0.4\).

Fig. 5
figure 5

The effects of the different colored noise parameters on the stationary PDF of the system displacement responses are compared, where solid lines result from analytical solutions in Sect. 3 and symbols result from MC simulation. a The noise intensity D are 0.03 and 0.1; b The noise correlation time \(\tau _1\) are 0.4 and 1.0

Full size image
Fig. 6
figure 6

The effects of the different constraint parameters on the evolutionary laws of mean square output voltage and mean output power are compared under two given correlation times \(\left( \tau _1 = 0.4\ \mathrm{{or}} \ 1.0\right) \), where blue and red lines result from analytical solutions in Sect. 3, and blue and red symbols result from MC simulation. a The position parameter \(\delta _{r}\) increases from 0.95 to 1.25; b the restitution coefficient e increases from 0.3 to 1.0; c the contact stiffness K increases from 5.0 to 13.0. (Color figure online)

Full size image
Fig. 7
figure 7

The evolutionary processes of mean square output voltage and mean output power with the noise intensity D rising from 0.005 to 0.125 are shown under two given correlation times \(\left( \tau _1 = 0.4\ \mathrm{{or}} \ 1.0\right) \), where blue and red lines result from analytical solutions in Sect. 3, and blue and red symbols result from MC simulation. (Color figure online)

Full size image

First, we evaluated the effect of the main parameters in the stochastic vibro-impact VEH model on the system response. Figures 4 and 5 show how the PDFs of the displacement response vary as a function of the constraint parameters (including the position parameters \(\delta _ {r}\), the restitution coefficient e and the contact stiffness K) and the noise parameters (including the noise intensity D and the correlation time \(\tau _ {1}\)); their PDFs are found to be bimodal. As shown in Fig. 4, the variables K and e are less affected by the system response than the variable \(\delta _r\). From Fig. 4a, it can be seen that the peak values of the PDF of the displacement response fall off rapidly as the parameter \(\delta _r\) increases, which indicates that the system jumps from a steady-state point to another steady-state point more frequently. However, increasing the other two variables (including e and K) did not cause any significant change in the peak PDF values, which can be seen in Fig. 4b, c. The influence of different colored noise parameters (including D and \(\tau _ {1}\)) on the PDF of the response of the system is then detailed in Fig. 5. It was found that increasing the noise parameters had a significant effect on the peak bimodal value of the PDF. They show opposed effects, namely that increasing the parameter \(\tau _{1}\) will increase the peak of the PDF of response, but increasing the parameter D decreases the peak of the PDF of response. These findings have important research significance. The lower PDF peak value of the VEH system response means that the maximum vibration displacement of the system is farther from the stable equilibrium point, and the system may have a larger vibration range, which will produce a higher energy harvesting efficiency. Thus, those parameters will inevitably result in a change in energy harvesting efficiency.

Fig. 8
figure 8

The effects of the different coupling parameters of the system on mean square output voltage and mean output power are shown under two given correlation times \(\left( \tau _1 = 0.4\ \mathrm{{or}} \ 1.0\right) \), where blue and red lines result from analytical solutions in Sect. 3, and blue and red symbols result from MC simulation. a The parameter \(\lambda \) increases from 0.03 to 0.09; b The linear electromechanical coupling coefficient \(\beta \) increases from 0.3 to 0.95. (Color figure online)

Full size image
Fig. 9
figure 9

The effects of the three different constraint physical parameters on PCE with the noise intensity D increasing from 0.005 to 0.125 are shown. a The position parameter \(\delta _{r}\) are 1.1, 1.2 and 1.3; b the restitution coefficient e are 0.4, 0.7 and 1.0; c the contact stiffness K are 1.0, 7.0 and 13.0

Full size image
Fig. 10
figure 10

The effects of the three different constraint physical parameters on PCE with the correlation time \(\tau _1\) increasing from 0.1 to 1.1 are shown. a The position parameter \(\delta _{r}\) are 1.1, 1.2 and 1.3; b the restitution coefficient e are 0.4, 0.7 and 1.0; c the contact stiffness K are 1.0, 7.0 and 13.0

Full size image

Secondly, for any given correlation time of colored noise, the effects of different constraint parameters and noise intensities on the evolution patterns of mean square output voltage \(E\left[ V_{\tau _{1}}^{2}\right] \) and mean output power \(E\left[ P_{\tau _{1}}\right] \) are shown in Figs. 6 and 7, respectively. We find that increasing \(\delta _r\), e and D will result in both mean square output and mean output power increasing simultaneously, but the trends caused by \(\delta _r\) and D are more significant in comparison. However, for another parameter K, it has a different effect on the mean square output and mean output power of the proposed VEH system than the previous three parameters. Subsequently, we also studied the effect of the parameters \(\beta \) and \(\lambda \) on the mean square output and mean output power of the proposed VEH system, as shown in Fig. 8. As you can see from Fig. 8a, the value of mean square output decreases gradually with increasing parameter \(\lambda \), which is contrary to the finding shown by mean output power. Thus, the parameter \(\lambda \) has the opposite impact on mean square output and mean output power. Figure 8b shows that increasing the coefficient \(\beta \) would improve the mean square output and mean output power indicators. In parallel, we also studied the effect of \(\tau _ 1\) on the mean square output voltage and mean output power of the system, as shown in Figs. 6, 7 and 8. In comparison, we observed that mean square output and mean output power decreased with increasing \(\tau _1\).

Finally, to further understand the effects of the constraint parameters of the proposed model and the colored noise on energy harvesting performance, we choose the PCE as a physical quantity to evaluate the energy harvesting performance, and the influence laws are shown in Figs. 9 and 10. As shown in Fig. 9, the trajectory of the PCE curve is a downward parabola, indicating that there is an optimal noise intensity to maximize PCE, which is given by Eq. (37). Next, how another physical quantity of the colored noise (correlation time \(\tau _1\)) affects the PCE of the system under different constraint parameters is studied and shown in Fig. 10. It was found that increases in parameters \(\tau _1\) and K were detrimental to PCE, and increases in parameters \(\delta _r\) and e promoted PCE. The results of the above analysis provide further evidence of the influence of the system’s physical parameters on the stochastic response and energy harvesting performance. On the other hand, the theoretical analysis results are in good agreement with the numerical MC simulation, which validates the method of analysis proposed in this work.

5 Conclution

The main purpose of this paper is to explore the theoretical analysis of the stochastic response and harvesting performance of a bistable VEH system with bilateral Hertz-damp vibro-impact under the excitation of colored noise.

First, the system is transformed into two first-order stochastic differential equations using a transformation method from the equilibrium points of the bistable vibro-impact VEH system. Combined with the relation between the system’s total energy and the potential energy of the obstacle’s position, the Itô equation is derived using the quasi-conservative stochastic averaging method. The energy harvesting performance indexes, such as system response, mean square output voltage, RMS voltage, mean output power, and PCE, were obtained by solving the FPK equation corresponding to the Itô equation. Finally, the effectiveness of the proposed method is verified by an example. The effects of the stochastic bistable vibro-impact VEH system’s physical parameters on system response and collection performance are simultaneously investigated in detail, and the corresponding conclusions are given.

Theoretical analysis shows that increasing the position parameters \(\delta _r\), the restitution coefficient e, and the noise intensity D will decrease the peak value of the PDF of the displacement response, which will contribute to improved mean square output and mean output power, as well as improved energy harvesting performance. In contrast, the effects of the parameter K and the noise correlation time \(\tau _1\) on the mean square output and mean output power are the opposite of the previous parameters. It means that parameters K and \(\tau _1\) are not conducive to improved energy harvesting performance. Furthermore, we also explore the effects of the coupling parameters \(\lambda \) and the electromechanical coupling coefficient \(\beta \) on the mean square output and mean output power. We find that the mean square output will gradually decrease, and the MPO will gradually increase as the \(\lambda \) increases. On the other hand, an increase in \(\beta \) will increase both the mean square output and MPO.

In studying the PCE as a performance indicator of energy capture, we constructed a relationship between the noise intensity D and the optimal PCE for the system. In addition, we found that the PCE trend is inversely related to the noise correlation time \(\tau _1\). Next, we discussed the effects of Hertz-damp impact constraint parameters on the PCE and found that increased location parameter \(\delta _r\) and the restitution coefficient e, promoted the PCE. However, parameter K has the opposite effect on PCE as parameters \(\delta _r\) and e.

Finally, all the analysis results agree with the MC simulation results. The study results in this paper have significance for the engineering practice of the vibro-impact bistable VEH system with inelastic impact.