1 Introduction

Rotor systems, no matter how precisely designed, cannot avoid system faults due to machining and assembly errors. These faults include unbalances, bowed shafts, and fatigue cracks. Residual shaft bow can be caused by various reasons. For example, static bending can occur when heavy horizontal rotor systems remain nonrotating for extended periods. The amplitude of the force generated by the shaft bow is proportional to the size of the bow of the rotor, not the rotational speed of the rotor. Also, when rotor systems pass through resonance points, oscillations with large amplitudes occur as an intrinsic property of the system. It is a well-known fact that several nonlinearities depend on displacement in a system. It is natural to have an accurate understanding of the vibration characteristics of the system only when the effects of these nonlinearities are comprehensively considered. In particular, in systems with initial faults, accurately studying the response characteristics of these faults and combinations of various nonlinearities poses an important problem in the dynamic analysis of rotor systems.

Many researchers have studied the dynamic behavior of rotor systems taking into account the residual shaft bow and cubic nonlinearities of the system. Nicholas et al. investigated the effect of the residual shaft bow on the unbalance response of a Jeffcott rotor with rigid supports [1]. Flack et al. examined the dynamic behavior of a Jeffcott rotor with shaft bow and runout theoretically and experimentally [2]. Parkinson et al. investigated the synchronous whirl of a flexible shaft with an initial bend [3]. Shiau and Lee investigated the effect of the residual bow on the unbalance response characteristics of a simple supported rotor [4]. Darpe et al. investigated the dynamic behavior of rotor systems with shaft bow and transverse surface cracks [5]. Shen et al. studied the dynamic behavior of a rub-impact rotor system supported on a journal bearing [6]. Song et al. investigated the effect of the residual shaft bow on the dynamic behavior of the warped rotor through numerical simulations and experiments [7]. Chen and Kuo investigated the dynamic response of a geared rotor system with residual bow effect and translational motion [8]. Chen studied the dynamic behavior of a double-stage geared rotor system with a residual shaft bow [9]. Yang et al. investigated the dynamic behavior of rotor systems by combining initial bow, cubic nonlinearity, and rub coupling faults [10]. Saeed et al. examined the dynamic responses of asymmetric and cracked rotor systems taking into account the cubic nonlinearity of the Jeffcott rotor system [11,12,13,14]. Ri et al. analyzed the dynamic behavior of composite shaft-disk systems using the classical IHB method considering geometrical nonlinearity [15]. SFD is widely used to attenuate amplitude near resonance points. The authors have already published papers analyzing the dynamic behavior of rigid and flexible rotor systems supported on SFD using the modified IHB method [16,17,18]. Recently, many new generation devices such as magnetorheological fluid (MRF) dampers are being used in the automotive industry, and many studies are being conducted on them. Li et al. demonstrated that micro-MRF device is applicable when mechanical loading is less than 20N [19]. Versaci et al. used finite element method to study asymmetric MRF damper [20]. Sun et al. proposed a novel method to design MRF damper [21]. The studies on the dynamic behavior of system have been conducted not only in rotor systems but also in other systems. Żur et al. conducted the dynamic behavior and flutter analysis on the structures of panel, blade, shell and beam made of functionally graded graphene nanoplatelets reinforced composite (FG GPLRC) [22,23,24,25,26,27,28,29]. Kumar et al. made the dynamic analysis of the cylindrical shell structure subjected to static and time-varying radial loading [30]. Kiani et al. studied the dynamic behavior of the skew plate located in point supports [31].

All of the papers mentioned above considered the dynamic behavior near the resonance points of the system, taking into account the nonlinearities that appear in rotor systems. However, as discussed earlier, various faults such as unbalances and residual shaft bow must exist in rotor systems. Also in rotor systems there is a geometrical nonlinearity that depends on the displacements of the shaft. In rotor systems supported on SFDs, there are nonlinear forces generated by the fluid-film of the damper. The effects of these faults and each nonlinearity on the dynamic response characteristics of the system are not the same. Therefore, if only one aspect is considered when interpreting the dynamic behavior of a system, this cannot be considered an accurate method. The aim of this study is to accurately analyze the dynamic behaviors of the rotor systems with faults. In practical application, no matter how precisely the rotor systems are manufactured, there will certainly exist some faults. In order to build the mathematical model near to reality, such faults should be considered in the dynamic analysis of the system. In this paper, initial bow is considered as a fault of rotor system. The studies which investigate the dynamic behavior of system by considering even the cubic nonlinearity in the rotor system (with initial bow) supported by SFD remains unclear. Therefore, we analyzed the dynamic behavior of rotor systems by adding the effects of unbalances, shaft bow, disk weight, cubic nonlinearity, and nonlinear forces caused by the fluid-film of SFD to the equations of motion of Jeffcott rotor systems, and the effects of each factor on the system are investigated.

In Sect. 2, the equations of motion of Jeffcott rotor systems taking into account the residual shaft bow are written. This equation of motion includes the cubic nonlinearity of the system, the nonlinear forces arising from the fluid-film of the damper, and disk weight. Section 3 gives a method for calculating the nonlinear forces occurring in the fluid-film of SFD. Section 4 describes a method for solving the equation of motion of the system using the modified IHB method. Section 5 proceeds with the stability analysis of the calculated solution using the Floquet theory. Section 6 demonstrates the validity of the proposed model using the Runge–Kutta method and examines the change in the dynamic behavior of the system while changing the system parameters. In Sect. 7, the relevant conclusions are drawn based on the previous studies.

2 The equation of motion of the system

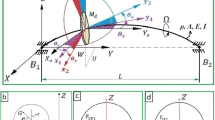
In this section, Lagrange's equation is used to construct the motion equation of system. Figure 1 shows a rotor system with an initial bow. The system is supported by SFDs on both sides of the shaft and the disk is loaded in the middle of the shaft. As can be seen from the figure, the shaft is already bent (bow) in the stationary state, and the amplitude becomes larger by the whirling motion of the shaft during rotation. In this case, the nonlinear forces related to the magnitude of the amplitude cannot be neglected in the dynamic analysis of the system.

Fig. 1
figure 1

Rotor system with an initial bow

Full size image

Figure 2 shows the relationship between global and local coordinate systems used in the dynamic analysis of the system. In the figure, O-XYZ is the global coordinate system, and O1 − X1Y1Z1 is the local coordinate system. The local coordinate system rotates with the shaft. r0 represents the size of the residual shaft bow. D is the center of mass of the disk and e is the distance between the shaft's center of rotation and the disk's center of mass. Initially, O1 and O2 are in the same position. When the shaft rotates, the rotor system receives centrifugal force due to mass eccentricity, so O1 moves to O2. In the figure, δ1 means the distance between O1 and O2. The green circle indicates the position of the disk in the rigid motion after t time from when the system starts to rotate. The blue circle indicates the position of the disk in the whirling motion after t time. The black circle is the orbit drawn by O1, the origin of the local coordinate system when the shaft rotates. Since the system considered in the paper proceeds with a synchronous whirl, the rotational speed of the shaft and the whirling frequency are the same [32]. Therefore, the phase angle β caused by the movement of the origin O1 of the local coordinate system can be expressed as follows [10].

$$ \beta = \omega t - \beta_{0} $$
(1)

where β0 is the phase angle caused by the initial shaft bow.

Fig. 2
figure 2

Relationships between global and local coordinate systems

Full size image

The equation of motion of a system can be written using Lagrange's equation [33].

$$ \frac{{{d}}}{{{{d}}t}}\left( {\frac{\partial L}{{\partial \dot{q}_{j} }}} \right) - \frac{\partial L}{{\partial q_{j} }} = Q_{j} ,\;\;\;\left( {j = 1,2, \ldots n} \right) $$
(2)
$$ L = T - U $$
(3)

Here, T is the kinetic energy of the system, and U is the strain energy of the system. \(\dot{q}\) and q denote generalized velocity and displacement. Q is the generalized external force. In the system considered in the paper, it is assumed that the shaft has no weight and the disk is rigid. Therefore, only the kinetic energy of the disk belongs to the kinetic energy of the system, and only the strain energy of the shaft belongs to the strain energy of the system. As shown in Fig. 2, the position vector OD in the global coordinate system can be written as follows.

$$ {\mathbf{OD}} = {\mathbf{OO}}_{2} + {\mathbf{O}}_{2} {\mathbf{D}} $$
(4)

If this vector is divided into X and Y directions of the global coordinate system and displayed, it can be written as follows [10].

$$ \begin{gathered} x_{D} = x + e\cos \omega t \hfill \\ y_{D} = y + e\sin \omega t \hfill \\ \end{gathered} $$
(5)

From this, the kinetic energy of the disk can be written as follows [34, 35].

$$ T = \frac{1}{2}m\dot{x}_{D}^{2} + \frac{1}{2}m\dot{y}_{D}^{2} = \frac{1}{2}m\left( {\dot{x} - e\omega \sin \omega t} \right)^{2} + \frac{1}{2}m\left( {\dot{y} + e\omega \cos \omega t} \right)^{2} $$
(6)

In the global coordinate system, the position vector OO2 can be written as follows.

$$ {\mathbf{OO}}_{{2}} {\mathbf{ = OO}}_{{1}} {\mathbf{ + O}}_{{1}} {\mathbf{O}}_{{2}} $$
(7)

If this vector is displayed in the X and Y directions of the global coordinate system in the same way as in the above, it is as follows [10].

$$ \begin{aligned} & x = x_{1} + r_{0} \cos \left( {\omega t - \beta_{0} } \right) \\ & y = y_{1} + r_{0} \sin \left( {\omega t - \beta_{0} } \right) \\ \end{aligned} $$
(8)

In Eq. (8), the displacement actually caused by the whirling motion of the shaft is x1 and y1. Therefore, δ1 can be expressed as follows [10].

$$ \delta_{1} = \sqrt {\left[ {x - r_{0} \cos \left( {\omega t - \beta_{0} } \right)} \right]^{2} + \left[ {y - r_{0} \sin \left( {\omega t - \beta_{0} } \right)} \right]^{2} } $$
(9)

The strain energy of the shaft is expressed as follows [34, 35].

$$ \begin{aligned} V & = \frac{1}{2}k\delta_{1}^{2} + \frac{1}{4}\alpha \delta_{1}^{4} = \frac{1}{2}k\left( {x - r_{0} \cos \left( {\omega t - \beta_{0} } \right)} \right)^{2} + \frac{1}{2}k\left( {y - r_{0} \sin \left( {\omega t - \beta_{0} } \right)} \right)^{2} \\ & \quad + \frac{1}{4}\alpha \left( {x - r_{0} \cos \left( {\omega t - \beta_{0} } \right)} \right)^{4} + \frac{1}{4}\alpha \left( {y - r_{0} \sin \left( {\omega t - \beta_{0} } \right)} \right)^{4} \\ & \quad + \frac{1}{2}\alpha \left( {x - r_{0} \cos \left( {\omega t - \beta_{0} } \right)} \right)^{2} \left( {y - r_{0} \sin \left( {\omega t - \beta_{0} } \right)} \right)^{2} \\ \end{aligned} $$
(10)

where α is the nonlinear stiffness coefficient. Using Lagrange's equation, the equation of motion is written as follows:

$$ \begin{aligned} & m\ddot{x} + kx = me\omega^{2} \cos \left( {\omega t} \right) + kr_{0} \cos \left( {\omega t - \beta_{0} } \right) + \alpha r_{0}^{3} \left[ {\cos^{3} \left( {\omega t - \beta_{0} } \right) + \sin^{2} \left( {\omega t - \beta_{0} } \right)\cos \left( {\omega t - \beta_{0} } \right)} \right] \\ & \quad - \alpha r_{0}^{2} \left[ {2\cos^{2} \left( {\omega t - \beta_{0} } \right)x + x + \sin \left( {2\omega t - 2\beta_{0} } \right)y} \right] - \alpha \left( {x^{3} + xy^{2} } \right) \\ & \quad + \alpha r_{0} \left[ {3\cos \left( {\omega t - \beta_{0} } \right)x^{2} + 2\sin \left( {\omega t - \beta_{0} } \right)xy + \cos \left( {\omega t - \beta_{0} } \right)y^{2} } \right] + F_{x} \\ \end{aligned} $$
(11)
$$ \begin{aligned} & m\ddot{y} + ky = me\omega^{2} \sin \left( {\omega t} \right) + kr_{0} \sin \left( {\omega t - \beta_{0} } \right) + \alpha r_{0}^{3} \left[ {\sin^{3} \left( {\omega t - \beta_{0} } \right) + \cos^{2} \left( {\omega t - \beta_{0} } \right)\sin \left( {\omega t - \beta_{0} } \right)} \right] \\ & \quad - \alpha r_{0}^{2} \left[ {\sin \left( {2\omega t - 2\beta_{0} } \right)x + 2\sin^{2} \left( {\omega t - \beta_{0} } \right)y + y} \right] - \alpha \left( {y^{3} + x^{2} y} \right) \\ & \quad + \alpha r_{0} \left[ {\sin \left( {\omega t - \beta_{0} } \right)x^{2} + 2\cos \left( {\omega t - \beta_{0} } \right)xy + 3\sin \left( {\omega t - \beta_{0} } \right)y^{2} } \right] - mg + F_{y} \\ \end{aligned} $$
(12)

where Fx and Fy are the nonlinear forces in the X and Y directions that occur in the fluid-film of the SFD. mg is the weight of the disk. To make calculations convenient, the following non-dimensional variables are introduced [16, 17].

$$ \tilde{x} = \frac{x}{c},\;\;\;\tilde{y} = \frac{y}{c},\;\;\;\tilde{e} = \frac{e}{c},\;\;\;\;\tilde{r}_{0} = \frac{{r_{0} }}{c},\;\;\;\;\tilde{t} = \omega_{0} t,\;\;\;\tilde{\Omega } = \frac{\omega }{{\omega_{0} }} $$
(13)

Here, ω0 is the natural frequency of the system and c is the radial clearance of the SFD. Putting the non-dimensional variables into Eqs. (11) and (12) and rearranging them, the following equation is obtained.

$$ \begin{aligned} & \ddot{\tilde{x}} + \tilde{x} = \tilde{e}\tilde{\Omega }^{2} \cos \left( {\tilde{\Omega }\tilde{t}} \right) + \tilde{r}_{0} \cos \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right) + \tilde{k}_{{{{NL}}}} \tilde{r}_{0}^{3} \left[ {\cos^{3} \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right) + \sin^{2} \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)\cos \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)} \right] \\ & \quad - \tilde{k}_{{{{NL}}}} \tilde{r}_{0}^{2} \left[ {2\cos^{2} \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)\tilde{x} + \tilde{x} + \sin \left( {2\tilde{\Omega }\tilde{t} - 2\beta_{0} } \right)\tilde{y}} \right] - \tilde{k}_{{{{NL}}}} \left( {\tilde{x}^{3} + \tilde{x}\tilde{y}^{2} } \right) + \\ & \quad + \tilde{k}_{{{{NL}}}} \tilde{r}_{0} \left[ {3\cos \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)\tilde{x}^{2} + 2\sin \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)\tilde{x}\tilde{y} + \cos \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)\tilde{y}^{2} } \right] + \tilde{F}_{x} \\ \end{aligned} $$
(14)
$$ \begin{aligned} & \ddot{\tilde{y}} + \tilde{y} = \tilde{e}\tilde{\Omega }^{2} \sin \left( {\tilde{\Omega }\tilde{t}} \right) + \tilde{r}_{0} \sin \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right) + \tilde{k}_{{{{NL}}}} \tilde{r}_{0}^{3} \left[ {\sin^{3} \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right) + \cos^{2} \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)\sin \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)} \right] \\ & \quad - \tilde{k}_{{{{NL}}}} \tilde{r}_{0}^{2} \left[ {\sin \left( {2\tilde{\Omega }\tilde{t} - 2\beta_{0} } \right)\tilde{x} + 2\sin^{2} \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)\tilde{y} + \tilde{y}} \right] - \tilde{k}_{{{{NL}}}} \left( {\tilde{y}^{3} + \tilde{x}^{2} \tilde{y}} \right) \\ & \quad + \tilde{k}_{{{{NL}}}} \tilde{r}_{0} \left[ {\sin \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)\tilde{x}^{2} + 2\cos \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)\tilde{x}\tilde{y} + 3\sin \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)\tilde{y}^{2} } \right] - \tilde{g} + \tilde{F}_{y} \\ \end{aligned} $$
(15)

Here, \(\tilde{k}_{{{{NL}}}} = \frac{{\alpha c^{2} }}{{\omega_{0}^{2} m}},\;\;\;\tilde{g} = \frac{g}{{\omega_{0}^{2} c}}\). The equation of motion of the system is expressed in matrix form as follows.

$$ {\mathbf{M\ddot{q}}} + {\mathbf{Kq}} = \tilde{e}\tilde{\Omega }^{2} {\mathbf{F}}_{u} + \tilde{r}_{0} {\mathbf{F}}_{1} + \tilde{k}_{{NL}} \tilde{r}_{0}^{3} {\mathbf{F}}_{2} - \tilde{k}_{{NL}} \tilde{r}_{0}^{2} {\mathbf{F}}_{3} - \tilde{k}_{{NL}} {\mathbf{F}}_{4} + \tilde{k}_{{NL}} \tilde{r}_{0} {\mathbf{F}}_{5} - \tilde{g}{\mathbf{G}} + {\mathbf{F}}_{{sdf}} $$
(16)
$$ {\mathbf{M}} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right]\;\;\;{\mathbf{K}} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right]\;\;\;{\mathbf{F}}_{u} = \left[ {\begin{array}{*{20}c} {\cos \left( {\tilde{\Omega }\tilde{t}} \right)} \\ {\sin \left( {\tilde{\Omega }\tilde{t}} \right)} \\ \end{array} } \right]\;\;\;{\mathbf{F}}_{1} = \left[ {\begin{array}{*{20}c} {\cos \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)} \\ {\sin \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)} \\ \end{array} } \right] $$
(17)
$$ {\mathbf{F}}_{2} = \left[ {\begin{array}{*{20}c} {\cos^{3} \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right) + \sin^{2} \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)\cos \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)} \\ {\sin^{3} \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right) + \cos^{2} \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)\sin \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)} \\ \end{array} } \right] $$
(18)
$$ {\mathbf{F}}_{3} = \left[ {\begin{array}{*{20}c} {{2}\cos^{2} \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)\tilde{x} + \tilde{x} + \sin \left( {{2}\tilde{\Omega }\tilde{t} - {2}\beta_{0} } \right)\tilde{y}} \\ {\sin \left( {{2}\tilde{\Omega }\tilde{t} - {2}\beta_{0} } \right)\tilde{x} + {2}\sin^{2} \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)\tilde{y} + \tilde{y}} \\ \end{array} } \right]\;\;\;{\mathbf{F}}_{4} = \left[ {\begin{array}{*{20}c} {\tilde{x}^{3} + \tilde{x}\tilde{y}^{2} } \\ {\tilde{y}^{3} + \tilde{x}^{2} \tilde{y}} \\ \end{array} } \right] $$
(19)
$$ {\mathbf{F}}_{5} = \left[ {\begin{array}{*{20}c} {3\cos \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)\tilde{x}^{2} + 2\sin \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)\tilde{x}\tilde{y} + \cos \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)\tilde{y}^{2} } \\ {\sin \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)\tilde{x}^{2} + 2\cos \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)\tilde{x}\tilde{y} + 3\sin \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)\tilde{y}^{2} } \\ \end{array} } \right] $$
(20)
$$ {\mathbf{G}} = \left[ {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \right]\;\;\;{\mathbf{F}}_{{{{sdf}}}} = \left[ {\begin{array}{*{20}c} {\tilde{F}_{x} } \\ {\tilde{F}_{y} } \\ \end{array} } \right]\;\;\;{\mathbf{q}} = \left[ {\begin{array}{*{20}c} {\tilde{x}} \\ {\tilde{y}} \\ \end{array} } \right] $$
(21)

In the system equation of motion (16), all other items except for the nonlinear forces caused by the fluid-film are known. In the next section, we introduce the method for calculating \(\tilde{F}_{x}\) and \(\tilde{F}_{y}\).

3 Calculation of nonlinear forces occurring in fluid-film in SFD

In this section, a methodology is described for the calculation of nonlinear forces occurred in the fluid-film of SFD. The method for calculating the nonlinear forces generated in the fluid-film of the damper has been introduced in many papers [36,37,38,39,40,41,42]. Since these contents are also introduced in our papers 16–18, they are briefly introduced to avoid duplication.

In SFD, the Navier–Stokes equations are simplified using the following assumptions [16,17,18].

  1. 1.

    The change in pressure through the film is very small, so ignore it.

  2. 2.

    Flow in circumferential and axial directions is basic.

  3. 3.

    Flow is incompressible and laminar.

  4. 4.

    Flow is steady.

  5. 5.

    The velocity component through the film is much smaller than the velocity component in the axial and circumferential directions.

  6. 6.

    The effect of fluid inertia can be ignored.

We can simplify the Navier–Stokes equations by applying the above assumptions and then applying the boundary conditions to obtain the Reynolds equation in fluid lubrication. The pressure distribution at the damper can be obtained from the Reynolds equation. Nonlinear forces occurring in the fluid-film of the damper are calculated by integrating this pressure distribution over the entire surface of the damper. For detailed information on this calculation process, please refer to the literature [16]. The nonlinear forces occurring in the fluid-film are expressed as follows [16].

$$ F_{r} = - \frac{{\mu RL^{3} }}{{c^{2} }}\left( {I_{1} \dot{\varepsilon } + I_{2} \varepsilon \dot{\phi }} \right) $$
(22)
$$ F_{t} = - \frac{{\mu RL^{3} }}{{c^{2} }}\left( {I_{2} \dot{\varepsilon } + I_{3} \varepsilon \dot{\phi }} \right) $$
(23)

Fr and Ft are the forces in the r and t directions in the rotating coordinate system (Fig. 3).μ is the fluid dynamic viscosity, and L and R are the length and radius of the damper. \(\varepsilon\) and \(\dot{\varepsilon }\) are the displacement and velocity in the r direction. \(\dot{\phi }\) is the angular velocity of the line OSOJ in Fig. 3. I1, I2, and I3 are denoted as [17].

$$ I_{1} = \int\limits_{{\theta_{1} }}^{{\theta_{1} + \pi }} {\frac{{\cos^{2} \theta }}{{\left( {1 + \varepsilon \cos \theta } \right)^{3} }}{{d}}\theta } ,\;\;\;I_{2} = \int\limits_{{\theta_{1} }}^{{\theta_{1} + \pi }} {\frac{\sin \theta \cos \theta }{{\left( {1 + \varepsilon \cos \theta } \right)^{3} }}{{d}}\theta } ,\;\;\;I_{3} = \int\limits_{{\theta_{1} }}^{{\theta_{1} + \pi }} {\frac{{\sin^{2} \theta }}{{\left( {1 + \varepsilon \cos \theta } \right)^{3} }}{{d}}\theta } $$
(24)
$$ \theta_{1} = \tan^{ - 1} \left( { - \frac{{\dot{\varepsilon }}}{{\varepsilon \dot{\phi }}}} \right) $$
(25)

θ1 is where the positive pressure region begins. Since the equations of motion of the system are written in a global coordinate system, these nonlinear forces must also be written in this coordinate system. This force can be expressed in the global coordinate system as follows [18].

$$ F_{x} = F_{r} \cos \phi - F_{t} \sin \phi $$
(26)
$$ F_{y} = F_{r} \sin \phi + F_{t} \cos \phi $$
(27)
Fig. 3
figure 3

The relationship between the global coordinate system and the rotating coordinate system

Full size image

In order to conveniently proceed with the calculation, non-dimensional variables are introduced in Eq. (13). Using these parameters, we can express the nonlinear forces in the fluid-film as follows [16].

$$ \tilde{F}_{x} = - \tilde{B}\left[ {\left( {\tilde{I}_{1} \dot{\tilde{\varepsilon }} + \tilde{I}_{2} \tilde{\varepsilon }\dot{\tilde{\phi }}} \right)\;\cos \tilde{\phi } + \left( {\tilde{I}_{2} \dot{\tilde{\varepsilon }} + \tilde{I}_{3} \tilde{\varepsilon }\dot{\tilde{\phi }}} \right)\sin \tilde{\phi }} \right] $$
(28)
$$ F_{y} = - \tilde{B}\left[ {\left( {\tilde{I}_{1} \dot{\tilde{\varepsilon }} + \tilde{I}_{2} \tilde{\varepsilon }\dot{\tilde{\phi }}} \right)\sin \tilde{\phi } - \left( {\tilde{I}_{2} \dot{\tilde{\varepsilon }} + \tilde{I}_{3} \tilde{\varepsilon }\dot{\tilde{\phi }}} \right)\cos \tilde{\phi }} \right] $$
(29)

Here, \(\tilde{B} = \frac{{\mu RL^{3} }}{{m\omega_{0} c^{3} }}\). Equations (28) and (29) are the non-linear forces occurring in the fluid-film expressed by the non-dimensional variables used in the equation of motion (16) of the system. In the next section, the method for solving the system equation of motion is described.

4 The solution to the equation of motion of the system

In this section, a methodology is described to solve the motion equation of system constructed in Sect. 2. In the paper, the equation of motion of the system is solved by the IHB method. We have already published papers for analyzing the dynamic behavior of beam and rotor systems using the IHB method [15, 34, 35]. However, the classical IHB method cannot analyze the dynamic behavior of rotor systems involving nonlinear forces occurring in the fluid-film of the SFD. Therefore, the authors proposed a modified IHB method to conduct a dynamic analysis of these systems at resonance points and analyzed the dynamic behavior of rotor systems supported by SFD using this method [16,17,18]. The equation of motion (16) of the system is solved by combining the classical IHB method and the modified IHB method. Of course, these equations can be solved using only the modified IHB method, but the classical IHB method is used together to reduce the amount of computation during iterative calculations. The nonlinear forces generated in the fluid-film are calculated using the modified IHB method, and the calculation of the remaining items is performed by the classical IHB method. The coupling between the two methods is achieved using a transformation matrix. Specific explanations of these methods are briefly described here because they are described in the articles published by the authors.

If it is set as \(\tau { = }\tilde{\Omega }\tilde{t}\), then the equation of motion of the system is written as follows.

$$ \tilde{\Omega }^{2} {\mathbf{Mq^{\prime\prime}}} + {\mathbf{Kq}} = \tilde{e}\tilde{\Omega }^{2} {\mathbf{F}}_{u} + \tilde{r}_{0} {\mathbf{F}}_{1} + \tilde{k}_{{{{NL}}}} \tilde{r}_{0}^{3} {\mathbf{F}}_{2} - \tilde{k}_{{{{NL}}}} \tilde{r}_{0}^{2} {\mathbf{F}}_{3} - \tilde{k}_{{{{NL}}}} {\mathbf{F}}_{4} + \tilde{k}_{{{{NL}}}} \tilde{r}_{0} {\mathbf{F}}_{5} - \tilde{g}{\mathbf{G}} + \tilde{\Omega }{\mathbf{F}}_{{{{sdf}}}} $$
(30)

In the IHB method, the iterative calculation proceeds by processing the residual. The residual for solving the equation of motion of the system is as follows.

$$ {\overline{\mathbf{R}}} = \tilde{e}\tilde{\Omega }_{{0}}^{{2}} {\overline{\mathbf{F}}}_{u} + \tilde{r}_{0} {\overline{\mathbf{F}}}_{1} + \tilde{k}_{{{{NL}}}} \tilde{r}_{0}^{3} {\overline{\mathbf{F}}}_{2} - \tilde{k}_{{{{NL}}}} \tilde{r}_{0}^{2} {\overline{\mathbf{F}}}_{3} - \tilde{k}_{{{{NL}}}} {\overline{\mathbf{F}}}_{4} + \tilde{k}_{{{{NL}}}} \tilde{r}_{0} {\overline{\mathbf{F}}}_{5} - \tilde{g}{\overline{\mathbf{G}}} + \tilde{\Omega }_{{0}} {\overline{\mathbf{F}}}_{{{{sdf}}}} - \left( {\tilde{\Omega }_{{0}}^{{2}} {\overline{\mathbf{M}}} + {\overline{\mathbf{K}}}} \right){\mathbf{A}} $$
(31)
$$ {\overline{\mathbf{M}}} = \int\limits_{0}^{2\pi } {{\mathbf{S}}^{T} {\mathbf{M}}} {\mathbf{S^{\prime\prime}}}{{d}}\tau ,\;\;{\overline{\mathbf{K}}} = \int\limits_{0}^{2\pi } {{\mathbf{S}}^{T} {\mathbf{K}}} {\mathbf{S}}{{d}}\tau ,\;\;{\overline{\mathbf{F}}}_{u} = \int\limits_{0}^{2\pi } {{\mathbf{S}}^{T} } {\mathbf{F}}_{u} {{d}}\tau ,\;\;{\overline{\mathbf{F}}}_{1} = \int\limits_{0}^{2\pi } {{\mathbf{S}}^{T} } {\mathbf{F}}_{1} {{d}}\tau ,\;\;{\overline{\mathbf{F}}}_{2} = \int\limits_{0}^{2\pi } {{\mathbf{S}}^{T} } {\mathbf{F}}_{2} {{d}}\tau $$
(32)
$$ {\overline{\mathbf{F}}}_{3} = \int\limits_{0}^{2\pi } {{\mathbf{S}}^{T} } {\mathbf{F}}_{3} {{d}}\tau ,\;\;{\overline{\mathbf{F}}}_{4} = \int\limits_{0}^{2\pi } {{\mathbf{S}}^{T} } {\mathbf{F}}_{4} {{d}}\tau ,\;\;{\overline{\mathbf{F}}}_{5} = \int\limits_{0}^{2\pi } {{\mathbf{S}}^{T} } {\mathbf{F}}_{5} {{d}}\tau ,\;\;{\overline{\mathbf{G}}} = \int\limits_{0}^{2\pi } {{\mathbf{S}}^{T} } {\mathbf{G}}{{d}}\tau ,\;\;{\overline{\mathbf{F}}}_{{{\text{sfd}}}} = {\mathbf{TF}}_{{{\text{sfd}}}}^{f} $$
(33)

Here, S and \({\mathbf{S^{\prime\prime}}}\) is expressed as follows.

$$ {\mathbf{S}}{ = }\left[ {\begin{array}{*{20}c} {1} & {0} & {{\text{c}}\tau } & {0} & {{\text{s}}\tau } & {0} & {{\text{c2}}\tau } & {0} & \cdots & {{\text{s3}}\tau } & {0} & {{\text{c4}}\tau } & {0} & {{\text{s4}}\tau } & {0} \\ {0} & {1} & {0} & {{\text{c}}\tau } & {0} & {{\text{s}}\tau } & {0} & {{\text{c2}}\tau } & \cdots & {0} & {{\text{s3}}\tau } & {0} & {{\text{c4}}\tau } & {0} & {{\text{s4}}\tau } \\ \end{array} } \right] $$
(34)
$$ {\mathbf{S^{\prime\prime}}}{ = }\left[ {\begin{array}{*{20}c} 0 & 0 & { - {\text{c}}\tau } & 0 & { - {\text{s}}\tau } & \cdots & 0 & { - {\text{16c4}}\tau } & 0 & { - {\text{16s4}}\tau } & 0 \\ 0 & 0 & 0 & { - {\text{c}}\tau } & 0 & \cdots & { - 9{\text{s3}}\tau } & 0 & { - {\text{16c4}}\tau } & 0 & { - {\text{16s4}}\tau } \\ \end{array} } \right] $$
(35)
$$ {\mathbf{A }}{ = }\left[ {\begin{array}{*{20}c} {a_{{{10}}} } & {a_{{{20}}} } & {a_{{{11}}} } & {a_{{{21}}} } & {b_{{{11}}} } & {b_{{{21}}} } & {a_{{{12}}} } & {a_{{{22}}} } & {b_{{{12}}} } & {b_{{{22}}} } & {a_{{{13}}} } & {a_{{{23}}} } & {b_{{{13}}} } & {b_{{{23}}} } & {a_{{{14}}} } & {a_{{{24}}} } & {b_{{{14}}} } & {b_{{{24}}} } \\ \end{array} } \right]^{T} $$
(36)

cτ means cos(τ), sτ means sin(τ), c2τ means cos(2τ), and s2τ means sin(2τ) ···. T is the transformation matrix and is expressed as follows [16,17,18].

$$ {\mathbf{T}} = \int\limits_{0}^{2\pi } {{\mathbf{S}}^{T} {\mathbf{S}}} {{d}}\tau $$
(37)

Fsfd and \({\mathbf{F}}_{{{\text{sfd}}}}^{f}\) has the following relationship [16,17,18].

$$ {\mathbf{F}}_{{{\text{sfd}}}} = \sum\limits_{k = 1}^{5} {c_{j,k - 1} \cos \left( {k - 1} \right)} \tau + \sum\limits_{p = 1}^{4} {d_{j,k - 1} \sin \left( {k\tau } \right)} = {\mathbf{SF}}_{{{\text{sfd}}}}^{f} $$
(38)
$$ {\mathbf{F}}_{{{\text{sfd}}}}^{f} = \left[ {\begin{array}{*{20}c} {c_{{{10}}} } & {c_{{{20}}} } & {c_{{{11}}} } & {c_{{{21}}} } & {d_{{{11}}} } & {d_{{{21}}} } & {c_{{{12}}} } & {c_{{{22}}} } & {d_{{{12}}} } & {d_{{{22}}} } & {c_{{{13}}} } & {c_{{{23}}} } & {d_{{{13}}} } & {d_{{{23}}} } & {c_{{{14}}} } & {c_{{{24}}} } & {d_{{{14}}} } & {d_{{{24}}} } \\ \end{array} } \right]^{T} $$
(39)

Here, j can have values of 1 and 2. 1 means the X-direction, and 2 means the Y-direction. Equation (38) means that f in the frequency domain can be obtained by performing Fourier transformation on Fsfd in the time domain.

In Eq. (31), \({\overline{\mathbf{M}}},\;{\overline{\mathbf{K}}},\;{\overline{\mathbf{F}}}_{u} ,\;{\overline{\mathbf{F}}}_{1} ,\;{\overline{\mathbf{F}}}_{2}\) and \({\overline{\mathbf{G}}}\) do not change during iterative calculations. For a detailed expression of these matrices, refer to the literature 17. However, \({\overline{\mathbf{F}}}_{3} ,\;{\overline{\mathbf{F}}}_{4} ,\;{\overline{\mathbf{F}}}_{5}\) and \({\overline{\mathbf{F}}}_{{{\text{sfd}}}}\) must be recalculated at every iteration step because they change according to the change in column vector A. An algorithm for solving the equations of motion of a system is presented in the literature [16,17,18]. In this algorithm, MATLAB's library function fsolve is used. In this function, the Jacobian matrix of the residual is used to find the next solution in the iteration step. This Jacobian matrix can be written as follows.

$$ \frac{{\partial {\overline{\mathbf{R}}}}}{{\partial {\mathbf{P}}}} = \tilde{e}\frac{{\partial \tilde{\Omega }_{0}^{2} {\overline{\mathbf{F}}}_{u} }}{{\partial {\mathbf{P}}}} - \tilde{k}_{{{{NL}}}} \tilde{r}_{0}^{2} \frac{{\partial {\overline{\mathbf{F}}}_{3} }}{{\partial {\mathbf{P}}}} - \tilde{k}_{{{{NL}}}} \frac{{\partial {\overline{\mathbf{F}}}_{4} }}{{\partial {\mathbf{P}}}} + \tilde{k}_{{{{NL}}}} \tilde{r}_{0} \frac{{\partial {\overline{\mathbf{F}}}_{5} }}{{\partial {\mathbf{P}}}} + \frac{{\partial \tilde{\Omega }_{0} {\overline{\mathbf{F}}}_{{{{sdf}}}} }}{{\partial {\mathbf{P}}}} - \frac{{\partial \left( {\tilde{\Omega }_{0}^{2} {\overline{\mathbf{M}}} + {\overline{\mathbf{K}}}} \right){\mathbf{A}}}}{{\partial {\mathbf{P}}}} $$
(40)
$$ {\mathbf{P}} = \left[ {\begin{array}{*{20}c} {\mathbf{A}} & {\tilde{\Omega }_{0} } \\ \end{array} } \right] $$
(41)

Also in Eq. (40), \(\frac{{\partial {\overline{\mathbf{F}}}_{3} }}{{\partial {\mathbf{P}}}}{,}\;\frac{{\partial {\overline{\mathbf{F}}}_{4} }}{{\partial {\mathbf{P}}}}{,}\;\frac{{\partial {\overline{\mathbf{F}}}_{5} }}{{\partial {\mathbf{P}}}}\) and \(\frac{{\partial \tilde{\Omega }_{0} {\overline{\mathbf{F}}}_{{{{sdf}}}} }}{{\partial {\mathbf{P}}}}\) have to be recalculated at every iteration step because they depend on the change in column vector A. Specific expressions of \(\frac{{\partial \tilde{\Omega }_{0}^{2} {\overline{\mathbf{M}}\mathbf{A}}}}{{\partial {\mathbf{P}}}}\), \(\frac{{\partial {\overline{\mathbf{K}}\mathbf{A}}}}{{\partial {\mathbf{P}}}}\), \(\frac{{\partial \tilde{\Omega }_{0}^{2} {\overline{\mathbf{F}}}_{u} }}{{\partial {\mathbf{P}}}}\) and \(\frac{{\partial \tilde{\Omega }_{0} {\overline{\mathbf{F}}}_{{{{sdf}}}} }}{{\partial {\mathbf{P}}}}\) can be referred to in the literature [17]. The calculation of \(\frac{{\partial {\overline{\mathbf{F}}}_{3} }}{{\partial {\mathbf{P}}}}{,}\;\frac{{\partial {\overline{\mathbf{F}}}_{4} }}{{\partial {\mathbf{P}}}}\) and \(\frac{{\partial {\overline{\mathbf{F}}}_{5} }}{{\partial {\mathbf{P}}}}\) is clear from the definition of \({\overline{\mathbf{F}}}_{3} ,\;{\overline{\mathbf{F}}}_{4}\) and \({\overline{\mathbf{F}}}_{5}\) shown in Eq. (33), so we will not describe it. If it is difficult to calculate the Jacobian matrix of the equation in the fsolve function, this matrix can be approximated using finite differences [43]. However, if this method is used, the calculation time is long and it may not be possible to calculate the Jacobian matrix near the resonance points. Therefore, to solve equations faster and more accurately, you must use analytical derivatives.

5 Stability analysis of the calculated solution

In this section, the stability analysis of the solutions calculated in Sect. 4 is made. Among the solutions of nonlinear vibration equations, there are stable and unstable solutions. Of these solutions, only stable solutions can be realized in reality. In the paper, stability analysis of the calculated solutions is performed using Floquet theory. The authors have already presented papers for stability analysis in rotor systems using Floquet theory [16,17,18, 35]. Therefore, only the changed contents are briefly described here.

Assume that the system has a small perturbation Δq. In this case, the displacement of the system can be written as follows [16].

$$ {\mathbf{q}} = {\mathbf{q}}_{0} + \Delta {\mathbf{q}} $$
(42)

Putting Eq. (42) into Eq. (30) gives Eq. (43).

$$ \tilde{\Omega }^{2} {\mathbf{M}}\Delta {\mathbf{q^{\prime\prime}}} + {\mathbf{K}}\Delta {\mathbf{q}} = - \tilde{k}_{{{{NL}}}} \tilde{r}_{0}^{2} \Delta {\mathbf{F}}_{3} - \tilde{k}_{{{{NL}}}} \Delta {\mathbf{F}}_{4} + \tilde{k}_{{{{NL}}}} \tilde{r}_{0} \Delta {\mathbf{F}}_{5} + \tilde{\Omega }\Delta {\mathbf{F}}_{{{{sdf}}}} $$
(43)
$$ \Delta {\mathbf{F}}_{3} { = }\left[ {\begin{array}{*{20}c} {{2}\cos^{2} \left( {\tau - \beta_{0} } \right){ + 1}} & {\sin \left( {{2}\tau - {2}\beta_{0} } \right)} \\ {\sin \left( {{2}\tilde{\Omega }\tilde{t} - {2}\beta_{0} } \right)} & {{2}\sin^{2} \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right){ + 1}} \\ \end{array} } \right]\;\;\;\Delta {\mathbf{F}}_{4} = \left[ {\begin{array}{*{20}c} {{3}\tilde{x}^{{2}} { + }\tilde{y}^{2} } & {{2}\tilde{x}\tilde{y}} \\ {{2}\tilde{x}\tilde{y}} & {{3}\tilde{y}^{{2}} + \tilde{x}^{2} } \\ \end{array} } \right] $$
(44)
$$ \Delta {\mathbf{F}}_{{5}} = \left[ {\begin{array}{*{20}c} {6\cos \left( {\tau - \beta_{0} } \right)\tilde{x} + 2\sin \left( {\tau - \beta_{0} } \right)\tilde{y}} & {2\sin \left( {\tau - \beta_{0} } \right)\tilde{x} + 2\cos \left( {\tau - \beta_{0} } \right)\tilde{y}} \\ {2\sin \left( {\tau - \beta_{0} } \right)\tilde{x} + 2\cos \left( {\tau - \beta_{0} } \right)\tilde{y}} & {2\cos \left( {\tau - \beta_{0} } \right)\tilde{x} + 6\sin \left( {\tau - \beta_{0} } \right)\tilde{y}} \\ \end{array} } \right] $$
(45)
$$ \Delta {\mathbf{F}}_{{{{sdf}}}} { = }\frac{{\partial {\mathbf{F}}_{{{{sdf}}}} }}{{\partial {\mathbf{q}}}}\Delta {\mathbf{q}} + \frac{{\partial {\mathbf{F}}_{{{{sdf}}}} }}{{\partial {\mathbf{q^{\prime}}}}}\Delta {\mathbf{q^{\prime}}} $$
(46)

If we write Eq. (43) using the state space form, it is as follows [16].

$$ {\mathbf{X^{\prime}}} = {\mathbf{Q}}\left( \tau \right){\mathbf{X}} $$
(47)
$$ {\mathbf{X}} = \left[ {\begin{array}{*{20}c} {\Delta {\mathbf{q}}} & {\Delta {\mathbf{q^{\prime}}}} \\ \end{array} } \right]^{T} ,\;\;{\mathbf{Q}} = \left[ {\begin{array}{*{20}c} {\mathbf{0}} & {\mathbf{I}} \\ {{\mathbf{Q}}_{21} } & {{\mathbf{Q}}_{22} } \\ \end{array} } \right] $$
(48)
$$ {\mathbf{Q}}_{21} = - \frac{1}{{\tilde{\Omega }^{2} }}{\mathbf{M}}^{ - 1} \left( {{\mathbf{K}} + \tilde{k}_{{{{NL}}}} \tilde{r}_{0}^{2} \Delta {\mathbf{F}}_{3} + \tilde{k}_{{{{NL}}}} \Delta {\mathbf{F}}_{4} - \tilde{k}_{{{{NL}}}} \tilde{r}_{0} \Delta {\mathbf{F}}_{5} - \tilde{\Omega }\frac{{\partial {\mathbf{F}}_{{{{sdf}}}} }}{{\partial {\mathbf{q}}}}} \right),\;\;\;{\mathbf{Q}}_{22} = \frac{1}{{\tilde{\Omega }}}{\mathbf{M}}^{ - 1} \frac{{\partial {\mathbf{F}}_{{{{sdf}}}} }}{{\partial {\mathbf{q^{\prime}}}}} $$
(49)

Since the processing for Eq. (47) is specifically described in the literature 42, it is omitted here. The description of the Floquet theory is also omitted because it is specifically introduced in the literature [44] published by the authors.

6 Results and discussion

In this section, the effectiveness of the model proposed in this paper is evaluated at first, and then the dynamic characteristic of the system is investigated according to the changes of parameters. In order to prove the validity of the proposed solution method, the results calculated using the solution method introduced in Sect. 4 are compared with the results calculated using the Runge–Kutta method (Fig. 4). When calculating using the IHB method, the amplitude of the amplitude is calculated as follows [16].

$$ a = \sqrt {a_{11}^{2} + b_{11}^{2} } $$
(50)
Fig. 4
figure 4

Comparison of the results calculated using the proposed method and the Runge–Kutta method

Full size image

The parameters of the system are \(\tilde{e} = 0.1, \, \;\tilde{B} = 0.01,\; \, \tilde{k}_{{{{NL}}}} = 1.0,\; \, \tilde{g} = 0.0\), and the responses of the system are compared by changing the residual shaft bow \(\tilde{r}_{0}\) to 0.1, 0.2, and 0.3. In the figure, the solid lines are stable solutions and the dotted lines are unstable solutions. The black circles are solutions calculated using the Runge–Kutta method, and the other colored circles indicate where saddle-node bifurcations occur. Saddle-node bifurcations occur when a Floquet multiplier leaves the unit circle through + 1 [44]. A library function of Matlab, ode45, is a function embodying Runge–Kutta method, which is used to calculate the response of system. In the present paper, this function is used to achieve a numerical integration on the following formula.

$$ \begin{aligned} & \frac{{{{d}}\tilde{x}_{1} }}{{{{d}}\tilde{t}}} = \tilde{x}_{2} \\ & \frac{{{{d}}\tilde{x}_{2} }}{{{{d}}\tilde{t}}} = - \tilde{x}_{1} + \tilde{e}\tilde{\Omega }^{2} \cos \left( {\tilde{\Omega }\tilde{t}} \right) + \tilde{r}_{0} \cos \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right) + \tilde{k}_{{{{NL}}}} \tilde{r}_{0}^{3} \left[ {\cos^{3} \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right) + \sin^{2} \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)\cos \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)} \right] \\ & - \tilde{k}_{{{{NL}}}} \tilde{r}_{0}^{2} \left[ {2\cos^{2} \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)\tilde{x}_{1} + \tilde{x}_{1} + \sin \left( {2\tilde{\Omega }\tilde{t} - 2\beta_{0} } \right)\tilde{y}} \right] - \tilde{k}_{{{{NL}}}} \left( {\tilde{x}_{1}^{3} + \tilde{x}_{1} \tilde{y}_{1}^{2} } \right) \\ & + \tilde{k}_{{{{NL}}}} \tilde{r}_{0} \left[ {3\cos \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)\tilde{x}_{1}^{2} + 2\sin \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)\tilde{x}_{1} \tilde{y}_{1} + \cos \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)\tilde{y}^{2} } \right] + \tilde{F}_{x} \\ \end{aligned} $$
(51)
$$ \begin{aligned} & \frac{{{{d}}\tilde{y}_{1} }}{{{{d}}\tilde{t}}} = \tilde{y}_{2} \\ & \frac{{{{d}}\tilde{y}_{2} }}{{{{d}}\tilde{t}}} = - \tilde{y}_{1} + \tilde{e}\tilde{\Omega }^{2} \sin \left( {\tilde{\Omega }\tilde{t}} \right) + \tilde{r}_{0} \sin \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right) + \tilde{k}_{{{{NL}}}} \tilde{r}_{0}^{3} \left[ {\sin^{3} \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right) + \cos^{2} \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)\sin \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)} \right] \\ & - \tilde{k}_{{{{NL}}}} \tilde{r}_{0}^{2} \left[ {\sin \left( {2\tilde{\Omega }\tilde{t} - 2\beta_{0} } \right)\tilde{x}_{1} + 2\sin^{2} \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)\tilde{y}_{1} + \tilde{y}_{1} } \right] - \tilde{k}_{{{{NL}}}} \left( {\tilde{y}_{1}^{3} + \tilde{x}_{1}^{2} \tilde{y}_{1} } \right) \\ & + \tilde{k}_{{{{NL}}}} \tilde{r}_{0} \left[ {\sin \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)\tilde{x}_{1}^{2} + 2\cos \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)\tilde{x}_{1} \tilde{y}_{1} + 3\sin \left( {\tilde{\Omega }\tilde{t} - \beta_{0} } \right)\tilde{y}_{1}^{2} } \right] - \tilde{g} + \tilde{F}_{y} \\ \end{aligned} $$
(52)

where \(\tilde{x} = \tilde{x}_{1} ,\;\;\;\frac{{{{d}}\tilde{x}}}{{{{d}}\tilde{t}}} = \tilde{x}_{2} ,\;\tilde{y} = \tilde{y}_{1} ,\;\;\;\frac{{{{d}}\tilde{y}}}{{{{d}}\tilde{t}}} = \tilde{y}_{2}\). In other words, Eqs. (51) and (52) are derived from Eqs. (14) and (15), respectively.

As can be seen from the figure, the results calculated using the two methods are completely consistent. In Fig. 5, the dynamic responses of the system are considered while changing the parameter indicating the damping ability of the SFD. In this case, the parameters of the system are \(\tilde{e} = 0.1{, }\;\tilde{r}_{0} = 0.0{, }\;\tilde{k}_{{{{NL}}}} = 0.0{, }\;\tilde{g} = 0.0\). This means that there is no residual shaft bow in the system and neither the cubic nonlinearity nor the mass of the disk is taken into account. In other words, there are only nonlinear forces generated by the fluid-film of the SFD in this system. As can be seen in the figure, all solutions are stable and in other cases, saddle-node bifurcations can be seen in the system. Also, as the value increases, the damping ability of the SFD increases, so it can be seen that the amplitude of the amplitude decreases at the resonance points. In Fig. 6, the response characteristics of the system are considered while changing the cubic nonlinearity of the system.

Fig. 5
figure 5

Response characteristics when changing the damping ability of SFD

Full size image
Fig. 6
figure 6

Changes in response characteristics according to changes in \(\tilde{k}_{{{{NL}}}}\)

Full size image

In this case, the parameters of the system are \(\tilde{e} = 0.1{, }\;\tilde{B} = 0.0{,}\; \, \tilde{r}_{0} = 0.0{,}\; \, \tilde{g} = 0.0\). This means that there is no residual shaft bow in the system and the mass of the disk is not taken into account. It also means that the rotor system is simply supported, not by SFD.

As can be seen from the figure, it can be seen that the system is more inclined to the right as the cubic nonlinearity coefficient increases.

Figures 7, 8 and 9 show the response characteristics when the system parameter is fixed \(\tilde{e} = 0.1{, }\;\tilde{r}_{0} = 0.{0,}\;\;\tilde{g} = 0.0\) and \(\tilde{B}\) is changed to 0.005, 0.01, and 0.05. That is, there are only cubic nonlinearity and nonlinear forces due to fluid-film in the system. In Fig. 7, the damping capacity of SFD is the smallest, and in Fig. 9, the damping capacity is the largest.

Fig. 7
figure 7

Response characteristics when \(\tilde{B} = 0.{005}\)

Full size image
Fig. 8
figure 8

Response characteristics when \(\tilde{B} = 0.{01}\)

Full size image
Fig. 9
figure 9

Response characteristics when \(\tilde{B} = 0.{05}\)

Full size image

From the figures, it can be seen that the response of the system is determined by the relative magnitude of \(\tilde{B}\) and \(\tilde{k}_{{{{NL}}}}\). In other words, it can be seen that as the size of \(\tilde{B}\) is relatively small, the system response approaches the response when only cubic nonlinearity is considered, and in the opposite case, it approaches the response when only nonlinear forces due to the fluid-film are considered.. That is, as the coefficient of cubic nonlinearity increases, it is inclined to the right more strongly, but as the value of \(\tilde{B}\) is increased, it is inclined weakly. An increase in the coefficient of cubic nonlinearity means an increase in the ratio of shaft length to diameter. In other words, as this ratio increases, the response of the system at resonance points depends a lot on cubic nonlinearity, but as this ratio decreases, it is more related to nonlinear forces generated by the fluid-film of the SFD. This shows that the analysis of the dynamic response of the system should be carried out by comprehensively considering the nonlinearity that may occur in the system. In the stability analysis in this case, only saddle-node bifurcations occurred as in the previous analysis. In Figs. 7 and 8, unstable solutions exist in all cases. However, in Fig. 9, it can be seen that only stable solutions exist when the coefficient of cubic nonlinearity is 0, but unstable solutions occur when this coefficient increases. This is also a reason to comprehensively consider all nonlinearities in the dynamic analysis of the system. In other words, when the nonlinearities existing in the system are comprehensively considered, it can be seen that not only the response characteristics but also the properties of the solution are changed compared to when only one type of nonlinearity is considered. Figure 10 shows the response characteristics when the residual shaft bow is changed to 0.0, 0.1, 0.2, and 0.3 when the system parameter is \(\tilde{e} = 0.1{,}\; \, \tilde{B} = 0.005{,}\; \, \tilde{k}_{{{{NL}}}} = 1.5{,}\; \, \tilde{g} = 0.{0}\). As can be seen from the figure, it can be seen that the amplitude at the resonance points increases as the initial bow increases. It can also be seen that there are stable and unstable solutions in all cases, and only saddle-node bifurcations occur.

Fig. 10
figure 10

Changes in response characteristics according to the size of the residual shaft bow (\(\tilde{B} = 0.005\))

Full size image

Figures 11 and 12 show the change in response characteristics when the system parameters are the same as in the case of Fig. 10, and only the damping capacity of the SFD is changed to 0.01 and 0.05.

Fig. 11
figure 11

Changes in response characteristics according to the size of the residual shaft bow (\(\tilde{B} = 0.0{1}\))

Full size image
Fig. 12
figure 12

Changes in response characteristics according to the size of the residual shaft bow (\(\tilde{B} = 0.05\))

Full size image

Even in these cases, it can be seen that there is little change in the form in the response characteristics of the system, and only the magnitude of the amplitude increases as the initial bow increases. It can also be seen that only saddle-node bifurcations occur as in the case of Fig. 10.

The cases considered so far are cases where the mass of the disk is ignored. Therefore, since the response characteristics in the X and Y directions are the same, only the displacements in the X direction are considered. However, when the mass of the disk is considered, the displacements in these two directions are not the same. Figure 13 shows the changes in response characteristics in the X and Y directions when the system parameters are fixed to \(\tilde{e} = 0.1{, }\;\tilde{B} = 0.01{,}\; \, \tilde{r}_{0} = 0.2{,}\; \, \tilde{g} = 0.3\), and \(\tilde{k}_{{{{NL}}}}\) changed to 0.5, 1.0, and 1.5. As can be seen from the figure, the change in displacement in the two directions is different, and it can be seen that the stability analysis is also different from the case discussed earlier. In all of the previous cases, only saddle-node bifurcations occurred. The square markers in Fig. 13 indicate that period-doubling bifurcations occur. These bifurcations occur when a Floquet multiplier leaves the unit circle through -1 [44]. If the weight of the disk is not taken into account when performing the analysis, the existence of this bifurcation will not be known, and an error will occur. This is because period-2 motion occurs at the location where this bifurcation occurs. Since the present study analyzes period-1 motion, it is not possible to know the exact magnitude of the amplitude in the frequency–response curve. An interpretation of this motion can be found in the literature [18]. Therefore, the mass of the disk must be considered when performing the dynamics of horizontally placed rotor systems.

Fig. 13
figure 13

Changes in response characteristics according to changes in \(\tilde{k}_{{{{NL}}}}\)

Full size image

Figure 14 shows the response characteristics when the system parameters are fixed as \(\tilde{e} = 0.1{, }\;\tilde{B} = 0.01,\; \, \tilde{k}_{{{{NL}}}} = 1,\; \, \tilde{g} = 0.3\), and the residual shaft bow is changed. As shown in the figure, it can be seen that period-doubling bifurcations also occur at this time. As mentioned above, since only period-1 motion is considered in the present study, the exact magnitude of the amplitude cannot be known at the locations where these bifurcations occur. However, using the Runge–Kutta method, a set of properties can be known. Therefore, using this method, the time histories, Poincaré sections, and orbits of the disk's center of mass calculated in the case of \(\tilde{\Omega } = 0.9\) and \(\tilde{\Omega } = {2}{\text{.4}}\) in the response characteristics shown in Fig. 14 are shown below.

Fig. 14
figure 14

Changes in response characteristics according to changes in \(\tilde{r}_{0}\)

Full size image

As shown in Fig. 14, the solution at \(\tilde{\Omega } = 0.9\) is stable, and the solution at \(\tilde{\Omega } = {2}{\text{.4}}\) is unstable. As shown in the results of Figs. 15, 16, 17, 18, 19 and 20 calculated using the Runge–Kutta method, period-1 motion in \(\tilde{\Omega } = 0.9\) and period-2 motion in \(\tilde{\Omega } = {2}{\text{.4}}\). All the solutions calculated using the Runge–Kutta method are stable solutions [43]. Therefore, the results shown in Figs. 18, 19 and 20 are the curves for a stable motion, which is period-2. Results calculated using the numerical integration method are highly dependent on the choice of initial values. In the paper, the initial value is selected as follows [16].

$$ {\mathbf{q}} = {\mathbf{SA}} $$
(51)
Fig. 15
figure 15

Time history (\(\tilde{\Omega } = 0.9\))

Full size image
Fig. 16
figure 16

Poincaré sections (\(\tilde{\Omega } = 0.9\))

Full size image
Fig. 17
figure 17

Disk's center of mass while orbit (\(\tilde{\Omega } = 0.9\))

Full size image
Fig. 18
figure 18

Time history (\(\tilde{\Omega } = {2}{\text{.4}}\))

Full size image
Fig. 19
figure 19

Poincaré sections (\(\tilde{\Omega } = {2}{\text{.4}}\))

Full size image
Fig. 20
figure 20

Disk's center of mass while orbit (\(\tilde{\Omega } = {2}{\text{.4}}\))

Full size image

S can be seen in Eq. (34) and is set as τ = 0. A can be seen in Eq. (36) and is a value obtained when the calculation is performed using the modified IHB method. If we take the stability analysis performed in Figs. 15, 16, 17, 18, 19 and 20 as an example, A is a solution in \(\tilde{\Omega } = 0.9\) or a solution in \(\tilde{\Omega } = {2}{\text{.4}}\).

As mentioned above, in the rotor systems with initial bow, the cubic nonlinearity of system and the nonlinear forces occurred in the fluid-film of SFD greatly affect the dynamic behavior of the system. In consideration of initial bow, amplitude becomes larger, and the influence of the cubic nonlinearity and the nonlinearity in SFD on the system changes. In addition, in consideration of disk weight, the response characteristic in X and Y axes changes. Therefore, the system faults and the nonlinearities existing in the system should be comprehensively considered to precisely analyze the dynamic characteristic of the system.

7 Conclusion

In the paper, the effect of cubic nonlinearity in rotor systems with a residual shaft bow (supported by an SFD) and nonlinear forces generated in the SFD fluid-film on the system dynamics is investigated. In addition, the effect of the initial bow and disk mass on the dynamic properties of rotor systems is investigated. The results of examining each nonlinearity individually and simultaneously show that the analysis should proceed by considering all nonlinearities simultaneously in the dynamic analysis of rotor systems. However, when the shaft length and diameter ratio are small, the model can be approximated by considering only the nonlinear forces caused by the fluid-film, and only the cubic nonlinearity when the shaft length and diameter are large. Also, the initial bow affects the displacement characteristics of the system and increases the amplitude of the response curves. The mass of the disk varies the amplitude characteristics in the X and Y directions and also changes the properties (stability aspect) of the solution. Therefore, the nonlinear sources existing in the system, faults that may appear in the system, and factors that may affect the dynamic characteristic analysis are comprehensively analyzed. It is necessary to proceed with the analysis by taking this into account to proceed with an accurate simulation.