1 Introduction

The transmission of information between neurons is carried out by sequences of spikes [1]. The differential in the charged ions’ concentration inside and outside the membrane determines a neuron’s membrane potential. When a neuron transmits information, charged ions move in and out of the cell membrane to generate an action potential. According to the Maxwell electromagnetic induction theorem, the movement of charged ions can trigger time-varying electromagnetic fields [2]. The impact of magnetic fields on information transmission to neurons can help us better understand and explore life’s mysteries.

The memristor is the fourth basic circuit element, representing the mathematical relationship between charge and flux [3]. Coexistence attractor [4,5,6], hidden attractor [7,8,9], hyperchaotic attractor [10,11,12], circular chaotic attractors [13], and other phenomena have been identified in the research of chaos based on memristor. Such complicated dynamics have been exploited to encrypt [14,15,16]. Memristors have been used in circuit elements to simulate biological synaptic functions [17,18,19]. Various types of memristors were also being proposed [20], Fractional-order memristor [21,22,23], local active memristor [24,25,26], and so on.

Inspired by the magnetic flux physical characteristics of memristor [3], Ma et al. proposed introducing magnetic flux into the neuron model [27]. HR neuron model under electromagnetic radiation in 2016 to obtain a variety of discharge modes [28]. Based on this theory, the dynamic behaviors of different neuron models under electromagnetic radiation were explored [29,30,31,32]. For example, under the stimulation of electromagnetic radiation, FHN neurons can produce hidden extreme multistability phenomena [29]. Complex hidden cluster discharge patterns can be formed when the electromagnetic induction effect is applied to HR neurons [30]. The electrical activities of neurons under the electric fields were also considered in Refs. [31, 32]. Introducing external electromagnetic radiation through an inductor coil, Ref. [33] proposed a new neuron model under the influence of time-varying electric and magnetic fields and external electromagnetic radiation. By introducing Hamiltonian energy to measure magnetic field energy, the relationship between different neuron discharge modes and energy under electromagnetic radiation was studied, such as HR neuron [34,35,36], FHN neuron [37, 38], and Izhikevich neuron [39, 40]. The researchers looked beyond the effects of electromagnetic radiation on neurons to neural networks. In Refs. [41,42,43,44], the chaotic dynamic behavior of the Hopfield neural network under the influence of external electromagnetic radiation on some neurons has been studied. The impact of different external stimuli on the chaotic dynamics of the Hopfield neural network was studied, and the energy transfer phenomenon of the neural network under other incentives was learned from the perspective of Hamiltonian energy [45]. The modulation of different kinds of external electromagnetic stimulation on the dynamics of the Newman–Watts small-world neural network model proved the feasibility of external electromagnetic stimulation in controlling the evolution of the neural network model [46].

Neurons communicate with one another via synapses [47, 48]. Neurons may also receive input from inhibitory or excitatory postsynaptic potentials. The excitatory synapse can increase firing usually, and the inhibitory synapse makes possible a reduction in neuronal firing [49]. Sometimes, increased arrival rates of inhibitory input can enhance firing rates, and increased excitatory input rates can decrease firing rates [50]. Synapses in the neurological system are classified as electrical or chemical synapses [51]. Electrical synapses convey messages to postsynaptic neurons via electric currents. Chemical synapses transmit information via neurotransmitters, which either excite or inhibit postsynaptic neurons depending on the neurotransmitter. Chemical synapses are characterized by unidirectional transmission and delay because neurotransmitters can only pass from the presynaptic membrane to the postsynaptic membrane. It would be interesting to discover another efficient method of signaling communication between neurons. In [52], scholars studied magnetic field coupling, the interaction between neuron magnetic fields, and proposed the coupling neuron model. When magnetic field coupling and electrical synaptic coupling exist in neural networks, magnetic field coupling can regulate the collective behavior of neural networks [53, 54]. In the case that magnetic field coupling, electric field coupling and synaptic coupling simultaneously act on the Newman–Watts small-world neuronal network, standard deviation and synchronization factors are introduced to provide helpful guidance for signal transmission between neurons [55]. The above studies suggest that magnetic field coupling is another way of neuron signal propagation. In [52,53,54,55], the influence of magnetic field coupling is considered. In [52, 53], it is considered that magnetic field coupling promotes phase synchronization of neurons. In [54, 55], Magnetic field coupling was considered to regulate neuron activity, but only excitatory neuron networks were considered.

However, it is a pity that the split of magnetic field coupling into excitatory and inhibitory magnetic field coupling was not considered in previous researches [52,53,54,55]. Excitatory and inhibitory synapses are two types of synapses [47]. As magnetic field coupling is another means of neuron signal communication, the regulation of inhibitory and excitatory magnetic field coupling on neuronal dynamical properties should also be considered. Based on the above discussion, this paper puts forward the concept of excitation and inhibition of magnetic field coupling and proposes the corresponding theoretical model. According to Abe’s theorem, the direction of the magnetic field is determined by the law of ion movement. Therefore, the excitation and inhibition of neurons can be indicated by the direction of the magnetic field. The magnetic fields of the two neurons are superimposed on each other, either in the same direction or opposite. The excitatory magnetic field coupling and inhibitory magnetic field coupling models are proposed. It is verified that excitatory magnetic field coupling can promote the firing of neurons, inhibitory magnetic field coupling can inhibit the corresponding neuron, and the increasing coupling intensity to a certain degree makes the neuron reach the static state.

The following of this paper is organized as follows; Sect. 2 splits magnetic field coupling into excitatory and inhibitory magnetic field coupling; Sect. 3 studies two magnetic field coupling states under four discharge modes; Sect. 4 summarizes the full text.

2 Model description and scheme considered

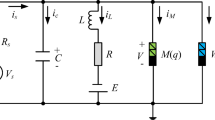
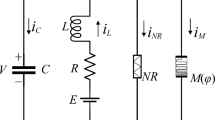
Synapses are the connections between neurons. And the importance of magnetic coupling as a possible way of transmitting information between neurons is undeniable. To study the modulation of dynamical properties of coupling neurons by excitatory and inhibitory magnetic field coupling. In this paper, we consider the response of the magnetic field coupled HR model to external stimulus currents in two cases: Case I. Excitatory magnetic field coupling model; Case II. Inhibitory magnetic field coupling model.

2.1 Excitatory magnetic field coupling model

In [52], a model of interaction between neuron magnetic fields was presented. In Refs. [53, 55, 56], electrical synapses and magnetic fields were used for information interaction between neurons. And the two neurons connected by magnetic coupling were both excited, so it can be considered that the magnetic coupling connecting the two excited neurons is also excitatory magnetic coupling. The corresponding excitatory magnetic field coupling model is shown below:

$$\begin{aligned} \left\{ \begin{array}{l} {{\dot{x}}_1} = {y_1} - a{x_1}^3 + b{x_1}^2 - {z_1} + {I_\mathrm{ext}} - k\rho ({\varphi _1}){x_1}\\ {{\dot{y}}_1} = c - d{x_1}^2 - {y_1}\\ {{\dot{z}}_1} = r[s({x_1} + 1.6) - {z_1}]\\ {{\dot{\varphi }}_1} = {k_1}{x_1} - {k_2}{\varphi _1} + {G_\mathrm{ex}}({\varphi _2} - {\varphi _1})\\ {{\dot{x}}_2} = {y_2} - a{x_2}^3 + b{x_2}^2 - {z_2} + {I_\mathrm{ext}} - k\rho ({\varphi _2}){x_2}\\ {{\dot{y}}_2} = c - d{x_2}^2 - {y_2}\\ {{\dot{z}}_2} = r[s({x_2} + 1.6) - {z_2}]\\ {{\dot{\varphi }}_2} = {k_1}{x_2} - {k_2}{\varphi _2} + {G_\mathrm{ex}}({\varphi _1} - {\varphi _2}), \end{array} \right. \end{aligned}$$
(1)

where x, y, z and \(\varphi \) describe the membrane potential, recovery variables of slow current and adaptive current, and magnetic flux, respectively. \({I_\mathrm{ext}}\) is the external stimulus current, the memristor coupling magnetic flux and membrane potential. Its conductivity is \(\rho ( \varphi )=\alpha +3\beta \varphi ^2 \). \({G_\mathrm{ex}}({\varphi _1} - {\varphi _2})\) and \({G_\mathrm{ex}}({\varphi _2} - {\varphi _1})\), represent the interaction of two magnetic fields. \({G_\mathrm{ex}}\) means the coupling strength of the corresponding excitatory magnetic field, and the other parameters (a, b, c, d, k, r, s, \({k_1}\), \({k_2}\)) are constants as (1.0, 3.0, 1.0, 5.0, 1, 0.006, 4, 0.5, 0.5).

Table 1 Cases of different firing states according to magnetic field coupling types
Full size table

2.2 Inhibitory magnetic field coupling model

It is well known that synapses can be divided into inhibitory and excitatory. Inhibitory synapses connect the neurons, and the presynaptic neuron is activated while the postsynaptic neuron is inhibited. In this paper, magnetic field coupling is another way of neuron information transmission. Therefore, there is also a corresponding inhibitory magnetic field coupling. That is, the upper-level neuron is activated while the lower-level neuron is inhibited, and they communicate with one another via magnetic field coupling. In this work, we propose the inhibitory magnetic field model coupling two neurons as:

$$\begin{aligned} \left\{ \begin{array}{l} {{\dot{x}}_1} = {y_1} - a{x_1}^3 + b{x_1}^2 - {z_1} + {I_\mathrm{ext}} - k\rho ({\varphi _1}){x_1}\\ {{\dot{y}}_1} = c - d{x_1}^2 - {y_1}\\ {{\dot{z}}_1} = r[s({x_1} + 1.6) - {z_1}]\\ {{\dot{\varphi }}_1} = {k_1}{x_1} - {k_2}{\varphi _1} - {G_\mathrm{in}}({\varphi _2} + {\varphi _1})\\ {{\dot{x}}_2} = {y_2} - a{x_2}^3 + b{x_2}^2 - {z_2} + {I_\mathrm{ext}} - k\rho ({\varphi _2}){x_2}\\ {{\dot{y}}_2} = c - d{x_2}^2 - {y_2}\\ {{\dot{z}}_2} = r[s({x_2} + 1.6) - {z_2}]\\ {{\dot{\varphi }}_2} = {k_1}{x_2} - {k_2}{\varphi _2} + {G_\mathrm{in}}({\varphi _1} + {\varphi _2}), \end{array} \right. \end{aligned}$$
(2)

where \({G_\mathrm{in}}\) is the coupling strength of the corresponding inhibitory magnetic field.

It is well known that adjusting the applied excitation current can alter the firing pattern of neurons. To explore the influence of different degrees of magnetic field coupling intensity on neuronal firing mode under other circumstances, we studied two magnetic field coupling cases with four different firing patterns, as shown in Table 1.

Table 2 Equilibrium points and their corresponding eigenvalues and stabilities (\({I_\mathrm{ext}}=3.2\))
Full size table

2.3 Stability analysis for the equilibrium states

The equilibrium Eq. (3) is found by zeroing the left side of Eq. (1)

$$\begin{aligned} \left\{ \begin{array}{l} {y_1} - a{x_1}^3 + b{x_1}^2 - {z_1} + {I_\mathrm{ext}} - k\rho ({\varphi _1}){x_1} = 0\\ c - d{x_1}^2 - {y_1} = 0\\ r[s({x_1} + 1.6) - {z_1}] = 0\\ {k_1}{x_1} - {k_2}{\varphi _1} + {G_\mathrm{ex}}({\varphi _2} - {\varphi _1}) = 0\\ {y_2} - a{x_2}^3 + b{x_2}^2 - {z_2} + {I_\mathrm{ext}} - k\rho ({\varphi _2}){x_2} = 0\\ c - d{x_2}^2 - {y_2} = 0\\ r[s({x_2} + 1.6) - {z_2}] = 0\\ {k_1}{x_2} - {k_2}{\varphi _2} + {G_\mathrm{ex}}({\varphi _1} - {\varphi _2}) = 0, \end{array} \right. \end{aligned}$$
(3)

The equations may be solved using MATLAB, and the real solution is the equilibrium point. The following approach is used to construct the Jacobian matrix corresponding to Eq. (1).

$$\begin{aligned} J = \left( {\begin{array}{*{20}{c}} {{J_{11}}}&{}1&{}{ - 1}&{}{{J_{14}}}&{}0&{}0&{}0&{}0\\ {{J_{21}}}&{}{ - 1}&{}0&{}0&{}0&{}0&{}0&{}0\\ {{J_{31}}}&{}0&{}{{J_{33}}}&{}0&{}0&{}0&{}0&{}0\\ {{J_{41}}}&{}0&{}0&{}{{J_{44}}}&{}0&{}0&{}0&{}{{J_{48}}}\\ 0&{}0&{}0&{}0&{}{{J_{55}}}&{}1&{}{ - 1}&{}{{J_{58}}}\\ 0&{}0&{}0&{}0&{}{{J_{65}}}&{}{ - 1}&{}0&{}0\\ 0&{}0&{}0&{}0&{}{{J_{75}}}&{}0&{}{{J_{77}}}&{}0\\ 0&{}0&{}0&{}{{J_{84}}}&{}{{J_{85}}}&{}0&{}0&{}{{J_{88}}} \end{array}} \right) \end{aligned}$$
(4)

where

$$\begin{aligned}&{J_{11}}=2b{x_1}-3a{x_1^2}-k(\alpha +3 \beta \varphi _1^2); {J_{21}}=-2d{x_1};\\&\quad {J_{31}}={J_{75}}=rs; {J_{85}}={J_{41}}={k_{1}};\\&\quad {J_{14}}=-6k\beta \varphi _1x_1; {J_{33}}={J_{77}}=-r;\\&\quad {J_{88}}={J_{44}}=-{k_2}-{G_\mathrm{ex}}; {J_{48}}={J_{84}}={G_\mathrm{ex}};\\&\quad {J_{55}}=2b{x_2}-3a{x_2^2}-k (\alpha +3 \beta \varphi _2 ^2); {J_{65}}=-2d{x_2};\\&\quad {J_{58}}=-6k\beta \varphi _2x_2. \end{aligned}$$

The eigenvalues of the appropriate equilibrium point are calculated by substituting it into the Jacobian matrix.

The related equilibrium Eq. (5) is found by zeroing the left side of Eq. (2).

$$\begin{aligned} \left\{ \begin{array}{l} {y_1} - a{x_1}^3 + b{x_1}^2 - {z_1} + {I_\mathrm{ext}} - k\rho ({\varphi _1}){x_1} = 0\\ c - d{x_1}^2 - {y_1} = 0\\ r[s({x_1} + 1.6) - {z_1}] = 0\\ {k_1}{x_1} - {k_2}{\varphi _1} - {G_\mathrm{in}}({\varphi _2} + {\varphi _1}) = 0\\ {y_2} - a{x_2}^3 + b{x_2}^2 - {z_2} + {I_\mathrm{ext}} - k\rho ({\varphi _2}){x_2} = 0\\ c - d{x_2}^2 - {y_2} = 0\\ r[s({x_2} + 1.6) - {z_2}] = 0\\ {k_1}{x_2} - {k_2}{\varphi _2} + {G_\mathrm{in}}({\varphi _1} + {\varphi _2}) = 0, \end{array} \right. \end{aligned}$$
(5)

The Jacobian matrix of (2) is yielded as

$$\begin{aligned} J = \left( {\begin{array}{*{20}{c}} {{J_{11}}}&{}1&{}{ - 1}&{}{{J_{14}}}&{}0&{}0&{}0&{}0\\ {{J_{21}}}&{}{ - 1}&{}0&{}0&{}0&{}0&{}0&{}0\\ {{J_{31}}}&{}0&{}{{J_{33}}}&{}0&{}0&{}0&{}0&{}0\\ {{J_{41}}}&{}0&{}0&{}{{J_{44}}}&{}0&{}0&{}0&{}{{J_{48}}}\\ 0&{}0&{}0&{}0&{}{{J_{55}}}&{}1&{}{ - 1}&{}{{J_{58}}}\\ 0&{}0&{}0&{}0&{}{{J_{65}}}&{}{ - 1}&{}0&{}0\\ 0&{}0&{}0&{}0&{}{{J_{75}}}&{}0&{}{{J_{77}}}&{}0\\ 0&{}0&{}0&{}{{J_{84}}}&{}{{J_{85}}}&{}0&{}0&{}{{J_{88}}} \end{array}} \right) \end{aligned}$$
(6)

where

$$\begin{aligned}&{J_{11}}=2b{x_1}-3a{x_1^2}-k (\alpha +3 \beta \varphi _1^2); {J_{21}}=-2d{x_1}; \\&\quad {J_{31}}={J_{75}}=rs; {J_{85}}={J_{41}}={k_{1}};\\&\quad {J_{14}}=-6k\beta \varphi _1x_1; {J_{33}}={J_{77}}=-r;\\&\quad {J_{44}}= -{k_2}-{G_\mathrm{in}}; {J_{48}}=-{G_\mathrm{in}};\\&\quad {J_{55}}=2b{x_2}-3a{x_2^2}-k (\alpha +3\beta \varphi _2 ^2); {J_{65}}=-2d{x_2};\\&\quad {J_{58}}=-6k\beta \varphi _2x_2;{J_{84}}={G_\mathrm{in}}; {J_{88}}=-k_2+G_\mathrm{in}. \end{aligned}$$

The equilibrium point of an actual number solution is first found by solving equations and then replaced into the Jacobian matrix, and the stability of the equilibrium point is determined by its eigenvalue. Table 2 summarizes the findings.

Neither excitatory nor inhibitory magnetic field coupling has an equilibrium point when \({G_\mathrm{ex}}\)=0 or \({G_\mathrm{in}}=0\). The applied excitation current determines the equilibrium point in excitatory magnetic field coupling. The excitatory magnetic field coupling intensity has a minor effect on the eigenvalue but no impact on the equilibrium point. The inhibitory magnetic field coupling intensity can affect both the equilibrium point and the eigenvalue in the inhibitory magnetic field coupling. The stability of the equilibrium point varies from unstable equilibrium point to stable equilibrium point as the magnetic field coupling strength increases.

3 Numerical results and discussion

In numerical study, this section uses the fourth order Runge–Kutta algorithm to solve the dynamic equation with a transient period of 1200. Neurons in the model of the initial value are set to \((x_1, y_1, z_1, \varphi _1, x_2, y_2, z_2, \varphi _2 ) = (0.2, 0.5, 0.1, 0.1, 0.3, 0.8, 0.2, 0.0)\), the other parameters are chosen as a=1.0, b=3.0, c=1.0, d=5.0, r=0.006, s=4, k=1, \(k_1\)=0.5, \(k_2\)=0.5, \(\alpha \)=0.1, \(\beta \)=0.02. For clear illustration, the influence of applied current on the electrical activity of neurons can be illustrated by the inter-spike interval (ISI) bifurcation diagram as shown in Fig. 1.

Fig. 1
figure 1

Bifurcation diagram of neuron membrane potential and different external stimulus signals

Full size image
Fig. 2
figure 2

Two neurons with different initial values were sampled with different excitation (the blue is the response of the first neuron, and the orange is the response of the second neuron). a \({I_\mathrm{ext}}=1.8\); b \({I_\mathrm{ext}}\) =2.3; c \({I_\mathrm{ext}}\) =3.2; d \({I_\mathrm{ext}}\) =4; The initial values are selected as (0.2, 0.5, 0.1, 0.1, 0.3, 0.8, 0.2, 0.0)

Full size image

ISI reflects the distance between two peaks in the firing sequence diagram of neurons. The firing modes of the HR neuronal models experienced several major transitions. When the external stimulus \({I_\mathrm{ext}}\) is too tiny, the neuron is in a quiescent state. With the increase of external stimulation, the neuron experiences spike discharge, burst discharge, chaotic discharge and periodic oscillation. We can select the appropriate external excitation current to control the firing mode of neurons, as shown in Fig. 2.

Various modes of electrical activity can be triggered by selecting the right applied excitation current. And two neurons with different initial values fired in the same pattern without synaptic coupling and magnetic coupling. When the external excitation current is fixed, the regulation of excitatory and inhibitory magnetic field coupling on neuronal dynamical properties under different discharge modes is explored through bifurcation analysis of magnetic field coupling intensity.

3.1 Inhibitory magnetic field coupling

In case 1, two neurons with different initial values at peak discharge were selected to change the intensity of magnetic field coupling, and the effect of magnetic field coupling on neuron firing mode was detected. Bifurcation of ISI with parameter \({G_\mathrm{in}}\) and neuron firing patterns are shown in Figs. 3 and 4.

Fig. 3
figure 3

Bifurcation diagram of neuronal firing ISI with different Inhibitory magnetic field coupling intensity, \({I_\mathrm{ext}}=1.8\); (the blue is the response of the first neuron, and the orange is the response of the second neuron) The inserted figure is an enlarged version

Full size image
Fig. 4
figure 4

Sampled time series for membrane potential, \({I_\mathrm{ext}}=1.8\) (the blue is the response of the first neuron, and the orange is the response of the second neuron). a \({G_\mathrm{in}}=0\); b \({G_\mathrm{in}}=0.2\); c \({G_\mathrm{in}}=0.8\); d \({G_\mathrm{in}}=2\)

Full size image

It has been discovered that changing the magnetic coupling strength alters the firing mode of neurons. With the increase of magnetic field coupling intensity, the firing mode of neuron 1 becomes more and more complex, and the observed spikes become more and more intensive. To observe the bifurcation diagram in greater detail, zoom in on the bifurcation diagram near \({G_\mathrm{in}}=0.8\). The neuron starts to inhibit the firing until the magnetic field coupling intensity reaches a certain degree. We can find that the bifurcation diagram disappears, indicating that the neuron is stationary. With the increase of magnetic coupling intensity, the amplitude and frequency of the membrane potential of neuron 2 became smaller and smaller and reached the quiescent state before neuron 1.

In case 2, the intensity of magnetic field coupling was changed to detect the influence of magnetic field coupling on neuron firing mode. The bifurcation diagram of ISI and the time series diagram are shown in Figs. 5 and 6.

Fig. 5
figure 5

Bifurcation diagram of neuronal firing ISI with different Inhibitory magnetic field coupling intensity, \({I_\mathrm{ext}}=2.3\) (the blue is the response of the first neuron, and the orange is the response of the second neuron)

Full size image
Fig. 6
figure 6

Sampled time series for membrane potential, \({I_\mathrm{ext}}=2.3\) (the blue is the response of the first neuron, and the orange is the response of the second neuron). a \({G_\mathrm{in}}=0\); b \({G_\mathrm{in}}=0.2\); c \({G_\mathrm{in}}=0.8\); d \({G_\mathrm{in}}=2\)

Full size image

With the increase of excitation current, more inhibitory magnetic field coupling is needed to make the neuron reach the quiescent state. The different discharge patterns of the two neurons were observed. The two neurons move from the same firing mode to a different one due to inhibitory magnetic coupling. Figure 6 shows the existence of burst discharge and Subthreshold oscillation [57] and the existence of burst discharge and chaotic state. Moreover, when the neuron is stationary, the membrane potential of neuron 1 is lower than that of neuron 2.

Fig. 7
figure 7

Bifurcation diagram of neuronal firing ISI with different Inhibitory magnetic field coupling intensity, \({I_\mathrm{ext}}=3.2\) (the blue is the response of the first neuron, and the orange is the response of the second neuron)

Full size image
Fig. 8
figure 8

Sampled time series for membrane potential, \({I_\mathrm{ext}}=3.2\) (the blue is the response of the first neuron, and the orange is the response of the second neuron). a \({G_\mathrm{in}}=0\); b \({G_\mathrm{in}}=0.2\); c \({G_\mathrm{in}}=0.8\); d \({G_\mathrm{in}}=2\)

Full size image

In case 3, two neurons with different initial values at chaotic discharge were selected to change the intensity of magnetic field coupling, and the effect of magnetic field coupling on neuron firing mode was detected. Bifurcation of ISI with parameter \({G_\mathrm{in}}\) and neuron firing patterns are shown in Figs. 7 and 8.

As seen from the diagram, neurons can have a variety of discharge modes by adjusting the magnetic field coupling intensity. With the increase of magnetic field coupling intensity, the discharge modes of the two neurons change from chaos state to burst state and period-1 discharge and static form.

In case 4, two neurons at periodic oscillation were selected to change the intensity of magnetic field coupling, and the effect of magnetic field coupling on neuron firing mode was detected. Bifurcation of ISI with parameter \({G_\mathrm{in}}\) and neuron firing patterns are shown in Figs. 9 and 10.

Fig. 9
figure 9

Bifurcation diagram of neuronal firing ISI with different Inhibitory magnetic field coupling intensity, \({I_\mathrm{ext}}=4\) (the blue is the response of the first neuron, and the orange is the response of the second neuron)

Full size image
Fig. 10
figure 10

Sampled time series for membrane potential, \({I_\mathrm{ext}}=4\)(the blue is the response of the first neuron, and the orange is the response of the second neuron). a \({G_\mathrm{in}}=0\); b \({G_\mathrm{in}}=0.2\); c \({G_\mathrm{in}}=0.8\); d \({G_\mathrm{in}}=2\)

Full size image
Fig. 11
figure 11

Bifurcation diagram of neuronal firing ISI with different excitatory magnetic field coupling intensity, \({I_\mathrm{ext}}=1.8\) (the blue is the response of the first neuron, and the orange is the response of the second neuron)

Full size image
Fig. 12
figure 12

Sampled time series for membrane potential, \({I_\mathrm{ext}}=1.8\) (the blue is the response of the first neuron, and the orange is the response of the second neuron). a \({G_\mathrm{ex}}=0\); b \({G_\mathrm{ex}}=0.2\); c \({G_\mathrm{ex}}=0.8\); d \({G_\mathrm{ex}}=2\)

Full size image

The discharge mode can be controlled by selecting suitable magnetic coupling intensity. The two neurons move from the same firing mode to a different one due to inhibitory magnetic coupling. When \({G_\mathrm{in}}=2\), the neuron firing pattern is subthreshold oscillation rather than resting, as shown in Fig. 10d. And with the increase of external stimulus current, the two neurons need more inhibitory magnetic coupling strength to reach the resting state.

Fig. 13
figure 13

Bifurcation diagram of neuronal firing ISI with different excitatory magnetic field coupling intensity, \({I_\mathrm{ext}}=2.3\) (the blue is the response of the first neuron, and the orange is the response of the second neuron)

Full size image
Fig. 14
figure 14

Sampled time series for membrane potential, \({I_\mathrm{ext}}=2.3\) (the blue is the response of the first neuron, and the orange is the response of the second neuron). a \({G_\mathrm{ex}}=0\); b \({G_\mathrm{ex}}=0.2\); c \({G_\mathrm{ex}}=0.8\); d \({G_\mathrm{ex}}=2\)

Full size image
Fig. 15
figure 15

Bifurcation diagram of neuronal firing ISI with different excitatory magnetic field coupling intensity, \({I_\mathrm{ext}}=3.2\) (the blue is the response of the first neuron, and the orange is the response of the second neuron)

Full size image
Fig. 16
figure 16

Sampled time series for membrane potential, \({I_\mathrm{ext}}=3.2\) (the blue is the response of the first neuron, and the orange is the response of the second neuron). a \({G_\mathrm{ex}}=0\); b \({G_\mathrm{ex}}=0.2\); c \({G_\mathrm{ex}}=0.8\); d \({G_\mathrm{ex}}=2\)

Full size image

3.2 Excitatory magnetic field coupling

In case 1, two neurons with peak discharge were stimulated by an excitatory coupling magnetic field. Then the coupling intensity was changed to observe the firing of the neurons without synaptic coupling; the results are presented in Figs. 11 and 12.

With the increase of magnetic coupling intensity, the two neurons’ firing mode becomes more and more complex, and the observed spikes become denser. The firing mode of neurons changes from peak discharge to period-2 discharge.

In case 2, two neurons with burst discharge were stimulated by an excitatory coupling magnetic field. Then the coupling intensity was changed to observe the neurons firing without synaptic coupling. The results are presented in Figs. 13 and 14.

Table 3 Different ways to couple HR neurons
Full size table

Neurons firing in period-2 discharge flip to firing in a period-3 discharge after being activated by an excitatory magnetic coupling. And it was found that excitatory magnetic fields made neurons asynchronous.

Fig. 17
figure 17

Bifurcation diagram of neuronal firing ISI with different excitatory magnetic field coupling intensity, \({I_\mathrm{ext}}=4\) (the blue is the response of the first neuron, and the orange is the response of the second neuron)

Full size image

In case 3, two neurons with chaotic discharge were stimulated by an excitatory coupling magnetic field, and then the coupling intensity was changed to observe the discharge of the neurons without synaptic coupling. The results are presented in Figs. 15 and 16.

The bifurcation diagram shows that the two neurons are in chaotic discharge, but through the sequence diagram, we can find that the excitatory magnetic coupling promotes the neuron discharge.

Fig. 18
figure 18

Sampled time series for membrane potential, \({I_\mathrm{ext}}=4\) (the blue is the response of the first neuron, and the orange is the response of the second neuron). a \({G_\mathrm{ex}}=0\); b \({G_\mathrm{ex}}=0.2\); c \({G_\mathrm{ex}}=0.8\); d \({G_\mathrm{ex}}=2\)

Full size image

In case 4, two neurons with Periodic oscillation were stimulated by an excitatory coupling magnetic field, and then the coupling intensity was changed to observe the discharge of the neurons without synaptic coupling. The results are presented in Figs. 17 and 18.

In conclusion, the effects of excitatory and inhibitory magnetic field coupling on neuron discharge differ. Excitatory magnetic field coupling can benefit neuron firing but also affect neuron firing patterns, complicating electrical activity. Inhibitory magnetic field coupling can enhance neuron firing when the coupling intensity is small but can inhibit neuron firing when the coupling intensity is vital. The neurons enter a static state when the magnetic coupling strength reaches a critical point. As the external stimulus current increases, more inhibitory magnetic field coupling strength is required to make the neuron enter the quiescent state.

4 Conclusions

Sequences of spikes carry out the information of neurons; neurons can modulate the firing patterns of other neurons using magnetic fields. Like synapses, magnetic coupling acts as a means of transmitting data between neurons. Thus, the magnetic coupling may have properties similar to synaptic coupling. This paper divided the magnetic field coupling into excitation and inhibition magnetic field coupling, and two coupling models are established, respectively. The method of transmitting neuron information through magnetic field coupling is further improved. It increases the magnetic coupling strength of the excitatory model, which promotes neuronal electrical activity. A high enough inhibitory magnetic coupling causes the neuron to become quiescent. Table 3 lists the two neurons’ synaptic and magnetic coupling models. Chemical synaptic coupling is unidirectional; information can only be transmitted from the presynaptic neuron to the postsynaptic neuron. Chemical synapses have a time delay due to synaptic cleft. Magnetic coupling is the ability of neurons to interact with each other. It is bi-directional and has no time delay. It is divided into excitatory synapses and inhibitory synapses. Moreover, the neuronal magnetic field not only affects postsynaptic neurons but also has a diffusion effect. Because neurons are exposed to the integrated magnetic fields of other neurons, the next step of this paper is to study the interaction of magnetic fields of multiple neurons.