Rogue waves of the fifth-order Ito equation on the general periodic travelling wave solutions background

Abstract

In this paper, on the background of general periodic travelling wave solutions, we construct rogue wave solutions of the fifth-order Ito equation. In particular, those solutions cover the known results in the literature. By means of the Darboux transformation, we derive one-, two- and three-fold rogue wave solutions on the periodic travelling wave solutions background. We provide several illustrations of such rogue waves and analyze their generation mechanisms.

1 Introduction

Rogue waves (also called freak waves, giant waves and extreme waves) are unexpectedly large-amplitude waves which are much higher than those of the surrounding waves [1]. They appear from nowhere and disappear without a trace [2] and can exist in different physical contexts including in the open ocean and in coastal areas [1, 3, 4]. Over the years, many progresses have been achieved in the study of the physical mechanisms of the rogue wave phenomenon. Many physical models of the rogue wave phenomenon have been intensively developed, and various laboratory experiments have been conducted, such as in optical fibers [5, 6] and water wave tank [7]. It is believed that the occurrence of rogue waves is related to the modulation instability of the plane waves or periodic waves [8]. Mathematically, the rational solution of the nonlinear Schrödinger (NLS) equation can be used to described the mechanisms of rogue wave phenomenon [9]. This kind of rogue wave solution has a localized hump with a peak amplitude and approaches a nonzero constant background as time goes to $\pm \infty$. Since the NLS equation is completely integrable, the hierarchy of rational solutions in this equation can be constructed by the Darboux transformation (DT) from a nonzero plane wave background [10,11,12].

Recently, it has been shown that rogue waves can also arise from the periodic wave background [13,14,15,16,17,18,19]. These waves (referred as rogue periodic waves) can be used to illustrate interesting nonlinear phenomena in various physical contexts, such as rogue waves in the water wave flume and in nonlinear fibers with oscillating background [6, 20,21,22]. Recent study by Pelinovsky and Chen shows that rogue periodic wave solutions on the periodic wave background for many nonlinear evolution equations can be constructed by combining the nonlinearization of spectral problem with the DT method [14, 16, 17], such as the NLS equation [14, 15], the modified Korteweg–de Vries (mKdV) equation [16, 17], the Hirota equation [18, 19] and the sine-Gordon equation [23].

In this paper, we consider the fifth-order Ito equation

$$\begin{aligned} q_t+\left( 6q^5+10\left( q q_x^2+q^2q_{xx}\right) +q_{xxxx}\right) _x=0, \end{aligned}$$

(1)

which was firstly proposed by Ito in Ref. [24]. Eq. (1) is the second member in the mKdV hierarchy of equations, and its many integrable properties have been studied [24,25,26,27]. The spectral problem of Eq. (1) can be written as

$$\begin{aligned} \varPhi _x&=\mathrm{U}(q;\lambda )\varPhi ,\mathrm{U}(q;\lambda )=\lambda \sigma _3+ Q,\end{aligned}$$

(2a)

$$\begin{aligned} \varPhi _t&=\mathrm{V}(q;\lambda )\varPhi ,\mathrm{V}(q;\lambda )=-16\lambda ^5\sigma _3-16\lambda ^4 Q\nonumber \\&\quad +\,\lambda ^3V_3+\lambda ^2V_2+\lambda V_1+V_0, \end{aligned}$$

(2b)

with

$$\begin{aligned}&\sigma _3=\left( \begin{array}{cc} 1 &{} 0\\ 0 &{} -1 \end{array}\right) ,Q=\left( \begin{array}{cc} 0 &{} q\\ -q &{} 0 \end{array}\right) ,\\&V_3=8\sigma _3\left( Q^2-Q_x\right) , V_2=4\left( 2Q^3-Q_{xx}\right) , \\&V_1=-2\left( 6Q^4+2Q_x^2-4QQ_{xx}\right. \\&\left. \qquad -\,12Q^2Q_x+2Q_{xxx}\right) ,\\&V_0=-6Q^5+10QQ_x^2+10Q^2Q_{xx}-Q_{xxxx}, \end{aligned}$$

where $\varPhi =(\varphi _1,\varphi _2)^T$ (the superscript T represents matrix transpose) is the vector eigenfunction and $\lambda$ is the spectral parameter. The zero curvature equation $U_t-V_x+[U,V]=0$ is exactly equivalent to Eq. (1).

It is easy to check that Eq. (1) admits two families of the normalized periodic travelling wave solutions given by

$$\begin{aligned}&q(x,t)=\mathrm{dn}(x-c_{dn} t;k),~ c_{dn}=6-6k^2+k^4,\nonumber \\\end{aligned}$$

(3)

$$\begin{aligned}&q(x,t)=k \mathrm{cn}(x-c_{cn} t;k),~ c_{cn}=1-6k^2+6k^4,\nonumber \\ \end{aligned}$$

(4)

where dn and cn are Jacobian elliptic functions and k $\in (0,1)$ is the elliptic modulus.

In Ref. [25], the rogue wave solutions of Eq. (1) have been derived on the background of Jacobi elliptic function solutions (3) and (4). In the present work, we plan to make a further study on rogue wave solutions of Eq. (1). Firstly, we derive the general periodic travelling wave solutions of Eq. (1) by reducing this high-order equation to a solvable first-order ordinary differential equation. In particular, these solutions include the elliptic function solutions (3) and (4). Secondly, on the background of the general periodic travelling wave solutions, our main aim is to construct rogue wave solutions of Eq. (1), which cover the known results in the literature [25]. Thirdly, based on obtained solutions, we analyze the generation mechanisms of rogue periodic waves.

The rest of this paper is arranged as follows. In Sect. 2, we derive general periodic travelling wave solutions of Eq. (1). Particularly, these solutions can reduce to the elliptic function solutions (3) and (4). In Sect. 3, on the periodic travelling wave solutions background, we determine eigenvalues and eigenfunctions of spectral problem. In Sect. 4, we construct the N-fold DT of Eq. (1) and present the one-, two- and three-fold transformation formulas. In Sect. 5, we provide the second solution of spectral problem. In Sect. 6, we construct rogue wave solutions on the periodic travelling wave solutions background. Section 7 is devoted to the conclusion and discussion.

2 General periodic travelling wave solutions

We assume that the travelling wave solution of Eq. (1) takes the form

$$\begin{aligned} q(x,t)=q(\xi ), \xi =x-c\,t, \end{aligned}$$

(5)

where c is a real constant representing the wave speed. Substituting Eq. (5) into Eq. (1) and integrating the resulting equation once with respect to $\xi$, we have

$$\begin{aligned} q^{(4)}+10(q^2q^{\prime \prime }+qq^{\prime 2})-cq+6q^5=c_0, \end{aligned}$$

(6)

where $c_0$ is a real integral constant and the prime sign denotes the differentiation with respect to $\xi$. By virtue of the sub-equation method [28], Eq. (6) can be reduced to the following elliptic equation

$$\begin{aligned} q_\xi ^2=P(q),P(q)=-q^4+a_2q^2+a_1q+a_0, \end{aligned}$$

(7)

with $c=a_2^2-2a_0$ and $c_0=-\frac{1}{2}a_1a_2$. Taking the derivative of Eq. (7) with respect to $\xi$ successively, we have

$$\begin{aligned}&q^{\prime \prime }+2q^3-a_2q-\frac{1}{2}a_1=0,\end{aligned}$$

(8)

$$\begin{aligned}&q^{(3)}+6q^2q^{\prime }-a_2q^{\prime }=0, \end{aligned}$$

(9)

where two constants $a_1$ and $a_2$ are to be undetermined.

It is known that Eq. (7) admits two explicit families of periodic solutions [29], namely: (I) the polynomial P(q) has four simple real roots $Q_1$, $Q_2$, $Q_3$ and $Q_4$. Without loss of generality, one can order the roots as $Q_4\le Q_3\le Q_2\le Q_1$; (II) the polynomial P(q) has two simple real roots $b\le a\,(a, b \in \mathbb {R})$, and a pair of complex conjugate roots $\alpha \pm i\beta \,(\alpha , \beta \in \mathbb {R})$.

For the first case, the exact periodic travelling wave solution of Eq. (1) can be expressed as

$$\begin{aligned} q(\xi )= & {} Q_4+\frac{(Q_1-Q_4)(Q_2-Q_4)}{(Q_2-Q_4)+(Q_1-Q_2)\mathrm{sn}^2(\rho \xi ;\kappa )},\nonumber \\ \end{aligned}$$

(10)

with

$$\begin{aligned} {\left\{ \begin{array}{ll} 4\rho ^2=(Q_1-Q_3)(Q_2-Q_4), \\ 4\rho ^2\kappa ^2=(Q_1-Q_2)(Q_3-Q_4), \\ \end{array}\right. } \end{aligned}$$

(11)

where $\rho >0$ and the parameter $\kappa \in (0,1)$ is the elliptic modulus. Moreover, by Viète’s formulas, we have

$$\begin{aligned} {\left\{ \begin{array}{ll} a_2=-(Q_1Q_2+Q_1Q_3+Q_1Q_4+Q_2Q_3\\ \qquad +\,Q_2Q_4+Q_3Q_4),\\ a_1=Q_1Q_2Q_3+Q_1Q_2Q_4+Q_1Q_3Q_4\\ \qquad +\,Q_2Q_3Q_4,\\ a_0=-Q_1Q_2Q_3Q_4,\\ Q_1+Q_2+Q_3+Q_4=0. \end{array}\right. } \end{aligned}$$

(12)

Remark 1

For $a_1=0$, we can obtain $Q_4=-Q_1$ and $Q_3=-Q_2$ because P(q) is an even function. Thus, one immediately has $a_2=Q_1^2+Q_2^2,a_0=-Q_1^2Q_2^2$ and $Q_1=\rho (1+\kappa ),Q_2=\rho (1-\kappa )$ from Eqs. (11) and  (12). Accordingly, the periodic travelling wave solution (10) can reduce to

$$\begin{aligned} q(\xi )=Q_1\mathrm{dn}(Q_1\xi ;k), k=\sqrt{1-\frac{Q_2^2}{Q_1^2}}. \end{aligned}$$

(13)

For the particular case of $Q_1=1$ and $Q_2=\sqrt{1-k^2}$, the solution (13) becomes the normalized dnoidal wave solution (3).

For the second case, we can easily know that Eq. (1) has the following periodic travelling wave solution

$$\begin{aligned} q(\xi )=a+\frac{(b-a)(1-\mathrm{cn}(\rho \xi ;\kappa ))}{1+\delta +(\delta -1)\mathrm{cn}(\rho \xi ;\kappa )}, \end{aligned}$$

(14)

with

$$\begin{aligned} {\left\{ \begin{array}{ll} \delta ^2=\frac{(b-\alpha )^2+\beta ^2}{(a-\alpha )^2+\beta ^2},\\ \rho ^2=\sqrt{\left( (a-\alpha )^2+\beta ^2\right) \left( (b-\alpha )^2+\beta ^2\right) },\\ 2\rho ^2\kappa ^2=\rho ^2-(a-\alpha )(b-\alpha )+\beta ^2, \end{array}\right. } \end{aligned}$$

(15)

where $\delta >0$, $\rho >0$. In a similar procedure, by Viète’s formulas, we have the following relations

$$\begin{aligned} {\left\{ \begin{array}{ll} a_2=-(ab+2\alpha (a+b)+\alpha ^2+\beta ^2),\\ a_1=2ab\alpha +(a+b)(\alpha ^2+\beta ^2),\\ a_0=-ab(\alpha ^2+\beta ^2),\\ a+b+2\alpha =0. \end{array}\right. } \end{aligned}$$

(16)

Remark 2

If $a_1=0$, we can obtain $b=-a,\alpha =0$ and $\delta =1$. The periodic travelling wave solution (14) can reduce to

$$\begin{aligned} q(\xi )= & {} a\mathrm{cn}(\rho \xi ;\kappa ),\rho =\sqrt{a^2+\beta ^2},\nonumber \\ \kappa= & {} \frac{a}{\sqrt{a^2+\beta ^2}}. \end{aligned}$$

(17)

In the case of $a=k$ and $\beta =\sqrt{1-k^2}$, Eq. (17) becomes the normalized cnoidal wave solution (4).

3 Eigenvalues and eigenfunctions of spectral problem

3.1 Nonlinearization of spectral problem

By introducing the following Bargmann constraint [30]:

$$\begin{aligned} q=\phi _1^2+\phi _2^2+\psi _1^2+\psi _2^2, \end{aligned}$$

(18)

where the vector function $(\phi _j,\psi _j)^T$ corresponds to the solution of spectral problem (2a) and (2b) with $\lambda =\lambda _j$ $(j=1,2)$, one can derive the finite-dimensional Hamiltonian system from Eq. (2a)

$$\begin{aligned} \frac{\mathrm{d}\phi _j}{\mathrm{d}x}=\frac{\partial H_0}{\partial \psi _j},\frac{\mathrm{d}\psi _j}{\mathrm{d}x}=-\frac{\partial H_0}{\partial \phi _j},(j=1,2), \end{aligned}$$

(19)

where $H_0(\phi _1,\phi _2,\psi _1,\psi _2)=\lambda _1\phi _1\psi _1+\lambda _2\phi _2 \psi _2+\frac{1}{4}(\phi _1^2+\phi _2^2+\psi _1^2+\psi _2^2)^2$. By direct calculation, then another conserved quantity can be derived from Hamiltonian system (19)

$$\begin{aligned}&H_1(\phi _1,\phi _2,\psi _1,\psi _2)\nonumber \\&\quad =4(\lambda _1^3\phi _1\psi _1+\lambda _2^3 \phi _2\psi _2)\nonumber \\&\qquad -\,4(\lambda _1\phi _1\psi _1+\lambda _2\phi _2\psi _2)^2\nonumber \\&\qquad -\,(\lambda _1(\phi _1^2-\psi _1^2)+\lambda _2(\phi _2^2-\psi _2^2))^2\nonumber \\&\qquad +\,2\left( \phi _1^2+\phi _2^2+\psi _1^2+\psi _2^2\right) \nonumber \\&\qquad \times \left( \lambda _1^2(\phi _1^2+\psi _1^2)+\lambda _2^2 (\phi _2^2+\psi _2^2)\right) . \end{aligned}$$

(20)

For convenience, we introduce $F_0=4H_0$ and $F_1=4H_1$.

Taking the derivative of Eq. (18) with respect to x successively, we can derive the differential equations about $q(\xi )$

$$\begin{aligned}&q^{\prime }=2\lambda _1(\phi _1^2-\psi _1^2)+2\lambda _2(\phi _2^2-\psi _2^2),\end{aligned}$$

(21)

$$\begin{aligned}&q^{\prime \prime }+2q^3=a_2q-4\lambda _2^2(\phi _1^2+\psi _1^2)\nonumber \\&\quad -4\lambda _1^2 (\phi _2^2+\psi _2^2),\end{aligned}$$

(22)

$$\begin{aligned}&q^{(3)}+6q^2q^{\prime }-a_2q^{\prime }=-8\lambda _1\lambda _2\nonumber \\&\quad \times \left( \lambda _2 (\phi _1^2-\psi _1^2)+\lambda _1(\phi _2^2-\psi _2^2)\right) ,\end{aligned}$$

(23)

$$\begin{aligned}&q^{(4)}+10q^2q^{\prime \prime }+10qq^{\prime 2}+6q^5\nonumber \\&\quad -a_2\left( q^{\prime \prime }+2q^3\right) +2a_0q=0, \end{aligned}$$

(24)

where

$$\begin{aligned} a_2= & {} 2F_0+4\lambda _1^2+4\lambda _2^2,\end{aligned}$$

(25)

$$\begin{aligned} a_0= & {} 4F_0(\lambda _1^2+\lambda _2^2)+8\lambda _1^2\lambda _2^2-F_0^2-F_1,\end{aligned}$$

(26)

$$\begin{aligned} F_0= & {} 4\lambda _1\phi _1\psi _1+4\lambda _2\phi _2\psi _2+q^2,\end{aligned}$$

(27)

$$\begin{aligned} F_1= & {} 16(\lambda _1^3\phi _1\psi _1+\lambda _2^3\phi _2\psi _2)-(F_0-q^2)^2\nonumber \\&+2q\left( q^{\prime \prime }+2q^3-2F_0q\right) -q^{\prime 2}. \end{aligned}$$

(28)

It is known that the Hamiltonian system (19) allows the following Lax representation [30, 31]

$$\begin{aligned} L_x=[U,L], \end{aligned}$$

(29)

with

$$\begin{aligned} L=\begin{pmatrix} 1-\frac{2\lambda _1\phi _1\psi _1}{\lambda ^2-\lambda _1^2} -\frac{2\lambda _2\phi _2\psi _2}{\lambda ^2-\lambda _2^2} &{} \frac{\phi _1^2}{\lambda -\lambda _1} +\frac{\psi _1^2}{\lambda +\lambda _1}+\frac{\phi _2^2}{\lambda -\lambda _2} +\frac{\psi _2^2}{\lambda +\lambda _2} \\ -\frac{\phi _1^2}{\lambda +\lambda _1}-\frac{\psi _1^2}{\lambda -\lambda _1} -\frac{\phi _2^2}{\lambda +\lambda _2}-\frac{\psi _2^2}{\lambda -\lambda _2}&{}-1 +\frac{2\lambda _1\phi _1\psi _1}{\lambda ^2-\lambda _1^2}+\frac{2\lambda _2\phi _2\psi _2}{\lambda ^2-\lambda _2^2}\end{pmatrix}. \end{aligned}$$

(30)

From the determinant of above matrix L, the following two important differential constraints on q can be derived as below:

$$\begin{aligned}&(q^{\prime \prime }+2q^3-2F_0q)^2-16\lambda _1^2\lambda _2^2q^2-2q^{\prime }\nonumber \\&\quad \times \, (q^{(3)}+6q^2q^{\prime }-a_2q^{\prime })\nonumber \\&\quad -\,2(F_0-q^2)(8\lambda _1^2\lambda _2^2+q^{\prime 2}\nonumber \\&\quad -\,2qq^{\prime \prime }-3q^4+a_2q^2-a_0)\nonumber \\&\quad -\,4(\lambda _1^2+\lambda _2^2)\left( q^{\prime 2}+(F_0-q^2)^2\right) =0, \end{aligned}$$

(31)

and

$$\begin{aligned}&(q^{(3)}+6q^2q^{\prime }-2F_0q^{\prime })^2+\left( F_0^2+F_1+q^{\prime 2}\right. \nonumber \\&\quad \left. -2qq^{\prime \prime }-3q^4+2F_0q^2\right) ^2\nonumber \\&\quad -\,4(\lambda _1^2+\lambda _2^2)\times (q^{\prime \prime }+2q^3-2F_0q)^2\nonumber \\&\quad -\,16\lambda _1^2 \lambda _2^2\left( q^{\prime 2}+(F_0-q^2)^2\right) \nonumber \\&\quad +\,32\lambda _1^2\lambda _2^2q(q^{\prime \prime }+2q^3-2F_0q)=0. \end{aligned}$$

(32)

Note that the detailed derivation process of the above two constraints can be seen in Ref. [17].

3.2 Eigenvalues

In this subsection, we will determine the location of eigenvalues of spectral problem (2). Inserting the second-order derivative of Eq. (7) into Eq. (24), we obtain

$$\begin{aligned} q^{\prime 2}-2q^{\prime \prime }-3q^4+a_2q^2-a_0=0. \end{aligned}$$

(33)

With the use of Eqs. (23) and (33), we can rewrite Eqs. (31) and (32) in the following forms:

$$\begin{aligned}&(q^{\prime \prime }+2q^3-2F_0q)^2-4(\lambda _1^2+\lambda _2^2)\left( q^{\prime 2}\right. \nonumber \\&\quad \left. +(F_0-q^2)^2\right) -16\lambda _1^2\lambda _2^2F_0=0,\end{aligned}$$

(34)

$$\begin{aligned}&4(\lambda _1^4+\lambda _1^2\lambda _2^2+\lambda _2^4)\left( q^{\prime 2} +(F_0-q^2)^2\right) \nonumber \\&\quad +16\lambda _1^2\lambda _2^2(\lambda _1^2+\lambda _2^2)(F_0-q^2) +16\lambda _1^4\lambda _1^4\nonumber \\&\quad -(\lambda _1^2+\lambda _2^2)(q^{\prime \prime }+2q^3-2F_0q)^2\nonumber \\&\quad +8\lambda _1^2 \lambda _2^2q(q^{\prime \prime }+2q^3-2F_0q)=0. \end{aligned}$$

(35)

Substituting Eqs. (21)–(22) into Eqs. (34)–(35), we get

$$\begin{aligned}&a_1^2=16(\lambda _1^2+\lambda _2^2)(F_0^2+a_0)+64\lambda _1^2\lambda _2^2F_0,\end{aligned}$$

(36)

$$\begin{aligned}&16(\lambda _1^4+\lambda _1^2\lambda _2^2+\lambda _2^4)(F_0^2+a_0)\nonumber \\&\quad +64\lambda _1^2 \lambda _2^2(\lambda _1^2+\lambda _2^2)F_0\nonumber \\&\quad +64\lambda _1^4\lambda _2^4 -(\lambda _1^2+\lambda _2^2)a_1^2=0. \end{aligned}$$

(37)

Furthermore, from Eqs. (36) and (37), we know that

$$\begin{aligned}&a_0=4\lambda _1^2\lambda _2^2-F_0^2,\end{aligned}$$

(38)

$$\begin{aligned}&a_1^2=64\lambda _1^2\lambda _2^2(F_0+\lambda _1^2+\lambda _2^2). \end{aligned}$$

(39)

From Eqs. (26) and (38), we can easily derive the following relation

$$\begin{aligned} F_1=4F_0(\lambda _1^2+\lambda _2^2)+4\lambda _1^2\lambda _2^2. \end{aligned}$$

(40)

By virtue of Eqs. (26), (38) and (39), the following form about $F_0$ is obtained

$$\begin{aligned} 4(F_0^2+a_0)(2F_0+a_2)=a_1^2, \end{aligned}$$

(41)

which can be viewed as a cubic equation with respect to $F_0$.

For the periodic travelling wave solution (10), based on Eqs. (12), the three roots of Eq. (41) are solved as follows:

$$\begin{aligned}&(1)F_0=\frac{1}{2}(Q_1Q_4+Q_2Q_3),\nonumber \\&(2)F_0=\frac{1}{2}(Q_1Q_3+Q_2Q_4),\nonumber \\&(3)F_0=\frac{1}{2}(Q_1Q_2+Q_3Q_4). \end{aligned}$$

(42)

Because there are three possible choices of the two eigenvalues $\lambda _1,\lambda _2$, we only need to consider one combination of the three eigenvalues, namely

$$\begin{aligned} \lambda _1= & {} \frac{1}{2}(Q_1+Q_2),\lambda _2=\frac{1}{2}(Q_1+Q_3),\nonumber \\ \lambda _3= & {} \frac{1}{2}(Q_2+Q_3). \end{aligned}$$

(43)

For the periodic travelling wave solution (14), from Eqs. (16), the three roots of Eq. (41) are solved as follows:

$$\begin{aligned} (1)F_0= & {} \frac{1}{8}(a^2+6ab+b^2)+\frac{1}{2}\beta ^2,\nonumber \\ (2)F_0= & {} -\frac{1}{4} (a+b)^2\pm \frac{i}{2}\beta (a+b). \end{aligned}$$

(44)

Then, the eigenvalues are located at

$$\begin{aligned} \lambda _1= & {} \frac{1}{4}(a-b)+\frac{i}{2}\beta ,\lambda _2=\frac{1}{4}(a-b) -\frac{i}{2}\beta ,\nonumber \\&\lambda _3=\frac{1}{2}(a+b). \end{aligned}$$

(45)

3.3 Eigenfunctions

In this subsection, we would like to determine the squared periodic eigenfunctions of spectral problem. We collect what have been obtained above and rewrite Eqs. (18), (21), (22) and (23) as a system of linear equations

$$\begin{aligned} {\left\{ \begin{array}{ll} \phi _1^2+\phi _2^2+\psi _1^2+\psi _2^2=q,\\ 2\lambda _1(\phi _1^2-\psi _1^2)+2\lambda _2(\phi _2^2-\psi _2^2)=q^{\prime },\\ 4\lambda _1^2(\phi _1^2+\psi _1^2)+4\lambda _2^2(\phi _2^2+\psi _2^2)=q^{\prime \prime }\\ \qquad +2q^3-2F_0q,\\ 8\lambda _1^3(\phi _1^2-\psi _1^2)+8\lambda _2^3(\phi _2^2-\psi _2^2)=q^{(3)}\\ \qquad +6q^2q^{\prime }-2F_0q^{\prime }. \end{array}\right. } \end{aligned}$$

(46)

By solving linear system (46) with Cramer’s rule, we obtain the relations of the squared eigenfunctions

$$\begin{aligned}&\phi _1^2+\psi _1^2=\frac{q^{\prime \prime }+2q^3-2F_0q-4\lambda _2^2q}{4(\lambda _1^2-\lambda _2^2)},\end{aligned}$$

(47)

$$\begin{aligned}&\phi _1^2-\psi _1^2=\frac{q^{(3)}+6q^2q^{\prime }-2F_0q^{\prime }-4\lambda _2^2 q^{\prime }}{8\lambda _1(\lambda _1^2-\lambda _2^2)}.\end{aligned}$$

(48)

$$\begin{aligned}&\phi _2^2+\psi _2^2=\frac{q^{\prime \prime }+2q^3-2F_0q-4\lambda _1^2q}{4(\lambda _2^2-\lambda _1^2)},\end{aligned}$$

(49)

$$\begin{aligned}&\phi _2^2-\psi _2^2=\frac{q^{(3)}+6q^2q^{\prime }-2F_0q^{\prime }-4\lambda _1^2 q^{\prime }}{8\lambda _2(\lambda _2^2-\lambda _1^2)}. \end{aligned}$$

(50)

By use of Eqs. (8), (9) and (25), Eqs. (47)-(50) can be simplified to the following forms

$$\begin{aligned}&\phi _1^2+\psi _1^2=\frac{a_1+8\lambda _1^2q}{8(\lambda _1^2-\lambda _2^2)},\end{aligned}$$

(51)

$$\begin{aligned}&\phi _1^2-\psi _1^2=\frac{\lambda _1q^{\prime }}{2(\lambda _1^2-\lambda _2^2)},\end{aligned}$$

(52)

$$\begin{aligned}&\phi _2^2+\psi _2^2=\frac{a_1+8\lambda _2^2q}{8(\lambda _2^2-\lambda _1^2)},\end{aligned}$$

(53)

$$\begin{aligned}&\phi _2^2-\psi _2^2=\frac{\lambda _2q^{\prime }}{2(\lambda _2^2-\lambda _1^2)}. \end{aligned}$$

(54)

Further, we can also rewrite Eqs. (27) and (28) as a linear system:

$$\begin{aligned} {\left\{ \begin{array}{ll} 4\lambda _1\phi _1\psi _1+4\lambda _2\phi _2\psi _2=F_0-q^2,\\ 16\lambda _1^3\phi _1\psi _1+16\lambda _2^3\phi _2\psi _2=F_1+F_0^2+q^{\prime 2}\\ \qquad -2qq^{\prime }-3q^4+2F_0q^2. \end{array}\right. } \end{aligned}$$

(55)

Solving Eqs. (55) with Cramer’s rule, we have

$$\begin{aligned}&\phi _1\psi _1=\frac{F_1+F_0^2+q^{\prime 2}-2qq^{\prime \prime }-3q^4+2F_0q^2+4 \lambda _2^2q^2-4\lambda _2^2F_0}{16\lambda _1(\lambda _1^2-\lambda _2^2)},\end{aligned}$$

(56)

$$\begin{aligned}&\phi _2\psi _2=\frac{F_1+F_0^2+q^{\prime 2}-2qq^{\prime \prime }-3q^4+2F_0q^2+4 \lambda _1^2q^2-4\lambda _1^2F_0}{16\lambda _2(\lambda _2^2-\lambda _1^2)}. \end{aligned}$$

(57)

By use of Eqs. (25), (33), (38) and (40), Eqs. (56) and (57) are simplified to the forms

$$\begin{aligned}&\phi _1\psi _1=\frac{\lambda _1(a_2-4\lambda _1^2-2q^2)}{8(\lambda _1^2-\lambda _2^2)},\end{aligned}$$

(58)

$$\begin{aligned}&\phi _2\psi _2=\frac{\lambda _2(a_2-4\lambda _2^2-2q^2)}{8(\lambda _2^2-\lambda _1^2)}. \end{aligned}$$

(59)

4 Darboux transformation

The DT method is a very important tool to construct the exact solutions of nonlinear integrable equations [32,33,34,35,36]. Assume that $\varPhi _j=[f_j(x,t),g_j(x,t)]^T$ $(1 \le j \le N)$ are N sets of linearly independent solutions of Eqs. (2a) and (2b) with different spectral parameters $\lambda _j$ $(1 \le j \le N)$. The N-fold DT of Eq. (1) can be constructed by the eigenfunction transformation

$$\begin{aligned} \varPsi _{[N]}= & {} T_{[N]}\varPsi , T_{[N]}\nonumber \\= & {} \left( \begin{array}{cc} \lambda ^N-\sum \limits _{j=1}^{N}a_{j}(x,t)\lambda ^{j-1}&{} -\sum \limits _{j=1}^{N}b_{j}(x,t)(-\lambda )^{j-1}\\ -\sum \limits _{j=1}^{N}c_{j}(x,t)\lambda ^{j-1}&{} \lambda ^N-\sum \limits _{j=1}^{N} d_{j}(x,t)(-\lambda )^{j-1} \end{array}\right) ,\nonumber \\ \end{aligned}$$

(60)

and the potential transformation

$$\begin{aligned} q_{[N]}(x,t)= & {} q(x,t)+2(-1)^{N-1}b_N\nonumber \\= & {} q(x,t)+2\frac{\tau _{N+1,N-1}}{\tau _{N,N}}, \end{aligned}$$

(61)

with

$$\begin{aligned} \tau _{M,L}=\left| \begin{array}{cc} F_{N\times M} &{}G_{N\times L} \\ G_{N\times M}&{}-F_{N\times L} \end{array}\right| , (M+L=2N) \end{aligned}$$

(62)

where the block matrices $F_{N {\times } M}=[{\lambda }_{j}^{m-1}{f}_{j}(x,t)]_ {\begin{array}{c} {1}{\leqslant } {j}{\leqslant } {N} \\ {1}{\leqslant } {m}{\leqslant } {M} \end{array}} \text {and} G_{{N}\times {L}}=[(-{\lambda }_{j})^{m-1}{g}_{j}(x,t)]_ {\begin{array}{c} {1}{\leqslant } {j}{\leqslant } {N} \\ {1}{\leqslant } {m}{\leqslant } {L} \end{array}}$.

For $N=1$, $N=2$ and $N=3$ in Eq. (61), the one-, two- and three-fold potential transformation formulas can be represented as

$$\begin{aligned} q_{[1]}(x,t)= & {} q(x,t)+ 2\frac{\left| \begin{array}{cc} f_1&{}\lambda _1f_1\\ g_1&{}-\lambda _1g_1\end{array}\right| }{\left| \begin{array}{cc} f_1&{}g_1\\ g_1&{}-f_1\end{array}\right| }, \end{aligned}$$

(63)

$$\begin{aligned} q_{[2]}(x,t)= & {} q(x,t)+ 2\frac{{\left| \begin{array}{cccc} f_1&{}\lambda _1f_1&{}\lambda _1^2f_1&{}g_1\\ f_2&{}\lambda _2f_2&{}\lambda _2^2f_2&{}g_2\\ g_1&{}-\lambda _1g_1&{}\lambda _1^2g_1&{}-f_1\\ g_2&{}-\lambda _2g_2&{}\lambda _2^2g_2&{}-f_2\end{array}\right| }}{\left| \begin{array}{cccc} f_1&{}\lambda _1f_1&{}g_1&{}-\lambda _1g_1\\ f_2&{}\lambda _2f_2&{}g_2&{}-\lambda _2g_2\\ g_1&{}-\lambda _1g_1&{}-f_1&{}-\lambda _1f_1\\ g_2&{}-\lambda _2g_2&{}-f_2&{}-\lambda _2f_2\end{array}\right| }, \nonumber \\\end{aligned}$$

(64)

$$\begin{aligned} q_{[3]}(x,t)= & {} q(x,t)\nonumber \\&+2\frac{{\left| \begin{array}{cccccc} f_1&{}\lambda _1f_1&{}\lambda _1^2f_1&{}\lambda _1^3f_1&{}g_1&{}-\lambda _1g_1\\ f_2&{}\lambda _2f_2&{}\lambda _2^2f_2&{}\lambda _2^3f_2&{}g_2&{}-\lambda _2g_2\\ f_3&{}\lambda _3f_3&{}\lambda _3^2f_3&{}\lambda _3^3f_3&{}g_3&{}-\lambda _3g_3\\ g_1&{}-\lambda _1g_1&{}\lambda _1^2g_1&{}-\lambda _1^3g_1&{}-f_1&{}-\lambda _1f_1\\ g_2&{}-\lambda _2g_2&{}\lambda _2^2g_2&{}-\lambda _2^3g_2&{}-f_2&{}-\lambda _2f_2\\ g_3&{}-\lambda _3g_3&{}\lambda _3^2g_3&{}-\lambda _3^3g_3&{}-f_3&{}-\lambda _3f_3\\ \end{array}\right| }}{\left| \begin{array}{cccccc} f_1&{}\lambda _1f_1&{}\lambda _1^2f_1&{}g_1&{}-\lambda _1g_1&{}\lambda _1^2g_1\\ f_2&{}\lambda _2f_2&{}\lambda _2^2f_2&{}g_2&{}-\lambda _2g_2&{}\lambda _2^2g_2\\ f_3&{}\lambda _3f_3&{}\lambda _3^2f_3&{}g_3&{}-\lambda _3g_3&{}\lambda _3^2g_3\\ g_1&{}-\lambda _1g_1&{}\lambda _1^2g_1&{}-f_1&{}-\lambda _1f_1&{}-\lambda _1^2f_1\\ g_2&{}-\lambda _2g_2&{}\lambda _2^2g_2&{}-f_2&{}-\lambda _2f_2&{}-\lambda _2^2f_2\\ g_3&{}-\lambda _3g_3&{}\lambda _3^2g_3&{}-f_3&{}-\lambda _3f_3&{}-\lambda _3^2f_3 \end{array}\right| }.\nonumber \\ \end{aligned}$$

(65)

5 The second solution of spectral problem

In this section, in order to obtain new solutions of Eq. (1) on the periodic background, we construct the second linearly independent solution $\varPhi = (\widetilde{\phi }_1,\widetilde{\psi }_1)^T$ of spectral problem (2a) and (2b) with the same eigenvalue $\lambda =\lambda _1$.

When $q(x,t)=q(x-ct)$ is a periodic travelling wave solution to Eq. (1), we need to consider that the eigenfunction $\varPhi (x,t)=\varPhi (x-ct)$ also satisfies the time evolution in spectral problem (2). Substituting the eigenfunction $\varPhi =(\phi _1(x-ct),\psi _1(x-ct))^T$ into Eq. (2b), we have

$$\begin{aligned}&\frac{\partial \phi _1}{\partial t}+c\frac{\partial \phi _1}{\partial x} =\frac{\partial \phi _1}{\partial t}+(a_2^2-2a_0)\frac{\partial \phi _1}{\partial x}\\&\quad =\frac{1}{2}(a_2+4\lambda _1^2)\left( 8\lambda _1^3\phi _1-\psi _1 (a_1+8\lambda _1^2(\phi _1^2+\psi _1^2))\right. \\&\qquad \left. +8\lambda _1^2(\phi _1^2\psi _1+\psi _1^3 -\frac{\partial \phi _1}{\partial x})\right) =0, \end{aligned}$$

where Eqs. (51), (52) and (58) have been used for simplification. In a similar procedure as above, we can also verify that

$$\begin{aligned} \frac{\partial \psi _1}{\partial t}+c\frac{\partial \psi _1}{\partial x}=0. \end{aligned}$$

Therefore, $\phi _1(x,t)=\phi _1(x-ct)$ and $\psi _1(x,t)=\psi _1(x-ct)$ satisfy the time evolution in spectral problem (2).

According to the work in Ref. [17], the second linearly independent solution $\varPhi =(\widetilde{\phi }_1,\widetilde{\psi }_1)^T$ of spectral problem (2a) and (2b) with $\lambda =\lambda _1$ has the following explicit form:

$$\begin{aligned} \widetilde{\phi }_1=\phi _1\theta _1-\frac{2\psi _1}{\phi _1^2+\psi _1^2}, \widetilde{\psi }_1=\psi _1\theta _1+\frac{2\phi _1}{\phi _1^2+\psi _1^2},\nonumber \\ \end{aligned}$$

(66)

where $\theta _1$ is a function of x and t to be determined. Substituting Eqs. (66) into Eq. (2a) with $\lambda =\lambda _1$, we obtain

$$\begin{aligned} \frac{\mathrm{d}\theta _1}{\mathrm{d}x}=-\frac{8\lambda _1\phi _1\psi _1}{(\phi _1^2+\psi _1^2)^2}. \end{aligned}$$

(67)

With the use of Eqs. (51) and (58), we can rewrite Eq. (67) as

$$\begin{aligned} \frac{\mathrm{d}\theta _1}{\mathrm{d}x}=\frac{64\lambda _1^2(\lambda _1^2-\lambda _2^2) (-a_2+4\lambda _1^2+2q^2)}{(a_1+8\lambda _1^2q)^2}, \end{aligned}$$

(68)

which can be integrated to the form

$$\begin{aligned} \theta _1= & {} -16(\lambda _1^2-\lambda _2^2)\left[ 4\lambda _1^2\int _{0}^{x} \frac{a_2-4\lambda _1^2-2q^2}{(a_1+8\lambda _1^2q)^2}\, dy \right. \nonumber \\&\left. +\theta _0(t)\right] , \end{aligned}$$

(69)

where $\theta _0(t)$ is a undetermined integral constant depending on t.

Next, substituting both solutions $\varPhi =(\phi _1,\psi _1)^T$ and $\varPhi =(\widetilde{\phi }_1,\widetilde{\psi }_1)^T$ into Eq. (2b) with $\lambda =\lambda _1$, we arrive at

$$\begin{aligned}&\frac{\mathrm{d}\theta _1}{\mathrm{d}t}=\frac{16\lambda _1(-a_0+8\lambda _1^4+a_2q^2+4\lambda _1^2q^2)}{(\varPhi _1^2+\psi _1^2)^2}\\&\qquad -\frac{8\lambda _1(a_2+4\lambda _1^2)q'}{(\varPhi _1^2+\psi _1^2)^2}\\&\quad =\frac{8\lambda _1(c-a_2^2+16\lambda _1^4+2a_2q^2+8\lambda _1^2q^2)}{(\varPhi _1^2+\psi _1^2)^2}\\&\qquad -\frac{8\lambda _1(a_2+4\lambda _1^2)q'}{(\varPhi _1^2+\psi _1^2)^2}. \end{aligned}$$

Further, substituting Eqs. (52), (58) and (67) into the above expression, we have

$$\begin{aligned} \frac{\mathrm{d}\theta _1}{\mathrm{d}t}+c\frac{\mathrm{d}\theta _1}{\mathrm{d}x}=-16(\lambda _1^2-\lambda _2^2)(a_2+4\lambda _1^2). \end{aligned}$$

Finally, we obtain the exact expression for $\theta _1(x,t)$:

$$\begin{aligned} \theta _1(x,t)= & {} -16(\lambda _1^2-\lambda _2^2)\nonumber \\&\times \left[ 4\lambda _1^2\int _{0}^{x} \frac{a_2-4\lambda _1^2-2q^2}{(a_1+8\lambda _1^2q)^2}\, dy +\tau t\right] ,\nonumber \\ \end{aligned}$$

(70)

with $\tau =a_2+4\lambda _1^2$.

For the non-periodic solutions $(\widetilde{\phi }_2,\widetilde{\psi }_2)^T$ and $(\widetilde{\phi }_3,\widetilde{\psi }_3)^T$, they can be obtained by the transformation $(\phi _1,\psi _1)^T\rightarrow (\phi _2,\psi _2)^T,(\phi _1,\psi _1)^T\rightarrow (\phi _3,\psi _3)^T$ and $\theta _1\rightarrow \theta _2,\theta _1\rightarrow \theta _3$ with the interchanges $\lambda _1\leftrightarrow \lambda _2$ and $\lambda _1\leftrightarrow \lambda _3$, respectively.

6 Rogue waves

In this section, we will construct the rogue wave solutions of Eq. (1) on the periodic background by using the second linearly independent solutions of spectral problem (2a) and (2b) for the eigenvalues $\lambda _1,\lambda _2$ and $\lambda _3$.

Substituting $f_1=\widetilde{\phi }_1$ and $g_1=\widetilde{\psi }_1$ given by Eqs. (66) into the one-fold DT formula (63), we obtain a new solution of Eq. (1)

$$\begin{aligned} q_{[1]}=q+\frac{4\lambda _1A_1}{\left( \phi _1^2+\psi _1^2\right) ^2\theta _1^2+4}. \end{aligned}$$

(71)

with

$$\begin{aligned} A_1=\frac{\phi _1\psi _1}{\phi _1^2+\psi _1^2}\left[ (\phi _1^2+\psi _1^2)^2 \theta _1^2-4\right] +2(\phi _1^2-\psi _1^2)\theta _1. \end{aligned}$$

Substituting $(f_1,g_1)^T=(\widetilde{\phi }_1,\widetilde{\psi }_1)^T$ and $(f_2,g_2)^T=(\widetilde{\phi }_2,\widetilde{\psi }_2)^T$ into the two-fold DT formula (64), we derive a new solution of Eq. (1)

$$\begin{aligned}&q_{[2]}\nonumber \\&\quad =q+\frac{4(\lambda _1^2-\lambda _2^2)(\lambda _1A_1B_2-\lambda _2A_2B_1)}{(\lambda _1^2+\lambda _2^2)B_1B_2-8\lambda _1\lambda _2A_1A_2-2 \lambda _1\lambda _2C_1C_2},\nonumber \\ \end{aligned}$$

(72)

where for $j=1,2$

$$\begin{aligned} A_j= & {} \frac{\phi _j\psi _j}{\phi _j^2+\psi _j^2}\left[ (\phi _j^2+\psi _j^2)^2 \theta _j^2-4\right] \\&+2(\phi _j^2-\psi _j^2)\theta _j,\\ B_j= & {} (\phi _j^2+\psi _j^2)^2\theta _j^2+4,\\ C_j= & {} \frac{\phi _j^2-\psi _j^2}{\phi _j^2+\psi _j^2}\left[ (\phi _j^2+\psi _j^2)^2 \theta _j^2-4\right] -8\phi _j\psi _j\theta _j. \end{aligned}$$

Similarly, by the substitution of $(f_1,g_1)^T=(\widetilde{\phi }_1,\widetilde{\psi }_1)^T$ , $(f_2,g_2)=(\widetilde{\phi }_2,\widetilde{\psi }_2)^T$ and $(f_3,g_3)=(\widetilde{\phi }_3,\widetilde{\psi }_3)^T$ into the three-fold DT formula (65), a new solution of Eq. (1) can be derived.

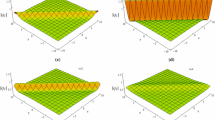
For the periodic travelling wave solution (10), we take $Q_1=2$, $Q_2=-0.25$, $Q_3=-0.75$ and $Q_4=-1$. Inserting them into Eqs. (43), we can obtain three different choices for the eigenvalue. Therefore, from one-fold DT formula (71), three new solutions of Eq. (1) can be derived. Their profile plots are presented in Fig. 1a–c. It is seen that they display a bright algebraic soliton propagating on the periodic background of the elliptic function solution (10). For the two-fold solution (72), there are also three different choices for two eigenvalues expressed by Eq. (43). In Fig. 2a–c, we display the plots of three solutions depending on the choices of different two eigenvalues. It is shown that two propagating solitons collide on the periodic background. The highest points of the plots are all at the center. These peaks at origin can be considered as rogue waves.

Fig. 1

The one-fold transformation solution (71) on the background periodic solution (10) with three different choices of eigenvalue

Fig. 2

The two-fold transformation solution (72) on the background of periodic solution (10) with three different choices of two eigenvalues

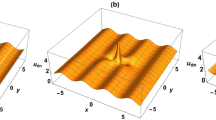
For the periodic travelling wave solution (14), we choose the parameters $a=1.5$, $b=-0.5$, $\alpha =-0.5$ and $\beta =2$. Inserting them into Eqs. (45), the values of three eigenvalues $\lambda _1$, $\lambda _2$ and $\lambda _3$ can be determined. For the one-fold transformation, there is only one possible choice for the eigenvalue, i.e., the real eigenvalue $\lambda _3$. In this case, the profile of the solution (71) is shown in Fig. 3a for $\lambda _3=0.5$, from which it is seen that the profile of the wave looks like a propagating soliton on the background of the periodic travelling wave. For the two-fold transformation, we choose a pair of complex conjugate eigenvalues $\lambda _1$ and $\lambda _2$. In this case, the solution describes a rogue wave in the center on the periodic background, as shown in Fig. 3b. For the three-fold transformation, three eigenvalues are all used in Eq. (45). From Fig. 3c, it is seen that two solitons collide on the periodic background and a rogue wave is located at the center.

Fig. 3

The one-, two-, and three-fold transformation solutions on the background of periodic solution (14)

Finally, it should be pointed out that the simulation results in Figs. 1, 2 and 3 agree well with the analytic solutions of Eq. (1), which is consistent with the theoretical analysis in Ref. [25]. Particularly for both initial background solutions (3) and (4), we can also numerically investigate the generation mechanism of rogue waves in Eq. (1). Of special interest, we have found that those simulation results can reduce to the rational and exponential solitons. Therefore, our simulation experiments can support the theoretical analysis for characteristics of rogue waves in Eq. (1).

7 Conclusion and discussion

In this paper, we have constructed rogue wave solutions of the fifth-order Ito equation on the background of general periodic travelling wave solutions. Based on the sub-equation method, we have presented the general periodic travelling wave solutions. By the Darboux transformation method, we have derived one-, two- and three-fold rogue wave solutions on the background of obtained periodic travelling wave solutions. We have provided several illustrations of such rogue waves and patterns of their interactions. As a result, since these solutions can describe phenomena of rogue waves on the periodic background, we expect that the results obtained in this work will be useful for physical experiments such as in nonlinear fiber optics with oscillating background.

In Ref. [25], some rogue wave solutions of Eq. (1) have been studied on the background of Jacobi elliptic function solutions (3) and (4). Through comparing our obtained results with those published previously, we find that the solutions in the present paper are more general than those. Finally, it is pointed out that the obtained results in our paper will be useful to further understand the generation of rogue waves, and they can be extended to the other Ito equations and the modified Korteweg–de Vries hierarchy of equations.