1 Introduction

Hysteresis is a nonlinear behavior that is present in several systems and devices. It is commonly related to the phenomena of ferromagnetism, plasticity, and friction, among others [56]. Some examples include mechanical, electronic and biomedical systems, as well as sensors and actuators such as magnetorheological dampers, piezoelectric actuators, and pneumatic control valves [20, 46, 50]. An intrinsic feature of such systems is the memory effect, meaning that the output depends on the history of the corresponding input.

In addition to the memory effect, the literature provides different definitions and conditions to distinguish such systems and characterize the hysteretic behavior. In some cases, the occurrence of hysteresis has been associated with the existence of several fixed points whenever these systems are subject to a constant [41] or time-varying [37] input signal. Additionally, hysteresis has also been defined as a hard nonlinearity that depends on the magnitude and rate of the input signal. These aspects can pose various performance limitations if not properly taken into account during the control design [50, 55]. Hence, a common goal is to attenuate the hysteretic behavior of the system [18, 57, 63] prior to feedback control design.

In many approaches, the compensation of hysteresis starts with obtaining a suitable model. In the literature, several hysteresis models have been proposed based on phenomenological, black-box, and gray-box modeling approaches.

In the realm of models based on first principles, important contributions have been made based on differential equations and operators [28], such as the Bouc–Wen model [58], the Duhem model [42], the Preisach model [26], and the Prandtl–Ishlinskii operator [15]. These models have been widely used to predict the hysteresis behavior due to their ability to describe a variety of hysteresis loops that resemble the proprieties of a wide class of real nonlinear hysteretic systems [53]. Besides, such models are known to be challenging for system identification techniques [48]. In some cases, as for the Bouc–Wen model that has a well-known structure, the challenge stems from the problem of estimating its parameters, which appear nonlinearly in the equation. This has led many works in the literature to focus on how to estimate the parameters of such a model, which often requires sophisticated optimization algorithms [16, 31, 60]. Apart from the computational effort required in the identification of phenomenological models, their application in the design of compensators is somewhat limited due to their structural complexity [28, 46].

From the point of view of black-box modeling, there are few works that compare techniques in the identification of hysteretic systems [43]. In this context, nonlinear autoregressive with exogenous inputs (NARX) models are considered a convenient choice due to their ability to predict a wide class of nonlinear behaviors [34, 35]. Nevertheless, very few works consider NARX models, especially in polynomial form, in the representation of hysteresis, and in most cases, the approach is black-box and structure selection is mostly ad hoc. Interesting works that fall in this category are [43], where the estimated model has 32 terms and [61] where a model with no less than 84 terms was estimated. Although these models can predict the temporal response of the hysteretic system, no critical analysis with respect to their ability to describe behaviors that are commonly used to characterize such systems, e.g., hysteresis loop, was done.

Related work was performed by Masri and co-workers using continuous-time polynomials [39] in a black-box fashion. As with the previous papers, the authors set off with a large model either 22 or 42 terms, but in a second stage, they prune the model by eliminating those terms with small coefficients. This procedure is known to lack robustness with respect to noise [1], as was confirmed by the authors in [39]. The need for a more careful structure selection procedure was also acknowledged by them. In a similar vein, apart from continuous-time monomials the authors in [14] use Chebyshev polynomials and point out that very compact models were possible to be obtained at the cost of some performance, but still presenting some important aspects of hysteresis. It should be emphasized that black-box modeling does not rely on prior knowledge about the system [10, 17, 25]. Consequently, relevant features that should be present in a model to reproduce hysteresis and an appropriate structure for designing compensators are not ensured by black-box techniques. Hence, the search for models that have specific features that are accurate and that have a suitable structure for designing compensators remains an open problem. Results in the field of neural networks can be found in [4, 6, 45].

As for the use of gray-box techniques, it is first pointed out that there are very few works in this field and that the term gray box is applied in a variety of ways. For instance, one of the very few papers to address some sort of gray-box modeling for hysteretic system is [61]. However, by gray box the authors refer to the use of physically inspired model structures. Specifically, they estimate parameters for LuGre and Maxwell slip models. Hence, despite the title of the paper, the problem addressed is the estimation of parameters for such well-established model structures. It can be argued that this falls into the category of gray-box modeling where the auxiliary information is the model structure itself. In this paper, we follow a different route in which the auxiliary information assumed is only that the system that produced the data is hysteretic.

A particular advantage of models obtained using gray-box techniques is that they can be tailored to reproduce specific relevant features [3]. For this purpose, the use of NARX models has been found appropriate [21, 36, 37, 59], since they have interesting features with respect to the ability to predict nonlinear behaviors and the structural flexibility. In addition, it has been argued that it is viable to enforce constraints on the model structure in order to make it suitable for designing compensators [44].

An important step in modeling the hysteresis nonlinearity was advanced in [37], in which sufficient conditions were presented for NARX models to display a hysteresis loop when subject to a certain class of input signals. An appealing feature is the performance and generality achieved with a simple model of 4 terms, which is promising for designing compensators. Additionally, the concept of a bounding structure \(\mathcal{H}\) formed by sets of stable equilibria and its implication on the existence of the hysteresis loop in the identified models was introduced in [37]. However, for more general cases, this concept and conditions need to be adapted. For instance, the conditions proposed in [37] are not sufficient to ensure the existence of multiple fixed points at steady state which is a very important feature for hysteretic systems [12, 41]. Despite this, to the best of the authors knowledge, there are no works in the literature of NARX polynomial models that guarantee such a feature. Also, the concept of bounding structure is limited to cases in which the sets of equilibria that form this structure are stable. As with [37], the approach proposed in this paper does not deal with non-local memory effect [40].

Finally, as for the compensation of hysteresis, there are some works in the literature that use specific models, such as Bouc–Wen [49] and the Prandtl–Ishlinskii operator [27, 50]. However, not every hysteretic system can be represented by such models. Besides, there are many challenges related to the estimation of the parameters of such nonlinear-in-the-parameter models. Also, their structural complexity represents an additional difficulty in the design of compensators. On the other hand, NARX polynomial models are both quite general and can present simple structure. However, the literature on the use of NARX models in the compensation of hysteresis is still scarce [22, 33]. One of the very few papers that are concerned with obtaining structurally simple NARX models that are particularly suitable for model-based control is [36]. Although the authors identify a compact model for a hysteretic system, they have not used the identified model in any control or compensation scheme. It is also important to note that the methodology proposed by them does not guarantee that the identified models are suitable for designing compensators. This can be verified by manipulating such a compact model in [36] to obtain a compensator following the strategies provided in the present work. As a result, it can be seen that the compensator obtained would have a singularity when the velocity variable is equal to zero. A similar problem would happen in [33]. The lack of NARX-based methods for hysteresis design can arguably be explained by the modeling problems that could not be solved in the context of black-box techniques. With such hurdles out of the way, simple model-based techniques can be now developed.

The main contributions of this work are: the proposition of a specific parameter constraint that ensures reproducing a key feature of hysteresis through identified NARX models. A framework is put forward to explain how the hysteresis loop results from an interplay of attracting and repelling regions in the input–output plane. Moreover, some structural specifications are enforced during the identification procedure in such a way that the identified NARX model can be effectively used to mitigate the hysteresis nonlinearity. Hence, two model-based compensation strategies are introduced. In the first, the compensation law is obtained through simple algebraic manipulations performed on the identified models. In the second strategy, the compensation law is directly identified from the data. It has been found that the compensators based on gray-box models outperform those that use models identified following black-box techniques.

This work is organized as follows: Sect. 2 presents the background. A constraint to ensure hysteresis in the identified models and a framework for understanding how the hysteresis loop is formed are provided in Sect. 3. Based on NARX models, two strategies to design compensators are detailed in Sect. 4. The numerical and experimental results for the model identification and the compensator design are, respectively, given in Sect. 5 and 6 . Section 7 presents the concluding remarks.

1.1 Notation

Below is a list of some of the symbols and variable used:

\(n_u,\,n_y\): maximum input and output lags;

\(n_\theta \): dimension of the parameter vector \({\varvec{\theta }}\);

\(\tau _{\mathrm{d}}\): pure time delay;

\(\tau _u,\,\tau _y\): arbitrary input and output delays;

\(\tau _{\mathrm{s}}\): number of time steps that \(y_k\) should be delayed with respect to \(u_k\);

\(\varSigma _y\): sum of parameters of all linear output regressors;

\(\phi _{1,k}\): first difference of the input \(u_k\);

\(\phi _{2,k}\): sign\((\phi _{1,k})\);

\({\bar{u}},\,{\bar{y}}\): steady-state values of \(u_k\) and \(y_k\);

\({\tilde{y}}\): output resulting from quasi-static analysis;

\(r_k,\, m_k\): reference and compensation signal;

\(\breve{\bullet }\): indicates a variable or function of the inverse model \(\breve{{\mathcal {M}}}\).

2 Background

A NARX model can be represented as [34]:

$$\begin{aligned} y_k = {\tilde{F}}\big (y_{k-1},\cdots ,y_{k-n_{y}}, \,u_{k-\tau _{\mathrm{d}}},\cdots ,u_{k-n_u}\big ), \end{aligned}$$
(1)

where \(y_k \in {\mathbb {R}}\) is the output at instant \(k \in {\mathbb {N}}\), \(u_k \in {\mathbb {R}}\) is the input, \(n_y\) and \(n_u\) are the maximum lags for the output and input, respectively, \(\tau _{\mathrm{d}} \in {\mathbb {N}}^{+}\) is the pure time delay, and \({\tilde{F}}(\cdot )\) is a nonlinear function of the lagged inputs and outputs.

This work considers a linear-in-the-parameters extended model set [13] of the NARX model (1) with the addition of specific functions, such as absolute value, trigonometric, and sign function. The goal is to choose functions that allow the models to predict systems whose nonlinearities cannot be well approximated using only regressors based on monomials of lagged input and output values. For instance, [13] recommends the addition of absolute value and sine functions as candidate regressors for the identification of a damped and forced nonlinear oscillator. In the case of the identification of systems with hysteresis, [37] shows that including the regressor given by sign of the first difference of the input, i.e., \(\mathrm{sign}(u_k-u_{k-1})\), in addition to polynomial terms is a sufficient condition to reproduce hysteresis. Therefore, in this work the models are of the type:

$$\begin{aligned} y_k= & {} F^{\ell }\big (y_{k-1},\cdots ,y_{k-n_{y}}, \,u_{k-1},\cdots ,u_{k-n_u}, \nonumber \\& \phi _{1,\,k-1}, \,\phi _{2,\,k-1} \big ), \end{aligned}$$
(2)

where \(\phi _{1,\,k}{=}u_k-u_{k-1}\), \(\phi _{2,\,k} {=} \mathrm{sign}(\phi _{1,\,k})\), and \(F^{\ell }(\cdot )\) is a polynomial function of the regressor variables up to degree \(\ell \in {\mathbb {N}}^{+}\). The addition of the regressors \(\phi _{1,\,k}\) and \(\phi _{2,\,k}\) does not affect the number, location, and stability of fixed points [7]. The definition of fixed points is given below.

Definition 1

(Fixed points [7]). The steady-state analysis of the model (2) is computed by taking \(y_k{=}{\bar{y}},\,\forall k\), \(u_k{=}{\bar{u}},\,\forall k\) and, consequently, \(\phi _{1,\,k}{=}u_k-u_{k-1}{=}0\) and \(\phi _{2,\,k}{=}\mathrm{sign}(\phi _{1,\,k}){=}0,\,\forall k\), yielding \({\bar{y}} = {\bar{F}}^{\ell }({\bar{y}},{\bar{u}})\), whose solution \({\bar{y}}\) for a given constant value of input \({\bar{u}}\) is defined as the fixed point, or equilibria, of model (2).  \(\square \)

The number of solutions for which the model remains invariant, given \({\bar{u}}\), depends on the maximum degree of output regressors in the model. Hysteretic models are characterized by the fact that any solution obtained with a constant input is an equilibria and, therefore, such models have a continuum of steady-state solutions, whose definition is given below which assumes that \(F^\ell \) is smooth.

Definition 2

(Continuum of steady-state solutions [41]). Let \(u_k{=}{\bar{u}},\,\forall k\), be any constant input of model (2). Hence, \(\phi _{1,\,k}{=}u_k-u_{k-1}{=}0\) and \(\phi _{2,\,k}{=}\mathrm{sign}(\phi _{1,\,k}){=}0,\,\forall k\), thus yielding \(y_k {=} F^{\ell }(y_{k-1},\cdots ,y_{k-n_{y}}, {\bar{u}})\), where \(y_k\) is the output at instant k given \({\bar{u}}\). If in steady state, for each constant \({\bar{u}}\), \(y_k\) converges and remains  at some constant value \({\bar{y}}\), then the model (2) has a continuum of steady-state solutions. \(\square \)

Evaluating model (2) along a data set of length N, the resulting set of equations can be expressed in matrix form as:

$$\begin{aligned} {\varvec{y}}=\varPsi \hat{{\varvec{\theta }}}+{\varvec{\xi }}, \end{aligned}$$
(3)

where \({\varvec{y}} \triangleq [y_k\,\, y_{k-1}\,\cdots \, y_{k+1-N}]^T \in {\mathbb {R}}^N\) is the vector of output measurements, \(\varPsi \triangleq [\psi _{k-1}^T;\, \cdots ;\, \psi ^T_{k-N}] \in {\mathbb {R}}^{N\times n_{\theta }}\) is the regressor matrix composed by the regressors vectors \(\psi _{k-j} \in {\mathbb {R}}^{n_{\theta }}\) which contains linear and nonlinear combinations of the variables that compose \(F^{\ell }(\cdot )\) in (2) weighted by the parameter vector \(\hat{{\varvec{\theta }}} \in {\mathbb {R}}^{n_{\theta }}\), \({\varvec{\xi }} \triangleq [\xi _k\,\, \xi _{k-1}\,\cdots \, \xi _{k+1-N}]^T \in {\mathbb {R}}^{N}\) is the residual vector and T indicates the transpose.

The unconstrained least squares batch estimator is given by \(\hat{{\varvec{\theta }}}_{\mathrm{LS}}=(\varPsi ^T\varPsi )^{-1}\varPsi ^T{\varvec{y}}.\) A set of equality constraints on the parameter vector is \({\varvec{c}}=S{\varvec{\theta }}\), where \({\varvec{c}} \in {\mathbb {R}}^{n_c}\) and \(S \in {\mathbb {R}}^{n_c\times n_{\theta }}\) are known constants. Then, the constrained least squares estimation problem is

$$\begin{aligned} \hat{{\varvec{\theta }}}_{\mathrm{CLS}} = \underset{{\varvec{\theta }}\,:\,{\varvec{c}}=S{\varvec{\theta }}}{\arg \min } \big [{\varvec{\xi }}^T{\varvec{\xi }}\big ], \end{aligned}$$
(4)

whose solution is [23]:

$$\begin{aligned} \hat{{\varvec{\theta }}}_{\mathrm{CLS}} {=} \hat{{\varvec{\theta }}}_{\mathrm{LS}}{-}(\varPsi ^T\varPsi )^{-1}S^T[S(\varPsi ^T\varPsi )^{-1}S^T]^{-1}(S\hat{{\varvec{\theta }}}_{\mathrm{LS}}{-}{\varvec{c}}). \nonumber \\ \end{aligned}$$
(5)

In this paper, the model structure is chosen using the error reduction ratio (ERR) [19] together with Akaike’s information criterion (AIC) [8]. Other approaches that have proved to be useful in more demanding contexts are presented in [9, 24, 38, 47, 51].

3 Identification of systems with hysteresis

Some of the features of hysteretic systems are: a characteristic loop behavior displayed on the input–output plane [12], several stable fixed points [41], and multi-valued mapping [21]. However, which and how these features can be used in the identification procedure remains an open problem.

In what follows, a constraint is proposed to ensure a key feature of hysteresis. Also, it is shown how the hysteresis loop can be seen as an interplay of attracting and repelling regions in the input–output plane of certain models. Then, in the sequel the resulting models will be used to design compensators. We start with a property (see [12, 37, 41]).

Property 1

An identified hysteretic model, under a constant input, has two or more real non-diverging equilibria. \(\square \)

In [37], Property 1 was attained by ensuring that the model had at least one fixed point under loading–unloading inputs, with different values for loading and unloading. Thus, in (2) \(\phi _{1,\,k}{=}u_k-u_{k-1}\) and \(\phi _{2,\,k} = \mathrm{sign}(\phi _{1,\,k})\), with \(\phi _{2,\,k} {=}1\) for loading, and \(\phi _{2,\,k} {=}-1\) for unloading.

Hysteresis is a nonlinear behavior that appears in both the static response and the dynamics. In some works, this nonlinearity is classified as quasi-static because the analyses are performed when the system is excited by a periodic signal that is very slow compared to the system dynamics [29].

Based on a static analysis of NARX models (2), we will show which constraints need to be considered in the identification procedure in order for Property 1 to be satisfied. Thereafter, a quasi-static analysis will be used to describe how hysteresis happens in these models and an illustrative example will be presented.

3.1 Static analysis

By means of static analysis, it is possible to determine the fixed points of a model, as described in Definition 1.

Assumption 1

(Systems with hysteresis). In order to comply with Property 1, following the recommendation of the literature, the identified models should not have the following regressors:

  1. (i)

    \(y^{p}_{k-\tau _y}\), \(y^{p}_{k-\tau _y}\phi _{1,\,k-\tau _u}^m\) and \(y^{p}_{k-\tau _y}\phi _{2,\,k-\tau _u}^m\) for \(p{>}1,\,\forall m\) [7],

  2. (ii)

    \(\mathrm{sign}(u_{k-\tau _u}-u_{k-\tau _u-1})^m=\phi ^m_{2,\,k-\tau _u}\) for \(m>1\) [37],

as will be shown in this paper, the following regressors can also be removed

  1. (iii)

    \(y^{p}_{k-\tau _y}u^m_{k-\tau _u}\) and \(u^m_{k-\tau _u}\) \(~\forall p,\,m\),

where \(\tau _y\) and \(\tau _u\) are any time lags. \(\square \)

The steady-state analysis is done by taking \(y_k={\bar{y}},\,\forall k\), \(u_k={\bar{u}},\,\forall k\) and, consequently, \(\phi _{1,\,k}=u_k-u_{k-1}=0\) \(\phi _{2,\,k}=\mathrm{sign}(\phi _{1,\,k})=0,\,\forall k\). For a model that complies with Assumption 1, we get \({\bar{y}}=\varSigma _y{\bar{y}}\), where \(\varSigma _y\) is the sum of all parameters of all linear output regressors. For the sake of clarity, we discuss the most common case, in which the hysteretic model only has one linear output term: \(\theta _1y_{k-1}\) [33, 37]. Hence, the model only has one fixed point for which stability analysis yields the following: if \(|\theta _1| < 1\) (\(|\theta _1| > 1\)), then \({\bar{y}}=0\) is a single asymptotically stable (diverging) equilibria and, as a result, Property 1 is not satisfied. To overcome this problem, with Definition 2 in mind, the following lemma is stated.

Lemma 1

Given that Assumption 1 holds, if \(\theta _1=1\), then the identified model has a continuum of solutions at steady state. \(\square \)

Proof

The steady-state analysis of a model that satisfies Assumption 1 and Lemma 1 yields \({\bar{y}}={\bar{y}}\) which is trivially true for any value \({\bar{y}}\). Hence, the model has a non-hyperbolic fixed point and will display a continuum of steady-state solutions  which will play the role required by Property 1. \(\square \)

Remark 1

Lemma 1 guarantees that the model fixed point is non-hyperbolic and in that way it will be able to guarantee multiple steady-state solutions. However, the case of a non-hyperbolic fixed point is known to be structurally unstable. Hence, unless the constraint in Lemma 1 is used, the probability of estimating a model with a non-hyperbolic fixed point is zero. If the model has more than one linear output term, the constraint in Lemma 1 becomes \(\varSigma _y=1\) and this will guarantee that the Jacobian matrix has one eigenvalue at 1. In order for the model to have a continuum of steady-state solutions, all the remaining eigenvalues of the Jacobian matrix evaluated at the fixed point must have modulus less than one. \(\square \)

3.2 Quasi-static analysis

The core idea of the framework proposed in [37] to identify models with a hysteresis loop is to build a bounding structure \(\mathcal{H}\) made of sets of equilibria and  to ensure that one set is stable during loading and the other one, during unloading. Such a scenario is effective, but it does not help to understand models with more complicated structures and with both attracting and repelling regions in the \(u \times y\) plane. This section aims at enlarging the scenario developed in [37].

In quasi-static analysis, it is assumed that the input \(u_k\) is a loading–unloading signal that is much slower than the system dynamics to the point that, at a given time k, the system will be in a certain attracting  region, avoiding any possible repelling  regions. Also, such regions depend on \(u_k\), \(\phi _{1,\,k}\) and \(\phi _{2,\,k}\). More specifically, there will be two sets of regions, one for loading and another for unloading.

In quasi-static analysis, we assume that \(y_k\approx y_{k-j}={\tilde{y}},~j=1,\,2,\ldots ,\,n_y\), such that (2) is given by

$$\begin{aligned} {\tilde{y}}\approx & {} F^{\ell }\big ({\tilde{y}}, \,u_{k-1},\cdots ,u_{k-n_u}, \, \phi _{1,\,k-1}, \,\phi _{2,\,k-1} \big ), \end{aligned}$$
(6)

which can be usually solved for \({\tilde{y}}\), especially if higher powers of the output are not in \(F^{\ell }(\cdot )\) [7]. This is achieved in practice by removing such group of terms from the set of candidates as done in Assumption 1. If the inputs are all constant, then \({\tilde{y}}\) will depend on such values.

Given a slow input, if \({\tilde{y}}\) is in an attractive region, then the model output moves toward an attracting solution. In what follows, \({\tilde{y}}_{\mathrm{L}}^{\mathrm{a}}\) and \({\tilde{y}}_{\mathrm{U}}^{\mathrm{a}}\) are, respectively, the solutions to (6) in attracting regions under loading and unloading; \({\tilde{y}}_{\mathrm{L}}^{\mathrm{r}}\) and \({\tilde{y}}_{\mathrm{U}}^{\mathrm{r}}\) are the counterparts in repelling regions. The conditions for \({\tilde{y}}\) to be attracting are

$$\begin{aligned} \left| \mathrm{eig} \left( \frac{\partial F^{\ell }(\mathbf{y},\,u_{k-1},\,\phi _{1,\,k-1},\, \phi _{2,\,k-1})}{\partial \mathbf{y}} \right) \right| <1 , \end{aligned}$$
(7)

where \(\mathbf{y}=[y_{k-1}\, \ldots y_{k-n_y}]^T\). This procedure resembles that of determining the stability of fixed points [7]. Here the Jacobian matrix is not evaluated at fixed points. Hence, we do not speak in terms of stable and unstable fixed points.

To illustrate how this helps to understand the formation of a hysteresis loop, consider the schematic representation in Fig. 1. The input is a loading–unloading signal such that \(u_{\mathrm{min}} \le u_k \le u_{\mathrm{max}},~\forall k\). The sets \({\tilde{y}}_{\mathrm{L}}^{\mathrm{a}}\), \({\tilde{y}}_{\mathrm{U}}^{\mathrm{a}}\), \({\tilde{y}}_{\mathrm{L}}^{\mathrm{r}}\) and \({\tilde{y}}_{\mathrm{U}}^{\mathrm{r}}\) are shown. Consider the point A, which takes place under loading; hence, only solutions \({\tilde{y}}_{\mathrm{L}}^{\mathrm{r}}\) and \({\tilde{y}}_{\mathrm{L}}^{\mathrm{a}}\) are active and should be considered. Given that the system is under the direct influence of \({\tilde{y}}_{\mathrm{L}}^{\mathrm{r}}\), which is responsible for pushing upwards (see vertical component \(y_{\mathrm{A}}\)), and it is the loading regime, there is a horizontal component \(u_{\mathrm{A}}\) (related to the input) that points to the right. The resulting effect is to pull the system along the loop in the NE direction. The same can be said for point B; however, at that point the vertical component is the result of the attracting action of \({\tilde{y}}_{\mathrm{L}}^{\mathrm{a}}\). A similar analysis can be readily done for the unloading regime, given by points D and E. At the turning points C and F, \(\phi _{2,\,k}\) switches from 1 to -1 and from -1 to 1, respectively. Hence, the analysis also switches from using \({\tilde{y}}_{\mathrm{L}}^{\mathrm{a}}\) and \({\tilde{y}}_{\mathrm{L}}^{\mathrm{r}}\), to using \({\tilde{y}}_{\mathrm{U}}^{\mathrm{a}}\) and \({\tilde{y}}_{\mathrm{U}}^{\mathrm{r}}\). This analysis is useful in Sect. 5 to understand the formation of hysteresis loops in identified models.

Fig. 1
figure 1

Schematic representation of hysteresis loop in the \(u \times y\) plane. Attracting sets are shown in black continuous lines, whereas the repelling sets are indicated in red dash dot. The hysteresis loop is indicated by dotted lines

Full size image

It is important to point out that the assumption that the set \({\tilde{y}}\) comes in two disjoint parts, either for loading or unloading, is a consequence of the solution of (6) being rational instead of polynomial. This is useful to analyze models with more general model structures. In addition, a NARX polynomial model, due to its simplicity, is typically unable reproduce a number of aspects found in more sophisticated hysteretic models, as in the Preisach model [26] and in the Masing model [30] that present some more subtle aspects of hysteresis.

It should be noted that the use of Lemma 1 enables to the model to “remember” its last state and remain there even when the input goes to zero (this was not the case in [37]). Also, since the hysteresis branches are here formed as a result of the position of fixed points, which depend on the model parameters which are fixed in this paper, so is the hysteresis loop. In order to enable the model to follow other branches, as seen in the Preisach model, we would need some mechanism for updating parameters recursively. This is not a concern in this work.

The following example illustrates the application of this analysis.

Example 1

Consider the following NARX model that complies with Assumption 1:

$$\begin{aligned} y_k= & {} \theta _1y_{k-1}+\theta _2\phi _{2,\,k-1}{+}\theta _3\phi _{1,\,k-1}u_{k-1} \nonumber \\&+\,\theta _4\phi _{2,\,k-1}\phi _{1,\,k-1}y_{k-1}{+}\theta _5\phi _{1,\,k-1}. \end{aligned}$$
(8)

In this case, the constraint \(\theta _1=1\) will be achieved using estimator (5) with \(c=1\) and \(S=[1\,\, 0\,\, 0\,\, 0\,\, 0]\). Hence, according to Lemma 1, the resulting model will have a continuum of steady-state solutions.

For a more complicated model structure, the constraint in Lemma 1 is still in the form \(1=S{\varvec{\theta }}\) (4) but with S having more than one element equal to one, e.g., as shown in [2] to obtain NARX models able to reproduce dead zone and in [5] for a quadratic nonlinearity.

The quasi-static analysis of model (8) is performed following the steps provided in Sect. 3.2. So rewriting this model as (6), we have

$$\begin{aligned} {\tilde{y}}\approx & {} \theta _1{\tilde{y}}{+}\theta _2{\phi }_{2,k-1}{+}\theta _3{\phi }_{1,k-1}u_{k-1} \\&+\,\theta _4{\phi }_{2,k-1}{\phi }_{1,k-1}{\tilde{y}} {+}\theta _5{\phi }_{1,k-1}, \end{aligned}$$

which can be described by

$$\begin{aligned} {\tilde{y}}({u},{\phi }_{1},{\phi }_{2}) {\approx } {\left\{ \begin{array}{ll} \dfrac{\theta _2+\theta _3{\phi }_{1}{u}+\theta _5{\phi }_{1}}{1-\theta _1-\theta _4{\phi }_{1}}, &{}\text {for} \,\,\,\,{\phi }_{2}{=}\,\,\,1; \\ \dfrac{-\theta _2+\theta _3{\phi }_{1}{u}+\theta _5{\phi }_{1}}{1-\theta _1+\theta _4{\phi }_{1}}, &{}\text {for} \,\,\,\,{\phi }_{2}{=}{-}1, \end{array}\right. } \end{aligned}$$
(9)

where the time indices have been omitted for simplicity. Therefore, the solution given at the top in (9) represents the set \({\tilde{y}}_{\mathrm{L}}\), while the bottom is the set \({\tilde{y}}_{\mathrm{U}}\).

To define whether the solutions to (9) are in the attracting or repelling regions, (7) should be computed for model (8). This yields

$$\begin{aligned}&-1< \theta _1 + \theta _4{\phi }_{2,k-1}{\phi }_{1,k-1}<1, \nonumber \\&\frac{-1-\theta _1}{\theta _4\phi _{2,k-1}}< {\phi }_{1,k-1} < \frac{1-\theta _1}{\theta _4\phi _{2,k-1}}. \end{aligned}$$
(10)

Since it is assumed that the input \(u_k\) is a loading–unloading signal, the conditions (10) to ensure that the solutions (9) are in attracting regions can be readily verified numerically. In Sects. 5 and  6, this analysis will be performed for the identified models. \(\square \)

4 Compensator design

Two procedures are proposed. The first one designs a compensator from a model \({\mathcal {M}}\) identified from u and y with output \({\hat{y}}_k\) (Sect. 4.2). The second is based on a model of the inverse relationship, in which case a model \(\breve{{\mathcal {M}}}\) is obtained to yield \({\hat{u}}_k\) (Fig. 2a and Sect. 4.3). Some of the algorithms and considerations adopted in the three main steps of system identification are also outlined in Fig. 2a.

4.1 Preliminaries

Given a nonlinear system \({\mathcal {S}}\), the first step is to obtain hysteretic models for \({\mathcal {S}}\) (Fig. 2a). In the second step, the identified model is used to design a compensator \({\mathcal {C}}\) that yields the compensation signal \(m_k\) for a given reference \(r_k\) (Fig. 2b).

Fig. 2
figure 2

Compensator design based on identified NARX models. a Model identification and b compensator design based on identified models

Full size image

In this paper, the following additional assumptions are made for NARX models (2).

Remark 2

For design, in models \({\mathcal {M}}\) and \(\breve{{\mathcal {M}}}\), \(y_k\) is replaced by \(r_k\) and \(u_k\) by \(m_k\), respectively. The motivation behind this is that \(y_k\) should ideally be equal to \(r_k\) under compensation, that is, when \(m_k\) is used as the input to the dynamical system. \(\square \)

4.2 Model-based compensation

In what follows, the main idea is to specify a general model structure for \({\mathcal {M}}\) to determine the compensation input \(m_{k-\tau _{\mathrm{d}}+1}\). The following assumption is needed.

Assumption 2

(The general case). It is assumed that: (i) the only regressor involving \(u_{k{-}\tau _{\mathrm{d}}}\) is linear; (ii) \(n_u>\tau _{\mathrm{d}}\); (iii) the compensation signal \(m_k\) is known up to time \(k{-}\tau _{\mathrm{d}}\); and (iv) the reference \(r_k\) is known up to time \(k{+}1\).

\(\square \)

Assumption 2 imposes conditions on the selection of the model structure (Fig. 2a). Note that (i) ensures that \(u_{k-\tau _{\mathrm{d}}}\) can be isolated; (ii) allows having as regressors input terms with a delay greater than \(\tau _{\mathrm{d}}\); and the other constraints guarantee that the control action can be computed from known values. Therefore, the model \({\mathcal {M}}\) is rewritten as:

$$\begin{aligned} A(q)y_k= & {} B(q)u_{k}{+}f\big (y_{k-1},{\cdots },y_{k-n_{y}},\nonumber \\&u_{k-\tau _{\mathrm{d}}-1},{\cdots }, u_{k-n_u}\big )\!, \end{aligned}$$
(11)

where \(q^{-1}\) is the backward time shift operator such that \(q^{-1}u_k{=}u_{k-1}\), and the linear regressors are grouped in \(A(q)y_k\) and \(B(q)u_{k}\) with

$$\begin{aligned} A(q)= & {} 1 - a_1q^{-1} - a_2q^{-2} - \cdots - a_{n_{y}}q^{-n_{y}}, \nonumber \\ \end{aligned}$$
(12)
$$\begin{aligned} B(q)= & {} b_{\tau _{\mathrm{d}}}q^{-\tau _{\mathrm{d}}} + \underbrace{b_{\tau _{\mathrm{d}}+1}q^{-\tau _{\mathrm{d}}-1} + \cdots + b_{n_{u}}q^{-n_{u}}}_{B^*(q)}, \nonumber \\ \end{aligned}$$
(13)

and \(f(\cdot )\) includes all the nonlinear terms and possibly the constant term of the NARX model (2). Using (13), model (11) can be rewritten as

$$\begin{aligned} A(q)y_k= & {} b_{\tau _{\mathrm{d}}} u_{k-\tau _{\mathrm{d}}}{+}B^*(q)u_{k}{+}f\big (y_{k-1}, \cdots , y_{k-n_{y}},\nonumber \\& u_{k-\tau _{\mathrm{d}}-1}, \cdots , u_{k-n_u} \big ). \end{aligned}$$
(14)

From Remark 2, we have

$$\begin{aligned} A(q)r_{k{+}1}= & {} b_{\tau _{\mathrm{d}}} m_{k-\tau _{\mathrm{d}}+1} {+}B^*(q)m_{k{+}1}{+}f\big (r_{k},\cdots ,\nonumber \\& r_{k-n_{y}{+}1}, m_{k-\tau _{\mathrm{d}}},\cdots ,m_{k-n_u{+}1}\big ), \end{aligned}$$
(15)

which, for convenience, has been written an instant of time ahead, i.e., \(k \rightarrow k+1\). From Assumption 2, the compensation input can be obtained from (15) as

$$\begin{aligned} m_{k-\tau _{\mathrm{d}}+1}= & {} \frac{1}{b_{\tau _{\mathrm{d}}} } \Big [A(q)r_{k{+}1}-B^*(q)m_{k{+}1}-f\big (r_k,\cdots ,\nonumber \\& r_{k-n_y{+}1}, m_{k-\tau _{\mathrm{d}}},\cdots ,m_{k-n_u{+}1}\big )\Big ]. \end{aligned}$$
(16)

Assumption 3

In the case of systems with hysteresis, it should be remembered that according to Assumption 1-(iii) regressors involving \(u^m_{k-\tau _u}\) \(~\forall m\) and any \(\tau _u\) are removed. Therefore, Assumption 2-(i) should read: the only regressor involving \(\phi _{1,\,k{-}\tau _{\mathrm{d}}}\) is linear, and the other items are maintained. \(\square \)

This is illustrated in the following example.

Example 2

Consider the NARX model that complies with Assumptions 1 and 3 described by:

$$\begin{aligned} y_k&=\theta _1y_{k-1}{+}\theta _2{\phi }_{2,\,k-2}{+}\theta _3{\phi }_{1,\,k-2}u_{k-2} \nonumber \\&\quad +\,\theta _4{\phi }_{2,\,k-2}{\phi }_{1,\,k-2}y_{k-1}{+}\theta _5{\phi }_{1,\,k-1}. \end{aligned}$$
(17)

Since \(\phi _{1,\,k}{=}u_k-u_{k-1}\) and \(\phi _{2,\,k} {=} \mathrm{sign}(\phi _{1,\,k})\), we have

$$\begin{aligned} y_k&=\theta _1y_{k-1}{+}\theta _2\mathrm{sign}(u_{k-2}\!-\!u_{k-3}){+}\theta _3[u_{k-2}\!-\!u_{k-3}]u_{k-2} \\&\quad +\,\theta _4\mathrm{sign}(u_{k{-}2}\!-\!u_{k\!-\!3})[u_{k{-}2}\!-\!u_{k{-}3}]y_{k{-}1}\\&\quad +\,\theta _5[u_{k{-}1}\!-\!u_{k\!-\!2}], \end{aligned}$$

which is in the form (11) and, therefore,

$$\begin{aligned} A(q)y_k= & {} B(q)u_{k}{+}f\big (y_{k-1},u_{k-2},\nonumber \\&u_{k-3},\mathrm{sign}(u_{k-2}-u_{k-3})\big ), \end{aligned}$$
(18)

where \(A(q) = 1 - \theta _1q^{-1}\), \(B(q) = \theta _5q^{-1} - \theta _5q^{-2}\), and

$$\begin{aligned} f(\cdot )= & {} \theta _2\mathrm{sign}(u_{k-2}-u_{k-3}){+}\theta _3[u_{k-2}-u_{k-3}]u_{k-2} \\&\,{+}\,\theta _4\mathrm{sign}(u_{k-2}-u_{k-3})[u_{k-2}-u_{k-3}]y_{k-1}. \end{aligned}$$

From Remark 2, the model (18) is recast as

$$\begin{aligned} A(q)r_{k{+}1} {=} \theta _5m_{k}{-}&\theta _5m_{k-1}{+}f\big (r_{k},m_{k-1},m_{k-2},\nonumber \\&\mathrm{sign}(m_{k-1}-m_{k-2})\big ), \end{aligned}$$
(19)

and, because Assumption 3 is satisfied, we have:

$$\begin{aligned} m_k= & {} \frac{1}{\theta _5} \Big [A(q)r_{k{+}1}{+}\theta _5m_{k-1} \nonumber \\&-f\big (r_k,m_{k-1},m_{k-2},\mathrm{sign}(m_{k-1}{-}m_{k-2})\big )\Big ], \nonumber \\= & {} \frac{1}{\theta _5}\Big [r_{k{+}1}-\theta _1r_{k}{+}\theta _5m_{k-1} \nonumber \\&-\,\theta _2\mathrm{sign}(m_{k-1}{-}m_{k-2})-\theta _3[m_{k-1}{-}m_{k-2}]m_{k-1} \nonumber \\&-\,\theta _4\mathrm{sign}(m_{k-1}{-}m_{k-2})[m_{k-1}{-}m_{k-2}]r_{k} \Big ] . \end{aligned}$$
(20)

\(\square \)

4.3 Compensation based on compensator identification

Here, the strategy is to identify NARX models \(\breve{{\mathcal {M}}}\) that describe the inverse relationship between u and y of \({\mathcal {S}}\). The advantage is that the compensator \({\mathcal {C}}\) is obtained directly from \(\breve{{\mathcal {M}}}\) (see Remark 2). However, some issues related to the identification procedure of these models need to be addressed. For simplicity, in this section, we assume that \(\tau _{\mathrm{d}}=1\).

For the inverse model \(\breve{{\mathcal {M}}}\), the output \({\hat{u}}_k\) depends on \(y_k\). Hence, in order to avoid the lack of causality, \(y_k\) should be delayed by \(\tau _{\mathrm{s}}\) time steps with respect to \(u_k\), yielding [62]:

$$\begin{aligned} {\hat{u}}_k {=} \breve{F}\big ({\hat{u}}_{k-1},\cdots ,{\hat{u}}_{k-n_{u}},y_{k-1{+}\tau _{\mathrm{s}}},\cdots ,y_{k-n_y+\tau _{\mathrm{s}}}\big ),\nonumber \\ \end{aligned}$$
(21)

where \(\breve{F}(\cdot )\) is the inverse nonlinear function and \({\hat{u}}_k \in {\mathbb {R}}\) and \(y_k \in {\mathbb {R}}\) are related as shown in Fig. 2a. It should be noted that \(\tau _{\mathrm{s}} \ge \tau _{\mathrm{d}}+1\), where usually the equality is preferred. Similar ways to avoid noncausal models can be found in the literature [33, 49].

Assumption 4

It is assumed that: (i) there is at least one regressor of the output \((y_k)^j\) for \(j \ge 1\); (ii) the compensation signal \(m_k\) is known up to time \(k-1\); and (iii) the reference \(r_k\) is known up to time \(k-1+\tau _{\mathrm{s}}\). \(\square \)

Assumption 4 should be observed during the structure selection of the inverse model \(\breve{{\mathcal {M}}}\). Note that (i) ensures that there is at least one input signal \(y_k\) in the identified models; (ii) and (iii) ensure that \(m_k\) to be computed at time k is the only unknown variable. Given Assumption 4 and Remark 2, the compensation signal \(m_k\) can be obtained directly from \(\breve{{\mathcal {M}}}\) as

$$\begin{aligned} m_k {=} \breve{F}\big (m_{k-1},\cdots ,m_{k-n_{u}},r_{k-1{+}\tau _{\mathrm{s}}},\cdots ,r_{k-n_y+\tau _{\mathrm{s}}} \big ).\nonumber \\ \end{aligned}$$
(22)

5 Numerical results

Two simulated examples are detailed in what follows. An experimental system is addressed in Sect. 6.

5.1 Identification of a bench test system

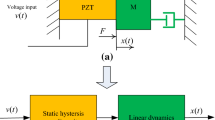
Consider the piezoelectric actuator with hysteretic nonlinearity modeled by the Bouc–Wen model [58] and whose mathematical model is given by [49]

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{h}}(t) &{}= ~A{\dot{u}}(t) - \beta |{\dot{u}}(t)|h(t) - \gamma {\dot{u}}(t)|h(t)|, \\ y(t) &{}=~d_{\mathrm{p}} u(t) - h(t), \end{array}\right. } \end{aligned}$$
(23)

where y(t) is the displacement, u(t) is the voltage applied to the actuator, \(d_{\mathrm{p}}=1.6\, \mathrm{\frac{\mu m}{V}}\) is the piezoelectric coefficient, h(t) is the hysteretic nonlinear term and \(A=0.9\, \mathrm{\frac{\mu m}{V}}\), \(\beta =0.008\, \mathrm{V^{-1}}\) and \(\gamma =0.008\, \mathrm{V^{-1}}\) are parameters that determine the shape and scale of the hysteresis loop.

Model (23) was integrated numerically using a fourth-order Runge–Kutta method with integration step \(\delta t=0.001\,\mathrm{s}\). The excitation signal was generated by low-pass filtering a white Gaussian noise [37]. In this work, a fifth-order low-pass Butterworth filter with a cutoff frequency of 1 Hz was used; see Fig. 3a. The sampling time is set to \(T_{\mathrm{s}}=\delta t=0.001\,\mathrm{s}\) and an input with frequency of 1 Hz is chosen to validate the identified models [49]. The data sets are \(50\,\mathrm{s}\) long \((N=50000)\). The identification data are shown in Fig. 3. The meta-parameters are \(\ell =3\) and \(n_y=n_u=1\). This choice is based on the discussion in [33, 37].

Fig. 3
figure 3

Identification data obtained from (23). a Excitation and b output

Full size image

5.1.1 Estimating \({\mathcal {M}}\)

In this example, we take \(n_u=2\) which is the smallest value that complies with Assumption 2-(ii), while \(n_y\) and \(\ell \) were chosen as detailed above. Using the data shown in Fig. 3, Assumption 1 and the ERR criterion the regressors were ranked according to importance. Then, AIC was used to determine the final number of parameters of the model:

$$\begin{aligned} y_k= & {} \theta _1y_{k-1}+\theta _2\phi _{1,\,k-1} +\theta _3\phi _{2,\,k-2}\phi _{1,\,k-2}u_{k-2} \nonumber \\&+\,\theta _4\phi _{2,\,k-2}\phi _{1,\,k-2}y_{k-1}+\theta _5\phi _{1,\,k-2}u^2_{k-2} \nonumber \\&+\,\theta _6\phi _{1,\,k-2}u_{k-2}y_{k-1}. \end{aligned}$$
(24)

Based on Lemma 1 and Example 1, for model (24) to fulfill Property 1, the constraint \(\theta _1=1\) should be imposed. This can be done using (5) with the constraint written as:

$$\begin{aligned} c = 1;\qquad S {=} [1 ~~ 0 ~~ 0 ~~ 0 ~~ 0 ~~ 0]. \end{aligned}$$
(25)

Hence, the parameter values estimated by the constrained least squares estimator (5) are shown in Table 1.

Table 1 Model parameters obtained with (5) and (25)
Full size table

A quasi-static analysis is performed (see Sect. 3.2 and Example 1). First, we write for (24) the corresponding to (6) as

$$\begin{aligned} {\tilde{y}}\approx & {} \theta _1{\tilde{y}}+\theta _2{\phi }_{1,k-1} +\theta _3{\phi }_{2,k-2}{\phi }_{1,k-2}u_{k-2}\\&+\,\theta _4{\phi }_{2,k-2}{\phi }_{1,k-2}{\tilde{y}}\!+\!\theta _5{\phi }_{1,k-2}u_{k-2}^2\!+\!\theta _6{\phi }_{1,k-2}u_{k-2}{\tilde{y}}, \end{aligned}$$

yielding

$$\begin{aligned} {\tilde{y}}({u},{\phi }_{1},{\phi }_{2}) {\approx } {\left\{ \begin{array}{ll} \dfrac{\theta _2{\phi }_{1}+\theta _3{\phi }_{1}{u}+\theta _5{\phi }_{1}{u}^2}{1-\theta _1-\theta _4{\phi }_{1}-\theta _6{\phi }_{1}{u}}, &{}\text {for} \,\,\,\,{\phi }_{2}{=}\,\,\,1; \\ \dfrac{\theta _2{\phi }_{1}-\theta _3{\phi }_{1}{u}+\theta _5{\phi }_{1}{u}^2}{1-\theta _1+\theta _4{\phi }_{1}-\theta _6{\phi }_{1}{u}}, &{}\text {for} \,\,\,\,{\phi }_{2}{=}-1, \end{array}\right. } \end{aligned}$$
(26)

where the time indices have been omitted for brevity.

The top expression in (26) gives the set \({\tilde{y}}_{\mathrm{L}}\), while the bottom one \({\tilde{y}}_{\mathrm{U}}\). Computing the derivative of (24) with respect to \(y_{k-1}\) and using (7), we obtain

$$\begin{aligned}&-1< \quad \theta _1 {+} \theta _4\phi _{1,k-2}{\phi }_{2,k-2}{+}\theta _6{\phi }_{1,k-2}u_{k-2} \quad<1, \nonumber \\&\frac{{-}1{-}\theta _1{-}\theta _4\phi _{1,k-2}{\phi }_{2,k-2}}{\theta _6\phi _{1,k-2}}< u_{k-2} < \frac{1{-}\theta _1{-}\theta _4\phi _{1,k-2}{\phi }_{2,k-2}}{\theta _6\phi _{1,k-2}}. \end{aligned}$$
(27)

Taking \({\phi }_{2,k-2}{=}1\) or \({\phi }_{2,k-2}{=}-1\), the conditions for attracting regions under load or unloading, respectively, are obtained. Considering the parameter values presented in Table 1 and a loading–unloading input signal, the points (26) and their attraction conditions (27) are computed numerically and shown in Fig. 4. Hence, in this way it is possible to see how model (24) is able to describe the hysteresis nonlinearity.

Fig. 4
figure 4

Results of quasi-static analysis for model (24) with input \(u_k{=}70\sin (2\pi k)\,\mathrm{V}\). The hysteresis loop indicated with (\(\cdots \)) is a result of the interaction of (—) attracting (\({\tilde{y}}_{\mathrm{L}}^{\mathrm{a}}\), \({\tilde{y}}_{\mathrm{U}}^{\mathrm{a}}\)) and (-\(\,\cdot \,\)-) repelling (\({\tilde{y}}_{\mathrm{L}}^{\mathrm{r}}\), \({\tilde{y}}_{\mathrm{U}}^{\mathrm{r}}\)) sets. ( ) indicates the orientation of the hysteresis loop. Compare to Fig. 1

Full size image

Model (24) is simulated with a loading–unloading input (see left side of Fig. 5) and, in cases where the input becomes constant, either during loading or unloading (see right side of Fig. 5), the system remains at the corresponding point of the hysteresis loop. This is a direct consequence of using Lemma 1. This feature is not generally present in identified models found in the literature.

Fig. 5
figure 5

Free-run simulation of model (24), a sinusoidal input of voltage \(u_k{=}40\sin (2\pi k)\,\mathrm{V}\) and in b the case where this input becomes constant during loading (\(\bullet \)) and unloading (\(\blacklozenge \)) with final value \(16.8\,\mathrm{V}\), temporal responses are in c and d while the hysteresis loops are in e and f, respectively. (—) represents original data and (- -) is the estimated model output

Full size image

The improvement due to using Lemma 1 is shown in Fig. 6. Despite different initial conditions, all models tend to the behavior of the dynamical system after a transient. The main difference is the ability of model (24) to predict the hysteretic behavior even when the input becomes constant. On the other hand, models estimated using black-box techniques and the model identified without using Lemma 1 [37] diverge. Most works in the literature [21, 33, 36, 43, 59, 61] do not test for this feature which in this paper is guaranteed by Lemma 1.

Fig. 6
figure 6

Model outputs to an input which is \(u_k{=}40\sin (2\pi k)\,\mathrm{V}\) up to a certain point and then remains constant; (—) the original output, (- -) model (24) that uses Lemma 1, (\(\cdots \)) a black-box model, (-\(\,\cdot \,\)-) a gray-box model but without considering Lemma 1 [37]

Full size image

5.1.2 Estimating \(\breve{{\mathcal {M}}}\)

The identified model that complies with Assumptions 1 and 4 is given by

$$\begin{aligned} {\hat{u}}_k= & {} \theta _1{\hat{u}}_{k-1}+\theta _2\breve{\phi }_{1,\,k-1} +\theta _3\breve{\phi }_{2,\,k-1}\breve{\phi }_{1,\,k-1}{\hat{u}}_{k-1} \nonumber \\&+\,\theta _4\breve{\phi }_{2,\,k-1}\breve{\phi }_{1,\,k-1}y_{k-1}+\theta _5\breve{\phi }_{2,\,k-1}y_{k-1}{\hat{u}}_{k-1} \nonumber \\&+\,\theta _6\breve{\phi }_{2,\,k-1}y^2_{k-1}, \end{aligned}$$
(28)

where \(\breve{\phi }_{1,\,k}=y_k-y_{k-1}\), \(\breve{\phi }_{2,\,k} = \mathrm{sign}(\breve{\phi }_{1,\,k})\), \({\hat{u}}_k\) is the estimated input (model output), and \(y_k\) is the output of system (23) (model input).

Note that the regressors of (24) and of (28) are different. In both cases, the regressors are automatically chosen from the pool of candidates using the ERR criterion. Nevertheless, also for (28), the steady-state analysis yields \(\bar{{\hat{u}}}{=}\theta _1\bar{{\hat{u}}}\), which is similar to the result found for model (24). Proceeding as before, the constrained least squares estimated parameters are shown in Table 1.

The formation of the hysteresis loop for this model (28) is shown in Fig. 7. The different orientation of the hysteresis loop has been discussed in [27].

Fig. 7
figure 7

Results of quasi-static analysis for model (28). For meaning of line patterns, refer to captions of Figs. 1 and  4

Full size image

The mean absolute percentage error (MAPE)

$$\begin{aligned} \mathrm{MAPE} = \frac{100 \sum _{k=1}^{N} |y_k-{\hat{y}}_k|}{N|\max ({\varvec{y}}) - \min ({\varvec{y}})|}, \end{aligned}$$
(29)

was computed for models (24) (28) and a black-box NARX polynomial model for sinusoidal input (Table 2). The results obtained for (28) are similar to those shown in Fig. 5 and are omitted for brevity.

Table 2 Model performance
Full size table

5.2 Compensation of a bench test system

Next, the models identified in the previous section are used to design compensators using the procedure illustrated in Fig. 2b.

5.2.1 Design of the compensation input signals

Applying the steps described in Sect. 4.2 to model (24), the following compensation signal is obtained

$$\begin{aligned} m_k= & {} \frac{1}{\theta _2}\Big [r_{k{+}1}-\theta _1r_{k}{+}\theta _2m_{k-1} \nonumber \\&-\,[\theta _3m_{k-1}{+}\theta _4r_{k}]\mathrm{sign}(m_{k-1}{-}m_{k-2})[m_{k-1}{-}m_{k-2}] \nonumber \\&-\,[\theta _5m^2_{k-1}{+}\theta _6m_{k-1}r_{k}][m_{k-1}-m_{k-2}]\Big ]. \end{aligned}$$
(30)

Similarly, following Sect. 4.3, after the change of variables in (28) the following compensator is obtained:

$$\begin{aligned} \breve{m}_k= & {} \theta _1\breve{m}_{k-1}{+}\theta _2[r_{k{+}1}-r_{k}] \nonumber \\&+\,[\theta _3\breve{m}_{k-1}+\theta _4r_{k{+}1}]\mathrm{sign}(r_{k{+}1}-r_{k})[r_{k{+}1}-r_{k}]\nonumber \\&+\,[\theta _5r_{k{+}1}\breve{m}_{k-1}+\theta _6r^2_{k{+}1}]\mathrm{sign}(r_{k{+}1}-r_{k}). \end{aligned}$$
(31)

The parameters of compensators (30) and (31) are given in Table 1.

5.2.2 Compensation performance

The designed compensators were applied to the piezoelectric actuator (23) with results summarized in Fig. 8. From the hysteresis loops (Fig. 8c), it is clear that a practically linear relation between the reference and the output was achieved. This would greatly facilitate the design and increase the performance of a feedback controller.

Fig. 8
figure 8

Hysteresis compensation for the piezoelectric actuator (23). a Compensation inputs, b outputs and in c hysteresis loops. (- -) results obtained with compensator (30) (\(\cdots \)) results with compensator (31), (-\(\,\cdot \,\)-) uncompensated system output and (—) reference \(r=40\sin (2\pi t)\,\mu \)m

Full size image

The accuracy achieved by each compensator was quantified by the MAPE index (29). In order to quantify the compensation effort, the normalized sum of the absolute variation in the input (NSAVI)

$$\begin{aligned} \mathrm{NSAVI}=\sum _{k=1}^{N-1} \frac{\big |m_{k+1}-m_k\big |}{\big |r_{k+1}-r_k\big |}, \end{aligned}$$
(32)

is calculated. These indices are shown in Table 3.

Table 3 Compensator performance
Full size table

The results shown in Fig. 8 and Table 3 indicate that the compensators may provide a significant improvement in the tracking performance of system (23). The tracking error was reduced by about \(93\%\) at the cost of a \(14\%\) increase in the compensation effort. Although the compensator strategies yield similar results, the design strategy of Sect. 4.2 yielded results with lower compensation effort and tracking error.

To further characterize the performance of the proposed designs, the influence of the sampling time \(T_{\mathrm{s}}\) was also investigated. In Fig. 9, it can be seen that the model accuracy somewhat deteriorates as \(T_{\mathrm{s}}\) is increased. It should be noted that even the largest values of \(T_{\mathrm{s}}\) in Fig. 9 are still comfortably small in terms of the sampling theorem. However, since one of the regressors is the first difference of the input, the identification of systems with hysteresis seems to be particularly sensitive to the sampling time [32]. Another conclusion that can be drawn from Fig. 9 is that, for both design strategies, the compensation performance is correlated to the model accuracy, and that the strategy in Sect. 4.2 (Fig. 9a) is somewhat less sensitive to such accuracy.

Fig. 9
figure 9

MAPE index (29) computed for the models and compensators described, respectively, by equations a (24) and (30); b (28) and (31). (\(\circ \)) model and (\(\bullet \)) tracking accuracies. (\(\blacktriangle \)) accuracy of uncompensated system

Full size image

Finally, the same analysis was carried out for situations with different shapes of the hysteresis loop varying \(\beta \) in the range \(0.004 \le \beta \le 0.1\) with increments of \(\varDelta =0.002\) (see Fig. 10). The results are quite similar to the ones described so far and are not shown.

Fig. 10
figure 10

Bouc–Wen hysteresis loops

Full size image

6 Experimental results

Both identification and compensation strategies are now applied to an experimental pneumatic control valve. This type of actuator is widely used in industrial processes, for which control performance can degrade significantly due to valve problems caused by nonlinearities [54] such as friction [11, 52], dead zone, dead band, and hysteresis [20]. Hence, in this section we aim at compensation hysteresis using the developed techniques.

The measured output is the stem position of the pneumatic valve, and the input is a signal that, after passing V/I and I/P conversion, becomes a pressure signal applied to the valve. The sampling time is \(T_{\mathrm{s}}=0.01\,\mathrm{s}\). For model identification, the input is set as white noise low pass filtered at \(0.1\,\mathrm{Hz}\). For model validation, the input is a sinusoid with frequency \(0.1\,\mathrm{Hz}\). Both data sets are \(200\,\mathrm{s}\) long (\(N=20000\)). The identification of the direct \({\mathcal {M}}\) and inverse \(\breve{{\mathcal {M}}}\) models was performed as in Sect. 5. The pool of candidate terms is generated with \(\ell =3\), \(n_{y}=1\) and \(n_{u}=2\). The model parameters are estimated using (5) in order to comply with Lemma 1.

The estimated model \({\mathcal {M}}\) is

$$\begin{aligned} y_k&=y_{k-1}-19.76\phi _{1,\,k-2}+19.32\phi _{1,\,k-1}\nonumber \\&\quad +\,9.44\phi _{2,\,k{-}2}\phi _{1,\,k{-}2}u_{k{-}2}{-}12.61\phi _{2,\,k{-}2}\phi _{1,\,k{-}2}y_{k{-}1}, \end{aligned}$$
(33)

and the inverse model \(\breve{{\mathcal {M}}}\) is

$$\begin{aligned} {\hat{u}}_k&={\hat{u}}_{k{-}1}+86.67\breve{\phi }_{1,\,k{-}1}-85.02\breve{\phi }_{1,\,k{-}2}{-}0.98\breve{\phi }_{1,\,k{-}1}y_{k{-}2} \nonumber \\&\quad +\,1.72\breve{\phi }_{2,\,k{-}2}\breve{\phi }_{1,\,k{-}2}y_{k{-}2}{-}1.13\breve{\phi }_{2,\,k{-}2}\breve{\phi }_{1,\,k{-}2}{\hat{u}}_{k{-}1}, \end{aligned}$$
(34)

which was estimated from a smoothed version of \(y_k\) obtained by quadratic regression. This is done only to estimate \(\breve{{\mathcal {M}}}\) to avoid the error-in-the-variables problem, since \(y_k\) serves as the input for \(\breve{{\mathcal {M}}}\). Each model performance is given in Fig. 11 and Table 4.

Fig. 11
figure 11

Left column refers to model (33) and right column to model (34). a input \(u_k{=}0.56\sin (0.2\pi k)+3\,\mathrm{V}\) and c the corresponding measured output (—) y and (- -) model (33) free-run simulation; b smoothed version of y in c; d the corresponding output which is \(u_k\) in a and (- -) model (34) free-run simulation. e and f show the same data as c and d, respectively

Full size image
Table 4 Experimental model performance
Full size table
Fig. 12
figure 12

Hysteresis compensation for the pneumatic valve. a Compensation inputs, b and c its temporal responses and in d and e the hysteresis loops. (- -) illustrates the results obtained with compensator (35), (\(\cdots \)) refers to the results by using compensator (36), (-\(\,\cdot \,\)-) the system output without compensation, and (—) the reference \(r{=}0.56\sin (0.2\pi t){+}3\,\mathrm{V}\)

Full size image

Models (33) and (34) are used to implement the strategies described in Sects. 4.2 and 4.3 , thus yielding, respectively, the following compensation inputs:

$$\begin{aligned} m_k= & {} \frac{1}{19.32}\Big [r_{k{+}1}{-}r_{k}{+}19.32m_{k{-}1}{+}19.76[m_{k{-}1}{-}m_{k{-}2}] \nonumber \\&{-}9.44\mathrm{sign}(m_{k-1}-m_{k{-}2})[m_{k{-}1}-m_{k{-}2}]m_{k{-}1} \nonumber \\&{+}12.61\mathrm{sign}(m_{k{-}1}{-}m_{k{-}2})[m_{k{-}1}{-}m_{k{-}2}]r_{k}\Big ]\!, \end{aligned}$$
(35)

and

$$\begin{aligned} \breve{m}_k= & {} \breve{m}_{k{-}1}{+}86.67[r_{k{+}1}-r_{k}]{-}85.02[r_{k}-r_{k{-}1}] \nonumber \\&{-}0.98[r_{k{+}1}{-}r_{k}]r_{k}{+}1.72\mathrm{sign}(r_{k}{-}r_{k{-}1})[r_{k}{-}r_{k{-}1}]r_{k}\nonumber \\&{-}1.13\mathrm{sign}(r_{k}-r_{k{-}1})[r_{k}-r_{k{-}1}]\breve{m}_{k-1}. \end{aligned}$$
(36)

Experimental compensation results are shown in Fig. 12 and assessed in Table 5. Note that both approaches significantly reduce the tracking error.

Table 5 Performance of the compensation step. Experimental results
Full size table

The compensation produced by (36) is smoother than the one obtained with (35); see Fig. 12a. This occurs because, for the compensator (36), the argument of the sign function depends on the difference of the reference signal, while, for the compensator (35), it depends on the difference of the autoregressive variable which usually produces stronger oscillations and sudden changes; see Fig. 12a, e.g., in the range of \(51{-}53\,\mathrm{s}\). As a result, larger compensation effort is required as quantified by NSAVI (32) in Table 5.

7 Conclusions

This work addressed the problems of identification and compensation of hysteretic systems. In the context of system identification, the contribution is twofold. First, we build models with regressors that use the sign function of the first difference of the input, as proposed by [37], and present an additional condition in order to guarantee a continuum of steady-state solutions, which is an important ingredient for hysteresis [12, 41]. To this aim, a particular constraint on the parameters is presented in Lemma 1. As a consequence, the identified models are able to describe both dynamical and static features of the hysteresis nonlinearity, whose comparison with other identified models that do not use Lemma 1 is provided in Fig. 6. Second, following a quasi-static analysis of these models, a schematic framework is proposed to explain how the hysteresis loop occurs on the input–output plane; see Fig. 1.

In the field of identification, there are promising approaches based on computational intelligence, such as those reviewed in [48]. However, this paper uses NARX polynomials due to the structural simplicity and fair generality. Such features allow: (i) using constraints such that simple models display hysteresis and (ii) using such models in compensator design by simple manipulations.

In the context of hysteresis compensation, this paper proposes two strategies to design compensators. An important aspect of such procedures is that they show how to restrict the pool of candidate regressors aiming at solving the compensation problem. Such strategies are not limited to hysteresis and can be extended to other nonlinearities.

The effectiveness of the compensation schemes is illustrated by means of numerical and experimental tests. For the strategy described in Sect. 4.2, the compensation law is obtained from the identified model by simple algebraic manipulations. In the case of the strategy introduced in Sect. 4.3, the compensators are identified directly from the data. The compensators designed by both strategies can be readily employed in online compensation schemes.

Based on both numerical and experimental results, it has been observed that the quality of the achieved compensation is correlated with the accuracy of the identified model (compare Table 2 with Table 3 and Table 4 with Table 5). Also, our results suggest that the compensation effort tends to be lower and more effective whenever the identified models are more accurate. In particular, compensators based on gray-box models clearly outperformed those based on black-box models.

Finally, as a general remark, we noticed that the identified models have a discontinuity due to the sign function used in some regressors. When the model has many such terms, it sometimes happens that the compensation signal presents abrupt transitions. The use of smoother functions in place of the sign function, in order to alleviate this problem, will be investigated in the future.