1 Introduction

Fractal phenomenon, since it was first introduced by Mandelbrot [1], has been attracting widespread interest. Fractal characteristic basically is based on self-similarity and refers to complexity of a system which is represented by the fractal dimension. The fractal dimension has found application in analysis of time series and determination of the nonlinear dynamical properties. As an example, it is used in bioscience for the determination of anomalies of the human body [2,3,4], in physics for the examination of solar activity [5], in atmospheric research for the analysis of rainfall data series [6], in mechanical engineering for damage detection of steel beam [7], in materials science for the measurement of silicon content in pig iron [8] and for assessing structural properties of materials [9] and in finance for the analysis of stock market indices [10].

There are number of algorithms used to calculate fractal dimension. Among them, especially, Higuchi’s algorithm [11] comes forward for its simplicity and efficiency. In 1988, Higuchi introduced his algorithm which approximates the fractal dimension directly from time series by means of the length of the irregular curve. So, in comparison with other methods especially that reconstructs the attractor phase space, Higuchi’s algorithm runs faster and can be applied to shorter time series for the estimation of the dimensional complexity of time series.

In this work, we extend Higuchi’s fractal dimension (HFD) analysis from monoscale to multiscale. In 2005, Costa et al. [12] introduced the multiscale complexity measure for biological signals. According to Costa, because of complexity of biological systems, they need to work across multiple spatial and temporal scales. So, they developed multiscale entropy (MSE) analysis by combining sample entropy as a complexity measure and coarse-graining procedure as a scaling filter.

Since then, multiscale analysis have been enriching by the works of scientists who noticed the benefits of observing information in multiple scales. Entropy-based multiscale evaluations have been the main focus in these works. A number of versions of multiscale permutation entropy have been applied for the observation of the dynamical characteristics of EEG data [13,14,15]. Modified version for multiscroll chaotic systems was introduced [16], and modified multiscale entropy for short term time series was developed [17]. More recently, improved version of multiscale permutation entropy [18] and multiscale transfer entropy were proposed [19].

We apply the same idea for HFD in order to investigate how complexity features of time series change through multiple scales. For the choice of scaling filter, several useful filter options were tested and the mean filter as the coarse-graining procedure come forward among them as the most efficient one. As a result, we introduce multiscale Higuchi’s fractal dimension (MSHG) analysis by putting together coarse-graining procedure as a scaling filter and HFD as a complexity measure. Then, we demonstrate the MSHG analysis on stochastic time series and chaotic time series.

We also examine how the relationship between complexity measure fractal dimension (D) and long-range dependence measure Hurst exponent (H) which is formulized as \(D=2-H\) changes in multiscale. We again experiment MSHG on the same set of chaotic time series and stochastic time series. The results show that as the relationship in monoscale holds through multiple scales with MSHG for the stochastic time series, it diverges for the chaotic time series. Therefore, such distinguishing observations in multiscale based on H and D can be useful for characterizing time series whether they possess stochastic or chaotic properties.

The rest of the paper is organized as follows. In subsequent section, which filtering method, how and why chosen is given in detail. All examined methods are briefly explained, and the comparative results are presented. Then, in Sect. 2, the most efficient method, mean filter and Higuchi’s fractal dimension algorithm which comprise MSHG are elaborated. In Sect. 3, MSHG is demonstrated on selected chaotic time series and stochastic time series extensively. Section 4 looks into the relationship between D and H in multiple scales in a fresh way by conducting MSHG and Hurst algorithms in parallel in successively scaled group of time series. In the final section, all findings are summarized with concluding comments.

Fig. 1
figure 1

Multiscale overlapping coarse-graining algorithm

Full size image

2 Methodology

The proposed method for the analysis of complex characters of time series that we call it multiscale Higuchi’s fractal dimension (MSHG) incorporates a scaling part and the complexity measurement part. For the scaling part, the coarse-graining algorithm is the most used in the multiscale literature although there are many filters especially employed in image processing. In this section, we firstly look at some good candidates among these filters by giving brief instructions and comparing their effectiveness on all chaotic and stochastic time series under examination. Gaussian filter, Wiener filter, mean shift filter, bilateral filter, total variation filter, standard deviation filter, max filter, harmonic mean filter and gradient filter are the filters examined as an alternative to mean filter.

2.1 Scaling filters

2.1.1 Coarse-graining procedure

Coarse-graining procedure or the mean filter is a moving average process. It is applied to time series in an order by using a scale factor \(\tau \) with a low-pass filter. In our study, overlapping window is used to minimize data loss to a single one in each step. As a result of windowing, in each step, data series change. The information in each interval which is related to other intervals can be captured by each window.

For one-dimensional time series of \({x_1, x_2,\ldots ,x_N}\), coarse-graining procedure is described as

$$\begin{aligned} y_{n,\tau }={1\over \tau }\sum _{i=0}^{\tau -1} x_{n+i}, \end{aligned}$$
(1)

where, consecutively, n, N, i and \(\tau \) denote the subscript of coarse-grained data series, the length of data series, the loop key and the scale factor. The length of each coarse-grained time series becomes \(N-\tau \). Equation 1 gives each data point on each scale. The procedure is also given with an illustration describing it visually in Fig. 1. As scale 1 is the original time series, at each scale, values of consecutive data pairs are averaged to obtain the value of each point of subsequent scale. As a consequence of this downsampling, the length of data is shortened on each scale. However, it keeps the loss of data at minimum by reducing the length of the series only by one which serves to transfer more information through scales, comparison with other coarse-graining procedures which consume more number of data points.

2.1.2 Gaussian filter

Gaussian filter has got many applications, especially in image processing. In Gaussian filter, simply, the average of weighting values replace the intensity value of the pixel and its neighbor pixels. The Gaussian filter use convolution of required Gaussian function g. This function that is governed by the variance \(\sigma ^2\) is described as

$$\begin{aligned} g(x,y,\sigma )={1\over 2\pi \sigma ^2}\mathrm{{e}}^{-({x^2+y^2\over 2\sigma ^2})}, \end{aligned}$$
(2)

where x and y are the distances in the horizontal axis and vertical axis consecutively. Equation 2 is used to estimate the coefficients for a Gaussian template and then convolved [20]. The Gaussian filter can be applied in one or more dimensions. The advantage of the Gaussian filter compared to direct averaging is the enhanced performance as a result of maintaining more features.

2.1.3 Wiener filter

The Wiener filter is actually a linear estimation of a signal. It is, especially advantageous while working with noisy signals. Therefore, it finds wide-range applications for linear prediction, signal restoration and system identification. For an original signal x and an additive noise n, the Wiener filter is described as

$$\begin{aligned} W(u,v)={H^{*}(u,v) S_{xx}(u,v)\over \mid H(u,v)\mid ^2 S_{xx}(u,v)+S_{nn}(u,v)}, \end{aligned}$$
(3)

where u, v are the location parameters of frequency. H(u, v) is blurring or degradation filter, and \(H^*\) is its conjugate. \(S_{xx}(u,v)\) denotes the power spectrum of the original signal which is computed by the Fourier transform of the signal autocorrelation. \(S_{nn}(u,v)\) is the power spectrum of the additive noise which is acquired by the Fourier transform of the noise autocorrelation [21].

2.1.4 Mean shift filter

Mean shift filtering is primarily related to data clustering. It has many applications in the areas of computer vision, smoothing, segmentation and tracking. As to Fukunaga’s introduction, the mean shift vector is

$$\begin{aligned} m(x)={\sum _{i=1}^n g({x-x_i\over h})x_i\over \sum _{i=1}^n g({x-x_i\over h})}-x, \end{aligned}$$
(4)

where h is bandwidth radius, n is data point in observations \(x_i\) where \(i=1,\dots ,n\) in d-dimension space \(R^d\) and \(g(x)=-K(x)\). Here, K is a kernel (for instance Gaussian kernel which is the most popular one) employed in order to estimate probability density. The algorithm works by iteratively calculating the mean of a window around a data point as shifting the center of the window until the convergence. The mean shift vector is computed until the convergence for each point \(x_i\) according to a selected search window. The algorithm looks for a local maximum of density of a distribution [22, 23].

2.1.5 Bilateral filter

Bilateral filter operates as a smoothing filter by replacing each point with the nonlinear combination of the neigbouring values. Its applications can be found in denoising, optical-flow estimation, texture editing and so on. As I denotes an image and p, q represent some pixel positions, bilateral filter is described as

$$\begin{aligned} BF[I]_p={1\over W_p}\sum _{q\in S}G_{\sigma _s}(\Vert p-q\Vert )G_{\sigma _r}\big (I_p-I_q\big )I_q.\nonumber \\ \end{aligned}$$
(5)

The normalization factor \(W_p\) in Eq. 5 is

$$\begin{aligned} W_p=\sum _{q\in S}G_{\sigma _s}(\Vert p-q\Vert )G_{\sigma _r}\big (I_p-I_q\big ), \end{aligned}$$
(6)

and the two-dimensional Gaussian kernel \(G_\sigma (x)\) in Eq. 6 is

$$\begin{aligned} G_\sigma (x)={1\over 2\pi \sigma ^2}\mathrm{{exp}}\left( {-x^2\over 2\sigma ^2}\right) . \end{aligned}$$
(7)

So, based on Eq. 7, \(G_{\sigma _s}\) is the Gaussian kernel associated with location which decreases the effects of far points and \(G_{\sigma _r}\) is the Gaussian related to value which decreases the effects of points q with an intensity value different from \(I_p\) [24, 25].

2.1.6 Total variation filter

The total variation algorithm was first introduced for image denoising and reconstruction [26]. For a signal x with an additive noise n which is observed in the form of \(y=x+n\), in order to estimate x, total variation filtering measures the amount of changes between signal values and is described as the minimization of following formula:

$$\begin{aligned} J(x)=\Vert y-x \Vert _2^2+\lambda \Vert Dx\Vert _1, \end{aligned}$$
(8)

where \(\lambda \) denotes the regularization parameter. The L1 norm matrix \(\Vert Dx\Vert _1\) given in Eq. 8 can also be expressed as

$$\begin{aligned} \sum _{n=2}^N |x(i)-x(i-1)|, \end{aligned}$$
(9)

for \(1\le i\le N\) for N-point signal x(i) in Eq. 9 [27].

2.1.7 Standard deviation filter

As the name suggests, with the standard deviation filter, the standard deviation of the data points in a particular range neighborhood is used. Then, these are returned to the place of every data point. The standard deviation formula is given below as

$$\begin{aligned} \mathrm{{SD}}=\sqrt{{\sum (x_i-{\bar{x}})^2\over r*c-1}}, \end{aligned}$$
(10)

where \(x_i\) denotes the value of particular pixel and \({\bar{x}}\) denotes the mean of the pixel values in the filter range. Besides, r and c are the size of the filter in rows and columns, respectively [28].

2.1.8 Max and Min filter

Max filter and min filter are classified among nonlinear filters. They filter an image by refining only the minimum or maximum of all pixels in a local region \(R_{u,v}\) of an image. Each pixel in an image is assigned a new value equal to the maximum or minimum value in a neighborhood around itself. This process is summarized as

$$\begin{aligned} I'(u,v)\leftarrow \min \{I(u+i,v+j)\mid (i,j)\in R\}, \end{aligned}$$
(11)
$$\begin{aligned} I'(u,v)\leftarrow \max \{I(u+i,v+j)\mid (i,j)\in R\}, \end{aligned}$$
(12)

where R denotes the filter region, I and \(I'\) denote the original image and the filtered image, u and v denote the position parameters. Algorithms replace every value in time series by the maximum or minimum in a determined range [29].

2.1.9 Harmonic mean filter

Harmonic mean filter, in essence, is a different version of mean filter. It is quite useful for the removal of Gaussian noise as well as preserving edge features. For two dimensional space, the harmonic mean filter is given as

$$\begin{aligned} HM(I)={mn\over \sum _{(i,j)\in W}{1\over I(x+i,y+j)}}, \end{aligned}$$
(13)

where x and y denote coordinates over the image and I, i and j denote the coordinates in a window W with the size of m, n which are the length of each dimension [30, 31]. The algorithm works as replacing every value by the harmonic mean value in a determined range.

2.1.10 Gradient filter

The gradient of the function I at position (u, v) is given as a vector:

$$\begin{aligned} \nabla I(u,v)=\bigg ( \begin{matrix} I_x(u,v)\\ I_y(u,v) \end{matrix} \bigg )=\bigg ( \begin{matrix} {\partial I\over \partial x}(u,v)\\ {\partial I\over \partial y}(u,v) \end{matrix} \bigg ). \end{aligned}$$
(14)

Basically, the partial derivatives of horizontal and vertical lines constitute the gradient function merely consists of. There are the horizontal and vertical gradient filters respond to swift changes in horizontal axis and the vertical axis, respectively [29].

Gradient filter based on the vector given in Eq. 14 calculates the magnitude of the gradient of an image which is the rate of increase and described as

$$\begin{aligned} |\nabla I|=\sqrt{\bigg ({\partial I\over \partial x}(u,v)\bigg )^2+\bigg ({\partial I\over \partial y}(u,v)\bigg )^2}. \end{aligned}$$
(15)

Because the magnitude does not vary when the image is rotated or oriented in a different position, it is especially used in edge detection.

2.1.11 Findings on scaling filters

All scaling filters selected for this study are the member of low pass filter family. Among these filters, while mean filter defined in Eq. 1 is one of the most used filter in practice, Gaussian filter which exercises the convolution of Gaussian function given in Eq. 2 is also very popular in image processing applications. The Wiener filter described in Eq. 3 as a dependent of the power spectrum of the signal and additive noise with a degradation filter is preferred in linear prediction. Mean shift filter whose algorithm is summarized in Eq. 4 computes the mean of a window until the convergence. Bilateral filter smoothes images while preserving edges according to Eq. 5. Total variation filter is a slope-preserving method which searches for the minimum of Eq. 8. Standard deviation filter based on Eq. 10 is employed by computing standard deviation of data points in the filter range. Max and min filter presented in Eqs. 11 and 12 basically calculate the maximum and minimum values of data points in filter region. Harmonic mean filter as modification of mean filter operates by replacing data points in a local region by the value calculated by Eq. 13. In gradient filter algorithm, the magnitude of the gradient given in Eq. 15 based on the partial derivatives of horizontal and vertical lines is computed.

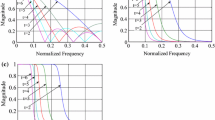
For the examination of these filters, built-in functions of Mathematica v11.0.1.0 are used. Results are presented in a way to allow comparisons. Because almost each pair result is closely identical, only figures for fractional Brownian motion (fBm) are given in Fig. 2 to avoid repetition and for clear presentation. As the data sets, five different fBm processes are generated with Hurst exponent values of 0.25, 0.40, 0.50, 0.60 and 0.75 and represented with different colors for providing distinguishable observations.

Figure 2 consists of ten subfigures. Each subfigure belongs to each filter in the list of scaling filters under investigation. These subfigures show fractal dimension value on y axis and scale value on x axis. The number of scales on which D values are calculated and plotted is 12.

As observed in subfigures of Fig. 2, mean filter, Gaussian filter, mean shift filter, bilateral filter, total variation filter, standard deviation filter produce similar patterns albeit with different values in each scale. It is not really clear to determine the most efficient scaling filter because of such close patterns. However, the most used filter, mean filter and Gaussian filter are applied to upcoming analysis side by side and observations show us mean filter is slightly more consistent for all the data series. So, the choice of scaling filter for the rest of our calculation arises as mean filter.

Although the mean filter acts slightly better with Higuchi’s algorithm, it is not easy to generalize it to other multiscale methods. In our previous studies, for example, in the application of correlation dimension algorithm in multiscale, Gaussian filter had generated more stable results than mean filter as well as other filters tested. Therefore, for now, for each algorithm, when analysis is made in multiscale, the choice of scaling filter is better to be made after testing variety of filters until developing an efficient uniform method for this purpose. For not diverging from the main purpose of this study, this subject of the choice of scaling filter is not presented in detail any further.

Fig. 2
figure 2

MSHG results of all filters. a Mean filter, b Gaussian filter, c Wiener filter, d Mean shift filter, e Bilateral filter, f Total variation filter, g Standard deviation filter, h Max filter, i Harmonic mean filter, j Gradient filter

Full size image

2.2 Fractal dimension

Complex interlinked systems like stock markets, human heart, neural structures, the digital networking systems are generally made up of multiple subsystems governed hierarchically show nonlinear deterministic characteristics and stochastic characteristics. A complex system can be examined for learning about its behavior by measuring its particular signals that indicate nonlinearity, sensitivity to initial conditions, long memory, severe volatility and nonstationarity [32].

Fractal theory gives effective method for characterizing complex structure of such systems. Fractals are interpreted by a non-integral dimension named as fractal dimension. The fractal phenomenon is found everywhere and studied in many fields of science like in finance for the analysis of price variations [33] and stock markets [34], in physics for the detection of periodic components in seismograms [35] or in engineering for porous media [36] and so on.

Fractal structure is characterized with self-similarity, and its complexity is measured by its fractal dimension which is easier to be computed from data sets. There are numerous methods for the measurement of fractal dimension like Higuchi, Kantz, Maragos and Sun or Burlaga and Klein and so on. Among them, Higuchi’s fractal dimension (HFD) is a fast nonlinear computational method which yields more accurate result in comparison with others [37]. Shifts in the structure of time series in a time domain over a specific characteristic frequency make it hard to find out power law indices and a characteristic time scale from the power spectrum. Stable indices and time scale related to the characteristic frequency can be provided by the HFD method even there are very limited data points available [11].

2.3 Higuchi’s fractal dimension algorithm

Higuchi’s fractal dimension algorithm is described as follows [11]. Giving a N-length one-dimensional time series with equal intervals \(x(1), x(2),\ldots ,x(n)\), a new time series \(X_k^m\) is constructed as

$$\begin{aligned}&X_k^m:x(m),x(m+k),x(m+2k),\nonumber \\&\quad \ldots ,x\left( m+int\left[ {N-m\over k}\right] .k\right) , \end{aligned}$$
(16)

where k as an integer is the time interval and number of new time series sets and \(m=1,2,\ldots ,k\). Therefore, Eq. 16 gives k number of new time series. The length of each new time series obtained by \(X_k^m\) is defined as

$$\begin{aligned} L_m(k)= & {} \left( {1\over k}\left\{ \left[ \sum _{i=1}^{\mathrm{{int}}[{N-m\over k}]}|x(m+ik)\right. \right. \right. \nonumber \\&\left. \left. \left. -x(m+(i-1).k)|\right] {N-1\over \mathrm{{int}}[{N-m\over k}.k]}\right\} \right) , \end{aligned}$$
(17)

where \({N-1\over \mathrm{{int}}[{N-m\over k}]}\) is the normalization factor for the curve length of k sets of constructed time series. By Eq. 17, the length of the curve for the interval k is obtained by computing the average value over k series of \(L_m(k)\) as

$$\begin{aligned} L(k)={1\over k}\sum _{m=1}^{k}L_m(k). \end{aligned}$$
(18)

Then, based on Eq. 18, the fractal dimension \(D_f\) is described by

$$\begin{aligned} L(k)\sim k^{D_\mathrm{{f}}}. \end{aligned}$$
(19)

So, the complexity measure \(D_\mathrm{{f}}\) can be calculated by the least-squares linear best fit procedure as finding the slope of the curve on the graph of \(\mathrm{{ln}}(L(k))-\mathrm{{ln}}(1/k)\) based on Eq. 19. \(D_\mathrm{{f}}\) takes values ranging between 1 and 2.

In our study, HFD, a measure of self-similarity and complexity of time series, is extended to multiple scales which is provided by coarse-graining scaling filter. So, new procedure named MSHG allows uncovering different characteristics which helps to understand and identify the nature of time series under examination. To do this, HFD value of each scale gathered by scaling filter is calculated. Then, all HFD values in y axis versus scale number in x axis are plotted. The pattern of the plot and values shows the particular characteristics of different time series. In the following section, on various time series data sets in different classes, namely stochastic and chaotic time series, MSHG is demonstrated in detail.

3 Applications

3.1 Stochastic time series

Applications and demonstrations on specific time series of MSHG algorithm start in this section with stochastic time series of white noise, fractional Brownian motion (fBm) and fractional Gaussian noise (fGn) generated by Mathematica’s related process functions

As fBm and fGn are self-similar stochastic processes with long-range dependence, white noise is a random noise. fGn and fBm are related processes since fGn is the increments of fBm. fBm is a Gaussian process with mean function \(\mu t\) and its covariance function is written as

$$\begin{aligned} \gamma (t,s)={\sigma ^2\big (s^{2H}+t^{2H}-|t-s|^{2H}\big ) \over 2}. \end{aligned}$$
(20)

Fractional Gaussian noise process is also a Gaussian noise with mean function \(\mu \) and covariance function

$$\begin{aligned} \gamma (t,s)={\sigma ^2\big (|t-s-1|^{2H}-2|t-s|^{2H}+|t-s+1|^{2H}\big )\over 2},\nonumber \\ \end{aligned}$$
(21)

where \(\sigma \) is volatility and H is the Hurst exponent \(H\in (0,1)\).

The Hurst exponent quantifies the Hurst phenomenon which describes the long-range dependence of the fBm given in Eq. 20 and fGn defined in Eq. 21 [38].

If H is set to 0.5, the process is Brownian motion and independently distributed. When H is different from 0.5, the observations are not independent and system is short-term memory process if \(H<0.5\) and long-term memory process if \(H>0.5\).

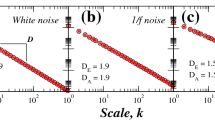
As a set of stochastic time series, white noise, fGn (\(H=0.5\)) and fBm (\(H=0.25, 0.75\)) processes are exercised with the length of 1250 time steps. The results are presented in Fig. 3 which shows similar patterns for every time series in different ranges.

Fig. 3
figure 3

MSHG results of stochastic processes

Full size image

3.2 Financial time series

MSHG is continued to be tested on stochastic time series particularly with financial time series processes in this section. For this purpose, two important processes of FARIMA and FIGARCH are utilized.

3.2.1 FARIMA

Autoregressive fractionally integrated moving average model (FARIMA), in a similar sense to FIGARCH, is a modification of autoregressive process (AR) and moving average process (MA) models allowing fractional differencing.

MA(q) model is written as

$$\begin{aligned} X_t=\mu +\sum _{i=1}^{q}\theta _i\epsilon _{t-i}+\epsilon _t. \end{aligned}$$
(22)

And AR(p) is given as

$$\begin{aligned} X_t=\mu +\sum _{i=1}^{p}\phi _i X_{t-i}+\epsilon _t, \end{aligned}$$
(23)

where \(\mu =E[y_t]\), \(\theta \) and \(\phi \) are the parameters of the MA model and AR model consecutively. \(\epsilon \) is the white noise process with the properties of \(E(\epsilon _t)=0\) and \(var(\epsilon _t)=\sigma ^2\) [39].

ARIMA(p, d, q) as a combination of AR(p) defined in Eq. 23 and MA(q) given in Eq. 22 models is described as follows [40]:

$$\begin{aligned}&\left( 1-\sum _{i=1}^p\phi _i B^i\right) (1-B)^d (X_t-\mu )\nonumber \\&\quad =\left( 1+\sum _{i=1}^q\theta _i B^i\right) \epsilon _t, \end{aligned}$$
(24)

where \((1-B)^d\) is the difference operator as d takes integer values. B represents the backshift operator. It works in the notation as \(B^i X_t=X_{t-i}\).

So, ARIMA models given in Eq. 24 are especially powerful when it comes to short-range dependence [41]. And, when d is allowed to take fractional values, it is suggested that the model becomes better at capturing long-range dependence [42]. Then, as denoting the autoregressive order, the difference coefficient and the moving average order with p, d and q, in general form FARIMA(p, d, q) process can be described as

$$\begin{aligned} \phi (B)(1-B)^d X_t=\theta (B)\epsilon _t, \end{aligned}$$
(25)

where \(d\in (-0.5, 0.5)\), \(\phi (B)=1-\phi _1 B-\cdots -\phi _p B^p\), \(\theta (B)=1+\theta _1 B+\cdots +\theta _q B^q\) and \((1-B)^d\) is the fractional difference operator.

3.2.2 FIGARCH

Fractionally integrated generalized autoregressive conditional heteroskedastic (FIGARCH) process is a class of GARCH process with more persistence on the conditional variance which allows estimation long memory of conditional volatility.

The GARCH model allows the conditional variance to be dependent upon previous own lags. The GARCH(p, q) is

$$\begin{aligned} \sigma _{t}^2=\alpha _0+\sum _{i=1}^q\alpha _i \epsilon _{t-i}^2+\sum _{j=1}^p\beta _j\sigma _{t-j}^2, \end{aligned}$$
(26)

where \(\alpha _i\ge 0\) and \(\beta _j\ge 0\) are the parameters and \(\sigma _{t}^2\) is the conditional variance. The conditional variance of error term of a model \(\epsilon _t\) with the properties of \(\epsilon _t\sim N(0,\sigma _t^2)\) is written as

$$\begin{aligned} \sigma _{t}^2= & {} var(\epsilon _t|\epsilon _{t-1},\epsilon _{t-2},\ldots )\nonumber \\= & {} E[(\epsilon _t)^2|\epsilon _{t-1},\epsilon _{t-2},\ldots ]. \end{aligned}$$
(27)

The GARCH(p, q) model given in Eq. 26 can be expressed in a form that shows that it is effectively an ARMA(m, p) model for the conditional variance as

$$\begin{aligned} \epsilon _t^2[1-\alpha _1(B)-\beta _1(B)]=\alpha _0+[1-\beta _1(B)]v_t, \end{aligned}$$
(28)

where \(v_t\) is mean zero serially uncorrelated

$$\begin{aligned} v_t=\epsilon _t^2-\sigma _t^2, \end{aligned}$$
(29)

and \(m\equiv \max \{p,q\}\). The GARCH process is defined to be integrated in variance. So, based on Eqs. 27, 28 and 29, IGARCH can be written in the same notation as

$$\begin{aligned}&[1-\alpha _1(B)-\beta _1(B)](1-B)\epsilon _t^2\nonumber \\&\quad =\alpha _0+[1-\beta _1(B)]v_t, \end{aligned}$$
(30)

when,

$$\begin{aligned} \sum _{i=1}^p\beta _i+\sum _{j=1}^q \alpha _j=1. \end{aligned}$$
(31)

If fractional difference operator d is added to IGARCH(p, q) given in Eq. 30 with the condition of Eq. 31, then FIGARCH(p, d, q) is obtained and described as

$$\begin{aligned} \phi (B)(1-B)^d u_t^2=\omega +[1-\beta (B)] v_t, \end{aligned}$$
(32)

where \(0<d<1\) and \(\phi (B)\equiv [1-\alpha _1(B)-\beta _1(B)]\) is of order \(m-1\) [43].

FIGARCH process has got fractional and long memory properties but does not possess chaotic properties [44]. Identifying these properties is useful considering that MSHG results of the chaotic times series are compared with stochastic time series in the subsequent section.

3.2.3 MSHG results of FIGARCH and FARIMA

For the application of MSHG on FIGARCH(p, d, q) in Eq. 32 and FARIMA(p, d, q) in Eq. 25, sample data series for both processes are generated with the length of 1250 data points, and then, figures of HFD vs. number of scales are formed as presented in Fig. 4. FIGARCH and FARIMA lines follow the same pattern as it was in MSHG results of white noise, fGn and fBm presented in previous section. These similar pattern although occurring in various values may suggest that it is a property of stochastic time series in multiscale. In the next section, MSHG is run on several chaotic time series and its results are compared with the findings in this section whether or not these time series with different characteristics produce unique patterns.

Fig. 4
figure 4

MSHG results of FIGARCH and FARIMA

Full size image

3.3 Chaotic systems

A chaotic system is a complex dynamic nonlinear deterministic system which is unpredictable in the long term because of its sensitivity to changes of initial conditions. Even the smallest change at one point can cause a very large shift in future point as a result of information transmission through following data points. There are various methods and algorithms like HFD to measure the complexity of such characteristic systems in monoscale. In this section, MSHG is applied to examine the feature of complexity of chaotic time series in multiscale. The chaotic time series data set we use comprises three chaotic time series which are generated from two-dimensional chaotic discrete maps of Henon map, Duffing map and Ikeda map.

3.3.1 Henon map

Michel Henon introduced Henon map in 1976 with

$$\begin{aligned} x_{n+1}= & {} 1-a x_n^2 +y_n, \end{aligned}$$
(33)
$$\begin{aligned} y_{n+1}= & {} b x_n, \end{aligned}$$
(34)

where a, b parameters are given the values of 1.4 and 0.3 to obtain chaotic Henon time series for the calculation [45].

3.3.2 Duffing map

By assigning 2.75 and 0.2 values to a and b parameters in

$$\begin{aligned} x_{n+1}= & {} y_n, \end{aligned}$$
(35)
$$\begin{aligned} y_{n+1}= & {} -b x_n +a y_n-y_n^3, \end{aligned}$$
(36)

Duffing chaotic time series are acquired [46].

3.3.3 Ikeda map

These three equations,

$$\begin{aligned} x_{n+1}= & {} 1+u(x_n \cos (z)-y_n \sin (z)), \end{aligned}$$
(37)
$$\begin{aligned} y_{n+1}= & {} u(x_n \sin (z)+y_n \cos (z)), \end{aligned}$$
(38)
$$\begin{aligned} z= & {} 0.4-\left( {6 \over {1+x_n^2+y_n^2}}\right) , \end{aligned}$$
(39)

govern the Ikeda map [47]. Time series can be generated by setting u parameter to 0.918.

The result of MSHG calculations of these three chaotic time series generated by using Eqs. 33, 34, 35, 36, 37, 38 and 39 with the length of 1250 data points are summarized in Fig. 5. Lines emerging on D-Scale plane seem quite irregular and leading through uncertain directions. These patterns are very different from the ones revealed with stochastic time series. In comparison with stochastic time series, more irregular and jagged lines through consecutive scales of the chaotic time series figure take the place of smooth and horizontal lines of the stochastic time series.

Fig. 5
figure 5

MSHG results of chaotic maps

Full size image

4 HFD and Hurst exponent link in multiscale

The aim of this section is to investigate the relationship between HFD and H in multiscale. Through previous sections, MSHG method has been introduced and demonstrated on time series with different characteristics. With MSHG method, HFD is expanded on multiple scales and its distinguishing revelations are presented. In a similar sense, Hurst exponent calculations are exercised on multiple scales numerically, in order to examine the link between H and HFD also holds in multiple scales.

4.1 Hurst exponent

Hurst exponent (H) as a measure of long memory dependence has also been studied and applied in wide range of different fields such as in hydrology [48],in medicine and biology [49], in astrophysics [50], in finance [51] and so on. Hurst exponent was introduced in 1951 by H. E. Hurst while investigating river flows of the Nile basin [52]. The method developed was called rescaled range or R/S analysis. Letting \(X_n\) be the inflow of to the dam in the original problem or any time series in period \(n=1,2,\ldots ,k\), the rescaled adjusted range statistic is

$$\begin{aligned} R/S(k) ={\max {\begin{array}{c} {0\le j\le k} \end{array}}\left\{ \sum _{n=1}^j X_n-{j\over k}\sum _{n=1}^k X_n\right\} -{\min \begin{array}{c} 0\le j\le k \end{array}}\left\{ \sum _{n=1}^j X_n-{j\over k}\sum _{n=1}^k X_n\right\} \over \sqrt{{1\over k}\sum _{j=1}^k\left( X_j-{{1\over k}\sum _{j=1}^{k}X_j}\right) ^2}}. \end{aligned}$$
(40)

The numerator is called the adjusted range, and the denominator is the sample standard deviation in Eq. 40 where \(j=1,2,\dots ,k\). After examination of many different time series, Hurst found that \(R/S(k)\approx k^H c\) for large k where c denotes some constant [53].

Hurst exponent (H) takes values between 0 and 1. If \(H=0.5\), the system is independently distributed and Brownian motion. However, if H value is different from 0.5, then system possesses memory of previous points and no longer identified as independent. It is described as a short-term memory or anti-persistent system if \(H<0.5\) and long-term memory or persistent system if \(H>0.5\).

Mandelbrot later introduced a method which has been widely used. H is computed by Mandelbrot’s method [54] described as

$$\begin{aligned} R/S_t=ct^H, \end{aligned}$$
(41)

after taking logarithms of both sides, formula becomes linearized as,

$$\begin{aligned} \mathrm{{log}}(R/S_t)=\mathrm{{log}}(c)+H\mathrm{{log}}(t)), \end{aligned}$$
(42)

where \(R/S_t\) is,

$$\begin{aligned} R/S_t= & {} \left[ 1/M\sum _{m=1}^M\big (R_{I_m}/\sigma _{I_m}\big )\right] =c t^H, \end{aligned}$$
(43)
$$\begin{aligned} R_{I_m}= & {} \max \big (X_{k,m}\big )-\min \big (X_{k,m}\big ), \end{aligned}$$
(44)
$$\begin{aligned} X_{k,m}= & {} \sum _{k=1}^n \big (N_{k,m}-\mu _{I_m}\big ), \end{aligned}$$
(45)

where, \(\sigma \), \(\mu \), \(I_m\), N, \(N_{k,m}\), successively denote the standard deviation, the mean of M sub-periods for \(m=1,2,\ldots ,M\), each of the M subperiods, the number of points in time series, each element of a given time series. Also, as c represents some constant, \(t=N/M\) and \(k=1,2,\ldots ,t\) [55].

Time series of N observations are divided to t length of M subperiods. Standard deviation and mean of each subperiods are calculated. Then, by calculation of variation \(R_{I_m}\) given in Eq. 44 dependent on \(X_{k,m}\) calculated as in Eq. 45 provides to estimation of the mean \(R/S_t\) in Eq. 43 by \(R_{I_m}/\sigma _{I_m}\) of all subperiods. Finally, H value can be computed by a linear regression of Eq. 42 as a solution of relationship given in Eq. 41.

4.2 The relationship between fractal dimension and Hurst exponent

Mandelbrot [1] first introduced the relationship between Hurst exponent and fractal dimension as

$$\begin{aligned} D=2-H \end{aligned}$$
(46)

where, H denotes the Hurst exponent and D denotes fractal dimension which is calculated by Higuchi’s algorithm in this study and denoted with HFD.

The relationship described in Eq. 46 that theoretically relates HFD to H value is investigated in multiscale by making use of MSHG and calculating H value scale by scale simultaneously on the same stochastic time series and chaotic time series used in previous section.

Fig. 6
figure 6

Fractal dimension (D) and Hurst exponent (H) relationship in multiscale. a White noise, b fBm, c fGn, d FIGARCH, e FARIMA, f Henon, g Duffing, h Ikeda

Full size image

This algorithm is used to find H values on each scale which is obtained by coarse-graining procedure. Number of scales are limited to 12. Each H value against its related scale is plotted as it is repeated for MSHG simultaneously. Besides, for each scale, sum of H and D values are calculated and plotted to observe how \(D+H=2\) relationship appears.

These calculations are made for all stochastic time series (white noise, fGn, fBm, FIGARCH, FARIMA) and chaotic time series (Henon, Duffing, Ikeda) sets used in previous section. Each stochastic time series is generated by computing mean path of numerous sample random processes. Plots obtained for each time series are presented on a single figure (Fig. 6) in order to provide efficient viewing. Subfigures are lined up starting from stochastic time series through financial time series to chaotic time series. In subfigures, when y axis shows D and H values, x axis represents the number of scale.

In Fig. 6, subfigures from a to e present the changes of H and D values individually as well as \(D+H\) in multiscale for the stochastic time series. As it is clearly seen that even though H and D patterns are different for almost all stochastic time series in various degrees, \(D+H\) value converge at the value of 2, especially after the scale 4 by supporting the relationship generalized by Eq. 46.

However, the subfigures coming after e, displaying the results of MSHG and H algorithms for the chaotic time series, Henon, Duffing and Ikeda indicate irregular and diverging patterns from the relationship of \(D+H=2\) observed in the subfigures of the stochastic time series. While any firm convergence is not quite detected, around the number of 2.5 or between ranges of 2 and 2.5, the sum of D and H seems to fluctuate through until the last computed scale of 12. These such variant observations show that how distinguishing properties the stochastic time series and the chaotic time series possess in terms of H, D and the sum of H and D in multiple scales revealed by MSHG and H methods.

5 Conclusions

This study introduces the multiscale Higuchi’s fractal dimension (MSHG) method as a new complexity measure which captures multiscale properties for time series by employing mean filter as the coarse-graining procedure as a scaling filter and Higuchi’s fractal dimension algorithm as a self-similarity and complexity measurement method.

The choice of the most suitable scaling filter is experimented by applying a number of popular filtering methods on the stochastic and chaotic time series for which several filters are shown to be potentially effective as an addition to commonly used coarse-graining procedure in the multiscale literature. Consequently, the mean filter with an overlapping window is used for providing stable and effective results with the minimal data loss at each step. Also, Higuchi’s fractal algorithm is employed because of its more accurate and faster execution even with the smaller data sets than the alternative algorithms for the computation of fractal dimension.

MSHG method is demonstrated on various selected stochastic time series and chaotic time series. Distinguishing results between these two different class of time series clearly are observed as supporting method’s applicability and functionality as an alternative extension of current multiscale and monoscale complexity measuring methods.

Hurst exponent quantifies the persistence or long-range dependence of time series and has an infamous relationship of \(D+H=2\) with the self-similarity and complexity measure of fractal dimension. Furthermore, how this relationship between Hurst exponent and fractal dimension stands in multiple scales is examined by employing MSHG algorithm and stretching Hurst calculation with long-established Maldelbrot’s method through multiple scales simultaneously, once again on the same time series data sets. While this relationship is observed to be holding for the stochastic time series, contrary evidence is emerged for the chaotic time series. The outcomes of these calculations, clearly, point out specific patterns for the stochastic time series and chaotic time series, through multiple scales with regard to the sum value of D and H which suggests the possible use of these unique multiscale features for the categorization of time series.