On the efficacy of charging a battery using a chaotic energy harvester

Abstract

Introduction of stiffness nonlinearities to broaden the frequency bandwidth of vibratory energy harvesters has the adverse influence of complicating the response behavior of the harvester. As such, unlike linear energy harvesters, for which direct performance metrics can be easily developed, it is not always easy to develop metrics to assess the performance of nonlinear energy harvesters. One particular issue arises when the harvester operates in its chaotic regime resulting in an unpredictable response, under which the harvester’s performance is hard to assess. In this paper, we present a statistical technique to estimate the charging time of a battery being charged by a chaotic vibratory input. The proposed approach, which accounts for the presence of a rectifier circuit, a buck converter, and the dependence of the battery voltage on the state of charge, only requires the knowledge of the probability density function of the open-circuit voltage of the harvester. Using the proposed technique, it is also possible to obtain the optimal duty cycle of the buck converter. Results of the proposed methodology were compared to numerical data generated using MATLAB’s Simscape toolbox demonstrating excellent agreement. Not only does the proposed technique provide a valuable tool to assess performance of a chaotic energy harvester, but it can also be easily applied to other chaotic and random energy sources.

1 Introduction

The advent of vibratory energy harvesting as an effective means for harnessing energy to maintain low power consumption electronics has created various new research problems worthy of investigation. Most of such problems deal with finding the optimal conditions to maximally transfer energy from a vibration source to an electric load. Examples include: (i) active and passive tuning of the mechanical/electrical properties of the harvester to achieve resonance coupling between the source and the load [1,2,3,4,5,6], (ii) enhancing the electromechanical properties of the transduction materials [7, 8], (iii) designing charging circuits capable of dealing with very low power inputs [9,10,11], and (iv) understanding the response of the harvester under random and non-stationary excitations [12,13,14,15,16,17,18,19,20].

One particular research thrust is focused on devising means to improve the bandwidth of the harvester and reduce its sensitivity to variations in the excitation characteristics [21,22,23,24,25,26]. The motivation behind such research stems from a shortcoming in the very fundamental operation principle of the harvester itself. In particular, typical energy harvesters are linear electromechanical oscillators that operate based on the principle of resonance. The amplitude of the harvester’s resonance response drops sharply when the excitation frequency shifts away from the harvester’s natural frequency. Thus, operating the harvester outside the resonance bandwidth reduces its already small power output even further worsening the energy harvesting efficiency. This, combined with the fact that most excitation sources have non-stationary characteristics, necessitates the design of energy harvesters with a broader effective bandwidth.

An efficacious approach to broaden the effective bandwidth of the harvester and reduce its sensitivity to variations in the excitation characteristics lies in intentionally introducing stiffness nonlinearities into the harvester’s restoring force [21]. Because stiffness nonlinearities result in a response frequency which depends on the response amplitude, introducing nonlinearities can extend the coupling between the environmental excitation and the harvester to a wider range of frequencies. Consequently, unlike linear energy harvesters, the resulting response amplitude of a nonlinear energy harvester does not drop sharply as the excitation frequency shifts away from the resonance frequency of the harvester.

However, nonlinear energy harvesters have their own shortcomings. In particular, the nonlinearity complicates the response behavior of the harvester because it produces regions in the frequency domain where coexisting responses with competing basins of attraction exist. Therefore, depending on the initial conditions, the harvester can end up producing very different levels of power for the same exact excitation parameters. Moreover, the nonlinearity can result in chaotic responses and bifurcations that occur as the excitation parameters vary. As such, unlike linear energy harvesters, for which direct performance metrics can be easily developed, it is not always easy to develop metrics to assess the performance of nonlinear energy harvesters.

One particular problem arises when the harvester operates in its chaotic regime resulting in an unpredictable yet bounded response. These chaotic responses are a very common occurrence for nonlinear energy harvesters with bi-stable characteristics. It has been shown that, following a cascade of period doubling bifurcations, a chaotic region appears over a relatively wide excitation frequency bandwidth for moderate levels of excitation [24, 27, 28]. While many studies in the literature focused on understanding the response of an energy harvester to random inputs [29,30,31,32,33], to the authors’ knowledge none dealt with understanding the response when the response is deterministic yet chaotic in nature. It is therefore the goal of this paper to establish a metric to assess the performance of a chaotic energy harvester.

In our approach of this paper, the charging time of a storage device, i.e., a battery, is chosen as a metric for performance assessment. In the process, we will devise a new methodology by which the charging time of a battery can be estimated solely based on the characteristics of the chaotic open-circuit voltage of the harvester. The proposed approach accounts for the presence of a rectifier circuit, a buck converter, and the dependence of the battery voltage on the state of charge.

To achieve this goal, the rest of the paper is organized as follows: Sect. 2 provides an overview of the system components, i.e., the harvester, the rectifier, the buck converter, and the battery. Sect. 3 investigates the open-circuit response of the harvester. Section 4 demonstrates the process of estimating the charging time of the battery for a single-period harmonic input. Section 5 devises a methodology to estimate the charging time for a chaotic signal. Finally, Sect. 6 presents the pertinent conclusions.

2 Overview of the system components

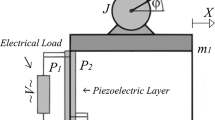
Figure 1 shows a typical harvesting system that consists of four main components: a harvester, a full-wave rectifier, a buck converter, and a battery. The harvester transforms external harmonic vibrations into an alternating electric current. The rectifier and the filter capacitor, $C_{\mathrm{R}}$, rectify the incoming electrical signal from the harvester and reduce the variance of the signal so that it becomes closer to a DC current source. The resulting output is fed into the buck converter, which maximizes the transferred power to the load by matching the impedances of the source and load. This is achieved by stepping down the voltage and stepping up the current. The output current from the buck converter is then used to charge the battery. In what follows, we provide more detailed discussions of each system component.

Fig. 1

A schematic of the harvester and associated electric components

2.1 Harvester

While the analysis presented in this paper can be applied to any energy source with a chaotic output; here we focus on vibration types of energy harvesting. The harvester used in this paper is the bi-stable axially loaded piezoelectric harvester analyzed by Masana and Daqaq in 2011 [27]. The harvester, shown in Fig. 2, has a bi-stable potential function, U(x), with two potential wells separated by a potential barrier. As such, the harvester can perform intra- and inter-well motions and has been shown to exhibit complex dynamic responses, which includes inter-well chaos. The harvester consists of a clamped–clamped aluminum beam with two piezoelectric patches attached to either side of its surface. The clamped boundary conditions were created using carefully designed aluminum clamps with one of the clamps placed on a linear sliding bearing such that it can be used to exert an axial load. The rest of the geometric and material properties of the axially loaded harvester are listed in Table 1.

Fig. 2

Schematic representation of the bi-stable harvester

In Masana’s and Daqaq experiments, the beam was subjected to a compressive static axial loading of magnitude, $P=39.3\,\hbox {N}$, which was beyond the critical buckling load of the beam, $P_{{\mathrm{cr}}}=37.6\,\hbox {N}$. The static load forced the beam to buckle into a nonzero static equilibrium position. To simulate the environmental vibrations, the whole setup was then subjected to a transverse dynamic acceleration, $\ddot{x}_b(t)$, generated by an electrodynamic shaker. In response to these excitations, the beam starts to perform finite amplitude oscillations about the static position. Depending on the magnitude and frequency of the input acceleration, the beam would either undergo small oscillations about the buckled position (intra-well motion) or large amplitude snap-through motion between the static equilibria (inter-well motion). These oscillations produce a dynamic strain in the piezoelectric patches, which, in turn, produces an electric voltage, $V_{\mathrm{p}}$, across the terminals of the piezoelectric elements.

Under the assumptions that the static mid-span deflection of the beam is small and that the external excitation frequency is always close to the frequency of the lowest vibration mode, which is assumed to be free of any internal resonances or an external combination resonance with any of the other modes, Masana and Daqaq [27] showed that the dynamics of the mid-span deflection of the beam can be well approximated by using a damped bi-stable oscillator whose dynamics is given by:

$$\begin{aligned} m\ddot{x}+c_m {\dot{x}}+\frac{\text {d} U}{\text {d}x} +\alpha V_{\mathrm{p}}= -m \lambda \ddot{x}_b, \end{aligned}$$

(1)

where x represents the mid-space deflection of the beam, m is the effective mass of the harvester, $c_m$ is a linear mechanical damping coefficient, $U(x)=-\frac{1}{2} a x^2+ \frac{1}{4} b x^4$ is the mechanical potential energy of the beam, a and b are constants determined experimentally, $\alpha$ is the piezoelectric electromechanical coupling coefficient, $V_{\mathrm{p}}$ is the voltage generated across the piezoelectric capacitor, $C_{\mathrm{p}}$, and $\lambda$ is a constant representing the projection of the base acceleration, $\ddot{x}_b$, onto the first vibration mode. As shown in Fig. 1, the voltage, $V_{\mathrm{p}}$, depends on the effective dynamics of the circuit. Under open-circuit conditions, $C_{\mathrm{p}} V_{\mathrm{p}}=\alpha {\dot{x}}$, or $V_{\mathrm{p}}=V_{{\mathrm{oc}}}=\alpha x/C_{\mathrm{p}}$. The current, $i_s$, generated by the harvester in the absence of an external electric load is equal to $\alpha {\dot{x}}$.

Table 1 Material and geometric properties of the harvester

Using the parameters listed in Table 1, the coefficients in Eq. (1) can be calculated as following [27]: $m=0.0232159\,{\hbox {kg}}$, $a=-6.8712 \times 10^4\,\hbox {N/m}, b=7.6135 \times 10^{10}\,\hbox {N/m}^3$, $\alpha =2.24503\times 10^{-4}\,\hbox {N/V}, c_m= 0.2\,\hbox {kg/s}$, and $C_{\mathrm{p}}=4.61487\,\hbox {nF}$.

2.2 Rectifier

A full-wave rectifier typically with a capacitor $C_{\mathrm{R}}$ at its output rectifies the alternating signal generated by the harvester. Here each solid-state diode in the rectifier is assumed to have a cutoff voltage of 0.7 V and a negligibly small series resistance. The value of the filter capacitor, $C_{\mathrm{R}}$, is chosen to be sufficiently large ($C_{\mathrm{R}}=5\,\upmu \hbox {F}$) such that it has a very slow discharge rate so that the rectified voltage is almost constant. The series resistance of the capacitance is assumed to be negligible.

2.3 Battery

While the analysis presented in this paper is valid for any type of battery, a GMB-300910 rechargeable lithium ion battery with a capacity $Q=12\,\hbox {mAh}$ was used here for the purpose of simulating the results presented throughout this paper. The cutoff voltage of the cell is 3 V while the maximum charge voltage is 4.23 V. The change of the open-circuit voltage of the battery, $V_{{\mathrm{B}}}$, is governed by a polynomial function of the state of charge z; $V_{\mathrm{B}}(z)=\sum _{i=0}^N \beta _i z^i$. For this specific battery, the best polynomial fit yielded $V_{{\mathrm{B}}}(z)= 3.0 + 3.31496 z - 6 z^2 + 3.9 z^3$. The battery is modeled using an equivalent electric circuit consisting of an open-circuit voltage connected in series to a internal resistance $R_0=0.35\,\Omega$, which is used to reflect the instantaneous drop of terminal voltage when a current passes through the cell. Since battery polarization happens at a very slow time scale when compared to the harvester’s dynamics, its influence on the dynamics is neglected.

The battery draws a current $i_{b}$ from the buck converter causing charges to accumulate in the cell according to ${\dot{z}}=\frac{\eta _c}{Q} z$, where $\eta _c=0.98$ is the Columbic efficiency of the cell. The accumulation of charges causes the cell voltage, $V_{{\mathrm{B}}}$, to increase as stated earlier. This process continues until the battery is fully charged when $z\approx 1$. Using a constant direct current of 12 mA, this battery was shown to have a charging time of 2.5 h [34].

2.4 Buck converter

A buck converter is implemented to maximize the power transfer from the harvester to the battery by matching the impedance of both. This is achieved by stepping down the voltage of the rectifier output and stepping up the associated current. This process is essential, or otherwise, a large portion of the energy generated by the harvester is reflected back to the source. In particular, a piezoelectric energy harvester has a large terminal voltage but produces very little current. Only a small portion of the voltage is needed to overcome the rectifier and battery voltage. The buck converter steps down the voltage to the necessary voltage while using the resulting power to boost up the current, and therewith improves the power transfer. For an ideal buck converter, the following holds:

$$\begin{aligned} V_{\mathrm{B}} i_b = V_{\mathrm{R}} i_r, \quad V_{\mathrm{B}} = k V_{\mathrm{R}}, \quad i_b = \frac{1}{k} i_r \end{aligned}$$

(2)

where, as shown in Fig. 1, $i_b$ and $i_r$ are, respectively, the battery and rectifier currents; $V_{\mathrm{B}}$ and $V_{\mathrm{R}}$ are, respectively, the battery and rectifier voltages, and $0<k<1$ is the voltage conversion ratio, which is determined by the duty cycle of the converter. k is the key parameter to be optimized for maximum power transfer.

3 Open-circuit response

The response of the harvester for open-circuit conditions was first simulated using a harmonic base acceleration of magnitude $\ddot{x}_b=13\,\hbox {m/s}^2$. Bifurcation maps of the mid-span deflection x of the harvester and the associated open-circuit voltage $V_{{\mathrm{oc}}}$ versus the excitation frequency are depicted in Fig. 3. The maps were obtained by integrating Eq. (1) at each excitation frequency for sufficiently long time, which allows the system to reach steady state, then recording the points at which the velocity vanishes. To obtain the open-circuit voltage, the harvester was disconnected from the battery and the piezoelectric resistance was assumed to approach infinity. This results in an open-circuit voltage $V_{{\mathrm{oc}}}=\alpha x/C_{\mathrm{p}}$.

Fig. 3

Bifurcation maps of a the mid-span deflection of the beam and b the associated open-circuit voltage versus the excitation frequency. Dashed lines represent the equilibrium points of the harvester. Here, $B_{\mathrm{L}}$ denotes the large orbit branch of solutions, $B_r$ denotes the small-orbit branch, CH denoted chaos, pd denotes a period doubling bifurcation, and cf denotes a cyclic-fold bifurcation

Fig. 4

Time histories of the harvester’s steady-state displacement for a harmonic base acceleration of $\ddot{x}_b=13\,\hbox {m/s}^2$ magnitude and different excitation frequencies a 53 Hz, b 52 Hz, and c 50 Hz

It is evident that, at this acceleration level, the harvester performs complex dynamic responses characterized by coexisting intra- and inter-well motions. Depending on the initial conditions in the range of frequencies 40–46 Hz and 52–60 Hz, the harvester can either perform small periodic oscillations, $B_r$, within a single potential well or large periodic oscillations, $B_{\mathrm{L}}$, between the two wells. Again, depending on the initial conditions, in the range of frequencies 44–51 Hz, the harvester can either perform cross-well chaotic motions (CH) or large amplitude inter-well motions, $B_{\mathrm{L}}$. The size of the chaotic window is loosely bounded by two bifurcations: a cycling fold (cf) bifurcation near 44 Hz and a period doubling bifurcation (pd) near 52 Hz.

In this system, transition to chaos occurs when the intra-well response undergoes a sequence of period doubling bifurcations as the excitation frequency is reduced. For instance, as shown in Fig. 4a, at an excitation frequency of 53 Hz the response is periodic with a frequency matching the excitation frequency. As the excitation frequency is reduced to 52 Hz, the response period doubles as shown in Fig. 4b, and the harvester’s response becomes periodic with a frequency that is half the frequency of the excitation. Further reduction in the excitation frequency results in a cascade of period doubling bifurcations that ultimately results in a chaotic response as shown in Fig. 4c for an excitation frequency of 50 Hz. The chaotic response continues to exist for a range of frequencies down to an excitation frequency of around 46 Hz—except for a small window of periodic responses near 48 Hz. The chaotic attractor ultimately disappears in a boundary crisis near an excitation frequency of 46 Hz [35].

4 Periodic oscillations

As stated earlier, our main objective is to estimate the charging time of the battery using characteristic data of the open-circuit voltage of the harvester. We first treat the simplest case where the harvester’s mechanical oscillations and, hence, the generated input current $i_s$ ($= \alpha {\dot{x}}$) is a single-period periodic function. Here, $i_s=I_o \sin (\omega t)$, where $I_o$ and $\omega$ are the amplitude and frequency of the generated current, respectively. When the piezoelectric element undergoes strain, charges of equal magnitude and opposite sign build on either side of its surface resulting in a voltage difference across its electrodes. Initially, this voltage difference, $V_{{\mathrm{oc}}}=\frac{I_o}{C_{\mathrm{p}} \omega }\int _0^t\sin (\omega \tau ) {\text {d}}\tau$, is too small to overcome the threshold voltage, $V_{{\mathrm{TH}}}$, which is equal to the activation voltage of the diodes, $2V_{\mathrm{D}}$, plus the rectifier voltage, $V_{\mathrm{R}}$, i.e., $V_{{\mathrm{TH}}}=2 V_{\mathrm{D}}+V_{\mathrm{R}}$. As a result, an internal current loop, $i_p$, forms within the piezoelectric element. During that time, the voltage across the piezoelectric element, $V_{\mathrm{p}}$, is equal to the open-circuit voltage, $V_{{\mathrm{oc}}}$.

Fig. 5

Variation in a voltage and b current with time for $i_s=1\times 10^{-4} \sin (100\pi t)\,{\hbox {Amp}}$

When the open-circuit voltage $V_{{\mathrm{oc}}}$ overcomes the threshold voltage $V_{{\mathrm{TH}}}$, a current $i_r$ flows through the full-wave rectifier and, as shown in Fig. 5a, the voltage across the piezoelectric element, $V_{\mathrm{p}}$, becomes equal to the threshold voltage, $V_{{\mathrm{TH}}}$. During this current conduction period, the current $i_r$ is approximately equal to the input current $i_s$. Once $V_{{\mathrm{oc}}}$ drops below $V_{{\mathrm{TH}}}$, the current $i_r$ drops back to zero for a time period, $t_{{\mathrm{cr}}}$, wherein $-V_{{\mathrm{TH}}}<V_{{\mathrm{oc}}}<V_{{\mathrm{TH}}}$. When $V_{{\mathrm{oc}}}$ drops below $-V_{{\mathrm{TH}}}$, the oppositely polarized diodes are activated again and $V_{{\mathrm{oc}}}$ becomes equal to $-V_{{\mathrm{TH}}}$. During this period, the current $i_r$ is equal to negative $i_s$ as shown in Fig. 5b.

To calculate the time required to fully charge the battery, we first find $i_b$. Following Eq. (2), the mean current $\langle i_b \rangle$ can be approximated using the mean value of $i_r$ as:

$$\begin{aligned} \langle i_b \rangle =\frac{\langle i_r \rangle }{k}= \frac{\pi }{\omega k}\int _{t_{{\mathrm{cr}}}}^{\pi /\omega } |i_s| \text {d}t, \end{aligned}$$

(3)

where $t_{{\mathrm{cr}}}$ is the time interval when the current $i_r=0$. This time interval corresponds to $-V_{{\mathrm{TH}}}<V_{{\mathrm{oc}}}<V_{{\mathrm{TH}}}$ and can be calculated by knowing that $t_{{\mathrm{cr}}}$ is the time required for the voltage, $V_{{\mathrm{oc}}}$, to rise from $-V_{{\mathrm{TH}}}$ to $V_{{\mathrm{TH}}}$. Knowing that

$$\begin{aligned} V_{{\mathrm{oc}}}=\frac{1}{C_{\mathrm{p}}} \int _0^t I_o \sin \omega \tau \text {d} \tau \end{aligned}$$

(4)

and letting $V_{{\mathrm{oc}}}=V_{{\mathrm{TH}}}$, we obtain

$$\begin{aligned} \cos (\omega t_{{\mathrm{cr}}})= 1-\frac{C_{\mathrm{p}} \omega V_{{\mathrm{TH}}}}{I_o}. \end{aligned}$$

(5)

Substituting Eq. (5) into Eq. (3), we obtain

$$\begin{aligned} \langle i_b \rangle = \frac{2}{k \pi } (2I_o-C_{\mathrm{p}} \omega V_{{\mathrm{TH}}}). \end{aligned}$$

(6)

The time required to fully charge the battery can then be obtained by using the state of charge equation

$$\begin{aligned} {\dot{z}}= \frac{\eta _c}{Q} \langle i_b \rangle =\frac{2\eta _c}{ Q k \pi } (2I_o-C_{\mathrm{p}} \omega V_{{\mathrm{TH}}}). \end{aligned}$$

(7)

Upon separating the variable, z, from time, t, and integrating, we obtain the following expression for the charging time

$$\begin{aligned} t_f=\int _0^1 \frac{ \pi k Q }{2\eta _c(2 I_o-C_{\mathrm{p}} \omega V_{{\mathrm{TH}}})}\text {d} z. \end{aligned}$$

(8)

Bearing in mind that $V_{{\mathrm{TH}}}=2 V_{\mathrm{D}}+V_{\mathrm{B}}(z)/k$ is a function of the state of charge, the previous integral can only be computed analytically for special cases of $V_{\mathrm{B}}(z)$. When $V_{\mathrm{B}}(z)$ is constant, Eq. (8) reduces to

$$\begin{aligned} t_f=\frac{\pi Q}{ 2\eta _c (2I_o -C_{\mathrm{p}} \omega (2V_{\mathrm{D}}+\frac{V_{{\mathrm{B}}}}{k}))}. \end{aligned}$$

(9)

The charging time can be further expressed in terms of the open-circuit voltage, $V_{{\mathrm{oc}}}$, by knowing that $V_{{\mathrm{oc}}}=\frac{1}{C_{\mathrm{p}} \omega } I_o$. This yields

$$\begin{aligned} t_f=\frac{\pi Q}{ 2\eta _c C_{\mathrm{p}} \omega (2(V_{{\mathrm{oc}}} - V_{\mathrm{D}})+\frac{V_{{\mathrm{B}}}}{k}))}. \end{aligned}$$

(10)

Similarly, for battery voltage that depends linearly on the state of charge, i.e., $V_{\mathrm{B}}(z)=V_1 +V_2 z$, we obtain

$$\begin{aligned} t_f=\frac{\pi k Q}{ 2\eta _c V_2 C_{\mathrm{p}} \omega } \ln \left( \frac{2 k (V_{{\mathrm{oc}}}-V_{\mathrm{D}})-V_1)}{2 k (V_{{\mathrm{oc}}}-V_{\mathrm{D}})-V_1-V_2}\right) , \end{aligned}$$

(11)

and for a quadratic dependence $V_{\mathrm{B}}(z)=V_1 +V_2 z+V_3 z^2$,

$$\begin{aligned} t_f=\frac{\pi k Q}{ \eta _c C_{\mathrm{p}} \omega } \frac{\left( \tan ^{-1} \frac{ V_2}{\sqrt{4V_3(V_1-2k(V_{{\mathrm{oc}}}-V_{\mathrm{D}}))-V^2_2}}-\tan ^{-1} \frac{ V_2+2V_3}{\sqrt{4V_3(V_1-2k(V_{{\mathrm{oc}}}-V_{\mathrm{D}}))-V^2_2}}\right) }{\sqrt{4V_3(V_1-2k(V_{{\mathrm{oc}}}-V_{\mathrm{D}}))-V^2_2}}. \end{aligned}$$

(12)

For higher-order polynomial functions of z, it becomes more efficient to integrate Eq. (8) numerically to obtain $t_f$.

To optimize the power flow form the harvester to the battery, it is essential to obtain the optimal voltage conversion ratio of the converter. To this end, we maximize the mean value of the battery current with respect to k, which yields

$$\begin{aligned} k_{{\mathrm{opt}}}=\frac{2 V_{\mathrm{B}}(z)}{V_{{\mathrm{oc}}} -2 V_{\mathrm{D}}}. \end{aligned}$$

(13)

The battery charging time obtained analytically is compared to numerical results obtained by simulating the response of the combined system using the Simpscape toolbox in MATLAB. Results are depicted in Fig. 6 illustrating excellent agreement between the model and the simulations. Clearly, it shows that there exists an optimal voltage conversion ratio, $k_{{\mathrm{opt}}}$, at which the charging time is minimized. On either side of the $k_{{\mathrm{opt}}}$, the charging time increases rapidly. It can also be noted that underestimation of the optimal voltage conversion ratio results in a much sharper increase in the charging time than overestimation. Thus, it is much safer to operate the converter at voltage conversion ratios that are slightly higher than the optimal value.

Fig. 6

Battery charging time for a base acceleration of $13\,\hbox {m/s}^2$ and a frequency of 40 Hz. The solid line represents analytical data while the markers represent numerical simulation results obtained via the Simscape toolbox in MATLAB

5 Chaotic signal

Estimation of the charging time for chaotic signals requires knowledge of the expected value of the current, $i_b$, which enters the battery. As shown in Fig. 7, the current $i_b$ take two values: a value of zero when $-V_{{\mathrm{TH}}}<V_{{\mathrm{oc}}}<V_{{\mathrm{TH}}}$, and the value of $|i_s|$ otherwise. Since the signal is chaotic, the exact timings of those time intervals are unknown. Instead, we can rely on the response statistics of the open-circuit voltage, $V_{{\mathrm{oc}}}$, to estimate the charging time. To this end, we first assume that the chaotic open-circuit voltage signal can be described by a stationary random variable whose probability distribution function (PDF) is obtained by using a sufficiently long portion of the chaotic signal itself [36]. In other words, we use a portion of the time history of the open-circuit voltage to estimate the PDF, ${\mathcal {P}}(V_{{\mathrm{oc}}})$, of the chaotic voltage. Once ${\mathcal {P}}(V_{{\mathrm{oc}}})$ is obtained, the probability that the open-circuit voltage is in the interval $-V_{{\mathrm{TH}}}< V_{{\mathrm{oc}}} < V_{{\mathrm{TH}}}$ can be calculated using

$$\begin{aligned} p(-V_{{\mathrm{TH}}}< V_{{\mathrm{oc}}} < V_{{\mathrm{TH}}})=\int _{ -V_{{\mathrm{TH}}}}^{ V_{{\mathrm{TH}}}} {\mathcal {P}}(V_{{\mathrm{oc}}}) \text {d} V_{{\mathrm{oc}}}. \end{aligned}$$

(14)

Fig. 7

Variation in the voltage $V_{\mathrm{p}}$ and currents $i_s$ and ib with time. Shaded time intervals represent voltages when $-V_{{\mathrm{TH}}}< V_{{\mathrm{oc}}} < V_{{\mathrm{TH}}}$ and $i_b=0$

Since chaos in the system emanates from bi-stability, the PDF of the voltage signal exhibits a bimodal distribution that can be constructed by adding two or more normal distributions as follows:

$$\begin{aligned} {\mathcal {P}}(V_{{\mathrm{oc}}})=\sum _{i=1}^n\frac{\alpha _i}{\sqrt{2 \pi \sigma ^2_i}} \exp \left( -\frac{(V_{{\mathrm{oc}}}-m_i)^2}{2\sigma ^2_i}\right) , \end{aligned}$$

(15)

where $m_i$ and $\sigma _i$ are, respectively, the means and variances of the normal distributions and $\alpha _i$ are weighting factors. Using the software Mathematica, time histories of the open-circuit voltage were used to construct a best-fit PDF following Eq. (15). In Fig. 8, the convergence of the PDF of the open-circuit voltage was studied as the number of excitation cycles used in the estimation of the PDF is increased. Starting with a small set which contains data from the first 250 excitation cycles $N=250$, the length of the data sets was increased until convergence was achieved. We noticed that there is a negligible change in the PDF beyond $N=4000$. At this value, we note that the PDF becomes almost symmetric about $V_{{\mathrm{oc}}}=0$, which is expected given that the bi-stable potential function describing the dynamics of the harvester is symmetric about the unstable equilibrium point.

Fig. 8

Probability density function of the chaotic signal for different numbers of excitation cycles

Once the PDF is obtained, the probability that the voltage is in the interval $-V_{{\mathrm{TH}}}< V_{{\mathrm{oc}}} < V_{{\mathrm{TH}}}$ can be computed using Eq. (14). The average current in the battery can then be obtained using

$$\begin{aligned} \langle i_b \rangle = k(1-p(-V_{{\mathrm{TH}}}< V_{{\mathrm{oc}}} < V_{{\mathrm{TH}}})) I_{{\mathrm{avg}}}, \end{aligned}$$

(16)

where $I_{{\mathrm{avg}}}$ is the mean of $|i_s|$ in the time intervals when the open-circuit voltage satisfies $|V_{{\mathrm{oc}}}| > V_{{\mathrm{TH}}}$. A crude way to estimate $I_{{\mathrm{avg}}}$ is to assume that it can be approximated by the mean of $|i_s|$ over the whole data set, i.e., $I_{{\mathrm{avg}}} \approx \langle |i_s| \rangle$. This assumption is accurate when the time intervals where $-V_{{\mathrm{TH}}}< V_{{\mathrm{oc}}} < V_{{\mathrm{TH}}}$ are extremely small, which is the case when k is close to one. However, as shown in Fig. 9, when k becomes small, the time intervals where $-V_{{\mathrm{TH}}}< V_{{\mathrm{oc}}} < V_{{\mathrm{TH}}}$ become longer resulting in a larger error in the assumption that $I_{{\mathrm{avg}}}$ can be approximated by using the mean of $|i_s(t)|$ over the whole data set.

Fig. 9

Intervals where the voltage is in the region $-V_{{\mathrm{TH}}}< V_{{\mathrm{oc}}} < V_{{\mathrm{TH}}}$. Light shades represent the case when $k=0.1$ while dark shades represent the case when $k=1$

Fig. 10

Probabilistic sinusoidal model of $i_{s}$ and $V_{{\mathrm{oc}}}$ for two different $V_{{\mathrm{TH}}}$

Fig. 11

PDFs of a the current, $i_s$, and b the voltage $V_{{\mathrm{oc}}}$ for $\ddot{x}_b=13\,\hbox {m/s}^2$ and an excitation frequency of 50 Hz

Fig. 12

Variation in the average current ratio with the duty cycle, k, for $V_o = 60\,\hbox {V}$, $V_{{\mathrm{B}}} = 3.7\,\hbox {V}$ and $V_{\mathrm{D}} = 0.7\,\hbox {V}$

To overcome this issue, we propose an approach to estimate $I_{{\mathrm{avg}}}$ as a function of k based on our understanding of how the open-circuit voltage, $V_{{\mathrm{oc}}}$, and the generated current, $i_s$, are related. Because of the capacitive nature of the piezoelectric transducer, $V_{{\mathrm{oc}}}$ and $i_s$ are $90^\circ$ out of phase. Thus, as shown in Fig. 10, when the voltage is large, the current is small, and vice versa. To obtain $I_{{\mathrm{avg}}}(k)$, the current, $i_s$, and voltage, $V_{{\mathrm{oc}}}$, are first assumed to be purely sinusoidal of the following form:

$$\begin{aligned} i_s = I_o \cos {\theta }, \quad V_{{\mathrm{oc}}}=V_o \sin {\theta }, \end{aligned}$$

(17)

where $I_o$ and $V_o$ are the amplitudes of the current and voltage, respectively. The values of $I_o$ and $V_{o}$ are not arbitrary, but are chosen such that, on average, the assumed sinusoidal form is a best representation of the original chaotic signal. To find $I_o$ and $V_o$, we carefully inspect the PDF of the current and voltage as shown in Fig. 11. Note that while the PDF of the voltage is bimodal, the PDF of the current follows a normal distribution. Thus, for the current, choosing $I_o$ to be the mean of $|i_s|$, i.e., $I_o=\langle |i_s| \rangle$ is a good assumption to capture the essence of the current signal on average. On the other hand, since $V_{{\mathrm{oc}}}$ follows a bimodal distribution, using $\langle |V_{{\mathrm{oc}}}| \rangle$ to estimate $V_o$ will underestimate the real contribution of the input voltage. In such a scenario, it makes more sense to choose $V_o$ such that the average power of the sinusoidal signal is equal to the average power of the chaotic signal. This yields

$$\begin{aligned} V_{o} = \frac{\pi }{2}\frac{\langle |V_{{\mathrm{oc}}} i_s|\rangle }{\langle |i_s| \rangle }. \end{aligned}$$

(18)

Next to estimate $I_{{\mathrm{avg}}}$ as function of k, we find the phase angle, $\theta _{{\mathrm{TH}}}$, at which the current $i_{s}$ flows to the battery. This occurs when $|V_{{\mathrm{oc}}}| \ge V_{{\mathrm{TH}}}$ (shaded regions in Fig. 10). Thus, the phase angle can be expressed as

$$\begin{aligned} \sin {\theta _{{\mathrm{TH}}}} = \frac{V_{{\mathrm{TH}}}}{V_o}. \end{aligned}$$

(19)

The average current $I_{{\mathrm{avg}}}$ during the current conduction time can then be calculated as

$$\begin{aligned} I_{{\mathrm{avg}}}= & {} \frac{1}{\pi /2 - \theta _{{\mathrm{TH}}}} \int ^{\pi /2}_{\theta _{{\mathrm{TH}}}} I_o \cos {\theta } \text {d}\theta \end{aligned}$$

(20)

$$\begin{aligned}= & {} \frac{\langle |i_s| \rangle }{\pi /2 - \theta _{{\mathrm{TH}}}} \left( 1 - \frac{V_{{\mathrm{TH}}}}{V_o} \right) . \end{aligned}$$

(21)

Fig. 13

Charging time of the battery as function of the duty cycle k. Dashed lines represent results obtained using $I_{{\mathrm{avg}}}=\langle |i_s(t)| \rangle$ while the solid line represents results obtained using Eq. (21). Markers represent data obtained using MATLAB Simscape toolbox

Fig. 14

Variation in the charging time with the duty cycle for the different PDFs shown in Fig. 8

Figure 12 depicts variation of the average current ratio, $I_{{\mathrm{avg}}}/\langle |i_s| \rangle$, with the voltage conversion ratio k. It can be clearly seen that the variation reflects the desired trend, that is, for large values of k, $I_{{\mathrm{avg}}}$ approaches $\langle |i_s| \rangle$, while for small values of k, $I_{{\mathrm{avg}}}$ is much smaller than $\langle |i_s| \rangle$. When $V_{{\mathrm{TH}}}$ is larger than $V_o$, $I_{{\mathrm{avg}}}$ is zero and no current flows from the harvester to the battery.

Using Eq. (16) in conjunction with Eq. (21), we estimate the charging time, $t_f=\pi Q/(\eta _c \langle i_b\rangle )$, of the battery for an excitation frequency of 50 Hz and a base acceleration of $13\,\hbox {m/s}^2$. These specific excitation parameters yield a chaotic response as shown earlier in Fig. 3. The PDF of the open-circuit voltage was constructed using 4000 excitation cycles resulting in the bimodal distribution shown in Fig. 8. The PDF was then used to calculate the charging time as function of the duty cycle, k, of the converter. Results shown in Fig. 13 depict the charging time using $I_{{\mathrm{avg}}}=\langle |i_s(t)| \rangle$ (dashed line) and as obtained using Eq. (21). It can be clearly seen that Eq. (21) results in a charging time that is in very good agreement with the numerical simulations (markers) obtained by MATLAB Simscape toolbox. On the other hand, results based on the average current, $\langle |i_s(t)| \rangle$, clearly underestimate the charging time of the battery. It is also worth noting that the numerical simulations obtained using the Simscape toolbox are computationally expensive due to the discrete nature of the diodes. Thus, the analytical approach described in this paper provides an effective technique to estimate the charging time especially when knowing that the PDF of the chaotic signal will need to be generated only once.

Fig. 15

a Probability density function of the chaotic open-circuit voltage, $V_{{\mathrm{oc}}}$, as obtained for different applied harmonic base accelerations. Numbers at the end of the arrows pointing to each PDF represent the magnitude and frequency of the base acceleration at which the chaotic open-circuit voltage was obtained. b Variation of the charging time with k

To study the sensitivity of the results to the shape of the PDF, we generated the curves of the charging time for the PDFs shown in Fig. 8. As shown in Fig. 14, it appears that the charging time is not very sensitive to variations in the shape of the PDF. While the PDF associated with the 250 cycles data set looks very different from that associated with $N=4000$, the charging time curves are similar with a maximum difference of about $7\%$ between the two curves. We also generated the charging time curves for different chaotic signals obtained using different excitation levels, as shown in Fig. 15. When comparing the results obtained using the chaotic signal to those shown in Fig. 6 for a periodic signal, it becomes evident that, at the optimal duty cycle, the charging time of the battery is at least four times longer when using the chaotic input.

The optimal voltage ratio, $k_{{\mathrm{opt}}}$, associated with the chaotic input can be obtained by maximizing the current $i_b$ as given by Eq. (16) with respect to k. The process, which involves setting the derivative of $i_b$ with respect to k to zero, yields a complex nonlinear equation for $k_{{\mathrm{opt}}}$ that can only be solved numerically. For the case involving the ($13\hbox { m/sec}^2$, 50 Hz) base acceleration, the numerical optimization yields $k_{{\mathrm{opt}}}= 0.145$. A simpler, yet still accurate way of estimating $k_{{\mathrm{opt}}}$ is to use Eq. (13), but with $V_{oc}= V_o$ as obtained using Eq. (18) that is;

$$\begin{aligned} k_{{\mathrm{opt}}}=\frac{2 V_{\mathrm{B}}(z)}{V_{o} -2 V_{\mathrm{D}}}. \end{aligned}$$

(22)

Equation (22) yields $k_{{\mathrm{opt}}}=0.152$ ($4\%$ error).

6 Conclusion

In this paper, we devised a methodology to estimate the time required to charge a battery via a chaotic input. The proposed approach, which accounts for the rectifier circuit, a buck converter, and the battery dependence on the state of charge, requires only the knowledge of the chaotic open-circuit voltage of the harvester and the design parameters of the harvesting circuit. Results obtained using the proposed methodology agree very well with numerical simulations obtained using the Simscape toolbox in MATLAB. Using the new approach, we were able to estimate the optimal voltage conversion ratio of the buck converter as function of the battery voltage. Results also illustrate that charging the battery using a chaotic input is not very efficient and takes longer time when compared to periodic inputs. Not only does the proposed technique provide a valuable tool to assess performance of a chaotic energy harvester, but it can also be easily applied to other chaotic and random energy sources.