1 Introduction

With the development of science and technology, an increasing number of mechanical and automatic devices have been applied in industrial production. Many of these devices have an important property that the number of system control inputs is less than the system degrees of freedom, which means that this kind of system is an underactuated system [1,2,3]. The most common reason for the occurrence of underactuation is the system dynamics itself, such as for helicopters [4] and underwater vehicles [5]. Underactuation can also occur due to the goal of reducing the load for certain applications such as in flexible robots [6]. Additionally, when some actuators of a fully actuated system fail, the system will become an underactuated system. Since many commonly used systems are underactuated systems, research on this kind of systems is highly important.

Crane systems, including overhead cranes [7,8,9,10], container cranes [11], rotary cranes [12], tower cranes [13,14,15] and offshore cranes [16,17,18], are typical underactuated systems that are also effective transportation tools and are widely used in many industrial environments such as factories, harbors and construction sites. To reduce costs, the transported payload cannot be directly controlled but is rather dragged by a trolley or a jib through a rope, giving rise to underactuation of the crane system. Most of the industrial crane systems used to date are manually manipulated by experienced workers. However, manual manipulation has some disadvantages such as poor transportation accuracy and low operational efficiency. In addition, this kind of manipulation task is very complex and requires high operational ability of the workers. Furthermore, a long working time may cause fatigue, which is very dangerous and may lead to serious accidents. Additionally, this system may be affected by properties such as dead zones [19] and time delays, which will also increase the control difficulty. Therefore, it is very important to design effective automatic control strategies for crane systems.

Among all crane systems, the overhead crane system is the most widely used. Generally, the control objective of overhead crane systems includes two components: The first is to make the trolley reach its destination quickly and accurately, while the second is to effectively suppress the unactuated payload swing. The control problem of an overhead crane system has attracted the attention of researchers worldwide, and many interesting research results have been presented. Based on whether feedback signals are needed, these results can be divided into two categories. The first category is the open-loop control methods such as trajectory planning methods and input shaping methods. By carefully analyzing the crane system kinematic characteristics, suitable trajectories can be planned for the trolley, with the state coupling behavior considered in the planning process, following which the trolley can reach the desired position, while the payload swing is suppressed [20,21,22,23,24]. For example, in [24], a time-optimal trajectory planning method is proposed for the overhead crane based on the differential flatness theory together with the B-spline technique. Similar to the trajectory planning methods, input shaping methods are also designed for overhead cranes by properly shaping the trolley acceleration signals to achieve payload swing suppression [25,26,27].

Open-loop methods can achieve proper control performance in gentle operational conditions, such as in an indoor environment, while because no feedback signal is needed, the extra cost for some sensors can be reduced. However, when the operational conditions are complex with unavoidable external disturbances, the control performance of open-loop methods may be degraded. To overcome this disadvantage, some closed-loop control methods have been designed that show good robustness. In [28,29,30], the partial feedback linearization technique is used to design control methods for the overhead crane system, and proper control performance is obtained. To deal with system parameter uncertainties, some researchers have designed a series of adaptive control-based methods in [31,32,33]. In addition, to deal with unknown external disturbances and obtain better robustness, sliding mode-based methods have also been successfully extended to control crane systems [34, 35]. To deal with the input saturation problem, together with some state constraints, some model predictive control-based methods are proposed in [36,37,38]. Currently, intelligent control methods, such as fuzzy control [39,40,41] and neural network-based control [42,43,44], are being developed quite rapidly. Some intelligent control methods have also been successfully extended to achieve the crane control objective [45, 46]. When the hook mass cannot be ignored or the payload shape is too large to be ignored, the payload may swing around the hook, and the crane system behaves more as a double-pendulum system. To some extent, the double-pendulum crane model is more precise and complex than the commonly used single-pendulum crane model. Some effective control methods have been proposed for this kind of crane system. Please see [47,48,49,50,51,52] for more details.

Currently, with social progress, safety concerns are becoming increasingly important in industry. Suitable control strategies for overhead crane systems are urgently needed to improve safety and avoid possible accidents. To the best of our knowledge, most existing control methods for overhead cranes focus mainly on the transportation objective, while the important emergency braking problem is usually ignored. However, since the working environment may be very complex, some emergency situations may occur, and to ensure safety, emergency braking methods must be designed. Different from the widely researched transportation problem, the emergency braking problem is highly challenging. Generally, the control objectives of emergency braking have two contradictory components, known as fast trolley braking and effective payload swing suppression. A too sudden trolley braking may lead to a large payload swing angle, which is dangerous and should be avoided. In addition, to avoid possible collisions with obstacles, the payload safety limit should also be satisfied during the entire braking process. However, since the payload position is not directly actuated by the control input, it is difficult to address the requirement of the payload safety limit. Since both transient performance and steady performance need to be considered, this emergency braking problem is very difficult and remains unsolved.

A careful search of the literature revealed that the emergency braking problem has been widely investigated for several other systems, particularly for motor vehicles [53, 54]. However, this important issue has not been widely studied for crane systems due to their underactuation property. In [55], the braking problems in overhead crane drives are considered and solved by designing a braking hardware circuit system for the actuating motor of the overhead crane system. Additionally, [56] proposes a fuzzy motion control method for an auto-warehousing crane with braking considered. However, the methods discussed in [55, 56] are designed to make the trolley stop when the transportation is finished and cannot deal with emergency situations. Currently, the most commonly used emergency braking method for overhead cranes in industry is directly setting the trolley actuating force to zero, thus stopping the trolley. Since no swing suppression is considered, this industrial braking method is likely to give rise to large payload swing, which is dangerous. In [57], a switching-based braking method is proposed for overhead cranes, and the performance of the method is proved by rigorous mathematical calculations. However, the objectives of swing suppression and fast trolley braking cannot be achieved simultaneously, which means that large payload swing may still occur. Our previous study [58] proposes a fuzzy logic-based braking method that makes the trolley brake quickly while simultaneously suppressing the payload swing. However, unfortunately, there is no theoretical proof for the performance of this method.

To solve this challenging problem, in this paper, we design a new emergency braking controller for an overhead crane that achieves fast trolley braking and effective swing suppression at the same time. Additionally, the payload safety limit is also theoretically ensured to avoid possible collisions. To the best of our knowledge, the proposed controller is the first emergency controller with rigorous closed-loop stability analysis that ensures trolley braking, payload swing suppression and the payload safety limit simultaneously and therefore is of great significance. Specifically, we first analyze the mechanical energy of the overhead crane system and recognize the passivity of this system. Then, based on the energy function and utilizing the barrier Lyapunov function technique, a Lyapunov function candidate is constructed, based on which the braking control law is obtained. Next, using the Lyapunov stability theory and LaSalle’s invariance theorem, the stability of the closed-loop system is proved. Additionally, various experiments are implemented using a self-built crane test bed that further illustrate the superior performance of the proposed method. The main merits of the proposed method are as follows: 1. Different from the industrial braking method, the proposed method can achieve trolley braking and payload swing suppression simultaneously, making the braking process more safe. 2. To the best of our knowledge, this method is the first emergency braking method with rigorous theoretical closed-loop analysis that ensures fast trolley braking and payload swing suppression simultaneously. 3. The payload position safety limit is theoretically ensured, avoiding possible collisions with obstacles.

The rest part of this paper is organized as follows. Sect. 2 gives the dynamic model of the overhead crane system together with the detailed control objective of emergency braking. The control method design process and the closed-loop stability analysis are described in Sect. 3, which forms the core of this paper. In Sect. 4, to comprehensively verify the performance of the proposed method, several groups of experimental tests are implemented. At last, the entire paper is summarized in Sect. 5.

2 Problem statements

In this paper, we consider the emergency braking problem for an overhead crane system with the following dynamic model [57]:

$$\begin{aligned}&(M+m)\ddot{x}+ml\ddot{\theta }\cos \theta -ml \dot{\theta }^2\sin \theta =F, \end{aligned}$$
(1)
$$\begin{aligned}&ml^2\ddot{\theta }+ml\cos \theta \ddot{x}+mgl\sin \theta =0, \end{aligned}$$
(2)

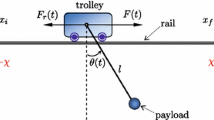
where M and m represent the masses of the trolley and the payload, respectively, l is the rope length, g is the gravity acceleration constant, x(t) is the trolley displacement, \(\theta (t)\) is the payload swing angle and F(t) is the actuating force acting on the trolley. For this kind of overhead crane system, an emergency situation is shown in Fig. 1, where \(x_{{{r}}}\) denotes the position of the obstacle in the transportation path of the payload. To deal with this emergency situation and avoid probable collisions, emergency braking is necessary and is of great significance. Generally, the braking objective of an overhead crane system consists of the following two aspects:

Fig. 1
figure 1

Schematic figure of an emergency situation

Full size image
  1. 1.

    The trolley should decelerate in a timely fashion and stop quickly, while the payload swing is suppressed during the braking process, which can be expressed as follows:

    $$\begin{aligned} \dot{x}(t)\rightarrow 0,\quad \theta (t)\rightarrow 0,\quad \dot{\theta }(t)\rightarrow 0. \end{aligned}$$
  2. 2.

    To avoid possible collisions with obstacles and ensure system safety, during the entire braking process, the payload horizontal displacement should be limited to a safe domain. That is,

    $$\begin{aligned} x_{{{p}}}(t) < x_{{{r}}}, \end{aligned}$$
    (3)

    where \(x_{{{p}}}(t)\) represents the payload horizontal displacement, which can be calculated by the following relationship:

    $$\begin{aligned} x_{{{p}}}=x+l\sin \theta . \end{aligned}$$
    (4)

    \(x_{{{r}}}\) denotes the payload safety limit, which can be determined by the obstacle displacements.

Generally, the following assumption is usually used in many crane control-related papers [7,8,9,10,11,12,13,14,15,16,17,18]:

Assumption 1

In practice, the payload is usually beneath the trolley, which means that the payload swing angle usually satisfies the following condition:

$$\begin{aligned} -\pi /2<\theta (t)<\pi /2. \end{aligned}$$
(5)

Additionally, it is clear that when the braking begins, possible collisions should not occur, which means that the following relationship should be obeyed:

$$\begin{aligned} x_{{{p}}}(0)<x_{{{r}}}. \end{aligned}$$
(6)

Without loss of generality, the time when the emergency braking begins is set to zero.

Based on the system model shown in (1) and (2), we find that the overhead crane system is a typical underactuated system. In addition, high coupling exists in the system dynamics, and inappropriate trolley braking may cause large payload swing, which is extremely dangerous. All of these factors increase the difficulty of the design of a suitable braking control method for overhead crane systems. In this paper, we focus on this important problem and propose a novel braking control method that makes the trolley brake quickly while simultaneously suppressing the payload swing. The payload safety limit is also considered and ensured. In the next section, we will describe the designed process of our method in detail.

3 Controller design and stability analysis

This section gives the detailed process of emergency braking controller design, as well as the corresponding closed-loop system stability analysis. In particular, we first analyze the system mechanical energy and demonstrate the passivity property of the overhead crane system. Then, to obtain better swing suppression performance, some additional items are constructed to enhance the coupling behavior between the trolley movement and the payload swing. After that, a novel emergency braking controller is designed that successfully achieves the braking objectives. At last, the closed-loop system stability is analyzed using Lyapunov stability theory and LaSalle’s invariance principle.

3.1 Emergency braking controller design

The expression for the mechanical energy of an overhead crane system is given by [57]

$$\begin{aligned} E&=\frac{1}{2}(M+m)\dot{x}^2+ml \dot{x}\dot{\theta }\cos \theta +\frac{1}{2}m l^2 \dot{\theta }^2 \nonumber \\&\quad +\,mgl(1-\cos \theta ). \end{aligned}$$
(7)

Taking the time derivative of (7), we have the following relationship:

$$\begin{aligned} \dot{E}&=(M+m)\ddot{x}\dot{x}+ml\ddot{x} \dot{\theta }\cos \theta +ml\dot{x}\ddot{\theta }\cos \theta \nonumber \\ {}&\quad -\,ml\dot{x}\dot{\theta }^2\sin \theta +ml^2\ddot{\theta }\dot{\theta }+mgl\sin \theta \dot{\theta } \nonumber \\&=\dot{x}[(M+m)\ddot{x}+ml\ddot{\theta }\cos \theta -ml\dot{\theta }^2\sin \theta ] \nonumber \\ {}&\quad +\,\dot{\theta }(ml\ddot{x}\cos \theta +ml^2\ddot{\theta }+mgl\sin \theta ). \end{aligned}$$
(8)

Substituting (1) and (2) into (8), we obtain

$$\begin{aligned} \dot{E}=F\cdot \dot{x}, \end{aligned}$$
(9)

illustrating the passivity property of the overhead crane system. Based on this, to achieve the objective of trolley braking, we can directly design a trolley velocity negative feedback controller as follows:

$$\begin{aligned} F=-k_E \dot{x}, \end{aligned}$$
(10)

where \(k_E\in \mathbb {R}^+\) denotes a positive control gain. It is observed that the controller (10) decreases the system energy and further achieves the trolley braking objective. However, we also find that (10) does not contain any swing angle signal-related items, making it unable to achieve satisfactory payload swing suppression performance. To overcome this disadvantage, the important swing angle signal should be contained in the braking controller.

Based on the relationship shown in (9), we design a scalar function \(V_1(t)\) with the following relationship:

$$\begin{aligned} \dot{V}_1=F\cdot [\dot{x}-\beta \cdot \varphi (\theta ,\dot{\theta })], \end{aligned}$$
(11)

where \(\beta \in \mathbb {R}^+\) represents a positive parameter and \(\varphi (\theta ,\dot{\theta })\) denotes a function of the payload swing angle and the angular velocity signal. Doing some calculations, we obtain

$$\begin{aligned} \dot{V}_1=\dot{E}-\beta F\cdot \varphi (\theta ,\dot{\theta }). \end{aligned}$$
(12)

Then, we need to design a positive definite function \(E_{{{s}}}(t)\) with the following relationship:

$$\begin{aligned} \dot{E}_{{{s}}}=-\beta F\cdot \varphi (\theta ,\dot{\theta }). \end{aligned}$$
(13)

Next, we need to construct a suitable structure of \(\varphi (\theta ,\dot{\theta })\) that ensures that (13) is integrable and further obtain the expression of \(V_1(t)\).

Based on the relationship shown in (13), \(E_{{{s}}}(t)\) can be obtained by performing the following integration:

$$\begin{aligned} E_{{{s}}}=&-\beta \int F\cdot \varphi (\theta ,\dot{\theta })\hbox {d}t \\ =&-\beta \int (M+m)\ddot{x}\cdot \varphi (\theta ,\dot{\theta }) \hbox {d}t \\&-\,\beta \int (ml\ddot{\theta }\cos \theta -ml \dot{\theta }^2\sin \theta )\varphi (\theta ,\dot{\theta }) \hbox {d}t. \end{aligned}$$

To design a suitable \(\varphi (\theta ,\dot{\theta })\), we first consider the second part of \(E_{{{s}}}(t)\), which can be rewritten as follows:

$$\begin{aligned}&-\beta \int (ml\ddot{\theta }\cos \theta -ml \dot{\theta }^2\sin \theta )\varphi (\theta ,\dot{\theta }) \hbox {d}t\nonumber \\&\quad =-\beta \int \Bigg \{ml\frac{\hbox {d}(\dot{\theta }^2)}{\hbox {d}t}\cdot \frac{\cos \theta \varphi (\theta ,\dot{\theta })}{2\dot{\theta }} \nonumber \\&\qquad +\,ml\dot{\theta }^2\cdot [-\sin \theta \varphi (\theta ,\dot{\theta })]\Bigg \}\hbox {d}t. \end{aligned}$$
(14)

To make this part integrable, \(\varphi (\theta ,\dot{\theta })\) should be designed with the following relationship established:

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t}\Bigg [\frac{\cos \theta \varphi (\theta ,\dot{\theta })}{2\dot{\theta }}\Bigg ]=-\sin \theta \varphi (\theta ,\dot{\theta }). \end{aligned}$$

Based on this requirement, \(\varphi (\theta ,\dot{\theta })\) is designed as

$$\begin{aligned} \varphi (\theta ,\dot{\theta })=\dot{\theta } \cos \theta . \end{aligned}$$
(15)

(14) can be further shown as

$$\begin{aligned}&-\beta \int (ml\ddot{\theta }\cos \theta -ml \dot{\theta }^2\sin \theta )\varphi (\theta ,\dot{\theta }) \hbox {d}t\nonumber \\&\quad =-\beta \int (ml\ddot{\theta }\cos ^2\theta \dot{\theta }-ml\dot{\theta }^3\sin \theta \cos \theta ) \hbox {d}t\nonumber \\&\quad =-\frac{1}{2}\beta ml \dot{\theta }^2\cos ^2\theta +C_1, \end{aligned}$$
(16)

where \(C_1\) denotes a to-be-determined constant.

In addition, we should also test whether the first part of \(E_{{{s}}}(t)\) is integrable. Substituting (15) into the first part of \(E_{{{s}}}(t)\), we obtain the following relationship:

$$\begin{aligned}&-\beta \int (M+m)\ddot{x}\cdot \varphi (\theta ,\dot{\theta }) \hbox {d}t\nonumber \\&\quad =-\beta \int (M+m)\ddot{x}\dot{\theta } \cos \theta \hbox {d}t. \end{aligned}$$
(17)

Next, based on the dynamic model of the overhead crane, we have

$$\begin{aligned} \cos \theta \ddot{x}=-g\sin \theta -l\ddot{\theta }. \end{aligned}$$
(18)

Substituting (18) into (17), we further obtain

$$\begin{aligned}&-\beta \int (M+m)\ddot{x}\cdot \varphi (\theta ,\dot{\theta }) \hbox {d}t \nonumber \\&\quad =\beta \int [(M+m)g\sin \theta \dot{\theta }+(M+m)l\ddot{\theta }\dot{\theta }]\hbox {d}t \nonumber \\&\quad =-\beta (M+m)g\cos \theta +\frac{1}{2}\beta (M+m) l\dot{\theta }^2+C_2, \end{aligned}$$
(19)

where \(C_2\) denotes a to-be-determined constant. Therefore, it is concluded that the choice of (15) is effective.

Then, based on (16) and (19), \(E_{{{s}}}(t)\) can be expressed as follows:

$$\begin{aligned} E_{{{s}}}&=-\frac{1}{2}\beta ml \dot{\theta }^2\cos ^2\theta +C_1-\beta (M+m)g\cos \theta \\&\quad +\frac{1}{2}\beta (M+m) l\dot{\theta }^2+C_2 \\&=\frac{1}{2}\beta M l\dot{\theta }^2+\frac{1}{2}\beta m l\dot{\theta }^2\sin ^2\theta -\beta (M+m)g\cos \theta \\&\quad +\,C_1+C_2. \end{aligned}$$

To ensure that \(E_{{{s}}}(t)\) is positive definite, the constant \(C_1+C_2\) can be set as \(C_1+C_2=\beta (M+m)g\), and then, it is found that

$$\begin{aligned} E_{{{s}}}=&\frac{1}{2}\beta M l\dot{\theta }^2+\frac{1}{2}\beta m l\dot{\theta }^2\sin ^2\theta \nonumber \\&+\,\beta (M+m)g(1-\cos \theta )\ge 0. \end{aligned}$$
(20)

Then, we obtain

$$\begin{aligned} V_1=E+E_{{{s}}},\quad \dot{V}_1=F\cdot (\dot{x}-\beta \cos \theta \dot{\theta }). \end{aligned}$$
(21)

To facilitate the subsequent descriptions, we define an auxiliary signal variable as

$$\begin{aligned} \varepsilon =x-\beta \sin \theta ,~\dot{\varepsilon }=\dot{x}-\beta \cos \theta \dot{\theta }. \end{aligned}$$
(22)

Thus, we have

$$\begin{aligned} \dot{V}_1=F\cdot \dot{\varepsilon }. \end{aligned}$$

Furthermore, to ensure system safety, during the braking process, the safety limit shown in (3) must be satisfied. Based on this requirement, we construct the following positive definite scalar function based on the idea of the barrier Lyapunov function [59]:

$$\begin{aligned} V_2=\frac{\alpha \dot{\varepsilon }^2}{2(x_{{{r}}}-x_{{{p}}})^2}, \end{aligned}$$
(23)

where \(\alpha \in \mathbb {R}^+\) denotes a positive parameter. Furthermore, to design a suitable emergency braking controller, we choose the following positive definite function as a Lyapunov function candidate:

$$\begin{aligned} V=V_1+V_2. \end{aligned}$$
(24)

Taking the time derivative of (24), we obtain

$$\begin{aligned} \dot{V}&=F\cdot \dot{\varepsilon }+\frac{\alpha \dot{\varepsilon }}{(x_{{{r}}}-x_{{{p}}})^4}[\ddot{\varepsilon }(x_{{{r}}}-x_{{{p}}})^2+(x_{{{r}}}-x_{{{p}}})\dot{x}_{{{p}}}\dot{\varepsilon }] \nonumber \\&=\dot{\varepsilon }\Bigg [ F+\frac{\alpha \ddot{\varepsilon }}{(x_{{{r}}}-x_{{{p}}})^2} +\frac{\alpha \dot{x}_{{{p}}}\dot{\varepsilon }}{(x_{{{r}}}-x_{{{p}}})^3} \Bigg ] \nonumber \\&=\dot{\varepsilon }\Bigg [F+ \frac{\alpha (\ddot{x}-\beta \cos \theta \ddot{\theta }+\beta \dot{\theta }^2\sin \theta )}{(x_{{{r}}}-x_{{{p}}})^2}\nonumber \\&\quad + \frac{\alpha \dot{x}_{{{p}}}\dot{\varepsilon }}{(x_{{{r}}}-x_{{{p}}})^3} \Bigg ]. \end{aligned}$$
(25)

By utilizing (1) and (2), \(\ddot{x}(t),~\ddot{\theta }(t)\) can be expressed as follows:

$$\begin{aligned} \ddot{x}&=\frac{F}{M+m\sin ^2\theta }+\frac{mg \sin \theta \cos \theta +ml\dot{\theta }^2\sin \theta }{M+m\sin ^2\theta }, \end{aligned}$$
(26)
$$\begin{aligned} \ddot{\theta }&=-\frac{\cos \theta \ddot{x}}{l}-\frac{g\sin \theta }{l}. \end{aligned}$$
(27)

Then, based on (26) and (27), we have the following relationship:

$$\begin{aligned}&\ddot{x}-\beta \cos \theta \ddot{\theta } \nonumber \\&\quad =\ddot{x}+\frac{\beta \cos ^2\theta \ddot{x}}{l} +\frac{\beta g \sin \theta \cos \theta }{l}\nonumber \\&\quad =\Big (1+\frac{\beta \cos ^2\theta }{l}\Big ) \frac{1}{M+m\sin ^2\theta }\cdot F+\frac{\beta g\sin \theta \cos \theta }{l}\nonumber \\&\qquad +\,\Big (1+\frac{\beta \cos ^2\theta }{l}\Big ) \frac{mg \sin \theta \cos \theta +ml\dot{\theta }^2\sin \theta }{M+m\sin ^2\theta }. \end{aligned}$$
(28)

Taking the time derivative of (4), we obtain

$$\begin{aligned} \dot{x}_{{{p}}}=\dot{x}+l \cos \theta \dot{\theta }. \end{aligned}$$
(29)

Substituting (4), (28) and (29) into (25) and performing some simplifications, we obtain

$$\begin{aligned} \dot{V}&=\dot{\varepsilon }\Bigg [ F+ \frac{\alpha (l+\beta \cos ^2\theta )}{l(x_{{{r}}}-x-l\sin \theta )^2(M+m\sin ^2\theta )}\cdot F \nonumber \\&\quad +\frac{\alpha (mg \sin \theta \cos \theta +ml\dot{\theta }^2\sin \theta )}{(x_{{{r}}}-x-l\sin \theta )^2(M+m\sin ^2\theta )}\Big (1+\frac{\beta \cos ^2\theta }{l}\Big ) \nonumber \\&\quad +\frac{\alpha \beta g\sin \theta \cos \theta }{l(x_{{{r}}}-x-l\sin \theta )^2}+\frac{\alpha \beta \dot{\theta }^2\sin \theta }{(x_{{{r}}}-x-l\sin \theta )^2} \nonumber \\&\quad +\frac{\alpha (\dot{x}+l\cos \theta \dot{\theta })\dot{\varepsilon }}{(x_{{{r}}}-x-l\sin \theta )^3} \Bigg ]. \end{aligned}$$
(30)

Defining the auxiliary variables

$$\begin{aligned} A&=1+ \frac{\alpha (l+\beta \cos ^2\theta )}{l(x_{{{r}}}-x-l\sin \theta )^2(M+m\sin ^2\theta )}, \end{aligned}$$
(31)
$$\begin{aligned} B&=\frac{\alpha (mg \sin \theta \cos \theta +ml\dot{\theta }^2\sin \theta )}{(x_{{{r}}}-x-l\sin \theta )^2(M+m\sin ^2\theta )}\Big (1+\frac{\beta \cos ^2\theta }{l}\Big ) \nonumber \\&\quad + \frac{\alpha \beta g\sin \theta \cos \theta }{l(x_{{{r}}}-x-l\sin \theta )^2}+\frac{\alpha \beta \dot{\theta }^2\sin \theta }{(x_{{{r}}}-x-l\sin \theta )^2} \nonumber \\&\quad +\frac{\alpha (\dot{x}+l\cos \theta \dot{\theta })\dot{\varepsilon }}{(x_{{{r}}}-x-l\sin \theta )^3}, \end{aligned}$$
(32)

(30) can be rewritten in the following form:

$$\begin{aligned} \dot{V}=\dot{\varepsilon }(A\cdot F+B). \end{aligned}$$
(33)

Then, we can design the emergency braking control law as

$$\begin{aligned} F=\frac{1}{A}(-k\dot{\varepsilon }-B), \end{aligned}$$
(34)

where \(k\in \mathbb {R}^+\) denotes a to-be-determined positive control gain.

In the next part, the satisfactory performance of the proposed emergency braking control law will be demonstrated by rigorous mathematical analysis.

3.2 Closed-loop stability analysis

We will prove that using the designed emergency braking controller (34), the detailed emergency braking objectives can be achieved. The main results are summarized by the following theorem:

Theorem 1

The proposed emergency braking control method can achieve fast trolley braking and suppress the payload swing simultaneously. That is,

$$\begin{aligned} \lim _{t\rightarrow \infty }\dot{x}(t)\rightarrow 0,\quad \lim _{t\rightarrow \infty }\theta (t)\rightarrow 0,\quad \lim _{t\rightarrow \infty }\dot{\theta }(t)\rightarrow 0. \end{aligned}$$
(35)

Additionally, during the entire braking process, the payload position safety limit is ensured to avoid possible collisions with obstacles, in the sense that

$$\begin{aligned} x_{{{p}}}(t)< x_{{{r}}}. \end{aligned}$$
(36)

Proof

Substituting (34) into (33), we have

$$\begin{aligned} \dot{V}=-k\dot{\varepsilon }^2 \le 0. \end{aligned}$$
(37)

Therefore, it is found that \(V(t)\le V(0)\) and \(V(t)\in \mathcal {L}_{\infty }\). Based on the expression for V(t) shown in (7), (20), (21), (23) and (24), the following relationship is obtained:

$$\begin{aligned} \dot{x},\dot{\theta },\frac{\dot{\varepsilon }^2}{(x_{{{r}}}-x_{{{p}}})^2}\in \mathcal {L}_{\infty }. \end{aligned}$$

Considering that \(x_{{{p}}}=x+l\cos \theta \) and \(\varepsilon =x-\beta \sin \theta \), it is obtained that

$$\begin{aligned} \dot{x}_{{{p}}}=\dot{x}-l\sin \theta \dot{\theta },\qquad \dot{\varepsilon }=\dot{x}-\beta \cos \theta \dot{\theta }. \end{aligned}$$

It is further concluded that \(\dot{x}_{{{p}}},\dot{\varepsilon },\frac{1}{(x_{{{r}}}-x_{{{p}}})^2}\in \mathcal {L}_{\infty }\) and \(x_{{{p}}}(t)\) is continuous.

Next, we will prove that \(x_{{{p}}}<x_{{{r}}}\) in the entire control process. At the beginning, this relationship is satisfied since the overhead crane is static and the payload is far from the safety limit \(x_{{{r}}}\). Since \(x_{{{p}}}(t)\) is continuous, assume that the payload position \(x_{{{p}}}(t)\) reaches the safety limit \(x_{{{r}}}\) at the time T. It is found that \(\lim _{t\rightarrow T^{-}}x_{{{p}}}(t)=x_{{{r}}}^{-}\). Then, it is concluded that \(\lim _{t\rightarrow T^{-}}\frac{1}{(x_{{{r}}}-x_{{{p}}})^2}=+\infty \), contradicting the relationship that \(\frac{1}{(x_{{{r}}}-x_{{{p}}})^2}\in \mathcal {L}_{\infty }\). Thus, it is found that this assumption is not established, and \(x_{{{p}}}<x_{{{r}}}\) is satisfied in the entire control process. Then, based on the structure of the auxiliary variable A in (31), it is found that \(A >0\), which means that there is no singularity for the controller (34). Additionally, since we have \(\dot{x},~\dot{\theta },~\dot{\varepsilon },~\frac{1}{(x_{{{r}}}-x_{{{p}}})^2}\in \mathcal {L}_{\infty }\), it is concluded that \(F(t)\in \mathcal {L}_{\infty }\). Then, using the dynamic model in (1) and (2), we can further conclude that \(\ddot{x}(t),~\ddot{\theta }(t) \in \mathcal {L}_{\infty }\). In summary, all of the system signals are bounded.

Now, we will use LaSalle’s invariance principle to prove the asymptotic stability of the closed-loop system. First, we define the set

$$\begin{aligned} S\triangleq \{(q,\dot{q})|\dot{V}=0\} \end{aligned}$$
(38)

and then define the largest invariance set in S as \(\varOmega \). From (37), it is observed that in \(\varOmega \), we have

$$\begin{aligned} \dot{\varepsilon }=\dot{x}-\beta \cos \theta \dot{\theta }=0. \end{aligned}$$
(39)

Taking the time derivative of (39), we obtain

$$\begin{aligned} \ddot{x}=\beta \cos \theta \ddot{\theta }-\beta \dot{\theta }^2 \sin \theta . \end{aligned}$$
(40)

Substituting (40) into (1) and performing some simplifications, we obtain the following relationship:

$$\begin{aligned} \Big ( M+m+\frac{ml}{\beta } \Big ) \ddot{x}=F. \end{aligned}$$
(41)

On the other hand, from (34), it is seen that

$$\begin{aligned} A\cdot F+B=-k \dot{\varepsilon }. \end{aligned}$$
(42)

Substituting the detailed expressions of A and B shown in (31) and (32) into (42), we find that

$$\begin{aligned} F+\frac{\alpha \ddot{\varepsilon }}{(x_{{{r}}}-x_{{{p}}})^2}+\frac{\alpha \dot{x}_{{{p}}} \dot{\varepsilon }}{(x_{{{r}}}-x_{{{p}}})^3}=-k\dot{\varepsilon }. \end{aligned}$$
(43)

Since \(\dot{\varepsilon }=0\), it is directly found that \(\ddot{\varepsilon }=0\). Then, based on (43), it is obtained that

$$\begin{aligned} F=0. \end{aligned}$$
(44)

Using (41), we can further obtain that

$$\begin{aligned} \ddot{x}=0. \end{aligned}$$
(45)

Next, we need to analyze \(\dot{\theta }(t)\). Here, we decide to analyze the cases when \(\dot{\theta }\equiv 0\) and \(\dot{\theta }\ne 0\) to finish the proof.

  • Case 1 Assume that \(\dot{\theta } \equiv 0\) in the set \(\varOmega \). From (39), we obtain that \(\dot{x}=0\). Then, utilizing (2) and (45), it is found that

    $$\begin{aligned} \sin \theta =0. \end{aligned}$$
    (46)

    Then, considering the range of \(\theta (t)\) shown in (5), we further obtain that

    $$\begin{aligned} \theta =0. \end{aligned}$$
    (47)

  • Case 2 Assume that \(\dot{\theta }(t)\) is not identically zero in the set \(\varOmega \). Therefore, there must exists at least one point \(\dot{\theta }(t_{{{a}}})\ne 0\). Since \(\ddot{\theta }\in \mathcal {L}_{\infty }\), it is observed that \(\dot{\theta }(t)\) is continuous. Therefore, in the neighborhood of \(\dot{\theta }(t_a)\), expressed as \(\varOmega _{{{a}}}\), the following relationship is always satisfied:

    $$\begin{aligned} \dot{\theta }\ne 0. \end{aligned}$$
    (48)

    Now, we continue the analysis in \(\varOmega _{{{a}}}\). Substituting (44) and (45) into (1) and (2) and performing some calculations, we obtain

    $$\begin{aligned} \dot{\theta }^2\sin \theta +\frac{g}{l}\sin \theta \cos \theta =0. \end{aligned}$$
    (49)

    Taking the time derivative of (49), we obtain

    $$\begin{aligned} 2\dot{\theta }\ddot{\theta }\sin \theta +\dot{\theta }^3\cos \theta +\frac{g}{l}\cos ^2\dot{\theta }-\frac{g}{l}\sin ^2\theta \dot{\theta }=0. \end{aligned}$$
    (50)

    Based on the crane dynamic model and the relationship \(\ddot{x}=0\), we further have the following relationship:

    $$\begin{aligned} \ddot{\theta }=-\frac{g}{l}\sin \theta . \end{aligned}$$
    (51)

    Substituting (51) into (50) and considering that \(\dot{\theta }\ne 0\), we have

    $$\begin{aligned} -\frac{3g}{l}\sin ^2\theta +\dot{\theta }^2\cos \theta +\frac{g}{l}\cos ^2\theta =0. \end{aligned}$$
    (52)

    Similarly, taking the time derivative of (52) and performing some calculations, we obtain

    $$\begin{aligned} -\frac{8g}{l}\sin \theta \cos \theta +2\ddot{\theta }\cos \theta -\dot{\theta }^2\sin \theta =0. \end{aligned}$$
    (53)

    Next, substituting (51) into (53), we further obtain

    $$\begin{aligned} \frac{10g}{l}\sin \theta \cos \theta +\dot{\theta }^2\sin \theta =0. \end{aligned}$$
    (54)

    From (49) and (54), it is found that

    $$\begin{aligned} \sin (2\theta )=0. \end{aligned}$$
    (55)

    Utilizing (5), it is obtained that \(\theta (t)=0\) and \(\dot{\theta }(t)=0\), contradicting (48). Therefore, the assumption that \(\dot{\theta }(t)\) is not identically zero in the set \(\varOmega \) is incorrect.

Additionally, based on the fact that \(\theta (t)=0,~\dot{\theta }(t)=0\), together with the relationship shown in (39), we can further obtain \(\dot{x}(t)=0\). In summary, we can conclude that in the largest invariance set \(\varOmega \), \(\dot{x}(t),~\dot{\theta }(t)\) and \(\theta (t)\) are all equal to zero. Based on LaSalle’s invariance principle, it is known that \(\dot{x}(t),~\dot{\theta }(t)\) and \(\theta (t)\) all converge to zero asymptotically. Additionally, it is also proved that the payload position safety limit is always satisfied, and the entire control objective of emergency braking is achieved. \(\square \)

Remark 1

In this paper, we consider the emergency braking problem of an overhead crane. For this control problem, it is required that the trolley should brake quickly and the payload swing should be effectively suppressed. In addition, the payload safety limit should be considered and satisfied to avoid possible collisions. To achieve these control objectives, in our work, an emergency braking controller is designed, and the closed-loop system is analyzed rigorously. It is proved that by using the proposed method, the trolley brakes quickly, while the payload swing is effectively suppressed. Additionally, it is also proved that in the entire braking process, the payload safety limit is satisfied. Furthermore, some experiments have also been implemented, and the obtained results verify the effectiveness of the proposed method. In summary, it is concluded that the proposed method achieves all of the objectives of emergency braking, instead of only making the states converge to the steady states.

Remark 2

During the controller design process, we do not consider the upper bound of the trolley actuating force, and it is assumed that the actuated motor of the trolley can provide a sufficiently large braking force. With this assumption, there is no need to analyze the shortest safe distance because, if the payload is very close to the safety limit, a sufficiently large braking force can be provided to make the payload stop immediately, and the safety limit can be further satisfied. In our future work, we will consider the upper bound of the braking force and analyze the shortest safe distance of a certain overhead crane state.

Fig. 2
figure 2

Mechanical structure of the used overhead crane test bed

Full size image

Remark 3

From the expression of V(t), it is found that V can be continuous if both \(\dot{\varepsilon }\) and \(x_{{{p}}}-x_{{{r}}}\) vanish simultaneously. However, during the boundedness proof, it is observed that the fact that both \(\dot{\varepsilon }\) and \(x_{{{p}}}-x_{{{r}}}\) vanish simultaneously does not affect the proof. To summarize, it is concluded that by using the proposed method, the safety limit is satisfied in the entire control process.

4 Experimental results

To verify the proper performance of the proposed emergency braking method, a series of experiments are implemented using a self-built overhead crane test bed.

The detailed mechanical structure of the self-built crane test bed is shown in Fig. 2. It is observed that the trolley can horizontally move along a rail, while the trolley movement is actuated by a 400 W SYNTRON alternating current (AC) servo motor produced by HollySys Automation Technologies, Ltd. The payload is connected to the trolley by a steel rope, and a 100 W SYNTRON AC servo motor is used to actuate the payload lifting movement. The trolley horizontal displacement and the payload vertical displacement can be measured in real time using the encoders equipped in the corresponding servo motors. Additionally, to measure the important payload swing angle, two half-arcs are installed on the trolley. When the payload swings around the trolley, the steel rope will drive the rotations of these two half-arcs, and the angular encoders equipped at the rotating shafts of the arcs measure the swing angle in real time. Moreover, for the software control system, as shown in Fig. 3, a motion control board produced by Googol Technology together with a personal computer is utilized to control the servo motors. In particular, the control signals are first calculated using MATLAB/Simulink installed in the Windows XP environment of the host PC and then transferred to the corresponding servo motor actuator by the motion control board. Additionally, the measured system state signals are also collected by the motion control board and then sent to the PC. Based on the hardware requirements, the sample time is set as \(5~{\mathrm{ms}}\). By careful measurements, the physical parameters of this crane test bed are shown as follows:

$$\begin{aligned} M=4.6~{\mathrm{kg}},~m=5~{\mathrm{kg}},~l=1.05~{\mathrm{m}}. \end{aligned}$$
Fig. 3
figure 3

Control system of the used overhead crane test bed

Full size image

To verify the performance of the designed emergency braking method, we first use a preceding method to make the trolley move to its destination prior to the braking. Then, at the switching time, the preceding method is switched to the emergency braking method, and the emergency braking begins. To comprehensively demonstrate the effectiveness of the proposed method, we implement three groups of experiments. In the first group, both a trajectory planning-based method and a proportional –derivative (PD) control method are chosen as the preceding crane control method to demonstrate the braking performance of our braking method. Then, to demonstrate the adaptability of our method, some system parameters are changed in the second group. The last group shows the experimental results of a commonly used industrial braking method as a comparison to further illustrate the satisfactory performance of our method.

Group 1 In this group of experiments, to verify the effectiveness of the proposed braking control method,Footnote 1 the original trolley target position is set as \(x_{{{d}}}=1.5~{\mathrm{m}}\), while two commonly used crane control methods are chosen as the preceding method.

The first one is a trajectory planning-based control method [60] with the following trolley reference trajectory:

$$\begin{aligned} x_{\mathrm{ref}}=x_{{{d}}}\Big (\xi +\frac{l\ddot{\xi }}{g} \Big ), \end{aligned}$$
(56)

where \(x_{\mathrm{ref}}\) denotes the reference trajectory of the trolley movement, l is the rope length, g is the gravity acceleration constant and \(\xi (t)\) denotes an auxiliary trajectory with the following expression:

$$\begin{aligned} \xi (t)&=252\gamma ^{11}+1386\gamma ^{10}-3080\gamma ^9 \\&\quad +\,3456\gamma ^8-1980\gamma ^7+462\gamma ^6, \end{aligned}$$

where \(\gamma \) is defined as \(\gamma =t/T\), while T denotes the predetermined transportation time, which is set as \(T=6~{\mathrm{s}}\) in our experiments. The second control method is the PD control method given by the following expression:

$$\begin{aligned} F=-k_{{{p}}}(x-x_{{{d}}})-k_{{{d}}} \dot{x}, \end{aligned}$$
(57)

where \(k_{{{p}}},~k_{{{d}}} \in \mathbb {R}^+\) are the positive potential and derivative control gains, respectively. In the experiments, the control gains of the PD controller are set to \(k_{{{p}}}=130\) and \(k_{{{d}}}=100\).

For the emergency braking, the payload position safety limit is set as \(x_{{{r}}}=1~{\mathrm{m}}\) for both the trajectory planning-based method and the PD control method. The braking control gains are set as \(k=30,~\beta =4\) and \(\alpha =0.01\) for the trajectory planning-based method and \(k=34.5,~\beta =2.5\) and \(\alpha =0.01\) for the PD control method.Footnote 2 The experimental results are shown in Figs. 4 and 5. Each figure contains 4 subfigures that show the trajectories of the payload horizontal position, the trolley displacement, the payload swing angle and the actuating control force, from top to bottom. From these two figures, it is observed that by using the proposed method, the trolley can brake quickly with the payload swing effectively suppressed simultaneously. Additionally, the payload position safety limit is satisfied during the entire braking process, avoiding possible collisions with obstacles. By comparing Figs. 4 and 5, we can summarize that even when the preceding control method is changed, the proposed emergency braking method can still obtain superior control performance with all of the braking objectives achieved, in agreement with the mathematical analysis in Sect. 3. We conclude that the designed emergency braking method achieves the braking objectives described in (35) and (36).

Fig. 4
figure 4

Experimental results of the proposed braking method (preceding method: trajectory planning-based method. Payload mass: \(m=5~{\mathrm{kg}}\). Rope length: \(l=1.05~{\mathrm{m}}\). Switching time: \(t=4~{\mathrm{s}}\)). Solid line: experimental results; red dashed line: payload position safety limit: \(x_{{{r}}}=1~{\mathrm{m}}\)

Full size image
Fig. 5
figure 5

Experimental results of the proposed braking method (preceding method: PD control method. Payload mass: \(m=5~{\mathrm{kg}}\). Rope length: \(l=1.05~{\mathrm{m}}\). Switching time: \(t=3~{\mathrm{s}}\)). Solid line: experimental results; red dashed line: payload position safety limit: \(x_{{{r}}}=1~{\mathrm{m}}\)

Full size image

Group 2 In this group of experiments, to demonstrate the adaptability of the proposed method, this method is tested in various working situations different from that in Group 1. Specifically, the preceding method in this group is chosen as the trajectory planning-based method shown in (56), and we change some system parameters in the experiments, including the payload position safety limit, the rope length and the payload mass, as shown in the following three cases:

  • Case 1 Changed payload position safety limit. To test the effectiveness of the proposed method, in this case, the payload position safety limit for the trajectory planning-based method is changed to \(x_{{{r}}}=0.9~{\mathrm{m}}\).

  • Case 2 Changed rope length. Instead of \(l=1.05~{\mathrm{m}}\) as in Group 1, the rope length in this case is changed to \(l=0.8~{\mathrm{m}}\) and \(l=0.9~{\mathrm{m}}\).

  • Case 3 Changed payload mass. A new \(1~{\mathrm{kg}}\) payload is used here to test the designed braking method.

The control gains of the braking method in this group are set as \(k=30,~\beta =4\) and \(\alpha =0.01\) in Case 1, \(k=20,~\beta =6\) and \(\alpha =0.01\) in Case 2, and \(k=20,~\beta =12\) and \(\alpha =0.01\) in Case 3. The experimental results are shown in Figs. 6, 7, 8 and 9. From these figures, we find that even though the working situations are changed, the proposed method can still obtain proper control performance with the entire braking control objective achieved, ensuring system safety.

Fig. 6
figure 6

Experimental results of the proposed braking method (preceding method: trajectory planning-based method. Payload mass: \(m=5~{\mathrm{kg}}\). Rope length: \(l=1.05~{\mathrm{m}}\). Switching time: \(t=4~{\mathrm{s}}\)). Solid line: experimental results; red dashed line: payload position safety limit: \(x_{{{r}}}=0.9~{\mathrm{m}}\)

Full size image
Fig. 7
figure 7

Experimental results of the proposed braking method (preceding method: trajectory planning-based method. Payload mass: \(m=5~{\mathrm{kg}}\). Rope length: \(l=0.8~{\mathrm{m}}\). Switching time: \(t=4~{\mathrm{s}}\)). Solid line: experimental results; red dashed line: payload position safety limit: \(x_{{{r}}}=1~{\mathrm{m}}\)

Full size image
Fig. 8
figure 8

Experimental results of the proposed braking method (preceding method: trajectory planning-based method. Payload mass: \(m=5~{\mathrm{kg}}\). Rope length: \(l=0.9~{\mathrm{m}}\). Switching time: \(t=4~{\mathrm{s}}\)). Solid line: experimental results; red dashed line: payload position safety limit: \(x_{{{r}}}=1~{\mathrm{m}}\)

Full size image
Fig. 9
figure 9

Experimental results of the proposed braking method (preceding method: trajectory planning-based method. Payload mass: \(m=1~{\mathrm{kg}}\). Rope length: \(l=1.05~{\mathrm{m}}\). Switching time: \(t=4~{\mathrm{s}}\)). Solid line: experimental results; red dashed line: payload position safety limit: \(x_{{{r}}}=1~{\mathrm{m}}\)

Full size image

Group 3 This group will show the control performance of a commonly used industrial braking control method as a comparison. Based on our cooperation with an industrial crane factory, it is found that in industry, to make the overhead crane system brake, the commonly used braking method is to directly set the trolley actuating force to zero so that the trolley decelerates due to the friction between the wheels and the track. Based on this, in the experiment, to imitate the industrial braking method, when the braking begins, the trolley actuating force is directly set as zero, and the existing friction makes the trolley brake. The preceding control method used in this group is also the trajectory planning-based method, and the emergency braking begins at \(4~{\mathrm{s}}\). Moreover, the payload position safety limit is set as \(x_{{{r}}}=1~{\mathrm{m}}\). The experimental results are shown in Fig. 10. It is found that using the industrial braking method, the trolley stops very quickly. Even though the industrial braking method can ensure the objective of trolley braking, since no swing suppression is considered, this method may lead to unavoidable large payload swing, which is still dangerous. On the other hand, the proposed emergency braking method achieves fast trolley braking and effective payload swing suppression simultaneously, which is clearly safer. In summary, we can conclude that the proposed emergency braking method provides better control performance compared with the commonly used braking method in industry.

Fig. 10
figure 10

Experimental results of the commonly used braking method in industry (preceding method: trajectory planning-based method. Payload mass: \(m=5~{\mathrm{kg}}\). Rope length: \(l=1.05~{\mathrm{m}}\). Switching time: \(t=4~{\mathrm{s}}\)). Solid line: experimental results; red dashed line: payload position safety limit: \(x_{{{r}}}=1~{\mathrm{m}}\)

Full size image

5 Conclusion

This paper focuses on the emergency braking problem of overhead crane systems and proposes a novel braking control method that simultaneously achieves trolley braking and payload swing suppression. Additionally, the important payload position safety limit is also ensured to avoid possible collisions with obstacles. In particular, the crane system is shown to be passive, and an energy shaped function is designed to enhance the coupling behavior between the system states and further obtain better swing suppression performance. Additionally, the idea of the barrier Lyapunov function is also used to ensure the payload safety limit. The closed-loop system stability is rigorously proved by mathematical analysis. A series of experiments are implemented to verify the satisfactory performance of the proposed method. In our further studies, we will also seek to design optimal control laws to solve this troublesome control problem and obtain better control performance.