Nonlinear dynamics of piezoelectric-based active nonlinear vibration absorber using time delay acceleration feedback

Abstract

In this paper, dynamic analysis of an active nonlinear vibration absorber using lead zirconate titanate (PZT) stack actuator has been carried out considering time delay in the acceleration feedback. Here the primary system is modelled as a harmonically base excited system with a nonlinear spring, damper and mass which is subjected to an external harmonic force. The smart absorber consists of a nonlinear spring, mass and damper system along with a linear spring connected in series with the PZT stack actuator. In the proposed model, the active control force is produced by the combination of spring and the PZT stack actuator which requires less voltage compared to that of the conventional system where the actuator is directly connected to the primary system and one can tune the frequency ratio of the absorber actively. The nonlinear governing equation of motion of the system is derived and solved by using a modified harmonic balance method. The steady-state response is obtained by using Newton’s method, and the stability of the system is studied using the reduced equations. It has been shown that the proposed novel vibration absorber which has inbuilt fail-safe design can absorb the vibration of the system more effectively with negligible damping than the available passive and active vibration absorbers. Also, the Den Hartog’s equal peaks are achieved when the primary system is subjected to both harmonic force and base excitation.

1 Introduction

There are many physical vibrating systems such as automobiles [1, 2], railways [3], ships [4], space crafts [5,6,7], machining systems like turning, milling, boring or drilling system [8,9,10,11], buildings and bridges [12, 13] which undergo severe vibration and need reduction in vibration by using passive or active vibration absorbers or isolators. Generally, vibration absorber consists of a spring and a mass system which is connected to the primary vibrating system to absorb its vibration [14]. In the tuned vibration absorber, the complete vibration suppression of the primary system takes place only at the resonating frequency when the external excitation frequency matches with the natural frequency of the primary system and that of the absorber [15, 16]. It is observed that by the addition of a damper to the tuned vibration absorber, it is impossible to completely eliminate the steady-state response of the primary system [17, 18]. Due to this, many optimization techniques such as fixed point and H-infinity optimization are developed to reduce the amplitude of the resonating vibration [15] and ${H}_{2}$ optimization is used to minimize the total vibrational energy of the primary system [17, 18]. There are many studies on the passive dynamic vibration absorber, and a recent one includes the work of Buki et al. [19] where a vib-bracelet is designed and developed to attenuate 85% of the vibration of the forearm tremor in a human hand. The mass ratio between the absorber and the primary system plays a significant role in the suppression of the vibration and most of the researchers taken it as 1:20 [11,12,13]. The high mass ratio increases the overall structural weight of the system. But with the use of various optimization techniques [20,21,22], model design [23,24,25] along with the advanced materials such as piezoelectric actuator and sensor [26], shape memory alloy [27], voice coil motor [28], electrodynamic vibration absorber [29], magnetostrictive elastomers and dampers [30,31,32] and other smart materials, one may go for lower mass ratio to absorb the vibration of the system for a larger band of operating frequencies [33, 34].

The active control techniques use various feedback methods such as displacement, velocity or acceleration and/or combination of these to attenuate the vibration of the primary mass [35, 36]. Cheung et al. [37] analytically designed a damped hybrid vibration absorber (HVA) with a low mass ratio by obtaining optimum parameters such as tuning frequency, control gain and damping ratio using fixed point theory for of the absorber to suppress the vibration of an SDOF primary system subjected to external harmonic force excitation. They also showed the proposed optimized HVA outshine in suppressing the vibration of a beam under uniformly distributed load. The absorber used for suppressing the vibration of the primary mass vibrates itself at a higher amplitude which arises due to the nonlinear behaviour of the system, which may be evident from the frequency response of the absorber. Also, many dynamical systems are inherently nonlinear because of prolonged use and various applications [4]. The nonlinear vibration absorber is more practical in nature, but its limit of vibration suppression is not adequate as a passive vibration absorber. So in such systems, active vibration absorber is more useful than the passive vibration absorber. Habib et al. [38] derived the formulae for the optimal stiffness and damping ratio of the nonlinear passive dynamic vibration absorber (DVA) which shows two equal peaks in the frequency response at the nonlinear resonating amplitude of the primary system. Gatti [39] studied the efficacy of cubic nonlinear stiffness in the tuned mass damper (TMD) to suppress the vibration of an SDOF primary system under harmonic excitation for a wider band of operating frequency than the linear TMD. They used the harmonic balance method (HBM) and Floquet’s theory to obtain the response of the system and study the effect of hardening and softening nonlinear stiffness on the frequency response and stability of the system. Rizos et al. [40] designed and experimented pre-stressed leaf-springs-based tuned mass damper with four PZT stack actuators to mitigate vibration of the primary structure, which undergoes free, force and base excitation for a wide band of operating frequencies. They also observed and characterize various nonlinearity developed in the system in suppressing the vibration. Renault et al. [41] investigated the enhanced performance of nonlinear dynamic vibration absorber by tracking anti-resonances in frequency response curve using coupled numerical technique and HBM. Cirillo et al. [42] explored the qualitative and structural behaviour of a two-degree-of-freedom nonlinear system under harmonic excitation by bifurcation and singularity theory. They used a single harmonic term in HBM to obtain the frequency response of the system. Kucera et al. [43] analysed vibration suppression of an SDOF system under harmonic disturbance for an extended range of operating frequency by an active vibration absorber using both delayed and non-delayed acceleration feedback. They verified the analytical results with the experimental results and showed that with a distributed delay, vibration suppression of the primary system was achieved for the wider excitation frequency range. Bonkhorst [44] analytically (HBM) and experimentally studied to suppress the vibration of a cubic nonlinear SDOF primary system by an optimal viscoelastic DVA for broadband operating frequency. Carbajal and Navarro [45] analysed an active vibration control scheme to suppress the multi-frequency harmonic vibrations of a primary Duffing oscillator by connecting a passive damped vibration absorber. They proposed a robust active vibration controller and used the method of multiple scales for analytical study. Ji [46] designed a nonlinear vibration absorber tuned under three to one internal resonance to suppress primary resonance of an SDOF nonlinear oscillator having cubic nonlinearity using the method of multiple scales.

From the above literature review, it is observed that most of the work on the dynamic vibration absorbers is based on linear primary and secondary systems and very few researchers have studied the nonlinear vibration absorber to absorb the vibration of the nonlinear primary system. Though several studies have been made on PZT patch actuators for vibration suppression, in very few literature PZT stack actuators are used [40, 43, 47,48,49]. Though accelerometers are commonly used for vibration measurement [7], most of the studies considered displacement or velocity feedback [5, 11, 21, 28, 33,34,35,36,37, 45, 47,48,49,50,51,52] instead of acceleration feedback of the system which shows better vibration suppression [53,54,55,56]. Hence, few studies have been made on acceleration feedback. Further, in most cases, the time delay in the feedback between sensing and actuation is ignored. In few works, both the external forcing and base excitation are considered to obtain the Den Hartog’s equal peaks for the nonlinear primary and secondary systems. Hence, in the present work, an attempt has been made to develop a novel vibration absorber for suppressing the vibration of the nonlinear primary system with nonlinear absorber containing a linear spring with PZT stack actuator and time delay acceleration feedback system. In the next section, the mathematical modelling of the proposed active nonlinear vibration absorber (ANVA) is presented.

2 Mathematical modelling of the system

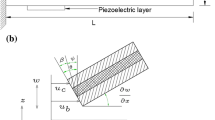
Figure 1 shows the PZT stack actuator-based active nonlinear vibration absorber connected to a harmonically based excited single-degree-of-freedom primary system with nonlinear spring, mass and a damper. In this figure, $m_i ,c_i ,k_i ,$ and $k_{i3}$ denote mass, damping, linear and nonlinear stiffness of the primary system ($i=1$) and the absorber ($i=2$). The primary system is subjected to an external harmonic force $F_{11} \cos (\Omega _1 t)$ and a base excitation $Y_0 \cos (\Omega _2 t)$. The active control force $F_\mathrm{c}$ is produced by the combination of a PZT stack actuator with stiffness $k_P^E$ and a linear spring with stiffness $k_3$. The governing equations of motion of the system in terms of the displacements of the primary system ($x_1$) and the secondary system ($x_2$) are described by two ordinary coupled nonlinear differential equations of motion using Newton’s second law or d’Alembert’s principle which are given follows.

$$\begin{aligned}&m_1 \ddot{x}_1 +c_1 \left( {{\dot{x}}_1 -{\dot{y}}} \right) +c_2 \left( {{\dot{x}}_1 -{\dot{x}}_2 } \right) \nonumber \\&\quad +\,k_1 \left( {x_1 -y} \right) +k_{13} \left( {x_1 -y} \right) ^{3}+k_2 \left( {x_1 -x_2 } \right) \nonumber \\&\quad +\,k_{23} \left( {x_1 -x_2 } \right) ^{3}=F_{11} \cos \left( {\Omega _1 t} \right) -F_\mathrm{c} \end{aligned}$$

(1)

$$\begin{aligned}&m_2 \ddot{x}_2 +c_2 \left( {{\dot{x}}_2 -{\dot{x}}_1 } \right) +k_2 \left( {x_2 -x_1 } \right) \nonumber \\&\quad +\,k_{23} \left( {x_2 -x_1 } \right) ^{3}=F_\mathrm{c} \end{aligned}$$

(2)

Fig. 1

PZT stack actuator-based active nonlinear vibration absorber

In the absence of controlling force $F_\mathrm{c}$, spring stiffness $k_3$ and base excitation, Eqs. (1) and (2) can be reduced to that of Cirillo et al. [42] and Habib et al. [57]. The active control force produced by the PZT stack actuator and the spring stiffness $k_3$ in series may be written as $F_\mathrm{c} =k_\mathrm{r} \left( {x_1 +\delta _0 -x_2 } \right)$ where the equivalent stiffness $k_\mathrm{r} ={\left( {k_3 k_p^E } \right) }/{\left( {k_3 +k_p^E } \right) }$ and $\delta _0$ is the nominal displacement of the PZT stack actuator at the juncture of the primary system. The nominal displacement of the actuator can be written as $\delta _0 =nd_{33} V$ [35], where n, $d_{33}$ and V denote the number of wafers in the PZT actuator, dielectric charge constant and the voltage applied to the actuator, respectively. The PZT actuator acts both as a sensor and as an actuator. First, it senses the acceleration of the primary mass due to the external disturbance and then provides actuation by a counteracting force on the primary mass. During the process, the time delay in the acceleration feedback is considered as $\tau$. The voltage applied to the PZT actuator by the time delay $\tau$ in the acceleration feedback can be written as $V=k_\mathrm{c} \left( {\ddot{x}_1 \left( {t-\tau } \right) } \right)$, where $k_\mathrm{c}$ denote controller gain in the acceleration feedback. Substituting the value of V in the active control force $F_\mathrm{c}$, the modified equation can be written as follows.

$$\begin{aligned} F_\mathrm{c} =k_\mathrm{r} \left( {x_1 -x_2 +nd_{33} k_\mathrm{c} \ddot{x}_1 \left( {t-\tau } \right) } \right) \end{aligned}$$

(3)

Equations (1) and (2) are rewritten below in the non-dimensional form by assuming non-dimensional time $\tau _1 =\omega _1 t$ where $\omega _1 =\sqrt{k_1 /m_1 }.$

$$\begin{aligned}&\ddot{u}_1 +2\xi _1 {\dot{u}}_1 -2\xi _2 {\dot{u}}_2 +u_1 +\alpha _{13c} u_1 ^{3} \nonumber \\&\qquad -\,\left( {\alpha +\alpha _\mathrm{r} } \right) u_2 -\beta u_2 ^{3} \nonumber \\&\quad =F_1 \cos \Omega \tau _1 +Y\cos \left( {\Omega \tau _1 -\gamma } \right) \nonumber \\&\qquad +\,\alpha _{13c} \left( {Y\cos \left( {\Omega \tau _1 -\gamma } \right) } \right) ^{3} \nonumber \\&\qquad +\,3\alpha _{13c} \left( {\begin{array}{l} u_1 ^{2}Y\cos \left( {\Omega \tau _1 -\gamma } \right) - \\ u_1 \left( {Y\cos \left( {\Omega \tau _1 -\gamma } \right) } \right) ^{2} \\ \end{array}} \right) \nonumber \\&\qquad -\,F_{c1} \ddot{u}_1 \left( {\tau _1 -\tau } \right) \end{aligned}$$

(4)

$$\begin{aligned}&\mu \ddot{u}_2 +2\xi _2 {\dot{u}}_2 +\left( {\alpha +\alpha _\mathrm{r} } \right) u_2 +\beta u_2 ^{3} \nonumber \\&\quad =F_{c1} \ddot{u}_1 \left( {\tau _1 -\tau } \right) -\mu \ddot{u}_1 \end{aligned}$$

(5)

where

$$\begin{aligned}&u_1 =x_1 /x_0 ,u_2 =\left( {x_2 -x_1 } \right) /x_0 ,\\&\mu =\frac{m_2 }{m_1 },\xi _1 =\frac{c_1 }{2m_1 \omega _1 },\\&\xi _2 =\frac{c_2 }{2m_1 \omega _1 },\alpha =\frac{k_2 }{k_1 },\\&\alpha _\mathrm{r} =\frac{k_\mathrm{r} }{k_1 }, \\&Y=Y_0 /x_0 ,\alpha _{13} =\frac{k_{13} x_0 ^{2}}{k_1 },\\&\beta =\frac{k_{23} x_0 ^{2}}{k_1 },F_1 =\frac{F_{11} }{m_1 \omega _1 ^{2}x_0 },\\&F_{c1} =\alpha _\mathrm{r} k_\mathrm{c} nd_{33} ,\Omega =\frac{\Omega _1 }{\omega _1 }, \\&\frac{\Omega _2 }{\omega _1 }=\Omega -\gamma ,\gamma =\hbox {phase}, x_0 =\hbox { reference length} \end{aligned}$$

It may be noted that Eqs. (4) and (5) are written by considering the relative displacement of the absorber, i.e. $u_2 =\left( {x_2 -x_1 } \right) /x_0 ,$ by which the complexity associated with the expansion of the nonlinear term $\left( {x_2 -x_1 } \right) ^{3}$ reduces and one can easily obtain the solution. The approximate solution of Eqs. (4) and (5) is discussed in the following section.

2.1 Approximate solution by HBM

In this section, the steady-state solution of Eqs. (4) and (5) are obtained by using the harmonic balance method.

$$\begin{aligned} u_1= & {} A\left( {\tau _1 } \right) \cos \left( {\Omega \tau _1 -\varphi _1 \left( {\tau _1 } \right) } \right) \end{aligned}$$

(6)

$$\begin{aligned} u_1 \left( {\tau _1 -\tau } \right)= & {} A\left( {\tau _1 } \right) \cos \left( {\Omega \left( {\tau _1 -\tau } \right) -\varphi _1 \left( {\tau _1 -\tau } \right) } \right) \nonumber \\ \end{aligned}$$

(7)

$$\begin{aligned} u_2= & {} B\left( {\tau _1 } \right) \cos \left( {\Omega \tau _1 -\varphi _2 \left( {\tau _1 } \right) } \right) \end{aligned}$$

(8)

Unlike in the previous literature in this paper, both the amplitudes ($A\left( {\tau _1 } \right) ,B\left( {\tau _1 } \right)$) and the phases ($\varphi _1 \left( {\tau _1 } \right) , \varphi _2 \left( {\tau _1 } \right)$) are considered to be slowly varying function of time $\tau$ such that one can neglect the following terms: ${\ddot{A}},\ddot{\varphi }_1 ,\ddot{B},\ddot{\varphi }_2 ,{\dot{A}}{\dot{\varphi }}_1 ,{\dot{B}}{\dot{\varphi }}_2 ,{\dot{\varphi }}_1 ^{2},\dot{\varphi }_2 ^{2}.$ Substituting Eqs. (6)–(8) in Eqs. (4) and (5) and equating coefficient of $\sin \Omega \tau _1$ and $\cos \Omega \tau _1$ terms, Eqs. (4) and (5) can be written in the following compact matrix form:

$$\begin{aligned} \left[ {{\begin{array}{llll} {a_1 }&{} {a_2 }&{} {a_3 }&{} {a_4 } \\ {a_5 }&{} {a_6 }&{} {a_7 }&{} {a_8 } \\ {a_9 }&{} {a_{10} }&{} {a_{11} }&{} {a_{12} } \\ {a_{13} }&{} {a_{14} }&{} {a_{15} }&{} {a_{16} } \\ \end{array} }} \right] \left\{ {{\begin{array}{l} {{\dot{A}}} \\ {{\dot{\varphi }}_1 } \\ {{\dot{B}}} \\ {{\dot{\varphi }}_2 } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{l} {b_1 } \\ {b_2 } \\ {b_3 } \\ {b_4 } \\ \end{array} }} \right\} \end{aligned}$$

(9)

where $a_1$–$a_{16}$ and $b_1$–$b_4$ are given in “Appendix-I”

From Eq. (9), the following amplitude and phase equations are obtained.

$$\begin{aligned} {\dot{A}}= & {} f_1 \left( {A,B,\varphi _1 ,\varphi _2 } \right) , \end{aligned}$$

(10)

$$\begin{aligned} {\dot{\varphi }}_1= & {} f_3 \left( {A,B,\varphi _1 ,\varphi _2 } \right) , \end{aligned}$$

(11)

$$\begin{aligned} {\dot{B}}= & {} f_2 \left( {A,B,\varphi _1 ,\varphi _2 } \right) , \end{aligned}$$

(12)

$$\begin{aligned} {\dot{\varphi }}_2= & {} f_4 \left( {A,B,\varphi _1 ,\varphi _2 } \right) . \end{aligned}$$

(13)

The steady-state solutions of the slow-flow equations are obtained from Eq. (9) by taking ${\dot{A}}={\dot{\varphi }}_{_1 } =\dot{B}={\dot{\varphi }}_{_2 } =0$, and the corresponding equations are given as follows.

$$\begin{aligned}&N_1 \cos \varphi _1 +N_2 \sin \varphi _1 +N_3 \cos \varphi _2 \nonumber \\&\quad +\,N_4 \sin \varphi _2 +N_{b1} =0 \end{aligned}$$

(14)

$$\begin{aligned}&\quad -\,N_1 \sin \varphi _1 +N_2 \cos \varphi _1 -N_3 \sin \varphi _2 \nonumber \\&\quad +\,N_4 \cos \varphi _2 -F_1 +N_{b2} =0 \end{aligned}$$

(15)

$$\begin{aligned}&N_5 \cos \varphi _2 +N_6 \sin \varphi _2 \nonumber \\&\quad +\,N_7 \sin \varphi _1 +N_8 =0 \end{aligned}$$

(16)

$$\begin{aligned}&\quad -\,N_5 \sin \varphi _2 +N_6 \cos \varphi _2 \nonumber \\&\quad +\,N_7 \cos \varphi _1 +N_9 =0 \end{aligned}$$

(17)

where $N_1$–$N_9$, $N_{b1}$ and $N_{b2}$ are given in “Appendix-I.”

It may be noted that in the conventional HBM one has to do the stability analysis using the original equation after getting the response [58] but in the present case, both the response and stability analysis can be performed simultaneously by using the reduced Eqs. (10)–(13). The stability of the steady-state equations of the slow-flow equation thus obtained is ensured by the negative real part of the eigenvalues of the Jacobian matrix which is given in “Appendix-I.” The steady-state solutions of the slow-flow Eqs. (14)–(17) are solved by using Newton’s method and are discussed in the following section.

Fig. 2

Frequency response of the a primary system and the b absorber

3 Results and discussions

In this section, the performance of the active nonlinear vibration absorber (ANVA) is studied for a mass ratio of 1:20 (i.e. $\mu =0.05)$ by using the frequency response curves (FRC), time responses phase portraits and Poincare’ section for various system parameters such as cubic nonlinear stiffness in the primary system $\alpha _{13} ,$ cubic nonlinear stiffness of the absorber $\beta ,$ controlling force $F_{c1} ,$ time delay $\tau ,$ amplitude of base excitation Y, amplitude of harmonic force excitation $F_1$ and stiffness of the spring $k_3$ between the PZT stack actuator and the absorber. The FRC for the primary system and the ANVA are found out by numerically solving the four equations [Eqs. (14)–(17)] by using the Newton’s method. It may be noted that these equations are obtained by using HBM. These results are initially compared with the developed SIMULINK model (“Appendix-II”) by solving Eqs. (4) and (5). Further, it is compared by studying Eqs. (4) and (5) using the fourth-order Runge–Kutta method. The command ode45 is used for the system without delay, and dde23 is used for the system with delay. These comparisons will be discussed in the subsequent sections. The stiffness and damping parameters for the ANVA are taken from the work of Habib et al. [38], and Mallik and Chatterjee [35] have been referred for the properties of PZT stack actuator. With reference to Eqs. (4) and (5), the non-dimensional natural frequency of the primary system is $\omega _1 =1$, the damping ratio of the primary system $\xi _1 =$ 0.001 and for the absorber is $\xi _2 =$ 0.0064, linear stiffness ratio between the absorber and the primary system is $\alpha +\alpha _\mathrm{r} =$ 0.0454, external forcing amplitude $F_1 = 0.1$ and $x_0 =1.$ The amplitude of the external forcing $F_1$ is considered to be equal to 0.1 in Sects. 3.1–3.5, 3.7 and 3.8, and in other subsections $F_1$ values are varied from 0.0005 to 1.5 while all other system parameters are kept same in all sections as mentioned above.

In Sects. 3.1–3.6, 3.8 and 3.9, frequency responses, time responses phase portraits, Poincare’ section and basin of attractions of the system are studied by considering only the external harmonic excitation $F_1 \cos \Omega \tau _1$, and hence, the amplitude of harmonic base excitation Y is considered to be zero. In other Sects. 3.7, 3.8 and 3.10, FRC of the system are studied for both external harmonic and base excitation where Y is not equal to zero. In the following subsection, the frequency response of the passive linear system is found out.

Fig. 3

Frequency response curve of the system for $\beta =0.001$ and $\beta =0.01$

Fig. 4

Frequency response of the system for $\alpha _{13} = 0.1$ and $\alpha _{13} = 1$

3.1 Passive linear system

The FRC of the primary system and the ANVA in the absence of any nonlinearity are shown in Fig. 2 with the optimal system parameters taken from Habib et al. [38]. The results obtained in the frequency responses by HBM using Newton’s method (marked in dots) are compared with the numerical simulations using the SIMULINK model (marked using circles), and they are found to be in good agreement as shown in Fig. 2a and b. From Fig. 2a, it is observed that the amplitude of the two resonating peaks is the same and equals to 0.62 at a frequency, $\Omega =0.89$ and 1.05. The response amplitude of the primary system at resonance (i.e. $\Omega =1$) is 0.54. The absorber response is shown in Fig. 2b where the response amplitude at the peaks and the valley is 2.102 and 2.05, respectively. These results are similar to the earlier theoretical analysis [36, 38, 59] and the experimental studies [60, 61]. In the literature ([38], Fig. 2a), the amplitude of external excitation is taken as $F_1 =0.001$ and they observed linear behaviour with a maximum amplitude of $6.2\times 10^{-3}.$ In the present work, the forcing amplitude $F_1 =0.1$, (100 times more) and the corresponding response amplitude is found to be 0.62, which is also 100 times more than the response amplitude in [38]. Hence, both results are consistent as per the superposition rule for the linear system.

This validates the use of harmonic balance method (HBM) formulation for the linear case, and validation for the nonlinear cases is given subsequent sections. In the next subsection, the effect of cubic nonlinear stiffness in the absorber on the FRC is studied.

3.2 Effects of cubic nonlinear stiffness in the absorber for the passive system

The FRC of the primary system and the passive absorber are shown in Fig. 3 for two values of cubic nonlinear stiffness $\beta$ equals to 2.2% (0.001) and 22% (0.01) of the linear stiffness of the absorber. It is observed from Fig. 3a that for $\beta = 0.001,$ the first resonating peak is at 0.86 for $\Omega =0.92$ and the second peak is at 0.53 for $\Omega =1.1$. Similarly, the response amplitude of 2.49 and 1.732 is observed for the absorber (Fig. 3b) at the same frequencies. From Figs. 2 and 3a, b, it is observed that when the operating frequency $\Omega$ is greater than 1, the response of the system is better which reduces the second peak response 15% lower than the linear system. For $\beta = 0.01$ it is observed from Fig. 3a that the response amplitude of the primary system increases sharply from 0.9 to 15 for $\Omega$ in the range of 0.9–0.972. Similar frequency response for the absorber is observed in Fig. 3d. The second peak amplitude of the primary system and the absorber is observed at $\Omega = 1.15$ with amplitude 0.31 and 1.12, respectively. The unstable solution in the frequency response is observed for $\Omega = 0.971$. It is inferred from Fig. 3 that for $\beta$ equals to 2.2% or 0.001 the system amplitude reduces 15% in the second peak, however, for an increase in $\beta$ value to 22% or 0.01 makes the system unstable and creates a larger response in the system. Hence the cubic nonlinear stiffness value in the absorber must be less than 2.2% of the absorber linear stiffness. So one may investigate the use of active vibration absorber if the nonlinearity is more than 2.2%. From these figures, one may observe that the results obtained from HBM and Newton’s method (marked in dots) also compared with the numerical simulations (marked circles) and are found to be in good agreement.

3.3 Effects of cubic nonlinear stiffness in the primary system

The FRC of the primary system and the passive absorber are shown in Fig. 4 for cubic nonlinear stiffness in the primary system $\alpha _{13}$ equal to 10%, i.e. 0.1 and 100%, i.e. 1 of the linear stiffness of the primary system. The FRC of the system obtained by Newton’s method (marked in dots) are also compared numerically by fourth-order Runge–Kutta method (marked using circles) by solving Eqs. (4) and (5) showing a good match with each other. For $\alpha _{13} = 0.1$, it is observed from Figs. 2a and 4a that the response amplitude in the first resonant peak decreases from 0.62 to 0.57, and at the second peak it increases from 0.62 to 0.66 than the linear primary system. The absorber frequency response is shown in Fig. 4b which shows similar characteristic as the primary system. For $\alpha _{13} = 1$, in Fig. 4a one can observe two saddle points at $\Omega =1.18$ and $\Omega =1.8$ showing jump-up and jump-down phenomena, respectively. The second peak in the frequency response is at 1.7 due to the hardening effect in the frequency response while the first peak amplitude is 0.39 at $\Omega =0.89.$ The FRC of the passive absorber are shown in Fig. 4b where the same nonlinear behaviour is observed as the primary system and the maximum response amplitude is found to be 2.32. The system response is unstable from $\Omega =1.18$ to 1.8. Hence for nonlinear stiffness in the primary system below 10%, the system does not show any appreciable changes in the FRC than the linear system, but when the primary system is highly nonlinear, then the response amplitude and unstable region increase as evident from Fig. 4.

Fig. 5

Frequency response of the system, a, b linear and nonlinear stiffness ($\alpha _{13} = 1$) in the primary system. c, d Nonlinear stiffness ($\beta = 0.01$) in the absorber (e, f) nonlinear stiffness in both the primary system ($\alpha _{13} = 1$) and the absorber ($\beta = 0.0042$)

It may be noted that the computational time required to obtain the FRC by SIMULINK (Figs. 2 and 3) or fourth-order Runge–Kutta method (Fig. 4) is more as one has to get the response at each frequency point. Time taken to obtain a single point on the response curve takes 1 min, so to obtain complete FRC which consists of more than 100 points it takes more than 1 h and 40 min, and also unstable points are difficult to obtain. Using the HBM method, the computational time required to obtain the plot is only 6 min, so one can use the proposed HBM method to reduce the computational time and study the stability of the response. Unlike other perturbation methods where the small divisor terms in the equation motion are required to obtain the solution but in HBM, one can use the procedure without ordering the equation. Further, in this modified HBM one can obtain the stability of the system by using the Jacobian matrix of the reduced equations. While the above-mentioned FRC show the response of the system with passive vibration absorber, in the next section the study has been carried out for active vibration absorber by using PZT stack actuator with acceleration feedback.

3.4 Active vibration absorber

In this section, the FRC of the proposed ANVA are found out for four different cases, namely linear, nonlinear spring in the primary system, nonlinear spring in the absorber and nonlinear spring in both the primary system and the absorber, with negative feedback controlling force $F_{c1} = 0.1$ and they are shown in Fig. 5. For the linear case, it is observed from Fig. 5a that with the active controlling force (blue colour) the response amplitude decreases from 0.62 (Fig. 2a) to 0.49 in the first peak (21%) at $\Omega = 0.8$, and for the second peak, it decreases from 0.62 (Fig. 2a) to 0.34 (45%) at $\Omega =1.2$. It may be observed that these peaks are occurring at different frequencies due to the presence of active force. The response amplitude at resonating frequency ($\Omega =1$) decreases from 0.54 (i.e. in passive case, Fig 2a) to 0.15 in the present active case which is a 72% reduction. But the response amplitude of the absorber increases from 2.4 to 3.6 (50%) for the first peak and from the same value to 2.6 (8%) in the second peak as shown in Figs. 2b and 5b. Further considering a realistic system where the primary system is considered to be highly nonlinear ($\alpha _{13} =1$), the FRC are shown in Fig. 5a (black colour). Unlike in Fig. 4a here, the frequency response of the primary system shows no unstable region and the amplitude of vibration reduces from 0.39 to 0.36 (7.7%) in the first peak and from 1.8 to 0.42 (77%) in the second peak. The FRC for the absorber (Fig. 5b) seem to be similar to the linear system, and no unstable region is found unlike in the case of Fig. 4b, but the amplitude of the response increases from 1.5 to 2.7 in the first peak and 2.3 to 2.8 in the second peak. Comparing the linear and the nonlinear responses, it is observed that the response amplitude for the linear system decreases 34% in the first peak, but at second peak it increases 14% while, at the resonating frequency, the response amplitude remains same as that of the nonlinear primary system. In Fig. 5c, d, the FRC of the system are studied for $\beta = 0.01$. From Fig. 5c, it is observed that by the applied controlling force a small range of unstable zone is found when $0.962<\Omega <0.965$ with jump-up and jump-down phenomena. In addition, the system shows an unstable region when $1.1195<\Omega <1.733$ showing Hopf bifurcation points at $\Omega =1.195$ and 1.733.

The response amplitude of the active nonlinear absorber (Fig. 5d) is higher than that of the passive case (Fig. 3d). In Fig. 5e, f, nonlinear stiffness in both the primary system ($\alpha _{13c} =1$) and the absorber ($\beta =0.0042$) are considered. It may be noted that here optimum nonlinear stiffness coefficients are considered from the work of Habib et al. [38]. It is observed from Fig. 5e that with the active force $F_{c1} = 0.1$, the response amplitude of the primary system reduces for $\Omega>$ 1.136 and shows saddle-node bifurcation points at $\Omega = 0.982$ and 1.136. Here, also it may be noted that at the resonant frequency, i.e. $\Omega = 1$, the nonlinear system has two stable and one unstable response out of which the lower stable response has a value which is less than that found in [38], where the $F_{c1} = 0$. From Fig. 5f, it is observed that the response amplitude of the absorber increases at the peaks than the passive vibration absorber.

From Fig. 5, it is observed that with the applied controlling force there is much decrease in the unstable region of operating frequency and also the vibration of the primary system; however, the amplitude of the absorber increases at the peaks. In the following section, nonlinear stiffness is considered in both the primary system and the absorber and the variation of controlling force on the frequency response is studied.

3.5 Variation of controlling force on the frequency response

The effect of four values of controlling force $F_{c1}$, viz. 0 (green colour), 0.1 (cyan colour), 0.2 (black colour) and 0.5 (blue colour) on the FRC of the system, is studied in this section.

Fig. 6

Frequency response of the system for variation in controlling force $F_{c1}$ for (a, b) $\alpha _{13} = 0.1$ and $\beta = 0.001$. c, d Basin of attraction of the primary system at $\Omega = 0.82$ and 0.889. Frequency response of the system with different $F_{c1}$ for e, f$\alpha _{13} = 1$ and $\beta = 0.01$

3.5.1 Nonlinear stiffness in both the primary system and the absorber

In Fig. 6a, b and e, f, the FRC of the system are shown by considering two values of nonlinear spring stiffness in both the primary system and the absorber. In Fig. 6a, b, the nonlinear stiffnesses $\alpha _{13c}$ and $\beta$ are considered equal to 0.1 and 0.001, respectively. From Fig. 6a, it is observed that with $F_{c1} =0$ the primary system shows two peaks with amplitude 0.69 and 0.54 at $\Omega$ equals to 0.92 and 1.08, respectively, with no unstable zone. But by increasing $F_{c1}$ values from 0 to 0.1, the amplitude of the two peaks shift and occur at $\Omega$ equals to 0.908 and 1.24. A minimum of 55% reduction in the vibration of the primary system is observed than for $F_{c1} = 0$ when $0.91<\Omega <2$, but the system shows an unstable frequency zone for a small range when $0.906<\Omega <0.91$ and the system has multiple solutions. The jump-up and jump-down phenomena are observed with saddle-node bifurcation points at $\Omega = 0.906$ and 0.911. Further increasing $F_{c1}$ values from 0.1 to 0.2, the primary system amplitude reduces to 0.003 (96%) than for $F_{c1} = 0$ when $\Omega>$ 0.96, but at the same time more hardening effect in the FRC is observed with instability zone when $0.888<\Omega <0.956$. Two saddle points are observed at $\Omega = 0.888$ with the jump-up amplitude height 0.7 and at $\Omega = 0.956$ with the jump-down amplitude height is 1.44 for $F_{c1}$ = 0.2. It is observed from the FRC that with the increase in the $F_{c1}$ at first peak the system amplitude increases, and for a very small range of operating frequency, the system shows unstable fixed point solution, but for a larger band the amplitude response reduces significantly. In Fig. 6c, d, basin of attraction for the primary system is plotted at the points D ($\Omega = 0.82$) and E ($\Omega = 0.889$) of Fig. 6a. From Fig. 6c at point D, one can observe a single stable point with response amplitude of 0.64. Also in Fig. 6d at point E, two stable points with response amplitude of 1.2 and 0.4, with a separatrics at response amplitude of 0.62, can be observed which are evident from the FRC curve shown in Fig. 6a. In Fig. 6b, the amplitude of the absorber for $F_{c1} = 0.1$ shows marginal higher amplitude for $\Omega>$1, but for $\Omega<$ 0.9 the absorber amplitude increases with the same unstable zone as discussed above. In Fig. 6e, f, highly nonlinear system is considered with $\alpha _{13}$ and $\beta$ equals to 1 and 0.01, respectively. In Fig. 6e, for $F_{c1} = 0$, two high peaks with amplitude equal to 0.87 and 0.35 at $\Omega =1.16$ and 1.18, respectively, with the stable and unstable solutions appear when $1.062<\Omega <1.162$. The jump-up amplitude of 0.32 and jump-down amplitude of 0.54 are observed at $\Omega =1.062$ and at 1.162, respectively. The Hopf bifurcation points are observed at $\Omega =1.103$ and at 1.163. The response amplitude at the first peak of the primary system that reduces from 0.87 to 0.56 with $F_{c1} =0.1$ compares to when $F_{c1} =0$ but creates a wider range of unstable zone with saddle-node bifurcation points at $\Omega =1.014$ and 1.146 and Hopf bifurcation points at $\Omega =1.172$ and 1.338. The same effects are also observed for $F_{c1} =0.2$ and 0.5 with more hardening effect and unstable region. The amplitude of the primary system at first peak ($\Omega =1.016$) decreases 80% with an increase in $F_{c1}$ from 0 to 0.5 but shows both stable and unstable fixed point solutions. However, the jump-up and jump-down amplitude height increases with more hardening effect. In Fig. 7a, f for $F_{c1} =0.2$ (black line), the time responses, phase portraits and Poincare’s section at point P ($\Omega =1.15$, stable point), Q ($\Omega =1.25$, unstable point) and R ($\Omega =1.52$, unstable point) of Fig. 6e are shown. From Fig. 7a, b, time response and fixed point response are observed at point P, and quasi-periodic responses are observed at points Q and R. From the phases portraits and Poincare’ section in Fig. 7a–h, existence of periodic, quasi-periodic and chaotic responses in addition to fixed point responses is clearly observed for different system parameters. Hence, one must choose the system parameters carefully to suppress the excessive vibration.

Fig. 7

Time responses a, b, phase portraits and Poincare’s section (c–f) at the frequency points P ($\Omega =1.15$), Q ($\Omega =1.25$), and R ($\Omega =1.52$) for $F_{c1} = 0.2$. g, h Phase portraits and Poincare’ section for $F_{c1}$ = 0.2 at $\Omega =1.08$ and $\Omega =1.32$

3.5.2 Linear system

The FRC of the linear system with a variation of $F_{c1}$ are shown in Fig. 8a, b. It is observed from Fig. 8a that with higher $F_{c1}$ the amplitude of the primary system reduces for all frequency of operation with no unstable zone and shows a significant decrease in the amplitude response at the second peak. The system with $F_{c1} =0.5$ shows around 90 % reduction in vibration than $F_{c1} =0$ for $\Omega >0.85$, but at the same time the absorber amplitude (Fig. 8b) at the peaks increases.

Fig. 8

Frequency response of the linear system for variation in controlling force $F_{c1}$

Hence from Fig. 8, it is observed that large vibration reduction in the primary system is achieved with higher values of $F_{c1}$ when the system is linear. But when both the primary system and absorber are nonlinear (Figs. 6, 7), then for a particular operating frequency higher controlling force may not be effective. It is also observed that a wider unstable range of frequency is obtained for $\alpha _{13}>$ 10% and $\beta>$2.2% of the linear stiffness of the system. So, one has to choose $F_{c1}$ values judiciously to suppress the vibration of the system for a broader range of operating frequency. In the following section, the effects of variation in the amplitude of external force excitation on the FRC are studied.

3.6 Effects of variation in the amplitude of external excitation

In Fig. 9, the effect of three values of amplitude of external excitation, viz. $F_1$ equals to 0.1 (cyan colour), 0.5 (black colour) and 1 (green colour) on the FRC of the system, is studied with zero control force and the results are compared with those obtained by numerically solving Eqs. 4 and 5 (marked in circles). In Fig. 9a, b, the FRC of the system are shown for $\alpha _{13}$ and $\beta$ equal to 0.1 and 0.01, respectively. From these figures, it is observed that with an increase in the amplitude of external excitation the peak response amplitude of system increases. For $F_1$ = 0.1, the jump-up and jump-down phenomena are observed with saddle-node bifurcation points at $\Omega$ equals to 1.005 and 1.087, respectively. An isolated stable and unstable branch are also observed when $1.25<\Omega <1.356.$ Further increase in the $F_1$ value from 0.1 to 1, the system response amplitude increases with a large increase in the jump-up and jump-down height as shown in Fig. 9a, b. The primary system shows only a single peak (Fig. 9a), but the absorber shows two peaks (Fig. 9b). Near the supercritical Hopf bifurcation (point S, $\Omega =1.4$), the time response of the primary system is found to be periodic with many harmonics, and for the absorber, it is found to be quasi-periodic. For other point near Hopf bifurcation point R ($\Omega =1.552$), both the primary system and the absorber have a quasi-periodic response which is clearly evident from Poincare’ section (Fig. 9c, d).

Fig. 9

Frequency response of the system for variation in the amplitude of external force $F_1$, a, b$\alpha _{13} = 0.1$ and $\beta = 0.01$. c–f Time response and Poincare’ section at S ($\Omega =1.4$) and R ($\Omega =1.552$) for $F_1 = 0.5$

In Fig. 10, the response of the highly nonlinear system is analysed for the variable amplitude of external excitation for three different frequencies, i.e. $\Omega =1.2$, 1 and 0.8. From Fig. 10a and c, it is observed that with $F_{c1} = 0.1$ and $\alpha _{13} = 1$ the response amplitude decreases and no unstable region is observed. The Hopf bifurcation points without active force are observed at $\Omega =0.062$ and $\Omega =0.104$ for $\Omega =1.2$. The effectiveness of the active force in suppressing the vibration is clearly observed for $0<F_1 <0.1$. In Fig. 10e–h, optimal nonlinear stiffness parameters ($\alpha _{13} =1$, $\beta =0.0042$) from the work of Habib et al. [38] are considered. From Fig. 10e and g, it is observed that with $F_{c1} =0.1$ the response amplitude of the primary system decreases for $F_1$ in the range of 0–0.1. Hopf bifurcation points are observed at $F_1 = 0.107$, 0.2 and 0.274 for $\Omega = 1.2$ without active force. But with $F_{c1} =0.1$ the Hopf bifurcation points are observed at $F_1 = 0.116, 0.124, 0.276$ and 0.432 for $\Omega =1.2$ and $F_1 =0.071$ and 0.115 for $\Omega = 1$. The response amplitude of the absorber increases with $F_{c1} =0.1$ compared to $F_{c1} =0$. From Fig. 10, it is observed that with $F_{c1} =0.1$ the response amplitude of the highly nonlinear primary system decreases with active force but for the higher amplitude of excitation, the effectiveness of controlling force is not observed. However, one can suppress the vibration for the higher amplitude of external excitation by increasing the controlling force. In the following section, the same system is studied where the primary system is also subjected base excitation.

Fig. 10

Response of the system for variation in the amplitude of external force $F_1$, a, b$\alpha _{13} = 1$ and $F_{c1} = 0$. c, d$\alpha _{13} = 1$ and $F_{c1} = 0.1$. e, f$\alpha _{13} = 1$, $\beta = 0.0042$ and $F_{c1} = 0$. g, h$\alpha _{13} = 1$, $\beta = 0.0042$ and $F_{c1} = 0.1$

Fig. 11

Frequency response curve with $Y= 0.01$ and $F_1 = 0.1$. Linear system (a, b) without and with controlling force. Nonlinear primary system (c, d) with $\alpha _{13} = 0.1$ and $\alpha _{13} = 1$

3.7 Active vibration absorber with both harmonic force and base excitation

Considering both external harmonic force and base excitation, the FRC of the system are shown in Fig. 11. In Fig. 11a–d, the amplitude of force $F_1$ and base excitation Y are considered to be equals to 0.1 and 0.01, respectively, and the phase ($\gamma$) is taken to be zero. In Fig. 12, the amplitude of force $F_1$ and base excitation Y are both taken as 0.1 and $\gamma =\pi /2$.

3.7.1 Linear system

Initially, the response for the primary system and the passive absorber is shown in Fig. 11a, b, where the response amplitude of the primary system at the two peaks is the same and equals to 0.69 and for the absorber, it is 2.33 and 2.29, respectively. Now applying controlling force $F_{c1}$ equals to 0.1, i.e. for the active system, the response amplitude of the primary system decreases from 0.69 to 0.55 (21%) in the first peak and from 0.69 to 0.41 (40%) in the second peak. Similarly, at the resonating frequency ($\Omega =1$), the amplitude of the primary system also decreases from 0.6 to 0.2 (67%). However, the response amplitude of the absorber (Fig. 11b) at the peaks is more in case of active vibration absorber than in passive vibration absorber.

3.7.2 Nonlinear stiffness in the primary system

Now considering $\alpha _{13} = 0.1$ in Fig. 11c, the response amplitude of the two peaks is found to be 0.52 and 0.41 at $\Omega$ equals to 0.82 and 1.21, respectively. From Fig. 11c, it can be observed that a reduction of 16% is achieved in the first peak and 41% in the second peak in the active vibration absorber than the passive vibration absorber (Fig. 4a). It may be noted that in Fig. 4a the primary system is subjected to only harmonic excitation force. For absorber (Fig. 11d), the two peaks are found to be 3.6 and 2.8, respectively. Now, considering the highly nonlinear primary system ($\alpha _{13} = 1$) in Fig. 11c, one can observe that the two resonating peaks are 0.42 and 0.52. It may be noted that 80% reduction in response amplitude in the second peak is observed in the active case in comparison with the passive case (Fig. 4a). However, for the absorber (Fig. 11d) the response amplitude at the peaks is found to be 3.14 and 3.16. From Fig. 10, it is clearly observed that the suppression of vibration of the primary system under harmonic force and base excitation can be achieved by applying the appropriate controlling force using the developed equations for the proposed absorber. Here the nonlinear system behaves much like a linear system by using the acceleration feedback-based control force.

3.7.3 Nonlinear stiffness in both the primary system and the absorber with a different nonzero phase between external force and base excitation

Considering nonlinear stiffness in both the primary system and the absorber with different phases between the external forcing and base excitation, the FRC are shown in Fig. 12. It is observed from these figures that the response amplitude of the system is more for $\gamma$ = 0 than $\gamma$ = 90$^{\circ }$ when $F_{c1} = 0$. Also, it is observed that the response amplitude of the primary system reduces with $F_{c1} =0.1$. The higher amplitude of the base excitation force in these figures produces higher response amplitude than that of Fig. 11. Here also similar nonlinear effects as stated in the previous sections are observed. In the following section, the effect of time delay in the active vibration absorber is investigated.

Fig. 12

Frequency response curve with $Y= 0.01$ and $F_1 = 0.1$. a, b$\alpha _{13} = 0.1$ and $\beta = 0.001$

3.8 Effects of time delay in active vibration absorber

The effects of four values of time delay $\tau$ = 0, 0.1, 1 and 10 on the FRC of the system are studied in this section for various parameters of nonlinear stiffness. In Sects. 3.8.1–3.8.4, FRC of the system are studied by considering only external force excitation, and in Sect. 3.8.5 both external force and base excitations are considered.

3.8.1 Linear system

In Fig. 13a, b, the FRC of the system are shown by considering a linear system. From Fig. 13a, it is observed that for $\tau$ equals to 0 and 0.1, the system does not show any unstable region but for $\tau$ equals to 1 and 10, a broader range of unstable region appears. The response amplitude at the first peak is 7% more at $\tau = 0$ than at $\tau = 0.1$, while at second peak it is 1% less. For $\tau =1$, the stable region is observed for 0.63 $>\Omega>$2.16, and for $\tau =10$, the system is completely unstable. In Fig. 13b, similar characteristics are observed with higher response amplitude. From Fig. 13a, b, it can be inferred that for $\tau =0.1$ the system vibration suppression is better compared to higher or lower time delay.

Fig. 13

Frequency response of the active linear system with variation in the time delays. $\tau =0$ cyan (stable), $\tau =0.1$ green (stable), $\tau =1$ black (stable) red (unstable), $\tau =10$ magneta (unstable). (Color figure online)

3.8.2 Nonlinear stiffness in the absorber

In Fig. 14a, b, only the nonlinear stiffness in the absorber is considered for $\beta = 0.001$. From Fig. 14a, it is observed that for $\tau = 0$ the primary system shows high response amplitude at the first peak with jump-up and jump-down phenomena at saddle-node bifurcation points $\Omega$ = 0.902 and 0.916, respectively, but for $\tau = 0.1$ the response amplitude at the first peak reduces to 65% with no unstable region. Further increasing $\tau$ to 1, it is observed that the system becomes more unstable with a stable region found for a narrow band of 1.112 $<\Omega<$ 1.228, while for $\tau =10$ no stable region is observed. From Fig. 14a, b, it is inferred that for $\beta =0.001$ a time delay of $\tau =0.1$ shows better vibration suppression and the system is stable than other time delays. In Fig. 14c, d, FRC of the system are shown by increasing the nonlinear stiffness, i.e. $\beta =0.01$. From Fig. 14c, it is observed that for $\tau =1$ the response amplitude near the first peak reduces to 90% than for $\tau =0$ or 0.1 and shows a stable region for $\Omega<$ 1.164, but for $\tau =10$ the system is completely unstable.

Fig. 14

Frequency response of the system for different time delays (a, b) $\beta =0.001$ (c, d) $\beta =0.01$. $\tau =0$ cyan (stable) magneta (unstable), $\tau =0.1$ green (stable) blue (unstable), $\tau =1$ black (stable) red (unstable), $\tau =10$ magneta (unstable). (Color figure online)

The Hopf bifurcation points are observed for $\tau =1$ at $\Omega =1.165$ and 1.515, where the system stability changes from stable to unstable and vice versa respectively, which is more clearly shown in Fig. 14d. From Fig. 14a–d, it is concluded that for lower nonlinear stiffness in the absorber (2.2% or 0.001) the time delay of 0.1 shows better vibration suppression with no unstable region. For higher nonlinear stiffness in the absorber (22% or 0.01), the time delay of 1 shows better vibration suppression with no unstable region when the operating frequency $\Omega<$ 1.164.

3.8.3 Nonlinear stiffness in the primary system

In Fig. 15a, b, only the nonlinearity in the primary system is considered, i.e. $\alpha _{13} = 0.1$. From these figures, it is observed that for $\tau =0$ and 0.1 the response amplitude is stable. The response amplitude of the primary system for $\tau =0$ is 6% more at the first peak and 12% less at the second peak than for $\tau =0.1$. For $\tau =1$, the system shows an unstable region for 0.62 $<\Omega<$ 2.162, and for $\tau =10$, the system shows broader unstable region and an isolated stable and unstable branch for 0.996 $<\Omega<$ 1.071. From these figures, it can be inferred that for $\alpha _{13} = 0.1$ the delay in the range of 0–0.1 shows stable behaviour and less peaks response amplitude. In Fig. 15c, d the nonlinear stiffness is increased by considering $\alpha _{13} = 0.2$. Here also the same trend is observed as in Fig. 15a, b but for $\tau ={}^{\prime }10$ the isolated branch is merged with the stable and unstable branch. Further increasing the nonlinear stiffness, i.e. $\alpha _{13} = 1$ in Fig. 15e, f, the close orbit opens up for $\tau ={}^{\prime }10$ and shows stable region for 0.931 $<\Omega<$ 1.04. The Hopf bifurcation points are observed at frequency points $\Omega =0.93$ and 1.04. A comparison of time responses at frequency marked K ($\Omega =0.92$, unstable) and L ($\Omega =0.94$, stable of the Fig. 15e, f) is shown in Fig. 15g, h. From the time responses in Fig. 15g, h, one can observe fixed point response at L point and a higher periodic response amplitude at K point which evident from the FRC of Fig. 15e, f. From Fig. 15a–h, it can be inferred that for time delay equals to 0 and 0.1 the system amplitude is less than higher delay and no unstable region is observed for nonlinear stiffness in the primary system equals to 0.1–1. Also, the system amplitude at both peaks decreases with increasing $\alpha _{13}$ from 0.1 to 1. For $\tau = 1$ and 10, the response amplitude and unstable region are more pronounced and only for a limited range of frequency the system is stable.

Fig. 15

Frequency response of the system for different time delays (a, b) $\alpha _{13} = 0.1$ (c, d) $\alpha _{13} = 0.2$ (e, f) $\alpha _{13} = 1$. g, h Time responses at frequency K ($\Omega = 0.92$) and L ($\Omega = 0.94$). $\tau =0$ cyan (stable), $\tau =0.1$ green (stable), $\tau =1$ black (stable) red (unstable), $\tau =10$ yellow (stable) magneta (unstable). (Color figure online)

3.8.4 Nonlinear stiffness in both absorber and primary system

In Fig. 16a, b, $\alpha _{13}$ and $\beta$ are considered equals to 0.1 and 0.001, respectively, and the colour code is same as in Fig. 14. From Fig. 16a, it is observed that for $\tau =0$ the response amplitude at first peak increases by 18% while at the second peak it is decreased by 8% than for $\tau =0.1$ and shows unstable solution at the first peak with two saddle-node bifurcation points at $\Omega =0.906$ and 0.911. For $\tau =1$, the unstable region broadens with Hopf bifurcation points are at $\Omega = 0.628, 1.123$ and 1.479. The system becomes complete unstable for $\tau =10$ and shows a single peak. It is inferred from these figures that for $\tau =0.1$ the system response amplitude shows better vibration suppression for a broader range of operating frequency when $\alpha _{13} =0.1$ and $\beta =0.001$ with no unstable region.

3.8.5 Nonlinear primary system with both external force and base excitation

Considering both external harmonic force $F_1 =0.1$ and base excitation $Y=0.1$, the FRC of the system for the above four-time delays $\tau$ are shown in Fig. 17a, b. From Fig. 17a, b, one can observe for $\tau = 0$ and 0.1 the response amplitude of the system is less and shows no unstable range of operating frequency than for higher time delays $\tau =1$ or 10. For $\tau =1$, the Hopf bifurcation points are observed at $\Omega =0.62$ where the system stability changes from stable to unstable as shown in red colour. For $\tau =10$, the system shows Hopf bifurcation points at $\Omega = 0.964$, 1.017, 1.018 and 1.073. It is observed from these figures that for time delay $\tau = 0$ and 0.1 the system is stable and response amplitude is less than higher time delay 1 or 10. In the following section, effects of the spring stiffness $k_3$ attached to PZT stack actuator in the active vibration absorber are investigated.

Fig. 16

Frequency response of the system with different time delay for $\alpha _{13} =0.1$ and $\beta =0.001$. $\tau =0$ cyan (stable) magneta (unstable), $\tau =0.1$ green (stable), $\tau =1$ black (stable) $\tau =1$ red (unstable), $\tau =10$ magneta (unstable). (Color figure online)

Fig. 17

Frequency response of the system with different time delay with $Y=0.1$ and $\alpha _{13} = 0.1$. $\tau =0$ cyan (stable) magneta (unstable), $\tau =0.1$ green (stable), $\tau =1$ black (stable) $\tau =1$ red (unstable), $\tau =10$ yellow (stable) $\tau =10$ magneta (unstable). (Color figure online)

3.9 Effects of the spring stiffness attached to PZT stack actuator

The displacement of the nonlinear primary system and the active nonlinear absorber is shown in Fig. 18 when the applied controlling force $F_{c1} = 0.005$ and stiffness $k_3 =0.05$ N/kg. The parameters are kept same as in the work of Habib et al. [38] which are $m_1 =1$ kg, $c_1 =0.002$ Ns/m, $k_1 =1$ N/m, $k_{13} =1$ N/m$^{3}$, $m_2 =0.05$ kg, $c_2 ={0.0128}$ Ns/m, $k_2 ={0.0454}$ N/m and $k_{23} ={0.0042}$ N/m$^{3}$. In Fig. 18, a comparison of the displacements of the primary system and the secondary system for the present case of ANVA and that of the Habib et al. [38] is shown. The response in both the cases is quasi-periodic for external excitation $F_1$ = 0.12. It shows clearly that in this case, the response of the primary system reduces 31% i.e. from 0.75 to 0.52. The vibration suppression of the nonlinear absorber is more noticeable in Fig. 18b where the amplitude reduces from 2.4 to 0.32 (87%) with the active control force.

Fig. 18

Comparison of time responses with passive and active absorber for the (a) primary system and the (b) absorber with $F_1 ={0.12}$

In all the previous analysis, it is observed that with the applied controlling force $F_{c1}$, the response amplitude of the absorber at the peaks increases, but here it is shown that with proper stiffness value of $k_3$ one can reduce the vibration of both the absorber and the primary system. Also, it is observed that with the applied controlling force the system settles down more quickly than the passive vibration absorber. The stiffness of spring $k_3$ can be increased to provide more blocking force to the PZT stack actuator, and at the same time, spring stiffness $k_2$ can be decreased to maintain the optimum tuning ratio required to suppress the vibration of the primary system actively. The increase in spring stiffness $k_3$ suppresses the vibration of the absorber, and by the combination of both active control force and spring $k_3$, the required vibration suppression of the primary system and the absorber can be achieved. In the following section, the effect of spring stiffness $k_3$ is studied on FRC to obtain Den Hartog’s equal peaks when the primary system is subjected to both external harmonic and base excitation.

3.10 Effects of attached spring in the PZT stack actuator

While in the previous sections attempts were made to reduce the amplitude of the primary system, in this section it is tried to achieve the Den Hartog’s equal peaks in both the nonlinear primary system and the active nonlinear absorber, when the primary system is subjected to both external force and base excitation. While it is absolutely required to have equal peaks in the primary system to minimize its maximum response amplitude, sometimes due to space/kinematic constraint, it is also required to have equal peaks of the absorber to minimize its response amplitude. The equal peaks in the FRC are tried to achieve by variation of spring stiffness $k_3$ and $F_{c1}$. It may be noted that the taken system parameters are same as those in Habib et al. [38], where they obtained equal peaks in the FRC of the primary nonlinear system which is subjected to only external excitation force by considering nonlinear passive vibration absorber.

3.10.1 External force excitation

In Fig. 19a, b, the spring stiffness $k_3 =0.0005\hbox { N/kg}$, active control force $F_{c1} =0.0005$ and external harmonic force $F_1 =0.001$ are considered. From Fig. 18a, the two resonating peaks in the FRC of the primary system are observed to be 0.0042 and 0.0082 at $\Omega = 0.88$ and 1.08, respectively. The resonating peaks amplitude of the absorber (Fig. 19b) is at different amplitudes of 0.016 and 0.022 at $\Omega = 0.9$ and 1.07, respectively. It may be noted from Fig. 19a that with the applied controlling force the primary system amplitude is lesser at the first resonating peak than the passive nonlinear vibration absorber by Habib et al. [38]. In Fig. 19c, d, $F_1$ and $F_{c1}$ are increased to 0.01 and 0.005, respectively, keeping all other system parameters the same as in Fig. 19a, b. The difference between the resonating peak amplitudes and valley amplitude of both the primary system and the absorber reduces as shown in Fig. 19c, d. The maximum amplitude for the primary system is observed at the second peak with a value of 0.062 at $\Omega =1.08$. The maximum amplitude for the absorber is found to be 1.194 (Fig. 19d) at $\Omega = 1.08$. The resonating peak and the valley amplitude in the FRC for both the primary system and the absorber are minimized by increasing the active controlling force as observed from Fig. 19a–d, and also the Den Hartog’s equal peaks in the FRC of the nonlinear primary system and the active nonlinear vibration absorber can be found.

Fig. 19

Frequency response of the system with the external harmonic force for (a, b) $k_3 =0.0005$, $F_{c1} =0.0005$ and $F_1 =0.001$ (c, d) $k_3 =0.0005$, $F_{c1} =0.005$ and $F_1 ={0.01}$

3.10.2 Both harmonic external force and base excitation

Now in Fig. 20a, b to obtain equal peaks in the FRC for $Y=0.0012$ and $F_1 =0.001$, $F_{c1}$ and $k_3$ are increased to 0.05 while keeping all other system parameters same as in Fig. 19c, d. But it is found that with the increasing $F_{c1}$ and $k_3$, the primary system (Fig. 19a) shows a single peak of amplitude 0.13 at $\Omega =0.88$, and for absorber (Fig. 20b), the first resonant peak amplitude is 0.25 and a small resonating peak is observed with amplitude 0.34 at $\Omega =1.4$. So, in Fig. 20c, d the stiffness of $k_3$ spring is decreased to 0.005 from 0.05 while all other system parameters are kept the same as in Fig. 20a, b. It is observed from Fig. 20c, d that vibration suppression by the absorber is significantly better than in Fig. 19a, b in reducing the maximum amplitude for the primary system to 0.037 and 0.052 at $\Omega = 0.93$ and 1.09 respectively. But the two resonating peaks are found at different response amplitudes. In Fig. 20e, f, the comparison between the responses of the system is shown when the primary system is subjected to external harmonic excitation $F_1 =0.0012$ and base excitation $Y=0.0012$ for with and without using the attached spring $k_3$ to the PZT stack actuator. It is observed from Fig. 20e, f that for the same spring stiffness $k_3$ and $F_{c1}$ equals to 0.005 the vibration suppression is better for both the primary system and the absorber and also the response amplitude of the resonating peaks are same. From Fig. 20, it is observed that with applied controlling force the vibration suppression is better than the passive vibration absorber and also sensitiveness of the vibration for the system reduces which shows two equal peaks in the response curves when both external harmonic force and base excitation are acting on the primary system. With the proposed active nonlinear vibration absorber, the two resonating peaks amplitudes of the primary system are found to be 0.0062, which show better vibration suppression than the passive nonlinear vibration absorber. In Fig. 20f, the FRC of the absorber show the two resonating peaks amplitudes are slightly at a different amplitude of 0.015 and 0.017, respectively. From these curves, it is found that with the attached spring and PZT stack actuator combination the vibration suppression of both the system is reduced for a wider band of operating frequency when the primary system undergoes both harmonic force and base excitation. From Fig. 20 and Sect. 3.7, it is observed that the vibration suppression of the primary system is better than the work reported in [45, 46] where the mass ratio is considered to be 1:10.

Fig. 20

Frequency response of the system for $F_{c1} =0.05,F_1 =0.01$ and $Y=0.0012$, (a, b) $k_3 =0.05,$ (c, d) $k_3 =0.005$. Frequency response of the system for $F_{c1} =0.005,F_1 =0.0012$ and $Y=0.0012$ (e, f) (black) for $k_3 =0.005,$ and (blue) for $k_3 =0$. (Color figure online)

3.11 Reliability and cost of the proposed active nonlinear vibration absorber

In the proposed model, as both spring and actuator provide the controlling force, one can obtain higher controlling force by the PZT stack actuator due to the blocking force produced by the spring which is in series connection with the PZT stack actuator. Also, when the actuator, i.e. the active part, fails due to an electronic malfunction, then the passive optimal absorber can still protect the primary system from severe vibration. Thus, the proposed vibration absorber is more economical and fail-safe design. Also, it can be observed that the natural frequency of the primary system ($\omega _{n1} =\sqrt{{\left( {k_1 +k_2 +k_\mathrm{r} } \right) }/{k_1 }}$, $k_\mathrm{r} ={k_3 k_p^E }/{\left( {k_3 +k_p^E } \right) })$ does not change much with the variation of spring $k_3$ attached to the PZT stack actuator, but the natural frequency of the absorber ($\omega _{n2} =\sqrt{{\left( {k_2 +k_\mathrm{r} } \right) }/{\mu k_1 }}$, $\mu ={m_2 }/{m_1 })$ changes significantly as the absorber mass is 20 times smaller than the mass of the primary system. So the designer can tune the frequency of the absorber actively in accordance with the forcing frequency of the primary system by the spring and actuator combination for various other resonance conditions. The proposed active nonlinear vibration absorber shows better vibration suppression at resonance than (Figs. 16 and 17) from the work of Kučera et al. [43] where linear analysis is carried out experimentally considering delayed resonator. The vibration suppression by the proposed absorber is almost same (90%) of the vibration for the highly nonlinear primary system as in the experimental work of Bronkhorst et al. [44]. But in [44], the absorber mass is 20% of the primary mass, whereas in the present analysis the absorber mass is only 5% of the primary system. Hence, the proposed absorber is very much lighter than in [44]. The proposed absorber also gives better performance than the work of Xiang et al. [60] where absorber mass is similar to that in [44], i.e. 20% of the primary system where a higher damping ratio for the absorber is used. It may be noted that in the present case, very low damping ratio for the primary system ($\xi _1 =$ 0.001) and the absorber ($\xi _2 =$ 0.0064) is used. Hence, the present model is more reliable and cost-effective as a lighter weight absorber is used. These studies can find effective application in vibration suppression of many small and large machinery used in various industries.

4 Conclusions

In this work, the performance of the active nonlinear vibration absorber is investigated for the primary resonance condition by considering a new design in the active part where the PZT stack actuator is connected in series with a spring in the absorber configuration. The analysis is carried out by considering time delay in the acceleration feedback of the primary system when it undergoes both external harmonic force and base excitation. The steady-state response and its stability are obtained by using a modified harmonic balance method, where the amplitude and the phase are considered as a slowly varying function of time. Time responses, phase portraits, Poincare’ sections, basin of attractions, frequency responses with stable and unstable branches are plotted to investigate the effect of cubic nonlinear stiffness, controlling force, time delay, attached spring stiffness, the amplitude and frequency of external harmonic force and base excitation on the suppression of vibration of the system. The frequency response curves obtained by harmonic balance and Newton’s method are compared with those obtained by fourth-order Runge–Kutta method and are found to be in good agreement. Fundamentally based on nonlinearity, the considered systems are divided into four cases, viz. case-1: both the primary system and the absorber are linear, case-2: the primary system linear and the absorber are nonlinear, case-3: the primary system nonlinear and the absorber are linear, case-4: both the primary system and the absorber are nonlinear. Further considering the presence and absence of PZT stack actuator (active force), delay and base excitation, twenty different cases have been investigated in this work.

From the analysis, it can be observed that in case-2 with cubic nonlinear stiffness in the absorber below 2.2% the system behaves similar to case-1 and the response amplitude in case-2 is less at the second peak than the case-1. However, higher nonlinearity in the absorber stiffness (22%) increases the response amplitude of the system. In case-3 considering nonlinear stiffness of the primary system equals to 10% of the linear spring, the response amplitude remains same as that in case-1. But with higher nonlinear stiffness in the primary system, jump-up and jump-down phenomena are observed with higher amplitude in the second peak.

It is observed for the primary system that by suitably applying the controlling force by the spring and PZT stack actuator combination (30–90%) vibration suppression is achieved for case-1 and case-3 when the system undergoes both harmonic force and base excitation. Moreover, the highly nonlinear primary system in case-3 behaves like that of case-1 with no hardening effect with the applied active force. In case-2 with highly nonlinear absorber (22%) by applying active force the response amplitude reduces significantly but after the resonant frequency, supercritical Hopf bifurcation is observed. Comparing case-2 and case-4, it is observed that with same control force the attenuation in vibration in case-4 is more significant than in case-2. Similar to the case-3 here in case-4, Hopf bifurcation is observed which leads to periodic, quasi-periodic and chaotic responses with a change in the controlling force. It is also observed that with active force the response amplitude of the absorber remains almost same at the resonant frequency; however, at the peaks its response amplitude increases in all cases.

Further considering time delay, it is observed that the response amplitude is less for the time delay of 0.1 than in the case of 0, 1 and 10 in case-1, 3 and 4. But in case-2 with higher nonlinearity in the absorber, a time delay of 1 shows better vibration suppression. Hence depending on the actual system parameters, one should consider the proper delay to suppress the vibration. Also, the higher time delay of 10 makes the system completely unstable for most of the cases. It is also observed that by selecting the proper stiffness value of spring attached to the PZT stack actuator, the vibration of the absorber and the primary system can be attenuated. Further, it is also observed that with variation of both $k_3$ and $F_{c1}$, vibration of the primary system and the absorber are reduced up to 30% and 80%, respectively, and the Den Hartog’s equal peaks in the frequency response of the nonlinear primary system and the active nonlinear vibration absorber is achieved when the primary system undergoes both harmonic and base excitation. With the suggested parameters and the analysis on various coefficients of cubic nonlinear stiffness, active forces by the PZT stack actuator, time delays in the feedback and excitations amplitude on the system give a clear idea for the designer to know the response amplitude of the system and the operating frequency range to minimize the vibration of the system.

Appendices

Appendix-I

$$\begin{aligned} a_1= & {} -\,2\Omega \cos \varphi _1 +2\xi _1 \sin \varphi _1 \\&+\, 2F_{c1} \Omega \sin \varphi _1 \sin \Omega \tau \\&-\, 2F_{c1} \Omega \cos \varphi _1 \cos \Omega \tau \\ a_2= & {} 2\xi _1 A\cos \varphi _1 +2\Omega A\sin \varphi _1 \\&+\, 2F_{c1} A\Omega \sin \varphi _1 \cos \Omega _d \\&+\, 2F_{c1} A\Omega \cos \varphi _1 \sin \Omega \tau \\ a_3= & {} -\, 2\xi _2 \sin \varphi _2 \hbox {, }a_4 =-2\xi _2 B\cos \varphi _2 \\ a_5= & {} 2\Omega \sin (\varphi _1 )+2\xi _1 \cos (\varphi _1 ) \\&+\, 2F_{c1} \Omega \sin \varphi _1 \cos \Omega \tau \\&+\, 2F_{c1} \Omega \cos \varphi _1 \sin \Omega \tau \\ a_6= & {} -\, 2\xi _1 A\sin \varphi _1 +2\Omega A\cos \varphi _1 \\&-\, 2F_{c1} A\Omega \sin \varphi _1 \sin \Omega \tau \\&+\, 2F_{c1} A\Omega \cos \varphi _1 \cos \Omega \tau \\ a_7= & {} -\, 2\xi _2 \cos \varphi _2 \hbox {, }a_8 =2\xi _2 B\sin \varphi _2 \\ a_9= & {} -\, 2\mu \Omega \cos \varphi _1 -2F_{c1} \Omega \sin \varphi _1 \sin \Omega \tau \\&+\, 2F_{c1} \Omega \cos \varphi _1 \cos \Omega \tau \\ a_{10}= & {} 2\mu \Omega A\sin \varphi _1 -2F_{c1} A\Omega \sin \varphi _1 \cos \Omega \tau \\&-\, 2F_{c1} A\Omega \cos \varphi _1 \sin \Omega \tau \\ a_{11}= & {} -\,2\mu \Omega \cos \varphi _2 +2\xi _2 \sin \varphi _2 \\ a_{12}= & {} 2\xi _2 B\cos \varphi _2 +2\mu \Omega B\sin \varphi _2 \\ a_{13}= & {} 2\mu \Omega \sin \varphi _1 -2F_{c1} \Omega \sin \varphi _1 \cos \Omega \tau \\&-\, 2F_{c1} \Omega \cos \varphi _1 \sin \Omega \tau \\ a_{14}= & {} 2\Omega \mu A\cos \varphi _1 +2F_{c1} A\Omega \sin \varphi _1 \sin \Omega \tau \\&-\, 2F_{c1} A\Omega \cos \varphi _1 \cos \Omega \tau \\ a_{15}= & {} 2\mu \Omega \sin \varphi _2 +2\xi _2 \cos \varphi _2 \\ a_{16}= & {} -\, 2\xi _2 B\sin \varphi _2 +2\mu \Omega B\cos \varphi _2 \\ b_1= & {} N_1 \cos \varphi _1 +N_2 \sin \varphi _1 \\&+\, N_3 \cos \varphi _2 +N_4 \sin \varphi _2 +N_{b1} \\ b_2= & {} -\, N_1 \sin \varphi _1 +N_2 \cos \varphi _1 \\&-\, N_3 \sin \varphi _2 +N_4 \cos \varphi _2 -F_1 +N_{b2} \\ b_3= & {} N_5 \cos \varphi _2 +N_6 \sin \varphi _2 \\&+\, N_7 \sin \varphi _1 +N_8 \\ b_4= & {} -\, N_5 \sin \varphi _2 +N_6 \cos \varphi _2 \\&+\, N_7 \cos \varphi _1 +N_9 \\ N_1= & {} -\,2\xi _1 A\Omega ,N_2 =\left( {-\Omega ^{2}+1} \right) A, \\ N_3= & {} 2\xi _2 B\Omega ,N_4 =-\left( {\alpha B+0.75\beta B^{3}} \right) , \\ N_{b1}= & {} -\,\alpha _\mathrm{r} B\sin \varphi _2 +0.75\alpha _{13} A^{3}\sin \varphi _1 \\&-\, F_{c1} A\Omega ^{2}\sin \left( {\varphi _1 +\Omega \tau } \right) \\&-\, 0.75A^{2}Y\sin \left( {2\varphi _1 } \right) \cos \left( \gamma \right) \\&+\, 1.5\alpha _{13} AY^{2}\sin \varphi _1 \\&-\, 0.75\alpha _{13} AY^{2}\sin \varphi _1 \cos \left( {2\gamma } \right) \\&-\, Y\sin \left( \gamma \right) -0.75\alpha _{13} Y^{3}\sin \left( \gamma \right) \\&-\, 1.5\alpha _{13} A^{2}Y\sin \left( \gamma \right) \\&+\, 0.75\alpha _{13} A^{2}Y\cos \left( {2\varphi _1 } \right) \sin \left( \gamma \right) \\&-\, 0.75\alpha _{13} AY^{2}\sin \left( {2\gamma } \right) \cos \left( {\varphi _1 } \right) , \\ N_5= & {} -\,2\xi _2 B\Omega ,N_6 =-\mu \Omega ^{2}B+\alpha B+0.75\beta B^{3}, \\ N_7= & {} -\,\mu \Omega ^{2}A, \\ N_{b2}= & {} \alpha _\mathrm{r} B\cos \varphi _2 +0.75\alpha _{13} A^{3}\cos \varphi _1 \\&-\, F_{c1} A\Omega ^{2}\cos \left( {\varphi _1 +\Omega \tau } \right) -Y\cos \left( \gamma \right) \\&-\, 0.75\alpha _{13} Y^{3}\cos \left( \gamma \right) -1.5\alpha _{13} A^{2}Y\cos \left( \gamma \right) \\&-\, 0.75\alpha _{13} A^{2}Y\cos \left( \gamma \right) \cos \left( {2\varphi _1 } \right) \\&+\, 1.5\alpha _{13} AY^{2}\cos \left( {\varphi _1 } \right) \\&+\, 0.75\alpha _{13} AY^{2}\cos \left( {\varphi _1 } \right) \cos \left( {2\gamma } \right) \\&+\, 0.75\alpha _{13} A^{2}Y\sin \left( {2\varphi _1 } \right) \sin \left( \gamma \right) \\&+\, 0.75\alpha _{13} AY^{2}\sin \left( {2\gamma } \right) \sin \left( {\varphi _1 } \right) , \\ N_8= & {} -\,\alpha _\mathrm{r} B\sin \varphi _2 +F_{c1} A\Omega ^{2}\sin \left( {\varphi _1 +\Omega \tau } \right) , \\ N_9= & {} -\,\alpha _\mathrm{r} B\cos \varphi _2 +F_{c1} A\Omega ^{2}\cos \left( {\varphi _1 +\Omega \tau } \right) \end{aligned}$$

Jacobian matrix obtained as

$$\begin{aligned} J=\left[ {{\begin{array}{llll} {\frac{\partial f_1 }{\partial A}}&{} {\frac{\partial f_1 }{\partial \varphi _1 }}&{} {\frac{\partial f_1 }{\partial B}}&{} {\frac{\partial f_1 }{\partial \varphi _2 }} \\ {\frac{\partial f_2 }{\partial A}}&{} {\frac{\partial f_2 }{\partial \varphi _1 }}&{} {\frac{\partial f_2 }{\partial B}}&{} {\frac{\partial f_2 }{\partial \varphi _2 }} \\ {\frac{\partial f_3 }{\partial A}}&{} {\frac{\partial f_3 }{\partial \varphi _1 }}&{} {\frac{\partial f_3 }{\partial B}}&{} {\frac{\partial f_3 }{\partial \varphi _2 }} \\ {\frac{\partial f_4 }{\partial A}}&{} {\frac{\partial f_4 }{\partial \varphi _1 }}&{} {\frac{\partial f_4 }{\partial B}}&{} {\frac{\partial f_4 }{\partial \varphi _2 }} \\ \end{array} }} \right] , \end{aligned}$$

Appendix-II

Fig. 21

a MATLAB SIMULINK model of the system b subsystem model for passive nonlinear vibration absorber and linear primary system with external harmonic excitation. c Subsystem model for active nonlinear vibration absorber and nonlinear primary system under harmonic external force and base excitation by time delay acceleration feedback

The SIMULINK model for the passive and active system are shown in Fig. 21