Nonlinear planar modeling of massive taut strings travelled by a force-driven point-mass

Abstract

The planar response of horizontal massive taut strings, travelled by a heavy point-mass, either driven by an assigned force, or moving with an assigned law, is studied. A kinematically exact model is derived for the free boundary problem via a variational approach, accounting for the singularity in the slope of the deflected string. Reactive forces exchanged between the point-mass and the string are taken into account via Lagrange multipliers. The exact model is consistently simplified via asymptotic analysis, which leads to condense the horizontal displacement as a passive variable. The dynamic increment of tension, with respect the static one, is neglected in the governing equations, but evaluated a posteriori, as a higher-order quantity in a perturbation perspective. The equations are solved and rearranged in the form of an integral equation coupled with an integro-differential equation, thus extending a procedure already introduced in the literature. Numerical results, showing the importance of the horizontal reactive force on the quality of motion, are discussed, generalizing those relevant to massless strings.

1 Introduction

Engineering examples of structures travelled by moving load are mostly related to transport engineering, but not limited to it. Among them are the following: cable railways and funicular railways, railway transport vehicle like as trains and trams with pantograph sliding on an overhead electric line, space tethers, cranes (see, e.g., [1, 2]).

The modeling and the analysis of such structures is a complex research topic which has received the attention of many researches starting from the nineteenth century [1]. The literature on the subject is wide and rich and it differs for the structures analyzed, which are strings [3,4,5,6,7], cables [8, 9], beams [10,11,12,13,14] and plates [15, 16], and the modeling of the load, which can be schematized as: i) moving force [17, 18]; ii) moving mass [2, 19]; iii) moving oscillator [20, 21].

The study of such systems leads to the observation of complex phenomena and paradoxical behaviors. In particular, the Stokes paradox [3, 12], i.e., the discontinuity in the particle trajectory close to the end support, has aroused particular interest in the researchers [2, 22,23,24].

In this context, in [24] an extended model to discuss the paradox in the case of a taut string was proposed. In such paper, the authors formulated a kinematically exact model of massive string travelled by a point-mass driven by an assigned force, and therefore having unknown motion. The model accounts for horizontal and vertical displacements of the string, and therefore for the dynamic strain and tension which superimpose to the respective static parts. The boundary conditions for the free boundary problem were derived enforcing balance of force and energy at the singularity; as an alternative, a variational formulation was also indicated. Successive analysis, carried out in the contest of an asymptotic model and applied to the massless string, revealed the key role of the horizontal component of the reactive force, exchanged during the motion between the point-mass and the string. This reactive force is responsible for a peculiar behavior of the system, namely the point-mass either reaches the opposite end, or never reaches it, by inverting its motion.

In this paper, the exact model formulated in [24] is reconsidered. It is re-obtained via a modified variational approach. An asymptotic minimal nonlinear model is then derived, based on an order of magnitude evaluation of the involved quantities. Moreover, investigations are carried out for massive strings. A semi-analytical solution strategy is followed, by extending to the case of unknown motion a methodology first proposed by Smith [3], leading to a Volterra integral equation of the first kind, now coupled to an integro-differential equation.

This paper introduces some important novelties with respect to [24], namely: (a) here the equations are obtained via a variational approach in which, in order for the reactive forces appear, the compatibility between the point-mass and string is introduced via Lagrangian multipliers; (b) the nonlinear horizontal motion of the string is here analyzed after quasi-static condensation; (c) the dynamic tension is post-evaluated as a nonlinear effect, according to a perturbation strategy; (d) attention is devoted to the time evolution of the reactive force; (e) the influence on the response of the mass of string, neglected in [24], is investigated here; (f) both cases in which the motion of the mass is unknown or it is assigned, are studied, and in the latter case the attention is focused on the driving force needed to sustain the desired motion.

Differently from [24], in which vertical elastic supports were considered at the ends of the string, here, to simplify the formulation, fixed ends are taken. Although elastic springs regularize the mathematical model, by removing singularities at the ends, the numerical procedure adopted here has been checked to work even for fixed ends. The topic is discussed in “Appendix C”.

The presented here results could be useful for modeling, design and control of more complex structures such as networks of connected elastically strings loaded by moving masses or moving forces. Among such structures we can mention space tethers or pantograph-catenary systems.

2 An exact model

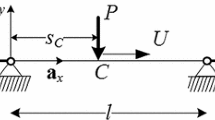
We consider a planar horizontal taut string, fixed at the ends, massive but weightless, travelled by a heavy point-mass (see Fig. 1). We mainly refer to the case in which the motion of the point-mass, sustained by an assigned driving force, is unknown. As opposite case, we will consider the more popular problem in which the motion of the point-mass is assigned, while the driving force is unknown.

Fig. 1

Horizontal taut string travelled by a heavy point-mass

The string is pre-stressed by a force $T_{0}$, and it has mass per unit length m. The point-mass M is loaded by a potential force ${\mathbf {F}}=D\left( t\right) \,{\mathbf {a}}_{x}-P\left( t\right) \,{\mathbf {a}}_{y}$, in which the horizontal component D is the driving force and the vertical component P is the sum of the self-weight and of an external vertical force, with t the time and ${\mathbf {a}}_{x},\,{\mathbf {a}}_{y}$ unit vectors. The point-mass is in-permanent contact with the string, by sliding without friction along it, and exchanging with it the reactive force $\pm \,{\mathbf {R}}$. This reaction induces a singularity in the response of the string, whose position depends on time.

If the driving force is assigned, i.e., if $D={\bar{D}}\left( t\right)$, the horizontal motion $x\left( t\right)$ of the point-mass is unknown. In this case, goal of the analysis is to find: (a) the horizontal and vertical motion of the string, (b) the horizontal and vertical motion of the point-mass; (c) the increment of stress in the string; (d) the reactive force. If the horizontal motion of the point-mass is instead assigned, i.e., if $x={\bar{x}}\left( t\right)$, the driving force $D\left( t\right)$ is unknown.

2.1 Kinematics

Let us take the pre-stressed straight equilibrium configuration of the unloaded string as reference configuration, and denote by $s\in \left[ 0,\,\ell \right]$ a material abscissa, with $\ell$ the (stretched) reference length. The current configuration of the string is described by the position vector ${\mathbf {r}}\left( s,t\right)$, constrained by the geometric boundary conditions:

$$\begin{aligned} \begin{aligned} {\mathbf {r}}\left( 0,t\right)&={\mathbf {0}},&{\mathbf {r}}\left( \ell ,t\right)&=\ell \,{\mathbf {a}}_{x}.\end{aligned} \end{aligned}$$

(1)

The unit extension $\varepsilon$ is taken as strain measure, namely:

$$\begin{aligned} \varepsilon =\left| {\mathbf {r}}'\right| -1, \end{aligned}$$

(2)

where a prime denotes partial differentiation with respect to s.

Let us denote by ${\mathbf {x}}\left( t\right)$ the current position of the point-mass, and by $\xi \left( t\right)$ the material abscissa of the string instantaneously occupied by the point-mass. Compatibility between point-mass and string requires that:

$$\begin{aligned} {\mathbf {x}}\left( t\right) ={\mathbf {r}}\left( \xi \left( t\right) ,t\right) . \end{aligned}$$

(3)

It should be noticed that $\xi \left( t\right)$ is always unknown, even in the case of assigned horizontal motion of the point-mass, since the string is free to stretch itself. Therefore, the problem is a free boundary problem.

As we said, the point-mass induces a singularity in the deflected shape of the string, which moves in the interval $\left[ 0,\,\ell \right]$. Accordingly, ${\mathbf {r}}\left( s,t\right)$ is continuous with its first derivatives in the interval $\left[ 0,\,\xi \right) \cup \left( \xi ,\,\ell \right]$; moreover, it is continuous at the singularity, i.e., ${\mathbf {r}}{}_{-}={\mathbf {r}}{}_{+},$ but its first space- and time-derivatives are discontinuous, i.e., ${\mathbf {r}}'_{-}\ne {\mathbf {r}}'_{+}$ and $\dot{{\mathbf {r}}}_{-}\ne \dot{{\mathbf {r}}}_{+}$, with ${\mathbf {r}}_{\pm }:=\underset{\epsilon \rightarrow 0}{\lim }\,{\mathbf {r}}\left( \xi \pm \epsilon ,\,t\right)$ and $\epsilon >0$. The jumps in the space and time-derivatives; however, are not independent, but related by the continuity condition of the total derivative of $\hat{{\mathbf {r}}}\left( t\right) :={\mathbf {r}}\left( \xi \left( t\right) ,t\right)$, which describes the motion of the singularity. Indeed:

$$\begin{aligned} \frac{\mathrm {d}\hat{{\mathbf {r}}}}{\mathrm {d}t}=\dot{{\mathbf {r}}}_{-}+{\dot{\xi }}\,{\mathbf {r}}'_{-}=\dot{{\mathbf {r}}}_{+}+{\dot{\xi }}\,{\mathbf {r}}'_{+}, \end{aligned}$$

(4)

in which the dot denotes partial time-differentiation, from which (Hadamard’s condition):

$$\begin{aligned} \llbracket \dot{{\mathbf {r}}}\rrbracket +{\dot{\xi }}\llbracket {\mathbf {r}}'\rrbracket ={\mathbf {0}}, \end{aligned}$$

(5)

where the double square bracket $\llbracket f\rrbracket :=f_{+}-f_{-}$ denotes the jump of the argument at the singularity.

If displacements ${\mathbf {u}}=u\left( s,t\right) \,{\mathbf {a}}_{x}+v\left( s,t\right) \,{\mathbf {a}}_{y}$ are introduced for the string, then:

$$\begin{aligned} \begin{aligned} {\mathbf {r}}&=\left( s+u\left( s,t\right) \right) \,{\mathbf {a}}_{x}+v\left( s,t\right) \,{\mathbf {a}}_{y},\\ \varepsilon&=\sqrt{\left( 1+u'\left( s,t\right) \right) ^{2}+v'^{2}\left( s,t\right) }-1. \end{aligned} \end{aligned}$$

(6)

2.2 Elastic law

Let us assume that the string is hyperelastic, and its potential per unit length is quadratic:

$$\begin{aligned} \phi \left( \varepsilon \right) :=T_{0}\,\varepsilon +\frac{1}{2}\,{EA}\,\varepsilon ^{2}. \end{aligned}$$

(7)

From the Green law, the tension $T=\frac{\partial \phi }{\partial \varepsilon }$ follows:

$$\begin{aligned} T=T_{0}+{EA}\,\varepsilon , \end{aligned}$$

(8)

in which $T_{0}$ is the prestress, and EA is the axial stiffness.

2.3 Hamilton principle

The equations of motion of the string-point-mass system can be derived by the variational Hamilton principle. Differently from [24], in which the compatibility condition (3) was directly substituted in the functional, here it is accounted for by the way of a Lagrange multiplier ${\mathbf {R}}$, in order to derive equations also for the reactive force exchanged between the string and the point-mass. The modified Hamilton functional reads:

$$\begin{aligned} \begin{aligned} \tilde{{\mathcal {H}}}\left[ {\mathbf {r}},{\mathbf {x}},\xi ,{\mathbf {R}}\right] :=&\intop _{t_{1}}^{t_{2}}\left[ {\mathcal {K}}_{m}+{\mathcal {K}}_{s}-{\mathcal {U}}_{s}+{\mathcal {W}}\right. \\&\left. -\,{\mathbf {R}}\cdot \left( {\mathbf {x}}-{\mathbf {r}}\left( \xi \left( t\right) ,t\right) \right) \right] \,\mathrm {d}t, \end{aligned} \end{aligned}$$

(9)

where:

$$\begin{aligned} \begin{aligned} {\mathcal {K}}_{m}&:=\frac{1}{2}\,M\,\dot{{\mathbf {x}}}\cdot \dot{{\mathbf {x}}},&{\mathcal {K}}_{s}&:=\frac{1}{2}\intop _{0}^{\ell }m\,\dot{{\mathbf {r}}}\cdot \dot{{\mathbf {r}}}\,\mathrm {d}s,\\ {\mathcal {U}}_{s}&:=\intop _{0}^{\ell }\phi \left( \varepsilon \right) \,\mathrm {d}s,&{\mathcal {W}}&:={\mathbf {F}}\cdot {\mathbf {x}}, \end{aligned} \end{aligned}$$

(10)

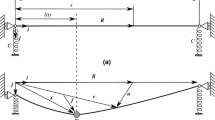
are, in the order, the kinetic energy of the point-mass, the kinetic energy of the string, the elastic potential energy of the string and the potential of the force ${\mathbf {F}}$ applied to the mass M. The principle requires $\delta \tilde{{\mathcal {H}}}=0$ for any admissible arguments and arbitrary times $t_{1},t_{2}$. Admissibility at the external boundaries, following Eq. (1), requires:

$$\begin{aligned} \delta {\mathbf {r}}\left( 0,t\right) =\delta {\mathbf {r}}\left( \ell ,t\right) =0,\qquad \forall \,t. \end{aligned}$$

(11)

Admissibility at singularity (internal boundary) requires that:

$$\begin{aligned} \delta \hat{{\mathbf {r}}}=\underset{\epsilon \rightarrow 0}{\lim }\,\frac{1}{\epsilon }\left\{ \left[ {\mathbf {r}}+\epsilon \,\delta {\mathbf {r}}\right] _{\xi \left( t\right) +\epsilon \,\delta \xi \left( t\right) ,t}-{\mathbf {r}}\left( \xi \left( t\right) ,t\right) \right\} , \end{aligned}$$

(12)

is continuous, i.e.,

$$\begin{aligned} \begin{aligned}&\delta \hat{{\mathbf {r}}}=\delta \mathbf {r_{-}}+{\mathbf {r}}'_{-}\,\delta \xi =\delta \mathbf {r_{+}}+{\mathbf {r}}'_{+}\,\delta \xi .\end{aligned} \end{aligned}$$

(13)

A geometrical interpretation of $\delta \hat{{\mathbf {r}}}$ is given in Fig. 2.

Fig. 2

Geometrical interpretation of $\delta \hat{{\mathbf {r}}}$: vertical component $\delta {\hat{v}}$

2.4 Equations of motion

By variational calculus, in which the moving singularity is accounted for, the following Euler–Lagrange equations for the variational problem are drawn (see “Appendix A” for a detailed derivation):

$$\begin{aligned}&\left( \frac{T}{1+\varepsilon }\,{\mathbf {r}}'\right) '-m\,\ddot{{\mathbf {r}}}={\mathbf {0}}, \end{aligned}$$

(14)

$$\begin{aligned}&{\mathbf {F}}-{\mathbf {R}}-M\,\ddot{{\mathbf {x}}}={\mathbf {0}}, \end{aligned}$$

(15)

(16)

(17)

$$\begin{aligned}&{\mathbf {x}}-{\mathbf {r}}\left( \xi \left( t\right) ,t\right) ={\mathbf {0}}, \end{aligned}$$

(18)

in which, from Eqs. (8) and (2):

$$\begin{aligned} T=T_{0}+EA\,\left( \left| {\mathbf {r}}'\right| -1\right) . \end{aligned}$$

(19)

The previous equations are a set of mixed partial/ordinary differential equations and internal boundary conditions, for the unknown ${\mathbf {r}},{\mathbf {x}},\xi ,{\mathbf {R}}$; they must be sided by the external boundary conditions (1), the continuity condition $\llbracket {\mathbf {r}}\rrbracket =0$, and the initial conditions:

$$\begin{aligned} \begin{aligned}&{\mathbf {r}}\left( s,0\right) ={\mathbf {r}}_{0}\left( s\right) ,&\dot{{\mathbf {r}}}\left( s,0\right) =\dot{{\mathbf {r}}}_{0}\left( s\right) ,\\&{\mathbf {x}}\left( 0\right) ={\mathbf {0}},&\dot{{\mathbf {x}}}\left( 0\right) ={\dot{\xi }}_{0}\,{\mathbf {r}}'_{0}\left( 0\right) ,\\&\xi \left( 0\right) =0,&{\dot{\xi }}\left( 0\right) ={\dot{\xi }}_{0}, \end{aligned} \end{aligned}$$

(20)

where ${\mathbf {r}}_{0}\left( s\right) ,\,\dot{{\mathbf {r}}}_{0}\left( s\right)$ are smooth functions satisfying compatibility at the ends, i.e., ${\mathbf {r}}_{0}\left( 0\right) ={\mathbf {0}}$, ${\mathbf {r}}_{0}\left( \ell \right) =\ell \,{\mathbf {a}}_{x},$$\dot{{\mathbf {r}}}_{0}\left( 0\right) =\dot{{\mathbf {r}}}_{0}\left( \ell \right) ={\mathbf {0}}$. The initial conditions, moreover, satisfy the point-mass-string compatibility at $s=0$, namely $\dot{{\mathbf {x}}}\left( 0\right) =\dot{{\mathbf {r}}}_{0}\left( 0\right) +{\dot{\xi }}_{0}\,{\mathbf {r}}'_{0}\left( 0\right)$.

Equations (14)–(18) are firstly derived in [24], by following a balance approach. It is worth noticing that they are kinematically exact. Equation (14) is the field equation, expressing balance of internal and inertia forces, acting on a generic element of string in the current configuration. This equation does not hold at the singularity. Equation (15) is the linear momentum equation for the point-mass, solicited by the external active force ${\mathbf {F}}$ and the internal reaction $-{\mathbf {R}}$.

Equation (16) is the internal boundary condition, expressing the balance of forces acting on an infinitesimal element of string which contains the singularity. In it, in addition to the reaction ${\mathbf {R}}$ and the jump between the internal forces at the ends of the element, a peculiar term proportional to ${\dot{\xi }}$ appears (which is absent in the usual engineering problems of immovable boundaries); it expresses the variation of the linear momentum of an infinitesimal segment of string of length ${\dot{\xi }}\,\mathrm {d}t$, which instantaneously passes from the right to left of the point-mass, undergoing a jump in velocity. By using the Hadamard condition (5), this equation can also be written as:

(21)

Equation (17) expresses the balance of energy (no dissipation) of a segment of string which contains the singularity (see [24] for more details). It can be transformed as follows, by using the definitions of strain, Eq. (2), the elastic law (8) and the expression of the elastic potential (7):

(22)

or, by collecting terms with the same powers of $\varepsilon$ and accounting for the continuity of their coefficients:

(23)

By assuming subsonic motions, it is ${\dot{\xi }}^{2}<\frac{{EA}}{m}=:c_{l}^{2}$, with $c_{l}$ the celerity of longitudinal waves; therefore, the energy balance condition entails:

(24)

Note that the condition is independent of prestress, and the magnitude in brackets is the Cauchy-Green one-dimensional strain. This equation is kinematically exact, subjected to the unique assumption that the elastic potential is quadratic.

2.5 Equations in terms of displacements

The set of Eqs. (14), (15), (21), (24), (18) can be recast in terms of displacements, via Eq. (6). The resulting equations turn out to be:

$$\begin{aligned}&\left[ \frac{T}{1+\varepsilon }\,\left( {\mathbf {a}}_{x}+{\mathbf {u}}'\right) \right] '=m\,\ddot{{\mathbf {u}}}, \end{aligned}$$

(25)

$$\begin{aligned}&{\mathbf {F}}-{\mathbf {R}}=M\,\ddot{{\mathbf {x}}}, \end{aligned}$$

(26)

(27)

(28)

$$\begin{aligned}&{\mathbf {x}}=\xi \,{\mathbf {a}}_{x}+{\mathbf {u}}\left( \xi ,t\right) , \end{aligned}$$

(29)

together with the continuity condition $\llbracket {\mathbf {u}}\rrbracket ={\mathbf {0}}$ and the initial conditions:

$$\begin{aligned} \begin{aligned}&{\mathbf {u}}\left( s,0\right) ={\mathbf {u}}_{0}\left( s\right) ,&\dot{{\mathbf {u}}}\left( s,0\right) =\dot{{\mathbf {u}}}_{0}\left( s\right) ,\\&{\mathbf {x}}\left( 0\right) ={\mathbf {0}},&\dot{{\mathbf {x}}}\left( 0\right) ={\dot{\xi }}\left( 0\right) \,\left( {\mathbf {a}}_{x}+{\mathbf {u}}_{0}'\left( 0\right) \right) ,\\&\xi \left( 0\right) =0,&{\dot{\xi }}\left( 0\right) ={\dot{\xi }}_{0}. \end{aligned} \end{aligned}$$

(30)

The reaction ${\mathbf {R}}$, of course, could be easily eliminated between Eqs. (26) and (27), as well ${\mathbf {x}}$ and $\ddot{{\mathbf {x}}}$ by Eq. (29), but this operation is avoided here, in view of the strategy of solution that will be followed ahead.

When the previous equations are projected onto the orthonormal basis, by introducing ${\mathbf {x}}=x\left( t\right) \,{\mathbf {a}}_{x}+y\left( t\right) \,{\mathbf {a}}_{y}$, they read:

$$\begin{aligned} \left[ \frac{T}{1+\varepsilon }\,\left( 1+u'\right) \right] '= & {} m\,\ddot{u},\nonumber \\ \left[ \frac{T}{1+\varepsilon }\,v'\right] '= & {} m\,\ddot{v}, \end{aligned}$$

(31)

$$\begin{aligned} D-R_{x}= & {} M\,\ddot{x},\nonumber \\ -P-R_{y}= & {} M\,\ddot{y}, \end{aligned}$$

(32)

(33)

(34)

$$\begin{aligned} x= & {} \xi +u\left( \xi ,t\right) ,\nonumber \\ y= & {} v\left( \xi ,t\right) , \end{aligned}$$

(35)

with the continuity conditions $\llbracket u\rrbracket =0$, $\llbracket v\rrbracket =0$ and the initial conditions. This is a set of scalar equations for the displacements of the string, u, v, the reactive forces $R_{x},R_{y}$, the coordinate of the point-mass x, y and the material abscissa of the current position of the point-mass, $\xi$. In the particular case in which the horizontal motion of the point-mass is assigned, i.e., $x={\bar{x}}\left( t\right)$, the right-hand member of Eq. (32a) must be substituted by the known term $\ddot{{\bar{x}}}\left( t\right)$, and the driving force D treated as an unknown.

3 A minimal nonlinear model

The equations of motion (31)–(35) are strongly nonlinear in the large displacement range, when the current tension T cannot be linearized around the pretension $T_0$. Here, however, a small displacement regime is postulated, in which the dynamic tension is considered as a small perturbation of the pretension. Consistently, a weakly nonlinear minimal model is formulated, able to capture the behavior of the point-mass-string system when its response is small but finite.

The following assumptions are introduced: (i) the dynamic strain is small ($\varepsilon \ll 1$ and therefore, also $u'\ll 1$); (ii) the horizontal displacements u are much smaller than the vertical displacements v, in the motions of interest; (iii) the pre-strain $\varepsilon _{0}:=\frac{T_{0}}{EA}$ is also small. This last assumption has important consequences (commonly accepted in the literature in dealing with strings and cables, see, e.g., [25]). It entails that the celerity of the transverse waves $c_{t}:=\sqrt{\frac{T_{0}}{m}}$ is much lower than the celerity of the longitudinal waves $c_{l}:=\sqrt{\frac{{EA}}{m}}$, so that the two motions develop on different time scales. In prevalent transverse nonlinear motions, the longitudinal response, due to the weak dynamic coupling, is of quasi-static type, i.e., it is driven by the transverse motion. Therefore, the horizontal inertia force $-m\,\ddot{u}$ is negligible with respect to the elastic force appearing in the same equation.

3.1 The horizontal motion of the string and the dynamic tension

Under the previous hypotheses, the first of Eq. (31) provides $T=T\left( t\right)$, i.e., $T=T_{0}+{EA}\,\varepsilon _{1}\left( t\right)$ in $\left[ 0,\xi \right)$ and $T=T_{0}+{EA}\,\varepsilon _{2}\left( t\right)$ in $\left( \xi ,\,\ell \right]$, with $\varepsilon _{1},\varepsilon _{2}$ two arbitrary functions of the time, only. However, the same assumption of small strain leads to simplify Eq. (34) into $\llbracket \varepsilon \rrbracket =0$, i.e., $\varepsilon _{1}=\varepsilon _{2}$. Therefore, the current tension T at a fixed time t, is not only stepwise constant in the domain, but, in the framework of the minimal model, it remains strictly constant in the whole domain.

By assuming for the strain the series expansion of the exact definition (2), i.e.,

$$\begin{aligned} \varepsilon =u'+\frac{1}{2}\,v'^{2}, \end{aligned}$$

(36)

we get that $u=O\left( v^{2}\right)$, or $v=O\left( \epsilon \right) ,\,u=O\left( \epsilon ^{2}\right) ,\,\varepsilon =O\left( \epsilon ^{2}\right)$, with $\epsilon$ a small parameter. By integrating the previous equation with $\varepsilon =\mathrm {const}$, and using the boundary conditions $u\left( 0\right) =u\left( \ell \right) =0$ and $\llbracket \varepsilon \rrbracket =0$, the displacement u is found as a passive variable (slave of v):

$$\begin{aligned} u=-\frac{1}{2}\intop _{0}^{s}v'^{2}\left( {\check{s}},t\right) \,\mathrm {d}{\check{s}}+\frac{s}{2\,\ell }\,\intop _{0}^{\ell }v'^{2}\left( s,t\right) \,\mathrm {d}s. \end{aligned}$$

(37)

Consequently, the dynamic tension reads:

$$\begin{aligned} {\tilde{T}}=\frac{{EA}}{2\,\ell }\intop _{0}^{\ell }v'^{2}\left( s,t\right) \,\mathrm {d}s. \end{aligned}$$

(38)

It should by noticed that, since EA is large, ${\tilde{T}}$ can be of the same order of $T_{0}$. As an example, if $\frac{{EA}}{T_{0}}=O\left( 10^{3}\right)$ (tightened steel string) and $v'=O\left( 10^{-2}\right)$, it is $\frac{{\tilde{T}}}{T_{0}}=O\left( 10^{-1}\right)$. For less tightened string, this ratio can easily increase to 1. However, in the framework of the minimal model, it will be assumed here, that ${\tilde{T}}\ll T_{0}$, this assumption to be checked a posteriori from Eq. (38), once the vertical response has been evaluated.

3.2 The vertical motion

With previous hypotheses and results, and by retaining the leading terms in each equations, the second of Eqs. (31), (32), (33) and (35) become:

$$\begin{aligned}&T_{0}\,v''=m\,\ddot{v}, \end{aligned}$$

(39)

$$\begin{aligned}&-P-R_{y}=M\,\ddot{y}, \end{aligned}$$

(40)

$$\begin{aligned}&\left( T_{0}-m\,{\dot{\xi }}^{2}\right) \llbracket v'\rrbracket +R_{y}=0, \end{aligned}$$

(41)

$$\begin{aligned}&y=v\left( \xi ,t\right) . \end{aligned}$$

(42)

The field equation (39) and the mechanical boundary condition (41) can be incorporated, as customary, in a unique equation, in which the Dirac delta appears:

$$\begin{aligned} \begin{aligned}&T_{0}\,v''+R_{y}\,\delta \left( s-\xi \right) =m\,\ddot{v}.\end{aligned} \end{aligned}$$

(43)

Note that $R_{y}$ is a first-order quantity. If it is eliminated between Eqs. (43) and (40), a classical equation, well-known in the literature, is obtained (see, e.g., [22] in the context of assigned motion of the point-mass), namely:

$$\begin{aligned} \begin{aligned} T_{0}\,v''=&\left[ P+M\left( \ddot{\xi }\,v'+{\dot{\xi }}^{2}\,v''_{\pm }+2\,{\dot{\xi }}\,{\dot{v}}'_{\pm }+\ddot{v}_{\pm }\right) \right] \delta \left( s-\xi \right) \\&+m\,\ddot{v}, \end{aligned} \end{aligned}$$

(44)

in which $\ddot{y}$ has been evaluated via Eq. (42).

3.3 The horizontal motion of the mass

In the same framework of approximation, the first of Eqs. (32), (33) and (35) become:

$$\begin{aligned}&D-R_{x}=M\,\ddot{x}, \end{aligned}$$

(45)

$$\begin{aligned}&\left( T_{0}-m{\dot{\xi }}^{2}\right) \llbracket u'\rrbracket +R_{x}=0, \end{aligned}$$

(46)

$$\begin{aligned}&x=\xi +u\left( \xi ,t\right) . \end{aligned}$$

(47)

Equation (46) supplies an important result, namely, that $R_{x}/T_{0}=O\left( \epsilon ^{2}\right)$is a second-order quantity, that therefore cannot be described in a purely linear context. Since $\llbracket \varepsilon \rrbracket =0$, from Eq. (36) it follows:

$$\begin{aligned} \llbracket u'\rrbracket =-\frac{1}{2}\llbracket v'^{2}\rrbracket \equiv -\llbracket v'\rrbracket \left\langle v'\right\rangle , \end{aligned}$$

(48)

where $\left\langle v'\right\rangle :=\frac{1}{2}\left( v'_{+}+v'_{-}\right)$ is the average value of the two (linearized) slopes at the singularity; therefore, from Eqs. (46) and (41), it is found that [24]:

$$\begin{aligned} \begin{aligned} R_{x}&=-R_{y}\left\langle v'\right\rangle .\end{aligned} \end{aligned}$$

(49)

This result has an important geometrical meaning, namely, at the leading order of approximation, the reaction ${\mathbf {R}}$is directed along the bisector of the angle formed by the two tangents at the singularity (see Fig. 3).

Fig. 3

Reaction ${\mathbf {R}}$ at the singularity

With Eqs. (49) and (47), by neglecting inertial terms concerning u (as done for the inertial term $-m\,\ddot{u}$ in Eqs. (31a)) and  (45) reads:

$$\begin{aligned} D+R_{y}\left\langle v'\right\rangle =M\,\ddot{\xi }. \end{aligned}$$

(50)

This nonlinear equation governs the horizontal motion of the mass. It is worth discussing the order of magnitude of the various terms here involved. By assuming $R_{y}/T_{0}=O\left( \epsilon \right)$ , it follows that:

• If the driving force is small, of the same order of magnitude of the horizontal reactive force $R_{x}$, i.e., if $\frac{D}{T_{0}}=O\left( \frac{R_{y}\left\langle v'\right\rangle }{T_{0}}\right) =O\left( \epsilon ^{2}\right)$, then $R_{x}$ strongly affects the motion of the point-mass, by rendering it nonlinear;

• If, in contrast, the driving force is sufficiently large, i.e., $\frac{D}{T_{0}}\ge O\left( \epsilon \right)$, the reaction $R_{x}$ can be neglected in Eq. (50), so that the horizontal motion of the point-mass uncouples from the vertical one, and the problem becomes linear.

From the previous consideration, it follows that the more interesting case occurs when the driving force is small. As an example, if $D=\mathrm {const}$ and small, it is not guaranteed that the point-mass reaches the right end of the string.

In the case of assigned horizontal motion of the mass, and in the framework of the minimal model for which $x\simeq \xi ,$ it turns out that $\xi ={\bar{\xi }}\left( t\right)$ is a known function. Hence, the free boundary problem changes into a simpler moving-boundary problem. Accordingly, the vertical motion of the string, governed by Eq. (44), uncouples from the horizontal motion, and furnishes the same results of the linear theory. However, differently from this latter, the minimal nonlinear model permits to post-evaluate the driving force via Eq. (50), and the dynamic increment of tension via Eq. (38).

3.4 Final nondimensional governing equations

By summarizing previous results, the minimal model is constituted by Eqs. (43), (40), (50), (42). When recast in nondimensional form, they read:

$$\begin{aligned}&v''+R_{y}\,\delta \left( s-\xi \right) =\ddot{v}, \end{aligned}$$

(51)

$$\begin{aligned}&-P-R_{y}=\mu \,\ddot{y}, \end{aligned}$$

(52)

$$\begin{aligned}&D+R_{y}\left\langle v'\right\rangle =\mu \,\ddot{\xi }, \end{aligned}$$

(53)

$$\begin{aligned}&y=v\left( \xi ,t\right) , \end{aligned}$$

(54)

with relevant boundary and initial conditions:

$$\begin{aligned}&v\left( 0,t\right) =v\left( 1,t\right) =0, \end{aligned}$$

(55)

$$\begin{aligned}&v\left( s,0\right) =0,&{\dot{v}}\left( s,0\right) =0, \end{aligned}$$

(56)

$$\begin{aligned}&y\left( 0\right) =0,&{\dot{y}}\left( 0\right) =0, \end{aligned}$$

(57)

$$\begin{aligned}&\xi \left( 0\right) =0,&{\dot{\xi }}\left( 0\right) ={\dot{\xi }}_{0}, \end{aligned}$$

(58)

in which the string has been taken at the rest at the initial time. In the previous equations, the following positions hold:

$$\begin{aligned} \begin{aligned} {\hat{s}}&:=\frac{s}{\ell },&{\hat{t}}&:=\frac{1}{\ell }\sqrt{\frac{T_{0}}{m}}t,&{\hat{v}}&:=\frac{v}{\ell },&{\hat{\xi }}&:=\frac{\xi }{\ell },\\ {\hat{y}}&:=\frac{y}{\ell },&\mu&:=\frac{M}{m\,\ell },&{\hat{D}}&:=\frac{D}{T_{0}},&{\hat{P}}&:=\frac{P}{T_{0}},\\ {\hat{R}}_{y}&:=\frac{R_{y}}{T_{0}},&\alpha&:=\frac{EA}{2\,T_{0}}, \end{aligned} \end{aligned}$$

(59)

hat has been omitted, and prime and dot denote differentiation with respect to the nondimensional independent variables. Note that ${\hat{P}}$ is independent of $\mu$ even in case in which the vertical force is the weight of the point-mass only, $P=Mg$.

Finally, the nondimensional horizontal displacement, horizontal reaction and dynamic tension, respectively, read:

$$\begin{aligned}&u = -\frac{1}{2}\intop _{0}^{s}v'^{2}\left( {\check{s}},t\right) \,\mathrm {d}{\check{s}}+\frac{s}{2}\,\intop _{0}^{1}v'^{2}\left( s,t\right) \,\mathrm {d}s, \end{aligned}$$

(60)

$$\begin{aligned}&R_{x} = -R_{y}\left\langle v'\right\rangle , \end{aligned}$$

(61)

$$\begin{aligned}&{\tilde{T}}= \alpha \intop _{0}^{\ell }v'^{2}\left( s,t\right) \,\mathrm {d}s. \end{aligned}$$

(62)

It appears that the vertical motion $v\left( s,t\right)$ is coupled to the horizontal motion of the mass. Coupling is due to the vertical reaction $R_{y}$, which, for a given vertical deflection $v\left( s,t\right)$, and according to the bisector rule in (49), produces a horizontal reaction $R_{x}\left( t\right)$, which, in turn, influences the horizontal motion of the mass $\xi \left( t\right)$; this latter, as a feedback, affects the vertical motion. The nonlinearity is related to the mechanism triggering $R_{x}$.

Once the problem (51)–(54) has been solved: the horizontal reaction $R_{x}$ is evaluated by Eq. (61); the horizontal motion of the string, $u\left( s,t\right)$, by Eq. (60); the motion of the point-mass as $x=\xi \left( t\right) +u\left( \xi \left( t\right) ,t\right)$, $y=v\left( \xi \left( t\right) ,t\right)$; the dynamic tension ${\tilde{T}}$ by Eq. (62).

4 Solution

Here, a semi-analytical strategy of solution, similar to that firstly proposed by Smith [3], but extended to account for the unknown motion, is followed. It consists of: (i) solving Eqs. (51) and (52) by the way of the convolution integral, in order to express $v\left( s,t\right)$ and $y\left( t\right)$ in terms of two unknowns $R_{y}\left( t\right) ,\;\xi \left( t\right)$; (ii) using the remaining Eqs. (53) and (54) to obtain a coupled integral-differential system in these latter quantities; (iii) numerically integrating the resulting equations.

The solution to Eq. (51) is sought in the form of a truncated series:

$$\begin{aligned} v\left( s,t\right) =\sum _{k=1}^{N_{e}}\phi _{k}\left( s\right) \,q_{k}\left( t\right) , \end{aligned}$$

(63)

where $\phi _{k}\left( s\right) :=\sqrt{2}\sin \left( \omega _{k}\,s\right)$, $\omega _{k}:=k\,\pi$, $k=1,2,3,\cdots$, are the eigenfunctions of the linear taut string, suitably normalized. By substituting Eq. (63) in Eq. (51) and by projecting on the eigenfunction basis, the following equations are obtained for the modal amplitudes:

$$\begin{aligned} \ddot{q}_{k}+\omega _{k}^{2}\,q_{k}=R_{y}\phi _{k}\left( \xi \right) ,\qquad k=1,2,\ldots N_{e}, \end{aligned}$$

(64)

which admit the solution:

$$\begin{aligned} q_{k}\left( t\right) =\frac{\sqrt{2}}{\omega _{k}}\int _{0}^{t}R_{y}\left( \tau \right) \sin \left( \omega _{k}\,\xi \left( \tau \right) \right) \sin \left( \omega _{k}\left( t-\tau \right) \right) \,\mathrm {d}\tau . \end{aligned}$$

(65)

Then, the solution (63) becomes:

$$\begin{aligned} \begin{aligned} v\left( s,t\right)&=\int _{0}^{t}R_{y}\left( \tau \right) K\left( s,t,\tau \right) \,\mathrm {d}\tau ,\end{aligned} \end{aligned}$$

(66)

where the following kernel appears:

$$\begin{aligned} \begin{aligned} K\left( s,t,\tau \right) :=&\sum _{k=1}^{N_{e}}\frac{2}{\omega _{k}}\sin \left( \omega _{k}\,s\right) \sin \left( \omega _{k}\,\xi \left( \tau \right) \right) \\&\cdot \sin \left( \omega _{k}\left( t-\tau \right) \right) . \end{aligned} \end{aligned}$$

(67)

On the other hand, the solution to Eq. (52) is:

$$\begin{aligned} y\left( t\right) =-\frac{P\,t^{2}}{2\,\mu }-\frac{1}{\mu }\int _{0}^{t}R_{y}\left( \tau \right) \left( t-\tau \right) \,\mathrm {d}\tau . \end{aligned}$$

(68)

To write Eqs. (53) and (54), it needs to evaluate $\left\langle v'\right\rangle$. Since the assumed vertical response of the string (66) is smooth, no jumps in $v'\left( s,t\right)$ can be described. However, as it is well-known in the Fourier theory, the series converges for large $N_{e}$ to the average value of the discontinuity, namely $v'\left( \xi ,t\right) \rightarrow \left\langle v'\right\rangle$. With this approximation:

$$\begin{aligned} \begin{aligned} \left\langle v'\right\rangle =&2\sum _{k=1}^{N_{e}}\cos \left( \omega _{k}\xi \left( t\right) \right) \int _{0}^{t}R_{y}\left( \tau \right) \sin \left( \omega _{k}\,\xi \left( \tau \right) \right) \\&\times \,\sin \left( \omega _{k}\left( t-\tau \right) \right) \,\mathrm {d}\tau . \end{aligned} \end{aligned}$$

(69)

By substituting Eqs. (66), (68),(69) in Eqs. (53), (54), it follows:

$$\begin{aligned} \begin{aligned} -\frac{P\,t^{2}}{2\,\mu }&=\int _{0}^{t}R_{y}\left( \tau \right) \left[ K\left( \xi \left( t\right) ,t,\tau \right) +\frac{t-\tau }{\mu }\right] \,\mathrm {d}\tau ,\\ \mu \,\ddot{\xi }&=D+2R_{y}\left( t\right) \sum _{k=1}^{N_{e}}\cos \left( \omega _{k}\xi \left( t\right) \right) \int _{0}^{t}R_{y}\left( \tau \right) \\&\times \,\sin \left( \omega _{k}\xi \left( \tau \right) \right) \sin \left( \omega _{k}\left( t-\tau \right) \right) \,\mathrm {d}\tau . \end{aligned} \end{aligned}$$

(70)

Equation (70) is an integro-differential system for the unknowns $R_{y}$ and $\xi$; they must be accompanied with initial conditions $\xi \left( 0\right) =0,\;{\dot{\xi }}\left( 0\right) ={\dot{\xi }}_{0}$. Here, they are numerically solved by the algorithm described in “Appendix B”.

5 Numerical results

Some numerical results are shown, to comment typical behaviors of the system, relevant to: (a) assigned, and, (b) unknown, horizontal motions of the point-mass. In the latter case, the role of the mass of the string is studied, and peculiar oscillatory motions of the point-mass are investigated. All the case studies concern a (steel) string of nondimensional mechanical parameter $\alpha =500.$ The number of the eigenfunctions appearing in the series (63) has been fixed to $N_{e}=30$, and the number of steps of numerical integrations to $N_{s}=1200$; these two numbers have been chosen with a suitable numerical convergence analysis.

Fig. 4

Trajectory of the point-mass for the case of assigned horizontal uniform motion, when $P=0.01$ and U variable: a$\mu =0.1$; b$\mu =1$

5.1 Assigned horizontal motion

First, the case in which the point-mass experiences an assigned uniform motion, $\xi =U\,t$, is considered. Here, U is the nondimensional velocity, which, according to the definitions (59), is the ratio between the dimensional velocity and the celerity of the transverse waves. As already said, the minimal model furnishes for this problem the same vertical response of the classical linear theory, but supplies additional information for the other quantities.

Figure 4 shows the motion of the mass for different values of the velocity U and for two values of the mass ratio, a small value $\mu =0.1$ (Fig. 4a), and a large value $\mu =1$ (Fig. 4b). In both cases, the vertical force has been fixed to a small value $P=0.01$, in order to investigate prevalent inertial effects. Figures report the trajectory y(x) of the point-mass, obtained by the parametric equations $x=x\left( t\right) ,\,y=y\left( t\right)$ by eliminating the parameter t. It emerges from the plots, the occurrence of the famous Stokes paradox [3, 12, 22], i.e., $y\left( 1\right) \ne 0$, which is exalted by large velocities U and large mass-ratios $\mu$. It is worth noticing that the lower is U, the larger is the number of reflected/transmitted waves which meet the point-mass; consequently, the lower is U and the curlier is the trajectory of the point-mass.

One of these cases, namely $P=0.01,\,\mu =0.1,\,U=0.9$, has been more widely detailed in Fig. 5. Here, several quantities have been plotted vs the abscissa x instantaneously occupied by the point-mass, namely: (a) the vertical position of the point-mass; (b) the vertical displacement of the string at midspan; (c) the driving force necessary to sustain the uniform motion; (d) the vertical reaction exchanged between the point-mass and the string; (e) the dynamic tension in the string; (f) the horizontal displacement of the string at midspan. It is seen that vertical displacements of the string and point-mass are small, of order $10^{-3},$ and the horizontal displacement of the string is even smaller, according to the hypotheses introduced. This is due to the fact that the point-mass and the vertical force are small too. The driving force and the vertical reactive force exhibit an oscillatory behavior around an average value, the former of order $10^{-4},$ the latter of order $10^{-2}$, thus confirming to be a second- and a first-order quantity, respectively. A peculiar phenomenon, however, is displayed: most of these quantities suddenly increase when the point-mass approaches the right end. In particular, the driving force and the dynamic tension become about twice the prestress of the string, while the vertical reaction becomes the quadruple. A similar behavior is displayed by the horizontal displacement at midspan, as a consequence of the large stretch of the string, while the vertical displacement at midspan is not affected by this behavior, since measured far from the right end. From these results, it clearly emerges that the minimal nonlinear model is unable to capture the mechanical behavior of the system when the mass is close to the right end.

Fig. 5

Detailed results for the case of assigned horizontal uniform motion, when $P=0.01$, $\mu =0.1$ and $U=0.9$ : a trajectory of the point-mass; b${\bar{v}}=v\left( \frac{1}{2},t\right)$; c driving force; d vertical reactive force; e dynamic tension; f${\bar{u}}=u\left( \frac{1}{2},t\right)$

Fig. 6

Comparison between massive (black lines) and massless (gray lines) taut string model, for the case of unknown horizontal motion, when $\mu =1$, $P=0.025$, $D=2\times 10^{-4}$ and ${\dot{\xi }}_{0}=0.03$: a trajectory of the point-mass; b${\bar{v}}=v\left( \frac{1}{2},t\right)$; c horizontal reactive force; d vertical reactive force; e dynamic tension; f${\bar{u}}=u\left( \frac{1}{2},t\right)$

5.2 Unknown horizontal motion

The case in which the motion of the point-mass is sustained by a driving force, is now examined, see Fig. 6. Attention is first focused on the role of the distributed string mass. By fixing the (small) driving force at $D=2\times 10^{-4}$, the initial velocity at ${\dot{\xi }}_{0}=0.03$, the (small) vertical force at $P=0.025$ and the mass parameter at $\mu =1$, the response of a massive string is compared with that of the massless string model, whose equations of motions are derived in “Appendix C”, namely Eqs. (98) and (99) (note that $\mu$ enters the definition (59) of the nondimensional time, so that $\mu =1$ for the massless string should be meant as a mere time scaling factor). Figures show that the response of the massive string is a small perturbation of the response of the massless string. This result can be justified by the fact that an unknown horizontal motion calls for small driving forces, of the same order of $R_{y}\left\langle v'\right\rangle$; moreover, also the initial velocity ${\dot{\xi }}_{0}$ must be small. As a consequence, the dynamics of the system is slow, of quasi-static type, entailing very small accelerations, so that the mass of string gives small contributions. If one requires ${\dot{\xi }}_{0}=0$ (results not reported), the two solutions further approach each other. It is worth noticing that in this case the point-mass reaches the end support without oscillations, due to the smallness of the vertical force.

Fig. 7

Oscillatory motion of the mass between the two supports, when $D=2\times 10^{-4}$ , $P=0.275$ and $\mu =0.1$: a material abscissa of the string instantaneously occupied by the point-mass; b vertical displacement of the point-mass; c dynamic tension

Figure 7 shows a case in which the point-mass oscillates between the two ends of the string, occurring for $\mu =0.1$, a small driving force $D=2\times 10^{-4}$, but a quite large vertical force $P=0.275$. The oscillatory character of motion is displayed: in Fig. 7a, which shows that the point-mass remains internal to the interval of the string, i.e., $0<\xi <1,\quad \forall t>0$; in Fig. 7b, which describes the oscillatory vertical motion of the point-mass; in Fig. 7c, which reports an analogous behavior for the dynamic stress. It is worth noticing that such a kind of motion does not occur for a small vertical force P; this has, in contrast, to overcome a threshold value. This occurrence is due to the fact that, in order to invert the motion of the point-mass, a sufficiently high horizontal reaction $R_{x}$ is needed, antagonist to the driving force. Since this reaction follows the bisector rule, a sufficiently large vertical force also is needed. On the other hand, such a large vertical force triggers large vertical displacements (up-to the order $10^{-1}$) which, in turn, produce very high dynamic increment of stress, up-to 25 times the pretension, for which the minimal model is inadequate. Therefore, a more refined model, at least including the dynamic stress in the equations of motion, is needed. Finally, it is worth mentioning that when oscillatory motions of the point-mass are investigated, significative differences between the massive and massless models are found. In particular, by keeping fixed the parameters $\mu$, D and ${\dot{\xi }}_{0}$, the value of P that triggers an oscillatory motion of the point-mass is larger for the massless string model.

6 Conclusions

The planar response of a horizontal taut string, travelled by a point-mass, either driven by an assigned horizontal force, or experiencing an assigned horizontal motion, has been analyzed. An exact nonlinear model, formulated by the authors in a previous paper, has been re-derived here in a variational way, in a slight different form, in order to make explicit the reactive forces exchanged between the point-mass and the string. Then, a minimal nonlinear model has been drawn from the exact model, by quasi-statically condensing the horizontal displacement of the string, and assuming that the incremental dynamic stress is small with respect to its static part. In the framework of a perturbation approach, the dynamic stress has however been post-evaluated as an higher-order quantity, on the ground of the lower-order solution. The nonlinear minimal model, although approximated, improves the classical linear model, namely:

• 1. When the horizontal motion of the point-mass is unknown (free boundary problem), the model describes the nonlinear interaction between the vertical response of the string and the horizontal response of the mass;

• 2. When the horizontal motion of the point-mass is known (moving boundary problem), the vertical response of the string coincides with that of the linear theory, but additional quantities can be post-evaluated, i.e., the horizontal displacement of the string, the driving force and the dynamic increment of tension.

The analysis of the equations of the minimal nonlinear model has revealed the role of the reactive force. It is directed along the bisector of the angle formed by the two tangents to the deflected profile of the string, at the singular point instantaneously occupied by the point-mass. The vertical component of the reaction is a first-order quantity, the horizontal component a second-order quantity. Two limit cases occur:

• 1. If the driving force is large, the horizontal reaction is negligible, and the system behaves as a linear system, in which the vertical response of the string is uncoupled from the horizontal motion of the point-mass;

• 2. If the driving force is small, the horizontal motion is truly unknown, and it exerts a feedback on the vertical motion via the vertical reaction.

From numerical simulations carried out, the following conclusion can be drawn:

• 1. When a uniform horizontal motion is assigned to the point-mass (this case was not considered in [24]), subjected to a small vertical load, the response strongly depends on the traveling velocity. Even for high values of this latter, the driving force, the dynamic stress and the horizontal response of the string are small, except in a boundary layer close to the right end, where they assume very large values, which make the minimal model (as well the linear one) inadequate.

• 2. When a small driving force and a small vertical force are applied to the point-mass, possessing a small initial velocity, the point-mass reaches the end support without oscillations. This result is in agreement with results of [24], where it was obtained for a massless string hanged on two elastic springs with non-zero compliance. The response is quasi-static, entailing that the influence of the distributed mass on the response is small.

• 3. When a massive string is considered, with small driving force but with large vertical load, oscillatory motions are observed, in which the point-mass approaches the right end and comes back. This result also is in agreement with results of [24]. However, it has been checked, that a large dynamic tension is triggered, so that these results should be confirmed by a more refined analysis. In this case significative differences between the massless and the massive model are observed.

Further studies must be performed, mainly to include the dynamic tension in the equations of motion, in order to allow it to increase up-to, and possibly overcome, the static tension.

Appendices

Appendix A: Variational derivation of the equations of motion

The Equations of motion (14)–(18) are derived by the stationary condition of the modified Hamilton principle (9), $\delta \tilde{{\mathcal {H}}}\left[ {\mathbf {r}},{\mathbf {x}},\xi ,{\mathbf {R}}\right] =0$, i.e.,

$$\begin{aligned} \begin{aligned}&\intop _{t_{1}}^{t_{2}}\left[ \delta {\mathcal {K}}_{m}+\delta {\mathcal {K}}_{s}-\delta {\mathcal {U}}_{s}+\delta {\mathcal {W}}-{\mathbf {R}}\cdot \left( \delta {\mathbf {x}}-\delta \hat{{\mathbf {r}}}\right) \right] \,\mathrm {d}t\\&\quad -\intop _{t_{1}}^{t_{2}}\delta {\mathbf {R}}\cdot \left( {\mathbf {x}}-{\mathbf {r}}\left( \xi \left( t\right) ,t\right) \right) \,\mathrm {d}t=0\qquad \forall \left( \delta {\mathbf {r}},\delta {\mathbf {x}},\delta \xi ,\delta {\mathbf {R}}\right) , \end{aligned} \end{aligned}$$

(71)

where the definitions (10) hold for ${\mathcal {K}}_{m},{\mathcal {K}}_{s},{\mathcal {U}}_{s},{\mathcal {W}}$ and (13) for $\delta \hat{{\mathbf {r}}}$.

The variations of non-integral in space terms are straightforward, namely:

$$\begin{aligned}&\intop _{t_{1}}^{t_{2}}\delta {\mathcal {K}}_{m}dt =\intop _{t_{1}}^{t_{2}}M\,\dot{{\mathbf {x}}}\cdot \delta \dot{{\mathbf {x}}}\,\mathrm {d}t=-\intop _{t_{1}}^{t_{2}}M\,\ddot{{\mathbf {x}}}\cdot \delta {\mathbf {x}}\,\mathrm {d}t, \end{aligned}$$

(72)

$$\begin{aligned}&\delta {\mathcal {W}} ={\mathbf {F}}\cdot \delta {\mathbf {x}}, \end{aligned}$$

(73)

where terms evaluated at $t_{1},t_{2}$ after integration by parts have been canceled. The variation of the terms which involve integrals on space, instead, is more complicated, since it calls for properly accounting for the presence of a singularity at $s=\xi$. By breaking the integration interval as:

$$\begin{aligned} \intop _{0}^{\ell }f\left( s\right) \,\mathrm {d}s=\intop _{0}^{\xi }f\,\mathrm {d}s+\intop _{\xi }^{\ell }f\,\mathrm {d}s, \end{aligned}$$

(74)

it follows that:

$$\begin{aligned} \delta \intop _{0}^{\ell }f\left( s\right) \,\mathrm {d}s= & {} \intop _{0}^{\ell }\delta f\,\mathrm {d}s+\left( \intop _{0}^{\xi +\delta \xi }f\,\mathrm {d}s-\intop _{0}^{\xi }f\,\mathrm {d}s\right) \nonumber \\&+\left( \intop _{\xi +\delta \xi }^{\ell }f\,\mathrm {d}s-\intop _{\xi }^{\ell }f\,\mathrm {d}s\right) \nonumber \\= & {} \intop _{0}^{\ell }\delta f\,\mathrm {d}s+\left[ f\left( \xi _{-}\right) -f\left( \xi _{+}\right) \right] \delta \xi \nonumber \\= & {} \intop _{0}^{\ell }\delta f\,\mathrm {d}s-\llbracket f\rrbracket \delta \xi , \end{aligned}$$

(75)

Accordingly:

$$\begin{aligned}&\delta {\mathcal {K}}_{s}=\intop _{0}^{\ell }m\,\dot{{\mathbf {r}}}\cdot \delta \dot{{\mathbf {r}}}\,\mathrm {d}s-\frac{1}{2}m\,\llbracket \dot{{\mathbf {r}}}\cdot \dot{{\mathbf {r}}}\rrbracket \delta \xi , \end{aligned}$$

(76)

$$\begin{aligned}&\delta {\mathcal {U}}_{s}:=\intop _{0}^{\ell }\frac{T}{1+\varepsilon }\,{\mathbf {r}}'\cdot \delta {\mathbf {r}}'\,\mathrm {d}s-\llbracket \phi \rrbracket \delta \xi , \end{aligned}$$

(77)

in which $\delta \phi =\frac{\partial \phi }{\partial \varepsilon }\,\delta \varepsilon =T\,\delta \varepsilon$ has been exploited, together with $\delta \varepsilon =\frac{{\mathbf {r}}'\cdot \delta {\mathbf {r}}'}{1+\varepsilon }$, following Eq. (2).

Next step calls for integrating by parts the last two expressions. By noticing that:

$$\begin{aligned} \begin{aligned}&\intop _{0}^{\ell }f\left( s,t\right) {\dot{g}}\left( s,t\right) \,\mathrm {d}s\\&\quad = -\intop _{0}^{\ell }{\dot{f}}\,g\,\mathrm {d}s+\intop _{0}^{\ell }\left( f\,g\right) ^{\bullet }\,\mathrm {d}s\\&\quad = -\intop _{0}^{\ell }{\dot{f}}\,g\,\mathrm {d}s+\frac{\mathrm {d}}{\mathrm {d}t}\left( \intop _{0}^{\ell }f\,g\,\mathrm {d}s\right) +{\dot{\xi }}\llbracket f\,g\rrbracket ,\\&\intop _{0}^{\ell }f\left( s\right) g'\left( s\right) \,\mathrm {d}s\\&\quad = -\intop _{0}^{\ell }f'g\,\mathrm {d}s+\left[ f_{-}g_{-}\right] _{0}^{\xi }+\left[ f_{+}g_{+}\right] _{\xi }^{\ell }\\&\quad = -\intop _{0}^{\ell }f'g\,\mathrm {d}s+\left[ f_{\,}g\right] _{0}^{\ell }-\llbracket f\,g\rrbracket , \end{aligned} \end{aligned}$$

(78)

it follows:

$$\begin{aligned} \intop _{t_{1}}^{t_{2}}\delta {\mathcal {K}}_{s}\,\mathrm {d}t=&-\intop _{t_{1}}^{t_{2}}\intop _{0}^{\ell }m\,\ddot{{\mathbf {r}}}\cdot \delta {{\mathbf {r}}}\,\mathrm {d}s\,\mathrm {d}t+\intop _{t_{1}}^{t_{2}}m\,{\dot{\xi }}\llbracket \dot{{\mathbf {r}}}\cdot \delta {\mathbf {r}}\rrbracket \,\mathrm {d}t \end{aligned}$$

(79)

$$\begin{aligned}&-\intop _{t_{1}}^{t_{2}}\frac{1}{2}m\llbracket \dot{{\mathbf {r}}}\cdot \dot{{\mathbf {r}}}\rrbracket \delta \xi \,\mathrm {d}t, \end{aligned}$$

(80)

(81)

where the arbitrariness of $t_{1},t_{2}$ and the external boundary conditions were accounted.

The last step concerns the treatment of the discontinuities at $s=\xi$. By remembering Eq. (13b), it follows:

$$\begin{aligned} \begin{aligned} \llbracket {\mathbf {f}}\left( s\right) \cdot \delta {\mathbf {r}}\rrbracket&={\mathbf {f}}_{+}\cdot \delta {\mathbf {r}}_{+}-{\mathbf {f}}_{-}\cdot \delta {\mathbf {r}}_{-}\\&={\mathbf {f}}_{+}\cdot \left( \delta \hat{{\mathbf {r}}}-{\mathbf {r}}'_{+}\delta \xi \right) -{\mathbf {f}}_{-}\cdot \left( \delta \hat{{\mathbf {r}}}-\delta \xi \,{\mathbf {r}}'_{-}\right) \\&=\llbracket {\mathbf {f}}\rrbracket \cdot \delta \hat{{\mathbf {r}}}-\llbracket {\mathbf {f}}\cdot {\mathbf {r}}'\rrbracket \delta \xi , \end{aligned} \end{aligned}$$

(82)

from which the terms in Eqs. (79) and (81) are rewritten as:

$$\begin{aligned} \llbracket \dot{{\mathbf {r}}}\cdot \delta {\mathbf {r}}\rrbracket&=\llbracket \dot{{\mathbf {r}}}\rrbracket \cdot \delta \hat{{\mathbf {r}}}-\llbracket \dot{{\mathbf {r}}}\cdot {\mathbf {r}}'\rrbracket \delta \xi , \end{aligned}$$

(83)

(84)

The term $\llbracket \dot{{\mathbf {r}}}\cdot {\mathbf {r}}'\rrbracket$ can be further transformed by using the relationship:

$$\begin{aligned} \llbracket \dot{{\mathbf {r}}}\cdot \dot{{\mathbf {r}}}\rrbracket +2\,{\dot{\xi }}\llbracket \dot{{\mathbf {r}}}\cdot {\mathbf {r}}'\rrbracket +{\dot{\xi }}^{2}\llbracket {{\mathbf {r}}}'\cdot {\mathbf {r}}'\rrbracket =0, \end{aligned}$$

(85)

which is obtained by manipulating as follows Eq. (4):

$$\begin{aligned} \begin{aligned} \dot{{\mathbf {x}}}\cdot \dot{{\mathbf {x}}}&=\left( \dot{{\mathbf {r}}}_{\pm }+{\dot{\xi }}\,{\mathbf {r}}'_{\pm }\right) \cdot \left( \dot{{\mathbf {r}}}_{\pm }+{\dot{\xi }}\,{\mathbf {r}}'_{\pm }\right) \\&=\dot{{\mathbf {r}}}_{\pm }\cdot \dot{{\mathbf {r}}}_{\pm }+2\,{\dot{\xi }}\,\dot{{\mathbf {r}}}_{\pm }\cdot {\mathbf {r}}'_{\pm }+{\dot{\xi }}^{2}\,{\mathbf {r}}'_{\pm }\cdot {\mathbf {r}}'_{\pm }. \end{aligned} \end{aligned}$$

(86)

By collecting all previous results, the variational principle (71) reads:

(87)

from which Eqs. (14)–(18) are finally derived.

Appendix B: Numerical solution of the integro-differential system

To solve the final Eq. (70), a numerical procedure is adopted, in which the trapezoidal rule for the integral and the forward finite differences for the time-derivatives are adopted. The following positions are first introduced for brevity:

$$\begin{aligned} \begin{aligned}&f\left( t\right) :=-\frac{P\,t^{2}}{2\,\mu },\\&{\mathcal {A}}\left( t,\tau \right) :=K\left( \xi \left( t\right) ,t,\tau \right) +\frac{t-\tau }{\mu },\\&{\mathcal {B}}\left( t,\tau \right) :=2\sum _{k=1}^{N_{e}}\cos \left( \omega _{k}\xi \left( t\right) \right) \sin \left( \omega _{k}\xi \left( \tau \right) \right) \\&\quad \sin \left( \omega _{k}\left( t-\tau \right) \right) . \end{aligned} \end{aligned}$$

(88)

The time interval $\left[ 0,t_{f}\right]$ is divided in $N_{s}>2$ equispaced time sub-intervals of amplitude $\Delta t=t_{f}/N_{s}$. The following notation is used:

$$\begin{aligned} \begin{aligned}&t_{i}=i\,\Delta t,&\tau _{j}=j\,\Delta t,&i,j=0,\,1,\,2,\cdots ,N_{s},\\&R_{yi}=R_{y}\left( t_{i}\right) ,&\xi _{i}=\xi \left( t_{i}\right) ,\\&{\mathcal {A}}_{ij}={\mathcal {A}}\left( t_{i},\tau _{j}\right) ,&{\mathcal {B}}_{ij}={\mathcal {B}}\left( t_{i},\tau _{j}\right) ,\\&f_{i}=f\left( t_{i}\right) ,&D_{i}=D_{i}\left( t_{i}\right) \end{aligned} \end{aligned}$$

(89)

The integral Eq. (70a) is approximated as:

$$\begin{aligned}&\left( \frac{1}{2}{\mathcal {A}}_{10}R_{y0}+\frac{1}{2}{\mathcal {A}}_{11}R_{y1}\right) \Delta t=f_{1},\nonumber \\&\left( \frac{1}{2}{\mathcal {A}}_{i0}R_{y0}+\sum _{j=1}^{i-1}{\mathcal {A}}_{ij}R_{yj}+\frac{1}{2}{\mathcal {A}}_{ii}R_{yi}\right) \Delta t=f_{i},\nonumber \\&i=2,\cdots ,N_{s}, \end{aligned}$$

(90)

and the integro-differential Eq. (70b), by accounting for the initial conditions, as:

$$\begin{aligned} \begin{aligned}&\xi _{0}=0,\\&\xi _{1}={\dot{\xi }}_{0}\,\Delta t,\\&\mu \,\frac{\xi _{2}-2\,\xi _{1}+\xi _{0}}{\Delta t^{2}}=D_{0},\\&\mu \,\frac{\xi _{3}-2\,\xi _{2}+\xi _{1}}{\Delta t^{2}}\\&\quad =D_{1}+R_{y1}\,\left( \frac{1}{2}{\mathcal {B}}_{10}R_{y0}+\frac{1}{2}\mathsf {{\mathcal {B}}}_{11}R_{y1}\right) \Delta t,\\&\mu \,\frac{\xi _{i+2}-2\,\xi _{i+1}+\xi _{i}}{\Delta t^{2}}=D_{i}\\&\qquad +R_{yi}\,\left( \frac{1}{2}\mathsf {{\mathcal {B}}}_{i0}R_{y0}+\sum _{j=1}^{i-1}{\mathcal {B}}_{ij}R_{yj}+\frac{1}{2}\mathsf {{\mathcal {B}}}_{ii}R_{yi}\right) \Delta t,\\&\quad \quad i=2,\cdots ,N_{s}. \end{aligned} \end{aligned}$$

(91)

Equations (90) and (91) can be solved in cascade by following the sequence:

$$\begin{aligned}&\xi _{0}= 0,\nonumber \\&\xi _{1}= {\dot{\xi }}_{0}\,\Delta t,\nonumber \\&R_{y0}= \frac{2\,f_{1}}{{\mathcal {A}}_{10}\,\Delta t},\nonumber \\&\xi _{2}= \frac{D_{0}\Delta t^{2}}{\mu }+2\,\xi _{1}-\xi _{0},\nonumber \\&R_{y1}= \frac{f_{2}}{{\mathcal {A}}_{21}\,\Delta t}-\frac{{\mathcal {A}}_{20}}{2{\mathcal {A}}_{21}}R_{y0},\nonumber \\&\xi _{3}= \frac{D_{1}\Delta t^{2}}{\mu }+2\,\xi _{2}-\xi _{1}+\frac{1}{2\mu }{\mathcal {B}}_{10}R_{y0}R_{y1}\Delta t^{3},\nonumber \\&R_{y\left( i-1\right) }= \frac{f_{i}}{{\mathcal {A}}_{i\left( i-1\right) }\,\Delta t}\nonumber \\&\quad -\frac{1}{{\mathcal {A}}_{i\left( i-1\right) }}\left( \frac{1}{2}{\mathcal {A}}_{i0}R_{y0}+\sum _{j=1}^{i-2}{\mathcal {A}}_{ij}R_{yj}\right) ,\nonumber \\&i=3,\cdots ,N_{s},\nonumber \\&\xi _{i+1}= \frac{D_{\left( i-1\right) }\Delta t^{2}}{\mu }+2\,\xi _{i}-\xi _{i-1}\nonumber \\&\quad +\frac{R_{y\left( i-1\right) }}{\mu }\,\left( \frac{1}{2}\mathsf {{\mathcal {B}}}_{\left( i-1\right) 0}R_{y0}+\sum _{j=1}^{i-2}\mathsf {{\mathcal {B}}}_{\left( i-1\right) j}R_{yj}\right) \Delta t^{3},\nonumber \\&i=3,\cdots ,N_{s}, \end{aligned}$$

(92)

in which ${\mathcal {A}}_{ii}={\mathcal {B}}_{ii}=0$ has been accounted for (i.e., ${\mathcal {A}}\left( t,t\right) ={\mathcal {B}}\left( t,t\right) =0$). In the case of assigned $\xi$-motion, the step relevant to the determination of $\xi _{i}$ is skipped and subsequently utilized for the determination of $D_{i}$.

Appendix C: Massless string

The equation of motion of the massless string is obtained by neglecting the inertia term in Eq. (51):

$$\begin{aligned}&v''+R_{y}\,\delta \left( s-\xi \right) =0. \end{aligned}$$

(93)

Equation (93) admits the solution:

$$\begin{aligned} v\left( s,t\right) ={\left\{ \begin{array}{ll} R_{y}\,\left( 1-\xi \right) \,s &{} 0\le s\le \xi \\ R_{y}\,\left( 1-s\right) \,\xi &{} \xi \le s\le 1 \end{array}\right. }. \end{aligned}$$

(94)

Substitution of Eq. (94) in Eq (54) yields:

$$\begin{aligned} y=v\left( \xi ,t\right) =R_{y}\,\left( 1-\xi \right) \,\xi , \end{aligned}$$

(95)

from which:

$$\begin{aligned} R_{y}=\frac{y}{\left( 1-\xi \right) \,\xi }. \end{aligned}$$

(96)

From Eq. (94), it follows that:

$$\begin{aligned} \left\langle v'\right\rangle =\frac{1}{2}\left( 1-2\,\xi \right) \,R_{y}. \end{aligned}$$

(97)

By using Eqs. (96) and (97), Eqs. (52) and (53) become:

$$\begin{aligned}&\mu \,\ddot{y}+\frac{y}{\left( 1-\xi \right) \,\xi }=-P, \end{aligned}$$

(98)

$$\begin{aligned}&\mu \,\ddot{\xi }+\frac{\left( 2\,\xi -1\right) y^{2}}{2\left( 1-\xi \right) ^{2}\,\xi ^{2}}=D. \end{aligned}$$

(99)

Equations (98) and (99) govern the problem of the massless string. Once such equations are solved for y and $\xi$, the vertical reaction and the displacement field of the string are evaluated via Eqs. (96) and (94), then the nondimensional horizontal displacement, the horizontal reaction and the dynamic tension computed through Eqs. (60), (61) and (62), respectively.

It is worth noting that some coefficients of Eqs. (98) and (99) exhibit singularities at $\xi =0$ or $\xi =1$. This situation does not occur if the string is hanging on two vertical elastic supports, as proven in [24]. Therefore, the springs regularize the mathematical model. To investigate the role of singularities, a numerical analysis (not shown here) was carried out, comparing results of Eqs. (98), (99) and those derived in [24], when a very small compliance of the springs is taken. The two models were found to be in excellent agreement, except for a very narrow layer close to the ends. Therefore, the simpler model was adopted.