Abstract
In this paper, the finite frequency fault detection (FD) problem is addressed for a class of nonhomogeneous Markov jump systems with nonlinearities and sensor failures. Compared with the existing sensor fault models that contain many known faulty modes, the fault model in this paper is more general since it not only covers more types of sensor failures but also does not need to know the fault information in advance. Then, by means of finite frequency stochastic performance indices, a novel FD scheme is proposed. Some new lemmas, in which the nonlinear item and nonhomogeneous Markov switching are dealt appropriately, are developed to capture the stability of the system and desired finite frequency performances. Then, by the derived lemmas, sufficient conditions with potentially less conservativeness are investigated to guarantee the existence of the FD filters. Finally, an application to HiMAT vehicle is given to illustrate the effectiveness of the derived theoretical results.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
In recent decades, it is witnessed that Markov jump systems (MJSs) have received intensive research attention due to their strong ability to model the practical systems with sudden parameter variations, such as manufacturing systems, economic systems, electrical systems and communication systems [1,2,3,4,5,6,7,8]. MJS is a kind of system that includes two parts, finite discrete jump modes and system states which are, respectively, governed by Markov process and discrete-time differential equations [9]. As the pivotal factor of Markov processes, transition probabilities (TPs) play important roles in determining relevant system performances. For normal MJSs with affirmatory and known TPs, great efforts have been made to concentrate on the problems of stable and stability, \({\mathcal {H}}_{\infty }\) estimation and filtering, and so on [10,11,12]. For more information, one can see [13] for a survey. Further, for semi-MJSs and MJSs with partially known even uncertain TPs, there were also fruitful results concerned with the similar problems mentioned above, for example, [14, 15] and the references therein. It should be noticed that these results have been presented in the case of the TPs are constant, i.e., the considered Markov chain is a homogeneous one. Nevertheless, in many practical systems, such a premise may be not satisfied. Taking the vertical take-off and landing (VTOL) system, which can be seen in [16], for example, it can be modeled into normal MJSs in an ideal situation. However, the derived jump probabilities will be varied when the system experiences sudden disturbances such as wind and temperature. Thus, it is a matter of course to consider nonhomogeneous MJSs, and consequently there are a few kinds of literature focusing on such kinds of systems, such as [16] proposed an \({\mathcal {H}}_{\infty }\) estimation method in discrete-time domain for the MJSs with time-varying TPs, [17] addressed a robust \({\mathcal {H}}_{\infty }\) filtering scheme for kinds of uncertain discrete-time nonhomogeneous MJSs. However, the research on such kinds of systems is still in its infancy and deserves further considerations.
On the other hand, FD plays an important role in modern control field due to the increasing demands on reliability and low maintenance costs [18,19,20,21,22]. And consequently, great research efforts have been made on the FD problem for MJSs. For example, [23] presented a generalized \({\mathcal {H}}_{2}\) FD method for two-dimensional MJSs, [24] dealt with the FD and isolation problem for MJSs based on a geometric method, [25] designed the FD filter for MJSs with nonlinear stochastic time delays, and [26] developed an FD strategy for discrete-time MJSs with partial knowledge of TPs. Further, from the references therein, one can see more information about the results of FD for MJSs. Nevertheless, this method cannot be utilized for nonhomogeneous MJSs with nonlinearities, especially when the sensors experience failures.
It should be also noticed that the methods mentioned above are all developed in time domain. However, for some fault signals, they usually occur in a certain frequency domain, such as the actuator stuck fault is always in low-frequency range. In such situations, the aforementioned FD methods are imprecise due to the signal frequency constraints were not considered. Consequently, the FD strategy proposed in a finite frequency domain is considered as a more practical one nowadays. Of course, with the aid of the generalized Kalman–Yakubovič–Popov (GKYP) lemma, many FD schemes have been investigated, such as in [28,29,30], but all of them are proposed for certain linear systems. However, it should be declared that for systems which are not linear time-invariant ones, the GKYP lemma cannot be utilized directly. And thus, it is valuable to explore the finite frequency FD method for such kinds of systems. Accordingly, there are a few results concerned with such a topic. For example, in [31], FD and isolation scheme have been presented in finite frequency domain for a switched stochastic system with multi-stochastic parameters, and in [18], FD strategy for fuzzy systems has been considered. Nevertheless, those developed methods cannot be utilized to detect the sensor faults that occurred in certain frequency range for nonhomogeneous MJSs, especially for such kinds of systems with nonlinearities, which cannot be ignored in practical cases when designing the system.
Motivated by the aforementioned points, it is imperative to develop a finite frequency FD strategy for nonhomogeneous MJSs with sensor failures and nonlinearities. Nevertheless, such an interesting topic is with some difficulties listed below: (1) How to model the possible sensor failures appropriately? (2) How to detect the failures with small amplitude? (3) How to deal with the nonlinearities and nonhomogeneous Markov switching when developing the solvable conditions in finite frequency domain? Specifically, in this paper, the listed questions are solved legitimately. Firstly, a novel sensor fault model is given, which is more general than existing ones, since it not only involves more kinds of failures but also does not need to know the fault information beforehand. And then, an FD strategy is presented, in which the residual is sensitive to the fault and the reference input in faulty case, meanwhile robust to the disturbance and the reference input in fault-free case. Subsequently, sufficient conditions with potentially less conservativeness are developed to capture the required performance for the system, in which the nonlinear item and nonhomogeneous Markov switching are dealt appropriately. And the FD filter gains can be characterized by derived conditions. Lastly, the effectiveness of the investigated FD scheme is verified by an application to HiMAT vehicle.
2 Modeling of the system and problem formulation
Consider a class of MJSs given in a probability space \(\{{{\varvec{\Omega }}},{\mathbf {F}},{\mathbf {P}}\}\) as the form of
where \(x(k)\in {\mathbf {R}}^{n}\) is the system state, \(y(k)\in {\mathbf {R}}^{m}\) is the measured output, \(w(k)\in {\mathbf {L}}_{2}[0,\infty )\) is the disturbance, \(s(k)\in {\mathbf {L}}_{2}[0,\infty )\) is the reference input with frequency \(\varpi _{s}\), \(\varpi _{s}\in \varXi _{\varpi _{s}}:=\{\varsigma (\varpi _{s}-\varpi _{s1})(\varpi _{s}-\varpi _{s2})\le 0|\varpi _{s}\in {\mathbf {R}}\}\). \(f(\cdot ,\cdot ):{\mathbf {R}}^{n}\times {\mathbf {R}}\rightarrow {\mathbf {R}}^{n}\) is a nonlinear function. Further, the parameter \(\{\alpha _{k}, k\ge 0\}\) represents a nonhomogeneous Markov stochastic process with range set of \(\mathbb {S}=\{1,2,\ldots ,N\}\) and TP matrix \(\varLambda (k)=(\lambda _{ij}(k))\) given by \(\lambda _{ij}(k)={\mathbf {P}}\{\alpha _{k+1}=j|\alpha _{k}=i\}\) with \(\lambda _{ij}(k)>0\), \(\forall i,j\in \mathbb {S}\) and \(\sum _{j\in \mathbb {S}}\lambda _{ij}(k)=1\). The system matrices \(A_{\alpha _{k}}\), \(E_{\alpha _{k}}\), \(B_{1\alpha _{k}}\), \(B_{2\alpha _{k}}\), \(C_{\alpha _{k}}\), \(D_{1\alpha _{k}}\), \(D_{2\alpha _{k}}\) are known matrices with proper dimensions, which characterize the relationships between the system variables. In the sequel of the paper, the subscript \(\alpha _{k}\) associated with \(\alpha _{k}=i\) is denoted by i.
Remark 1
It is noted that \(\varXi _{\varpi _{s}}\) is utilized to limit the frequency range. From the reference [27], it is obvious that \(\varXi _{\varpi _{s}}\) can characterize low-frequency (LF), middle-frequency (MF) and high-frequency (HF) domain when \(\varsigma =1\) by selecting the parameters as in Table 1 while characterize the full frequency domain when \(\varsigma =-1\) and \(\varpi _{s1}=\varpi _{s2}=0\).
Assumption 1
The nonlinear function \(f(\cdot ,\cdot )\) is assumed to be bounded as
where \(\tau _{\kappa i}\), \(\varTheta _{\kappa i}\), \((\kappa =1,\ldots ,{\mathfrak {K}})\) are known column vectors and positive definite matrices.
Remark 2
The description (2) in statistical sense is more general since it can involve various types of nonlinearities, such as the nonlinear stochastic sequences, whose powers are dependent on the sector-bounded nonlinear function of the system states.
In this paper, the time-varying TP matrix \(\varLambda (k)\) is considered to be with a polytopic structure described by
where \(o_{\imath }(k)\ge 0\), \(\imath \in {\mathfrak {L}}=\{1,2,\ldots ,L\}\) are scalar functions of k satisfying \(\sum _{\imath \in {\mathfrak {L}}}o_{\imath }(k)=1\), \(\varLambda ^{\imath }\) are known matrices, which denote the vertices of the polytope.
Remark 3
It is noticed that equation (3) characterized a kind of time-dependent Markov chain, and this kind of process is called as nonhomogeneous Markov process. Further, if the time-varying one is fixed, i.e., \(\varLambda (k)=\varLambda \), it is the normal homogeneous one, which performs as a special case of the considered process in this manuscript. In [16], the author proposed an \({\mathcal {H}}_{\infty }\) estimation method for a class of nonhomogeneous MJSs, in which the TP matrix \(\varLambda (k)\) is subject to the piecewise homogeneous as \(\varLambda ^{\sigma _{k}}\), \(\sigma _{k}\) takes values in a finite set with a finite mode, which is also a specific form of the considered one in this paper.
Further, when the sensors encounter possible failures, the following model will be adopted to describe the jth measured output
where \(\varrho ^{j}_{\iota }(k)\) denotes the unknown efficiency coefficient, and \(f^{j}(k)\) represents the stuck or drift fault with unknown bound occurred on the jth sensor with frequency \(\varpi _{f}\), \(\varpi _{f}\in \varXi _{\varpi _{f}}:=\{\varsigma (\varpi _{f}-\varpi _{f1})(\varpi _{f}-\varpi _{f2})\le 0|\varpi _{f}\in {\mathbf {R}}\}\). Moreover, \(\iota =0\) means the fault-free case in which \(\varrho ^{j}_{\iota }(k)=1\) and \(f^{j}(k)=0\), while \(\iota =1\) means faulty case, wherein \(0\le \varrho _{\iota }^{j}(k)\le 1\). Thus, we have
with \(\varrho _{\iota }(k)={\mathrm{diag}}\{\varrho ^{j}_{\iota }(k)\}\).
Remark 4
There are a few kinds of literature considering sensor failures, such as the multi-mode model has been adopted in [18]. However, some information about the fault in each mode should be exactly known beforehand, which restricts the application of the proposed method. In the model (5), \(\varrho _{\iota }(k)\) is assumed to be unknown. Such an assumption is more reasonable to describe the practical systems. Moreover, except outage and stuck ones, the model (5) can express more kinds of failures such as loss of effectiveness and drift phenomena compared to [18]; thus, it is more general.
The FD filter as the following form will be adopted to generate the residuals
where \({\hat{x}}(k)\in {\mathbf {R}}^{n}\) denotes the filter state, \(r(k)\in {\mathbf {R}}\) is the residual signal, \(A_{fi}\), \(B_{1fi}\), \(B_{2fi}\), \(C_{fi}\) and \(D_{fi}\) are filter gains. Then, by defining the augmented vector \({\tilde{x}}(k)=[\begin{array}{cc}x^{\mathrm{T}}(k)&{\hat{x}}^{\mathrm{T}}(k)\end{array}]^\mathrm{T}\), the whole FD systems together with the possible faults can be obtained as follows
where \({\mathcal {T}}=[\begin{array}{cc}I&0\end{array}]\), \({\mathcal {E}}_{i}^{\iota }=[\begin{array}{cc}E{i}^\mathrm{T}&0\end{array}]^\mathrm{T}\), and
Denoting the operator \(\Vert \cdot \Vert _{2}^{{\mathbf {E}}}=\sum _{0}^{\infty }\{\mathbf {E|\cdot |^{2}}\}^{1/2}\), and then the following definitions are firstly recalled.
Definition 1
The system (7) is stochastic stable (SS) if the inequality \(\Vert {\tilde{x}}(k)\Vert _{2}^{{\mathbf {E}}}<\infty \) holds \(\forall i\in \mathbb {S}\) when the system (7) is without disturbance and fault.
Definition 2
For all \(i\in \mathbb {S}\), the system (7) is with a finite frequency stochastic (FFS) \(H_{-}\)index \(\beta \) to s(k) if
holds under zero initial conditions for all the solutions in certain frequency domain satisfying
where \(\varpi _{s}=(\varpi _{s1}+\varpi _{s2})/2\).
Definition 3
For all \(i\in \mathbb {S}\), the system (7) is with a FFS \({\mathcal {H}}_{\infty }\) performance \(\gamma \) to s(k) if
holds under zero initial conditions for all the solutions in certain frequency domain satisfying (10).
Remark 5
It is obvious, from the Definitions 2–3, that \(\beta \) indicates the sensitivity to the reference input in finite frequency domain. On contrary, \(\gamma \) characterizes the robustness to it in a finite frequency range. And thus, the large \(\beta \) and the smaller \(\gamma \) they are, the better performance we can get.
Till now, the FD strategy to be addressed in this paper can be formulated as: For the considered nonhomogeneous MJSs (1) and the possible sensor failure, design a set of filters as form of (6) such that the dynamic of the system (7) is SS and the possible sensor failures can be detected effectively by satisfying the following requirement:
-
(a)
The system (7) is SS and with an \({\mathcal {H}}_{\infty }\) performance \(\gamma \) to the disturbance \(\omega (k)\).
-
(b)
In faulty case, the impact of s(k) on r(k) is maximized in certain frequency range, i.e., the system (7) is with a FFS \(H_{-}\)index \(\beta \) to s(k). Meanwhile in fault-free case, the impact is minimized in certain frequency range, i.e., with a finite frequency stochastic \({\mathcal {H}}_{\infty }\) performance \(\gamma _{d}\).
-
(c)
In faulty case, the impact of f(k) on r(k) is maximized in certain frequency range, i.e., the system (7) is with a FFS \(H_{-}\)index \(\beta _{f}\) to the fault.
Remark 6
In the proposed FD scheme which is presented above, it requires that the residual r(k) is sensitive to s(k) and f(k) in faulty cases instead of to f(k) only. This operation will make it possible to detect the fault with small amplitude. And the effectiveness will be shown in simulation further.
3 Main results
3.1 Performance analysis
In this subsection, the analysis conditions to capture the desired performances will be presented by the following lemmas and corollaries.
Lemma 1
The system (7) is SS and with a prescribed \({\mathcal {H}}_{\infty }\) performance \(\gamma \), \(\gamma >0\), to \(\omega (k)\) if there exist matrices \(P_{i\imath }^{\iota }=P_{i\imath }^{{\iota }{\mathrm{T}}}>0\) and scalars \(\delta _{\kappa i}^{\iota }\) such that the following inequalities
hold \(\forall i\in \mathbb {S}\), \(\kappa =1,2,\ldots ,{\mathfrak {K}}\), and \(\iota =0,1\), where
with
wherein \(\bar{{\mathcal {P}}}_{i}^{\iota }=\sum _{j=1}^{N}\sum _{\imath =1}^{L}\sum _{\jmath =1}^{L}o_{\imath }(k)\xi _{\jmath }(k)\lambda _{ij}^{\imath }P_{j\jmath }^{\iota }\), \({\mathcal {P}}_{i}^{\iota }=\sum _{\imath =1}^{L}o_{\imath }(k)P_{i\imath }^{\iota }\), \(\varOmega ^{'}={\mathcal {T}}^{\mathrm{T}}[\begin{array}{cccc}\varTheta _{1i}^{1/2}&\varTheta _{2i}^{1/2}&\cdots&\varTheta _{{\mathfrak {K}}i}^{1/2}\end{array}]\), \(\varOmega ^{''}={\mathrm{diag}}\{\delta _{1i}I,\delta _{2i}I,\ldots ,\delta _{{\mathfrak {K}}i}I\}\) with \(\xi _{\jmath }(k)=o_{\imath }(k+1)\).
Proof
Considering the following Lyapunov mode-dependent functional when \(f_{\iota }=0\) and \(s(k)=0\)
By the expression of (7), the forward difference defined as \(\Delta V_{i}(k)={\mathbf {E}}\{V({\tilde{x}}(k+1),k+1,j)\}-V({\tilde{x}}(k),k,i)\) can be derived as
Now, recalling the property
where a, b are nonzero vectors and M is an arbitrary matrix with suitable dimensions, one has
Further, (12) implies that \(\text {tr}(\tau _{\kappa i}\tau _{\kappa i}^{\mathrm{T}}{\mathcal {E}}_{i}^{{\iota {\mathrm{T}}}}\bar{{\mathcal {P}}}_{i}^{\iota }{\mathcal {E}}_{i}^{\iota })<\delta _{\kappa i}^{\iota }\). Consequently, when \(w(k)=0\), we have
Applying Schur’s complement to (13), it has \(\varPhi _{i}^{\iota '}<0\), then one has
where \(\xi =\inf \{\lambda _{\min }(-\varPhi _{i}^{\iota '})\}\), \(i\in \mathbb {S}\), which implies that
Thus, it can be deduced, from Definition 1, that the system (7) is SS.
Further, we are going to verify the \({\mathcal {H}}_{\infty }\) performance. Considering the index \({\mathfrak {I}}_{rw}=\sum _{k=0}^{\infty }\big [{\mathbf {E}}\{r^{\mathrm{T}}(k)r(k)-\gamma ^{2}\omega ^{\mathrm{T}}(k)\omega (k)\}\big ]\) under \({\tilde{x}}(0)=0\), which can be written into
where \(\varPhi _{i}^{\iota ''}={\mathfrak {J}}_{i}^{{\iota {\mathrm{T}}}}\varPsi _{i}^{\iota }{\mathfrak {J}}_{i}^{\iota }+{\mathfrak {V}}_{i}^{{\iota {\mathrm{T}}}}\varPi _{i}^{\iota }{\mathfrak {V}}_{i}^{\iota }-{\mathfrak {M}}_{i}^{{\iota {\mathrm{T}}}}\varUpsilon _{i}^{\iota }{\mathfrak {M}}_{i}^{\iota }\). It is obvious that the inequality (13) ensures that \({\mathfrak {I}}_{rw}<0\), that is \(\Vert r(k)\Vert _{2}^{{\mathbf {E}}}\le \gamma \Vert \omega (k)\Vert _{2}^{{\mathbf {E}}}\), which implies the system (7) is with an \({\mathcal {H}}_{\infty }\) performance \(\gamma \). The proof is completed. \(\square \)
Lemma 2
The system (7) is with a prescribed FFS \(H_{-}\)index \(\beta \), \(\beta >0\), to s(k) if there exist matrices \(P_{si\imath }^{\iota }=P_{si\imath }^{{\iota {\mathrm{T}}}}>0\), \(Q_{si\imath }^{\iota }=Q_{si\imath }^{{\iota {\mathrm{T}}}}>0\) and scalars \(\delta _{s\kappa i}^{\iota }\) such that
hold \(\forall i\in \mathbb {S}\), \(\kappa =1,2,\ldots ,{\mathfrak {K}}\), and \(\iota =1\), where
with \({\mathfrak {J}}_{si2}^{\iota }=[\begin{array}{cc}{\mathcal {B}}_{2i}^{{\iota {\mathrm{T}}}}&0\end{array}]^\mathrm{T}\), \({\mathfrak {V}}_{si1}^{\iota }\!=\![\begin{array}{cc}\varOmega ^{'}&0\end{array}]^\mathrm{T}\), \({\mathfrak {M}}_{si2}^{\iota }=[\begin{array}{cc}{\mathcal {D}}_{2i}^{{\iota {\mathrm{T}}}}&I\end{array}]^\mathrm{T}\), wherein \(\bar{{\mathcal {P}}}_{si}^{\iota }\!=\!\!\sum _{j=1}^{N}\sum _{\imath =1}^{L}\sum _{\jmath =1}^{L}o_{\imath }(k)\xi _{\jmath }(k)\lambda _{ij}^{\imath }P_{sj\jmath }^{\iota }\), \({\mathcal {P}}_{si}^{\iota }=\sum _{\imath =1}^{L}o_{\imath }(k)P_{si\imath }^{\iota }\), \(\varOmega _{s}^{''}={\mathrm{diag}}\{\delta _{s1i}I,\delta _{s2i}I,\ldots ,\delta _{s{\mathfrak {K}}i}I\}\). Furthermore, \(\gimel \ =\ \left[ \begin{array}{cc} 0 &{} 1\\ 1 &{} -2 \cos \varpi _{sl} \end{array} \right] \) in LF domain, \(\gimel =\left[ \begin{array}{ccc} 0 &{} e^{j\varpi _{sa}}\\ e^{-j\varpi _{sa}} &{} -2 \cos \varpi _{sb} \end{array} \right] \) in MF domain, \(\gimel =\left[ \begin{array}{ccc} 0 &{} -1\\ -1 &{} 2 \cos \varpi _{sh} \end{array} \right] \) in HF domain, wherein \(\varpi _{sa}=\frac{\varpi _{s1}+\varpi _{s2}}{2}\), and \(\varpi _{sb}=\frac{\varpi _{s2}-\varpi _{s1}}{2}\).
Proof
Under zero initial conditions and LF domain, pre- and post-multiplying the inequality (23) by \([{\tilde{x}}^{\mathrm{T}}(k)\ s^{\mathrm{T}}(k)]\) and its transpose, it is obvious that the following inequality can be obtained
On the one hand, for matrices \(P_{si\imath }^{\iota }>0\), define an energy functional \(V_{si}(k)={\tilde{x}}^{\mathrm{T}}(k)(\sum _{\imath =1}^{L}o_{\imath }(k)P_{si\imath }^{\iota }){\tilde{x}}(k)\) as the same form of (14), then from the inequality (22) and the proof to Lemma 1, one can prove \(\Delta V_{si}(k)\le [{\tilde{x}}^{\mathrm{T}}(k)\ s^{\mathrm{T}}(k)]\varPhi _{si}^{\iota '}[{\tilde{x}}^{\mathrm{T}}(k)\ s^{\mathrm{T}}(k)]^\mathrm{T}<0\) easily, where \(\varPhi _{si}^{\iota '}={\mathfrak {J}}_{si}^{{\iota {\mathrm{T}}}}(\bar{{\mathcal {P}}}_{i}^{\iota }\otimes {\mathrm{diag}}\{I, 0\}-{\mathcal {P}}_{si}^{\iota }\otimes {\mathrm{diag}}\{0, I\}){\mathfrak {J}}_{si}^{\iota }-{\mathfrak {V}}_{si}^{{\iota {\mathrm{T}}}}\varPi _{si}^{\iota }{\mathfrak {V}}_{si}^{\iota }\), that means the sum of the first three items in the left side of inequality (24) is larger than zero, which yields that
where \({\mathbb {I}}_{f}={\tilde{x}}^{\mathrm{T}}(k+1){\mathcal {Q}}_{si}^{\iota }{\tilde{x}}(k) + {\tilde{x}}^{\mathrm{T}}(k){\mathcal {Q}}_{si}^{\iota }{\tilde{x}}(k+1)-2 \cos \varpi _{sl}{\tilde{x}}^{\mathrm{T}}(k){\mathcal {Q}}_{si}^{\iota }{\tilde{x}}(k)\).
On the other hand, recalling the property (16) again and then summing \({\mathbb {I}}_{f}\) from \(k=0\) to \(\infty \), we have
Under zero initial conditions and LF domain, performing some calculations and Euler’s formula on the constraint (10), we have
Thus, for \({\mathcal {Q}}_{si}^{\iota }>0\), we have \(\sum _{k=0}^{\infty }\big ({\tilde{x}}(k){\tilde{x}}^{\mathrm{T}}(k+1)+ {\tilde{x}}(k+1){\tilde{x}}^{\mathrm{T}}(k)-2 \cos \varpi _{sl}{\tilde{x}}(k){\tilde{x}}^{\mathrm{T}}(k)\big ){\mathcal {Q}}_{si}^{\iota }\ge 0\), which implies \(\sum _{k=0}^{\infty }{\mathbb {I}}_{f}\ge 0\). Summing the inequality (25) from \(k=0\) to \(\infty \), one can easily obtain \(\Vert r(k)\Vert ^{{\mathbf {E}}}_{2}\ge \beta \Vert s(k)\Vert ^{{\mathbf {E}}}_{2}\) holds, that is the system (7) is with a LF stochastic \(H_{-}\)index. By the similar process, the conditions for MF and HF can be obtained naturally by choosing the suitable frequency parameters, and it is omitted here. The proof is completed. \(\square \)
Remark 7
If the system considered in this paper is a linear one rather than MJS, i.e., the system is independent on i, and it is without the nonlinear items \(f\big (x(k),\alpha _{k}\big )\), the condition in Lemma 2 can be reduced to the condition of GKYP lemma shown in [27]. Through such conditions, the finite frequency performance requirement has been transferred into time-domain conditions, which facilitated the design procedure.
Following the idea of Lemmas 1–2, the analysis conditions to capture the sensitivity performance to f(k) and the robustness performance to s(k) can be easily derived, which are shown in the following two corollaries.
Corollary 1
The system (7) is with a prescribed FFS \({\mathcal {H}}_{\infty }\) performance \(\gamma _{d}\), \(\gamma _{d}>0\), to s(k) if there exist matrices \(P_{di\imath }^{\iota }=P_{di\imath }^{{\iota {\mathrm{T}}}}>0\), \(Q_{di\imath }^{\iota }=Q_{di\imath }^{{\iota {\mathrm{T}}}}>0\) and scalars \(\delta _{d\kappa i}^{\iota }\) such that
hold \(\forall i\in \mathbb {S}\), \(\kappa =1,2,\ldots ,{\mathfrak {K}}\), and \(\iota =0\), where
with \({\mathfrak {V}}_{di1}^{\iota }=[\begin{array}{cc}\varOmega ^{'}&0\end{array}]^\mathrm{T}\), \(\varOmega _{d}^{''}={\mathrm{diag}} \{\delta _{d1i}I,\delta _{d2i}I,\ldots ,\delta _{d{\mathfrak {K}}i}I\}\), \(\bar{{\mathcal {P}}}_{di}^{\iota }=\sum _{j=1}^{N}\sum _{\imath =1}^{L}\sum _{\jmath =1}^{L}o_{\imath }(k)\xi _{\jmath }(k)\lambda _{ij}^{\imath }P_{dj\jmath }^{\iota }\), and \({\mathcal {P}}_{di}^{\iota }=\sum _{\imath =1}^{L}o_{\imath }(k)P_{di\imath }^{\iota }\).
Corollary 2
For the system (7) in faulty case, it is with a prescribed FFS \(H_{-}\)index \(\beta _{f}\), \(\beta _{f}>0\), to f(k) if there exist matrices \(P_{fi\imath }^{\iota }=P_{fi\imath }^{{\iota {\mathrm{T}}}}>0\), \(Q_{fi\imath }^{\iota }=Q_{fi\imath }^{{\iota {\mathrm{T}}}}>0\) and scalars \(\delta _{f\kappa i}^{\iota }\) such that
hold \(\forall i\in \mathbb {S}\), \(\kappa =1,2,\ldots ,{\mathfrak {K}}\), and \(\iota =1\), where
with \({\mathfrak {J}}_{fi2}^{\iota }=[\begin{array}{cc}{\mathcal {B}}_{3i}^{{\iota {\mathrm{T}}}}&0\end{array}]^\mathrm{T}\), \({\mathfrak {V}}_{fi1}^{\iota }=[\begin{array}{cc}\varOmega ^{'}&0\end{array}]^\mathrm{T}\), \({\mathfrak {M}}_{fi2}^{\iota }=[\begin{array}{cc}{\mathcal {D}}_{3i}^{{\iota {\mathrm{T}}}}&I\end{array}]^\mathrm{T}\), wherein \(\bar{{\mathcal {P}}}_{fi}^{\iota }=\sum _{j=1}^{N}\sum _{\imath =1}^{L}\sum _{\jmath =1}^{L}o_{\imath }(k)\xi _{\jmath }(k)\lambda _{ij}^{\imath }P_{fj\jmath }^{\iota }\), \({\mathcal {P}}_{fi}^{\iota }=\sum _{\imath =1}^{L}o_{\imath }(k)P_{fi\imath }^{\iota }\), \(\varOmega _{f}^{''}={\mathrm{diag}}\{\delta _{f1i}I,\delta _{f2i}I,\ldots ,\delta _{f{\mathfrak {K}}i}I\}\). Furthermore, \(\gimel _{f}=\left[ \begin{array}{cc} 0 &{} 1\\ 1 &{} -2 \cos \varpi _{fl} \end{array} \right] \) in LF domain, \(\gimel _{f}=\left[ \begin{array}{ccc} 0 &{} e^{j\varpi _{fa}}\\ e^{-j\varpi _{fa}} &{} -2 \cos \varpi _{fb} \end{array} \right] \) in MF domain, \(\gimel _{f}=\left[ \begin{array}{ccc} 0 &{} -1\\ -1 &{} 2\cos \varpi _{fh} \end{array} \right] \) in HF domain, wherein \(\varpi _{fa}=\frac{\varpi _{f1}+\varpi _{f2}}{2}\), and \(\varpi _{fb}=\frac{\varpi _{f2}-\varpi _{f1}}{2}\).
3.2 Fault detection filters synthesis
Based on the conclusions in above subsection, the linear conditions to design the FD filters will be developed thoroughly in this subsection.
Lemma 3
For the known scalar \(\epsilon \) and the real matrices Y, M, F, and E with appropriate dimensions subjecting \(F^{\mathrm{T}}F\le \epsilon ^{2}I\), the inequality \(Y+\mathbf He (MFE)<0\) holds if and only if there exists a scalar \(\sigma >0\) such that \(Y+\sigma MM^{\mathrm{T}}+\frac{1}{\sigma }\epsilon ^{2}E^{\mathrm{T}}E<0\).
Theorem 1
The system (7) is with a prescribed LF stochastic \(H_{-}\) index \(\beta \), \(\beta >0\), to s(k) if there exist matrices \(P_{si\imath }^{{\iota {\mathrm{T}}}}=P_{si\imath }^{\iota }=\left[ \begin{array}{cc}P_{si1\imath }^{\iota } &{} *\\ P_{si2\imath }^{\iota } &{} P_{si3\imath }^{\iota }\end{array}\right] >0\), \(Q_{si\imath }^{{\iota {\mathrm{T}}}}=Q_{si\imath }^{\iota }=\left[ \begin{array}{cc}Q_{si1\imath }^{\iota } &{} *\\ Q_{si2\imath }^{\iota } &{} Q_{si3\imath }^{\iota }\end{array}\right] >0\), \({\mathcal {Y}}_{i}\), \({\mathcal {M}}_{i}\), \({\mathcal {N}}_{i}\), \({\mathcal {G}}_{i}\), \({\mathcal {X}}_{3i}\), \({\mathcal {A}}_{fi}\), \({\mathcal {B}}_{1fi}\), \({\mathcal {B}}_{2fi}\), \({\mathcal {C}}_{fi}\), \({\mathcal {D}}_{fi}\) and scalars \(\delta _{s\kappa i}^{\iota }\) and \(\varepsilon _{s}\) such that
hold \(\forall i\in \mathbb {S}\), \(\kappa =1,2,\ldots ,{\mathfrak {K}}\), and \(\iota =1\), where
with \(\varGamma _{s22}^{1}={\mathcal {P}}_{si1}^{\iota }\!\!-\!2\cos \varpi _{sl}Q_{si1}^{\iota }+\mathbf He ({\mathcal {Y}}_{i}A_{i})+\varepsilon _{s}C_{i}^{\mathrm{T}}C_{i}\), \(\varGamma _{s22}^{2}={\mathcal {P}}_{si2}^{\iota }\!\!-\!2\cos \varpi _{sl}Q_{si2}^{\iota }+{\mathcal {M}}_{i}A_{i}+{\mathcal {A}}_{fi}^{\mathrm{T}}+{\mathcal {C}}_{fi}^{\mathrm{T}} \), \(\varGamma _{s22}^{3}={\mathcal {P}}_{si3}^{\iota }\!\!-\!2\cos \varpi _{sl}Q_{si3}^{\iota }+\mathbf He ({\mathcal {A}}_{fi}+{\mathcal {C}}_{fi})\), \(\varGamma _{s42}^{1}=B_{2i}^{\mathrm{T}}{\mathcal {Y}}_{i}^{\mathrm{T}}+{\mathcal {B}}_{2fi}^{\mathrm{T}}+{\bar{v}}_{1}{\mathcal {Y}}_{i}A_{i}+\varepsilon _{s}D_{2i}^{\mathrm{T}}C_{i}\), and \(\varGamma _{s42}^{2}=B_{2i}^{\mathrm{T}}{\mathcal {Y}}_{i}^{\mathrm{T}}+{\mathcal {B}}_{2fi}^{\mathrm{T}}+{\bar{v}}_{1}{\mathcal {A}}_{fi}+{\bar{v}}_{2}{\mathcal {C}}_{fi}\).
Proof
It is clear, from Lemma 2, that the conditions (22)–(23) guarantee the system (7) can be with a FFS \(H_{-}\)index \(\beta \). Expanding the inequality (22), the condition (32) can be easily derived. Further, we will focus on linearizing the inequality (23), which can be transformed into
where \(\mathbb {J}_{si}^{\iota }=\left[ \begin{array}{cc}{\mathfrak {J}}_{i1}^{\iota }&{} {\mathfrak {J}}_{si2}^{\iota }\\ 0 &{} I\end{array}\right] \), and then it can be equivalent to
by applying Finsler’s Lemma [18], where \({\mathcal {X}}_{1i}\) is the introduced slack matrix and \(v_{1}\) is a given scalar. And then, the above inequality can be transformed into
where
Exploiting Finsler’s Lemma again, (36) is equivalent to
where \({\mathcal {X}}_{2i}\) is the additional slack matrix. Further, the above inequality can be rewritten into
where \(\varGamma _{ss}^{2}={\mathrm{diag}}\left\{ \varGamma _{ss}^{1}+{\mathrm{diag}}\{0,\ {\mathfrak {V}}_{si}^{{\iota {\mathrm{T}}}}\varPi _{si}^{\iota }{\mathfrak {V}}_{si}^{\iota },\ 0 \}, -\varOmega _{s}^{''}\right\} \). Utilizing the same preceding method adopted above, the inequality (38) is equivalent to
where \({\mathcal {X}}_{3i}\) is the slack matrix introduced by Finsler’s lemma.
Without loss of generality, decomposing the matrices \({\mathcal {X}}_{1i}\), \({\mathcal {X}}_{2i}\) and the vectors \(v_{1}\), \(v_{2}\) into the form of \({\mathcal {X}}_{1i}=\left[ \begin{array}{cc}{\mathcal {Y}}_{i} &{} {\mathcal {N}}_{i}\\ {\mathcal {M}}_{i} &{} {\mathcal {N}}_{i}\end{array}\right] \), \({\mathcal {X}}_{2i}=\left[ \begin{array}{c}{\mathcal {G}}_{i} \\ {\mathcal {G}}_{i} \end{array}\right] \), and \(v_{1}=\left[ \begin{array}{cc}{\bar{v}}_{1}&0 \end{array}\right] \), \(v_{2}=\left[ \begin{array}{cc}{\bar{v}}_{2}&0 \end{array}\right] \). We expand the left part of equation (37) and rewrite it into the sum form of two parts. One part is the items with \(\varrho _{\iota }\), and the other is the left items without \(\varrho _{\iota }\). Recalling the fact of \(\varrho _{\iota }^{\mathrm{T}}\varrho _{\iota }\le I\), applying the Lemma 3, and defining the new variables
the condition (33) can be derived. The proof is completed. \(\square \)
Remark 8
Theorem 1 has presented the conditions to capture the LF stochastic \(H_{-}\)index. From Lemma 2, the conditions ensuring the desired MF and HF stochastic \(H_{-}\) indices can be easily derived by utilizing different \(\gimel \) and following the same proof process of Theorem 1.
Theorem 2
The system (7) is SS and with a prescribed \({\mathcal {H}}_{\infty }\) performance \(\gamma \), \(\gamma >0\), to \(\omega (k)\) if there exist matrices \(P_{i\imath }^{{\iota {\mathrm{T}}}}=P_{i\imath }^{\iota }=\left[ \begin{array}{cc}P_{i1\imath }^{\iota } &{} *\\ P_{i2\imath }^{\iota } &{} P_{i3\imath }^{\iota }\end{array}\right] >0\), \({\mathcal {Y}}_{i}\), \({\mathcal {M}}_{i}\), \({\mathcal {N}}_{i}\), \({\mathcal {G}}_{i}\), \({\mathcal {X}}_{3i}\), \({\mathcal {A}}_{fi}\), \({\mathcal {B}}_{1fi}\), \({\mathcal {B}}_{2fi}\), \({\mathcal {C}}_{fi}\), \({\mathcal {D}}_{fi}\) and scalars \(\delta _{\kappa i}^{\iota }\) and \(\varepsilon \) such that
hold \(\forall i\in \mathbb {S}\), \(\kappa =1,2,\ldots ,{\mathfrak {K}}\), and \(\iota =0,1\), where
Proof
Lemma 1 has presented the conditions to guarantee the SS and desired \({\mathcal {H}}_{\infty }\) performance to \(\omega (k)\). Equation (41) can be derived directly from (12). Further, we rewrite the inequality (13) into
where \(\mathbb {J}_{i}^{\iota }=\left[ \begin{array}{cc}{\mathfrak {J}}_{i1}^{\iota }&{} {\mathfrak {J}}_{i2}^{\iota }\\ 0 &{} I\end{array}\right] \), and then it can be equivalent to
from Finsler’s Lemma. We go on to split the above inequality into the form of
where
Then, utilizing Finsler’s Lemma again, one has (45) is equivalent to
Subsequently, for the item of \({\mathfrak {V}}_{i}^{{\iota {\mathrm{T}}}}\varPi _{i}^{\iota }{\mathfrak {V}}_{i}^{\iota }\), we adopt the same dealing method with the proof for Theorem 1, the condition (42) can be easily achieved. The proof is completed. \(\square \)
Further from Corollaries 1–2, following the similar route to prove Theorem 1 and choosing relative system matrices, the linear and solvable conditions can be derived, which are given in the following two theorems.
Theorem 3
For the system (7) in fault-free case, i.e., \(\varrho _{\iota }=I\) and \(\epsilon =0\), it is with a prescribed LF stochastic \({\mathcal {H}}_{\infty }\) performance \(\gamma _{d}\), \(\gamma _{d}>0\), to s(k) if there exist matrices \(P_{di\imath }^{{\iota {\mathrm{T}}}}=P_{di\imath }^{\iota }=\left[ \begin{array}{cc}P_{di1\imath }^{\iota } &{} *\\ P_{di2\imath }^{\iota } &{} P_{di3\imath }^{\iota }\end{array}\right] >0\), \(Q_{di\imath }^{{\iota {\mathrm{T}}}}=Q_{di\imath }^{\iota }=\left[ \begin{array}{cc}Q_{di1\imath }^{\iota } &{} *\\ Q_{di2\imath }^{\iota } &{} Q_{di3\imath }^{\iota }\end{array}\right] >0\), \({\mathcal {Y}}_{i}\), \({\mathcal {M}}_{i}\), \({\mathcal {N}}_{i}\), \({\mathcal {G}}_{i}\), \({\mathcal {X}}_{3i}\), \({\mathcal {A}}_{fi}\), \({\mathcal {B}}_{1fi}\), \({\mathcal {B}}_{2fi}\), \({\mathcal {C}}_{fi}\), \({\mathcal {D}}_{fi}\) and scalars \(\delta _{d\kappa i}^{\iota }\) such that the following inequalities
hold for all \(i\in \mathbb {S}\), \(\kappa =1,2,\ldots ,{\mathfrak {K}}\), and \(\iota =0\), where
with \(\varGamma _{d22}^{1}={\mathcal {P}}_{di1}^{\iota }\!\!-\!2\cos \varpi _{sl}Q_{di1}^{\iota }+\mathbf He ({\mathcal {Y}}_{i}A_{i}+{\mathcal {B}}_{1fi}C_{i})\), \(\varGamma _{d22}^{2}={\mathcal {P}}_{di2}^{\iota }\!\!-\!2\cos \varpi _{sl}Q_{di2}^{\iota }+{\mathcal {M}}_{i}A_{i}+{\mathcal {B}}_{1fi}C_{i}+{\mathcal {A}}_{fi}^{\mathrm{T}}+{\mathcal {C}}_{fi}^{\mathrm{T}}+{\mathcal {D}}_{fi}C_{i}\), \( \varGamma _{d22}^{3}={\mathcal {P}}_{di3}^{\iota }\!\!-\!2\cos \varpi _{sl}Q_{di3}^{\iota }+\mathbf He ({\mathcal {A}}_{fi}+{\mathcal {C}}_{fi})\), and \(\varGamma _{d32}^{1}=B_{2i}^{\mathrm{T}}{\mathcal {Y}}_{i}^{\mathrm{T}}+D_{2i}^{\mathrm{T}}{\mathcal {B}}_{1fi}^{\mathrm{T}}+{\mathcal {B}}_{2fi}^{\mathrm{T}}+D_{2i}^{\mathrm{T}}{\mathcal {D}}_{fi}^{\mathrm{T}}\).
Theorem 4
For the system (7) in faulty case, it is with a prescribed LF stochastic \(H_{-}\)index \(\beta _{f}\), \(\beta _{f}>0\), to f(k) if there exist matrices \(P_{fi\imath }^{{\iota {\mathrm{T}}}}=P_{fi\imath }^{\iota }=\left[ \begin{array}{cc}P_{fi1\imath }^{\iota } &{} *\\ P_{fi2\imath }^{\iota } &{} P_{fi3\imath }^{\iota }\end{array}\right] >0\), \(Q_{fi\imath }^{{\iota {\mathrm{T}}}}=Q_{fi\imath }^{\iota }=\left[ \begin{array}{cc}Q_{fi1\imath }^{\iota } &{} *\\ Q_{fi2\imath }^{\iota } &{} Q_{fi3\imath }^{\iota }\end{array}\right] >0\), \({\mathcal {Y}}_{i}\), \({\mathcal {M}}_{i}\), \({\mathcal {N}}_{i}\), \({\mathcal {G}}_{i}\), \({\mathcal {X}}_{3i}\), \({\mathcal {A}}_{fi}\), \({\mathcal {B}}_{1fi}\), \({\mathcal {B}}_{2fi}\), \({\mathcal {C}}_{fi}\), \({\mathcal {D}}_{fi}\) and scalars \(\delta _{f\kappa i}^{\iota }\) and \(\varepsilon _{f}\) such that
hold \(\forall i\in \mathbb {S}\), \(\kappa =1,2,\ldots ,{\mathfrak {K}}\), and \(\iota =1\), where
with \(\varGamma _{f22}^{1}={\mathcal {P}}_{fi1}^{\iota }\!\!-\!2\cos \varpi _{fl}Q_{fi1}^{\iota }+\mathbf He ({\mathcal {Y}}_{i}A_{i})+\varepsilon _{f}C_{i}^{\mathrm{T}}C_{i}\), \(\varGamma _{f22}^{2}={\mathcal {P}}_{fi2}^{\iota }\!\!-\!2\cos \varpi _{fl}Q_{fi2}^{\iota }+{\mathcal {M}}_{i}A_{i}+{\mathcal {A}}_{fi}^{\mathrm{T}}+{\mathcal {C}}_{fi}^{\mathrm{T}} \), and \(\varGamma _{f22}^{3}={\mathcal {P}}_{fi3}^{\iota }\!\!-\!2\cos \varpi _{fl}Q_{fi3}^{\iota }+\mathbf He ({\mathcal {A}}_{fi}+{\mathcal {C}}_{fi})\).
Remark 9
It is noticed from the Theorems 1–4 that some given vectors \({\bar{v}}_{1}\) and \({\bar{v}}_{2}\) are needed to derive the linear solvable conditions, and of course, different values will result in different performance levels. Particularly, but without loss of generality, it can be chosen as a unit vector.
Now, with the aid of the derived conditions in Theorems 1–4, a set of feasible solutions to the proposed design scheme can be obtained by the optimization problem stated as follows for acceptable \(\gamma \) and \(\gamma _{d}\):
where \(a_{\mathrm{s}}\) and \(a_\mathrm{f}\) are given weighting scalars subjecting to \(a_{\mathrm{s}}+a_\mathrm{f}=1\). After getting the solutions, the FD filter gains can be calculated according to (40).
The following algorithm presents the process to solve the above optimization problem.
Algorithm 1
- Step 1.:
-
Solving the following optimization problems to obtain the optimal values of the robustness performance indices \(\gamma \) and \(\gamma _d\),
$$\begin{aligned} \begin{array}{ll} &{} \min \quad \gamma \\ \mathrm{s.t.} &{} (41),(42),i\in \mathbb {S},\kappa =1,2,\ldots ,{\mathfrak {K}},\iota =0,1\\ \end{array} \\ \begin{array}{ll} &{} \min \quad \gamma _{d} \\ \mathrm{s.t.} &{} (47),(48),i\in \mathbb {S},\kappa =1,2,\ldots ,{\mathfrak {K}},\iota =0\\ \end{array} \end{aligned}$$ - Step 2.:
-
For the \(\gamma \) and \(\gamma _d\) derived in Step 1, solving (51). If it is solvable, break. Otherwise go to Step 3.
- Step 3.:
-
Increasing the values of \(\gamma \) and \(\gamma _d\) steply and separately, then solving (51). If it is solvable, break. Otherwise cycling in this step.
Remark 10
Normally, the scalars \(a_{\mathrm{s}}\) and \(a_\mathrm{f}\) are determined empirically according to the fault type that frequently occurred. For example, if the faults with large amplitude always occur, they can be chosen as \(a_{\mathrm{s}}=0.5\) and \(a_\mathrm{f}=0.5\). And if the faults with small amplitude always occur, we should increase the value of \(a_{\mathrm{s}}\) to strengthen the FD ability.
3.3 Detection threshold
After generating the residual signals, the last step is to determine the threshold and construct the detection logic. In this paper, the threshold \(J_{\mathrm{th}}\) will be chosen as
where \(J_\mathrm{{r}}(\tau )\) represents the average energy of the residual over the time window \([k_{0},k_{\tau }]\), which is denoted by
And then the detection logic can be made through
Remark 11
It should be emphasized that \(J_{\mathrm{th}}\) is just an ideally choice. In practice, it should be adjusted by \({\bar{J}}_{\mathrm{th}}=J_{\mathrm{th}}+\Delta J\), where \({\bar{J}}_{\mathrm{th}}\) means the adopted value, and \(\Delta J\) represents the worst-case value of systems related to dynamic inversion, such as parasitism in power systems. Furthermore, it is different for diverse systems, which do not cause \(J_\mathrm{{r}}(\tau )\) to exceed \({\bar{J}}_{\mathrm{th}}\).
4 Simulation examples
Here, a simulation example will be presented to validate the effectiveness of the proposed FD method. Considering the highly maneuverable aircraft technology (HiMAT) vehicle given in [32], choosing two operating points within the flight envelopes, whose trim conditions are shown in Table 2, as the switching modes, and the sampling period \(T=1s\), a switched system model under the reference input s(k) can be derived as the form of
where \(x(k)=[x_{1}(k)\quad x_{2}(k)]\), which represents the attack angle (deg) and the pitch rate (deg/s), respectively. The corresponding system matrices are
In addition, it is assumed that the derived system is switched under the direction of nonhomogeneous Markov chain with \(\mathbb {S}=\{1,2\}\) and TP been in a polytope, whose vertices are
Further, \(o_{\iota }(k)\), \(\iota =1,2,3\) are assumed to be as \(o_{1}(k)=0.7\), \(o_{2}(k)=0.3\cos ^{2}(k)\), \(o_{3}(k)=0.3\sin ^{2}(k)\). And thus, one has \(\varLambda (k)=0.1\varLambda ^{1}+0.3\cos ^{2}(k)\varLambda ^{2}+0.3\sin ^{2}(k)\varLambda ^{3}\).
Next, for the sake of illustrating the system performances can be influenced by signal frequency, solving the optimization problem (51) with \(\gamma =\gamma _{d}=1\) under \(a_{1}=0.8\) and \(a_{2}=0.2\), the derived indices \(\beta \) and \(\beta _{f}\) for different \(\varpi _{sl}\) and \(\varpi _{fl}\) are shown in Table 3.
From which, it is not difficult to see that the signal frequency affects the system performance definitely. And the signals in high frequency results in worse performance. Further, we are going to show the mutual restrictions between each performance by solving the optimization problem (51) under different situations with different \(\gamma \) and \(\gamma _{d}\) when \(a_{1}=0.8\) and \(a_{2}=0.2\) for \(\varpi _{sl}=\varpi _{fl}=0\). The results are shown in Table 4.
One can see, from Table 4, that the larger \(\gamma \) and \(\gamma _{d}\) are, the larger \(\beta \) and \(\beta _{f}\) can be obtained. That means it is contrary between the sensitivity performance \(\beta \), \(\beta _{f}\) and the attenuation performance \(\gamma \), \(\gamma _{d}\), and they cannot achieve the optimal identification simultaneously. Thus, one should find an equilibrium point between them when designing the practical FD systems.
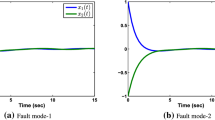
It should be stated here that this is the first attempt to develop the FD method in a finite frequency domain for nonhomogeneous MJSs with nonlinearities, especially with sensor failures. Though there are some results concerned on the finite frequency FD method, they are proposed for linear systems. Thus in this section, no comparison can be done meaningfully. In the following, to show the effectiveness of the proposed method, the system will be simulated for acceptable robustness level, i.e., \(\gamma =\gamma _{d}=1\) when \(a_{1}=0.8\) and \(a_{2}=0.2\). In such situation, from Table 4, it is shown that \(\beta =0.3072\), \(\beta _{f}=0.3329\). The filter gains are not listed here. Further, for the \(\varLambda (k)\) given above, a series of sequence \(\alpha _{k}\) can be produced. Without loss of generality, the one shown in Fig. 1 will be adopted in this simulation.
Furthermore, the model given in [33] will be utilized to generate the wind gust signal as the disturbance \(\omega (k)\), i.e., \(\omega (s)={\mathbf {W}}(s)d\), where d is Gaussian white noise and \({\mathbf {W}}(s)\) represents a random vertical gust process with the following form
where \(U_{0}\) means the trim velocity (fps) of the vehicle, \(\sigma _{w}\) denotes the rms vertical gust velocity (fps), \(L_{w}\) represents the characteristic length of turbulence (ft). One usual thunderstorm is with the value of \(\sigma _{w}=23\) fps, and \(L_{w}=1900\) ft. Within the above sequence \(\alpha _{k}\) and wind disturbance \(\omega (k)\), the system will be simulated under the following four fault cases, which are, respectively, corresponded to the fault types that (5) covered.
Case 1. The outage fault with parameters \(\varrho =0\) and \(f=0\) occurred when \(30<k<70\). The residual signal and its evaluation function are shown in Fig. 2. From the figure, one can see \(J_\mathrm{{r}}(\tau )>J_{\mathrm{th}}\) when \(k=32\). That is to say, the occurred fault can be detected two steps after it occurred, which shows the effectiveness of the developed FD method.
Case 2. The loss of effectiveness fault under the situation of \(\varrho =0.8\) and \(f=0\) occurred when \(30<k<70\). The residual signal and its evaluation function are given in Fig. 3. It is shown, from which, that the \(J_\mathrm{{r}}(\tau )\) exceeded the threshold \(J_{\mathrm{th}}\) when \(k=32\). It means the fault can be detected effectively and timely by the proposed FD method.
Case 3. The stuck fault with parameters \(\varrho =0\) and \(f=1\) occurred on the sensor when \(30<k<70\). Figure 4 presents the residual and its evaluation function. It is clear that the occurred fault could be detected timely since \(J_\mathrm{{r}}(\tau )>J_{\mathrm{th}}\) when \(k=32\).
Case 4. The drift fault under the case of \(\varrho =1\) and \(f=0.5\) occurred on the sensor when \(30<k<70\). The residual signal and its evaluation function are given in Fig. 5. It is shown that \(J_\mathrm{{r}}(\tau )\) exceeds the threshold \(J_{\mathrm{th}}\) at \(k=32\), which indicates the occurred fault can be detected successfully by the investigated FD approach.
In conclusion, from the simulation results for the above four faulty cases, we can see that even though there is a small time delay of detection after the fault occurred, the proposed FD method works well for every kind of fault that the model (5) covers. Such results exhibit the effectiveness of the proposed FD strategy.
5 Conclusion
In this study, the finite frequency FD problem has been presented for a class of nonhomogeneous MJSs with nonlinearities and sensor failures. Firstly, a novel model was presented to describe the sensor failures, and the FD scheme has been proposed for such kinds of sensor faults with the aid of finite frequency stochastic performance indices. Then, sufficient conditions to capture the desired performances were developed in terms of linear matrix inequalities, in which the nonlinearities and nonhomogeneous Markov switching were dealt into solvable items. Subsequently, the filter gains were characterized by solving an optimization problem. Finally, an application to the HiMAT vehicle has been presented to show the effectiveness of the proposed method. In addition, when the systems experience time delays as the types in [34,35,36] when transferring the information, the research of the FD method in finite frequency domain for such class of systems will be our future work.
References
Moon, J., Basar, T.: Risk-sensitive control of Markov jump linear systems: caveats and difficulties. Int. J. Control Autom. Syst. 15(1), 462–467 (2017)
Park, J.H., Shen, H., Chang, X.H., Lee, T.H.: Recent Advances in Control and Filtering of Dynamic Systems with Constrained Signals. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96202-3
Shi, P., Yin, Y.Y., Liu, F., Zhang, J.H.: Robust control on saturated Markov jump systems with missing information. Inf. Sci. 265(1), 123–138 (2014)
Wu, Z.-G., Shi, P., Shu, Z., Su, H.Y., Lu, R.Q.: Passivity-based asynchronous control for Markov jump systems. IEEE Trans. Autom. Control 62(4), 2020–2025 (2017)
Tao, J., Wu, Z.-G., Su, H.Y., Wu, Y.Q., Zhang, D.: Asynchronous and resilient filtering for Markovian jump neural networks subject to extended dissipativity. IEEE Trans. Cybern. https://doi.org/10.1109/TCYB.2018.2824853 (2018)
Shen, Y., Wu, Z.-G., Shi, P., Shu, Z., Karimi, H.R.: H-infinity control of Markov jump time-delay systems under asynchronous controller and quantizer. Automatica 99, 352–360 (2019)
Shen, H., Park, J.H., Wu, Z.G.: Finite-time synchronization control for uncertain Markov jump neural networks with input constraints. Nonlinear Dyn. 77, 1709–1720 (2014)
Qi, W., Kao, Y., Gao, X.: Passivity and passification for stochastic systems with Markovian switching and generally uncertain transition rates. Int. J. Control Autom. Syst. 15, 2174–2181 (2017)
Yao, X.M., Guo, L., Wu, L.G., Dong, H.R.: Static anti-windup design for nonlinear Markovian jump systems with multiple disturbances. Inf. Sci. 418(24), 169–183 (2017)
Ma, S.P., Boukas, E.K., Chinniah, Y.: Stability and stabilization of discrete-time singular Markov jump systems with time-varying delay. Int. J. Robust Nonlinear Control 20(5), 531–543 (2010)
Zhong, X.N., He, H.B., Zhang, H.G., Wang, Z.S.: Optimal control for unknown discrete-time nonlinear Markov jump systems using adaptive dynamic programming. IEEE Trans. Neural Netw. Learn. Syst. 25(12), 2141–2155 (2014)
Lam, J., Shu, Z., Xu, S., Boukas, E.K.: Robust \({\cal{H}}_{\infty }\) control of descriptor discrete-time Markovian jump systems. Int. J. Control 80, 374–385 (2007)
Shi, P., Li, F.B.: A survey on Markovian jump systems: modeling and design. Int. J. Control Autom. Syst. 13(1), 1–16 (2015)
Zhang, L.X., Boukas, E.K.: Stability and stabilization of Markovian jump linear systems with partly unknown transition probability. Automatica 45(2), 463–468 (2009)
Liu, X.H., Yu, X.H., Ma, G.Q., Xi, H.S.: On sliding mode control for networked control systems with semi-Markovian switching and random sensor delays. Inf. Sci. 337–338, 44–58 (2016)
Zhang, L.X.: \({\cal{H}}_{\infty }\) estimation for discrete-time piecewise homogeneous Markov jump linear systems. Automatica 45, 2570–2576 (2009)
Yin, Y.Y., Shi, P., Liu, F., Teo, K.L.: Filtering for discrete-time nonhomogeneous Markov jump systems witn uncertainties. Inf. Sci. 259(20), 118–127 (2014)
Li, X.-J., Yang, G.-H.: Fault detection in finite frequency domain for Takagi–Sugeno fuzzy systems with sensor faults. IEEE Trans. Cybern. 44(8), 1446–1458 (2014)
Zhao, D., Wang, Y.Q., Li, Y.Y., Ding, S.X.: \({\cal{H}}_{\infty }\) fault estimation for two-dimensional linear discrete time-varying systems based on Krein space method. IEEE Trans. Syst. Man Cybern. Syst. 48(12), 2070–2079 (2018)
Li, Y.Y., Karimi, H.R., Zhang, Q., Zhao, D., Li, Y.B.: Fault detection for linear discrete time-varying systems subject to random sensor delay: a Riccati equation approach. IEEE Trans. Circuits Syst. Regul. Pap. 65(5), 1707–1716 (2018)
Park, J.H., Mathiyalagan, K., Sakthivel, R.: Fault estimation for discrete-time switched nonlinear systems with discrete and distributed time varying delays. Int. J. Robust Nonlinear Control 26, 3755–3771 (2016)
Du, D., Xu, S.: Actuator fault detection for discrete-time switched linear systems with output disturbance. Int. J. Control Autom. Syst. 15, 2590–2598 (2017)
Wu, L.G., Yao, X.M., Zheng, W.X.: Generalized \({\cal{H}}_{2}\) fault detection for two-dimensional Markovian jump systems. Automatica 48(8), 1741–1750 (2012)
Meskin, N., Khorasani, K.: Fault detection and Isolation of discrete-time Markovian jump linear systems with application to a network of multi-agent systems having imperfect communication channels. Automatica 45(9), 2032–2040 (2009)
He, S.P., Liu, F.: Fuzzy model-based fault detection for Markov jump systems. Int. J. Robust Nonlinear Control 19(11), 1248–1266 (2009)
Dong, H.L., Wang, Z.D., Gao, H.J.: Fault detection for Markovian jump systems with sensor saturations and randomly varying nonlinearities. IEEE Trans. Circuits Syst. I Regul. Pap. 59(10), 2354–2362 (2012)
Iwasaki, T., Hara, S.: Generalized KYP lemma: unified frequency domain inequalities with design applications. IEEE Trans. Autom. Control 50(1), 41–59 (2005)
Wang, H., Yang, G.-H.: A finite frequency approach to filter design for uncertain discrete-time systems. Int. J. Adapt. Control Signal Process. 22, 533–553 (2008)
Wang, H., Yang, G.-H.: Integrated fault detection and control for LPV systems. Int. J. Robust Nonlinear Control 19, 341–363 (2009)
Yang, G.-H., Wang, H., Xie, L.H.: Fault detection for output feedback control systems with actuator stuck faults: a steady-state-based approach. Int. J. Robust Nonlinear Control 20, 1739–1757 (2010)
Long, Y., Park, J.H., Ye, D.: Transmission-dependent fault detection and isolation strategy for networked systems under finite capacity channels. IEEE Trans. Cybern. 47(8), 2266–2278 (2017)
Hou, Y.Z., Dong, C.Y., Wang, Q.: Adaptive control scheme for linear uncertain switched systems. In: AIAA Guidance, Navigation and Control Conference and Exhibit, Honolulu, Hawaii (2008)
Aouf, N., Boulet, B., Botez, R.: \({\cal{H}}_{2}\) and \({\cal{H}}_{\infty }\)-optimal gust load alleviation for a flexible aircraft. In: Proceeding of the American Control Conference, Chicago, Illinois, pp. 1872–1876 (2000)
Fang, M.: Synchronization for complex dynamical networks with time delay and discrete-time information. Appl. Math. Comput. 258(1), 1–11 (2015)
Que, H.Y., Fang, M., Wu, Z.-G., Su, H.Y., Huang, T.W., Zhang, D.: Exponential synchronization via aperiodic sampling of complex delayed networks. IEEE Trans. Syst. Man Cybern. Syst. https://doi.org/10.1109/TSMC.2018.2858247 (2018)
Zhao, D., Ding, S.X., Karimi, H.R., Li, Y.Y., Wang, Y.Q.: On robust Kalman filter for two-dimensional uncertain linear discrete time-varying systems: a least squares method. Automatica 99, 203–212 (2019)
Acknowledgements
This work was supported by 2017 Yeungnam University Research Grant. Also, the work of Y. Long and D. Ye was supported by NSFC (Nos. 61773187, 61773097), the Fundamental Research Funds for the Central Universities (No. N160402004).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
All the authors declare that there are no potential conflicts of interest and approval of the submission.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Long, Y., Park, J.H. & Ye, D. Finite frequency fault detection for a class of nonhomogeneous Markov jump systems with nonlinearities and sensor failures. Nonlinear Dyn 96, 285–299 (2019). https://doi.org/10.1007/s11071-019-04790-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-019-04790-4