Thermo-elastic buckling and post-buckling analysis of functionally graded thin plate and shell structures

Abstract

In this paper, we extend the Kirchhoff–Love model to thermal buckling and post-buckling analysis of functionally graded structures. The kernel idea of the proposed model consists of the consideration of large displacements and finite rotation to accurately model the thermal effects on buckling and post-buckling behavior of such structures. Both uniform and nonuniform temperature distributions are considered. Material properties of the FG structures are graded in the thickness direction and assumed to obey a power law distribution of the volume fraction of the constituents. The effectiveness and usefulness of the proposed model are highlighted through different numerical examples, and the effects of the volume fraction exponent, thermal loads, length-to-thickness ratio, boundary conditions and geometrical parameters on the buckling and post-buckling behavior of FGM structures are also examined.

1 Introduction

Buckling and post-buckling characteristics are one of the major design criteria for plates/panels for their optimal usage. Therefore, it is important to study the buckling and post-buckling characteristics of such structures under thermal loading for accurate and reliable design. Thin plates and shells are often used in many engineering applications such as aerospace, civil engineering and automobiles and notably curved panels, which are gained attention in rockets and hypersonic airplane where the thermal loading is a key factor. Furthermore, thermal stresses developed due to elevated temperature will lead to buckling failure of these slender structural members. Hence, the introduction of multifunctional materials which work under high-temperature loadings is one of the most challenging issues for both industrial and scientific communities. Recently, functionally graded materials known as (FGMs) have been regarded as a convenient strategy to handle thermal buckling and post-buckling problems due to their superior mechanical and thermal properties and their lightweight compared to other conventional engineering materials and structures. Typically, FGMs are made from a mixture of ceramic and metal and they are characterized by a gradual variation in their mechanical and thermal properties from one surface to the other. They have many gained applications in rocket engine components, space plan body, nuclear reactor components, first wall of fusion reactor, engine components, turbine blades and other engineering and technological applications. A detailed discussion on their design, processing and applications can be found in Koizumi [39, 40] Suresh and Mortensen [59] and Miyamoto et al. [47]. Equally, they present a good way of heat resistance such that they are able to withstand ultra-high temperature and extremely large thermal gradients. Such kinds of properties motivated many researchers to choose them as a promising candidates for multifunctional materials, especially that the material constitutive law is a key factor in the modeling process of shell analysis [5, 15, 25,26,27, 33, 34, 46, 69, 70, 72, 73]. On the other hand, and with the rapid progress of computer methods, the finite element method (FEM) is now the most widely used numerical tool, which constitutes an efficient method to model as well as to analyze the mechanical and thermal behavior of various shapes of structures. In particular, the modeling of thermal behavior of shell structures has attracted, over the past decades, the attention of many researchers using different FEM models. The first model, known as classical plate theory (CPT), is established based on the Kirchhoff–Love assumptions. The second model, labeled first-order shear deformation theory (FSDT), is developed by Mindlin, and it incorporates the effect of shear deformations. The third model, known as high-order shear deformation theory (HSDT), includes the Reddy’s and refined kinematic models and takes into account the parabolic distribution of transverse shear stresses. Each model allows a vast range of analysis, and according to the type of the studied structure (thin, moderately thick or thick) and its applicability domain (linear, nonlinear, static, dynamic, free vibration, buckling or post-buckling), one can choose the appropriate model to assess the desired investigation. The detailed information on these models can be found in the literature [10, 44, 54, 58, 62, 68]. The accuracy and computational costs of such models are still a great concern for many researchers, especially if the shell structure undergoes large displacements and finite rotations. For low computational effort and accurate results, the classical model constitutes a suitable choice favored by its simple implementation in the most finite element codes. A comparison between two-dimensional and three-dimensional finite element procedures, classical and refined generalized quadrature methods and analytical solution was presented in Tornabene et al. [62] for the free vibration investigations of composite cylindrical and spherical shells. Subsequently, a combination of the shear deformation theory and the modified couple stress theory was proposed by Civalek et al. to study the thermal vibration of microbeams [2] and nanobeams [13]. In view of this, the study of thermal buckling and post-buckling behavior of FGM structures has received, recently, a considerable attention in the literature. The major works related to this subject are briefly presented in the next paragraph.

Javaheri and Eslami provided exact solutions for thermal buckling of FGM plates using the CPT theory [36] or the HSDT theory [24, 37]. Also, an analytical investigation of thermal post-buckling of FG plates is presented by Shen [56] using the HSDT theory. Furthermore, many investigations dealing with thermal buckling and post-buckling of FG plates using the numerical procedure can be reported in Park and Kim [51], Zhao et al. [77], Tran et al. [65], Kandasamy et al. [41], Van Do and Lee [66], Zhang [75], Duc and Tung [19], Duc and Cong [16]. For the sake of completeness, it should be mentioned that many alternative numerical approaches, such as the generalized differential quadrature method or the isogeometric analysis, are applied successfully in the recent literature for shell structures under thermal loadings with complex shapes and based on high-order models [48, 67]. Although there are many researches conducted on thermal buckling and post-buckling of FGM plates, the number of studies related to this subject for FGM skew plates and notably for curved panels is rather limited. The thermal and mechanical buckling and post-buckling responses of skew plates using finite element procedure were obtained by Prabhu and Durvasula [52], Ganapathi and Prakash [30], Ganapathi et al. [31], Prakash et al. [53] and Jaberzadeh et al. [35]. Thermal buckling of cylindrical panels has been studied by Bhagat et al. [8], Bhagat and Jeyaraj [7]. Shen [57] obtained the analytical solutions for thermal post-buckling of FG cylindrical panels using the HSDT theory. In addition, Duc and his co-authors presented several works on the analysis of the nonlinear behavior of shells in thermal environment [17, 18, 21]. From some publications of Duc et al. [20, 22, 23], the nonlinear static and dynamic response of FG cylindrical panels in thermal environment can be improved by using stiffening components. Also, Anh el al. studied the nonlinear buckling response of thin FGM annular spherical shells subjected to external pressure and thermal loads [3]. Akbari et al. [1] studied the thermal buckling of FG conical shells using the classical shell theory. In [49], Nguyen et al. also studied the nonlinear response of carbon nanotube-reinforced composite truncated conical shells in thermal environment. Chan el al. [11] took nonlinearity into account and evaluated the dynamic response and vibration of FG truncated conical panel in thermal environments. Panda and his collaborators [43, 50] derived a finite element solutions of the buckling and post-buckling responses of FG shell panels in thermal environment. In addition, Liew et al. presented a finite element procedure to investigate the thermal buckling [76] and the post-buckling [45] behavior of the FGM cylindrical panels. Arefi et al. [4] analyzed the static behavior of a FG-CNTRC cylindrical pressure vessels subjected to pressure and thermal loadings by using the FSDT theory. Recently, Trabelsi et al. [63, 64] investigated the thermal buckling and post-buckling of FG plates and shells using a modified FSDT theory. As can be remarked from this report of the open literature, most of the papers used the FSDT or HSDT theories to predict thermal buckling and post-buckling behavior of FGM structures. Even these theories provide accurate results, and they require generally a prohibitive computational time due to the introduction of shear correction factors in FSDT theory and various kinematics variables in HSDT theory. So, to analyze thin structures, the Kirchhoff shell theory constitutes a suitable choice which can assure notably the compromise between good accuracy and low computational costs. Motivated by its simplicity and usefulness regarding thin shell structures, we have performed, in the present paper, its applicability for buckling and post-buckling analysis of FGM square, skew plates and curved panels under thermal loadings in the sense of nonlinear problem. Uniform and nonuniform temperature distributions through the thickness direction are considered. The material properties of FGM structures are determined via a power law distribution. Convergence studies and comparisons are carried out for the isotropic case in order to validate the efficiency of the present model. Then, parametric studies are conducted leading hence to perform the effects of power law index, length-to-thickness ratios, aspect ratios, thermal fields, boundary conditions on thermal buckling and post-buckling behavior of FGM structures.

2 Modeling of FGM structures

2.1 Effective material properties

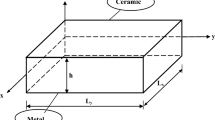
FGM structures are typically made from a mixture of ceramic and metal constituents. In fact, the ceramic phase provides the high temperature resistance due to its low thermal conductivity, while the ductile metal phase prevents fracture caused by stresses due to high temperature gradient in a very short period of time. Furthermore, the manufacturing process of a mixture of ceramic and metal constituents with a continuous variation in the volume fraction can be easily obtained. As a result, the volume fractions of the ceramic $V_{{\text {c}}}$ and metal $V_{{\text {m}}}$ phases can be expressed, according to a power law distribution as follows [55]:

$$V_{{\text {c}}}(z)=\left( \frac{z}{h}+\frac{1}{2}\right) ^p,\quad V_{{\text {c}}} + V_{{\text {m}}} =1.$$

(1)

where z is the thickness coordinate ($z\in [-h/2,h/2]$), h is the total thickness of the shell structure and p is the power law index which takes values greater than or equal to zero. The effective material properties of FGM structures, such as the modulus of elasticity E, the coefficient of thermal expansion $\alpha$ and the thermal conductivity K, which varies in the thickness direction z, can be expressed as:

$$P(T,z)= (P_{{\text {c}}}-P_{{\text {m}}}) V_{{\text {c}}}(z) + P_{{\text {m}}}.$$

(2)

where $P_{{\text {m}}}$ and $P_{{\text {c}}}$ denote the effective material properties of the metal and ceramic phases, respectively. According to the distribution of the temperature through the thickness, different profiles of temperature are considered as shown in Fig. 1.

Fig. 1

Temperature distributions through the thickness direction

The temperature dependence of the material properties of the metal or ceramic phases is given by:

$$P(T)=P_0 \left( P_{-1} T^{-1} + 1 + P_1 T + P_2 T^2 + P_3 T^3 \right) ,$$

(3)

where $P_0,P_{-1}, P_1, P_2$ and $P_3$ are the temperature coefficients and T is the temperature parameter in K. It should be noted that the Young’s modulus E and the thermal expansion coefficient $\alpha$ are considered as temperature dependent, while the Poisson’s ratio $\nu$ is assumed to be constant.

2.2 Uniform, nonuniform and linear temperature rises through the thickness direction

In order to accurately describe the effect of temperature rise through the thickness, uniform and nonuniform distributions are considered, in this investigation.

2.2.1 Uniform temperature rise

For an uniform distribution of the temperature rise, the initial temperature $T_i$ is uniformly raised to a final temperature $T_f$ for which the shell structure is buckled. Hence, the critical buckling temperature rise can be given by the following expression:

$$\Delta T_{{\text {cr}}}=T_f-T_i,$$

(4)

2.2.2 Nonuniform and linear temperature rises

In the case of nonuniform temperature distribution, the one-dimensional steady-state equation of heat transfer is solved as:

$$\begin{array}{ll}\left\{ \begin{array}{ll} \frac{{\text {d}}}{{\text {d}}z} \left[ K(z)\frac{{\text {d}}T}{{\text {d}}z} \right] =0,&{} -h/2 \prec z \prec h/2\\ T= T_{{\text {c}}},&{} z=h/2\\ T= T_{{\text {m}}},&{} z=-h/2\\ \end{array}\right. \end{array},$$

(5)

K(z) is the thermal conductivity of the shell structure, and $T_{{\text {c}}}$ and $T_{{\text {m}}}$ denote the temperature changes at the ceramic and metal sides, respectively. Similar to the coefficients of Young’s modulus and thermal expansion, the coefficient of thermal conductivity can be also written as a power form in function of z coordinate:

$$K(z)= (K_{{\text {c}}}-K_{{\text {m}}})\left( \frac{z}{h}+\frac{1}{2}\right) ^p + K_{{\text {m}}}.$$

(6)

Equation (5) can be solved using the Gauss integration method as follows:

$$\begin{array}{l l}\left\{ \begin{array}{l l} T(z)=T_{{\text {m}}}+\Delta T \cdot \eta (z)\\ \Delta T=T_{{\text {c}}}-T_{{\text {m}}}\\ \eta (z)=\frac{\int ^{z}_{-h/2}\frac{{\text {d}}z}{K(z)}}{\int ^{h/2}_{-h/2}\frac{{\text {d}}z}{K(z)}}\\ \end{array}\right. \end{array},$$

(7)

where $T_{{\text {c}}}$ and $T_{{\text {m}}}$ refer to ceramic-rich surface and metal-rich surface, respectively, and $\eta (z)$ is evaluated, numerically, by the Gauss numerical integration procedure. It should be mentioned that the linear temperature rise is obtained as a particular case by setting $p=1$.

3 Governing equations

The extension of the Kirchhoff shell model to thermal buckling and post-buckling analysis of FGM structures with geometrical nonlinearity type is presented here. The kinematics of the shell is briefly described. The initial and the deformed configurations are denoted by $C_0$ and $C_t$, respectively.

3.1 Geometry and kinematics

The position vectors of any material point q within the shell body in both reference $C_0$ and current $C_t$ configurations using convective curvilinear coordinates ${\varvec{\xi }} =(\xi ^1,\xi ^2,\xi ^3=z)$ read:

$${\varvec{X}}_q(\xi ^1,\xi ^2,z)={\varvec{X}}_p(\xi ^1,\xi ^2)+ z {\varvec{D}}(\xi ^1,\xi ^2), z\in \left[ -\frac{h}{2},\frac{h}{2} \right] ,$$

(8)

$${\varvec{x}}_q={\varvec{x}}_p+z {\varvec{d}}.$$

(9)

where ${\varvec{X}}_p$ and ${\varvec{D}}$ denote the position vector of an arbitrary point p of the mean reference surface in the initial configuration $C_0$ and the initial shell vector, respectively. h is the thickness of the shell and ${\varvec{d}}$ represents the shell director vector.

As a result, the Green–Lagrangian strain tensor ${\varvec{E}}$ can be given as follows Dammak et al. [12]:

$$\begin{array}{l l} \left\{ \begin{array}{l l} E_{\beta \gamma }=e_{\beta \gamma }+ z \chi _{\beta \gamma }\\ 2 E_{\beta 3}= \gamma _{\beta }\\ \end{array}\right. \end{array},$$

(10)

$e_{\beta \gamma }, \chi _{\beta \gamma }$ and $\gamma _{\beta }$ represent the membrane, the bending and the shear strains, respectively. Their corresponding variations are given as indicated in Dammak et al. [12]. In matrix notation, these components are expressed as follows:

$${\varvec{e}}= \left[ \begin{array}{c c c} e_{11}\\ e_{22}\\ 2e_{12}\\ \end{array} \right] , \quad {\varvec{\chi }}= \left[ \begin{array}{c c c} \chi _{11}\\ \chi _{22}\\ 2\chi _{12}\\ \end{array} \right] ,\quad {\varvec{\gamma }}= \left\{ \begin{array}{r c l} \gamma _{1}\\ \gamma _{2}\\ \end{array} \right\} .$$

(11)

According to the Kirchhoff hypothesis, the transverse shear strains are vanished. This assumption is considered under integral form on the element boundaries [12].

3.2 Variational formulation

Finite element formulation is derived from the variational principle for which the weak form of equilibrium is given by:

$$G = \int _A\left( {\varvec{N}} \cdot \delta {\varvec{e}}+ {\varvec{M}} \cdot \delta {\varvec{\chi }} \right) {\text {d}}A - G_{{\text {ext}}}=0,$$

(12)

$\delta {\varvec{e}}$ and $\delta {\varvec{\chi }}$ represent the variations of the shell strains, and ${\varvec{N}}$ and ${\varvec{M}}$ represent the membrane and bending stress resultants. Their expressions are given as follows:

$${\varvec{N}}=\left[ \begin{array}{c c c} N^{11}\\ N^{22}\\ N^{12}\\ \end{array} \right] , \quad {\varvec{M}}=\left[ \begin{array}{c c c} M^{11}\\ M^{22}\\ M^{12}\\ \end{array} \right] .$$

(13)

The components of stress resultants ${\varvec{N}}$ and ${\varvec{M}}$ are given by:

$$(N^{\alpha _\beta }, M^{\alpha _\beta })=\int _{-h/2}^{h/2} (1,z) S^{\alpha _\beta }{\text {d}}z,(\alpha ,\beta )=(1,2).$$

(14)

where $S^{\alpha _\beta }$ are the components of the second Piola–Kirchhoff stress tensor. For the generalized resultant of stress ${\varvec{R}}$ and strain ${\varvec{\Sigma }}$ vectors, they can be written as follows:

$${\varvec{R}}=\left[ \begin{array}{c c} {\varvec{N}}\\ {\varvec{M}}\\ \end{array} \right] ,\quad {\varvec{\Sigma }}=\left[ \begin{array}{c c} {\varvec{e}}\\ {\varvec{\chi }}\\ \end{array} \right] .$$

(15)

Therefore, the weak form of equilibrium can be rewritten as:

$$G({\varvec{\Phi }}, \delta {\varvec{\Phi }})= \int _A \delta {\varvec{\Sigma }}^{{\text {T}}} \cdot {\varvec{R}} {\text {d}}A - G_{{\text {ext}}}({\varvec{ \Phi }}, \delta {\varvec{\Phi }})=0.$$

(16)

where ${\varvec{\Phi }}=({\varvec{u}},{\varvec{d}})$ contains the displacement and shell vectors. Furthermore, Eq. (16) reflects a geometrical nonlinear problem which can be solved using the Newton iterative algorithm. The consistent tangent operator for the Newton solution procedure can be constructed by the directional derivative of the weak form in the direction of the increment $\Delta {\varvec{\Phi }}=(\Delta {\varvec{u}},\Delta {\varvec{d}})$. For geometrically nonlinear analysis, it is convenient to divide the tangent operator into geometric and material parts, denoted by $D_G G \cdot \Delta {\varvec{\Phi }}$ and $D_M G \cdot \Delta {\varvec{\Phi }}$, respectively, as follows:

$${D_G} \cdot \Delta {\varvec{\Phi }}={D_G} G \cdot \Delta {\varvec{ \Phi }}+{D_M} G \cdot \Delta {\varvec{\Phi }}$$

(17)

3.3 Material part

The variations in the generalized resultant of stress ${\varvec{ R}}$ with maintaining a constant strain lead to the definition of the material part of the tangent operator, which can be expressed as follows:

$${D_M} G \cdot \Delta {\varvec{\Phi }}= \int _A (\delta {\varvec{ \Sigma }}^{{\text {T}}} \cdot \Delta {\varvec{R}}) {\text {d}}A,$$

(18)

As a result, the material part of tangent modulus can be rewritten as:

$$\Delta {\varvec{R}}={\varvec{H}}_T \Delta {\varvec{\Sigma }} - {\varvec{R}}{\text {th}},\quad {\varvec{H}}_T=\left[ \begin{array}{r c} {\varvec{H}}_{11} &{} {\varvec{H}}_{12} \\ {\varvec{H}}_{12} &{} {\varvec{H}}_{22} \\ \end{array} \right] ,\quad \left( {\varvec{H}}_{11}, {\varvec{H}}_{12}, {\varvec{H}}_{22} \right) =\int _{-h/2}^{h/2} \left( 1, z, z^2 \right) {\varvec{H}} {\text {d}}z.$$

(19)

For the thermal generalized resultant of stress ${\varvec{R}}{\text {th}}=\left[ \begin{array}{c c c c} {\varvec{N}}{\text {th}} &{} {\varvec{M}}{\text {th}} \\ \end{array} \right] ^{{\text {T}}}$, its components are given by:

$$\begin{array}{l l l l} {\varvec{N}}{\text {th}}=\int _{-{h}/{2}}^{{h}/{2}} {\varvec{H}} \alpha (T,z) \Delta T \left[ \begin{array}{c c c} 1 \\ 1 \\ 0 \\ \end{array} \right] &{},\quad {\varvec{M}}{\text {th}}=\int _{-{h}/{2}}^{{h}/{2}} z {\varvec{H}} \alpha (T,z) \Delta T \left[ \begin{array}{c c c} 1 \\ 1 \\ 0 \\ \end{array} \right] \end{array},$$

(20)

where $\alpha (T,z)$ is the coefficient of thermal expansion and $\Delta T$ is the temperature change. The submatrix ${\varvec{H}}$ represents the in-plane elastic contribution of the constitutive equations in the material part, and its expression is given by:

$${\varvec{H}}=\frac{E(T,z)}{1-\nu ^2}\left[ \begin{array}{c c c} 1 &{} \nu &{} 0 \\ \nu &{} 1 &{} 0 \\ 0 &{} 0 &{} \frac{1-\nu }{2} \\ \end{array} \right] ,$$

(21)

E(T, z) and $\nu$ denote the Young’s modulus and the Poisson’s ratio, respectively.

3.4 Geometrical part

The geometrical part results from the variation in the virtual strains while holding stress resultants constant. Its form can be given as:

$${D_G} G \cdot \Delta {\varvec{\Phi }}= \int _A (\Delta \delta {\varvec{\Sigma }}^{{\text {T}}} \cdot {\varvec{R}}) {\text {d}}A,$$

(22)

The partition of this part into membrane and bending parts yields:

$${D_G} G \cdot \Delta {\varvec{\Phi }}= {D_G} {G_m} \cdot \Delta {\varvec{\Phi }}+{D_G} {G_b} \cdot \Delta {\varvec{\Phi }},$$

(23)

In the following, the discretization of the weak form of equilibrium as well as the material and geometrical parts is presented in detail.

4 Finite element approximations

4.1 Approximation of the displacement field

By neglecting the contribution of the shear strains, the geometry and the displacements are discretized by an isoparametric interpolation as Frikha et al. [28, 29] and Zghal et al. [71, 74]:

$$\delta {\varvec{u}}=\sum _{I=1}^{4} N^I \delta {\varvec{ u}}_I,\quad \delta {\varvec{d}}= \sum _{I=1}^{4} N^I \delta {\varvec{d}}_{I} + \sum _{K=5}^{8} P_K \delta \alpha _K {\varvec{ t}}_K,$$

(24)

$$\Delta {\varvec{u}}=\sum _{I=1}^{4} N^I \Delta {\varvec{ u}}_I,\quad \Delta {\varvec{d}}= \sum _{I=1}^{4} N^I \Delta {\varvec{d}}_{I} + \sum _{K=5}^{8} P_K \Delta \alpha _K {\varvec{ t}}_K,$$

(25)

$N^I$ are the standard isoparametric shape functions at nodal level I as indicated in Dhatt and Touzot [14] and Batoz and Dhatt [6]. Their expressions and the ones of $P_K$ are given, respectively, in Table 1 with ($\xi =\xi ^1, \eta =\xi ^2$). K and $\delta \alpha _k$ refer to the midpoint of the element boundaries and the variables associated with $\delta {\varvec{d}}$ on the boundaries, respectively. Its corresponding position is illustrated in Fig. 2. The direction of vector ${\varvec{t}}_K$, which is unit, is defined by the position of the nodes couple (I, J) as:

$${\varvec{t}}_K = ({\varvec{x}}_J - {\varvec{x}}_I)/L_K, \quad L_K=\left\| {\varvec{x}}_J - {\varvec{x}}_I \right\| ,$$

(26)

where $L_K$ is the $I-J$ side length. Considering the concept of Kirchhoff–Love under integral form on the element boundaries, $\Delta \alpha _K$ will be expressed in terms of the increment $\Delta {\varvec{\Phi }}=(\Delta {\varvec{u}},\Delta {\varvec{d}})$ [12].

Fig. 2

Position of the nodes couple (I, J)

Table 1 Shape functions $N^I$ and $P_K$ for the quadrilateral element

4.2 Nodal transformation

The shape function derivatives ${\overline{N}}_{,\alpha }^I$ ($\alpha =1,2$) in local Cartesian system and their corresponding ones in elementary system are given by:

$$\left\{ \begin{array}{r c l} {\overline{N}}_{,1}^I \\ {\overline{N}}_{,2}^I \\ \end{array} \right\} =\left[ {\varvec{J}} \right] ^{-1} \left\{ \begin{array}{r c l} N_{,\xi }^I \\ N_{,\eta }^I \\ \end{array} \right\} ,$$

(27)

where ${\varvec{J}}$ is the Jacobian transformation which relates the local Cartesian system to the parametric ones, with base vectors $\left\{ {\varvec{n}}_1^0, {\varvec{n}}_2^0, {\varvec{n}}^0 \right\}$, as follows:

$${\varvec{J}}=\left[ \begin{array}{r c l} {\varvec{n}}_1^0 \cdot {\varvec{A}}_1 &{} {\varvec{n}}_2^0 \cdot {\varvec{A}}_1 \\ {\varvec{n}}_1^0 \cdot {\varvec{A}}_2 &{} {\varvec{n}}_2^0 \cdot {\varvec{A}}_2 \\ \end{array} \right] ,$$

(28)

${\varvec{A}}_1$ and ${\varvec{A}}_2$ are the covariant base vectors of the mid-surface. The normal field to the mid-surface ${\varvec{n}}^0$ in the initial configuration $C_0$ is expressed by:

$${\varvec{n}}^0={\varvec{A}}_1 \wedge {\varvec{ A}}_2/\left\| {\varvec{A}}_1 \wedge {\varvec{A}}_2 \right\| ,$$

(29)

The construction of the nodal transformation yields:

$$\delta {\varvec{\Phi }}_I = {\varvec{\Pi }}_I \cdot \delta {\varvec{U}}_I,{\varvec{\Pi }}_I= \left[ \begin{array}{c c} {\varvec{I}} &{}{\varvec{0}} \\ {\varvec{0}} &{} {\overline{\varvec{\Lambda }}} \\ \end{array} \right] ,\quad I=1,\ldots ,4.$$

(30)

where the vectors $\delta {\varvec{\Phi }}_I$ and $\delta {\varvec{U}}_I$ are defined as follows:

$$\delta {\varvec{\Phi }}_I=\left[ \begin{array}{c c} \delta {\varvec{u}} &{} \delta {\varvec{d}} \\ \end{array} \right] _{I}^{T},\quad \delta {\varvec{U}}_I=\left[ \begin{array}{c c} \delta {\varvec{u}} &{} \delta {\varvec{\Theta }}\\ \end{array} \right] _{I}^{T}$$

(31)

The transformation ${\overline{\varvec{\Lambda }}}$ leads generally to a spatial description with 6DOF/node or a material description with 5DOF/node, and it can be expressed as follows:

$$\overline{\varvec{\Lambda }}= \left[ \begin{array}{cl} - {{\varvec{d}}}_{2}&{{\varvec{d}}}_{1} \end{array} \right] _{3 \times 2}.$$

(32)

The expressions of the directors and the rotations updating at nodes for both spatial and material descriptions are given in Table 2.

Table 2 Nodal updates

The discretization of the displacement field can be written at the global level as follows:

$$\delta {\varvec{\Phi }}_n = {\varvec{\Pi }}_n \cdot \delta {\varvec{U}}_n,\quad {\varvec{\Pi }}_n =\left[ \begin{array}{cccc} {\varvec{\Pi }}_1&{}{\varvec{0}}&{} {\varvec{0}} &{} {\varvec{0}}\\ {\varvec{0}} &{} {\varvec{\Pi }}_2 &{} {\varvec{0}}&{} {\varvec{0}}\\ {\varvec{0}} &{} {\varvec{0}} &{} {\varvec{\Pi }}_3&{}{\varvec{0}} \\ {\varvec{0}}&{}{\varvec{0}} &{}{\varvec{0}} &{} {\varvec{\Pi }}_4\\ \end{array} \right] .$$

(33)

All numerical examples given in Sect. 5 are obtained with the material description and 5DOF/node.

4.3 Approximation of the strain field

The finite element discretization of the membrane and bending parts of the strain field yields:

$$\delta {\varvec{e}}={\varvec{B}}_m \delta {\varvec{U}}_n,\quad \delta {\varvec{\chi }} = {\varvec{B}}_b \cdot \delta {\varvec{U}}_n,$$

(34)

where ${\varvec{B}}_m$ and ${\varvec{B}}_b$ are the discrete strain–displacement matrices. Their corresponding expressions are given in Table 3.

Table 3 Strain–displacement matrices

As a result, the variation in the generalized strain $\delta {\varvec{\Sigma }}$ can be given as:

$$\delta {\varvec{\Sigma }} = \left\{ \begin{array}{c c c c} \delta {\varvec{e}} \\ \delta {\varvec{\chi }} \end{array} \right\} = {\varvec{B}} \cdot \delta {\varvec{U}}_n, \quad {\varvec{B}} = \left[ \begin{array}{c} {\varvec{B}}_{m} \\ {\varvec{B}}_{b} \end{array} \right] .$$

(35)

4.4 Eigenvalue problem for thermal buckling analysis

The determination of the critical buckling temperature is achieved via the resolution of the eigenvalue problem, which can be written as follows:

$$(\varvec{K_{M}} + \lambda _{{\text {cr}}}\varvec{K_{G}}) \varvec{U_n} = 0.$$

(36)

where $K_{M}$ and $K_{G}$ represent the linear stiffness matrix and the geometric stiffness matrix, respectively, and $\lambda _{{\text {cr}}}$ is the critical temperature buckling parameter. The construction of the matrices $K_{M}$ and $K_{G}$ is carried out through the definition of the material and geometrical tangent operators, respectively. For that, we start with the material tangent operator which is given by the following expression:

$${\varvec{K}}_M=\int _A \varvec{B^{{\text {T}}}} {\varvec{H}}_T {\varvec{B}} {\text {d}}A.$$

(37)

In addition, the element residual ${\varvec{r}}$ can be deduced from the weak form of equilibrium Eq. (14) as:

$${\varvec{r}}=\int _A \varvec{B^{{\text {T}}}} {\varvec{R}} {\text {d}}A.$$

(38)

The geometric tangent operator can be expressed in matrix form as follows:

$$D_G G \cdot \Delta \Phi =\delta \Phi ^{{\text {T}}} \cdot {\varvec{K}}_{G} \cdot \Delta \Phi =\delta {\varvec{U}}_n^{{\text {T}}} \cdot \varvec{\Pi }_n^{{\text {T}}} \cdot {\varvec{K}}_{G} \cdot {\varvec{\Pi }}_n \cdot \Delta {\varvec{U}}_n.$$

(39)

where ${\varvec{K}}_{G}$ represents the global geometric tangent operator, which regroups the membrane and the bending contributions. For a couple of nodes (I, J), the expression of the matrix ${\varvec{K}}_{G}$ is given by:

$${{\varvec{K}}_{G}}_{IJ} = \left[ \begin{array}{c c c} UUM_{IJ} {\varvec{I}} + \varvec{UUF}_{IJ} &{} \varvec{UBF}_{IJ} \\ \varvec{BUF}_{IJ} &{} \varvec{BBF}_{IJ} \end{array} \right] ,$$

(40)

UUM and $\left( \varvec{UUF}, \varvec{UBF}, \varvec{BBF} \right)$ correspond to membrane and bending parts, respectively. Their expressions are as indicated in Table 4.

Table 4 Geometrical tangent matrix components

After the determination of the critical temperature buckling parameter via the resolution of the nonlinear eigenvalue problem described in Eq. (36), the post-buckling equilibrium path is obtained using the iterative and incremental procedure via the Newton–Raphson method.

5 Numerical results and discussion

In this section, numerical analysis of buckling and post-buckling responses of FG square, skew plates and cylindrical panels under thermal loadings is performed using the proposed four-node shell element with 5DOF/node (SQAD45). Validation study is firstly presented for both isotropic plates and cylindrical panels to check the accuracy of the present model in the prediction of the critical buckling temperature and the post-buckling responses of these structures subjected to different forms of temperature distributions. Then, the obtained results of FGM studied structures are examined in order to outline the capability of the present model to draw the thermal buckling and post-buckling responses of such structures with good accuracy.

5.1 Validation study

5.1.1 Isotropic square plate

For the verification of the thermal buckling response obtained from the present model, an isotropic square plate is first considered. The plate is meshed using $32\times 32$ of SQAD45 finite element, and its material properties are given as: Young’s modulus $E=1$ GPa, Poisson’s coefficient $\nu =0.3$ and thermal expansion coefficient $\alpha =2\times 10^{-6}/^{\circ }C$. The geometric properties of this plate are: the aspect ratio $a/b=1$ and the length-to-thickness ratio $a/h=100$ as shown in Fig. 3. The plate is assumed to be under two types of thermal loadings: uniform temperature rise and linear temperature distribution through the thickness. Table 5 presents the solutions of the critical buckling temperature $\Delta T_{{\text {cr}}}$ (in K) of the isotropic plates under different temperature distributions and for various boundary conditions obtained from the present formulation, as well as those provided from analytical method [32] and finite element methods [60]. The definition of the boundary condition is given as follows:

• Simply supported (S): $\left\{ \begin{array}{c} \hbox {u=w=}\Theta _1=0 \hbox { for side (AD) and (BC),}\\ \hbox {v=w=}\Theta _2=0 \hbox { for side (AB) and (DC),}\\ \end{array}\right.$

• Clamped $(C){:}\,u=v=w=\Theta _1=\Theta _2=0$,

The obtained results reveal a good agreement, and they are more closer to the analytical solution than the one derived from the finite element procedure, which affirms the capability of the present model in the prediction of thermal buckling behavior of square plates. In addition, the effect of the aspect ratio (a/b) on the critical buckling temperature of a simply supported isotropic plate under uniform temperature distribution is depicted in Fig. 4. The obtained results are presented in terms of nondimensional critical buckling temperature $\Delta T^*_{{\text {cr}}}=\alpha \times \Delta T_{{\text {cr}}} \times 10^{4}$, and they are compared to those available in the literature [9]. As can be seen from Fig. 4, a good agreement between the present results and those given by Bouazza et al. [9] is revealed. From Fig. 4, it can be also remarked that the nondimensional critical buckling temperature increases by the increase in the aspect ratio (a/b). In fact, as the aspect ratio (a/b) increases, the plate becomes less larger and hence more sensitive to the temperature parameter.

Table 5 Comparison study of critical buckling temperature $\Delta T_{{\text {cr}}}$ (in K) for isotropic square plates under different temperature distributions and for clamped (CCCC) and simply supported (SSSS) boundary conditions

Fig. 3

Schematic of the square plate

Fig. 4

Nondimensional critical buckling temperature $\Delta T_{{\text {cr}}}^*$ versus the aspect ratio a/b of the isotropic square plate under uniform temperature distribution with the geometrical ratio ($a/h=100$)

5.1.2 Isotropic skew plate

The effectiveness of the present model and its ability in the prediction of thermal buckling behavior of isotropic skew plates subjected to uniform temperature rise are now examined. The geometrical characteristics of the skew plate are depicted in Fig. 5 where $a/b=1$ and $a/h=1000$ as indicated in Prabhu and Durvasula [52] and Kant and Babu [42]. Its material properties such as Young’s modulus, the Poisson’s ratio and the thermal expansion coefficient are : $E=1$ GPa, $\nu =0.3$ and $\alpha =1\times 10^{-6}/^{\circ }$C, respectively. The definition of the boundary conditions for simply supported (S) or clamped (C) edges is given as mentioned earlier in Sect. 5.1.1. The comparison study is carried out using the present SQAD45 finite element for various skew angles ($\alpha =0^\circ , 15^\circ , 30^\circ$ and $45^\circ$). The nondimensional critical buckling temperatures ($\Delta T_{{\text {cr}}}^{*}=E \alpha b^{2} h \Delta T_{{\text {cr}}}/\pi ^{2} D$ with $D=E h^{3}/12(1-\nu ^{2}))$ of the clamped isotropic skew plate are listed in Table 6, as well as the corresponding results given by Prabhu and Durvasula [52] and Kant and Babu [42]. The present results are very closer to those obtained from the references Prabhu and Dur-vasula [52], Kant and Babu [42], which leads to validate the present formulation. Therefore, the current model is convenient for thermal buckling analysis of thin skew plates.

Fig. 5

Schematic and geometrical characteristics of the skew plate

Table 6 Comparison study of nondimensional critical buckling temperature $\Delta T_{{\text {cr}}}^{*}$ for the isotropic skew plate under uniform temperature distribution

5.1.3 Isotropic cylindrical panel

An isotropic cylindrical panel subjected to uniform temperature distribution is studied. The panel is meshed using $32\times 20$ of SQAD45 finite elements. Its geometry is illustrated in Fig. 6, and the corresponding properties are given as: the thickness $h=1$ mm, the thickness ratio $A/h=100$, the curvature ratio $R/A=2$, the aspect ratio $A/L=1$ and the angle $\theta = 15^\circ$. The material properties are given as follows Bhagat et al. [8]: $E=210$ GPa, $\nu =0.3$ and $\alpha =12.6\times 10^{-6}/^{\circ }$C. The critical buckling temperature $\Delta T_{{\text {cr}}}$ (in K) of the isotropic cylindrical panel under uniform temperature distribution is computed for various thickness ratios (A/h) and for different boundary conditions and compared to those given by Bhagat et al. [8]. A sequence of letters containing “C” or “F” is used to denote fully clamped (C) or free edges (F). Three combinations of boundary conditions are considered: CCCC, CCFC and CFCF. It should be mentioned that the first and third letters indicate the boundary condition applied to curved edge, while the latter letters refer to straight edge. From Fig. 7, it can be seen that the results obtained by the proposed model agree well with the solution of Bhagat et al. [8], which leads to verify the aptitude of the present formulation in the prediction of the thermal buckling behavior of isotropic cylindrical panels. Also, Fig. 7 shows that the critical buckling temperature decreases as the thickness ratio A/h increases for all combinations of boundary conditions. In fact, the more thin the cylindrical panel becomes, the more the stiffness of the panel is decreased. On the other hand, the fully clamped (CCCC) or clamped in three edges and free in one edge (CCFC) cylindrical panels lead to higher values of critical buckling temperatures compared to the other boundary condition (CFCF). This means that the applied boundary conditions have a significant effect on the thermal buckling strength of such structures.

Fig. 6

Geometry of the cylindrical panel

Fig. 7

Critical buckling temperature $\Delta T_{{\text {cr}}}$ (in K) of the isotropic cylindrical panel under uniform temperature rise versus thickness ratio (A/h) for different boundary conditions (CCCC, CCFC, CFCF)

5.2 Thermal buckling and post-buckling analysis of FGM structures

5.2.1 Thermal buckling responses of FGM plates and cylindrical panels

Here, the thermal buckling behavior of FGM structures is investigated. In fact, a series of analyses varying the power law index, the aspect ratios, the type of thermal loadings, boundary conditions and other geometrical parameters are carried out on FGM plates and cylindrical panels in order to show the effects of such parameters on the buckling behavior of these structures. For that, the thermal buckling of FGM square plate under uniform temperature distribution is first investigated (Table 7). The plate is made of aluminum (Al) and alumina (${\text {Al}}_2 {\text {O}}_3$) phases, and the adopted mesh involves $32\times 32$ of SQAD45 finite elements. The material properties are listed in Table 8. The geometrical characteristics of the plate are the same as mentioned in Kandasamy et al. [41]. Figure 8 depicts the obtained critical buckling temperatures $\Delta T_{{\text {cr}}}$ (in K) versus the power law index p compared to those given by Kandasamy et al. [41] under uniform temperature distribution with fully clamped (CCCC) and fully simply supported (SSSS) boundary conditions. A good agreement between the results implies that the present model has the capacity to reproduce the thermal buckling responses of FGM plates. It should be mentioned that the little difference between the results in the case of simply supported boundary condition and for $p\ge 1$ can be explained by the effect of shear deformations which is neglected in our approach. For the purpose of the validation of the present formulation with analytical and finite element methods [38, 41], further numerical results of the critical buckling temperature $\Delta T_{{\text {cr}}}$ (in K) of the FGM (Al/${\text {Al}}_2 {\text {O}}_3$) plates with geometrical characteristics: $a/b=1$ and $a/h=100$, under uniform temperature distribution and for simply supported boundary condition are provided in Table 7. For the different power law indexes (p), the present results show an excellent agreement with those published in the literature [38, 41], which highlight again the effectiveness and the reliability of the present model.

Table 7 Comparison study of critical buckling temperature $\Delta T_{{\text {cr}}}$ (in K) for FG simply supported (SSSS) square plates under uniform temperature distribution for different power law index values p

On the other hand, the effects of aspect ratio (b/a) on the critical buckling temperature of a clamped (Al/${\text {Al}}_2 {\text {O}}_3$) plate under uniform and nonuniform temperature distributions and for different power law index p values with length-to-thickness ratio ($a/h=100$) are shown in Fig. 9a, b. Based on these plots, it can be noted that the critical temperature parameter increases as the aspect ratio (b/a) increases and this is for both types of temperature distributions. In addition, the thermal buckling parameter decreases as the power law index p increases, which implies a rise in the stiffness of the FGM square plate.

Table 8 Material properties of aluminum (Al), alumina (${\text {Al}}_2 {\text {O}}_3$) and zirconia (${\text {ZrO}}_2$) phases [77]

Fig. 8

Critical buckling temperature $\Delta T_{{\text {cr}}}$ (in K) versus the power law index p of the rectangular plate under uniform temperature distribution for fully clamped (CCCC) and simply supported (SSSS) boundary conditions and with the geometrical ratios ($a/h=100, a/b=1$)

Fig. 9

Critical buckling temperature $\Delta T_{{\text {cr}}}$ (in K) of the FG clamped square plate with: a uniform temperature distribution and b nonuniform for different power law indexes p versus the aspect ratio b/a with length-to-thickness ratio ($a/h=100$)

In the second example, the thermal buckling analysis is performed for (Al/${\text {Al}}_2 {\text {O}}_3$) skew plate under uniform and nonuniform temperature distributions. The considered mesh is the same as mentioned earlier in Sect. 5.1.2. The used geometrical properties are as indicated in Jaberzadeh et al. [35]: $b/a=1,b/h=100$. Table 9 compares the critical buckling temperatures $\Delta T_{{\text {cr}}}$ (in K) of a clamped (CCCC) FGM skew plates under two sets of temperature distributions and with different power law indexes p. The comparison reveals an excellent agreement between the obtained results and those cited in Jaberzadeh et al. [35] leading hence to validate again the ability of the present model to reproduce with accuracy the thermal buckling behavior of FGM skew plates. According to Table 9, the relative error between the present result and those given by Jaberzadeh et al. [35] in the case of a skew angle ($\alpha =0^\circ , 15^\circ$ and $30^\circ$) does not exceed 1.3% for uniform temperature rise, while it can reach 36% in the case of nonuniform temperature distribution. In fact, the solution of the critical temperature of plate under nonuniform temperature rise in Jaberzadeh et al. [35] is achieved using the polynomial series method; however, in this study, the thermal buckling is computed using the Gauss integration method. So, the present method is more convenient for thermal buckling analysis of FGM structures under nonuniform temperature distribution. Furthermore, Table 10 illustrates the effect of boundary conditions and the power law index p on the critical buckling temperature $\Delta T_{{\text {cr}}}$ (in K) of the (Al/${\text {Al}}_2 {\text {O}}_3$) skew plate for uniform and nonuniform temperature rise. It can be seen that $\Delta T_{{\text {cr}}}$ increases as the power law index p decreases and this is for the two sets of temperature and for all the combinations of boundary conditions. In addition, for CCCC and SCSC boundary conditions, the values of critical buckling temperature are much greater than those for the fully simply supported (SSSS) skew plates. Thus, the more the plate is constrained, the more higher its rigidity becomes, which leads to high critical buckling temperature. In addition, the corresponding buckling mode shapes of the FGM skew plates are illustrated in Fig. 10.

Fig. 10

Buckling mode shapes of the FGM skew plates under uniform temperature rise with clamped edges

Table 9 Critical buckling temperature rise $\Delta T_{{\text {cr}}}$ (in K) of clamped Al/${\text {Al}}_2 {\text {O}}_3$ skew plate

Table 10 Critical buckling temperature rise $\Delta T_{{\text {cr}}}$ (in K) of Al/${\text {Al}}_2 {\text {O}}_3$ skew plate ($b/a=1, b/h=100, \alpha =30^{\circ }$) for different boundary conditions and different power law indexes p

The variation in buckling temperature versus the skew angle for the simply supported FGM skew plate under two studied thermal loads and for different power law indexes p is shown in Fig. 11a, b, respectively. The results of Fig. 11 indicate that as the skew angle of the plate increases, the critical buckling temperature parameter increases. In fact, for a skew angle higher than $30^{\circ }$, the increase in the thermal buckling parameter is more pronounced. Thus, a high values of skew angles induces the concentration of stresses at the corner of the FGM plate where its rigidity becomes more sensitive to the change in temperature. This observation is similar to those for fully clamped FGM skew plate illustrated in Fig. 12a, b. Moreover, when comparing the influence of thermal loading type on critical buckling behavior of FGM skew plate, it can be observed that the effect of nonuniform thermal load is more prominent than the uniform temperature rise. Further conclusions can be deduced from Figs. 13 and 14, which depict the effects of length-to-thickness ratio (a/h) and the aspect ratio (b/a) on thermal buckling behavior of clamped FGM skew plates under uniform temperature rise for different skew angles and with a power law index $p=5$. Figure 13 shows that the increase in the length-to-thickness ratio (a/h) induces a decrease in the critical buckling temperature parameter, and this is for all values of skew angles. In fact, the effect of the length-to-thickness ratio is more pronounced for FGM skew plate with a skew angle $\alpha =60^\circ$ compared to the other values of skew angles. This reveals that the skew angle has a significant effect on thermal buckling behavior of FGM skew plates. Furthermore, it can be remarked that when the length-to-thickness ratio ($a/h\ge 50$) increases, the FGM skew plate behaves as a thin structure and becomes hence less sensitive to the change in temperature. On the other hand, Fig. 14 illustrates the effect of the aspect ratio (b/a) on the critical buckling temperature of the FGM skew plate. It can be seen that the critical buckling temperature parameter rises with the increase in the aspect ratio (b/a) for all values of skew angles of the clamped FGM skew plate. This observation reflects that the variation in this geometrical parameter affects the flexural rigidity of the plate and hence the thermal buckling behavior of the FGM skew plate.

Fig. 11

Critical buckling temperature $\Delta T_{{\text {cr}}}$ (in K) versus the skew angle (in $^{\circ }$) of the SSSS FGM skew plate ($b/a=1, b/h=100$) subjected to: a uniform temperature rise and b nonuniform temperature rise for different power law index p

Fig. 12

Critical buckling temperature $\Delta T_{{\text {cr}}}$ (in K) versus the skew angle (in $^{\circ }$) of the CCCC FGM skew plate ($b/a=1, b/h=100$) subjected to: a uniform temperature rise and b nonuniform temperature rise for different power law indexes p

Fig. 13

Critical buckling temperature $\Delta T_{{\text {cr}}}$ (in K) versus length-to-thickness ratios (a/h) of the clamped (CCCC) FGM skew plate under uniform temperature rise for various skew angles and with a power law index value $p=5$

Fig. 14

Critical buckling temperature $\Delta T_{{\text {cr}}}$ (in K) versus aspect ratio (b/a) of the clamped (CCCC) FGM skew plate under uniform temperature rise for various skew angles and with a power law index value $p=5$

To illustrate the present approach for thermal buckling analysis of FGM shells, a clamped (Al/${\text {ZrO}}_2$) cylindrical panel under thermal loadings is considered with the properties as listed in Table 8. The geometric properties of the FGM panel are the same as mentioned in Zhao and Liew [76]: $L=0.2, R=1, h=0.002$. The considered mesh of the panel is $32\times 32$SQAD45 finite elements. Figure 15 presents the buckling temperature rise $\Delta T_{{\text {cr}}}$ (in K) versus the power law index p of the clamped FGM cylindrical panel under uniform in comparison with Zhao and Liew [76]. It is observed that a good agreement has been achieved in this comparison study.

Fig. 15

Critical buckling temperature rise for an Al/${\text {ZrO}}_2$ panel with two sides simply supported and two sides clamped (CSCS) under nonlinear temperature distribution with the geometrical ratios ($L=0.2, R=1, h=0.002$)

Figure 16 presents the buckling temperature rise $\Delta T_{{\text {cr}}}$ (in K) versus the power law index p of the Al/${\text {ZrO}}_2$ cylindrical panel under uniform and nonuniform temperature distributions with the geometrical ratios ($A/L=1, R/A=2$). For both thermal loadings, the critical temperature decreases when the power law index p increases. This is due to the decreases in the stiffness of the panel with a rise in this exponent. In fact, the high values of the power law exponent correspond to high portion of metal (Al) in comparison with the ceramic part (${\text {ZrO}}_2$). In addition, the panel under nonuniform temperature rise induces higher values of critical buckling temperature compared to panel under uniform temperature distribution. Therefore, the use of the numerical integration method and the dependency of the thermal load on the geometrical parameter can affect significantly the thermal buckling behavior of FGM cylindrical panels. Now, the effects of the thickness ratio (A/h) on the thermal buckling behavior of the clamped FGM cylindrical panel under the two sets of temperature distributions are examined in Fig. 17a, b. It can be observed that the critical temperature $\Delta T_{{\text {cr}}}$ (in K) decreases as the thickness ratio (A/h) increases and this for all thermal loading types. Indeed, the increase in the thickness ratio (A/h) induces a flat panel with a low values of buckling strength due to the decrease in the bending stiffness of the FGM cylindrical panel. In addition, the buckling temperature decreases as the power law exponent p rises, which leads to an increases in the stiffness of the panel. The two first mode shapes of the Al/${\text {ZrO}}_2$ cylindrical panel are plotted in Fig. 18.

Fig. 16

Critical buckling temperature $\Delta T_{{\text {cr}}}$ (in K) of a clamped FGM cylindrical panel versus the power law index p under different temperature distributions with the geometrical ratios ($A/L=1, R/A=2$)

Fig. 17

Critical buckling temperature $\Delta T_{{\text {cr}}}$ (in K) versus the thickness ratio (A/h) of a clamped FGM cylindrical panel subjected to: a uniform temperature rise and b nonuniform temperature rise for different power law indexes p and with the geometrical ratios ($A/L=1, R/A=2$) versus the thickness ratio (A/h)

Fig. 18

Buckling mode shapes of the FGM cylindrical panel under nonuniform temperature rise with two edges clamped and two edges simply supported

5.2.2 Thermal post-buckling responses of FGM plates and cylindrical panels

In order to validate the efficiency of the present formulation for thermal post-buckling analysis, two examples are considered for which the thermal post-buckling responses of isotropic square and skew plates are compared to the solutions available in the literature. Firstly, an isotropic square plate subjected to uniform temperature rise is examined. The geometrical and material properties of the plate are taken as indicated in Shen [56] where $a/b=1, a/h=10$ are the geometrical ratios, $E=1$ GPa is the Young’s modulus, $\nu =0.3$ is the Poisson’s coefficient and $\alpha =10^{-4}/^{\circ }$C is the thermal expansion coefficient. The plate is modeled using $32\times 32$ of SQAD45 finite elements. The obtained results are presented in terms of dimensionless critical temperature $T= \Delta T/\Delta T_{{\text {cr}}}$ with $\Delta T_{{\text {cr}}}=119.783$. As can be seen from Fig. 19, a good agreement between the obtained results and those provided by Shen [56] is revealed which leads to verify the effectiveness of the present model and draw hence its ability to predict the thermal post-buckling behavior of plates with good accuracy.

Fig. 19

Post-buckling path of the simply supported isotropic square plate subjected to uniform temperature distribution with the geometrical ratios ($a/h=10, a/b=1$)

Secondly, the thermal post-buckling path of a clamped isotropic skew plate under uniform temperature distribution is analyzed. The material properties and the geometric parameters are: $E=1$ GPa, $\nu =0.3, \alpha =10^{-4}/^{\circ }$C, $a/h=100$, and the skew angle is taken equal to $45^{\circ }$. The isotropic skew plate is meshed using $32\times 32$ of SQAD45 finite elements. Figure 20 depicts the obtained nondimensional temperature $T^*$ ($=E\alpha a^2 h T/\pi ^2D$, with $D= Eh^3/12(1-\nu ^2)$) compared to the result given by Prakash et al. [53]. An excellent agreement between the results is highlighted, which demonstrates the aptitude of the present formulation to predict the thermal post-buckling behavior of skew plates with good accuracy. It should be mentioned that the difference between the results at $\frac{w}{h}=0$, observed in Figs. 19 and 20, can be explained by the different used theories and methods in the resolution procedure. In fact, in our paper a finite element method is elaborated in the sense of nonlinear analysis with the introduction of large displacement and finite rotations while in Prakash et al. [53] and Shen [56] an analytical method is employed based on von Karman assumptions which include only the effect of membrane forces.

Fig. 20

Post-buckling path of the clamped isotropic skew plate subjected to uniform temperature distribution with the geometrical ratios ($a/h=100, a/b=1, \alpha =45^\circ$)

Now, the thermal post-buckling responses of FGM structures are examined for square plates, skew plates and cylindrical panels. Figure 21 depicts the thermal post-buckling curves of a clamped Al/${\text {Al}}_2 {\text {O}}_3$ FGM square plates under uniform temperature distribution for different power law coefficients p. The geometrical properties and the used mesh are the same as mentioned earlier in Sect. 5.2.1. In fact, the increases in the power index p produce less deflection and the thermal post-buckling path decreases. Figure 22 shows the thermal post-buckling behavior of a simply supported ${\text {Si}}_3{\text {N}}_4$/SUS304 FGM skew plates under nonuniform temperature distribution for different power law indexes p. The geometrical parameters are: $a/h=100, a/b=1$, skew angle $\alpha =45^\circ$ and the temperature-dependent material properties are listed in Table 11. It can be observed that as the power index p increases, the post-buckling response of the FG plate decreases. In fact, a high value of the power index p induces a rise in the volume fraction of ceramic portion, which is able to withstand high temperature. Therefore, the FGM materials show a good way of heat resistance. In addition, the effect of skew angle on the thermal post-buckling behavior of a simply supported ${\text {Si}}_3{\text {N}}_4$/SUS304 skew plates under nonuniform temperature distribution is also examined as depicted in Fig. 23. It can be seen that with an increase in the skew angle, the post-buckling path is reduced for an applied thermal load, which induces the high thermal load capacity of the FG skew plate with the rise in the skew angle. As a result, designer can adjust the thermal capacity of such structures with the variation in the skew angle geometrical parameter.

Fig. 21

Thermal post-buckling path of a clamped Al/${\text {Al}}_2 {\text {O}}_3$ FGM square plates under uniform temperature distribution for different power law indexes p and with the geometrical parameters ($a/h=100, a/b=1$)

Table 11 Temperature-dependent thermo-elastic coefficients of ${\text {Si}}3{\text {N}}4$ and SUS304 [53]

Fig. 22

Thermal post-buckling path of a simply supported ${\text {Si}}_3{\text {N}}_4$/SUS304 FGM skew plates under nonuniform temperature distribution for different power law indexes p and with the geometrical parameters ($a/h=100, a/b=1$, Skew angle $\alpha =45^\circ$)

Fig. 23

Thermal post-buckling path of a simply supported ${\text {Si}}_3{\text {N}}_4$/SUS304 FGM skew plates under nonuniform temperature distribution for different skew angles and with the geometrical parameters ($a/h=100, a/b=1$)

Figure 24 illustrates the post-buckling path of Al/${\text {ZrO}}_2$ cylindrical panels under uniform temperature load for different power law indexes p and with geometrical properties ($L=0.2, R=1, h=0.002$). As the temperature load increases, the nondimensional deflection increases. In addition, the thermal post-buckling response increases as the power index p increases. This can be explained by the flexural rigidity of the FGM panel, which is high with a fully ceramic phase ($p=0$) compared to the metallic part and can hence reach its maximum thermal load capacity. In Fig. 25, the thermal post-buckling curves evaluated for the clamped FGM cylindrical panel ($p=0.5$) under uniform and nonuniform temperature distributions are highlighted. The uniform temperature distribution leads to more deflection compared to the nonuniform temperature distribution, which induces the significant effect of temperature distribution profile on thermal post-buckling behavior of FGM structures. For the sake of completeness, it should be noted that the nondimensional deflections in the case of large displacement can reach to ($w/h=6$) as shown in Figs. 21, 24 and 25, whereas in the case of small displacements the deflection does not exceed ($w/h=1.5$) due to the inclusion of Von karman assumptions.

Fig. 24

Thermal post-buckling response for an Al/${\text {ZrO}}_2$ clamped (CCCC) panel under uniform temperature distribution with the geometrical parameters ($L=0.2, R=1, h=0.002$)

Fig. 25

Thermal post-buckling paths for an Al/${\text {ZrO}}_2$ clamped (CCCC) panel under uniform and nonuniform temperature rise through thickness with the geometrical ratios ($L=0.2, R=1, h=0.002$)

6 Conclusion

Thermal buckling and post-buckling analysis of FG square, skew plates and cylindrical panels is presented. The governing equations are developed using a finite rotation four-node shell element. This model allows the description of large deformations as well as the finite rotation which constitutes an amelioration compared to the standard Kirchhoff–Love model. In fact, the standard Kirchhoff–Love model used in the literature includes only membrane forces and remains limited to small deformations via the use of von Karman assumptions. The material properties of FGM structures are assumed to be graded along the thickness direction and temperature dependent. In numerical examples, comparison studies are firstly performed to verify the accuracy of the present finite element method and then a parametric study is conducted to show the effects of several parameters on the thermal buckling and post-buckling paths of FGM plates and cylindrical panels. From the numerical results, the following conclusions can be drawn:

• The present work allows the assessment of the critical buckling temperature and the post-buckling responses of FGM structures with a good efficiency and assures the compromise between good accuracy and low computational time.

• The critical buckling temperature of a clamped plate is greater than that of a simply supported ones. So, to delay the thermal buckling phenomena, a clamped boundary condition should be applied to the structure.

• The applied thermal loadings have a significant effect on the thermal buckling and post-buckling responses. In fact, the structure undergoes buckling at lower temperature when the applied thermal field is uniform through the thickness.

• The flexural rigidity of the FGM structures subjected to thermal loadings is highly dependent on the variation in the power law index.

• The stiffness of the FGM skew plates in thermal environment is highly dependent on the variation in the skew angle. Indeed, as the skew angle increases, the critical buckling temperature increases, and the post-buckling path is reduced.