Dynamics analysis and Hamilton energy control of a generalized Lorenz system with hidden attractor

Abstract

Hidden attractor can be found in some dynamic systems. More commonly, it can be excited by the stabilized equilibria, or be generated from the systems without equilibria. The generalized Lorenz system transformed from the Rabinovich system is researched by detecting the generating mechanism under different parameters and initial values, and then we have the good fortune to discover that the hidden attractor is coexisting with the states of stabilization, period, chaos, and even transient chaos. At the same time, the Hamilton energy function of the system is given to discuss the energy transform when the system undergoes a series of oscillations. The compositional principle can be used to design a new chaos control method, which is called Hamilton energy control. By numerical simulating, the feedback gain in the present control method is assigned and then controls the system with hidden attractor to expected states effectively. The feature of the control method can be indicated that the Hamilton energy can be detected during the oscillation control processes.

1 Introduction

Over the past half-century, painstaking research has been done about chaotic motions, and people have comprehended quite profoundly its characteristics, laws, and application in some fields. It was the effect of systems parameters; the nonlinear systems can show some rich dynamic characteristics such as the transition among period, chaos and hyperchaos [1,2,3], and crisis-induced intermittency [4, 5].

With research moves along, the relationship between chaos and engineering technology becomes tighter and tighter. Moreover, chaos has been applied in many important fields, so the construction of chaotic systems purposely has become a key subject. In the past some years, many nonlinear systems with interesting attractors were designed [6,7,8,9,10,11]; for example, Qi et al. [6] found new four-dimensional chaotic system, in which each equation contains a cubic term. This system displays two coexisting double-wing chaotic attractors [7]. In paper, Wei et al. [8] established a bending-torsion-shaft coupling multi-degree-of-freedom dynamic analysis model and then analyzed comprehensively the impact of system parameters on nonlinear dynamic. Some multi-scrolls attractor systems were also found by using all kinds of technical means. In paper [9], the multi-scrolls chaotic system was proposed by combining in a hand. In paper [10], the time-delay sampled-data chaotic system was introduced to product multi-scrolls chaotic attractor, which can lead to a more complex nonlinear system with richer chaotic behavior. In paper, Chen et al. [11] proposed a new chaotic system that could generate multi-scroll attractors by combining the two nonlinear function. In paper [12], two 3D chaotic systems without equilibrium were constructed Sprott A system, which could appear multi-scroll hidden attractors. In paper [13], a 3D fractional-order chaotic system was proposed; furthermore, the chaotic system had only one stable equilibrium and exhibited the hidden attractors. In paper [14], a new nonlinear system with hidden attractor was introduced, the cause of existing of hidden attractor was the lack of equilibrium. The researches about all types of chaotic attractors enrich the nonlinear theory and provide abundant materials for chaos secure communication.

The attractors mentioned above are excited by the unstable equilibrium points of systems, we call it self-excited attractor. However, there is a kind of unpredictable attractor, which is called hidden attractor. The basin of attraction does not touch unstable equilibria and is located far away from such points; meanwhile, the form of hidden attractor can be periodic or chaotic attractors. In recent years, some works have been done about the algorithms for finding hidden attractors [15,16,17,18,19,20,21] and analyses briefly [22,23,24,25,26]. Due to the generating mechanisms of hidden attractors, it is impossible to recognize and compute the special attractors using traditional methods. Meanwhile, the very small attraction basin and dimensions of hidden attractors result in failure to compute their integral curve by adopting random initial values. The finding of hidden attractor is proposed in classical Chua system in 2010 [15]. Kuznetsov et al. provided a way of using analytic numerical method to study hidden attractors and found the periodic solutions or hidden attractors by iteration calculating the initial values of harmonic linearized system. In paper, Zhao [20] located the hidden attractors in the Van der Pol–Duffing system; numerical results show that there are some interesting phenomenon, for example, the coexistence of hidden attractors and stable equilibria, the coexistence of hidden attractors and stable periodic solution, the coexistence of hidden attractors and chaotic attractors excited by the unstable equilibrium points. In paper, Dudkowski et al. [22] discussed some hidden attractors generating from Hilbert’s 16th problem, flows without fixed equilibria, flows with stable fixed equilibrium, flows with a line of fixed equilibria, electromechanical system without equilibria, electromechanical model of the drilling system, Rabinovich system, Glukhovskii–Dolzhanskii system and Rabinovich–Fabrikant system, respectively. In paper, Chen et al. [23] constructed a new memristive chaotic circuit, and the hidden attractors were found in the specific parameters setting. In paper, Zhang et al. [24] studied the complete synchronization between two nonlinear systems with hidden attractors, which was used to describe the local kinetic. Hidden attractors have some own unique dynamical characteristics, which are entirely different from self-excited attractors. Because of the undesirable dynamical behavior generating from hidden attractors when some practical nonlinear system is applied in engineering field, the research of coexisting hidden attractors has both physical meaning and high project application worth. From the viewpoint of applications, the hidden oscillate may cause unnecessary losses to our life and production, so it is necessity extremely to understand its mechanism and properties in order to grasp the most desirable chaotic motion better, and further lower the risk of the sudden jump to undesired behavior.

In the nonlinear chaotic circuit, a certain amount of energy is essential, and its release and storage between electric field and magnetic field are synchronous with the charge or discharge and the electromagnetic induction. According to mean field theory and Kirchhoff’s law, the energy exchange can be described by the dynamic equation of nonlinear oscillating circuits. Furthermore, for the actual oscillating circuits, the process of nondimension transform can be used to transform the electromagnetic field equations into dimensionless nonlinear dynamic equations that expect to be employed to estimate the energy exchange. At the same time, the state changes of the nonlinear dynamic systems are accompanied by the process of absorb and release of energy.

Next, it is an interesting job to look for an appropriate tool to detect the energy in a nonlinear system. Sarasola et al. [27] pointed out to us that the energy of a system can infer the dynamics process, but they developed an opposite approach and investigated a kind of variables function as the energy function to the given chaotic system. It is so exciting that Sarasola employed the Hamilton function as the energy function in a Hamilton system or general Hamilton system [28,29,30], and then calculated the Hamilton energy function for some classical chaotic systems. Torrealdea et al. [31, 32] found the average energy consumption of a Hindmarsh–Rose neuron and evaluated the energy consumption of the neuron during its signaling activity. Additionally, they analyzed whether a commonly accepted mathematical model of a neuron provides room for such a kind of trade-off. Moujahid et al. [33] studied the energy implications of synchronization phenomena in a pair of structurally flexible coupled neurons. Further, according to the Helmholtz theorem [34], Wang et al. [35] discussed the computing problems of Hamilton energy in a class of differential dynamic system and explained the physical interpretation of Hamilton energy function from the point of force fields work. In the method, they generalized the Helmholtz theorem in electromagnetic field theory to dimensionless dynamic systems. These studies are beneficial for us to extract the energy adopting the characteristic of expression, quantization, and awareness, and can help in the chaotic control greatly. In paper, Song et al. [36] calculated the Hamilton energy function for a Hindmarsh–Rose neuron and estimated the energy change induced by transition of electric modes. It was concluded that chaotic state consumes vast amounts of energy, whereas spiking state or bursting state and the energy function depended on external forcing. In paper, Ma et al. [37] discussed three kinds of attractors, that is, infinite attractors, attractors without equilibria and hidden attractors. Moreover, their Hamilton energy functions are designed and energy modulation on attractors is studied. They summarized that the Hamilton energy is dependent on all variables and initial values; meanwhile, the nonlinear dynamic systems need enough energy to keep various dynamic behaviors. In paper, Li and Yao [38] designed a new chaotic system with multi-scrolls attractors based on Chua circuit [39]; the mechanism is that a similar sine function induces the production of multi-scrolls attractors. In the meantime, the Hamilton energy of the new systems is discussed to analyze power consumption and found that energy is decreased when the number of attractor increases. The more complex dynamic behavior certainly consumes more energy, and then the value of Hamilton energy becomes low than before. In addition, we can design controllers by detecting the energy transport and aim to make the controllers reach the expected control goal associating with a minimum energy consumption.

Encouraged by those statements above, in this paper, we will discuss a generalized Lorenz system with a hidden attractor which is located in the given initial values. The period motion, chaos state, and transient chaos phenomenon can be found under different initial values, so the generalized Lorenz system depends on system parameters and initial values. The Hamilton energy function is given by a series of computations and analyzed the energy transform among different motion states. At last, a new control method is designed based on the Hamilton energy function and is used to control the system to different motion by a feedback gain.

We organized the paper as follows. In Sect. 2, the generalized Lorenz system with hidden attractors is discussed. In Sect. 3, the Hamilton energy of generalized Lorenz system with hidden attractors is defined. In Sect. 4, the new control method based on Hamilton energy is designed. Conclusion is given in Sect. 5.

2 The generalized Lorenz system with hidden attractors

Definition 1

[19, 40]. An attractor is called a self-excited attractor if its basin of attraction intersects with any open neighborhood of an unstable fixed point. Otherwise, it is called a hidden attractor.

Self-excited periodic and chaotic oscillations cannot cover all possible vibration types, for example, the types of hidden attractors that are moving away from unstable equilibrium, or come from the systems without equilibrium, or with no unstable equilibrium. Next, we will discuss the hidden attractors generated by the generalized Lorenz system.

2.1 The self-excited attractor from generalized Lorenz system

The generalized Lorenz system can be transformed from the Rabinovich system [41], and its dynamic equation is described as

$$\begin{aligned} \left\{ {\begin{array}{l} {\dot{x}}=-a(x-y)-byz \\ {\dot{y}}=cx-y-xz \\ {\dot{z}}=-dz+xy \\ \end{array}} \right. , \end{aligned}$$

(1)

where a, b, c, d are constants, which can hold the system (1) different states.

2.1.1 Symmetries

System (1) is symmetric under the transformation of $(x,\;y,\;z)\rightarrow (-x,\;-y,\;z)$, that is, system (1) is symmetric about z axis, and this characteristic remains the same to all the system parameters.

2.1.2 Dissipative

For this system, one has

$$\begin{aligned} \nabla V=\frac{\partial {\dot{x}}}{\partial x}+\frac{\partial {\dot{y}}}{\partial y}+\frac{\partial {\dot{z}}}{\partial z}=-a-1-d. \end{aligned}$$

Therefore, to ensure system (1) being dissipative, it is required that

$$\begin{aligned} -a-1-d<0. \end{aligned}$$

In this paper, in order to keep chaos characteristic, all the system parameters being selected will satisfy this condition.

2.1.3 Lyapunov dimension

The Lyapunov dimension can be defined as [42]

$$\begin{aligned} d_\mathrm{L} =j+\frac{\sum \nolimits _{i=1}^{i=j} {l_i } }{\left| {l_{j+1} } \right| }, \end{aligned}$$

where $l_1 \ge \cdots \ge l_n$, j is the largest integer to meet the conditions of $\sum \nolimits _{i=1}^{i=j} {l_i } \ge 0$ and $\sum \nolimits _{i=1}^{i=j+1} {l_i } \le 0$. For the system (1), we have the following rules:

• (1) $d_\mathrm{L} =0$, leading to stable equilibrium.

• (2) $d_\mathrm{L} =1$, leading to limit cycle.

• (3) $d_\mathrm{L} =2$, leading to quasiperiodic attractor

• (4) $d_\mathrm{L}$is a fraction, leading to chaos.

In the following, the above rules will be a computational tool to analyze the system (1).

2.1.4 The classical Lorenz system

When $a=10$, $b=0$, $c=28$, and $d=8/3$, system (1) becomes the classical Lorenz system and has three equilibria

$$\begin{aligned} S_0= & {} (0,\;0,\;0) \\ S_1= & {} (-8.4853,\;-8.4853,\;27) \\ S_2= & {} (8.4853,\;8.4853,\;27). \end{aligned}$$

For the zero equilibrium, we linearize the system (1) at the origin and get the Jacobian matrix:

$$\begin{aligned} J(S_o )=\left( {{\begin{array}{ccc} -a &{}\quad a&{}\quad 0 \\ c&{}\quad -1&{} \quad 0 \\ 0&{}\quad 0&{} \quad -d \\ \end{array}}} \right) \end{aligned}$$

and the characteristic equation can be given by

$$\begin{aligned} \det (\lambda I-J(S_o ))= & {} \lambda ^{3}+(a+c+1)\lambda ^{2} \\&+\,(a-ac-ad+d)\lambda -ad(c-1)=0; \end{aligned}$$

therefore, the three eigenvalues are calculated as

$$\begin{aligned} \lambda _1^0 =-2.6667, \lambda _2^0 =11.8277, \lambda _3^0 =-22.8277. \end{aligned}$$

Obviously, $S_0$ is unstable equilibrium (red dots in Fig. 1). Similarly, $S_1$ and $S_2$ are also unstable equilibria (red dots in Fig. 1) for the set of parameters, precisely because that

$$\begin{aligned} \lambda _1^{1,2}= & {} -13.8546, \lambda _2^{1,2} \\= & {} 0.0940+10.1945i, \lambda _3^{1,2} \\= & {} 0.0940-10.1945i. \end{aligned}$$

By numerical simulation, system (1) exhibits the classical Lorenz attractor like a butterfly [43], with respect to three equilibria. The equilibria $S_1$ and $S_2$ attract the unstable separatrices of the saddle zero equilibrium, as shown in Fig. 1, where the blue curve and green curve are all self-excited attractors.

Fig. 1

Attractors excited by the equilibria $S_0$, $S_1$, $S_2$ (the initial values are $x(0)=0.1, y(0)=0.2, z(0)=0.3$ (the blue curve)and $x(0)=-0.1, y(0)=-0.1, z(0)=-0.1$ (the green curve)). (Color figure online)

2.1.5 Coexistence of point attractor and strange attractor

With given parameters, the diverse attractors formed by triggering the nonlinear systems into different trajectories under different initial values are called coexisting attractors. The coexistence attractors present a rich diversity of stable states of nonlinear systems and have become a key research subjects recently. As you know, symmetric systems generally have coexisting attractors[44,45,46] because the attractors must appear in pairs or symmetrically. So the coexistence of different attractors can be found succeeded.

Now, the different parameters are set as $a=10$, $b=0$, $c=24.5$, and $d=8/3$; system (1) exhibits chaotic attractors as shown in Fig. 2a, accompanied by the three Lyapunov exponents:

$$\begin{aligned} \mathrm{LE}_1 =0.7988,\;\mathrm{LE}_2 =0,\;\mathrm{LE}_3 =-14.4641 \end{aligned}$$

and according to Kaplan–Yorke conjecture, the Lyapunov dimension is

$$\begin{aligned} d_\mathrm{L}= & {} k+\frac{1}{\left| {\lambda _{L,k+1} } \right| }\sum _{i=1}^k {\lambda _{L,i} } \\= & {} 2+\frac{\lambda _{L1} +\lambda _{L2} }{\left| {\lambda _{L3} } \right| } \\= & {} 2+\frac{0.7988+0}{\left| {-14.4641} \right| }=2.0552 \end{aligned}$$

which dominates the chaotic state of system (1) too.

The three equilibria of system (1) are calculated as the following:

$$\begin{aligned} S_0= & {} (0,\;0,\;0) \\ S_1= & {} (-7.9162,\;-7.9162,\;23.5) \\ S_2= & {} (7.9162,\;7.9162,\;23.5). \end{aligned}$$

In the same way, the three sets of eigenvalues corresponding to the equilibria $S_0$, $S_1$, $S_2$ can be calculated, respectively.

$$\begin{aligned}&\lambda _1^0 =-21.7865, \lambda _2^0 =\hbox {10.7865}, \lambda _3^0 =-\hbox {2.6667} \\&\lambda _1^{1, 2} =-13.6523, \lambda _2^{1, 2} =-\hbox {0.0072+9.5814i}, \\&\lambda _3^{1, 2} =-\hbox {0.0072}-\hbox {9.5814i} \end{aligned}$$

So for the sets of parameters $a=10$, $b=0$, $c=24.5$, and $d=8/3$, $S_0$ is unstable equilibrium, but $S_1$ and $S_2$ are stable equilibria (red dots in Fig. 2a). Figure 2a shows the attractors (the green curve and blue curve) excited by $S_0$ (starting from the neighborhood of $S_0$) which coexists with the stable equilibria.

Fig. 2

Coexisting attractors and the Lyapunov exponents of system (1). a Coexistence of self-attractors and the stable equilibria, the initial values are selected as: the blue curve: $x(0)=0.01, y(0)=0, z(0)=0$; the green curve: $x(0)=-0.01, y(0)=0, z(0)=0$. b Coexistence of self-attractors and hidden attractors, the initial values are selected as: the green curve: $x(0)=0.1, y(0)=0.001, z(0)=0$; the purple curve: $x(0)=-0.1, y(0)=0.001, z(0)=0$; the blue curve: $x(0)=0.3, y(0)=0.1, z(0)=0.6$. c The Lyapunov exponents of system (1) when $c\in [0,\;10]$. (Color figure online)

2.2 The hidden attractor from the generalized Lorenz system

When $a=-\,bc$, $b=-\,0.5$, $c=6.8$, and $d=1$, the three Lyapunov exponents are:

$$\begin{aligned} \mathrm{LE}_1 =0.2894,\;\mathrm{LE}_2 =0,\;\mathrm{LE}_3 =-5.6889 \end{aligned}$$

and the Lyapunov dimension is $d_\mathrm{L} =2.0508$, so the systems (1) display chaotic state.

The three equilibria of system (1) can be calculated by

$$\begin{aligned} S_0= & {} (0,\;0,\;0) \end{aligned}$$

(2)

$$\begin{aligned} S_1= & {} \left( {-\frac{a\sqrt{g}}{a+bg},\;-\frac{a\sqrt{g}}{a+bg},\;\frac{ag}{a+bg}} \right) \end{aligned}$$

(3)

$$\begin{aligned} S_2= & {} \left( {\frac{a\sqrt{g}}{a+bg},\;\frac{a\sqrt{g}}{a+bg},\;\frac{ag}{a+bg}} \right) , \end{aligned}$$

(4)

where

$$\begin{aligned} g=a/{2b^{2}(b(c-2)-a+\sqrt{(a-bc)^{2}+4ab})}. \end{aligned}$$

Further, one can get

$$\begin{aligned} S_0= & {} (0,\;0,\;0) \\ S_1= & {} (-3.4756,\;-3.4756,\;6.2801) \\ S_2= & {} (3.4756,\;3.4756,\;6.2801). \end{aligned}$$

We use the same method to calculate corresponding three eigenvalues of each equilibrium point:

$$\begin{aligned} \lambda _1^0= & {} -1, \lambda _2^0 =-7.1558, \lambda _3^0 =\hbox {2.7558} \\ \lambda _1^1= & {} -6.4481, \lambda _2^1 =0.5240+4.1138i, \\ \lambda _3^1= & {} 0.5240-4.1138i \\ \lambda _1^2= & {} 4.3988, \lambda _2^2 =-4.8994+2.3193i, \\ \lambda _3^2= & {} -4.8994+2.3193i. \end{aligned}$$

For the three equilibria, there are eigenvalues with positive value or positive real parts; obviously, $S_0$, $S_1$, and $S_2$ are unstable equilibria (red dots in Fig. 2b).

The unstable equilibria $S_1$ and $S_2$ attract the unstable separatrices of the equilibrium $S_0$, and the different attractors are simulated as shown in Fig. 2b. At two different sets of initial values, $S_1$ and $S_2$ excite the two attractors (the green curve and purple curve), whose trajectories all meet the equilibrium $S_0$. Meanwhile, under the initial value of $x(0)=0.3, y(0)=0.1, z(0)=0.6$, the system (1) displays a hidden attractor (the blue curve) that motions around the unstable equilibria $S_1$ and $S_2$ and exclude certainly by the saddle zero equilibrium $S_0$. Obviously, the chaotic attractor’s basin of attraction does not intersect with small neighborhoods of the unstable equilibria $S_0$, $S_1$, and $S_2$ and is located far away from such points. At the same time, there is a complex change with the different parameter c, due to the identical equation $a=-bc$, so parameter c has a large impact on the dynamic evolvement of system (1); the Lyapunov exponents calculated by choosing different c are shown in Fig. 2c.

Now, the impacts of parameters c on the hidden attractor will be discussed. Lyapunov exponents reflect the average emissivity between adjoining dots, so it can be employed to characterize the sensitivity of chaotic motion to initial condition. At the same time, Lyapunov exponents contain rich dynamic information, which results in one can master the systems dynamic characteristics of convergence or divergence when the Lyapunov exponent spectrum of a system is known. It is well known that the positive maximum Lyapunov exponent shows certain chaos features, while the other ones show stability or period features. According to Fig. 2c, we can easily find that the system (1) can transition among the three different states (stability, period, or chaos). For example, the system locates in the stability range in the region $c\in [1,\;6.6558)$ (three Lyapunov exponents take negative values) and then transit to the chaotic range in the region $c\in (6.6558,\;10]$ (one Lyapunov exponent takes positive values). At point $c=6.6558$, we will discuss the state below.

In more detail, the system (1) can display the following dynamical behavior varying $c\in [0,\;10]$.

(a) We fix the parameter as $c=3$; the three Lyapunov exponents of system (1) are all less than 0 (Fig. 2c); here, the following Lyapunov exponents can be calculated as:

$$\begin{aligned} \mathrm{LE}_1 =-0.3539,\;\mathrm{LE}_2 =-0.3543,\;\mathrm{LE}_3 ={-2.7918}. \end{aligned}$$

So system (1) is in a stable state, as shown in Fig. 2b. At this point, we have the following equilibria:

$$\begin{aligned} S_0= & {} (0,\;0,\;0) \\ S_1= & {} (-2.1094,\;-2.1094,\;2.4495) \\ S_2= & {} (2.1094,\;2.1094,\;2.4495) \end{aligned}$$

which can be easily verified to be unstable.

Due to the three unstable equilibria, there are self-excited attractors that occur in a state of stability. It can be seen that steady attractors (the blue curve) are “attracted “by one equilibrium. Figure 3 shows that the trajectories starting from initial values asymptotically approach the equilibria $S_2$ and $S_1$, respectively. At the same time, time responses are given and x converge to a fixed point(2.1094 or -2.1094, respectively). It is interesting that there is no hidden attractor using the above given parameters.

Fig. 3

Phase orbits and time responses of system (1) when $c=3$ (initial values of steady attractors are selected as: a $x(0)=0.1, y(0)=0.001, z(0)=0$, b $x(0)=-0.5, y(0)=-0.1, z(0)=-0.1)$

(b) When the parameter is chosen as $c=6.6558$, the three Lyapunov exponents can be calculated as:

$$\begin{aligned} \mathrm{LE}_1 =0,\;\mathrm{LE}_2 =-\,\hbox {0.0225},\;\mathrm{LE}_3 =-\,\hbox {5.3082}, \end{aligned}$$

which suggests that the system (1) shows a routine limit cycle for the fixed parameters $a=-bc,\;b=-0.5,\;c=6.6558,\;d=1$. At the same time, the two nonzero equilibria $S_{1,2} =(\pm \hbox {3.4338},\;\pm \hbox {1.7868},\hbox {6.1355})$ are stable focus nodes corresponding to the following eigenvalues

$$\begin{aligned} \lambda _1^{1,2}= & {} -5.2786, \lambda _2^{1,2} =-0.0246+\hbox {3.776}i, \\ \lambda _3^{1,2}= & {} -\hbox {0.0246}-\hbox {3.7765}i. \end{aligned}$$

The limit cycle with period-1 generated from the fixed initial values can be approximatively calculated as shown in Fig. 4. Fortunately, in that time frame of the 3rd time unit to 30th time unit, it can be seen clearly that system (1) has period-1 hidden attractor around the two stable equilibria $S_{1,2}$, respectively (the initial value of $x(0)=-3.8$, $y(0)=-2.1$, $z(0)=-3.1$ is employed for the blue curve and $x(0)=3.8$, $y(0)=2.1$, $z(0)=-3.1$ is employed for the green curve).

Fig. 4

Phase orbits and time responses of system (1) when $c=6.6558$

(c) When taking the point $c=6.8$, system (1) displays the interesting phenomenon that the hidden attractor coexists with the self-excited attractor as shown in Fig. 2b.

In addition, when $b\in [-2,\;0]$, the Lyapunov exponents calculated by choosing different b are shown in Fig. 5. For the boxed part, we can see the enlarged part in Fig. 5b more clearly.

Fig. 5

Lyapunov exponents of system (1) when $b\in [-2,\;0]$

Fig. 6

Phase orbits and time responses of system (1) when $b=-0.2$ (initial values of steady attractors are selected as: the green curve: $x(0)=16, y(0)=17, z(0)=18$; the blue curve: $x(0)=-16, y(0)=-17, z(0)=18)$. (Color figure online)

(a) We fix the parameter as $b=-0.2$; the three Lyapunov exponents of system (1) are all less than 0 as shown in Fig. 5, so system (1) is in steady state. At this point, the three equilibria are calculated as follows:

$$\begin{aligned} S_0= & {} (0,\;0,\;0) \\ S_1= & {} (-{3.4756},\;-{1.8069},\;{6.2801}) \\ S_2= & {} ({3.4756},\;{1.8069},\;{6.2801}). \end{aligned}$$

By numerical simulation, the system (1) displays steady attractors as shown in Fig. 6. The trajectories (the green curve and the blue curve) starting from different initial values asymptotically tend to the equilibria $S_1$ and $S_2$, respectively. At the same time, time responses are given and x converges to a fixed point (- 3.4756 or 3.4756, respectively). Similarly, by using the above given parameters, there is no hidden attractors when system (1) is in stable state.

Fig. 7

Attractors of the system (1) under different initial values

Fig. 8

Time responses of x(t) in system (1) (c and d are the part enlarged picture)

(b) When the parameter is chosen as $b=-\hbox {0.4261}$, system (1) has a zero Lyapunov exponent (the purple curve) as shown in Fig. 5, and the three Lyapunov exponents can be calculated as: $\mathrm{LE}_1 =0,\;\mathrm{LE}_2 ={-0.0225},\;\mathrm{LE}_3 ={-5.3082}$; this implies that there exists limit cycle attractor (the purple curve and the green curve) as shown in Fig. 7; the corresponding initial values are $x(0)=-0.01, y(0)=-0.02, z(0)=0.03$ and $x(0)=0.01, y(0)=0.02, z(0)=0.03)$ in system (1), and we will analyze the limit cycle attractor detailedly in Fig. 8. Fortunately, a hidden chaotic attractor (the blue curve, the corresponding initial value, and the three Lyapunov exponents are $x(0)=1.63, y(0)=2.25, z(0)=3.16$ and $\mathrm{LE}_1 =0.2508,\;\mathrm{LE}_2 = 0 ,\;\mathrm{LE}_3 ={-11.9511})$ can be detected coexisting with the self-excited limit cycle attractors as shown in Fig. 7.

Fig. 9

Transient chaos phenomenon and time response of system (1) when $b=-\hbox {0.4261}$ (c is the part enlarged picture)

Further analyzed by numerical simulation, the self-excited attractors plotted in Fig. 7 have finally evolved to the periodic states versus time t; the results of finding periodic attractor are described in Fig. 8. Nevertheless, the limit cycle with period-1 is approached by employing the gradually decreased amplitude. One can observe that the state variable x evolves from the irregular period to stable periodic state gradually; the corresponding phase diagrams are described in Fig. 8a–f (the purple curve and the green curve). In Fig. 8e, we can see that the purple trajectory from the initial of $x(0)=-0.01, y(0)=-0.02, z(0)=0.03$ stabilize to a limit cycle, and the final period-1 trajectory in the time unit $t\in [160,\;200]$ is shown in Fig. 8f. Additionally, there is the same case for the other coexisting self-excited attractors (the green curve).

Fig. 10

Two kinds of attractors and time responses of system (1) with different initial values There can also observe that system (1) has a transient chaos phenomenon when the initial values are given as $x(0)=23, y(0)=24, z(0)=25$, shown in Fig. 11, just like Fig. 9

Now, we continue to analyze the chaos characteristics of system (1) when $b=-{0.4261}$. The attractor and time response are plotted in Fig. 9 when the initial values are given as $x(0)=10, y(0)=10, z(0)=10$; obviously, the transient chaos phenomenon appears as the evolution of system (1). According to Fig. 9, system (1) displays chaotic state when time unit $t\in [0,\;70]$ and corresponds to the twin-scroll attractor TS (the blue curve in Fig. 9a), whereas, as time goes on, the time response of system (1) appears periodic state PS and corresponds to the contraction (the green curve in Fig. 9a) revolving around the equilibrium $S_1$. Furthermore, Fig. 9b presents the time response of x, which can describe the evolution of transient chaos more clearly and exactly. The above-mentioned process can be described as the system (1) changes from chaotic state into periodic state with time (the mechanism is the same to the above analysis in Fig. 8), that is, transient chaos phenomenon. The generating mechanism is that the twin-scroll chaotic attractor touches on an unstable periodic orbit near a critical value and leads to the happening of border crisis.

(c) When the parameter is chosen as $b=-0.46$, a positive Lyapunov exponent (the purple curve) can be seen in Fig. 5, so there exists a chaotic attractor in system (1). Here, the three equilibria are calculated as follows:

$$\begin{aligned} S_0= & {} (0,\;0,\;0) \\ S_1= & {} (-{3.4756},\;-{1.8069},\;{6.2801}) \\ S_2= & {} ({3.4756},\;{1.8069},\;{6.2801}). \end{aligned}$$

Numerical simulations are used to detect the chaotic behaviors when the different initial values are given. In Fig. 10, we can find that the hidden attractor and the periodic attractor are coexisted, just like Fig. 2b.

Fig. 11

Transient chaos phenomenon and time response of system (1) when $b=-0.46$

3 The Hamilton energy of generalized Lorenz system with hidden attractors

In this section, we will seek a variable function in the phase space as the Hamilton energy function. So in order to do that, the dynamic system (1) can be rewritten as

$$\begin{aligned} {\dot{x}}=f(x), \end{aligned}$$

(5)

where $x\in R^{n}$, f(x)is a smooth function.

By the Helmholtz theorem, the system (2) can be also regarded as the vector field to discuss the energy problems and be decomposed into the conservative field $f_c (x)$ and dissipative field $f_d (x)$ inevitably[26, 27], that is,

$$\begin{aligned} f(x)=f_c (x)+f_d (x). \end{aligned}$$

(6)

The change in energy comes from work done by electric field, and one can employ H(x, y, z) as the Hamilton energy function, which meets the following equations:

$$\begin{aligned}&\nabla H^{T}f_c (\cdot )=0 \end{aligned}$$

(7)

$$\begin{aligned}&\quad {\dot{H}}=\frac{\mathrm{d}H}{\mathrm{d}t}=\nabla H^{T}f_d (\cdot ). \end{aligned}$$

(8)

For the system (1), one has

$$\begin{aligned} f_c (x)= & {} \left( {\begin{array}{l} ay-byz \\ cx-xz \\ xy \\ \end{array}} \right) , f_d (x)=\left( {\begin{array}{l} -ax \\ -y \\ -dz \\ \end{array}} \right) . \end{aligned}$$

(9)

According to Eq. 6, the Hamilton energy function H(x, y, z) can be written as the following:

$$\begin{aligned} (ay-byz)\frac{\partial H}{\partial x}+(cx-xz)\frac{\partial H}{\partial y}+xy\frac{\partial H}{\partial z}=0. \end{aligned}$$

(10)

Then, a general solution of Eq. (10) is obtained as

$$\begin{aligned} H=\frac{1}{2}\left[ {x^{2}-\frac{a}{c}y^{2}+\left( {b-\frac{a}{c}} \right) z^{2}} \right] \end{aligned}$$

(11)

and its differential coefficient versus time can be described as

$$\begin{aligned} {\dot{H}}= & {} \frac{1}{2}\cdot 2x\cdot {\dot{x}}-\frac{a}{2c}\cdot 2y\cdot {\dot{y}} \\&\quad +\,\left( {\frac{b}{2}-\frac{a}{2c}} \right) \cdot 2z\cdot {\dot{z}} \\= & {} x\cdot {\dot{x}}-\frac{a}{c}\cdot y\cdot {\dot{y}}+\left( {b-\frac{a}{c}} \right) \cdot z\cdot {\dot{z}} \\= & {} x[-a(x-y)-byz] \\&\quad -\,\frac{a}{c}\cdot y(cx-y-xa) \\&\quad +\,(b-\frac{a}{c})\cdot z(-dz+xy) \\= & {} -ax^{2}+axy-bxyz-axy \\&\quad +\,\frac{a}{c}y^{2}+\frac{a}{c}xyz-dbz^{2} \\&\quad +\,bxyz+\frac{ad}{c}z^{2}-\frac{a}{c}xyz \\= & {} -ax^{2}+\frac{a}{c}y^{2}+\left( {dbz^{2}+\frac{ad}{c}} \right) z^{2} \\= & {} x\cdot (-ax)+\left( {-\frac{a}{c}y} \right) \cdot (-y) \\&\quad +\,\left( {b-\frac{a}{c}} \right) \cdot z\cdot (-dz) \\= & {} \nabla H^{T}f_d. \end{aligned}$$

Now, we will discuss the energy shift of system (1) by the Hamilton energy defined in Eq. (11).

(a) Parameter selection: $a=10$, $b=0$, $c=24. 5$, $d=8/3$.

For the system (1), we choose the parameters as $a=10$, $b=0$, $c=24.5$, and $d=8/3$; the simulations are shown in Figs. 14 and 15. It can be found in Fig. 12 that the curve starts from initial value and displays a periodic motion (the blue curve) when time unit $t\in [0,\;39]$, which can also be seen in Fig. 13 about the time response of state variable x. The curve continues to extend and crossovers to the negative value region and then goes back to the periodic orbitals after a period of chaotic motion (shown in Fig. 12a). From this beginning, the curve repetitive oscillates between the motions of periodicity and chaos (shown in Fig. 12b). In Fig. 11, the correspondence of time response and Hamilton energy is given. Obviously, some peaks emerge and smooth the shift to slower growth in the periodic orbitals. Once the chaos occurs (the green curve), some sharp peaks for the energy and time response are located concurrently dramatically. But, more remarkable, the larger values of the amplitude correspond to the smaller energy value just because that the dramatic chaos oscillation consumes large amounts of energy; for example, the sharp peaks $p^{+}$ and $q^{+}$ share the smaller energy value, whereas the mean peak $m^{+}$ shares the larger energy value. The three dots ($p^{+}$, $q^{+}$, and $m^{+}$) in Fig. 13a correspond to the three dots ($p^{-}$, $q^{-}$, and $m^{-}$) in Fig. 13b, respectively.

Fig. 12

Evolution of chaotic attractors in system (1)

Fig. 13

Time response of state variable x(t) and Hamilton energy H

(b) Parameter selection: $a=1.5$, $b=-0.5$, $c=3$, $d=1$.

We choose the parameters and initial values employed by Fig. 3, and the time response of state variable x and Hamilton energy H are calculated in Fig. 14. The attractor and time response plotted in Figs. 3 and 14 conform that system (1) is stable ultimately. If the stabilization line fixed on the constant 2.1094 is regarded as the baseline, state variables go through a sharp peaks at the 5th time unit, and then the energy function undergoes quick shift by reducing its value at the same time. After a period of state evolution, system (1) begins to stabilize gradually at the 15th time unit; correspondingly, the energy function stabilized around the fixed value. The phenomenon can be explained in the mechanism that system (1) needs a certain amount of energy to maintain steady state.

Fig. 14

Time response of state variable x(t) and Hamilton energy H

Fig. 15

Time response of state variable x(t) and Hamilton energy H

Fig. 16

The part enlarged picture of Fig. 15 and evolution process of system (1)

Fig. 17

Phase portraits of variables when the Hamilton energy is modulated

(c) Parameter selection: $a=2.98$, $b=-0.438$, $c=6.8$, $d=1$. We employ $x(0)=10, y(0)=10, z(0)=10$ as the initial values and analyze the change of Hamilton energy of the system (1). The time response of state variable x and Hamilton energy H are plotted in Fig. 15. Intuitively, one can find the transient chaos process that the trajectory starting from a periodic-like motion (the green curve) moves around one equilibrium until the 35th time unit, then undergoes the chaos oscillation (the red curve) around the two equilibria between the time unit 35 and 62, and finally reaches stabilization (the blue curve) from periodic state at the 62nd time unit. The evolution process of transient chaos phenomenon is observed in Fig. 16e, in which the colors of curve are consistent with the ones in Fig. 15a. As the enlarged picture, Fig. 16d presents the energy change when system (1) takes different motions. At the 35th time unit, the curve breaks the periodic-like state and then enters chaotic state accompanied by the more consume of energy at the critical moment of state transform, as shown in the dot $p^{1}$ (corresponding to the dot $o^{1})$. At the 58th time unit, the motion trajectory has relative minimum amplitude, so the relative less energy is consumed, as shown in the dot $p^{2}$ (corresponding to the dot$o^{2})$. At the critical moment, the rapid jump occurs in energy by adding it value as seen in the dots $p^{3}$ and $p^{4}$. At last, the energy has a stability value when system (1) achieved steady state gradually.

Fig. 18

Lyapunov exponents of system (1) when $k\in [0,\;0.68]$

Fig. 19

Bifurcation diagrams of system (1) when $k\in [0.35,0.68]$

Fig. 20

Evolutions of the feedback gain k, the time response of z(t), the Hamilton energy H

From these observations and the law of the conservation of energy, the energy oscillation is accompanied by the large amplitude when system (1) has more complex oscillation. For example, the chaos motion consumes more energy than periodic motion with the smaller amplitude value, and the smoother amplitude is embodied in energy function. It is interesting to find that the transient chaos phenomenon has more changes in the oscillation of energy function.

4 The new control method based on Hamilton energy

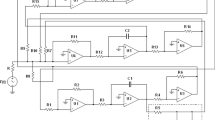
In this section, we present a new control method, that is, Hamilton energy control. According to Eq. 11, the energy function is dependent on all the variables and parameters of the system (1), so the evolution of different states for the system has great influence on energy function, as shown in Figs. 12, 13, 14, 15, and 16. On the contrary, the change of energy function should also affect the dynamical behavior of the chaotic system (1), as shown in Fig. 17.

Fig. 21

Attractors of system (1) a $k=0.1$; b $k=0.39$; c $k=0.66$

In order to verify the conclusion, we will design a controller and introduce into system (1); the dynamic function is set as follows:

$$\begin{aligned} \left\{ {\begin{array}{l} {\dot{x}}=-a(x-y)-byz \\ {\dot{y}}=cx-y-xz \\ {\dot{z}}=-dz+xy-kH \\ {\dot{H}}=-ax^{2}+a/cy^{2}+(-bd+ad/c)z^{2} \\ \end{array}} \right. \end{aligned}$$

(12)

where k is the feedback gain, H is the Hamilton energy of system (1), and we call the control method Hamilton energy control (or HE control for short). In the following, the state changes of system (1) will be investigated by using the feedback control. Firstly, the Lyapunov exponents are calculated when the value of feedback gain k ranges from 0 to 0.68, and the bifurcation diagrams with the value from 0.35 to 0.68, as exhibited in Figs. 18 and 19. It can be observed intuitively that the feedback gain k holds the system (1): the chaotic states at the interval $k\in [0,\;0.38]$ and the periodic motion at the interval $k\in [0.38,\;0.68]$. So on the whole, system (1) holds the motion process of evolution from chaotic state to periodic state, that is, the classic inverse period-doubling bifurcation.

It is found that the Hamilton energy in the system (1) changes greatly with increasing the feedback gain k. If we fix the parameters$k=0.1$, $k=0.39$, and $k=0.66$, the three different motion states of chaos (the blue curve), multi-periodic motion (the red curve), and period-1 motion (the purple curve) are shown in Figs. 20b and 21. The corresponding Hamilton energies are presented using different colors in Fig. 20c. By adjusting the feedback gain k, as shown in Fig. 20a, the system (1) can be controlled in different states effective; moreover, the energy transform is an essential part of dynamics system oscillation.

5 Conclusions

In this paper, the generating mechanism of hidden attractors in a generalized Lorenz system has been analyzed by numerical simulation. It is found that the hidden attractors are depending on the system parameters and initial values. According to the discussion about the motion states, the generalized Lorenz system has coexistence phenomena, including chaos, period, and transient chaos phenomenon. Then, the Hamilton energy function is calculated based on the Kirchhoff’s law and is said to relate to system parameters and initial values. Energy function is affected by parameters and initial values of the system (1) and can suppress the chaotic behavior in turn. At last, a new Hamilton energy control method is presented by the feedback gain. The advantage of the control method is that energy transform can be detected when controlling the system to the expected state.