1 Introduction

The problem of scavenging energy from ambient sources of vibration for powering up small-scale electronic devices such as micro-electro-mechanical systems (MEMS) is an active research topic and has a beneficial impact in the development of autonomous MEMS devices able to ensure their own power supply; see, for instance, [1] and references therein. A simple nonlinear mechanical attachment modeling such devices which exhibits relevant phenomena in the context of energy harvesting (EH), such as limit cycle (LC) oscillations and parametric amplification, is the Mathieu–van der Pol–Duffing-type equation [2, 3]. For instance, a certain type of radio frequency resonator can be designed by such an oscillator, as shown in [2, 4,5,6]. The sources of vibration present in the resonator are the self-sustained LC oscillations induced by a DC laser of sufficient amplitude and the parametric amplification produced by modulating the incident laser. In this case, the response of the oscillator can be frequency-locked near the resonance with a relatively large amplitude or quasi-periodic (QP) away from the resonance with a low amplitude [3, 7,8,9]. In such a system, energy can be harvested only in the frequency-locked regime near the resonance, while the QP regime should be avoided [10, 11]. However, it was shown in a series of papers [12,13,14] that in the presence of time delay, it is possible to exploit QP vibrations for scavenging energy in broadband of parameter space away from the resonance with a good performance. Indeed, in the presence of time delay large-amplitude QP vibrations can take place in certain ranges of excitation frequency and delay parameters.

In a recent paper [15], QP vibration-based EH has been studied in a delayed van der Pol oscillator coupled to an electromagnetic EH device. It was demonstrated that the modulation of the delay amplitude may give rise to stable large-amplitude QP vibrations in broadband of parameters. More recently, QP vibration-based EH was studied in a forced and delayed Duffing harvester device [16]. It was concluded that energy can be extracted from QP vibrations over broadband of excitation frequency away from the resonance, circumventing bistability and jump phenomena near the resonance. Moreover, EH from QP vibrations has been explored using a delayed electromagnetic coupling [17] and it was shown that an optimum value of the excitation frequency for which the QP vibrations amplitude and the output power are maximum can be obtained. In [17], the harvester is subjected to a delayed self-sustained vibration coupled to a delayed electromagnetic component, while in [16] the Duffing-type harvester is excited by an external forcing and the delay introduced in the mechanical attachment.

In the present paper, we consider the case where the nonlinear harvester is under self-sustained and parametric excitations and the delay is present in both mechanical and electrical components. Specifically, we consider a delayed Mathieu–van der Pol–Duffing-type resonator coupled to a delayed piezoelectric harvester circuit and we explore the effect of time delays on the performance of the harvester. This study can be viewed as an extension of the works provided in [16, 17]. For the sake of generality, it is assumed that the time delay present in the mechanical component is different from that present in the electric circuit.

The next section describes the harvester system and gives an approximation of the periodic response and power amplitudes near the principal parametric resonance using the multiple scales method. In Sect. 3, the QP response is approximated applying the second-step multiple scales method and the corresponding harvested power is provided. Section 4 provides the main results. Specifically, the influence of time delays and coupling parameters of the harvester device on the EH performance is examined. A summary of the results is given in the concluding section.

2 Model description and periodic energy harvesting

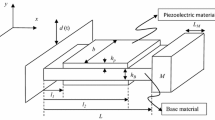
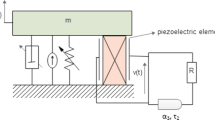
The energy harvester MEMS device considered consists of a Mathieu–van der Pol–Duffing resonator coupled to an electrical circuit through a piezoelectric device as shown in the schematic presented in Fig. 1. We assume that the mechanical and electrical components of the harvester are both under a time-delayed feedback such that the dimensionless governing equations for the system can be written as

$$\begin{aligned}&\ddot{x}(t)+[1-h \cos \omega t]x(t)-[\alpha -\beta x(t)^{2}]{\dot{x}}(t)\nonumber \\&\quad +\,\gamma x(t)^{3}-\chi v(t)= \alpha _{1} x(t-\tau _{1}) \end{aligned}$$
(1)
$$\begin{aligned}&{\dot{v}}(t)+\lambda v(t)+\kappa {\dot{x}}(t)=\alpha _{2} v(t-\tau _{2})\ \end{aligned}$$
(2)

Here x(t) is the relative displacement of the mass m and v(t) is the voltage across the load resistance. The coefficients h, \(\omega \) are, respectively, the amplitude and the frequency of the parametric excitation, \(\alpha \) and \(\beta \) the mechanical damping components, \(\gamma \) the stiffness, \(\chi \) the piezoelectric coupling term in the mechanical attachment, \(\kappa \) the piezoelectric coupling term in the electrical circuit and \(\lambda \) the reciprocal of the time constant of the electrical circuit. The parameters \(\alpha _{1}\), \(\alpha _{2}\) and \(\tau _{1}\), \(\tau _{2}\) are, respectively, the feedback gains and time delays in the mechanical and electric attachments. The current study is based on the linearized piezoelectric coupling in Eq. (1) although the piezoelectric constitutive equations are nonlinear [18,19,20].

Fig. 1
figure 1

Schematic of the EH system

Full size image

It is worth noticing that the delayed Mathieu–van der Pol–Duffing oscillator [Eq. (1) with \(\chi =0\)] has been investigated in [21]. Attention was focused on approximating QP and frequency-locked responses. In [7], the dynamic of such an oscillator under external forcing has been studied, while the undelayed forced Mathieu–van der Pol–Duffing oscillator, modeling an optically actuated radio frequency MEMS, was considered in [4, 9].

To study the response of the harvester system (1), (2) near the principal parametric resonance, we assume the resonance condition \(1=\frac{\omega ^{2}}{4}+\sigma \) where \(\sigma \) is a detuning parameter. Approximation of solutions is obtained using the method of multiple scales [22] by introducing a bookkeeping parameter \(\epsilon \) and scaling as \(\alpha =\epsilon {\tilde{\alpha }},\beta =\epsilon {\tilde{\beta }}, \gamma =\epsilon {\tilde{\gamma }}, \chi =\epsilon {\tilde{\chi }},h=\epsilon {\tilde{h}}, \alpha _{1}=\epsilon \tilde{\alpha _{1}}, \sigma =\epsilon {\tilde{\sigma }}\). Equations (1), (2) become

$$\begin{aligned}&\ddot{x}(t)+\frac{\omega ^{2}}{4}x(t)=\epsilon [({\tilde{\alpha }}-{\tilde{\beta }} x(t)^{2}){\dot{x}}(t)-{\tilde{\gamma }} x(t)^{3}\nonumber \\&\quad +\,{\tilde{\chi }} v(t)+ {\tilde{h}} \cos (\omega t) x(t)-{\tilde{\sigma }} x(t)+\tilde{\alpha _{1}} x(t-\tau _{1})]\ \end{aligned}$$
(3)
$$\begin{aligned}&{\dot{v}}(t)+\lambda v(t)+\kappa {\dot{x}}(t)=\alpha _{2} v(t-\tau _{2})\ \end{aligned}$$
(4)

We seek a solution of Eqs. (3) and (4) in the form:

$$\begin{aligned}&x(t)=x_{0}(T_{0},T_{1})+\epsilon x_{1}(T_{0},T_{1})+O(\epsilon ^{2})\ \end{aligned}$$
(5)
$$\begin{aligned}&v(t)=v_{0}(T_{0},T_{1})+\epsilon v_{1}(T_{0},T_{1})+O(\epsilon ^{2})\ \end{aligned}$$
(6)

where \(T_{0}=t\), and \(T_{1}=\epsilon t\). Using the time derivatives \(\frac{\mathrm{d}}{\mathrm{d}t}=D_{0}+\epsilon D_{1}+O(\epsilon ^{2})\) and \(\frac{\mathrm{d}^{2}}{\mathrm{d}t^{2}}=D_{0}^{2}+\epsilon ^{2} D_{1}^{2}+2\epsilon D_{0} D_{1}+O(\epsilon ^{2})\) where \(D_{i}^{j}=\frac{\partial ^{j}}{\partial ^{j} T_{i}}\), substituting (5), (6) into (3), (4) and balancing terms of like powers of \(\epsilon \), we obtain up to the second order

$$\begin{aligned}&D_{0}^{2}x_{0}+\frac{\omega ^{2}}{4}x_{0}=0\ \end{aligned}$$
(7)
$$\begin{aligned}&D_{0}v_{0}+ \lambda v_{0}+\kappa D_{0}x_{0}=\alpha _{2} v_{0\tau _{2}}\ \end{aligned}$$
(8)

and

$$\begin{aligned} D_{0}^{2}x_{1}+\frac{\omega ^{2}}{4}x_{1}= & {} -2D_{0} D_{1}x_{0}\nonumber \\&+\,({\tilde{\alpha }}-{\tilde{\beta }} x_{0}^{2})D_{0}x_{0} -{\tilde{\sigma }}x_{0}-{\tilde{\gamma }} x_{0}^{3}\nonumber \\&+\,{\tilde{\chi }} v_{0}+{\tilde{h}}\cos (\omega t)x_{0}+\tilde{\alpha _{1}} x_{1\tau _{1}}\ \end{aligned}$$
(9)
$$\begin{aligned} D_{0}v_{1}+\lambda v_{1}= & {} -D_{1}v_{0}-\kappa D_{0}x_{1}-\kappa D_{1}x_{0}\nonumber \\&+\,\alpha _{2} v_{1\tau _{2}}\ \end{aligned}$$
(10)

The first-order solution is given by

$$\begin{aligned} x_{0}(T_{0},T_{1})= & {} A(T_{1})e^{i\frac{\omega T_{0}}{2}}+{\bar{A}}(T_{1})e^{-\frac{\omega T_{0}}{2}}\ \end{aligned}$$
(11)
$$\begin{aligned} v_{0}(T_{0},T_{1})= & {} \frac{-\kappa i\omega A(T_{1})}{2\lambda +i\omega -2\alpha _{2} e^{-i\frac{\omega \tau _{2}}{2}}} e^{i\frac{\omega T_{0}}{2}}\nonumber \\&\quad +\, \frac{\kappa i\omega {\bar{A}}(T_{1})}{2\lambda -i\omega -2\alpha _{2} e^{i\frac{\omega \tau _{2}}{2}}} e^{-i\frac{\omega T_{0}}{2}} \end{aligned}$$
(12)

where \(A(T_{1})\) and \({\bar{A}}(T_{1}) \) are unknown complex conjugate functions. Substituting Eqs. (11), (12) into (9), (10) and eliminating the secular terms gives

$$\begin{aligned}&-i\omega (D_{1}A)+\frac{i{\tilde{\alpha }}\omega A}{2}-\frac{i{\tilde{\beta }}\omega }{2}A^{2}{\bar{A}}-{\tilde{\sigma }}A -3{\tilde{\gamma }}A^{2}{\bar{A}}\nonumber \\&\quad -\,\frac{\kappa i\omega {\tilde{\chi }}A}{2\lambda -2\alpha _{2}\cos (\frac{\omega \tau _{2}}{2})+i(\omega +2\alpha _{2}\sin (\frac{\omega \tau _{2}}{2}))} \nonumber \\&\quad +\,\frac{{\tilde{h}}}{2}{\bar{A}}+\tilde{\alpha _{1}}A e^{-\frac{i\omega \tau _{1}}{2}}=0\ \end{aligned}$$
(13)

Assuming \(A=\frac{1}{2}ae^{i\theta }\) where a and \(\theta \) are the amplitude and the phase, we obtain the modulation equations

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\mathrm{d}a}{\mathrm{d}t}=S_{1}a+S_{2}a^{3}+S_{3}a\sin (2\theta )\\ \displaystyle a\frac{\mathrm{d}\theta }{\mathrm{d}t}=S_{4}a+ S_{5}a^{3}+S_{3}a\cos (2\theta )\end{array} \right. \end{aligned}$$
(14)

in which \(S_{i} (i=1,\ldots ,5)\) are given in Appendix. The solution given by (11), (12) reads

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle x_{0}(T_{0},T_{1})=a \cos (\frac{\omega t}{2}+\theta )\\ \displaystyle v_{0}(T_{0},T_{1})=V \cos (\frac{\omega t}{2}+\theta +\arctan \frac{2\lambda -2\alpha _{2}\cos (\frac{\omega \tau _{2}}{2})}{\omega +2\alpha _{2}\sin (\frac{\omega \tau _{2}}{2})})\end{array} \right. \nonumber \\ \end{aligned}$$
(15)

with the condition \(\omega +2\alpha _{2}\sin (\frac{\omega \tau _{2}}{2})\ne 0\), and the voltage amplitude V is given by

$$\begin{aligned} V=\frac{\kappa \omega }{\sqrt{(2\lambda -2\alpha _{2}\cos (\frac{\omega \tau _{2}}{2}))^{2}+(\omega +2\alpha _{2}\sin (\frac{\omega \tau _{2}}{2}))^{2}}}a\nonumber \\ \end{aligned}$$
(16)

The steady-state response of system (14) obtained by setting \(\frac{\mathrm{d}a}{\mathrm{d}t}=\frac{\mathrm{d}\theta }{\mathrm{d}t}=0 \) corresponds to periodic solution of Eqs. (3) and (4). Eliminating the phase, the amplitude a is given by the equation

$$\begin{aligned}&(S_{2}^{2}+S_{5}^{2})a^{4}+(2S_{1}S_{2}+2S_{4}S_{5})a^{2}+S_{1}^{2}\nonumber \\&\quad +\, S_{4}^{2}-S_{3}^{2}=0 \end{aligned}$$
(17)

The condition for Eq. (17) to have two real roots is:

$$\begin{aligned} (2S_{1}S_{2}+2S_{4}S_{5})^{2}-4(S_{2}^{2}+S_{5}^{2})(S_{1}^{2}+S_{4}^{2}-S_{3}^{2})>0\nonumber \\ \end{aligned}$$
(18)

and the conditions for the stability of the steady-state response are:

$$\begin{aligned}&2(S_{1}S_{2}+S_{4}S_{5})>0 \end{aligned}$$
(19)
$$\begin{aligned}&S_{1}^{2}+S_{4}^{2}-S_{3}^{2}>0 \end{aligned}$$
(20)
Fig. 2
figure 2

Stability chart of the periodic solution in the plane \((\alpha _{1},\tau _{1})\); SP for stable periodic solution, UP for unstable periodic solution; \(h=0.25\), \(\omega =2\), \(\alpha =0.1\), \(\beta =0.2\), \(\gamma =0.05\), \(\lambda =0.05\), \(\kappa =0.5\), \(\chi =0.05\), \(\alpha _{2}=0.05\) and \(\tau _{2}=4.2\)

Full size image

The stability chart of the periodic solution is shown in Fig. 2 in which two regions can be distinguished. In the white region, where the conditions (19) and (20) are satisfied, a stable periodic (SP) solution is present, and within the gray regions, an unstable periodic (UP) one exists. The parameter values are chosen as in previous works [16, 17, 21]

The average power is obtained by integrating the dimensionless form of the instantaneous power \(P(t)= \lambda v(t)^{2}\) over a period T. This is given by

$$\begin{aligned} P_{av}=\frac{1}{T}\int _{0}^{T}\lambda v^{2}\mathrm{d}t\ \end{aligned}$$
(21)

where \(T=\frac{4\pi }{\omega }\). Hence, the average power expressed by \(P_{av}=\frac{\lambda V^{2}}{2}\) takes the form

$$\begin{aligned} P_{av}=\frac{1}{2}\left( \frac{\lambda \kappa ^{2}\omega ^{2}}{(2\lambda -2\alpha _{2}\cos (\frac{\omega \tau _{2}}{2}))^{2}+(\omega +2\alpha _{2}\sin (\frac{\omega \tau _{2}}{2}))^{2}}\right) a^{2}\nonumber \\ \end{aligned}$$
(22)

where the amplitude a is given by Eq. (17). Applying the maximization procedure, the maximum power reads

$$\begin{aligned} P_\mathrm{max}=\left( \frac{\lambda \kappa ^{2}\omega ^{2}}{(2\lambda -2\alpha _{2}\cos (\frac{\omega \tau _{2}}{2}))^{2}+(\omega +2\alpha _{2}\sin (\frac{\omega \tau _{2}}{2}))^{2}}\right) a^{2}\nonumber \\ \end{aligned}$$
(23)

Equations (17) and (23) will be used to study the effect of parameters on the steady-state response and on the output power of the harvester.

3 Quasi-periodic energy harvesting

Next, we investigate the QP response. Using the fact that the slow flow (14) is invariant under the transformation \(\theta \rightarrow -\theta +\frac{\pi }{2}\), \(S_{4}\rightarrow -S_{4}\), \(S_{5}\rightarrow -S_{5}\), system (14) can be rewritten in the form

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\mathrm{d}a}{\mathrm{d}t}=S_{1}a+S_{2}a^{3}+S_{3}a\sin (2\theta )\\ \displaystyle a\frac{\mathrm{d}\theta }{\mathrm{d}t}=s S_{4}a+s S_{5}a^{3}+S_{3}a\cos (2\theta )\end{array} \right. \end{aligned}$$
(24)

in which \(s=\pm 1\). This invariance property will be exploited, as in [16], to determine the boundaries of the QP modulation envelope given by taking \(s=1\) and \(s=-1\). Analytical approximate of the QP solution is carried out using the second-step multiple scales method on the slow flow (24) [23], written in its Cartesian form as

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\mathrm{d}u}{\mathrm{d}t}=(sS_{4}-S_{5})w+\mu \{S_{1}u+(S_{2}u+sS_{5}w)(u^{2}+w^{2})\}\\ \displaystyle \frac{\mathrm{d}w}{\mathrm{d}t}=-(sS_{4}+S_{3})u+\mu \{S_{1}w+(S_{2}w-sS_{5}u)(u^{2}+w^{2})\}\end{array} \right. \nonumber \\ \end{aligned}$$
(25)

where \(u=a \cos \theta \) and \(w=-a \sin \theta \) and \(\mu \) is a new bookkeeping parameter introduced in the system such that the unperturbed one has a basic solution. A periodic solution of the modulation equations (25), corresponding to the QP response of the original system (1), (2), is sought in the form

$$\begin{aligned}&u(t)=u_{0}(T_{0},T_{1})+\mu u_{1}(T_{0},T_{1})+O(\mu ^{2})\ \end{aligned}$$
(26)
$$\begin{aligned}&w(t)=w_{0}(T_{0},T_{1})+\mu w_{1}(T_{0},T_{1})+O(\mu ^{2})\ \end{aligned}$$
(27)

where \(T_{0}=t\) and \(T_{1}=\mu t\). In terms of the variables \(T_{i}\), we have \(\frac{\mathrm{d}}{\mathrm{d}t}=D_{0}+\mu D_{1}+O(\mu ^{2})\) where \(D_{i}^{j}=\frac{\partial ^{j}}{\partial ^{j} T_{i}}\). Substituting (26) and (27) into (25), and collecting terms of like powers of \(\mu \), we obtain the systems

$$\begin{aligned}&D_{0}^{2}u_{0}+\nu ^{2}u_{0}=0 \end{aligned}$$
(28)
$$\begin{aligned}&(sS_{4}-S_{3})w_{0}=D_{0}u_{0} \end{aligned}$$
(29)
$$\begin{aligned} D_{0}^{2}u_{1}+\nu ^{2}u_{1}= & {} -D_{0}D_{1}u_{0}+S_{1}D_{0}u_{0}+( S_{2}D_{0}u_{0}\nonumber \\&+\,sS_{5}D_{0}w_{0})(u_{0}^{2}+w_{0}^{2})\nonumber \\&-(sS_{4}-S_{3})D_{1}w_{0}\nonumber \\&+\,(S_{2}u_{0}+sS_{5}w_{0})D_{0}(u_{0}^{2}\nonumber \\&+\,w_{0}^{2})+( sS_{4}-S_{3})S_{1}w_{0}\nonumber \\&+(sS_{4}-S_{3})(S_{2}w_{0}\nonumber \\&-sS_{5}u_{0})(u_{0}^{2}+w_{0}^{2}) \end{aligned}$$
(30)
$$\begin{aligned}&(sS_{4}-S_{3})w_{1}=D_{0}u_{1}+D_{1}u_{0}\nonumber \\&-S_{1}u_{0}-(S_{2}u_{0} + sS_{5}w_{0})(u_{0}^{2}+w_{0}^{2})\nonumber \\ \end{aligned}$$
(31)

where \(\nu =\sqrt{S_{4}^{2}-S_{3}^{2}}\) is the frequency of the QP modulation. Up to the first order, the solution reads

$$\begin{aligned} u_{0}(T_{0},T_{1})= & {} R(T_{1})\cos (\nu T_{0}+\psi (T_{1})) \end{aligned}$$
(32)
$$\begin{aligned} w_{0}(T_{0},T_{1})= & {} \frac{-R(T_{1})\nu }{(sS_{4}-S_{3})}\sin (\nu T_{0}+\psi (T_{1})) \end{aligned}$$
(33)

where R and \(\psi \) are, respectively, the amplitude and the phase of the QP modulation. Substituting (32) and (33) into (30) and removing secular terms, we obtain the slow–slow flow

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\mathrm{d}R}{\mathrm{d}t}=S_{1}R+\left[ \frac{S_{2}}{2}+\frac{S_{2}\nu ^{2}}{2(sS_{4}-S_{3})^{2}}\right] R^{3}\\ \\ \displaystyle R\frac{\mathrm{d}\psi }{\mathrm{d}t}=\left[ \frac{\nu sS_{5}}{4(sS_{4}-S_{3})}+\frac{3\nu ^{3} sS_{5}}{8(sS_{4}-S_{3})^{3}}+\frac{3}{8\nu }sS_{5}(sS_{4}-S_{3})\right] R^{3}\end{array} \right. \nonumber \\ \end{aligned}$$
(34)

in which equilibria correspond to QP solutions of the original equations (1), (2). By setting \(\frac{\mathrm{d}R}{\mathrm{d}t}=0\), we obtain the nontrivial equilibrium

$$\begin{aligned} R=\sqrt{-\frac{S_{1}(sS_{4}-S_{3})}{sS_{2}S_{4}}}\ \end{aligned}$$
(35)

The boundaries of the QP modulation envelope are given by Eq. (35) with \(s=\pm 1\) and periodic solution of the slow flow (25) is approximated by

$$\begin{aligned} u(t)= & {} R \cos (\theta t) \end{aligned}$$
(36)
$$\begin{aligned} w(t)= & {} \frac{-R\nu }{(sS_{4}-S_{3})} \sin (\theta t) \end{aligned}$$
(37)

Explicitly, the QP response of the original system is given by

$$\begin{aligned} x(t)=u(t)\cos (\frac{\omega t}{2})+w(t)\sin (\frac{\omega t}{2}) \end{aligned}$$
(38)

Inserting Eq. (38) into Eq. (2), the QP voltage v(t) can be obtained using a convolution integral with the boundary condition \(v (0) = v (T)\) where \(T=\frac{2\pi }{\nu }\). This leads to

$$\begin{aligned} v(t)=-\kappa e^{(\alpha _{2} e^{\lambda \tau _{2}}-\lambda ) t}\int _{0}^{t}{\dot{x}}(t')e^{(\lambda -\alpha _{2} e^{\lambda \tau _{2}}) t'} \mathrm{d}t' \end{aligned}$$
(39)

Then, the total, the average and the maximum power outputs, in the QP regime, are, respectively, given by

$$\begin{aligned}&P_{QP}(t)= \lambda (\kappa e^{(\alpha _{2} e^{\lambda \tau _{2}}-\lambda ) t}\int _{0}^{t}{\dot{x}}(t')e^{(\lambda -\alpha _{2} e^{\lambda \tau _{2}}) t'} \mathrm{d}t')^{2} \end{aligned}$$
(40)
$$\begin{aligned}&P_{avQP}= \frac{\lambda \kappa ^{2}\nu ^{2}}{2[(\lambda -2\alpha _{2}\cos (\frac{\omega \tau _{2}}{2}))^{2}+(\nu +2\alpha _{2}\sin (\frac{\omega \tau _{2}}{2}))^{2}]}R^{2} \end{aligned}$$
(41)
$$\begin{aligned}&P_\mathrm{maxQP}= \frac{\lambda \kappa ^{2}\nu ^{2}}{[(\lambda -2\alpha _{2}\cos (\frac{\omega \tau _{2}}{2}))^{2}+(\nu +2\alpha _{2}\sin (\frac{\omega \tau _{2}}{2}))^{2}]}R^{2}\nonumber \\ \end{aligned}$$
(42)

where R is obtained from Eq. (35).

4 Main results

The influence of delay parameters on the power amplitude is presented in this section. In what follows, we fix the parameters: \(\alpha = 0.1, \beta = 0.2, \lambda = 0.05\) and \(\gamma = 0.05\). Figure 3 shows the variation of the amplitudes a and R of the periodic and the QP responses versus \(\omega \) (Fig. 3a) as well as the output power amplitudes \(P_\mathrm{max}\) (for the periodic response), \(P_\mathrm{maxQP}\) (for the QP response) versus the frequency \(\omega \) (Fig. 3b) in the case of the undelayed harvester device (\(\alpha _{1}=\alpha _{2}=0\) and \(\tau _{1}=\tau _{2}=0\)). The amplitude of the periodic response is given by (17), and the boundaries of the QP modulation envelope are obtained from Eq. (35) with \(s=\pm 1\). Also, the maximum power for periodic and QP vibrations are given, respectively, by Eqs. (23) and (42). The analytical prediction (solid lines for stable and dashed line for unstable) is compared to numerical simulation (circles) obtained by the method of Runge–Kutta of order 4. The plots in Fig. 3b show that in the absence of time delay, the periodic vibration-based EH performance is better than that of the QP vibrations.

Fig. 3
figure 3

Vibration and power amplitudes versus \(\omega \) for \(h=0.25\), \(\alpha _{1}=\alpha _{2}=0\), \(\tau _{1}=\tau _{2}=0\), \(\chi =0.05\), and \(\kappa =0.5\). Analytical prediction (solid lines for stable and dashed line for unstable) and numerical simulation (circles). QPR QP response, PR periodic response; QPP QP power, PP periodic power

Full size image

The frequency response curves in terms of amplitudes and power responses are illustrated in Fig. 4 in the case where the time delay is present only in the mechanical subsystem (\(\alpha _{1}\ne 0\), \(\tau _{1}\ne 0\) and \(\alpha _{2}=0\), \(\tau _{2}=0\)). It can be observed from Fig. 4 that the presence of a small delay amplitude in the mechanical component has no significant effect on the EH performance.

In Fig. 5 is shown by the black lines the influence of time delay introduced in both mechanical and electrical components (\(\alpha _{1}\ne 0\) and \(\alpha _{2}\ne 0\)) on the EH performance of the system. These are compared to the gray lines related to the case where the delay is present only in the mechanical subsystem (Fig. 4). It can be observed that introducing the delay in the electrical circuit causes a significant increase in the QP output power in a certain range of the frequency \(\omega \) just beyond the resonance (Fig. 5b, black lines).

Fig. 4
figure 4

Vibration and power amplitudes vs \(\omega \) for \(h=0.25\), \(\alpha _1=0.02\), \(\alpha _{2}=0\), \(\tau _{1}=5.2\), \(\tau _{2}=0\), \(\chi =0.05\) and \(\kappa =0.5\). Analytical prediction (solid and dashed lines) and numerical simulation (circles)

Full size image
Fig. 5
figure 5

Vibration and power amplitudes vs \(\omega \) for \(h=0.25\), \(\alpha _{1}=0.02\), \(\tau _{1}=5.2\), \(\tau _{2}=4.2\), \(\chi =0.05\), and \(\kappa =0.5\). Black lines for delayed electric circuit (\(\alpha _{2}=\lambda \)) and gray lines for undelayed circuit (\(\alpha _{2}=0\), Fig. 4)

Full size image

Figure 6 shows the variation of the amplitude of the responses (Fig. 6a) and the powers (Fig. 6b) versus the mechanical delay amplitude \(\alpha _{1}\) for \(\alpha _{2}=0\) (undelayed circuit, gray lines) and for \(\alpha _{2}=\lambda \) (delayed circuit, black lines). The analytical prediction is compared to numerical simulation (circles) obtained by using dde23 [24] algorithm. One can observe from Fig. 6b that for small values of \(\alpha _{1}\), energy can be extracted from periodic vibrations with low performance. Beyond a certain value of \(\alpha _{1}\), QP solution appears, offering the possibility to scavenging energy with better performance when the time delay is present in the electrical circuit (\(\alpha _{2}=\lambda \)).

Fig. 6
figure 6

Vibration and power amplitudes vs \(\alpha _{1}\), for \(h=0.25\), \(\omega =2\), \(\tau _{1}=5.2\), \(\tau _{2}=4.2\), \(\chi =0.05\) and \(\kappa =0.5\). Black (gray) lines for delayed (undelayed) electric circuit \(\alpha _{2}=\lambda \) (\(\alpha _{2}=0\))

Full size image

Next, a stability analysis of the QP solution is performed by examining the nontrivial solution of the slow–slow flow (34). Figure 7a shows this stability chart in the parameter plane (\(\alpha _{1},\tau _{1}\)) indicating the gray regions where stable QP (SQP) solutions take place and the white region corresponding to unstable QP (UQP) solutions. In Fig. 7b are shown time histories and the power output responses related to crosses 1, 2, 3 in Fig. 7a. From cross 3 to cross 2 or 1, a secondary Hopf bifurcation occurs. The evolution of the SQP domains in the parameter plane \((\alpha _{1},\tau _{1})\) is depicted in Fig. 8 for different values of the parametric excitation amplitude h. One observes that for small values of h, the SQP domain covers almost the entire parameter plane. When h is increased, the SQP domain divides into two parts that shift toward higher (positive and negative) values of the delay amplitude of the mechanical subsystem \(\alpha _{1}\). This indicates that for increasing values of h, QP vibration-based EH performance can be achieved for larger values of \(\alpha _{1}\) and over certain ranges of time delay \(\tau _{1}\).

Fig. 7
figure 7

Stability chart in the plane \((\alpha _{1},\tau _{1})\), b time and power histories corresponding to different regions picked from (a). SP stable periodic, SQP stable QP; \(h=0.25\), \(\omega =2\), \(\alpha _{2}=0.05\), \(\tau _{2}=4.2\), \(\chi =0.05\) and \(\kappa =0.5\)

Full size image

Finally, we show in Figs. 9, 10, respectively, the influence of the piezoelectric coupling coefficients \(\chi \) and \(\kappa \) on the output powers. It can be observed that for the given values of parameters, QP vibration-based EH can be extracted with a good performance for small negative values of \(\chi \) (Fig. 9b) or for large negative values of \(\kappa \) (Fig. 10b).

Fig. 8
figure 8

Evolution of the stability chart in the plane \((\alpha _{1},\tau _{1})\) for \(\omega =2\), \(\alpha _{2}=0.05\), \(\tau _{2}=4.2\), \(\chi =0.05\) and \(\kappa =0.5\), a \(h=0.02\), b \(h=0.15\), c \(h=0.16\), d \(h=1\). SP stable periodic, SQP stable QP

Full size image
Fig. 9
figure 9

Vibration and power amplitudes vs \(\chi \) for \(h=0.25\), \(\omega =2\), \(\alpha _{1}=0.02\), \(\tau _{1}=5.2\), \(\tau _{2}=4.2\) and \(\kappa =0.5\). Black (gray) line for delayed (undelayed) electric circuit \(\alpha _{2}=\lambda \) (\(\alpha _{2}=0\))

Full size image
Fig. 10
figure 10

Vibration and power amplitudes vs \(\kappa \) for \(h=0.25\), \(\omega =2\), \(\alpha _{1}=0.02\), \(\tau _{1}=5.2\), \(\tau _{2}=4.2\) and \(\chi =0.05\). Black (gray) line for delayed (undelayed) electric circuit \(\alpha _{2}=\lambda \) (\(\alpha _{2}=0\))

Full size image

5 Conclusions

QP vibration-based EH has been studied in [16] for a delayed and excited Duffing-type oscillator coupled to a piezoelectric circuit, and in [17] for a delayed van der Pol oscillator with a delayed electromagnetic coupling. In the former study, optimal values of external forcing for which the power is maximum were obtained, and in the later, it was demonstrated that the maximum power of the harvester is not necessarily accompanied by the maximum amplitude of the system response.

In the present work, we have studied QP vibration-based EH in a delayed Mathieu–van der Pol–Duffing-type resonator coupled to a delayed piezoelectric coupling mechanism. The study is carried out near the principal parametric resonance, and analytical approximations of the amplitudes of the QP response and the corresponding power output are obtained. Results show that for appropriate combination of time delay parameters, there exists a small range of the excitation frequency over which the energy harvested from QP vibrations is higher compared to the energy harvested from periodic ones. It was also concluded that beyond a certain value of the delay amplitude of the mechanical attachment, QP vibrations offer the possibility to scavenge energy with better performance when the delay is present in the electric circuit. Moreover, by increasing the amplitude of the parametric excitation, good QP vibration-based EH performance can be obtained only for higher values of the delay amplitude of the mechanical attachment.