Instability and stochastic analyses of a pad-on-disc frictional system in moving interactions

Abstract

A pad-on-disc frictional model, a rotating disc under acted by a pad, is established. The moving interaction between the coupled pad and disc is estimated using the Stribeck-type friction model, and the partial differential equation of the disc vibration is calculated using the finite difference method with moving load simulation procedure. Bifurcation diagram and phase portraits of the pad motion with 3-DOFs reveal that as the rotating speed is below a critical value, instability happens and stick–slip vibration is resulted for the pad. Then, eigenvalue analysis is applied to evaluate stability of the pad considering stochastic variation of frictional coefficients and contact effect. Probability distribution diagrams are presented to show that the higher initial displacement of preload or friction coefficient can bring occurrence of more probably instability in uncertain state.

1 Introduction

In a pad-on-disc frictional system, instability is usually occurred with high amplitude which has negative influences on the engineering. Many researches have been carried out for this problem with analytical, computational and experimental techniques. To investigate the frictional system of rotating brake disc acted by the fixed pad, the early achievements on system are attributed to the dry frictional stick–slip self-excited vibration [1] and unstable structural vibration [2]. Stick–slip refers to a fluctuation of friction force, sliding velocity with time or sliding distance changing [3].

For the stick–slip mechanism, the model of rigid body–rigid transmission belt also called “mass-on-moving-belt model” has been widely used previously [4]. Stick–slip is often caused by the nonlinear stiffness effect [5] or nonlinear discontinuity in $\mu -v$ friction curve [6]. To describe the occurrence of stick–slip, the critical excitation speed is pointed out by Thomsen [7]. In 2001, a dynamic system is presented by Galvanetto to get the mechanism of discontinuous bifurcations, and the results show that the stick–slip vibration can be affected by the non-smooth bifurcations [8]. Hereby, Stribeck-type coefficient is usually concluded in stick–slip analysis to analyse the system stability and determine the critical speed of the dynamic model [9].

However, using of the rigid belt model ignores the interaction between the brake pad and disc in transverse direction. To overcome this shortage, elastic or flexible brake disc models are adopted in recent investigations. A frictional system with a flexible thick plate for disc and two continuous beams for pads using the Mindlin’s theory is established by Beloiu and Ibrahim to account for the influence of flexible belt on the braking behaviours. The braking responses in time and frequency domains are investigated analytically and experimentally by considering the influence of nonlinearity and randomness of contact forces [10]. Nayfeh et al. reduced the order of a circular flexible uniform thickness disc and analysed its dynamical behaviour analytically [11]. More recently, an elastic annular disc model is adopted for the coupling system with separation and reattachment by Li et al. for investigating the friction-induced vibration in braking using the improved elastic disc model [12].

Table 1 Parameters

During braking, the time-dependent nature of the contacting interface in the pad–disc system is evident and must be considered even if at lower relative speed [13]. From the point of the rotating disc, its vibration is activated by the moving action of the rigid pad all the time. The influence of the moving force on system stability attracts more and more attentions and the moving load method is adopted in finite element method and experimental approaches in recent years. The deflection of a beam with moving force and the resonance velocity of the moving load are analysed by Yanmeni Wayou et al. [14]. An approximation solution of moving oscillator was investigated by Pesterev and Bergman to describe the variation of displacement and shear force in a one-dimensional distributed system with an arbitrarily varying speed [15]. Chen et al. analysed an axially accelerating viscoelastic string using the method of multiple scales. They found that the instability frequency intervals are influenced by the axial speed and the structure coefficient [16].

More recently, the eigenvalue analysis is widely used for investigating the stability of the disc–pad frictional system. Using the eigenvalue method, unstable frequencies of a braking system inspired by moving loads can be obtained via the finite element method [17, 18]. A linear complex-valued eigenvalue formulation for a disc with moving load is established by Cao et al. to calculate the stationary components of the disc brake [19]. Accordingly, Ouyang investigated the instability of a brake disc by presenting the relationship between eigenvalue and disc’s rotating speed [13]. Through the new technology, a disc brake stability-analysis model and a linear finite element system are constructed to get proper parameters for improving the stability in the proposed approach by Lü and Yu [20].

Some stochastic studies applied to the brake system have also been discussed recently. The most practical way to propagate the stochastic parameters is Monte Carlo simulation, which is not computationally efficient and cannot be applied to a large FE model directly [21]. Considering the brake systems, the statistical correlation analysis, basic statistical analysis of data and experimental data are mentioned in Ref [22]. For a pad-on-disc frictional system, stability of motion is influenced by many structural and operational parameters. Some of these parameters vary stochastically during frictional acting process, such as friction coefficient and contact effect. The negative slope in relation between the friction coefficient and relative velocity is one of the accounts related to the system instability. Generally, friction contact between elements of the system induces temperature increasing and stochastic varieties of friction coefficients. Some researches discuss the relation between material friction coefficient and temperature and its influence to the structure stability. According to Oberst and Lai, brake squeal depends mostly on the friction coefficients and pressure [23]. Therefore, the normal pressure given by the handler is another factor affecting the system stability which is stochastic and varied during braking. With regard to the contact pressure, the equilibrium and main frequency of the system are varied in the braking process where the stability of motion becomes stochastically varied. Considering these, a certain optimization method for the pad-on-disc frictional system with interval parameters is addressed by Lü and Yu [24]. Similarly, in their recent research, an instability analysis model considered imprecise uncertainty is established to study the squeal problems and discuss the evidence theory [25]. The stochastic analysis is also discussed using Kriging-based model and FE model by Nechak et al. [26]

The disc unstable mode mechanism of pad-on-disc model has been researched by using the finite element method [18, 27]. The mechanisms from stick–slip to binary flutter with mode coupling condition were also discussed in [27,28,29]. However, up to now, the eigenvalue analysis of stochastic interval parameters, the moving interactions and the flexible coupling between pad and disc have not been considered simultaneously in one numerical dynamical braking model.

This paper deals with a pad-on-disc, i.e. a rigid–flexible coupled frictional system. The vibration of disc is induced by the moving action of the pad and solved by the finite difference method using a moving load simulation procedure. Bifurcation analysis and the limit cycle motion of pad are put forward, and then, the pad’s stability is discussed based on the linear eigenvalue analysis. Stochastic instability of frictional coefficient and contact pressure is investigated using the probabilistic method.

The values referred in this paper are listed in Table 1.

2 Models

2.1 Dynamics model

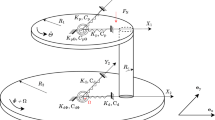
In the pad-on-disc frictional system, the disc is taken as an elastic basement rotating with a speed ${\Omega }$. The pad with subtended angle $\psi$ and inner radius $r_a$ is constrained by the callipers and act on the outer edge of disc. For simplicity, the pad is assumed as a rigid body and vibrates in circumferential direction ${{\varvec{X}}}$, vertical direction ${{\varvec{Y}}}$ and angular direction ${\varvec{\varPhi }}$. For the disc, lateral vibration ${{\varvec{W}}}$ is considered and equation of motion is established with respect to the polar coordinate of R (radial direction) and $\varTheta$ (circumferential direction). The stiffness in the system contains $k_{x}/k_{y}/k_{s}$ representing the effect of callipers; meanwhile, the contact stiffness between pads and disc are $k_{t1}/k_{t2}/k_{en}$. The corresponding damps are $c_{x}/c_{y}/c_{s}/c_{w}$ in tangential, normal, angle direction of pad and transverse direction of disc. In addition, $\varLambda$ is on behalf of the initial displacement with respect to the normal braking pressure.

Fig. 1

Model of a pad-on-disc system

The equations of motion of the pad and the disc are deduced, respectively, as

$$\begin{aligned} \left\{ \begin{array}{ll} &{}M{\ddot{X}}+k_{x}X+c_{x}{\dot{X}}+P \sin \varPhi \\ &{}\quad +k_{t2} \left( X-\frac{|F|}{k_{t1}}\right) \hbox {sgn}(V-{\dot{X}})\cos \varPhi =0 \\ &{}M{\ddot{Y}}+k_{y}(\Lambda +Y)+c_{y}{\dot{Y}}-P \cos \varPhi \\ &{}\quad +k_{t2} \left( X-\frac{|F|}{k_{t1}} \right) \hbox {sgn}(V-{\ddot{X}})\sin \varPhi =0 \\ &{}I_s {\ddot{\varPhi }}+k_{s}\varPhi +c_{s}{\dot{\varPhi }}+k_{t2} \left( X-\frac{|F|}{k_{t1}}\right) \times q/2=0\\ \end{array}\right. \end{aligned}$$

(2.1)

and

$$\begin{aligned}&\frac{\rho h\partial ^{2} W}{\partial T^{2} } + D\nabla ^{4} W + \frac{{c_{w} \partial W}}{{\partial T}} \nonumber \\&\qquad + \rho h\left( {\frac{{2{{\Omega }}\partial ^{2} W}}{{\partial \varTheta \partial T}} + \frac{{{{\dot{\Omega }}}\partial W}}{{\partial \varTheta }} + \frac{{{{\Omega }}^{2} \partial ^{2} W}}{{\partial \varTheta ^{2} }}} \right) \nonumber \\&\quad = H(R)H(\varTheta )\left\{ {N - [{F\hbox {sgn}({V - {\dot{X}}})} ]\frac{{\partial W}}{{R\partial \varTheta }}} \right\} \nonumber \\&\qquad \times \delta ({\varTheta - \sigma }) \end{aligned}$$

(2.2)

where D is flexural rigidity of the disc and $\sigma =\sigma (T)$ represents the circumferential position of moving load varying with time.

$$\begin{aligned}&\nabla ^{4}=\nabla ^{2}\nabla ^{2},\nabla ^{2}=\left( {\frac{\partial ^{2}}{\partial R^{2}}+\frac{\partial }{R\partial R}+\frac{\partial ^{2}}{R^{2}\partial \varTheta ^{2}}} \right) ,\nonumber \\&D=\frac{Eh^{3}}{12({1-\mu })}, H(R)=\left\{ {{\begin{array}{ll} 1,&{}\quad r_a<R<b \\ 0,&{}\quad \hbox {else} \\ \end{array} }} \right. ,\nonumber \\&H(\vartheta )=\left\{ {{\begin{array}{ll} 1,&{}\quad -\psi<\varTheta <\psi \\ 0,&{}\quad \hbox {else} \\ \end{array} }} \right. \end{aligned}$$

(2.3)

$$\begin{aligned}&\left\{ \begin{array}{ll} &{}P=\int \int \frac{k_{en} }{A_s }( {W-Y-R\varTheta \tan \varPhi })\alpha R\mathrm{d}R\mathrm{d}\varTheta \\ &{}\quad =\sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \frac{k_{en} }{m\cdot n}({W_{i,j} -Y_{i,j} })\alpha _{i,j} \\ &{}N=-P;\alpha _{i,j} =\frac{\max ( {0,W_{i,j} -Y_{i,j} } )}{| {W_{i,j} -Y_{i,j} } |};\\ &{}Y_{i,j} =Y+R_i \varTheta _j \tan \varPhi ; F=\mu |N| \end{array}\right. \end{aligned}$$

(2.4)

Here, i, j, m, n are the ith node in radial direction, jth node in circumferential direction, total number of radial nodes in contact area, total number of circumferential nodes in contact area, respectively. Hence, $W_{i,j}$, $Y_{i,j}$ are the local transverse response of disc, normal response of the pad with respect to the radial ith, circumferential jth node. $R_i$ and $\varTheta _j$ represent the radius length of the radial ith node and the angle of the circumferential jth node, also shown in Fig. 1. $P_{i,j}$ and $F_{i,j}$ are contact pressures and corresponding friction force between the pad and disc within the area of A, respectively.

Introduce the dimensionless variables and parameters

Equations (2.1) and (2.2) are rewritten as

(2.5)

2.2 Friction model

Friction models can be classified into two types, the static model and the dynamic model. Three widely used forms of static model to describe the friction properties are static friction model (used under the condition of no relative velocity from static to relative motion), the coulomb (friction model applied before occurrence of relative displacement between the contact parts) and Stribeck-type friction model.

The Stribeck effect refers to a phenomenon that the friction coefficient decreases with the increase in the relative velocity within a limit velocity range [3]. The negative slope in relation between the friction and relative velocity is known as the main reason of friction instability.

A universal friction model combined with these effects above which is also called the modified Stribeck-type friction coefficient $\mu (v_{r})$ can be expressed as

$$\begin{aligned} \mu (v_{r})=f_c +\left( {f_s -f_c } \right) e^{-\left( {{v_r }/{\tilde{v}_s }} \right) ^{\delta }} \end{aligned}$$

(2.6)

where $f_{c}$ and $f_{s}$ are the minimum and the maximum static friction coefficients, respectively. ${\widetilde{v_s}}=v_s \sqrt{\rho h^{2}/D}$ is the dimensionless Stribeck velocity, and $v_r$ the relative velocity. When $\delta = 1$, Eq. (2.6) is also known as Tustin index model (Fig. 2).

Fig. 2

Friction model: static friction $+$ Coulomb friction $+$ Stribeck effect

3 Numerical analysis

3.1 Moving load simulation

Considering a force ${\tilde{F}}$ moves along the edge of disc. To analyse its response under the moving load, the disc’s circumferential edge is discretized into 6n elements (the pad covers n elements depending on $\psi$). Let dt be the unit time and $\mathrm{d}\theta$ the unit space, the nodal force ${\tilde{F}}$ is subsequently allocated in every unit time.

For the moving load acted system, two conditions will be dealt with during calculation:

• a) $C\mathrm{d}\theta ={\tilde{\varOmega }}\mathrm{d}t$ (C is a positive integer). In this case, the load moves from one discrete point to the Cth one after each time step dt.

• b) $\mathrm{d}\theta =C{\tilde{\varOmega }}\mathrm{d}t$ (C is a positive integer). In this case, after each time step dt, the load moves at a place between the discrete points e and $e+1$. Dividing the space step $\mathrm{d}\theta$ into C equal sub-spaces, the load moves at the next sub-point after every time step dt. When the load ${\tilde{F}}$ moves at the ith one, $({e+\frac{i}{C}\mathrm{d}\theta })$ where $i=1,2\ldots C$, the load ${\tilde{F}}$ will be resoluted to the points e and $e+1$ as ${\tilde{F}}_e =\left( {1-\frac{i}{C}} \right) {\tilde{F}}$ and ${\tilde{F}}_{e+1} =(\frac{i}{C}){\tilde{F}}$, respectively (see Fig. 3).

Fig. 3

Moving load simulation. a Condition $C\mathrm{d}\theta ={\tilde{\Omega }}\mathrm{d}t$, b condition $\mathrm{d}\theta =C{\tilde{\Omega }}\mathrm{d}t$

3.2 Boundary conditions

Equations of motion (2.5) contain partial differential equation of disc and ordinary differential equations of pad, which can be solved by the finite difference method and Runge–Kutta method simultaneously. Considering the contact forces within the contact area moving along the outer edge of the elastic disc, the transverse response of disc is induced by successive change of the contact position between the pad and disc. Consider that the disc clamped at the inner radius ${\bar{r_a}}$ and free at the outer radius ${\bar{b}}$. The boundary conditions of the transverse response $w=w( {r,\theta ,t})$ are deduced as

$$\begin{aligned}&w |_{r={\bar{a}}}=0, \quad \left. {\frac{\partial w}{\partial r}} \right| _{r={\bar{a}}} =0\nonumber \\&\quad \hbox {at inner radius} \end{aligned}$$

(3.1)

$$\begin{aligned}&\left. {\frac{\partial ^{2}w}{\partial r^{2}}+\mu _0 \left( {\frac{1}{r}\frac{\partial w}{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}w}{\partial \theta ^{2}}} \right) } \right| _{r={\bar{b}}} =0\nonumber \\&\quad \hbox {at outer radius} \end{aligned}$$

(3.2)

$$\begin{aligned}&\left. {\left[ {\frac{\partial \left( {\nabla ^{2}w} \right) }{\partial r}+\frac{1-\mu }{r^{2}}\frac{\partial }{\partial \theta }\left( {\frac{\partial ^{2}w}{\partial r\partial \theta }-\frac{\partial w}{r\partial \theta }} \right) } \right] } \right| _{r={\bar{b}}} =0\nonumber \\&\quad \hbox {at outer radius} \end{aligned}$$

(3.3)

3.3 Bifurcation analysis

Linear eigenvalue method has been widely used for stability analysis of braking frictional systems. The matrix vibration equations of the pad are generally expressed as

$$\begin{aligned} \left[ M \right] \left[ {\ddot{Q}} \right] +\left[ K \right] \left[ Q \right] +\left[ C \right] \left[ {\dot{Q}} \right] +\left[ {G_h } \right] +\left[ {G_0 } \right] =0 \end{aligned}$$

(3.4)

where $\left[ {G_h } \right]$ and $\left[ {G_0 } \right]$ are the nonlinear contacting and constant forces and $\left[ M \right]$, $\left[ C \right]$, $\left[ K \right]$ and $\left[ Q \right]$, respectively, denote the mass matrix, the gyroscopic matrix, the damping matrix and the displacement vector of the pad.

The equilibrium position $( U )_0 =\left[ {{\begin{array}{l} {( Q )_0 } \\ {( {\dot{Q}} )_0 } \\ \end{array} }} \right]$, which depends on the rotating speed ${\Omega }$, can be obtained by setting all derivative terms to be zero, i.e. $\left[ K \right] \left( Q \right) _0 +\left[ {G_0 } \right] +\left[ {G_h } \right] _{{{\dot{Q}}}=0}=0$ and $\left( {\dot{Q}} \right) _0 =0$.

Introduce the perturbation vector and the state-space matrix, as follows:

$$\begin{aligned} \left[ U \right] =\left[ {{\begin{array}{c} Q \\ {\dot{Q}} \\ \end{array} }} \right] ,\,\left[ A \right] =\left[ {{\begin{array}{cc} 0&{} I \\ {-M^{-1}K}&{} {-M^{-1}C} \\ \end{array} }} \right] . \end{aligned}$$

The differential perturbation equation (3.5) is resulted from (3.4).

$$\begin{aligned} \left[ {\dot{U}} \right] =\left[ A \right] \left[ U \right] +\left[ {G_h } \right] +\left[ {G_0 } \right] \end{aligned}$$

(3.5)

Letting $SU=U-\left( U \right) _0$, investigate the stability at static equilibrium position $\left( U \right) _0$ which yields the perturbation equation (3.6). Here $[ {\tilde{A}} ]$ and $[ {\tilde{G}} ]$ are transformed by $\left[ A \right]$, $\left[ {G_h } \right]$ and $\left[ {G_0 } \right]$. [30]

$$\begin{aligned}{}[ {{\dot{SU}}} ]=[ {\tilde{A}} ][ {SU} ]+[ {\tilde{G}}] \end{aligned}$$

(3.6)

The eigenvalue corresponding to the matrix $[ {\tilde{A}} ]$ is

$$\begin{aligned} \lambda =\alpha \pm j\varpi \end{aligned}$$

(3.7)

where $\alpha$ and $\varpi$ correspond to the real and imaginary parts of the eigenvalue $\lambda$, respectively.

Numerical simulation shows that the angle displacement is very small, so we take $\sin \phi =0$ and $\cos \phi =1$. When the pad is in equilibrium, its velocity is near zero. So we have $\hbox {sgn}\left( {v-{\dot{x}}} \right) =1$. Influence of the disc vibration on instability of the pad is very slight, and it can be neglected.

Choose the variables $a_1 =\frac{k_{t2} }{k_{t1} }k_\mathrm{en}$, $a_2 =k_x +k_{t2}$, $a_3 =k_\mathrm{y} +k_\mathrm{en}$, $\mu _0 =f_c +\left( {f_s -f_c } \right) e^{\frac{v}{\widetilde{v_s }}}$. Letting ${\dot{x_0}}=0$, ${\dot{y_0}}=0$, ${\dot{\phi _0}}=0$, the equilibrium of the pad is determined as $x_0 =-\frac{k_\mathrm{y} \mu _0 a_1 {\varDelta }}{a_2 a_3 }$, $y_0 =-\frac{k_\mathrm{y} {\varDelta }}{a_3 }$ and $\phi _0 =\frac{k_\mathrm{y} qh{\varDelta }\mu _0 k_{t2} }{2k_\mathrm{s} a_3 }\left( {\frac{k_{en} }{k_{t1} }+\frac{a_1 }{a_2 }} \right)$.

Fig. 4

Eigenvalue analysis of the system with rotating velocities

Then, the state-space Jacobi matrix of the system is deduced as

$$\begin{aligned} \left[ {{\begin{array}{cccccc} 0&{} 1&{} 0&{} 0&{} 0&{} 0 \\ {-\frac{a_2 }{M\eta _0 }}&{} {m_1 }&{} {-\frac{\mu _0 a_1 }{M\eta _0 }}&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} 1&{} 0&{} 0 \\ 0&{} 0&{} {\frac{-a_3 }{M\eta _0 }}&{} {\frac{-c_y \sqrt{\eta _0 }}{M\eta _0 }}&{} 0&{} 0 \\ 0&{} 0&{} 0&{} 0&{} 0&{} 1 \\ {-\frac{k_{t2} h\frac{q}{2}}{I_s \eta _0 }}&{} {m_2 }&{} {-\frac{\frac{q}{2}ha_1 \mu _0 }{I_s \eta _0 }}&{} 0&{} {-\frac{k_s }{I_s \eta _0 }}&{} {-\frac{c_s \sqrt{\eta _0 }}{I_s \eta _0 }} \\ \end{array} }} \right] \end{aligned}$$

(3.8)

where

$$\begin{aligned} m_1 =\frac{-c_x \sqrt{\eta _0 }+\frac{a_1 k_\mathrm{y} {\varDelta }}{k_\mathrm{y} +k_{\mathrm{en}} }\frac{\left( {f_s -f_c } \right) }{\widetilde{v_s }}e^{\frac{v}{\widetilde{v_s }}}}{M\eta _0 } \end{aligned}$$

and

$$\begin{aligned} m_2 =\frac{\frac{k_{\mathrm{en}} k_\mathrm{y} q{\varDelta }h}{k_\mathrm{y} +k_{\mathrm{en}} }\frac{k_{t2} }{k_{t1} }\frac{\left( {f_s -f_c } \right) }{2{\widetilde{v_s }}}e^{\frac{v}{\widetilde{v_s }}}}{I_s \eta _0 }. \end{aligned}$$

Fig. 5

Phase portrait at different rotating speeds (${\varDelta }=0.1)$: a ${\widetilde{\Omega }}=35$, b ${\widetilde{\Omega }}=10$, c ${\widetilde{\Omega }}=20$

Let $\varDelta =0.1$, 0.2 and 0.3. Instability of the pad is occurred as at least one real part of eigenvalue becomes positive. While the rotating velocities decrease until 0, variation of the maximum real part of eigenvalues of the pad in terms of the rotating speed is shown in Fig. 4. One finds that the slope of the curve is varied with value of the initial pressure ${\varDelta }$. Larger initial pressure leads to the larger critical speed or early occurrence of the friction-induced instability. The equilibrium of the pad changes to be a limit cycle vibration. The image part of the pure eigenvalues represents frequency of the limit cycle. When ${\varDelta }=0.1$, the critical speed is ${\widetilde{\Omega }}=16.56$ and the eigenvalues are $-0.02\pm 1.0012{i}$, $-0.0478\pm 2.3934{i}$ and the pure eigenvalue pair $\pm 2.0904{i}$, respectively. The phase portraits of the pad vibration in x direction (circumferential motion) at ${\widetilde{\Omega }}=35,10$ and 20 are shown in Fig. 5.

Fig. 6

Bifurcation diagram of the tangential motion of the pad ($\varDelta =0.1$)

Typical bifurcation diagram of circumference motion of the pad (${\varDelta }=0.1$) with the variation of rotating speed ${\widetilde{\Omega }}$ is shown in Fig. 6. ${\widetilde{\Omega }}$ varies from 40 to 10 to simulate the braking procedure and also sweeps from 10 to 40 to obtain the reverse bifurcation process. When ${\widetilde{\Omega }}$ is larger enough, the pad stays in static equilibrium, which is defined as a relative-equilibrium state because it is attached and in slightly vibration together with the elastic disc [31]. At the critical speed ${\widetilde{\Omega }} =16.56$ (also called the Hopf bifurcation point), the relative equilibrium of the pad loses its stability and a large-amplitude limit cycle vibration with amplitude about 0.02 is resulted by the moving friction interaction. In other words, when the velocity is exceeded, the pad becomes unstable [30]. With the decrease in ${\widetilde{\Omega }}$ (positive direction), the limit cycle amplitude is shrunk gradually until zero. At negative direction, the amplitude of the limit cycle vibration is increasing until the saddle-node bifurcation point (speed) of the limit cycle at ${\widetilde{\Omega }}=30$, both the relative equilibrium and the stable limit cycle exist simultaneously within the speed range of 15.56–30. Initial conditions of motion determine which one is resulted.

Fig. 7

Tangential motion of the pad ($\varDelta =0.1$). a Stable focus (${\widetilde{\Omega }}=35$) and b friction-induced limit cycle (${\widetilde{\Omega }}=10$)

3.4 Limit cycle vibration of the pad

During braking, the disc’s rotating speed ${\widetilde{\Omega }}$ is persistently reduced until zero. According to the bifurcation diagram Fig. 6, a large-amplitude limit cycle vibration is resulted by the moving frictional interaction as ${\widetilde{\Omega }}$ is lower than the critical speed 15.56. The relative equilibrium and limit cycle vibration of the pad are presented by diagrams of time histories and phase portraits of the pad’s circumferential motion, as shown in Fig. 7a, b, respectively.

When ${\widetilde{\Omega }}=35$, vibration of the pad will be damped to a relative-equilibrium state. Figure 7a indicates that such the state is in fact a quasi-periodic motion with very small amplitude, until stable equilibrium with the value around $8.15\times 10^{-3}$ in x direction, which can be attributed to the sustained oscillation of the contacting force resulted from the disc transverse vibration. When ${\widetilde{\Omega }}$ decreases to 15.56, the Stribeck-type friction effect induced self-excited vibration (or stick–slip) appears and the limit cycle vibration with rather large amplitude in all directions of the pad is resulted. In this Hopf bifurcation, the stable relative-equilibrium motion transforms suddenly, after the bifurcation point, to be the stable limit cycle with larger amplitude. As the rotating speed continues to decrease, the amplitude of the limit cycle decreases steadily.

In terms of the quasi-periodic motion of pad, Fig. 8a–d shows the variation of the relative motion. In this case, the pad’s tangential velocity is always smaller than the rotating speed, so that the pad slides on the disc from the beginning to end. However, through the damping effect, the pad’s tangential velocity will be limited and the response will become a small-value periodic variation. On account of the pad’s small velocity, the friction coefficient will be settled in a range around 0.25 which is shown in Fig. 8b. Meanwhile, the friction force and contact pressure are damped as stable periodic variations of the pad coincidently. So a small-amplitude vibration is occurred by the decreased contact forces and pad’s tangential velocity.

For the stick–slip motion of the pad, its tangential velocity response is shown in Fig. 9a. During stick stage, the pad moves with the disc where the pad’s tangential speed is approximately equal to the disc’s linear speed at the outer edge $\left( {v_x =v} \right)$; namely, the pad stays still relative to the disc. In this stage, the pad’s tangential response reaches the highest amplitude rapidly and the friction coefficient $\mu$ becomes equal to the maximum static friction coefficient $f_{s}$ with respect to the condition $v_r =0$. Then, the pad starts slipping and the friction coefficient initially decreases with increasing velocity in the slip phase (shown in Fig. 9b). On account of the stick–slip self-excited vibration, the pad becomes unstable with high amplitude response.

Fig. 8

Variation of the relative motion and friction in relative-equilibrium state. a Relative velocity, b friction coefficient variation, c friction force variation, d contact pressure variation

Fig. 9

Variation of the relative motion and friction in stick–slip case. a Relative velocity and b friction coefficient variation

Conclusions are obtained in time-domain analysis that if the rotating speed is big enough, the pad is vibrating as a stable focus with small amplitude for the pad-on-disc system. As ${\widetilde{\Omega } }$ decreases, a friction-induced limit cycle appears for the pad and the stick–slip/limit cycle vibration takes place.

Frequency-domain analyses are also carried out to reveal the characteristic of motion of the pad-on-disc frictional system, from the relative equilibrium to a stable limit cycle, as shown by frequency spectra in Fig. 10, which are obtained by FFT technique for the pad’s tangential, normal and angle motions. Figure 11 represents the disc’s transverse motion after the friction-induced limit cycle vibration has happened (${\widetilde{\Omega }}=10$).

With reference to frequency analysis for the spectrum diagrams at lower rotating velocity, a periodical motion appears in the pad’s circumference direction with main frequency of 0.23 Hz, the second- order frequency of 0.45 Hz, the third-order frequency of 0.68 Hz, etc. also found in pad’s normal and angle directions. In Fig. 10b, d, the first-order frequency of 0.29 Hz of the disc can be found in pad’s normal direction and the natural frequency of 0.16 Hz in angle direction existed in Fig. 10d.

For the disc’s transverse response, equation of motion of disc is expanded by a finite difference model with inner edge and outer edge in radius direction, and continuation in circumferential direction. Calculation shows that the outer amplitude is larger than the inner one. In Fig. 11a, there are many frequency components, where the peak at 0.29 Hz is the first-order natural frequency of disc. The others with lower amplitude are 1.87 Hz of the second-order frequency and 5.03 Hz of the third-order frequency of disc, respectively. Also, one finds that pad’s main frequency of 0.23 Hz and the second-order frequency of 0.45 Hz in disc’s spectrums represent that deflection w depends on x, y and $\phi$, vice versa. Obviously, the dominant frequency is coincident in the whole disc and the first-order mode vibration always exists. However, the frequency distribution is different in the radial direction, that is, the second- and third-order natural frequencies are evident in the inner edge of disc but not distinct in the outer edge of disc.

Fig. 10

Spectra of the circumferential response of pad (${\widetilde{\Omega }}=10$) a x direction, b y direction, c $\phi$ direction, d y direction (${\widetilde{\Omega }}=35$)

Fig. 11

Spectra and vibration of the disc: a Spectra of disc’s transverse response at ${\widetilde{\Omega }}=10$, b disc’s transverse response, c disc radial outer edge response, d disc radial inner edge response

By comparison, amplitude of the first-order mode vibration increases along the radial direction, but the proportions with other frequencies are decreased. It should be pointed out that in the outer edge of disc, only the first-order mode can be induced in the disc acted by moving pad through numerical calculation. Considering the outer edge of the disc, the disc’s partial differential equation can be discretized by first-order dimensional reduction for further research.

4 Stochastic variations of parameters

Linear eigenvalue analysis is an available technology for pad stability analysis even for the uncertainty problems. In this section, the stability analyses are carried out considering of the stochastic contact pressure and friction coefficient, by using the eigenvalue analysis and Monte Carlo simulation.

The pad is completely hinged on the callipers, and the contact force on the pad can be changed through adjusting the displacement between the callipers and pad. We define the assumed or expected displacement as the initial displacement $\varDelta$, which results contact pressure $F_n =k_y \varDelta$ acting on the pad where $k_y$ is contact stiffness between calliper and pad. It should be noted that in a disc brake system, the pad may separate from the rotating disc occasionally with a small preload or low initial displacement, as revealed by Ouyang et al. [32] with the contact-point assumption.

Fig. 12

Distribution of instable points with initial normal pressure (variance $=$ 0.2)

Considering the complete contact case, the initial displacement varies between 0.01 and 0.30. Introduce the random normal distributed standard deviation $\delta _\varDelta$ with the mean value 0 and variance 0.2; then, the sample of initial displacement is obtained by ${\bar{\varDelta }}=\varDelta \left( {1+\delta _\varDelta } \right)$. Then, the distributions of the input variables and randomized instable probability are revealed in Fig. 12. This method employs a random generator to produce a considerable amount of samples over the processing domain. Then, the corresponding output distributions are achieved using the Monte Carlo simulation. For the interval initial displacement, the pad’s instability is occurred in probability at the instable state of ${\bar{\varDelta }}$ between 0.072 and 0.256. Choose 10 sampled points of ${\bar{\varDelta }}$ from the instable state, and the probabilities are shown in Table 2. However, away from the instable section, the probability seems to be 0 or 1. Apparently, the higher initial displacement of preload can bring occurrence of more probably instability in unstable state.

Similarly, the stochastic interval friction coefficient varies from 0.25 to 0.50 and the deviation $\delta _{f_s }$ is chosen to express the data fluctuation around $10^{4}$ samples, which satisfies the relation ${\bar{f_s}}=f_s \left( {1+\delta _{f_s } } \right)$. For the random inputs, the mean value is 0 and the variances are 0.1, 0.2, 0.25 and 0.3 as stochastic normal distributions shown, respectively, in Fig. 13a. It should be emphasized that the instable probability is calculated at a determinate rotating speed ${\tilde{\Omega }}=16$. Figure 13b and Table 3 display the unstable probabilities (10 typical samples) and distributions for the random friction coefficient obtained by the Monte Carlo simulation. With various input data fluctuations, the probabilistic response of $f_s$ is different that the bigger fluctuation can bring the smaller slope of probabilistic distributed curve.

Table 2 Probability results of samples ${\varDelta }$ (variance $=$ 0.2)

Fig. 13

Distribution of instable points with interval friction coefficient using different variances

Table 3 Probability results of samples $f_s$ at different variances

Fig. 14

Probability distribution of the instable points at different velocities (variance $=$ 0.20). a Via eigenvalue analysis, b via time-domain analysis ${\widetilde{\Omega }}=15$, c ${\widetilde{\Omega }}=10$, d ${\widetilde{\Omega }}=20$

Via linear eigenvalue analysis, the contact effect and friction coefficient are selected as stochastic interval variables using the two-dimensional probabilistic analysis. At the constant rotating velocity (${\widetilde{\Omega }}=15$), take the stochastic normal distributed parameters $\varDelta \in \left[ {0.01,0.30} \right]$ and $f_s \in \left[ {0.25,0.50} \right]$ with the mean value 0 and variance 0.2. Then, the instable probabilities are provided by eigenvalue calculation, and the probabilistic response surface is given in Fig. 14a. In time domain, instability is occurred with high amplitude in pad’s circumferential direction (see Sect. 3.4). Therefore, the pad’s time-domain amplitude is another index to measure the instability and the probability distribution of $\varDelta -f_s$ via time-domain analysis is shown in Fig. 14b. By comparison, this section is treated as a demonstration of the conclusion collected by eigenvalues. It should be stressed that in the Monte Carlo simulation, the accuracy of the results will be reliable with enough specimens. Thus, to verify the results by these two methods, the Monte Carlo simulation is applied twice with two groups of specimens. Apparently, the probability distributions tend to be coincident by approaches in Fig. 14a, b where a significant conclusion is obtained that the instability of the pad is relative to friction coefficient and initial displacement (normal pressure), and the critical instable point of the system is varied by the parameters probabilistically.

Fig. 15

Probability distribution of the instable points with different variances (${\widetilde{\Omega }}=15$). a variance $=$ 0.10, b variance $=$ 0.30

Under this case, the probability distributions at different velocities are analysed and the probability distributions at ${\widetilde{\Omega }}=10$ and ${\widetilde{\Omega }}=20$ are given in Fig. 14c, d. One finds that a stable region appears in $\varDelta -f_s$ curves, where the pad will be stable with parameters falling in the zone; however, the stable areas are varied with different rotating velocities. More specifically, a higher rotating velocity leads to a wider stable region. Meanwhile, the pad’s instability is probabilistically uncertain by the near of the stable region. In terms of the Monte Carlo simulation mentioned above, the lower initial displacement or friction coefficient is, the more stably the pad vibrates. In fact, lower friction coefficient and normal pressure lead to a lower friction force, which is applied to express the interaction of the contact effect affecting the pad’s stability. When the pad is stick to the disc, the friction force does positive work for the pad. Thus, if the stick–slip vibration is occurred at lower rotating velocity, the friction force will affect the pad’s stability with high energy, leading to the large instable probability around the sample point. In addition, the gradients in the probabilistic response surface are varied by different variances of the normal distributed inputs where the probability distributions with different variances are shown in Fig. 15.

Compared with the FE models [21, 26], stochastic instability can also be applied using the finite difference model with rigid pad–elastic disc coupling model to overcome the issue of computational workloads by the Monte Carlo simulation. Similarly, the pad’s instability is influenced by interval parameters of friction coefficient and contact pressure. Particularly, the model can also be improved, such as the pad’s transform by using the elastic pad model and disc’s circumferential vibration with more equations. Meanwhile, the contact stiffnesses can be more accurate with proper experiments.

5 Conclusions

A frictional pad-on-disc coupling model considered the moving interactions is investigated in this paper. Bifurcation analysis and the limit cycle motion of pad are conducted to get dynamical responses. The eigenvalue analysis is applied for studying stochastic variations of parameters.

Conclusions are summarized in the following.

• 1. The Hopf bifurcation happens for the pad as the rotating speed of disc is decreased across the critical speed. Then, the relative equilibrium of the pad loses its stability and a larger amplitude stick–slip is resulted by the friction interaction with the disc.

• 2. There are many frequency components in the disc vibration, but only the first-order mode frequency is dominant in circumferential vibration along the outer edge of disc obviously.

• 3. When stochastic variations of parameters are considered, instable regions in $\varDelta -f_s$ curves are varied with different rotating speeds, that is, the higher rotating speed leads to the wider stable region.

• 4. Lower initial displacement or friction coefficient leads to lower probability of instability. In the other words, the friction force is the dominant factor for the pad’s stability of motion with friction interaction.