1 Introduction

System identification is an alternative way of building models from observed sets of input and output data. During the past decades, there have been some significant advances in this research area for time invariant linear systems. However, most real systems exhibit a nonlinear form, and their modeling and identification are still challenging tasks due to the difficulty to establish a global model considering the diversity and complexity of nonlinear systems.

The block-oriented models such as (Wiener, Hammerstein, Wiener- Hammerstein\(\ldots \)) allow to build up models from simple blocks in order to find structures that are flexible enough to cover many relevant real nonlinear systems [1,2,3,4]. Among these systems, we can cite the Wiener system which is characterized by a linear part followed by a static nonlinear block; this model can approximate arbitrarily well most of linear dynamic processes with the output obtained using a nonlinear and soft sensor, as cited in [5, 6]; or when the linear dynamic system is connected to a memoryless nonlinearity, as a dead-zones or saturations [7]. In addition, they are utilized to describe a wide spectrum of industrial processes such as pH control systems, heat exchangers, distillation column, nonlinear microwave device and biological examples [8, 9].

On the other hand, the noninteger or fractional differentiation theory grew extensively since 1960, due to its better representation of the long memory behavior and infinite dimensional structure [10]. Furthermore, fractional order models based on this approach allow a better representation and understanding of physical phenomena, such as: heat and fluid flows, diffusive dynamics, mathematical and electrical engineering, biological processes [11,12,13,14,15,16,17,18].

Identification of fractional systems shows an important number of contributions and applications in real life. The great part of these studies have focused on the linear fractional models. In the literature some of the suggested identification procedures are based on the prediction error and output error (OE) methods; the least squares (LS) method has been applied, with the priori assumption that the fractional orders are be set [19]. The modified recursive least squares (RLS) and the recursive instrumental variable (RIV) algorithms have been used in [20]. The OE approach has been developed in [21].

Another promising idea to identify the fractional models is the use of the evolutionary algorithms, such as the genetic algorithms (GA) [22] and the particle swarm optimization (PSO) algorithm [23]. An overview on linear system identification is reported in [21].

Although some amount of knowledge on the topic of fractional system identification has been accumulated through literature, only few studies have been proposed for the fractional nonlinear system identification. They concern an output error approach such as in [24], where the Continuous Time Neural Networks (CTNN) have been used; [25] describes the system identification based on fractional Volterra series.

The block-oriented models have also been applied for the fractional order case [26,27,28,29,30,31]; however, the order is often not estimated and the major works consider the particular case of commensurate models where the fractional orders are multiple of the same basis \(\alpha \).

The Hammerstein structure has been applied in [26, 27]. The identification of the commensurate fractional order Hammerstein model is performed based on the instrumental variables (IV) [26]. In [27], the identification of neuro-fractional Hammerstein system has been reported. This approach use an iterative linear optimization algorithm in order to recover the fractional order and the degree of the fractional state space model, while the estimation of the other parameters is based in Lyaponove method.

The Wiener structure has also been used in [28,29,30]; where fractional Laguerre–Wiener system has been modeled using the orthonormal basis functions (OBF) and the identification is performed based on the RLS algorithm with the prior knowledge of the fractional order [28, 29]. The modified PSO heuristic, Self-Adaptive Velocity Particle Swarm Optimization (SAVPSO), estimates the parameters and the fractional order of a commensurate state space models [30].

In [31], the authors present a fractional approach for the initialization of a Wiener_Hammerstein model with fractional multiplicities of poles and zeros of the estimated Best Linear Approximation (BLA).

System identification involves two steps: the choice of the structure orders (linear block and nonlinear part orders) and the parametric identification. The drawback of the major proposed approaches in the literature, is the parametrization of the linear and the nonlinear blocks using input–output models, which induces the identification method to be dependent on the chosen orders model. The repeated task for the choice of the best orders structure requires tremendous computational effort, since the identification method is no longer suitable; the use of state space representation may be a solution to this problem.

In this paper, the identification of fractional Wiener system is developed and the general case of noncommensurate fractional order systems is considered.

The objective is the estimation of both its parameters and its fractional orders. To overcome the drawback of the proposed methods of the literature, state space representation of the nonlinear Wiener system is derived; moreover, state space models are often preferred to input–output models for dealing with multivariable systems as well as SISO systems. In this purpose, the Polynomial Nonlinear State Space (PNLSS) model which is the generalization of the state space model to the nonlinear case has been implemented for the Wiener system description. The identification is carried out based on a nonlinear optimization method, and the Levenberg Marquard (LM) algorithm is developed for the fractional PNLSS models. The estimation of both the linear part and nonlinear part of the Wiener system as well as the fractional orders is performed.

This paper is organized as follows:

Preliminary notions of the fractional calculus required to understand the used concepts in the paper are provided in Sect. 2. Section 3 describes the Wiener system in the fractional case, and its equations based on the Polynomial NonLinear Fractional State Space (PNLFSS) model are derived. In Sect. 4, the nonlinear optimization method in occurence LM algorithm is extended for the fractional case for the PNLFSS model and performed to identify the Wiener fractional system. In order to analyze the efficiency of the developed algorithm, simulation examples are carried out for different signal-to-noise ratios in Sect. 5. Finally, Sect. 6 concludes this paper and some perspectives are given.

2 Preliminary notions on fractional calculus

Various nonlinear systems exhibit fractional behavior and show long memory property and infinite dimensional structure; a further class based on the fractional derivative called fractional order models have been developed for their modeling.

Different definitions of the fractional differentiation operator have been reported in the literature such as

Riemann–Liouville type h-difference, Grunwald–Letnikov (GL) difference and Caputo difference [10, 32]. In this study, the one attributed to GL which is the most adequate for the simulation of discrete fractional order systems is used for numerical calculations [33]; it is expressed by the following equation :

$$\begin{aligned} \Delta ^{\alpha }f(kh)= \dfrac{1}{h^{\alpha }}\sum _{j=0}^{k}(-1)^{j} \begin{pmatrix} \alpha \\ j \end{pmatrix} f((k-j)h) \end{aligned}$$
(1)

\(\Delta \) is the discrete fractional derivation operator with initial time equal to zero, \(\alpha \) is a fractional value with \( \alpha \in R^{*+} \), \(k=0, 1, 2,\ldots , n\), is the number of samples and h the sampling interval which equals 1 in what follows.

$$\begin{aligned} \left( \begin{array}{l} \alpha \\ j \end{array}\right) \text { is the Newton binomial term defined by: } \end{aligned}$$
(2)
$$\begin{aligned} \left( \begin{array}{l} \alpha \\ j \end{array}\right) =\left\{ \begin{array}{ll} 1 &{}\quad \mathrm{for}\quad j=0\\ \frac{\alpha (\alpha -1) \cdots (\alpha -j+1)}{j!} &{}\quad \mathrm{for}\quad j>0 \end{array} \right. \end{aligned}$$
(3)

Equation (1) can be written under the form:

$$\begin{aligned} \Delta ^{\alpha }f(k)=\sum _{j=0}^{k} \beta (j) f(k-j) \end{aligned}$$
(4)

with the term :

$$\begin{aligned} \beta (j)= (-1)^{j} \begin{pmatrix} \alpha \\ j \end{pmatrix} \end{aligned}$$
(5)

where a recurrence relation between \(\beta (j)\) and \(\beta (j-1)\) can be deduced:

$$\begin{aligned} \beta (j)=\left\{ \begin{array}{ll} 1 &{}\quad \mathrm{for}\quad j=0\\ \beta (j-1) \frac{(j-1)(\alpha -1)}{j} &{}\quad \mathrm{for}\quad j>0 \end{array} \right. \end{aligned}$$
(6)

The fractional differentiation of a function f gives an overall characterization of this function at each instant k by considering the value of this function at all past times. Fractional systems are often closer to long memory systems, which can be described by a fractional state space model.

In the literature, it is quoted that, the state space representation is based on the fractional order difference operator definitions [32], in our work, we used the one based on GL difference operator given in [33], which is described by the following equations:

$$\begin{aligned} \left\{ \begin{array}{l} \Delta ^{(\alpha )}x(k+1)= Ax(k)+Bu(k) \\ y(k)=Cx(k)+Du(k)\\ \end{array} \right. \end{aligned}$$
(7)

\( x \in R^{n_{a}}\) is the state vector, \(u \in R\) is the input vector and \(y \in R\) is the output vector. \(\Delta ^{(\alpha )}x(k)\) is the state space fractional vector expressed as follows:

$$\begin{aligned} \Delta ^{(\alpha )}x(k)=[\Delta ^{\alpha _{1}}x_{1}(k) \quad \Delta ^{\alpha _{2}}x_{2}(k) \; \cdots \; \Delta ^{\alpha _{n}}x_{n}(k)]^{\mathrm{T}} \end{aligned}$$
(8)

and the fractional order vector is:

$$\begin{aligned} (\alpha ) = [ \alpha _{1} \quad \alpha _{2} \quad \cdots \quad \alpha _{n}]^{\mathrm{T}} \end{aligned}$$
(9)

In the particular case of fractional commensurate order system, the fractional orders \(\alpha \) of all the states \(x_{i}(k)\) are the same :

$$\begin{aligned} \alpha _{1}=\alpha _{2}= \cdots = \alpha _{n}=\alpha \end{aligned}$$
(10)

and

$$\begin{aligned} \Delta ^{(\alpha )}x(k)= & {} \left[ \Delta ^{\alpha }x_{1}(k) \quad \Delta ^{\alpha }x_{2}(k) \quad \cdots \quad \Delta ^{\alpha }x_{n_{a}}(k)\right] ^{\mathrm{T}} \nonumber \\= & {} \Delta ^{\alpha } [x_{1}(k) \quad x_{2}(k) \quad \cdots \quad x_{n}(k)]^{\mathrm{T}} \end{aligned}$$
(11)

The simulation of the fractional model (Eq. 7) can be performed using Eq. (4):

$$\begin{aligned} \Delta ^{(\alpha )}x(k)=\sum _{j=0}^{k} \beta (j) x(k-j) \end{aligned}$$
(12)

and

$$\begin{aligned} \Delta ^{(\alpha )}x(k+1)= x(k+1) + \sum _{j=1}^{k+1} \beta (j) x(k+1-j)\nonumber \\ \end{aligned}$$
(13)

The recurrence equation for the fractional state space simulation are as follows:

$$\begin{aligned} \left\{ \begin{array}{lll} \Delta ^{(\alpha )}x(k+1) = Ax(k)+Bu(k) \\ \quad x(k+1)=\Delta ^{(\alpha )}x(k+1)\\ \quad -\sum _{j=1}^{k+1} \beta (j) x(k-j+1)\\ y(k)=Cx(k)+Du(k) \end{array}\right. \end{aligned}$$
(14)

In order to make the simulations easier, we consider a limited length memory denoted L.

The fractional state space model described in this section is used as a part of the Wiener system in what follows.

3 Fractional order Wiener system description

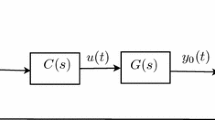
The conventional diagram of a Wiener system is depicted in Fig. 1, where a linear block is followed by a nonlinear block.

Fig. 1
figure 1

Wiener system

Full size image

In our case, the linear part is modeled by a discrete time fractional linear state space model of order \(n_{a}\), as given in Eq. (15), which is assumed asymptotically stable. The static nonlinear block is defined as a nonlinear basis function f(), which can be chosen as a polynomial of order r associated with the coefficients vector p (\(p=p_{1}, p_{2}, \ldots , p_{r}\)) as given in Eq. (16).

u(k) is the system input, v(k) is the linear part output and the input of the nonlinear part, therefore the intermediate unmeasured signal of the two blocks, y(k) is the nonlinear part output, e(k) is a disturbance noise and w(k) is the global Wiener system output.

$$\begin{aligned} \left\{ \begin{array}{lll} \Delta ^{(\alpha )} x(k+1)=A_{0}\, x(k)+ B_{0}\, u(k)\\ v(k)=C_{0}\, x(k) + D_{0}\, u(k) \end{array} \right. \end{aligned}$$
(15)
$$\begin{aligned} {y}(k)= & {} f(v(k))\nonumber \\= & {} \sum _{i=1}^{r}p_{i}v^{i}(k)\nonumber \\= & {} p_{1} v(k)+p_{2} v^{2}(k)+\cdots +p_{r} v^{r}(k) \end{aligned}$$
(16)

The Wiener system output is

$$\begin{aligned} {w}(k)={y}(k)+{e}(k) \end{aligned}$$
(17)

The substitution of the nonlinear block input v(k) by its expression of Eq. (15), yields to the following Wiener state space representation:

$$\begin{aligned} \left\{ \begin{array}{lll} \Delta ^{(\alpha )} x(k+1)=A_{0} x(k)+ B_{0} u(k)\\ y(k)= p_{1} v(k)+p_{2} v^{2}(k)+ \cdots +p_{r} v^{r}(k) \end{array} \right. \end{aligned}$$
(18)

In this case, the Wiener state space model contains nonlinear elements (polynomial), thus, the use of the polynomial nonlinear state space (PNLSS) model which is the generalization of the state space model to the nonlinear case is appropriate for its description.

3.1 Wiener System Description based on Polynomial Nonlinear State Space Model

The PNLSS model is a useful tool for the nonlinear system description with state space representation. It has been used in several studies for the integer case systems as reported in [34, 35]; our contribution in this work is to define the polynomial nonlinear fractional state space model with the acronym (PNLFSS) which will be used throughout this paper.

It consists of a fractional state space representation taking into account the nonlinear terms, which is described by these equations:

$$\begin{aligned} \left\{ \begin{array}{l} \Delta ^{(\alpha )}x(k+1) = Ax(k)+Bu(k)+ E\zeta (k) \\ y(k)=Cx(k)+Du(k)+F \eta (k) \end{array}\right. \end{aligned}$$
(19)

where x is the state, u the input and y the output. The matrices A, B, C and D contain linear coefficients, while, the nonlinear ones are given by the matrices E and F. The vectors \( \zeta (k) \) and \(\eta (k)\) include the nonlinear elements.

In the following, we will be limited to single input single output (SISO) systems. The Wiener system (Eq. 18), described by its fractional state space equation, can be modeled using PNLFSS. The equations linking these two models are developed:

$$\begin{aligned} \left\{ \begin{array}{lll} \Delta ^{(\alpha )} x(k+1)=A_{0} x(k)+ B_{0} u(k)\\ y(k)=\sum _{i=1}^{r}p_{i}v^{i}(k)\\ = \sum _{i=1}^{r}p_{i} \left( C_{0} x(k)+D_{0} u(k) \right) ^{i} \end{array} \right. \end{aligned}$$
(20)

Applying the multinomial expansion, the equations of the Wiener model PNLFSS can be derived. Let us consider two Wiener systems with the linear part of the same state order \(n_{a} = 2 \) and increasing complexity \( r = 2 \) and \( r = 3 \) for the polynomial nonlinear block.

  • Wiener case with \(n_{a}=2\) and \(r=2\):

    $$\begin{aligned} \left\{ \begin{array}{lll} \Delta ^{(\alpha )}x(k+1)=A_{0}x(k)+B_{0}u(k)\\ v(k)=C_{0}x(k)+D_{0}u(k)\\ y(k) =p_{1}v^{1}(k)+p_{2}v^{2}(k) \end{array} \right. \end{aligned}$$
    (21)

with \(C_{0}= [c_1\quad c_2]\), \(D_{0}=d\) and \(x = [x_1 \quad x_2]^\mathrm{T}\). The system output of Eq. (21) is given as follows:

$$\begin{aligned} y= & {} p_{1}v^{1}+p_{2}v^{2}\nonumber \\= & {} p_{1}\left( C_{0}x+D_{0}u\right) + p_{2}\left( C_{0}x+D_{0}u\right) ^{2} \end{aligned}$$
(22)
$$\begin{aligned} y= & {} p_{1}\left( c_{1}x_{1}+c_{2}x_{2} +du\right) \nonumber \\&+p_{2}\left( c_{1}x_{1}+c_{2}x_{2} +du\right) ^{2} \end{aligned}$$
(23)
$$\begin{aligned} y= & {} p_{1}c_{1}x_{1} +p_{1}c_{2}x_{2}+ p_{1}du\nonumber \\&+p_{2}[c_{1}^{2}x_{1}^{2}+2c_{1}c_{2}x_{1}x_{2} +2c_{1}dx_{1}u+c_{2}^{2}x_{2}^{2} \nonumber \\&+2c_{2}d x_{2}u+d^{2}u^{2}] \end{aligned}$$
(24)
$$\begin{aligned} \left\{ \begin{array}{ll} y&= \left[ \begin{array}{cc} p_{1}c_{1} \quad &{} p_{1}c_{2} \end{array} \right] \left[ \begin{array}{c} x_{1} \\ x_{2} \\ \end{array}\right] + \left[ p_{1}d \right] u\\ &{}\\ &{}\quad +\left[ \begin{array}{ccccccccc} p_{2}c_{1}^{2} &{} 2p_{2}c_{1}c_{2} &{} 2p_{2}c_{1}d &{} p_{2}c_{2}^{2} &{} 2 p_{2}c_{2}d &{} p_{2}d^{2} \\ \end{array} \right] \left[ \begin{array}{c} x_{1}^{2} \\ x_{1}x_{2} \\ x_{1}u \\ x_{2}^{2} \\ x_{2}u \\ u^{2} \end{array} \right] \\ \end{array}\right. \end{aligned}$$
(25)

The PNLFSS model is deduced:

$$\begin{aligned} \left\{ \begin{array}{lll} \Delta ^{(\alpha )} x(k+1)&{}=&{}A_{0} x(k)+ B_{0} u(k)\\ y&{}=&{} p_{1} \left[ \begin{array}{cc} c_{1}, \quad &{} c_{2} \end{array} \right] \left[ \begin{array}{c} x_{1} \\ x_{2} \\ \end{array}\right] + p_{1} \left[ d \right] u\\ &{}\\ &{} &{} \begin{array}{lll} + p_{2}\left[ \begin{array}{ccccccccc} c_{1}^{2} &{} 2c_{1}c_{2} &{} 2c_{1}d &{} c_{2}^{2} &{} 2 c_{2}d &{} d^{2} \end{array} \right] \left[ \begin{array}{c} x_{1}^{2} \\ x_{1}x_{2} \\ x_{1}u \\ x_{2}^{2} \\ x_{2}u \\ u^{2} \end{array} \right] \end{array} \end{array} \right. \end{aligned}$$
(26)

The separation of the linear part and the nonlinear part of model Eq.(26) yields to its corresponding PNLFSS model equations; it can be summarized in Table 1, for the linear part matrices (A, B, C and D), matrix E and vector \( \xi \), and Table 2 for the nonlinear elements \(\eta \) and its coefficients F.

In this case, the matrix \( E = 0 \), and \( \xi = 0\) and \(\eta \) contains the monomials expansion of u and x for \(r = 2\).

Table 1 Wiener case with \(n_{a}=2\) and \(r=2\)
Full size table
Table 2 Wiener case with \(n_{a}=2\) and \(r=2\)
Full size table

We can notice that the vector F contains elements of C, D and \(p_{2}\).

  • Wiener case with \(n_{a}=2\) and \(r=3\): In this case, the multinomial expansion generates an important number of elements when r increases.

    $$\begin{aligned} \left\{ \begin{array}{rcl} \Delta ^{(\alpha )}x(k+1)&{}=&{} A_{0}x(k)+B_{0}u(k)\\ v(k)&{}=&{} C_{0}x(k)+D_{0}u(k)\\ y(k)&{}=&{}p_{1}v^{1} (k)+p_{2}v^{2} (k)+p_{3}v^{3}(k) \end{array} \right. \end{aligned}$$
    (27)

Then

$$\begin{aligned} y= & {} p_{1}\left( c_1x_{1}+c_{2} x_{2}+du\right) +p_{2}\left( c_{1}x_{1}+c_{2}x_{2}+du\right) ^{2}\nonumber \\&+p_{3}\left( c_{1}x_{1}+c_{2}x_{2}+du\right) ^{3} \end{aligned}$$
(28)
$$\begin{aligned} y= & {} p_{1}c_1x_{1} + p_{1}c_{2}x_{2} + p_{1}du\nonumber \\&+\, p_{2} [c_{1}^{2}x_{1}^{2} + 2c_{1}c_{2}x_{1}x_{2} + 2c_{1}dx_{1}u \nonumber \\&+\, c_{2}^{2}x_{2}^{2} + 2c_{2}dx_{2}u + d^{2}u^{2}] \nonumber \\&+\, p_{3}[c_{1}^{3}x_{1}^{3} + 3c_{1}^{2}c_{2}x_{1}^{2}x_{2} + 3c_{1}^{2}dx_{1}^{2}u \nonumber \\&+\, 3c_{1}c_{2}^{2}x_{1}x_{2}^{2} + 6c_{1}c_{2}dx_{1}x_{2}u + 3c_{1}d^{2}x_{1}u^{2} \nonumber \\&+\, c_{2}^{3}x_{2}^{3}+3c_{2}^{2}dx_{2}^{2}u + 3c_{2}d^{2}x_{2}u^{2}+d^{3}u^{3}] \end{aligned}$$
(29)

and

$$\begin{aligned} \left\{ \begin{array}{lll} \Delta ^{(\alpha )} x(k+1)&{}=&{}A_{0} x(k)+ B_{0} u(k)\\ y&{}=&{} p_{1}\left[ \begin{array}{cc} c_{1}, \quad &{} c_{2} \end{array} \right] \left[ \begin{array}{c} x_{1} \\ x_{2} \\ \end{array}\right] + p_{1}\left[ d \right] u\\ &{}\\ &{} &{} \begin{array}{lll} +\left[ \begin{array}{c} p_{2} c_{1}^{2} \\ 2p_{2}c_{1}c_{2} \\ 2p_{2}c_{1}d \\ p_{2}c_{2}^{2} \\ 2p_{2}c_{2}d \\ p_{2}d^{2} \\ p_{3}c_{1}^{3} \\ 3p_{3}c_{1}^{2}c_{2} \\ 3p_{3}c_{1}^{2}d \\ 3p_{3}c_{1}c_{2}^{2} \\ 6p_{3}c_{1}c_{2}d \\ 3 p_{3}c_{1}d^{2} \\ p_{3}c_{2}^{3} \\ 3p_{3}c_{2}^{2}d \\ 3p_{3}c_{2}d^{2} \\ p_{3}d^{3} \end{array} \right] ^{T} \left[ \begin{array}{c} x_{1}^{2}\\ x_{1}x_{2} \\ x_{1}u \\ x_{2}^{2} \\ x_{2}u \\ u^{2} \\ x_{1}^{3} \\ x_{1}^{2} x_{2} \\ x_{1}^{2}u \\ x_{1}x_{2}^{2}\\ x_{1}x_{2}u \\ x_{1}u^{2} \\ x_{2}^{3} \\ x_{2}^{2}u \\ x_{2}u^{2} \\ u^{3} \\ \end{array} \right] \end{array} \end{array} \right. \end{aligned}$$
(30)

For this second case, \(n_{a}=2\), \(r=3\), the state equation of the PNLFSS representation remains unchanged, while the corresponding elements of the \(\eta \) and the vector F are given in Table 3. We notice that the number of parameters of transformed models grows strongly when increasing the nonlinear block order r as reported in the literature.

Table 3 Wiener case with \(n_{a}=2\) and \(r=3\)
Full size table

The Wiener PNLFSS representation can be written in the general case, as follows:

$$\begin{aligned} \left\{ \begin{array}{lll} \Delta ^{(\alpha )}x(k+1)=Ax(k)+Bu(k)\\ x(k+1)=Ax(k)+Bu(k)\\ -\sum _{j=1}^{k+1} \beta (j) x(k-j+1)\\ y(k)=Cx(k)+Du(k)+F \eta (k) \end{array} \right. \end{aligned}$$
(31)

with:

$$\begin{aligned} \left\{ \begin{array}{lll} F&{}=&{}\left[ p_{2}Z^{2} \quad \ldots \, \quad p_{r}Z^{r}\right] \\ Z&{}=&{}\left[ c_{1} \quad \, \ldots \, \quad c_{n_{a}} \quad d \right] \end{array} \right. \end{aligned}$$
(32)
$$\begin{aligned}&\left\{ \begin{array}{l} \eta (k)= \left[ \xi ^{2}(k) \quad \, \ldots \,\quad \xi ^{r}(k)\right] \\ \xi (k)= \left[ x_{1}(k)\quad \, \ldots \, \quad x_{na}(k) \quad u(k)\right] \end{array} \right. \end{aligned}$$
(33)

Note that the component number of the vector F is high (according to the orders \(n_{a}\) and r) and that F contains the elements of the matrices C, D and the vector p; moreover, we have redundancy of these parameters.

The objective of this study is the fractional Wiener model identification described by the PNLFSS model.

In the following, to unify the parameter estimates, we assume that the first nonzero coefficient of the nonlinear function equals 1, namely, \(p_{1} = 1\).

Therefore, we have to estimate the parameters of the fractional Wiener system contained in the matrices A, B, C, D, F and the fractional order \(\alpha \).

As reported in the literature, the difficulty in nonlinear systems identification is to deal with the curse of dimensionality (high dimension of the F vector), moreover, the redundancy of the non linear subsystem parameters \(p_{i}\) occurs as they appear in the vector F.

Bearing these facts in mind, the present study circumvents this problem by estimating just the elements of \(p_{i}\) ( \(i = 2, ..., r\)) instead of the elements of vector F; this way, the drawback of estimating an overparameterized model is avoided.

In this case, however, the Wiener system described with its PNLFSS model is nonlinear in the parameters and a nonlinear optimization method (LM algorithm) is developed for its identification in the next section.

4 Fractional system identification using LM algorithm

As the output of the model is nonlinear in the parameters, an output error method based on the LM algorithm is developed. This latter uses a nonlinear programming technique and allows better parameters adjusting based on the criterion variations.

Without loss of generality, the controllable canonical form is considered. Therefore, the Wiener linear part is:

$$\begin{aligned} \left\{ \begin{array}{lll} \Delta ^{(\alpha )} x(k+1)= \left[ \begin{array}{cccc} 0 &{} 1 &{} \ldots &{} 0 \\ \vdots &{} &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \ldots &{} 1 \\ a_{1} &{} a_{2} &{} \ldots &{} a_{n_{a}} \end{array} \right] x(k)+\left[ \begin{array}{c} 0 \\ \vdots \\ 1 \end{array} \right] u(k)\\ \\ v(k)= \left[ \begin{array}{ccc} c_{1} \,\quad c_{2} \,\quad \ldots \,\quad c_{n_{a}} \end{array} \right] x(k)+\left[ \begin{array}{c} d \end{array} \right] u(k) \end{array} \right. \end{aligned}$$
(34)

The vector of parameters \(\theta \) of length (\(n_{\theta }=3n_a+r\)) to be estimated is given by:

$$\begin{aligned} \theta= & {} [ a_{1} \,\quad \ldots \,\quad a_{n_{a}} \,\quad c_{1} \,\quad \ldots \, \quad c_{n_{a}} \,\quad \nonumber \\&d \,\quad p_{2} \,\quad \ldots \,\quad p_{r} \,\quad \alpha _{1} \,\quad \ldots \,\quad \alpha _{n_{a}} ] \end{aligned}$$
(35)

All the parameters in this Wiener system are explicitly given in the model of Eq. (31); the use of the PNLFSS model avoid the cross combination of the nonlinear block coefficients with the ones of the linear block, and here \((p_{2} \, \ldots \, p_{r})\) are contained in the F vector.

The optimization method consists on the minimization of a residual between the output data \( y_{k} \) and the output estimate \( \hat{y}_{k} \). Therefore, the mean quadratic prediction error of the output evaluate the criterion J.

$$\begin{aligned} J=\dfrac{1}{N} \sum _{k=1}^{N} \varepsilon _{k}^{2} \end{aligned}$$
(36)

with the output prediction error:

$$\begin{aligned} \varepsilon _{k}=y_{k}-\hat{y}_{k} \end{aligned}$$
(37)

LM algorithm [36] is manipulated according to the following recurrence equation:

$$\begin{aligned} \theta _{(i+1)}=\theta _{(i)}-\left\{ \left[ J_{\theta \theta }^{\prime \prime }+ \lambda I \right] ^{-1}J_\theta ^{'}\right\} _{\hat{\theta }=\theta _{(i)}} \end{aligned}$$
(38)

where \(\lambda \) is the monitoring parameter, \(J_\theta ^{'} \) the Gradient and \(J_{\theta \theta }^{\prime \prime }\) is the Hessian defined by the following equations:

$$\begin{aligned} \left\{ \begin{array}{l} J_\theta ^{'}=\dfrac{-2}{N} \left( \sum \limits _{k=1}^N \varepsilon _k \; \sigma _{y/\theta }\right) \\ \\ J_\theta ^{\prime \prime }=\dfrac{2}{N} \left( \sum \limits _{k=1}^N \sigma _{y/\theta }\; \sigma _{y/\theta }^T\right) \end{array} \right. \end{aligned}$$
(39)

with \(\sigma _{y/\theta } \) the output sensitivity function.

$$\begin{aligned} \displaystyle \sigma _{y/\theta }=\frac{\partial \hat{y}(k,\theta )}{\partial \theta } \end{aligned}$$
(40)

The main part of this algorithm for nonlinear systems is the crucial calculation of the Gradient and the Hessian based on the sensitivity functions at each iteration; these are developed in the next subsection.

5 Parameters sensitivity functions calculation

The sensitivity functions translate the effect of a variation of a parameter in the system output [37]. For the fractional Wiener PNLFSS, the sensitivity functions expression are derived obtained by the differentiation with respect to the elements of \(\theta _{i}\) as follows:

$$\begin{aligned} \left\{ \begin{array}{llll} \Delta ^{(\alpha )} \frac{\partial x(k+1)}{\partial \theta _{i}} &{}=&{}\frac{\partial }{\partial \theta _{i}} ( A x(k) + B u(k))\\ \\ \frac{\partial y(k)}{\partial \theta _{i}}&{}=&{} \frac{\partial }{\partial \theta _{i}} (C x(k) + D u(k) + F \eta (k)) \end{array} \right. \end{aligned}$$
(41)
$$\begin{aligned} \left\{ \begin{array}{llll} \Delta ^{(\alpha )} \frac{\partial x(k+1)}{\partial \theta _{i}}=\frac{\partial A}{\partial \theta _{i}}x(k)+ A \frac{\partial x(k)}{\partial \theta _{i}}\\ \qquad +\frac{\partial B}{\partial \theta _{i}}u(k)+ B \frac{\partial u(k)}{\partial \theta _{i}}\\ \\ \frac{\partial y(k)}{\partial \theta _{i}}= \frac{\partial C}{\partial \theta _{i}} x(k)+C \frac{\partial x(k)}{\partial \theta _{i}}+ \frac{\partial D}{\partial \theta _{i}} u(k)\\ +D \frac{\partial u(k)}{\partial \theta _{i}} + \frac{\partial F}{\partial \theta _{i}} \eta (k)+F \frac{\partial \eta (k)}{\partial \theta _{i}} \end{array} \right. \end{aligned}$$
(42)

with:

$$\begin{aligned} \left\{ \begin{array}{lll} \frac{\partial x(k)}{\partial \theta _{i}} &{}= &{} \sigma _{x/{\theta _{i}}}\quad \text {the state sensitivity function} \ /\theta _{i}\\ \\ \frac{\partial x(k+1)}{\partial \theta _{i}} &{}= &{} \sigma _{x_{(k+1)}/{\theta _{i}}}\\ \\ \frac{\partial y(k)}{\partial \theta _{i}} &{}=&{} \sigma _{y/{\theta _{i}}} \quad \text {the output sensitivity function} \ / \theta _{i} \\ \\ \frac{\partial u(k)}{\partial \theta _{i}}&{}=&{}0\\ \\ \frac{\partial \eta (k)}{\partial \theta _{i}} &{}= &{} \frac{\partial \eta (k)}{\partial x(k)} \frac{\partial x(k)}{\partial \theta _{i}} = \eta ^{'} \sigma _{x/{\theta _{i}}}\\ \\ with \eta ^{'}&{}=&{} \frac{\partial \eta (k)}{\partial x(k)} = \left[ \frac{\partial \eta (k)}{\partial x_{1}(k)} \; \ldots \; \frac{\partial \eta (k)}{\partial x_{n_{a}}(k)} \right] \end{array} \right. \end{aligned}$$
(43)

with \(i=1, \; ..., n_{\theta }\).

The sensitivity functions can be written under a fractional compact pseudo state space model as follows:

$$\begin{aligned} \left\{ \begin{array}{lll} \Delta ^{(\alpha )}\left[ \sigma _{x_{(k+1)}/{\theta _{i}}}\right] = A \;\sigma _{x/{\theta _{i}}}\\ +\left[ \begin{array}{l} \frac{\partial A}{\partial {\theta _{i}}} \frac{\partial B}{\partial {\theta _{i}}} 0 \end{array}\right] \left[ \begin{array}{c} x \\ u\\ \eta \end{array}\right] \\ &{} \\ \sigma _{y/{\theta _{i}}}= (C+F \eta ^{'}) \sigma _{x/{\theta _{i}}}\\ +\left[ \begin{array}{l} \frac{\partial C}{\partial {\theta _{i}}} \frac{\partial D}{\partial {\theta _{i}}} \frac{\partial F}{\partial {\theta _{i}}} \\ \end{array}\right] \left[ \begin{array}{c} x \\ u\\ \eta \end{array}\right] \end{array}\right. \end{aligned}$$
(44)

In the case of the controllable canonical form \(\frac{\partial B}{\partial {\theta _{i}}}=0 \) and the representation (44) reduces to:

$$\begin{aligned} \left\{ \begin{array}{l} \Delta ^{(\alpha )} \left[ \sigma _{x_{(k+1)} / {\theta _{i}}}\right] = A \ \sigma _{x/{\theta _{i}}} \\ \quad +~\left[ \begin{array}{l} \frac{\partial A}{\partial {\theta _{i}}} \ 0 \ 0 \end{array}\right] \left[ \begin{array}{c} x \\ u\\ \eta \end{array}\right] \\ \sigma _{y/{\theta _{i}}}= (C+F \eta ^{'}) \ \sigma _{x/{\theta _{i}}}\\ \quad +~\left[ \begin{array}{l} \frac{\partial C}{\partial {\theta _{i}}} \ \frac{\partial D}{\partial {\theta _{i}}} \ \frac{\partial F}{\partial {\theta _{i}}} \\ \end{array}\right] \left[ \begin{array}{c} x \\ u\\ \eta \end{array}\right] \\ \end{array}\right. \end{aligned}$$
(45)

The LM algorithm is based on the sensitivity functions calculation with respect to each parameter of \(\theta \), which are expressed as follows:

$$\begin{aligned} \left\{ \begin{array}{lll} \Delta ^{(\alpha )} \left[ \sigma _{x_{(k+1)}/{a_{i}}} \right] = A \sigma _{x/{a_{i}}} \quad + I_{n_{a}j} x\\ \\ \sigma _{y_/{a_{i}}}=(C+F \eta ^{'}) \sigma _{x/{a_{i}}} \end{array} \right. \end{aligned}$$
(46)

\( I_{n_{a}j} \) is a zero matrix with a single element equal to one at entry \( (n_{a},j) \).

$$\begin{aligned} \left\{ \begin{array}{lll} \Delta ^{(\alpha )} \left[ \sigma _{x_{(k+1)}/{c_{i}}} \right] = A \sigma _{x/{c_{i}}}\\ \\ \sigma _{y_/{c_{i}}}= (C+F \eta ^{'}) \sigma _{x/{c_{i}}} \\ + \left[ \frac{\partial C}{\partial {c_{i}}} \; \; \frac{\partial F}{\partial {c_{i}}} \right] \left[ \begin{array}{c} x \\ \eta \end{array}\right] \end{array} \right. \end{aligned}$$
(47)
$$\begin{aligned} \left\{ \begin{array}{lll} \Delta ^{(\alpha )} \left[ \sigma _{x_{(k+1)}/{d}} \right] = A \sigma _{x/{d}}\\ \\ \sigma _{y_/{d}}= (C+F \eta ^{'}) \sigma _{x/{d}}\\ +\left[ \frac{\partial D}{\partial {d}} \; \; \frac{\partial F}{\partial {d}} \right] \left[ \begin{array}{c} u \\ \eta \end{array}\right] \end{array} \right. \end{aligned}$$
(48)

In order to reduce the computation load of the algorithm, the sensitivity functions with respect to the vector p are calculated instead of those of the F vector. For example, for the case \(r=2\), \(p=[1 \quad p_{2}]\), the length of F vector is 6, while for \(r=3\), \(p=[1 \quad p_{2} \quad p_{3}]\) and F length is 16; in this way, the computation of the sensitivity functions with respect to p instead of the sensitivity function with respect to F, reduces drastically the algorithm complexity.

$$\begin{aligned} \left\{ \begin{array}{lll} \Delta ^{(\alpha )} \left[ \sigma _{x_{(k+1)}/{p_{i}}} \right] = A \sigma _{x/{p_{i}}}\\ \\ \sigma _{y_/{p_{i}}}= (C+F \eta ^{'}) \sigma _{x/{p_{i}}} + \left[ \frac{\partial F}{\partial {p_{i}}}\right] \left[ \eta \right] \end{array} \right. \end{aligned}$$
(49)

with

$$\begin{aligned} \frac{\partial F}{\partial {p}}=\left[ Z^{2} \quad Z^{3} \; \ldots \; Z^{r} \right] \end{aligned}$$
(50)

The sensitivity function with respect to each fractional order \(\alpha \) is calculated using the numerical approximation of the derivative :

$$\begin{aligned} y(k,\alpha +\delta \alpha )-y(k,\alpha ) \simeq \delta \alpha \frac{\partial y}{\partial \alpha } = \delta \alpha \sigma _{y/{\alpha }} \end{aligned}$$
(51)

with

$$\begin{aligned} \sigma _{y/{\alpha }}=\dfrac{y(k,\alpha +\delta \alpha )-y(k,\alpha )}{\delta \alpha } \end{aligned}$$
(52)

with \( \delta \alpha \) being a small variation of \(\alpha \).

At each iteration, the sensitivity functions are evaluated in order to calculate the gradient \(J^{'}\) and the Hessian \(J^{\prime \prime }\) and thus, update the parameter vector \(\theta \).

The developed identification method performance is evaluated with numerical simulations.

6 Simulation examples

In this section, numerical examples are profiled in order to evaluate and illustrate the performance of the proposed approach. Indeed, the Fractional Wiener model is considered for the commensurate and the general noncommensurate case.

In the following examples, the input u(k) is a random persistent excitation sequence of zero mean and unit variance. The disturbance e(k) is taken as a white noise sequence of zero mean.

In order to test the efficiency of the estimator, the simulations are performed in the noise-free case, then with data affected by white noise sequence for different signal-to-noise ratios (SNR). In the presence of noise, we perform the Monte Carlo simulation, and 50 runs of the simulation for each level of noise are achieved.

6.1 Example 1

In this example, the fractional Wiener model in the commensurate case is tested with the linear part of order \(n_a = 3\) and nonlinear part order \(r = 3\). Therefore, it is described by the equations below:

$$\begin{aligned} \left\{ \begin{array}{lll} \Delta ^{0.3}x(k+1)&{}=&{} \begin{array}{lll} \left[ \begin{array}{ccc} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \\ -0.2 &{} -0.4 &{} -0.3 \end{array} \right] \end{array} x(k)+ \left[ \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right] u(k) \\ \\ v(k)&{}=&{} \left[ \begin{array}{ccc} 0.3 \,\quad 0.2 \,\quad 0.1 \end{array} \right] x(k)+ \left[ \begin{array}{c} 0.1 \end{array} \right] u(k), \\ \\ y(k)&{}=&{}v(k)+0.1v^{2}(k)+0.5v^{3}(k) \end{array} \right. \end{aligned}$$
(53)

The PNLFSS model is deduced and the parameter vector to be estimated is:

$$\begin{aligned} \theta= & {} [-0.2 \quad -0.4 \quad -0.3 \quad 0.3 \quad 0.2\nonumber \\&\quad \; 0.1 \quad \; 0.1 \quad \; 0.1 \quad \; 0.5 \quad \; 0.3]. \end{aligned}$$
(54)

However, the identification procedure requires the parametric identification as well as the choice of the model structure. In this purpose, the structure is selected based on several tests of different structure choices and the criterion evolution is investigated for 20 iterations.

Table 4 gives the results of evolution of the criterion versus the structure, and Fig. 2 confirms that the order of linear part and nonlinear part are, respectively, \(n_{a}= 3\) and \(r = 3 \ (J = e-8)\). Based on the best criterion result, the use of the \(n_{a}=3\) and \(r=3\) is confirmed.

Table 4 Evolution of the criterion versus the structure
Full size table
Fig. 2
figure 2

Evolution of the criterion versus the structure

Full size image

The parameters mean value using the Monte Carlo simulation are given in Table 5 for different SNR.

Table 5 Means of the parameters \(\theta _{i}\)
Full size table

From the table, we can see that good parameter estimation is obtained. In fact, in the noise-free case, the output prediction error is null, as shown in Fig. 3, with the quadratic criterion \(J \simeq e-15\). Therefore, a perfect adequacy between the output response of the estimated model and the data is shown in Fig. 4.

While Figs. 5 and 6 show the output data and the output of the estimated model in the presence of noise SNR = 34 dB and SNR = 15 dB, respectively. These figures show a good adequacy, that demonstrate the efficiency of the estimator.

Fig. 3
figure 3

Prediction error for noise-free case

Full size image
Fig. 4
figure 4

Estimated and simulated outputs for noise-free case

Full size image
Fig. 5
figure 5

Estimated and simulated outputs for \(\mathrm{SNR}=34\;\mathrm{dB}\)

Full size image
Fig. 6
figure 6

Estimated and simulated outputs for \(\mathrm{SNR}=15\;\mathrm{dB}\)

Full size image

6.2 Example 2

Here, a fractional Wiener model in the noncommensurate case is considered, whose the linear part is of order \( n_{a}=2\) and the nonlinear part of order \( r=3 \). The model is described by:

$$\begin{aligned} \left\{ \begin{array}{lll} \Delta ^{(\alpha )}x(k+1)= \begin{array}{lll} \left[ \begin{array}{ccc} 0 &{} 1 \\ -0.1 &{} -0.4 \end{array} \right] \end{array} x(k)+ \left[ \begin{array}{c} 0 \\ 1 \end{array} \right] u(k) \\ \\ v(k)= \left[ \begin{array}{ccc} 0.3 \,\quad 0.2 \end{array} \right] x(k)+ \left[ \begin{array}{c} 0.1 \end{array} \right] u(k) \\ y(k)=v(k)+0.3v^{2}(k)+0.4v^{3}(k) \end{array} \right. \end{aligned}$$
(55)

with \((\alpha )=[0.2 \,\quad 0.5].\)

The vector of parameters to be estimated is :

$$\begin{aligned} \theta =\left[ -0.1 \quad -0.4 \quad 0.3 \quad 0.2 \quad 0.1 \quad 0.3 \quad 0.4 \quad 0.2 \quad 0.5 \right] \nonumber \\ \end{aligned}$$
(56)

The validation of the structure is determined based on the values of the criterion for different orders of \(n_{a}\) and r, as given in Table 6; Fig. 7 shows its evolution, for 20 iterations. Therefore, it is confirmed that the order of linear part and nonlinear part are, respectively, \(n_{a} =2\) and \(r=3\).

Fig. 7
figure 7

Evolution of the criterion versus the structure

Full size image
Table 6 Evolution of the criterion versus the structure
Full size table

Using this above result, Table 7 provides the results of the simulation carried out in the absence of noise, and the mean values of the estimated parameters with data affected by white noise sequence for different SNR.

Table 7 Means of the parameters \(\theta _{i}\)
Full size table

The results in Table 7 show that the proposed approach restores accurately the parameters. This can be observed in the plot sketched in Fig. 8, which is practically null with the quadratic criterion \(J = e-16\). Figure 9 shows a perfect correspondence of the output response of the estimated model and the data for the noise-free case.

Figures 10 and 11 represent the system output of the estimated model and the simulated one, in the presence of noise, respectively, for SNR = 34 dB and SNR = 15 dB.

Fig. 8
figure 8

Prediction error for noise-free case

Full size image
Fig. 9
figure 9

Estimated and simulated outputs for noise-free case

Full size image
Fig. 10
figure 10

Estimated and simulated outputs for \(\mathrm{SNR}=34\;\mathrm{dB}\)

Full size image
Fig. 11
figure 11

Estimated and simulated outputs for \(\mathrm{SNR}=15\;\mathrm{dB}\)

Full size image

As a result, the effectiveness of the proposed method has been validated with these simulation examples, and the good performance of the estimator is confirmed for both the commensurate fractional case and the general noncommensurate order one, even in the presence of noise.

7 Conclusion

The aim of this work is the identification of a Wiener system in the fractional case, using the fractional nonlinear state space representation.

This nonlinear block-oriented structure can be described using the PNLFSS model and the link between these two representations has been derived.

Moreover, this state space model avoids the difficulty of having the coefficients cross product of the linear and nonlinear parts to occur.

The Wiener PNLFSS model identification task has been solved using an output error identification method, based on the LM algorithm, adapted to estimate the parameters of the nonlinear Wiener model as well as its fractional orders.

It is based on the crucial calculation of sensitivity functions, which have been developed from the PNLFSS model.

As reported in the literature, the number of parameters of the transformed models grows strongly when increasing the nonlinear block order r, in our case the F vector which contains the non linear block coefficients.

However, in the proposed approach, to overcome the drawback of the complex sensitivity functions computation (view the heavy load of the F elements in the PNLFSS model), we have derived a new formulation by just computing the sensitivity functions with respect to the \(p_{i}\) elements of the nonlinear part, and simultaneously reducing the computational load of the method.

In order to illustrate the performance of the proposed algorithm, numerical simulation examples are tested. These latters are carried out in the absence of noise, in both the commensurate and non commensurate cases, and the method estimates the parameters with a very good accuracy. In the presence of noise, a Monte Carlo simulation is performed for different signal-to-noise ratios, and satisfactory results are obtained, which highlights the efficiency of the developed method, even though the results accuracy decreases for a large amount of noise.

In the future, the proposed method will be extended to identify a cascaded Wiener-Hammerstein model.