Adaptive Reactionless Null Space Planning and Control of Free-Floating Space Manipulator After Capturing Unknown Rotating Target

Abstract

On the basis of the momentum conservation equations and recursive least squares with forgetting factor, a new adaptive reactionless planning algorithm is proposed for the reaction null-space motion of the free-floating space manipulator after capturing an unknown rotating target. First, the Lagrange dynamic model of the manipulator is established. Second, the adaptive reactionless planning algorithm is designed to update the null-space solutions for joint rates in online manner. To go to a step further, the desired motion generated by adaptive reactionless planning is produced by driving joints with the PID controller. Finally, on the basis of Lyapunov method, the stability of the proposed scheme is proved theoretically, and the effectiveness of the designed scheme is verified by computer simulation.

1 Introduction

With the development of space technology, the dynamics and control of space robot systems have attracted the attention of researchers from all over the world [1, 2]. Because space is the environment characterized by microgravity and strong radiation, the risks of astronauts performing missions in space are extremely high. The manipulator has been gradually used to replace astronauts for space operations. It is an important and basic mission for space manipulator to capture unknown target. In order to maintain good communication, space manipulator system must move in a stable attitude after capturing the unknown rotating target by the designed controller [3, 4]. Bandyopadhyay et al. [5] proposed a robust nonlinear tracking control law, for the combined aerospace system after capturing a larger target, which can stabilize the combined system in the presence of bounded disturbances and uncertainties. Matunaga et al. [6] designed a scheme that use impact to suppress the angular momentum of non-cooperative rotating targets, and then proposed a bumper damper control method based on collision push to eliminate the rotational motion of the captured target. However, the end effector with passive damper needs to contact the rotating target multiple times to reduce the target angular momentum, which makes the control of the entire robot system difficult to stabilize and coordinate. Yiping et al. [7] built the dynamics model of the overall system composed of the space manipulator and target, and performed stable control of the space robot system after capturing the target. Jing et al. [8] designed an adaptive control scheme combined with saturation function, using a high-precision nonlinear filter to replace the measurement of the speed term, and carried out the stable control of the capture operation of the dual-arm space manipulator under the condition of limited input torque. The above methods are easily limited in the complex environment. Nenchev et al. [9] proposed a reaction null-space motion control law (RNS) to keep joint rates of the manipulator within the set of RNS motion solutions and the disturbance-free operation based on RNS has been experimentally verified by the Engineering Test Satellite VII (ETS-VII). Yoshida et al. [10] proposed a distributed momentum control (DMC) strategy with RNS motion to capture free-floating rotating satellites. RNS motion control is applied to the pre-shock and post-shock control phases known situation. Nakanishi et al. [11] adopted the redundant control technology to develop a distributed momentum control algorithm to realize the distribution and absorption of the initial angular momentum of the captured target, and to control the attitude of the base while satisfying the tracking control of the end effector.

In the above methods in articles [5,6,7,8] do not adopt reactionless null space planning, but study different controllers to control the attitude of the machine. The uncontrollability is to high to adapt to the complex space environment. The researches in articles [9,10,11] although consider the reactionless null space planning of the base attitude after capturing the target, but these all need to know the specific parameter information of the captured target, and cannot solve the problem of zero disturbance to base attitude when the inertial parameters of the captured target are unknown. In view of the above problems, this paper proposes a new adaptive reactionless planning algorithm. This algorithm combines the momentum conservation equations and recursive least squares (RLS) method with forgetting factor to adaptively obtain a set of joint rates of reaction null-space motion. Then, the desired motion is produced by driving the joints with velocity-based controller where joint torques are computed as per the PID control law for the whole motion. Using the recursive least squares method with forgetting factor not only ensures the speed of convergence, but also effectively prevents the phenomenon of data saturation and reduces the total prediction error.

2 Dynamic Model

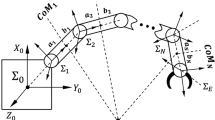
Figure 1 shows a triple-link manipulator system with a capture target, which is composed of free-floating base $B_{0}$, rigid links $B_{1}$, $B_{2}$, $B_{3}$ and End gripper $P$. The system is comprised of 4 rigid bodies where the target is assumed to be rigidized by the end-effector to the last link of the arm when the capture is established. $J_{i}$ is the joint connecting $B_{i - 1}$ and $B_{i} (i = 1,2,3)$. $C_{i}$ is the centroid of $B_{i} (i = 1,2,3)$. $C_{g}$ is the mass center of the system. $\sum_{I}$ is the inertial reference coordinate system. $\sum_{B}$ is the inertial coordinate frame of $B_{0}$. $I_{i}$ and $m_{i} (i = 0,1,2,3)$ are the inertial moment and mass of the ith link. $r_{{\text{g}}}$ is the position vector of the centroid of the system. $r_{i}$ is the position vector of the centroid of $B_{i} (i = 0,1,2,3)$. $P_{{\text{e}}}$ is the position vector of the end of the manipulator arm. $a_{{\text{i}}}$ and $b_{{\text{i}}}$ are position vectors from $J_{i}$ to $C_{i}$ and from $C_{i}$ to $J_{i + 1} (i = 1,2,3)$, respectively. $b_{{0}}$ is the vector of the position of the origin of the $B_{1}$ coordinate system in the $B_{0}$ centroid coordinate system. $M$ is the total mass of the system. $z_{{\text{i}}} ({\text{i}} = 0,1,2,3)$ the unit vector associated with each revolute joint $i$. $\omega_{e}$ is the end-effector angular velocity at the end of the manipulator. $\omega_{0}$ is the angular velocity of the $B_{0}$. $v_{{\text{e}}}$ is the end-effector linear velocity. $v_{{0}}$ is the linear velocity of the $B_{0}$. $\dot{\theta }_{i} (i = 0,1,2,3)$ is the joint rate associated with each revolute joint i.

Fig. 1

Free-floating space manipulator and target

$\tilde{\user2{v}}_{0}$ is a skew-symmetric matrix of vector ${\varvec{v}}_{0} = [x,y,z]^{{\text{T}}}$, defined as:

$${\varvec{v}}_{0} = \left[ {\begin{array}{*{20}c} 0 & { - z} & y \\ z & 0 & { - x} \\ { - y} & x & 0 \\ \end{array} } \right]$$

As shown in Fig. 1, it is easy to write the position relation as:

$$r_{i} = p_{i} + a_{i} = r_{0} + b_{0} + \mathop \Sigma \limits_{k = 1}^{i - 1} (a_{k} + b_{k} ) + a_{i}$$

(1)

$$p_{e} = r_{3} + b_{3} = r_{0} + b_{0} + \mathop \Sigma \limits_{k = 1}^{i - 1} (a_{k} + b_{k} )$$

(2)

where $r_{{\text{i}}}$ is the position vector of the mass center of each arm; ${\varvec{p}}_{e}$ denotes the position vector of the end-effector from the origin of the inertial frame.

The linear velocity of center of mass of link $i$ and the end-effector linear velocity can be obtained by differentiating both sides of Eqs. (1) and (2) as follows:

$$\begin{gathered} v_{i} = \dot{r}_{i} = v_{0} + {\varvec{\omega}}_{0} \times (r_{i} - r_{0} ) + \hfill \\ \, \mathop \Sigma \limits_{k = 1}^{i} [z_{k} \times (r_{i} - p_{k} )]\dot{\theta }_{k} \hfill \\ \end{gathered}$$

(3)

$$\begin{gathered} v_{e} = \dot{p}_{e} = v_{0} + {\varvec{\omega}}_{0} \times (p_{e} - r_{0} ) + \hfill \\ \, \mathop \Sigma \limits_{k = 1}^{3} [z_{k} \times (p_{e} - p_{k} )]\dot{\theta }_{k} \hfill \\ \end{gathered}$$

(4)

The angular velocity of link $i$ and the angular velocity vector of the last link can be written as:

$${\varvec{\omega}}_{i} = {\varvec{\omega}}_{0} + \mathop \Sigma \limits_{k = 1}^{i} z_{k} \dot{\theta }_{k}$$

(5)

$${\varvec{\omega}}_{e} = {\varvec{\omega}}_{0} + \mathop \Sigma \limits_{k = 1}^{3} z_{k} \dot{\theta }_{k}$$

(6)

Write Eqs. (4) and (6) as matrices:

$$\left[ {\begin{array}{*{20}c} {v_{e} } \\ {{\varvec{\omega}}_{e} } \\ \end{array} } \right] = J_{b} \left[ {\begin{array}{*{20}c} {v_{0} } \\ {{\varvec{\omega}}_{0} } \\ \end{array} } \right] + J_{m} \dot{\user2{\theta }}$$

(7)

where

$$J_{b} = \left[ {\begin{array}{*{20}c} {E_{3} } & { - \tilde{p}_{0e} } \\ {\varvec{O}} & {E_{3} } \\ \end{array} } \right] \in R^{6 \times 6} ,\tilde{p}_{0e} = p_{e} - r_{0}$$

(8)

$$J_{m} = \left[ {\begin{array}{*{20}c} {z_{1} \times (p_{e} - p_{1} )} & {z_{2} \times (p_{e} - p_{2} )} & {z_{3} \times (p_{e} - p_{3} )} \\ {z_{1} } & {z_{2} } & {z_{3} } \\ \end{array} } \right] \in R^{6 \times 3}$$

(9)

where ${\varvec{J}}_{b}$ and ${\varvec{J}}_{m}$ are Jacobi matrices associated with free-floating base motion and manipulator motion, respectively, and $\tilde{\user2{p}}_{0e}$ is the vector of position from the vector centroid of the carrier to the end-effector of the manipulator:

$${\varvec{P}} = \mathop \sum_{i = 0}^{3} m_{i} \dot{\user2{r}}_{i}$$

(10)

$${\varvec{L}} = \mathop \sum_{i = 0}^{3} ({\varvec{I}}_{i} \omega_{i} + {\varvec{r}}_{i} \times m_{i} \dot{\user2{r}}_{i} )$$

(11)

The matrix form of Eqs. (10) and (11) can be written as:

$$\left[ {\begin{array}{*{20}c} {\varvec{P}} \\ {\varvec{L}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {M{\varvec{E}}_{3} } & {M\tilde{\user2{r}}_{0g}^{T} } \\ {\varvec{0}} & {{\varvec{H}}_{\omega } } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\varvec{v}}_{0} } \\ {{\varvec{\omega}}_{0} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {{\varvec{J}}_{T\omega } } \\ {{\varvec{H}}_{\omega \theta } } \\ \end{array} } \right]\dot{\user2{\theta }} + \left[ {\begin{array}{*{20}c} {\varvec{0}} \\ {{\varvec{r}}_{g} \times {\varvec{P}}} \\ \end{array} } \right]$$

(12)

where

$${\varvec{H}}_{\omega } = \mathop \sum_{i = 1}^{3} \left( {{\varvec{I}}_{i} + m_{i} \left( {\tilde{\user2{r}}_{gi} } \right)^{T} \tilde{\user2{r}}_{0i} } \right) + {\varvec{I}}_{0} \in {\varvec{R}}^{3 \times 3}$$

(13)

$${\varvec{H}}_{\omega \theta } = \mathop \sum_{i = 1}^{3} \left( {{\varvec{I}}_{i} {\varvec{J}}_{Ri} + m_{i} \tilde{\user2{r}}_{gi} {\varvec{J}}_{Ti} } \right) \in {\varvec{R}}^{3 \times 3}$$

(14)

$${\varvec{J}}_{{{\rm T}\omega }} = \mathop \sum_{i = 1}^{3} m_{i} {\varvec{J}}_{Ti} \in {\varvec{R}}^{3 \times 3}$$

(15)

$${\varvec{J}}_{{{\rm T}\iota }} = \left[ {\begin{array}{*{20}c} {{\varvec{z}}_{1} \times ({\varvec{r}}_{i} - {\varvec{p}}_{1} )} & {{\varvec{z}}_{2} \times ({\varvec{r}}_{i} - {\varvec{p}}_{2} )} & \cdots & {{\varvec{z}}_{i} \times ({\varvec{r}}_{i} - {\varvec{p}}_{i} )} & 0 & \cdots & 0 \\ \end{array} } \right] \in {\varvec{R}}^{3 \times 3}$$

(16)

$${\varvec{J}}_{Ri} = \left[ {\begin{array}{*{20}c} {{\varvec{z}}_{1} } & {{\varvec{z}}_{2} } & \cdots & {{\varvec{z}}_{i} } & 0 & \cdots & 0 \\ \end{array} } \right] \in {\varvec{R}}^{3 \times 3}$$

(17)

$${\varvec{r}}_{g} = \frac{{\sum\nolimits_{i = 0}^{3} {m_{i} {\varvec{r}}_{i} } }}{M},{\varvec{r}}_{gi} = {\varvec{r}}_{i} - {\varvec{r}}_{g} ,{\varvec{r}}_{0i} = {\varvec{r}}_{i} - {\varvec{r}}_{0}$$

(18)

By using the second Lagrange equation, the dynamic equations of free-floating space manipulator system can be obtained as:

$${\mathbf{D(q)}}\mathop {\mathbf{q}}\limits^{{{\mathbf{ \cdot \cdot }}}} {\mathbf{ + C(q,}}\mathop {\mathbf{q}}\limits^{{\mathbf{ \cdot }}} {\mathbf{)}}\mathop {\mathbf{q}}\limits^{{\mathbf{ \cdot }}} {\mathbf{ = \tau }}$$

(19)

where the generalized coordinates are ${\mathbf{q}} = [\begin{array}{*{20}c} {\begin{array}{*{20}c} {x_{0} } & {y_{0} } & {\theta_{0} } \\ \end{array} } & {\theta_{1} } & {\begin{array}{*{20}c} {\theta_{2} } & {\theta_{3} } \\ \end{array} } \\ \end{array} ]^{{\text{T}}}$ and ${\varvec{\tau}} = [\begin{array}{*{20}c} {\tau_{x} } & {\tau_{y} } & {\tau_{0} } & {\tau_{1} } & {\tau_{2} } & {\tau_{3} } \\ \end{array} ]^{{\text{T}}}$ is the driving torque.

$${\mathbf{D}}({\mathbf{q}}) = {\varvec{H}}_{\omega } - \left[ {{\varvec{J}}_{T\omega }^{T} \user2{ H}_{\omega \theta }^{T} } \right]^{T} \left[ {\begin{array}{*{20}c} {M{\varvec{E}}_{3} } & {M\tilde{\user2{r}}_{0g}^{T} } \\ {\varvec{0}} & {{\varvec{H}}_{\omega } } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\varvec{J}}_{T\omega } } \\ {{\varvec{H}}_{\omega \theta } } \\ \end{array} } \right]$$

(20)

$${\mathbf{C}}\left( {{\mathbf{q,}}\user2{\dot{q}}} \right) = \user2{\dot{D}\dot{q}} - \frac{\partial }{{\partial {\mathbf{q}}}}\left( {\frac{1}{2}\user2{\dot{q}}^{T} D\user2{\dot{q}}} \right)$$

(21)

3 Adaptive Reactionless Planning and Control

3.1 Adaptive Reactionless Planning

Reaction null-space (RNS) motion control was proposed by Nenchev et al. to minimize coupling disturbance for the free-floating space manipulator. RNS motion is defined as a set of joint rates producing zero disturbance to the base. A manipulator system with non-zero degree of redundancy (DOR) is required for the existence of RNS solutions.

Now, the RNS concept is proposed for the basic scenario, in which the initial linear and angular momenta of both manipulator and target relative to the defined inertial frame are zero (${\varvec{P}}$, $L$ = 0), that is, neither translation nor rotation is relative to the inertial frame. According to (12), the angular momentum equation can be simplified to:

$${\varvec{H}}_{\omega } {\varvec{\omega}}_{0} \user2{ + H}_{\omega \theta } \dot{\user2{\theta }} = 0$$

(22)

By substituting the desired angular velocity of the base, ${\varvec{\omega}}_{0}$ = 0, into (22) and solving the remaining homogeneous equation, we obtain the null-space solutions for joint rates:

$$\dot{\user2{\theta }}_{RNS} = ({\varvec{E}} - {\varvec{H}}_{\omega \theta }^{ + } {\varvec{H}}_{\omega \theta } )\dot{\user2{\zeta }}$$

(23)

where ${\varvec{E}} \in {\varvec{R}}^{n}$ is the n-order identity matrix; ${\varvec{H}}_{\omega \theta }^{ + }$ is the generalized inverse of ${\varvec{H}}_{\omega \theta }$; and $\dot{\user2{\zeta }} \in {\varvec{R}}^{n}$ is an arbitrary vector in units of ${{rad} \mathord{\left/ {\vphantom {{rad} s}} \right. \kern-0pt} s}$; $({\varvec{E}} - {\varvec{H}}_{\omega \theta }^{ + } {\varvec{H}}_{\omega \theta } )$ represents the mapping of matrix ${\varvec{H}}_{\omega \theta }$ to its zero space.

From the existence condition of RNS [12], the solution (23) exists if:

$$\begin{gathered} dim(RNS) = dim({\varvec{E}} - {\varvec{H}}_{\omega \theta }^{ + } {\varvec{H}}_{\omega \theta } ) \hfill \\ \, = n - rank({\varvec{H}}_{\omega \theta } ) > 0 \hfill \\ \end{gathered}$$

(24)

where recall n is the DOF of the arm. In this paper, the object of this study is a triple-link manipulator system with free-floating base, from which n = 3, $rank({\varvec{H}}_{\omega \theta } ) = 1$, $\begin{aligned} dim(RNS) & = 3 - 1 \\ \, & = 2 > 0 \\ \end{aligned}$ can be obtained, which satisfies the solution condition of RNS motion.

In practical applications of space manipulator, it is important to avoid base attitude disturbances, and base translation does not bring obvious adverse effects. Therefore, this paper only studies the change of the spatial attitude of the base, and then it can be assumed that the linear momentum of the system before capturing the target is zero. After the capture, it is supposed that the system is not subject to any external forces, which follow the law of conservation of momentum. Hence, when the manipulator captures a rotating target with unknown parameters (the initial angular momentum is not zero), the total angular momentum of the system can be written as:

$${\varvec{L}} = {\varvec{L}}_{m} + {\varvec{L}}_{t}$$

(25)

where ${\varvec{L}}_{m}$ and ${\varvec{L}}_{t}$ are the angular momentum of the space manipulator and the target, respectively.

As per Eq. (12), the angular momentum of the system after capturing a tumbling target can be written as:

$${\varvec{H}}_{\omega } {\varvec{\omega}}_{0} + {\varvec{H}}_{\omega \theta } \dot{\user2{\theta }} = {\varvec{L}} = {\varvec{L}}_{m} + {\varvec{L}}_{t}$$

(26)

The matrices ${\varvec{H}}_{\omega }$ and ${\varvec{H}}_{\omega \theta }$ in Eq. (26) include the inertia term of the target by assuming that the target becomes rigidly attached to the end-effector. if the detailed parameters of the captured target are known, and the base attitude is not disturbed, that is ${\varvec{\omega}}_{0} = 0$, the joint rates of reaction null space motion for the manipulator will be computed according to the generalization of Eq. (23) as:

$$\dot{\user2{\theta }}_{r} = {\varvec{H}}_{\omega \theta }^{ + } {\varvec{L}} + ({\varvec{E}} - {\varvec{H}}_{\omega \theta }^{ + } {\varvec{H}}_{\omega \theta } )\dot{\user2{\zeta }}$$

(27)

where $\dot{\user2{\theta }}_{r}$ is the joint rates of reaction null space motion of the space manipulator where the target parameters are known.

According to Eq. (27), if the manipulator motion are governed by nonzero ${\varvec{\omega}}_{0}$, the general solution of the joint rates will be written as:

$$\dot{\user2{\theta }} = {\varvec{H}}_{\omega \theta }^{ + } ({\varvec{L}} - {\varvec{H}}_{\omega } {\varvec{\omega}}_{0} ) + ({\varvec{E}} - {\varvec{H}}_{\omega \theta }^{ + } {\varvec{H}}_{\omega \theta } )\dot{\user2{\zeta }}$$

(28)

Equation (27) can be regarded as a special solution of Eq. (28) in the case of ${\varvec{\omega}}_{0} = 0$, and Eq. (28) is the general solution of the joint rate of Eq. (27). Subtract formula (28) from formula (27):

$$\dot{\user2{\theta }}_{r} - \dot{\user2{\theta }} = \user2{K\omega }_{0}$$

(29)

where ${\varvec{K}} = {\varvec{H}}_{\omega \theta }^{ + } {\varvec{H}}_{\omega }$. To satisfy the planning objective, it is obvious that if $\dot{\user2{\theta }}$ is infinitely close to $\dot{\user2{\theta }}_{r}$, ${\varvec{\omega}}_{0}$ will converges to zero, and then zero disturbance of the base attitude will be achieved.

When the parameters of the capture target are unknown, the specific elements in matrix ${\varvec{K}}$ are unknown and the base attitude cannot be controlled directly by Eq. (29). However, the benefit of Eq. (29) is apparent when it is utilized as a regressor form for deriving an adaptive control algorithm, so the recursive least squares (RLS) algorithm is employed to adaptively update ${\varvec{K}}$ in online method. Then the joint rates of reaction null space will be solved, and write Eq. (30) as follows:

$$\user2{\hat{\dot{\theta }}}_{r} - \dot{\user2{\theta }} = \user2{\hat{K}\omega }_{0}$$

(30)

where $\dot{\user2{\theta }}$ and ${\varvec{\omega}}_{0}$ are the actual joint rate and the base angular velocities, and the symbol “$\wedge$” is employed to denote the unknown post-capture vector and matrices, which incorporate the properties of the unknown target after capturing the unknown target.

The idea of recursive least squares can be written as:

$$\begin{gathered} {\text{New estimated parameters}} = \hfill \\ {\text{Previous estimated parameters}} + \hfill \\ {\text{Correction value}} \hfill \\ \end{gathered}$$

(31)

Define the prediction error formula as:

$${\varvec{e}}(k) = \user2{\hat{\dot{\theta }}}_{r} (k - 1) - \dot{\user2{\theta }}_{r} (k) - \hat{\user2{K}}(k - 1){\varvec{\omega}}_{0} (k)$$

(32)

where $\user2{\hat{\dot{\theta }}}_{r} (k - 1)$ and $\hat{\user2{K}}(k - 1)$ represent the estimates of $\dot{\user2{\theta }}_{r}$ and ${\varvec{K}}$ at the time of the previous (k-1) sampling, respectively.

The recursive least squares (RLS) algorithm has been known to provide extremely fast initial convergence. However, the RLS algorithm is prone to data saturation as the data increases, which will lead that as the system parameters change, it is no longer possible to effectively estimate the ${\varvec{K}}$ matrix. Hence, it is necessary to employ the forgetting factor to discount old data to minimize the total prediction error, and the following cost function is defined:

$$J = \sum\limits_{k = 1}^{l} {\lambda^{l - k} \left\| {e_{k} } \right\|^{2} }$$

(33)

where the value range of the forgetting factor is $0 < \lambda \le 1$.

The measured data is time-varying weighted by Eq. (33), and the newer the data, the greater the weight. In order to make an online estimate of the ${\varvec{K}}$ matrix and minimize the value of Eq. (33), the least squares parameter estimation with forgetting factor is established as follows:

$$\begin{gathered} \hat{\user2{K}}(k) = \hat{\user2{K}}(k - 1) + \hfill \\ \, [\user2{\hat{\dot{\theta }}}_{r} (k - 1) - \dot{\user2{\theta }}(k) - \hat{\user2{K}}(k - 1){\varvec{\omega}}_{0} (k)]{\varvec{N}}(k) \hfill \\ \end{gathered}$$

(34)

where

$${\varvec{N}}(k) = \frac{{{\varvec{\omega}}_{0} (k)^{T} {\varvec{Q}}(k - 1)}}{{\lambda + {\varvec{\omega}}_{0} (k)^{T} {\varvec{Q}}(k - 1){\varvec{\omega}}_{0} (k)}}$$

(35)

$${\varvec{Q}}(k) = \frac{1}{\lambda }\left[ {{\varvec{Q}}(k - 1) - \frac{{{\varvec{Q}}(k - 1){\varvec{\omega}}_{0} (k){\varvec{\omega}}_{0} (k)^{T} {\varvec{Q}}(k - 1)}}{{\lambda + {\varvec{\omega}}_{0} (k)^{T} {\varvec{Q}}(k - 1){\varvec{\omega}}_{0} (k)}}} \right]$$

(36)

It is noted that ${\varvec{N}}(k) \in {\varvec{R}}^{1 \times 3}$ is a row vector. The initial value of ${\varvec{Q}}(k) \in {\varvec{R}}^{3 \times 3}$ can be taken as ${\varvec{Q}}(0) = \alpha {\varvec{E}}$. The $\alpha$ is a sufficiently large positive real number $(10^{4} \sim 10^{10} )$. A value of forgetting factor $\lambda$ must very close to 1, generally not less than 0.9, if $\lambda = 1$ is degraded to the ordinary RLS algorithm.

Therefore, Eq. (30) can be written as the predicted form of the K-time RNS motion solution:

$$\user2{\hat{\dot{\theta }}}_{r} (k) = \dot{\user2{\theta }}(k) + \hat{\user2{K}}(k){\varvec{\omega}}_{0} (k)$$

(37)

The steps to adaptively update ${\varvec{K}}$ and obtain the $\user2{\hat{\dot{\theta }}}_{r} (k)$ in online method are summarized below:

Initialization (based on the known pre-capture parameters of the manipulator).

• Step1: Initialization (based on the known pre-capture parameters of the manipulator)

  $$\begin{gathered} {\varvec{Q}}(0) = \alpha {\varvec{E}} \\ \hat{\user2{K}}(0) = {\varvec{H}}_{\omega \theta }^{ + } {\varvec{H}}_{\omega } \\ \user2{\hat{\dot{\theta }}}_{r} (0) = {\varvec{H}}_{\omega \theta }^{ + } {\varvec{L}}_{m} + \left[ {{\varvec{E}} - {\varvec{H}}_{\omega \theta }^{ + } {\varvec{H}}_{\omega \theta } } \right]\dot{\user2{\zeta }} \\ \end{gathered}$$

  (38)

• Step 2: Measure (or simulate)$\dot{\user2{\theta }}(k)$ and ${\varvec{\omega}}_{0} (k)$.

• Step 3:Update $\hat{\user2{K}}(k)$ according to formulas (34), (35) and (36).

• Step 4:Using $\hat{\user2{K}}(k)$, update the $\dot{\user2{\theta }}_{r} (k)$ from (37).

• Step 5: $k \to k + 1$, Return to step 2 until the end of control.

3.2 PID Controller Design

When the angular velocity of the space manipulator joint is set to $\user2{\hat{\dot{\theta }}}_{r} (k)$, the PID controller is designed to produce $\user2{\hat{\dot{\theta }}}_{r} (k)$ to achieve zero disturbance to the base attitude, and the PID control law is:

$${\varvec{\tau}} = K_{{\text{P}}} \dot{e}(k) + K_{I} \sum\limits_{i = 0}^{k} {\dot{e}(i)} + K_{{\text{D}}} \dot{e}(k - 1)$$

(39)

where $\dot{\user2{e}}(k)\user2{ = \hat{\dot{\theta }}}_{r} (k) - \dot{\user2{\theta }}(k)$ is the joint rate error at the time of the k sampling; $\dot{e}(k - 1)$ is the joint rate error at the time of the previous (k-1) sampling; $\sum\limits_{i = 0}^{k} {\dot{e}(i)}$ is the sum of all previous joint rate errors.

The overall control scheme of the system is shown in Fig. 2.

Fig. 2

Adaptive reactionless planning and control scheme

3.3 Stability Proof

The stability of the proposed planning algorithm is analyzed under the assumption that the algorithm is implemented at a sufficiently high sampling rate to ensure a relatively small change in ${\varvec{K}}$ between two consecutive samples. On this basis, the $i$ component of the $i$ line of matrix $\hat{\user2{K}}$ is used to analyze the various components of the prediction error ${\varvec{e}}(k)$, according to Eq. (32):

$$e_{i} (k) = \hat{\dot{\theta }}_{ir} (k - 1) - \dot{\theta }_{i} (k){\varvec{\omega}}_{0}^{T} (k)\hat{\user2{K}}_{i}^{T} (k - 1)$$

(40)

where $\hat{\user2{K}}_{i}$ is the $i(i = 1,2,3)$ row of matrix $\hat{\user2{K}}$, and matrix ${\varvec{Q}}$ and regression vector ${\varvec{\omega}}_{0}$ are the same as in Eqs. (34) through (36), and therefore have:

$$\hat{\user2{K}}_{i}^{T} (k) = \hat{\user2{K}}_{i}^{T} (k - 1) + \overline{\user2{N}}(k){\varvec{e}}_{i} (k)$$

(41)

$$\overline{\user2{N}}(k) = \frac{{{\varvec{\omega}}_{0} (k)^{T} {\varvec{Q}}(k - 1)}}{{\lambda + {\varvec{\omega}}_{0} (k)^{T} {\varvec{Q}}(k - 1){\varvec{\omega}}_{0} (k)}}$$

(42)

$${\varvec{Q}}(k) = \frac{1}{\lambda }\left[ {{\varvec{Q}}(k - 1) - \frac{{{\varvec{Q}}(k - 1){\varvec{\omega}}_{0} (k){\varvec{\omega}}_{0} (k)^{T} {\varvec{Q}}(k - 1)}}{{\lambda + {\varvec{\omega}}_{0} (k)^{T} {\varvec{Q}}(k - 1){\varvec{\omega}}_{0} (k)}}} \right]$$

(43)

Introduce a scalar Lyapunov function as shown below:

$$V_{i} (k) = \tilde{\user2{K}}_{i} (k){\varvec{Q}}^{ - 1} (k)\tilde{\user2{K}}_{i}^{T} (k)$$

(44)

where $\tilde{\user2{K}}_{i} (k) = \hat{\user2{K}}_{i} (k) - {\varvec{K}}_{i} (k)$, ${\varvec{K}}_{i} (k - 1) \approx {\varvec{K}}_{i} (k)$

(based on the assumption that the sampling frequency is high enough and the prediction error between two consecutive samples is small). Subtract ${\varvec{K}}_{i}^{{\text{T}}} (k)$ from both sides of Eq. (41) to get it:

$$\begin{gathered} \tilde{\user2{K}}_{i}^{T} (k) = \tilde{\user2{K}}_{i}^{T} (k - 1) + \hfill \\ \, \overline{\user2{N}}(k)\left[ {\user2{\hat{\dot{\theta }}}_{ir} (k - 1) - \dot{\user2{\theta }}_{i} (k) - {\varvec{\omega}}_{0}^{T} (k)\hat{\user2{K}}_{i}^{T} (k - 1)} \right] \hfill \\ \end{gathered}$$

(45)

Write Eq. (30) as follows in discrete form

$$\user2{\hat{\dot{\theta }}}_{ir} (k - 1) - \dot{\user2{\theta }}_{i} (k) = {\varvec{\omega}}_{0}^{T} (k)\hat{\user2{K}}_{i}^{T} (k)$$

(46)

Using formula (41) and formula (46) is substituted for formula (45) to obtain

$$\begin{gathered} \tilde{\user2{K}}_{i}^{T} (k) = \lambda \frac{1}{\lambda }\left[ \begin{gathered} {\varvec{Q}}(k - 1) - \hfill \\ \frac{{{\varvec{Q}}(k - 1){\varvec{\omega}}_{0} (k){\varvec{\omega}}_{0} (k)^{T} {\varvec{Q}}(k - 1)}}{{\lambda + {\varvec{\omega}}_{0} (k)^{T} {\varvec{Q}}(k - 1){\varvec{\omega}}_{0} (k)}} \hfill \\ \end{gathered} \right]* \hfill \\ \, {\varvec{Q}}^{ - 1} (k - 1)\tilde{\user2{K}}_{i}^{T} (k - 1) \hfill \\ \end{gathered}$$

(47)

Equation (47) may also be abbreviated to the following form

$$\tilde{\user2{K}}_{i}^{T} (k) = \lambda {\varvec{Q}}(k){\varvec{Q}}^{ - 1} (k - 1)\tilde{\user2{K}}_{i}^{T} (k - 1)$$

(48)

Consider the following relationship

$$\begin{gathered} V_{i} (k) - \lambda V_{i} (k - 1) = \left[ {\tilde{\user2{K}}_{i} (k) - \tilde{\user2{K}}_{i} (k - 1)} \right]{\varvec{Q}}^{ - 1} (k)\tilde{\user2{K}}_{i}^{T} (k) \hfill \\ = - \frac{{\tilde{\user2{K}}_{i} (k - 1){\varvec{\omega}}_{0} (k){\varvec{\omega}}_{0} (k)^{T} {\varvec{Q}}(k - 1)}}{{\lambda + {\varvec{\omega}}_{0} (k)^{T} {\varvec{Q}}(k - 1){\varvec{\omega}}_{0} (k)}}{\varvec{Q}}^{ - 1} (k)\tilde{\user2{K}}_{i}^{T} (k) \hfill \\ \end{gathered}$$

(49)

Using formulas (44) and (48), and prescribing A, Eq. (49) may be written as:

$$\begin{gathered} V_{i} (k) - V_{i} (k - 1) = - \lambda \frac{{\tilde{\user2{K}}_{i} (k - 1){\varvec{\omega}}_{0} (k){\varvec{\omega}}_{0} (k)^{T} \tilde{\user2{K}}_{i}^{T} (k - 1)}}{{\lambda + {\varvec{\omega}}_{0} (k)^{T} {\varvec{Q}}(k - 1){\varvec{\omega}}_{0} (k)}} - \hfill \\ \, (1 - \lambda )V_{i} (k - 1) \le 0 \hfill \\ \end{gathered}$$

(50)

Since the gain matrix ${\varvec{Q}}$ is a positively definite symmetric matrix, it can be seen by Eq. (49) that $V_{i} (k)$ must be a positive scalar function without incrementing, completing the proof of stability.

4 Simulation

In order to verify the effectiveness of the planning and control algorithm proposed in this paper and visualize the motion state of the space manipulator, this paper develops a co-simulation platform using MSC. Adams and Matlab/Simulink software. It is assumed that prior to target capture, the angular momentum and linear momentum of the space manipulator system are equal to zero. It is suppose that after capture, the target is rigidized by the gripper relative to the end-effector within 0.1 s and the system begins adaptive reactionless control immediately. The combined simulation time is 120 s. Adams and Matlab/Simulink exchange data every 0.025 s, and Matlab/Simulink calculates in 0.0001 s.

Space manipulator system model parameters: mass of target $m_{{\text{t}}} { = }250{\text{ kg}}$, angular velocity of target ${\varvec{\omega}}_{t} = 0.2{\text{ rad/s}}$, $m_{0} = 500.7{\text{ kg}}$, $m_{i} { = 10}{\text{.7 kg(}}i{ = 1,2,3)}$, $I_{0} { = 83}{\text{.33 kg}} \cdot {\text{m}}^{2}$, $I_{i} { = 1}{\text{.05 kg}} \cdot {\text{m}}^{2} (i = 1,2,3)$, $b_{0} = 0.6{\text{ m}}$, $l_{i} { = 1}{\text{m}} (i = 1,2,3)$, $a_{i} = b_{i} = 0.5{\text{ m(}}i{ = 1,2,3)}$.

System control parameters: Forgetting factor $\lambda = 0.99$, Positive scale factor $\alpha = 10^{4}$, $\dot{\zeta }(0) = [\begin{array}{*{20}c} {0.1} & {0.1} & {0.1} \\ \end{array} ]^{{\text{T}}}$, $K_{P} = {\text{diag}}(1500,1500,1500)$, $K_{I} = {\text{diag}}(0.1,0.1,0.1)$, $K_{D} = {\text{diag}}(20,20,20)$.

The simulation results are shown in Figs. 3, 4, 5, 6, 7 and 8. Figures 3 and 4 show the base attitude and base angular velocity after capturing the target without adaptive reactionless control, respectively. Figures 5, 6, 7 and 8 show the base attitude, the base angular velocity, the joint rate error and joint rate after capturing the target with adaptive reactionless control, respectively.

Fig. 3

Base attitude without adaptive reactionless planning and control

Fig. 4

Base angular velocity without adaptive reactionless planning and control

Fig. 5

Base attitude with adaptive reactionless planning and control

Fig. 6

Base angular velocity with adaptive reactionless planning and control

Fig. 7

Joint rate error with adaptive reactionless planning and control

Fig. 8

Joint rate with adaptive reactionless planning and control

As can be seen from Figs. 3 and 4, if no control is added to the manipulator after capturing the unknown rotating target, the angular velocity of the base is not zero, and the base is significantly deflected, which the maximum change in the attitude angle of the base within 120 s reaches $- 0.53{\text{ rad}}$. To go a step further, it can be seen from the above comparison of Figs. 3 and 5 and that the base attitude deflection angle is significantly reduced, which the maximum deviation of the base attitude within 120 s in adaptive reactionless control is $- 4.66 \times 10^{ - 4} {\text{ rad}}$ within the allowable range. From the comparison of Figs. 4 and 6 and, it can be observed that the disturbance of the base attitude is quickly suppressed and the angular velocity of the base attitude is rapidly converged to near zero in adaptive reactionless control, which realizes the non-disturbance of the base attitude.

Furthermore, from the Fig. 6, it can be noted that the system has a peak of size ${{ - 7.14 \times 10^{ - 5} {\text{ rad}}} \mathord{\left/ {\vphantom {{ - 7.14 \times 10^{ - 5} {\text{ rad}}} s}} \right. \kern-0pt} s}$ in the base angular velocity at 24 s. It can be seen that the peak of the angular velocity of the base is due to the rapid change of the joint angular velocity and the closed-loop PID controller can not quickly track the expected joint rates obtained by the adaptive algorithm according to the existence of the corresponding peak of the angular velocity error of the joint of the manipulator at 24 s in Fig. 7 and the rapid change of the angular velocity of the joint of the manipulator in Fig. 8 around 24 s.

5 Conclusions

The Lagrange dynamic model of a free-floating triple-link manipulator is established to update the actual angular velocity of each member of the space manipulator. The expression with unknown parameters of RNS joint rates is derived according to the momentum conservation equations after the free-floating space manipulator capture the rotating target. To go a step further, the recursive least squares method with forgetting factor is proposed, in which the forgetting factor is introduced to discount old data to minimize the total prediction error and the expression of RNS joint rates is made into a recursion form. Then unknown parameters and the null-space solutions for joint rates can be adaptive updated online by the proposed planning algorithm, and the desired joint rates is produced by driving joints with the PID controller to complete the adaptive reactionless planning and control. Simulation results show that the proposed method can obtain the RNS motion of the free-floating manipulator under the condition that the target inertial properties are unknown.