Chaotic thermal convection of couple-stress fluid layer

Abstract

In this work we study the pattern of bifurcations and intermittent-chaos of non-Newtonian couple-stress shallow fluid layer subject to heating from below. The couple-stress parameter delays onset of convection, synchronizes chaotic behavior, and decreases the heat transfer . Some global aspects of the dynamics such as homoclinic bifurcations and transition to chaos are explored. The effects of particle size on the intermittent-chaos regime at particular normalized Rayleigh number, say $r=166.1$, are investigated. With the increase in couple-stress parameter, the present Lorenz-like system synchronizes to a steady state via a series of periodic solutions interspersed with intervals of chaotic behaviors.

1 Introduction

Investigation on the pattern of convection is very important for understanding underlying mechanism of chaotic evolution and its intermittent behavior. Over several decades thermal convection for Newtonian fluids has been extensively studied and focused mainly on the stability of the fluid layer at the onset of convection [1, 2]. A new direction of research in this field has been emerged after the pioneering work of Lorenz [3] who used the Rayleigh–Bénard convection problem to model equations for weather forecasting. He showed that depending upon the Rayleigh number, the dimensionless ratio of the destabilizing buoyancy force to the stabilizing viscous force, the low-dimensional system exhibits random, aperiodic behaviors. The system undergoes a sequence of local and global bifurcations at the transitional regime.

The understanding of convection patterns, bifurcations, onset of chaotic motion and its control depending upon material parameters of non-Newtonian fluids is important for applications in science and technology. Among available non-Newtonian fluid models, the couple-stress fluid model is very simple and easy for analysis. This kind of fluid is realistic in different aspects. The couple-stress and also micropolar fluids have widespread applications in medical and engineering sciences such as lubrication technology of loaded bearings [4,5,6,7,8], peristaltic transport of bio-fluids in conduits [9,10,11,12], blood flow through stenotic arteries [13, 14], extrusion of polymer fluids (see Refs. [15,16,17] for micropolar fluids), and cooling of metallic plate in a bath. The effects of couple-stresses on fluid flows were extensively studied by Stokes [18] in different geometries. The main feature of fluid couple-stresses is to introduce size-dependent effects on flows based on the material constant and dynamic viscosity, which are not present in classical viscous fluid models.

The stability of a layer of couple-stress fluid heated from below was first studied by Ahmadi [19]. Using linear stability theory, Banyal [20] derived a necessary condition for the onset of stationary convection. A global nonlinear stability analysis for thermo-convection of a couple-stress fluid has been studied by Sunil et al. [21]. They showed that the critical Rayleigh numbers at the onset of convection for both linear and nonlinear stability analysis are exactly the same and the couple-stress fluid is thermally more stable than the ordinary fluid. Recently, Jawdat et al. [22] studied numerically the effects of couple-stresses on chaotic convection. The convection of couple-stress fluid is delayed with increase in particle size in the fluid. At the onset of convection there is a direct proportion between the Rayleigh number and the couple-stress parameter (square of the dimensionless ratio of the particle size to the depth of the fluid layer).

The motivation of the present study is to focus the effects of particle size on convection and transition to chaos of couple-stress fluids subject to heating from below. This will be useful in understanding engineering transports such as heat transfer in fluids with long-chain molecules, melting and solidification of liquid crystals, polymeric suspensions, and lubrication technology under the framework of microcontinuum hypothesis which enables to assume each macrovolume element to contain a microstructure, allowing polar effects such as the presence of couple-stresses and body couple.

We explore the effects of particle size on the thermo-convective motion of a horizontal couple-stress fluid layer by employing a low-dimensional approach. This leads to three-dimensional Lorenz-like model equations with four control parameters, namely the Prandtl number $\sigma$, the normalized Rayleigh number r, the modified couple-stress parameter c, and a geometrical parameter b. The effects of the couple-stress parameter on the stability, bifurcations, transition to chaos, and intermittent-chaos are investigated. The first Lyapunov quantity determines the stability of the bifurcating periodic orbit emerging via the Hopf bifurcation. How the system reaches the convection-less state with increasing values of couple-stress parameter is shown graphically and analyzed. Analysis reveals that the synchronization of chaos to a steady state takes place through a series of periodic motions interspersed with chaotic behavior and non-stable limit cycle.

2 Convection model for couple-stress fluid

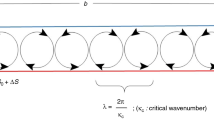
We consider gravity-driven thermal convection of a shallow, horizontally unbounded layer of an incompressible couple-stress fluid of depth h confined between two thermally conducting stress-free parallel planes subject to heating of the lower plane. A Cartesian coordinate system (x, y, z) is adopted with x-axis along the lower surface and z-axis vertically upward. Let $T_{0} + \varDelta T$ and $T_{0}$ be the temperature on the lower and upper surfaces, respectively. A schematic diagram of the flow domain with boundary conditions and other relevant thermo-physical parameters with clockwise and anticlockwise convection rolls is displayed in Fig. 1.

Fig. 1

A physical sketch of thermo-fluid convection problem in a shallow fluid layer of depth h depicting convective rolls. The upper and lower boundaries are held at an isothermal temperatures ${T_0}$ and ${T_0+\varDelta T}$, respectively

Then, the relevant hydrodynamic motion and heat transfer equations are written as [1, 18]

$$\begin{aligned}&\rho _0 \frac{\mathrm {d} \mathbf {V}}{\mathrm {d} t}=-\nabla p+\left( \mu -\mu '\nabla ^{2}\right) \nabla ^{2} \mathbf {V}-\rho g \hat{\mathbf {k}}\,, \end{aligned}$$

(1)

$$\begin{aligned}&\frac{\mathrm {d} T}{\mathrm {d} t}=\kappa \nabla ^{2} T, \end{aligned}$$

(2)

where $\mathrm {d}/{\mathrm {d} t} \equiv \partial / \partial t+(\mathbf {V}\cdot \nabla )$. By adopting the Boussinesq approximation, the density variation in the buoyancy term is taken as $\rho =\rho _{0}\left[ 1-\alpha (T-T_{0}) \right]$, and the incompressibility condition is $\nabla \cdot \mathbf {V}=0$.

Taking vector curl of (1) the pressure term is dropped out. In two-dimensional case all flow variables become independent of the y coordinate. Then, the velocity vector can be expressed in terms of stream function $\psi (x,z,t)$ as $\mathbf {V}=\left( -{\partial \psi }/{\partial z}, 0, {\partial \psi }/{\partial x} \right)$. Introducing the layer depth h as the length scale, $h^{2}/\kappa$ as the time scale and $\varDelta T$ as the temperature scale, the evolution equations for the perturbation field to the steady state of Eqs. (1) and (2) are written in dimensionless form as

$$\begin{aligned}&\frac{\partial }{\partial t} \left( \nabla ^{2}\psi \right) +\frac{\partial \left( \nabla ^{2}\psi ,\psi \right) }{\partial (z,x)}\nonumber \\&\quad =\sigma \left( 1-c_s\nabla ^{2}\right) \nabla ^{4}\psi +\sigma Ra \frac{\partial \theta }{\partial x}, \end{aligned}$$

(3)

$$\begin{aligned}&\frac{\partial \theta }{\partial t}+\frac{\partial (\theta , \psi )}{\partial (z,x)}=\frac{\partial \psi }{\partial x}+\nabla ^{2}\theta , \end{aligned}$$

(4)

where $\theta$ represents the (dimensionless) temperature deviation from the conducting state temperature and $\frac{\partial (f_1, f_2)}{\partial (z,x)}$ denotes $\left( \frac{\partial f_1}{\partial z}\frac{\partial f_2}{\partial x}-\frac{\partial f_1}{\partial x}\frac{\partial f_2}{\partial z} \right)$ for arbitrary $f_1$ and $f_2$.

In the above equations, the dimensionless parameters are $\sigma ={\mu }/{(\rho _0 \kappa )}$ the Prandtl number, $Ra={\rho _0 g \alpha \varDelta T h^3}/{(\kappa \mu )}$ the Rayleigh number, and the couple-stress parameter $c_s=a^2$, where $a=d/h$ and $d=({\mu '}/{\mu })^{1/2}$. The quantity d has the dimension of length and therefore can be associated with the molecular length scale of the couple-stress fluid. The dimensionless quantity a represents the ratio of the particle size to the depth of the fluid layer. Thus, for a particular fluid layer depth, the effects of couple-stresses increase with the particle size in the fluid. However, the molecular size and flow length scale must have some limitations and do not exceed the limitation of continuum theory for constitutive equations.

Now we shall precise the boundary conditions of this thermo-convective problem. Since the two bounding surfaces are stress-free, the boundary conditions for the dimensionless stream function $\psi$ are written as

$$\begin{aligned} \psi =\frac{\partial ^2\psi }{\partial z^2}=0 \quad \text { on }\quad z=0, 1. \end{aligned}$$

(5)

In addition, since the temperature is fixed on the boundaries, we have

$$\begin{aligned} \theta =0 \quad \text { on }\quad z=0, 1. \end{aligned}$$

(6)

For spatiotemporal evolution, the variables $\psi$ and $\theta$ are expanded in Fourier series of x and z, following Lorenz [3], as

$$\begin{aligned} \left. \begin{array}{ll} \psi (x,z,t)&{}=\frac{\sqrt{2}\, \varLambda }{\pi k}X(\tau )\sin {(kx)}\sin {(\pi z)} \\ \theta (x,z,t)&{}=\frac{\sqrt{2}\, \varLambda ^3}{\pi k^2 Ra}Y(\tau )\cos {(kx)}\sin {(\pi z)}\\ &{}\quad - \frac{\varLambda ^{3}}{\pi k^{2} Ra} Z(\tau )\sin {(2\pi z)} \end{array} \right\} \end{aligned}$$

(7)

where $\varLambda =\pi ^2+k^2$, k being the horizontal wavenumber, and $\tau =\varLambda t$ is the rescaled time variable. Obviously, the boundary conditions (5) and (6) are satisfied. Projecting Eqs. (3) and (4) onto the modes of Eq. (7), we obtain the following three-dimensional nonlinear system

$$\begin{aligned} \left. \begin{array}{l} \dot{X}=\sigma (Y-cX)\\ \dot{Y}=rX-Y-XZ\\ \dot{Z}=XY-bZ \end{array} \right\} \end{aligned}$$

(8)

where dot denotes derivative with respect to dimensionless time $\tau$, $r=Ra/Ra_c$ is the normalized Rayleigh number with $Ra_c=\varLambda ^3/k^2$, $c=1+\varLambda c_s$ the modified couple-stress parameter, and $b=4\pi ^2/\varLambda$ a geometrical parameter lying in $0<b<4$. In Eq. (8), the mode X represents the velocity field and the other two modes Y and Z describe, respectively, the change in the temperature along the horizontal and vertical directions. In the absence of fluid couple-stresses (i.e., $c_s=0$), Eq. (8) reduces to Lorenz system [3] corresponding to Newtonian fluid. Note that very recently Layek and Pati [23] derived a five-dimensional generalized Lorenz system for hyperbolic heat propagation in Newtonian fluid media.

The present nonlinear system (8) possesses two important properties. First, it is invariant under the transformation $(X, Y, Z)\rightarrow (-X,-Y, Z)$. Second, the flow divergence $\nabla \cdot (\dot{X}, \dot{Y}, \dot{Z})=-(1+b+c\sigma )$ is negative always. So, the system is dissipative and its solutions are bounded in the phase space.

3 Bifurcations from the steady solutions

In this section, we study the stability and bifurcations of the system (8) at its equilibrium or fixed points. The equilibrium points (or constant solutions or steady solutions) of (8) can be obtained by solving the equations $\dot{X}=0$, $\dot{Y}=0$, $\dot{Z}=0$, i.e., $Y=cX$, $rX-Y-XZ=0$, $XY=bZ$, which, after simplification, give a trivial solution $E_0=(0,0,0)$ and two symmetric non-trivial equilibrium solutions $E_\pm =(\pm \sqrt{b(r-c)/c}, \pm \sqrt{bc(r-c)}, r-c)$. Physically, the trivial solution $E_0$ represents the conducting state (state of no convection) of the couple-stress fluid layer, while the non-trivial solutions $E_{\pm }$ correspond to the steady convective state of the fluid layer.

The stability of the system (8) at the trivial equilibrium point $E_0$ can be obtained by linearizing it about $E_0$ and taking trial solutions of the form $\exp {(s\tau )}$. This gives the characteristic equation

$$\begin{aligned} \det { \begin{pmatrix} &{}s+c\sigma &{} -\sigma &{} 0\\ &{} -r &{} s+1 &{} 0\\ &{}0 &{} 0 &{}s+b \end{pmatrix}} =0. \end{aligned}$$

(9)

From Eq. (9), we have one characteristic root (eigenvalue) as $s=-b$ and the other two eigenvalues satisfy

$$\begin{aligned} s^2+(1+c\sigma )s+\sigma (c-r)=0. \end{aligned}$$

(10)

The stability of $E_0$ can be determined by the signs of the eigenvalues. It is stable if all of the three eigenvalues have negative real part; it is unstable if the real part of at least one eigenvalue is positive. The system undergoes a bifurcation at $E_{0}$ if it has either a zero eigenvalue or a pair of purely imaginary eigenvalues. Physically, a bifurcation in the thermo-convective motion corresponds to an onset of instability in the fluid layer.

Since b is positive, the eigenvalue $s=-b$ is negative always and so the onset of instability in the static solution $E_0$ depends on the roots of Eq. (10) only. Setting $s=0$ in (10), an exchange of stability (onset of stationary convection) takes place at the normalized Rayleigh number $r_p=c$ and it becomes $r_p=1$ for Newtonian fluids ($c_s=0$). In this work, the parameters k and $\sigma$ are taken as $\pi /\sqrt{2}$ and 10, respectively. Then, $b=8/3$ and $r_p=c=1+(3/2)\pi ^2c_s$. Since the roots of (10) are always real, the system cannot exhibit overstable motion (oscillatory onset of convection). So the onset of instability sets in only via stationary modes (pitchfork bifurcation), when r increases $r_p$. In the neighborhood of the bifurcation point $r_p$ the system has three steady solutions. One is the static solution $E_0$ which is always unstable for $r>r_p$, and the other two are the finite amplitude convective solutions $E_{\pm }$ existing only when $r>r_p$. Using normal form theory [24, 25], the non-trivial solutions are supercritical (stable) in the neighborhood of the pitchfork bifurcation point.

For stability of the convective solutions $E_\pm$ beyond $r_p$, we consider only the positive solutions since they are symmetric in nature. For linear stability of $E_+$, we first apply a small perturbation to $E_+$ as follows:

$$\begin{aligned} x_{2}=X-x_0,\, y_{2}=Y-cx_0, \, z_{2}=Z-(r-c), \end{aligned}$$

(11)

where $x_0=\sqrt{b(r-c)/c}$. Using (11) into Eq. (8), the perturbation equations are obtained as

$$\begin{aligned} \left. \begin{array}{lll} \dot{x}_{2}=\sigma y_{2}-c\sigma x_{2}\\ \dot{y}_{2}=cx_{2}-y_{2}-x_0 z_{2}-x_{2}z_{2}\\ \dot{z}_{2}=cx_{0}x_{2}+x_{0}y_{2}-bz_{2}+x_{2}y_{2} \end{array} \right\} \end{aligned}$$

(12)

with the origin as an equilibrium point. Linearizing (12) about the origin and assuming exponential evolution in time for the perturbation admits the following cubic equation for the eigenvalues

$$\begin{aligned} s^3+a_1 s^2+a_2 s+a_3=0, \end{aligned}$$

(13)

where $a_1=1+b+c\sigma$, $a_2=br/c+\sigma b c$, and $a_3=2 b \sigma (r-c)$.

Following Routh–Hurwitz stability criteria, the necessary (but not sufficient) condition [26] for linear stability of $E_+$ is that the quantities $a_1$, $a_2$, $a_3$, and f are all positive, where $f=a_1a_2-a_3$. Under this condition, the eigenvalues from Eq. (13) have negative real part. The instability sets in when at least one eigenvalue crosses the origin (for real eigenvalues) or a pair of eigenvalues cross the imaginary axis (for complex eigenvalues) to the positive half-plane. In the former case, the coefficient $a_3$ must change its sign first, whereas for the latter case the quantity f changes its sign first [26].

Thus, depending on the quantities $a_{3}$ and f one can find the critical Rayleigh number at the onset of instability in the convective solutions. Since $r>c$ for the convective solutions, we have $a_{3}>0$ always. So, the possibility of existence of instability now depends on f alone. In this case, the system undergoes a Hopf bifurcation in the neighborhood of $E_+$ provided the coefficients $a_j\, (j=1,2,3)$ satisfy the relation $a_1a_2-a_3=0$, which gives the critical normalized Rayleigh number at the onset of the Hopf bifurcation as $r_h=\sigma c^2(3+b+c\sigma )/(c\sigma -b-1)$, provided $\sigma >(1+b)/c$. At the Hopf bifurcation point $r_h$, the linearized system has a pair of purely imaginary eigenvalues $s_{\pm }=\pm i \omega$ ($i=\sqrt{-1}\,$) with the frequency of oscillation $\omega =\sqrt{\frac{2\sigma bc(1+c\sigma )}{c\sigma -b-1}}$. The third eigenvalue $s_3=-(1+b+c\sigma )$ is real and negative. Appearance of Hopf bifurcation at $r=r_h$ indicates that an infinitesimal perturbation to the steady convective state of the fluid layer may result in oscillatory motion in the system.

4 Sub- and supercritical Hopf bifurcations

By knowing how the solution $E_{+}$ loses its stability via Hopf bifurcation as r is increased through the critical value $r_h$, one can categorize the Hopf bifurcation into two types, namely supercritical and subcritical Hopf bifurcations. By supercritical Hopf bifurcation, it generally means that the bifurcation destabilizes the equilibrium point $E_{+}$ to a unique small-amplitude stable limit cycle whose periodic orbit can be detected numerically. On the other hand, for subcritical Hopf bifurcation no such small-amplitude limit cycle will be created after the bifurcation. In this case, $E_{+}$ loses its stability by absorbing a saddle limit cycle. A quantity that determines the type of the Hopf bifurcation is the first Lyapunov quantity, usually denoted by $l_1$(see Kuznetsov [27] for details). The Hopf bifurcation is supercritical if $l_1<0$ and subcritical when $l_1>0$. For $l_1=0$, we have codimension-2 degenerate Hopf bifurcation.

In order to determine whether the Hopf bifurcation is sub- or supercritical we follow the technique described in Hassard et al. [28] based on normal form theory. First, we fix the parameter r at the Hopf bifurcation point $r_h$. The eigenvectors corresponding to the eigenvalues $s_{+}=i\omega$ and $s_3=-(1+b+c\sigma )$ are obtained as

$$\begin{aligned} e_+=\begin{pmatrix} 1\\ c+i\frac{\omega }{\sigma }\\ \frac{\omega ^2-i(1+c\sigma )\omega }{\sigma x_0} \end{pmatrix} \quad \text {and }\quad e_3=\begin{pmatrix} -\frac{\sigma }{1+b}\\ 1\\ \frac{b(1+b+c\sigma )}{(1+b)x_0} \end{pmatrix}, \end{aligned}$$

respectively, where $x_0=\sqrt{\frac{b(1+c\sigma )(1+b+c\sigma )}{(c\sigma -b-1)}}$.

Let us now apply the transformation $(x_{2},y_{2},z_{2})'=\mathbf {A}(x_1,y_1,z_1)'$ to Eq. (12), where ‘$'$’ denotes transposition and the matrix $\mathbf {A}$ is given by

$$\begin{aligned} \mathbf {A}= & {} (\text {Re}\,e_+, -\text {Im}\,e_+,e_3)\\= & {} \begin{pmatrix} 1 &{} 0 &{} -\frac{\sigma }{1+b}\\ c &{} -\frac{\omega }{\sigma } &{} 1\\ \frac{\omega ^2}{\sigma x_0} &{} \frac{(1+c\sigma )\omega }{\sigma x_0} &{} \frac{b(1+b+c\sigma )}{(1+b)x_0} \end{pmatrix}. \end{aligned}$$

This gives the following normalized system

$$\begin{aligned} \left. \begin{array}{lll} \dot{x}_{1}=-\omega y_{1}+F_{1}(x_{1}, y_{1}, z_{1})\\ \dot{y}_{1}=\omega x_{1}+F_{2}(x_{1}, y_{1}, z_{1})\\ \dot{z}_1=-(1+b+c\sigma )z_1+F_3(x_1,y_1,z_1) \end{array} \right\} \end{aligned}$$

(14)

The functions $F_1$, $F_2$, and $F_3$ in (14) are given by

$$\begin{aligned} F_{1}(x_{1}, y_{1}, z_{1})&=\frac{l x_{0}}{1+b} P(x_{1}, y_{1}, z_{1})\\&\quad -\frac{l(1+c\sigma )}{x_{0}(1+b)^{2}}Q(x_{1}, y_{1}, z_{1}),\\ F_{2}(x_{1}, y_{1}, z_{1})&=\frac{l x_{0}(1+b+c\sigma )}{\omega (1+b)} P(x_{1}, y_{1}, z_{1})\\&\quad +l\frac{\omega ^{2}+b(1+b+c\sigma )}{x_{0}\omega (1+b)^{2}}Q(x_{1},y_{1},z_{1}),\\ F_{3}(x_{1}, y_{1}, z_{1})&=\frac{l x_{0}}{\sigma } P(x_{1}, y_{1}, z_{1})\\&\quad -\frac{l(1+c\sigma )}{(1+b)\sigma x_{0}} Q(x_{1}, y_{1}, z_{1}), \end{aligned}$$

where P, Q, and l are as follows:

$$\begin{aligned} P(x_1,y_1,z_1)&=\left\{ (1+b)x_{1}-\sigma z_1\right\} \\&\quad \left( c\sigma x_1-\omega y_{1}+\sigma z_{1} \right) ,\\ Q(x_1,y_1,z_1)&=\left\{ (1+b)x_1-\sigma z_1\right\} \\&\quad \left\{ (1+b)\omega ^{2}x_{1}+\omega (1+b)(1+c\sigma )y_1 \right. \\ {}&\quad \left. +\,b\sigma (1+b+c\sigma )z_1 \right\} ,\\ \text {and } \qquad l&=1/\left( \omega ^2+(1+b+c\sigma )^2 \right) . \end{aligned}$$

The normal form theory requires the evaluation of the following quantities for Eq. (14),

$$\begin{aligned} g_{11}&=\frac{1}{4}\left[ \frac{\partial ^2F_1}{\partial x_1^2}+\frac{\partial ^2F_1}{\partial y_1^2}+i\left( \frac{\partial ^2F_2}{\partial x_1^2}+\frac{\partial ^2F_2}{\partial y_1^2} \right) \right] \\&=\frac{l}{2}(\alpha _1+i\beta _1),\\ g_{02}&=\frac{1}{4} \left[ \frac{\partial ^2F_1}{\partial x_1^2}-\frac{\partial ^2F_1}{\partial y_1^2} -2\frac{\partial ^2F_2}{\partial x_1\partial y_1} \right. \\ {}&\quad \left. +\,i\left( \frac{\partial ^2F_2}{\partial x_1^2}-\frac{\partial ^2F_2}{\partial y_1^2}+2\frac{\partial ^2F_1}{\partial x_1\partial y_1} \right) \right] \\&=\frac{l}{2}(\alpha _2+i\beta _2),\\ g_{20}&=\frac{1}{4}\left[ \frac{\partial ^2F_1}{\partial x_1^2}-\frac{\partial ^2F_1}{\partial y_1^2}+2\frac{\partial ^2F_2}{\partial x_1\partial y_1}\right. \\ {}&\quad \left. +\,i\left( \frac{\partial ^2F_2}{\partial x_1^2}-\frac{\partial ^2F_2}{\partial y_1^2}-2\frac{\partial ^2F_1}{\partial x_1\partial y_1} \right) \right] \\&\quad =\frac{l}{2}(\alpha _3+i\beta _3),\\ G_{21}&=\frac{1}{8}\left[ \frac{\partial ^3 F_1}{\partial x_1^3}+\frac{\partial ^3F_1}{\partial x_1\partial y_1^2}+\frac{\partial ^3F_2}{\partial x_1^2\partial y_1}+\frac{\partial ^3F_2}{\partial y_1^3}\right. \\ {}&\quad \left. +\,i\left( \frac{\partial ^3F_2}{\partial x_1^3}+\frac{\partial ^3F_2}{\partial x_1\partial y_1^2}-\frac{\partial ^3F_1}{\partial x_1^2\partial y_1}-\frac{\partial ^3F_1}{\partial y_1^3} \right) \right] \\&\quad =0,\\ h_{11}&=\frac{1}{4}\left( \frac{\partial ^2F_3}{\partial x_1^2}+\frac{\partial ^2 F_3}{\partial y_1^2} \right) \\&\quad =\frac{l}{2}\alpha _4,\\ h_{20}&=\frac{1}{4}\left( \frac{\partial ^2F_3}{\partial x_1^2}-\frac{\partial ^2 F_3}{\partial y_1^2}-2i\frac{\partial ^2F_3}{\partial x_1\partial y_1} \right) \\&\quad =\frac{l}{2}(\alpha _4+i\beta _4),\\ G_{110}&=\frac{1}{2}\left[ \frac{\partial ^2F_1}{\partial x_1\partial z_1}+\frac{\partial ^2F_2}{\partial y_1\partial z_1}\right. \\ {}&\quad \left. +\,i\left( \frac{\partial ^2F_2}{\partial x_1\partial z_1}-\frac{\partial ^2F_1}{\partial y_1\partial z_1} \right) \right] =\frac{l}{2}(\alpha _5+i\beta _5),\\ G_{101}&=\frac{1}{2}\left[ \frac{\partial ^2F_1}{\partial x_1\partial z_1}-\frac{\partial ^2F_2}{\partial y_1\partial z_1}\right. \\ {}&\quad \left. +\,i\left( \frac{\partial ^2F_2}{\partial x_1\partial z_1}+\frac{\partial ^2F_1}{\partial y_1\partial z_1} \right) \right] =\frac{l}{2}(\alpha _6+i\beta _6), \end{aligned}$$

where $\alpha _j$, $\beta _j$, $j=1,2,\dots , 6$ are given below

$$\begin{aligned} \alpha _1&=x_0 c\sigma -(1+c\sigma )\omega ^2/x_0,\\ \alpha _2&=\alpha _1-(1+c\sigma )\left( \omega ^2+b(1+b+c\sigma )\right) /x_0\\&\quad +x_0(1+b+c\sigma ),\\ \alpha _3&=\alpha _1+(1+c\sigma )\left( \omega ^2+b(1+b+c\sigma )\right) /x_0\\&\quad -x_0(1+b+c\sigma ),\\ \alpha _4&=x_0 c(1+b)-\omega ^2(1+b)(1+c\sigma )/(\sigma x_0),\\ \alpha _5&=2 x_0\sigma -2 b \sigma (1+c\sigma )(1+b+c\sigma )/(x_0 (1+b)), \\ \alpha _6&=2\sigma (1+c \sigma )\omega ^2/(x_0(1+b))\\&\quad -2x_0 c\sigma ^2/(1+b), \end{aligned}$$

and

$$\begin{aligned} \beta _1&=x_0 c\sigma (1+b+c\sigma )/\omega \\&\quad +\omega (\omega ^2+b(1+b+c\sigma ))/x_0,\\ \beta _2&=\beta _1-\omega (1+c\sigma )^2/x_0-x_0\omega ,\\ \beta _3&=\beta _1+\omega (1+c\sigma )^2/x_0+x_0\omega ,\\ \beta _4&=\omega (1+b)(1+c\sigma )^2/(\sigma x_0)+x_0\omega (1+b)/\sigma ,\\ \beta _5&=-\frac{x_0\sigma (c\sigma +b+1)(c\sigma -b-1)}{\omega (1+b)} \\&\quad -\frac{\sigma \left( \omega ^4-b^2(1+b+c\sigma )^2 \right) }{x_0\omega (1+b)}\\&\quad -\frac{x_0\omega \sigma }{1+b}-\frac{\sigma \omega (1+c\sigma )^2}{x_0(1+b)},\\ \beta _6&=-\frac{x_0\sigma (c\sigma +b+1)(c\sigma -b-1)}{\omega (1+b)}\\&\quad -\frac{\sigma \left( \omega ^4-b^2(1+b+c\sigma )^2 \right) }{x_0\omega (1+b)} \\&\quad +\frac{x_0\omega \sigma }{1+b}+\frac{\sigma \omega (1+c\sigma )^2}{x_0(1+b)}. \end{aligned}$$

Now solving the equations $s_{3} w_{11}=-h_{11}$ and $(s_3-2i\omega )w_{20}=-h_{20}$, we have

$$\begin{aligned}&w_{11}=\frac{l}{2(1+b+c\sigma )}\alpha _4, \quad \\&\quad \text {and } w_{20}=\frac{l}{2 \left\{ (1+b+c\sigma )^2+4\omega ^2\right\} }(\alpha _7+i\beta _7), \end{aligned}$$

where $\alpha _7=(1+b+c\sigma )\alpha _4+2\omega \beta _4$ and $\beta _7=(1+b+c\sigma )\beta _4-2\omega \alpha _4$. Using the above quantities, we obtain

$$\begin{aligned} g_{21}= & {} G_{21}+2G_{110}w_{11}+G_{101}w_{20}\\= & {} \frac{l^2}{4(1+b+c\sigma )\left\{ (1+b+c\sigma )^2+4\omega ^2\right\} }\\&\times (\alpha _8+i\beta _8), \end{aligned}$$

where

$$\begin{aligned}&\alpha _8=2\left\{ (1+b+c\sigma )^2+4\omega ^2\right\} \\&\quad \alpha _4\alpha _5+(1+b+c\sigma )(\alpha _6 \alpha _7-\beta _6\beta _7),\\&\quad \text {and } \beta _8=2\left\{ (1+b+c\sigma )^2+4\omega ^2\right\} \\&\quad \alpha _4\beta _5+(1+b+c\sigma )(\alpha _6\beta _7+\alpha _7\beta _6). \end{aligned}$$

Finally, we calculate

$$\begin{aligned} C_1(r_h)&=\frac{i}{2\omega }\left( g_{20}g_{11}-2|g_{11}|^2-\frac{1}{3}|g_{02}|^2 \right) +\frac{g_{21}}{2}\\&=\frac{l^2}{8}\left[ \frac{\alpha _8}{(1+b+c\sigma )(4\omega ^2+(1+b+c\sigma )^2)} \right. \\ {}&\quad -\frac{\alpha _1\beta _3+\beta _1\alpha _3}{\omega } +i\left\{ \frac{\alpha _1\alpha _3-\beta _1\beta _3}{\omega } \right. \\ {}&\quad -2\left( \alpha _1^2+\beta _1^2 \right) -\frac{\alpha _2^2+\beta _2^2}{3} \\ {}&\quad \left. \left. +\frac{\beta _8}{(1+b+c\sigma )(4\omega ^2+(1+b+c\sigma )^2)} \right\} \right] . \end{aligned}$$

The nature of the Hopf bifurcation for the normalized system (14) can be determined by the first Lyapunov quantity [27]

$$\begin{aligned} l_1(c_s)&=\frac{\text {Re}\, C_1(r_h)}{\omega }\nonumber \\&=\frac{l^2}{8}\left[ \frac{2(4\omega ^2+(1+b+c\sigma )^2)\alpha _4\alpha _5+(1+b+c\sigma )^2(\alpha _4\alpha _6-\beta _4\beta _6)+2\omega (1+b+c\sigma ) (\beta _4\alpha _6+\alpha _4\beta _6)}{\omega (1+b+c\sigma )(4\omega ^2+(1+b+c\sigma )^2)}\right. \nonumber \\&\qquad \qquad \left. -\frac{\alpha _1\beta _3+\beta _1\alpha _3}{\omega ^2} \right] . \end{aligned}$$

(15)

The stability of the Hopf bifurcation depends on the sign of $l_1$. The determination of the sign of $l_1$ from (15) is very difficult analytically because of its complicated expression. So numerical simulations are desirable for the sign of $l_1$ over the parameter range. The variation of $l_1$ with the couple-stress parameter $c_s$ is displayed graphically in Fig. 2. As shown, the value of $l_1$ decreases with the increase in couple-stress parameter $c_s$, but it never reaches zero value. Hence, the Hopf bifurcation at $r=r_h$ is always subcritical type, like in Lorenz system. However, as $c_s$ is increased, the hardness of the stability boundary at $r=r_h$ gradually decreases (hard to soft bifurcations). The quantity $r_h$ is increasing nonlinearly with couple-stress parameter $c_s$. So it delays the transition to chaotic convection.

Fig. 2

Variation of the first Lyapunov quantity $l_1$ with the couple-stress parameter $c_s$

Fig. 3

The oscillatory decaying phase trajectories (projected onto the X–Y plane) to the equilibrium points $E_{\pm }$ for the parameters values: a $r=35$, $c_{s}=0.1$ and b $r=35$, $c_{s}=0.3$

Fig. 4

Existence of homoclinic orbits for a $r=43.4092$, $c_{s}=0.1$, and b $r=295.755$, $c_{s}=0.5$

5 Nonlinear behaviors: homoclinic explosion and the transition to chaos

So far we have discussed the effects of couple-stress parameter on the stability of the steady solutions and local bifurcation scenarios for the Lorenz-like system (8). In this section, we explore some global aspects of the dynamics, viz. homoclinic bifurcation and the transition to chaos. In nonlinear dynamics, a homoclinic bifurcation and the corresponding changes in dynamics are crucially important. This global behavior leads to change in deterministic dynamics from being robust and predictable to being chaotic [29].

Consider the range of the normalized Rayleigh number r between $r_{p}$ and $r_{h}$. Within this range, one can find a point (say $r_{s}$) beyond which all the trajectories started near the origin on its unstable manifold decay spirally toward one of the equilibrium points $E_{\pm }$. The trajectories on the positive half-space decay toward the point $E_{+}$, while those on the negative half-space decay toward $E_{-}$ (Fig. 3 illustrates flow trajectories behaviors).

As r is increased, the amplitude of oscillation of the flow trajectories becomes larger and larger with r until it reaches a critical value, $r_{0}$, beyond which the trajectories that attracted to $E_{+}$ now cross over this point and move toward the point $E_{-}$ and vice versa. An interesting feature is observed when r attains the critical value $r_{0}$. At this point, the trajectories started near the origin on its unstable manifold attracted to its stable manifold, creating a closed orbit surrounding the point $E_{+}$ or $E_{-}$, which connects the origin with itself (see Fig. 4). Such an orbit is called a homoclinic orbit. The bifurcation associated with a homoclinic orbit at the origin for $r=r_{0}$ is known as the homoclinic bifurcation or ‘homoclinic explosion’ [30]. It is a global bifurcation at the origin that cannot be revealed by the linearization technique. Note that homoclinic bifurcations play a role where the transition to chaos occurs immediately for a critical value of the parameter (see Broer and Takens [31] and references therein). The values of $r_{0}$ at the onset of the homoclinic bifurcation are listed in Table 1 for increasing values of $c_{s}$. The critical value increases with the increase in $c_s$, resulting in the delay of homoclinic bifurcation of the system.

Table 1 Approximate values of $r_{0}$ for increasing couple-stress parameter $c_{s}$

Fig. 5

Phase portrait (on X-Y plane) (left) and time history (X vs. time $\tau$) (right) of the solution of (8) for $c_s=0.1$ at different reduced Rayleigh numbers a $r=68$, b $r=74$, c $r=76$. As displayed, the time interval of random oscillation increases with r. After the chaotic oscillation, the flow trajectory decays spirally to the equilibrium point $E_{-}$

For r just above $r_0$, the system has non-stable periodic orbit surrounding either of the points $E_\pm$ in a strange invariant set created through the homoclinic bifurcation. For r near $r_0$, the periodic orbit is found to pass very close to the origin. But it moves away from the origin decreasing its period of oscillation with r. Eventually, it shrinks to the equilibrium point $E_+$ or $E_-$ when r is increased to $r_h$.

For the flow trajectory beyond the critical value for homoclinic orbit, $r_0$, we see that as r increases the trajectory wanders randomly around the non-trivial equilibrium points $E_{\pm }$, eventually decays to either of them. The average time interval of wandering is finite; it expands with r. Finally, the time interval tends to infinity when r attains another critical value $r_1(<r_h)$. Figure 5a–c display the phase portrait on the X-Y plane and time history (X versus $\tau$), which clearly indicate the chaotic and decaying behaviors for three different values of r at fixed value of $c_s$. For $r=r_{1}$, the trajectory of the strange attractor wanders chaotically around the points $E_\pm$. It takes infinitely large time to decay toward the equilibrium points. This phenomenon of chaotic wandering before the onset of the subcritical Hopf bifurcation was reported by Kaplan and Yorke [32] and by Yorke and Yorke [33], and they termed it as ‘preturbulence’ [32], or ‘metastable chaos’ [33].

Fig. 6

Bifurcation diagram (Z vs. $c_s$) of the intermittent-chaos at the normalized Rayleigh number $r=166.1$ representing the local extrema of Z in the post-transient solution of Z(t) as a function of the couple-stress parameter $c_s$. The other parameters are fixed at $\sigma =10$, $b=8/3$. The white stripes correspond to the periodic windows

The numerically computed values of $r_1$ (listed in Table 2) increase with the couple-stress parameter $c_s$, which clearly indicates the suppression effects of fluid couple-stresses on the chaotic evolution of the present system.

Table 2 Approximate values of $r_1$ for increasing couple-stress parameter $c_s$

6 Intermittency, intermittent-chaos, and synchronization of couple-stress fluid convection

Intermittency is a typical route of chaos in deterministic nonlinear systems. It is characterized by long periods of regular motion interrupted by random, aperiodic short-duration bursts. These chaotic bursts become more frequent in course of time evolution [25, 34]. The intermittency phenomenon in the Lorenz system was first studied numerically by Pomeau and Manneville [35]. They showed that the Lorenz system exhibits an intermittent transition to chaos at the critical normalized Rayleigh number $r_T\approx 166.06$. In this section, we investigate the effects of couple-stress parameter $c_s$ on the dynamics of the intermittent-chaos at $r=166.1>r_T$.

We now focus our attention on the bifurcation diagram of the system. Figure 6 displays the bifurcation diagram representing the local extrema of Z in the post-transient solution of Z(t) at $r=166.1$ as a function of the couple-stress parameter $c_s$. The white stripes in the bifurcation diagram correspond to periodic windows.

In this connection we define Poincaré map which is useful for analyzing complex dynamics of nonlinear systems. There exists a map where each state $(\phi , \dot{\phi })$ is connected to the next state $P(\phi , \dot{\phi })$. In other way, whenever $\phi (t)$ is a solution of the system, one obtains $P(\phi (t_{n}), \dot{\phi }(t_{n}))=(\phi (t_{n+1}), \dot{\phi }(t_{n+1}))$, $n=0,1,2,\ldots$. This map is called the Poincaré return map or period map or stroboscopic map. However, for construction of bifurcation diagram from Poincaré map the selection of appropriate Poincaré section is very important [30, 36].

Fig. 7

Phase portrait of the intermittent-chaos(at $r=166.1$) projected onto the X-Y plane (left) and the corresponding Poincaré map (right) for the couple-stress parameter: a $c_s=0.0$, b $c_s=0.001$

It is clear from the bifurcation diagram that the sequence of events through which the chaotic motion at $c_s=0$ synchronizes to a steady state as $c_s$ is increased. In the broad spectrum of the chaotic regimes, there exist periodic motions of certain periods. The periods can be determined by using the Poincaré return map. Here all post-transient return maps are constructed on the plane $Z=165$. The evolutions of the flow trajectories for intermittent-chaos (at $r=166.1$) with increasing values of $c_s$ are represented graphically in Figs. 7, 8, 10, 11, 12, and 13.

Figure 7a presents the Poincaré return map depicting intermittent-chaos at $r=166.1$ and $c_s=0$. As shown, two hooks appear on the Poincaré section. Actually, the hooks in the Poincaré map correspond to the contraction of nearby solution trajectories which causes one or more unstable periodic orbits to become stable. As a result, the system undergoes homoclinic explosion to a stable periodic orbit which can be detected numerically as $c_s$ is increased (see Sparrow [30], Vadasz and Olek [36]). As expected, a periodic solution is obtained at $c_s=0.001$ displayed in Fig. 7b, and the orbit is of period-4.

Above $c_{s}\approx 0.0036$, the solution becomes chaotic again. For $c_s=0.005$, the chaotic attractor is displayed graphically in Fig. 8a. The chaotic solution can also be confirmed by calculating the Lyapunov exponents [37]. Being three-dimensional, the present nonlinear system has three Lyapunov exponents (LEs). A chaotic attractor of (8) is quantified by Lyapunov spectra with a positive Lyapunov exponent. For periodic/quasi-periodic attractors, the largest LE is zero. For fixed point attractors, all the three LEs are negative [37]. The variation of the two leading Lyapunov exponents, say $\lambda _{1,2},$ with the couple-stress parameter $c_s\,\epsilon [0,0.22]$, is displayed graphically in Fig. 9a. In this range of ${c_s}$, the Kaplan–Yorke dimension (or the Lyapunov dimension) can be easily calculated. This enables one to estimate the fractal dimension of the underlying attractor displayed in the figures. The Kaplan–Yorke dimension of an attractor of system (8) with Lyapunov exponents $\lambda _{1}\ge \lambda _{2}\ge \lambda _{3}$ is defined as $D_{KY}=m+\frac{\sum _{j=1}^{m}\lambda _{j}}{|\lambda _{m+1}|}$, where m is the largest positive integer such that $\sum _{j=1}^{m}\lambda _{j}\ge 0$ [38]. If no such positive integer m exists, then $D_{KY}=0$. The variation of $D_{KY}$ with $c_s$ is presented graphically in Fig. 9b.

Fig. 8

Evolution of the flow trajectory of the intermittent-chaos (at $r=166.1$) projected onto the X-Y plane (left) and the corresponding Poincaré map (right) for a $c_s=0.005$, b $c_s=0.007$

Fig. 9

Variation of a the Lyapunov exponents $\lambda _{1,2}$ and b the Kaplan–Yorke dimension $D_{KY}$ with the couple-stress parameter $c_s$

Fig. 10

Phase portrait of the intermittent-chaos(at $r=166.1$) projected onto the X-Y plane (left) and the corresponding return map (right) for a $c_s=0.012$, b $c_s=0.01486$

The two hooks in the return map (see Fig. 8a) indicate the existence of periodic orbits via homoclinic explosion. A period-8 periodic orbit is obtained at $c_s=0.007$ (see Fig. 8b). Similarly, other periodic orbits can be found by varying the control parameter $c_s$. All these periodic orbits emerge via homoclinic explosions.

A period-3 periodic orbit is obtained for $c_s=0.01486$ (see Fig. 10b). Also, period-6 periodic solutions are found at $c_s=0.101$ (see Fig. 11b), $c_s=0.0186$, $c_s=0.11003$, and $c_s=0.174758$. Note that when $c_s$ exceeds the value $c_s=0.174758$, a chaotic solution emerges again. In this case, however, the return map contains no hook, as illustrated in Fig. 12 for $c_s=0.2$.

Fig. 11

Phase trajectory of the intermittent-chaos (at $r=166.1$) projected onto the X-Y plane (left) and the corresponding Poincaré section at $Z=165$ (right) for the couple-stress parameter: a $c_s=0.09$, b $c_s=0.101$

Fig. 12

Evolution of the flow trajectory of the intermittent-chaos (at $r=166.1$) projected onto the X-Y plane (left) and the corresponding return map (right) for the couple-stress parameter $c_s=0.2$

An interesting result is obtained when $c_s$ attains the value $c_s=0.209802$. At this point, a semi-stable limit cycle emerges in the system which signifies a synchronization of the chaotic motion to a steady state. The projection of the limit cycle on the X–Y plane is presented in Fig. 13a. For further increase in $c_s$, the limit cycle disappears and the solution becomes steady for ever. The trajectory of the steady-state solution projected onto the X-Y plane is displayed in Fig. 13b for $c_s=0.22$.

Finally, with increasing couple-stress parameter the synchronization of intermittent-chaos to a steady state takes place via a series of periodic motions interspersed with chaos. However, the chaotic solution of the system at $r=28$ below $c_s\approx 0.009$ directly synchronizes to a steady state.

Fig. 13

Phase trajectory at the final state at particular $r=166.1$ projected onto the X-Y plane when a $c_s=0.209802$, and b $c_s=0.22$

7 Summary and concluding remarks

This is a study exploring the effects of particle size on thermo-convective motion of horizontal couple-stress fluid layer heated from below under a low-dimensional approach represented by Lorenz-like equations. The stability, local and global bifurcations, transition to chaos, intermittent-chaos, and synchronization to steady state are analyzed for this system. The main results are summarized below:

• (i) The equilibrium solution $E_0$ undergoes a supercritical pitchfork bifurcation when r reaches the critical value $r_p=c$, and for $r>r_p$, the solution $E_0$ becomes unstable and two non-trivial solutions $E_{\pm }$ are born.

• (ii) The solutions $E_\pm$ are stable as long as $r<r_h$, where $r_h=\sigma c^2(3+b+c\sigma )/(c\sigma -b-1)$, $\sigma >(1+b)/c$ . At $r=r_h$, the convective solutions $E_{\pm }$ undergo a Hopf bifurcation, resulting a transition from stationary to oscillatory convection.

• (iii) Using first Lyapunov quantity, the Hopf bifurcation is of subcritical type. However, the hardness of the stability boundary at $r=r_h$ decreases with the couple-stress parameter $c_s$.

• (iv) For global aspects of dynamics of the nonlinear system (8) we found that between $r_p$ and $r_h$ there exists a critical normalized Rayleigh number, $r_0$, where the system exhibits homoclinic loops connecting the origin with itself and the system undergoes a homoclinic bifurcation in the neighborhood of the origin.

• (v) Beyond $r_0$, the trajectory wanders randomly around the equilibrium points $E_\pm$ and decays eventually to either of them. The average time interval of wandering expands with increasing r, and finally, it becomes infinitely large when r attains another critical value $r_1(<r_h)$.

• (vi) The synchronization of intermittent-chaos takes place via a series of periodic motion interspersed with intervals of chaotic behaviors. The saddle limit cycles are formed finally, and the system reaches the motionless conduction state.

Finally, the modeled system is useful in engineering transports such as heat transfer in fluids with long-chain molecules, melting and solidification of liquid crystals, polymeric suspension, lubrication technology, and bio-fluid transports.