Three-dimensional energy channeling in the unit-cell model coupled to a spherical rotator II: unidirectional energy channeling

Abstract

This work is the second one in a two-part series devoted to the analysis of complex nonlinear mechanism of energy channeling emerging in a locally resonant three-dimensional, unit-cell model, and the current paper considers unidirectional energy channeling. The considered system comprises an external mass subjected to a symmetric three-dimensional linear local potential with an internal spherical rotator. The present study specifically focuses on the analysis of three-dimensional, dissipative mechanism of irreversible (unidirectional) energy transport across mutually orthogonal directions realized in the limit of low-energy excitations. In particular, this study unveils the special transient regimes of three-dimensional partial and complete transformation of in-plane vibrations of the external element to out-of-plane vibrations. Similar to the results reported in the first part of the series, this three-dimensional energy flow is fully governed by the motion of the internal spherical rotator coupled to the external mass. Analysis of this peculiar response regime is based on regular multi-scale asymptotic analysis resulting in a reduced order dissipative slow-flow model. Results of the analysis are substantiated by the numerical simulations of the full model.

1 Introduction

Passive vibration absorption and isolation in mechanical structures remains one of the most extensively studied areas of theoretical and applied mechanics. The well-known engineering solutions providing efficient vibration suppression are based on the linear tuned mass dampers (TMD) attached to the externally loaded system. These simple absorption devices turn out to be rather efficient in attenuating unwanted vibrations over a relatively narrow bandwidth (mainly in the vicinity of fundamental resonance). Since the pioneering works of Frahm [1] and Den Hartog [2], the TMDs have been extensively applied in quite diverse areas [3,4,5].

Alternative approach providing a broader bandwidth of efficient vibration suppression is based on the nonlinear attachments appended to the primary structure. In some recent studies [6,7,8,9] it was shown that a properly tuned, essentially nonlinear attachment commonly referred to as nonlinear energy sink (NES) demonstrates tremendous capability of unidirectional energy pumping from the externally excited primary structure. This phenomenon of unidirectional energy transport from the primary excited structure to the internal, nonlinear substructure is usually referred to as a targeted energy transfer (TET). It is important to emphasize that in contrast to the linear TMDs, their essentially nonlinear counterparts (i.e., properly tuned NESs) are capable of suppressing unwanted vibrations developed in the externally loaded primary structure over a wide frequency band. Till date, several configurations of NESs have been proposed. These include the nonlinear absorber attached through purely nonlinear spring, vibro-impact absorbers [10,11,12], and internal rotators [13,14,15].

Of late, the concept of unidirectional energy transfer has been extended to two-dimensional structures. Thus, the new phenomena of bidirectional and unidirectional energy (and wave) channeling have been reported in [16,17,18,19] for a locally resonant, unit-cell model subject to the two-dimensional local potential and incorporating internal rotator. The first two studies have analyzed the intrinsic mechanisms of the reversible as well as irreversible energy flow from the axial to the lateral vibrations of the outer element in the limit of low and high energy excitations. The analytical study of the same model [18] has unveiled entire families of special (non-stationary) response regimes manifested by unusual synchronization of the external energy beats (i.e., energy beating between the axial and the lateral oscillations of the outer element) with the angular velocity of the rotator. The latest study [19] has addressed a more complex phenomenon of passive (reversible and irreversible), two-dimensional wave-wave transformations emerging in the quasi-one-dimensional chain of linearly coupled elements incorporating internal rotators.

Recently, the concept of two-dimensional energy channeling has been extended to the three-dimensional case where the outer element is subject to a three-dimensional local potential and incorporates an internal spherical rotator. This forms the first part of the two-part series considering three-dimensional regime of complete energy transport from in-plane vibrations of the outer element to the out-of-plane vibrations [20].

In this work we primarily focus on the asymptotic analysis of the transient regimes of three-dimensional, unidirectional energy flow mechanism emerging in the limit of low-energy excitations. This phenomenon is manifested by partial/complete irreversible energy transport from arbitrarily oriented in-plane vibrations of the external element to out-of-plane vibrations. As it will be shown in this paper, this energy exchange is fully governed by the motion of the internal spherical rotator. Using a regular multi-time-scale analysis we derive the slow-flow model depicting the evolution of amplitudes and phases of the three-dimensional vibrations of the external element as well as the slow dynamics of the internal spherical rotator. Further analysis of the complex slow-flow model enables complete analytical description of the intrinsic mechanisms governing the regimes of transient irreversible energy channeling. Numerical simulations of the original system are found to be in extremely good correspondence with the analysis.

The current paper is structured as follows. In Sect. 2 we describe the mathematical model considered in the present study. Numerical evidence of the regimes of complete as well as the partial unidirectional energy channeling is presented in Sect. 3. Section 4 is devoted to the mathematical analysis of the non-stationary regimes of unidirectional energy channeling. Section 4.1 considers development of an asymptotic model, and Sect. 4.2 comprehensively dwells on analytical and numerical study of the derived slow-flow model and provides comparison with the numerical simulations of the original mathematical model. We conclude this exposition discussing the main highlights of this work in Sect. 5.

2 Mathematical model

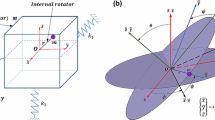
Similar to the first part of the paper, we consider a three-dimensional unit-cell oscillator model comprising the locally resonant external mass (of mass M) with an internal rotator (of mass m concentrated at a radius r). The external mass oscillates in a three-dimensional linear local potential. The dynamical description of the external mass is considered in Cartesian coordinates, whereas the Euler angles define the orientation of the internal rotator. The schematic of the system under consideration is shown in Fig. 1a, while the coordinate system considered for the internal rotator is shown in Fig. 1b. The coordinates of the internal rotator are given by,

$$\begin{aligned} x_m ( t )= & {} x_M ( t )+r\hbox {cos}( {\psi ( t )} )\nonumber \\ y_m ( t )= & {} y_M ( t )+r\hbox {cos}( {\theta ( t )} )\hbox {sin}( {\psi ( t )} )\nonumber \\ z_m ( t )= & {} z_M ( t )+r\hbox {sin}( {\theta ( t )} )\hbox {sin}( {\psi ( t )} ) \end{aligned}$$

(1)

where $x_M ,y_M$ and $z_M$ ($x_m ,y_m$ and $z_m$) are the generalized coordinates of the external mass (internal rotator).

Fig. 1

a Schematic of the system under consideration, b Definition of Euler angles modeling the orientation of the internal rotator $(\phi =0)$

The kinetic energy and the potential energy of the system under consideration are given by,

$$\begin{aligned} T= & {} \frac{m}{2}\left\{ {\left( {\frac{dx_m }{dt}} \right) ^{2}+\left( {\frac{dy_m }{dt}} \right) ^{2}+\left( {\frac{dz_m }{dt}} \right) ^{2}} \right\} \nonumber \\&+\frac{M}{2}\left\{ {\left( {\frac{dx_M }{dt}} \right) ^{2}+\left( {\frac{dy_M }{dt}} \right) ^{2}+\left( {\frac{dz_M }{dt}} \right) ^{2}} \right\} \quad \quad \end{aligned}$$

(2a)

$$\begin{aligned} V= & {} \left\{ {\frac{k_1 }{2}x_M^2 } \right\} +\left\{ {\frac{k_2 }{2}y_M^2 } \right\} +\left\{ {\frac{k_3 }{2}z_M^2 } \right\} \end{aligned}$$

(2b)

where $k_i$ is the linear stiffness coefficient. We consider velocity-dependent linear damping at the hub of the internal rotator and the corresponding Rayleigh dissipation function is given by

$$\begin{aligned} R= & {} \frac{\tilde{\mu }}{2}\{(\dot{x}_m-\dot{x}_M)^2+(\dot{y}_m-\dot{y}_M)^2+(\dot{z}_m-\dot{z}_M)^2\}\nonumber \\= & {} {\frac{\tilde{\mu }}{2}}r^2\{\dot{\theta }^2\sin ^2(\psi )+\dot{\psi }^2\} \end{aligned}$$

(2c)

Considering the Euler–Lagrange equations we derive the equations of motion of the damped 5 degree of freedom system under consideration and are correspondingly

$$\begin{aligned}&({m+M})\frac{d^{2}x_M }{dt^{2}}-mr\cos \left( \psi \right) \left( {\frac{d\psi }{dt}} \right) ^{2}\nonumber \\&\qquad -\,mr\sin \left( \psi \right) \frac{d^{2}\psi }{dt^{2}}+k_1 x_M =0 \end{aligned}$$

(3a)

$$\begin{aligned}&\left( {m+M} \right) \frac{d^{2}y_M }{dt^{2}}-mr\sin \left( \psi \right) \left\{ \sin \left( \theta \right) \frac{d^{2}\theta }{dt^{2}}\right. \nonumber \\&\qquad \left. +\,\cos \left( \theta \right) \left( {\left( {\frac{d\theta }{dt}} \right) ^{2}+\left( {\frac{d\psi }{dt}} \right) ^{2}} \right) \right\} \nonumber \\&\qquad +\,mr\cos \left( \psi \right) \left\{ {\cos \left( \theta \right) \frac{d^{2}\psi }{dt^{2}}-2\sin \left( \theta \right) \frac{d\theta }{dt}\frac{d\psi }{dt}} \right\} \nonumber \\&\qquad +\,k_2 y_M =0 \end{aligned}$$

(3b)

$$\begin{aligned}&\left( {m+M} \right) \frac{d^{2}z_M }{dt^{2}}+mr\sin \left( \psi \right) \left\{ \cos \left( \theta \right) \frac{d^{2}\theta }{dt^{2}}\right. \nonumber \\&\qquad \left. -\,\sin \left( \theta \right) \left( {\left( {\frac{d\theta }{dt}} \right) ^{2}+\left( {\frac{d\psi }{dt}} \right) ^{2}} \right) \right\} \nonumber \\&\qquad +\,mr\cos \left( \psi \right) \left\{ {\sin \left( \theta \right) \frac{d^{2}\psi }{dt^{2}}+2\cos \left( \theta \right) \frac{d\theta }{dt}\frac{d\psi }{dt}} \right\} \nonumber \\&\qquad +\,k_3 z_M =0 \end{aligned}$$

(3c)

$$\begin{aligned}&mr\sin \left( \psi \right) \left\{ 2r\cos \left( \psi \right) \frac{d\theta }{dt}\frac{d\psi }{dt}-\sin \left( \theta \right) \frac{d^{2}y_M }{dt^{2}}\right. \nonumber \\&\qquad \left. +\,\cos \left( \theta \right) \frac{d^{2}z_M }{dt^{2}}+\sin \left( \psi \right) \frac{d^{2}\theta }{dt^{2}} \right\} \nonumber \\&\qquad +\,\tilde{\mu } r\frac{d\theta }{dt}\sin ^{2}\left( \psi \right) =0 \end{aligned}$$

(3d)

$$\begin{aligned}&mr\left\{ -\sin \left( \psi \right) \frac{d^{2}x_M }{dt^{2}}+\cos \left( \psi \right) \cos \left( \theta \right) \frac{d^{2}y_M }{dt^{2}}\right. \nonumber \\&\quad +\,\cos \left( \psi \right) \sin \left( \theta \right) \frac{d^{2}z_M }{dt^{2}}+r\frac{d^{2}\psi }{dt^{2}}\nonumber \\&\quad \left. -\,r\sin \left( \psi \right) \cos \left( \psi \right) \left( {\frac{d\theta }{dt}} \right) ^{2} \right\} +\tilde{\mu } r\frac{d\psi }{dt}=0\quad \end{aligned}$$

(3e)

where M is the mass of the three-dimensional linear oscillator (external mass), m is the mass of the internal spherical rotator, r is the radius of the internal rotator (see Fig. 1a), $k_1 =k_2 =k_3 =k$ is linear stiffness coefficient of the elastic springs acting on the external mass in the x-, y-, and z- directions, respectively. $x_M , y_M , z_M$ denote the displacement of the external mass along the x-, y-, and z- directions respectively, whereas $\theta , \psi$ - are the nutation and spin angles of the internal spherical rotator (see Fig. 1b). In order to transform (3) into non-dimensional form we consider regular system rescaling and non-dimensionalization:

$$\begin{aligned} x= & {} \frac{x_M }{r}; y=\frac{y_M }{r}; z=\frac{z_M }{r}\nonumber \\ \tau= & {} t\sqrt{\frac{k_1 }{M+m}}; \varepsilon =\frac{m}{M+m};\mu =\frac{\tilde{\mu } \sqrt{m+M}}{m\sqrt{k_1 }} \end{aligned}$$

(4)

The mass ratio $\varepsilon$ is considered as a small system parameter ($0<\varepsilon \ll 1$) in this study and for subsequent asymptotic analysis. We consider small order viscous damping, i.e., $\tilde{\mu } =\varepsilon \nu$, where $\nu =O\left( 1 \right)$. Correspondingly, the non-dimensional equations of motion read,

$$\begin{aligned}&\ddot{x}+\varepsilon \sin (\psi )\ddot{\psi }=-x+\varepsilon \cos (\psi )\dot{\psi }^2; \end{aligned}$$

(5a)

$$\begin{aligned}&\ddot{y}-\varepsilon \sin (\psi )\sin (\theta )\ddot{\theta }+\varepsilon \cos (\psi )\cos (\theta )\ddot{\psi }\nonumber \\&\quad =-y+\varepsilon \sin (\psi )\cos (\theta )(\dot{\theta }^2+\dot{\psi }^2)\nonumber \\&\qquad +\,2\varepsilon \cos (\psi )\sin (\theta )\dot{\theta }\dot{\psi };\end{aligned}$$

(5b)

$$\begin{aligned}&\ddot{z}-\varepsilon \sin (\psi )\cos (\theta )\ddot{\theta }+\varepsilon \cos (\psi )\sin (\theta )\ddot{\psi }\nonumber \\&\quad =-z+\varepsilon \sin (\psi )\sin (\theta )(\dot{\theta }^2+\dot{\psi }^2)\nonumber \\&\qquad +\,2\varepsilon \cos (\psi )\cos (\theta )\dot{\theta }\dot{\psi }; \end{aligned}$$

(5c)

$$\begin{aligned}&-\sin (\theta )\ddot{y}+\cos (\theta )\ddot{z}+\sin (\psi )\ddot{\theta }\nonumber \\&\quad =-2\cos (\psi )\dot{\theta }\dot{\psi }-\varepsilon v\sin ({\psi })\dot{\theta }; \end{aligned}$$

(5d)

$$\begin{aligned}&-\sin (\psi )\ddot{x}+\cos (\psi )\cos (\theta )\ddot{y}\nonumber \\&+\cos (\psi )\sin (\theta )\ddot{z}+\ddot{\psi }\nonumber \\&\quad =\sin (\psi )\cos (\psi )\dot{\theta }-\varepsilon v\dot{\psi } \end{aligned}$$

(5e)

where over-dot denotes derivative with respect to non-dimensional time $\tau$. It is evident from (5) that $\varepsilon$ scales the magnitude of the nonlinear terms of the elastic forces applied on the external mass, as well as the coupling strength between the spherical rotator and the external mass. As we are primarily interested in understanding the fundamental (1:1:1) resonant interaction between the motion of the external mass along the three orthogonal directions, we consider symmetric springs (i.e., $k_1 =k_2 =k_3 =k)$.

We are primarily interested in low-energy excitations resulting in low amplitude displacement of the external mass $x,y,z\approx O\left( \varepsilon \right)$ as well as higher amplitude excursions of the internal spherical rotator $\theta ,\psi \approx O\left( 1 \right)$. Thus, the external mass oscillates with a fast resonant frequency, whereas the internal spherical rotator executes oscillations at a slower time scale as evidenced by the numerical simulations and asymptotic analysis in the following sections. The numerical evidence of the phenomena of unidirectional energy transport is presented in the next section.

Fig. 2

Response corresponding to unidirectional complete energy channeling for $x\left( 0 \right) =0, y\left( 0 \right) =0.003, z\left( 0 \right) =0.0052,\theta \left( 0 \right) =\pi /3, \psi \left( 0 \right) =0,\nu =0.15$. a x displacement, b y displacement, c z displacement of external mass, d rotator angle $\theta$, e rotator angle $\psi$. The response of the internal rotator in Cartesian coordinates f $\tilde{x}$ displacement, g $\tilde{y}$ displacement, h $\tilde{z}$ displacement

3 Numerical evidence of the three-dimensional unidirectional energy transport from $( {y-z})$ in-plane oscillations to x- direction out-of-plane oscillations

Before embarking on the asymptotic analysis, it would be prudent to numerically investigate the peculiar non-stationary regimes manifested by intense, spatial energy transport. Accordingly, we present the time histories of the response of the external mass subjected to in-plane $\left( {y-z} \right)$ initial excitation. The time histories of the response in x-, y- and z- directions are presented in Fig. 2. Unless otherwise stated we consider $\varepsilon =0.01$ all through this exposition. As it can be observed from the results of Fig. 2, the initial conditions are such that the response of the external mass is initially localized in the $\left( {y-z} \right)$ in-plane oscillations, whereas the internal spherical rotator is initially at rest and is oriented along an arbitrary direction. As the system evolves, initial energy imparted to the external mass to oscillate in $y-z$ plane gets effectively channeled to the x direction, i.e., the initial ($y-z$) in-plane oscillations of the external mass are completely transformed to horizontal oscillations (along the x- direction). This non-stationary regime of energy transport between the in-plane and the out-of-plane vibrations is unidirectional in the sense that the energy gets entrapped in the x- direction and does not flow back to the $y-z$ plane. The considered response regime is governed by strong resonant interactions between the three generalized coordinates of the external mass coupled through the internal motion of the spherical rotator. We consider the transformed equations of motion to circumvent the singularity whenever $\psi =0$ by considering Cartesian coordinates for both external mass and internal rotator as described in “Appendix 1” of [20]. However, since the response of the internal rotator is presented in angular coordinates (instead of Cartesian coordinates) in Fig. 3d, e, one can observe the singularities in angle $\theta$ (ref. Fig. 3d) whenever $\psi =0$. The observed singularity is a numerical artifact owing to Cartesian to Euler angles coordinate transformation. The corresponding response of the internal rotator in Cartesian coordinates is shown in Fig. 3f, g, and h where no singularities are observable. Alternatively, one can also employ switching algorithms in the numerical simulations to avoid these singularities [21, 22]. The Lissajous curves corresponding to the motion of the external mass exhibiting the three-dimensional channeling regime are presented in Fig. 3a, b for the initial 1500 time units of the numerical simulations. As can be observed, the energy is predominantly localized in the $y-z$ plane and oscillation along the x- direction is sufficiently small. In contrast, the final 500 time units of the numerical simulation presented in Fig. 3c, d exhibit a radically different behavior. As can be observed, the motion is localized along the x- direction with sufficiently large amplitude oscillations, whereas the oscillations in the $y-z$ are negligibly small. Such a behavior denotes energy locking/entrapment in the x- direction. In the present study this regime is termed as complete unidirectional energy channeling. However, such mechanism of energy channeling is not generic, but corresponds to a very specific choice of initial orientation of the internal rotator and will be considered analytically in Sect. 4.

Fig. 3

Lissajous curves corresponding to unidirectional complete energy channeling for $x\left( 0 \right) =\hbox { }x\left( 0 \right) =0, y\left( 0 \right) =0.003, z\left( 0 \right) =0.0052,\theta \left( 0 \right) =\pi /3, \psi \left( 0 \right) =0,\nu =0.15.$ a $x-y$ configuration plane b $x-z$ configuration plane corresponding to initial 1500 time units of the simulation c $x-y$ configuration plane d $x-z$ configuration plane corresponding to final 500 time units of the simulation

Fig. 4

Response corresponding to unidirectional partial energy channeling for $x\left( 0 \right) =0, y\left( 0 \right) =0.003, z\left( 0 \right) =0.0052,\theta \left( 0 \right) =\pi /3, \psi \left( 0 \right) =\pi /6,\nu =0.15$ a x displacement, b y displacement, c z displacement of external mass, d rotator angle $\theta$, e rotator angle $\psi$

Fig. 5

Lissajous curves corresponding to unidirectional partial energy channeling for $x\left( 0 \right) =0, y\left( 0 \right) =0.003, z\left( 0 \right) =0.0052,\theta \left( 0 \right) =\pi /3, \psi \left( 0 \right) =\pi /6,\nu =0.15$. a $x-y$ configuration plane b $x-z$ configuration plane corresponding to initial 1500 time units of the simulation c $x-y$ configuration plane d $x-z$ configuration plane corresponding to final 500 time units of the simulation

However, considering an arbitrary orientation of the internal rotator leads to partial unidirectional energy exchange between the $y-z$ plane and the x- direction. Similar to the previous case, we consider initial conditions such that the energy is initially localized in $y-z$ plane and the internal rotator is stationary and arbitrarily oriented as shown in Fig. 4. As the system evolves, the energy gets distributed in all the three directions in the form of oscillations of the external mass and the motion is delocalized. This process of mild energy exchange between ($y-z$) in-plane oscillations to the x- direction out-of-plane oscillations of the external mass happens unidirectionally. This behavior is considered as partial unidirectional energy channeling. The Lissajous curves corresponding to the motion of the external mass exhibiting the three-dimensional channeling regime are presented in Fig. 5a, b for the initial 1500 time units of the numerical simulations. As can be observed from the results shown in Fig. 5a, b, the initial energy provided in the $y-z$ plane is delocalized and starts flowing back and forth between $y-z$ plane and the x- direction. However, from Fig. 5c, d it can be observed that eventually the energy is locked in both $y-z$ plane and the x- direction and no further exchange is possible. This can be verified from the fact that $\psi$ reaches a steady-state stationary value.

In the following section, we consider analytical and numerical study of intrinsic mechanisms which govern the non-stationary regimes corresponding to the out-of-plane, unidirectional energy channeling. Additionally, there exists a similar class of channeling response regimes restricted solely to the in-plane energy flow between any two mutually orthogonal directions and is considered in “Appendix 3” [16]. Before proceeding with further analysis, it would be prudent to rigorously define the considered energy channeling mechanisms in this exposition. Unidirectional energy channeling refers to the nonrecurrent (complete/incomplete) energy exchange between any two orthogonal orientations of the external mass. The analysis of these intriguing regimes invoking regular multi-time-scale asymptotic analysis is considered in Sect. 4.2. With the application of asymptotic analysis, the global dynamics of the original dynamical system (5) spanning a ten-dimensional phase space can be substantially simplified. We emphasize that the present exposition dwells only on weak excitations and the resulting regimes of partial and complete (in-plane and out-of-plane) energy channeling.

4 Analytical study of the three-dimensional stationary and non-stationary regimes (unidirectional energy channeling) exhibited by the locally resonant unit-cell model

In the present section we consider a comprehensive analytical study of the intrinsic dynamics of stationary and non-stationary regimes of unidirectional energy channeling. We begin Subsect. 4.1 by considering regular multi-time-scale analysis resulting in a reduced slow-flow model describing the evolution of the amplitudes and phases of the response of the external mass as well as the motion of the internal spherical rotator. Subsect. 4.2.1 considers the analysis of stationary dynamics, whereas Subsect. 4.2.2 dwells on the non-stationary dynamics of out-of-plane unidirectional energy channeling.

4.1 Multi-time-scale analysis

It is worthwhile noting once again that the outer element of the system under consideration is subject to a symmetric, three-dimensional potential, such that its linearized natural frequencies in x-, y- and z- directions are identical and equal to unity. Therefore, in the unperturbed case ($\varepsilon =0$) the general motion of the outer element lies on the resonance manifold admitting the exact resonance condition of (1:1:1) between all the three frequency components. The light-mass internal rotator inertially couples the oscillations of the latter along the x-, y- and z- axes. Given the fact that the linearized natural frequencies of the outer element along the x-, y- and z- axes satisfy the basic (1:1:1) resonance conditions and its oscillations along these axes are weakly coupled ($\varepsilon >0$), we expect the formation of transient regimes of resonant energy exchanges between the three components of motion of the outer element. It is important to emphasize that all the regimes of resonant energy transport under consideration are manifested by the resonant interactions between the three components of the response of the outer element being off resonance with the motion of internal, spherical rotator. Thus, considering the 1:1:1 resonant interaction between the motions of the external mass along the three mutually perpendicular directions, we introduce the complex variables [23] in the following form,

$$\begin{aligned} X=\dot{x} +ix; Y=\dot{y}+iy; Z=\dot{z}+iz \end{aligned}$$

(6)

The complex representation of classical equations of motion of a system of linear oscillators is quite extensively used in the domain of quantum mechanics and solid-state physics. The representation basically incorporates in a single variable both velocity and displacement as the real and imaginary parts, respectively. Further, the displacements and velocities of the oscillators can be visually presented as equal length vectors rotating in opposite directions. Thus, it would be enough to find only one complex function for each oscillator and thereby completely determining both displacement and velocity. This representation leads to simplified equations of motion, and the order of differential equations of motion reduces by one. Accordingly,

$$\begin{aligned}&\dot{X} - iX - \varepsilon \cos \left( \psi \right) {\dot{\psi }^2} - \varepsilon \sin \left( \psi \right) \ddot{\psi }= 0 \end{aligned}$$

(7a)

$$\begin{aligned}&\dot{Y} - iY - \varepsilon \sin \left( \psi \right) \left\{ {\cos \left( \theta \right) \left( {{{\dot{\theta }}^2} + {{\dot{\psi }}^2}} \right) + \sin \left( \theta \right) \ddot{\theta }} \right\} \nonumber \\&\qquad +\, \varepsilon \cos \left( \psi \right) \left\{ { - 2\sin \left( \theta \right) \dot{\theta }\dot{\psi }+ \cos \left( \theta \right) \ddot{\psi }} \right\} = 0 \end{aligned}$$

(7b)

$$\begin{aligned}&\dot{Z} - iZ + \varepsilon \sin \left( \psi \right) \left\{ { - \sin \left( \theta \right) \left( {{{\dot{\theta }}^2} + {{\dot{\psi }}^2}} \right) + \cos \left( \theta \right) \ddot{\theta }} \right\} \nonumber \\&\qquad +\, \varepsilon \cos \left( \psi \right) \left\{ {2\cos \left( \theta \right) \dot{\theta }\dot{\psi }+ \sin \left( \theta \right) \ddot{\psi }} \right\} = 0 \end{aligned}$$

(7c)

$$\begin{aligned}&2\cos \left( \psi \right) \dot{\theta }\dot{\psi }- \sin \left( \theta \right) \left\{ {\dot{Y} - \frac{i}{2}\left( {Y + {Y^*}} \right) } \right\} \nonumber \\&\qquad + \cos \left( \theta \right) \left\{ {\dot{Z} - \frac{i}{2}\left( {Z + {Z^*}} \right) } \right\} \nonumber \\&\qquad + \sin \left( \psi \right) \ddot{\theta }+ \varepsilon \nu \sin \left( \psi \right) \dot{\theta }= 0 \end{aligned}$$

(7d)

$$\begin{aligned}&\qquad - \sin \left( \psi \right) \left\{ {\dot{X} - \frac{i}{2}\left( {X + {X^*}} \right) } \right\} \nonumber \\&\qquad + \cos \left( \theta \right) \cos \left( \psi \right) \left\{ {\dot{Y} - \frac{i}{2}\left( {Y + {Y^*}} \right) } \right\} \nonumber \\&\qquad + \,\cos \left( \psi \right) \sin \left( \theta \right) \left\{ {\dot{Z} - \frac{i}{2}\left( {Z + {Z^*}} \right) } \right\} \nonumber \\&\qquad +\, \ddot{\psi }- \sin \left( \psi \right) \cos \left( \psi \right) {\dot{\theta }^2} + \varepsilon \nu \dot{\psi }= 0 \end{aligned}$$

(7e)

In order to analyze the dynamics in the limit of low-energy excitations, we invoke the regular multi-time-scale procedure ($\tau _0 =\tau , \tau _1 =\varepsilon \tau$) and consider the regular expansions of the generalized coordinates

$$\begin{aligned} X( \tau )= & {} \varepsilon X_0 ( {\tau _0 ,\tau _1 } )+\varepsilon ^{2}X_1 ( {\tau _0 ,\tau _1 } )+O( {\varepsilon ^{3}} )\nonumber \\ Y( \tau )= & {} \varepsilon Y_0 ( {\tau _0 ,\tau _1 } )+\varepsilon ^{2}Y_1 ( {\tau _0 ,\tau _1 } )+O( {\varepsilon ^{3}} )\nonumber \\ Z( \tau )= & {} \varepsilon Z_0 ( {\tau _0 ,\tau _1 } )+\varepsilon ^{2}Z_1 ( {\tau _0 ,\tau _1 } )+O( {\varepsilon ^{3}} )\nonumber \\ \theta ( \tau )= & {} \theta _0 ( {\tau _0 ,\tau _1 } )+\varepsilon \theta _1 ( {\tau _0 ,\tau _1 } )+O( {\varepsilon ^{2}} )\nonumber \\ \psi ( \tau )= & {} \psi _0 ( {\tau _0 ,\tau _1 } )+\varepsilon \psi _1 ( {\tau _0 ,\tau _1 } )+O( {\varepsilon ^{2}} ) \end{aligned}$$

(8)

Incorporating (8) in (7) and expanding in rational powers of the small parameter $\varepsilon$ considering slow modulation of the angular coordinates and thereby neglecting the nonlinear components, one obtains the following equations at the leading order (O(1)),

$$\begin{aligned} {\ddot{\theta }_0} = 0;~{\ddot{\psi }_0} = 0 \end{aligned}$$

(9)

Where the over-dots represent derivatives with respect to fast time-scale $\tau _0$ and the solutions of (9) are considered in the following form,

$$\begin{aligned} \theta _0 =P\left( {\tau _1 } \right) +\tau _0 Q\left( {\tau _1 } \right) ; \psi _0 =R\left( {\tau _1 } \right) +\tau _0 S\left( {\tau _1 } \right) \nonumber \\ \end{aligned}$$

(10)

where P, Q, R, S are functions of the slow time-scale $\tau _1$. In the scope of the present work we are primarily interested only in the slow evolution of the amplitudes and specifically in the limit of low-energy excitations of the external mass. Thus, we preclude the fast rotation of the internal spherical rotator by considering $Q\left( {\tau _1 } \right) =S\left( {\tau _1 } \right) =0$. Thus, the slow evolution of both angular coordinates takes the form

$$\begin{aligned} \theta _0 =P\left( {\tau _1 } \right) ; \psi _0 =R\left( {\tau _1 } \right) \end{aligned}$$

(11)

Considering $O\left( \varepsilon \right)$ approximation, we have

$$\begin{aligned}&{\dot{X}_0} - i{X_0} = 0; \end{aligned}$$

(12a)

$$\begin{aligned}&{\dot{Y}_0} - i{Y_0} = 0; \end{aligned}$$

(12b)

$$\begin{aligned}&{\dot{Z}_0} - i{Z_0} = 0; \end{aligned}$$

(12c)

$$\begin{aligned}&\sin \left( {{\psi _0}} \right) {\ddot{\theta }_1} - \sin \left( {{\theta _0}} \right) \left\{ {{{\dot{Y}}_0} - \frac{i}{2}\left( {{Y_0} + Y_0^*} \right) } \right\} \nonumber \\&\qquad + \cos \left( {{\theta _0}} \right) \left\{ {{{\dot{Z}}_0} - \frac{i}{2}\left( {{Z_0} + Z_0^*} \right) } \right\} = 0; \end{aligned}$$

(12d)

$$\begin{aligned}&{\ddot{\psi }_1} - \sin \left( {{\psi _0}} \right) \left\{ {{{\dot{X}}_0} - \frac{i}{2}\left( {{X_0} + X_0^*} \right) } \right\} \nonumber \\&\qquad + \cos \left( {{\theta _0}} \right) \cos \left( {{\psi _0}} \right) \left\{ {{{\dot{Y}}_0} - \frac{i}{2}\left( {{Y_0} + Y_0^*} \right) } \right\} \nonumber \\&\qquad + \cos \left( {{\psi _0}} \right) \sin \left( {{\theta _0}} \right) \left\{ {{{\dot{Z}}_0} - \frac{i}{2}\left( {{Z_0} + Z_0^*} \right) } \right\} = 0\nonumber \\ \end{aligned}$$

(12e)

The $O(\varepsilon )$ approximation corresponding to the motion of the external mass is a decoupled set of oscillators (12a–c) wherein the external mass (of unit mass) oscillates with same frequency in all the three directions. The corresponding solutions are considered in the form,

$$\begin{aligned} {X_0}= & {} {x_0}\left( {{\tau _1}} \right) {e^{i{\tau _0}}}; \end{aligned}$$

(13a)

$$\begin{aligned} {Y_0}= & {} {y_0}\left( {{\tau _1}} \right) {e^{i{\tau _0}}}; \end{aligned}$$

(13b)

$$\begin{aligned} {Z_0}= & {} {z_0}\left( {{\tau _1}} \right) {e^{i{\tau _0}}} \end{aligned}$$

(13c)

where the amplitudes $x_0$, $y_0$, and $z_0$ are functions of slow time variable $\tau _1$. Incorporating these solutions into (12d, e), one has

$$\begin{aligned}&\sin \left( {{\psi _0}} \right) {\ddot{\theta }_1} \nonumber \\&\quad = i\sin \left( {{\theta _0}} \right) \left\{ {{y_0}{e^{i{\tau _0}}} - \frac{1}{2}\left( {{y_0}{e^{i{\tau _0}}} + y_0^*{e^{ - i{\tau _0}}}} \right) } \right\} \nonumber \\&\qquad -\, i\cos \left( {{\theta _0}} \right) \left\{ {{z_0}{e^{i{\tau _0}}} - \frac{1}{2}\left( {{z_0}{e^{i{\tau _0}}} + z_0^*{e^{ - i{\tau _0}}}} \right) } \right\} \nonumber \\ \end{aligned}$$

(13d)

$$\begin{aligned}&{\ddot{\psi }_1} = \frac{i}{2}\sin \left( {{\psi _0}} \right) \left\{ {{x_0}{e^{i{\tau _0}}} - x_0^*{e^{ - i{\tau _0}}}} \right\} \nonumber \\&\qquad -\frac{i}{2}\cos \left( {{\theta _0}} \right) \cos \left( {{\psi _0}} \right) \left\{ {{y_0}{e^{i{\tau _0}}} - y_0^*{e^{ - i{\tau _0}}}} \right\} \nonumber \\&\qquad - \frac{i}{2}\cos \left( {{\psi _0}} \right) \sin \left( {{\theta _0}} \right) \left\{ {{z_0}{e^{i{\tau _0}}} - z_0^*{e^{ - i{\tau _0}}}} \right\} \end{aligned}$$

(13e)

Since the above differential equations are in terms of fast time-scale $\tau _0$, all the slow time-varying terms can be effectively considered to be constant (at this particular time scale). Therefore, (13d, e) can be integrated twice yielding,

$$\begin{aligned} \theta _1= & {} \frac{i}{2\sin \left( {\psi _0 } \right) }\left[ \sin \left( {\theta _0 } \right) \left\{ {-y_0 e^{i\tau _0 }+y_0^*e^{-i\tau _0 }} \right\} \right. \nonumber \\&\left. -\cos \left( {\theta _0 } \right) \left\{ {-z_0 e^{i\tau _0 }+z_0^*e^{-i\tau _0 }} \right\} \right] \end{aligned}$$

(14a)

$$\begin{aligned} \psi _1= & {} \frac{i}{2}\left[ \sin \left( {\psi _0 } \right) \left\{ {-x_0 e^{i\tau _0 }+x_0^*e^{-i\tau _0 }} \right\} \right. \nonumber \\&-\cos \left( {\theta _0 } \right) \cos \left( {\psi _0 } \right) \left\{ {-y_0 e^{i\tau _0 }+y_0^*e^{-i\tau _0 }} \right\} \nonumber \\&\left. -\cos \left( {\psi _0 } \right) \sin \left( {\theta _0 } \right) \left\{ {-z_0 e^{i\tau _0 }+z_0^*e^{-i\tau _0 }} \right\} \right] \nonumber \\ \end{aligned}$$

(14b)

Proceeding to the next order of approximation $O({\varepsilon ^2})$ we have

$$\begin{aligned}&2ix'_0 + {x_0}{\sin ^2}\left( {{\psi _0}} \right) - {y_0}\cos \left( {{\theta _0}} \right) \sin \left( {{\psi _0}} \right) \cos \left( {{\psi _0}} \right) \nonumber \\&\qquad -\, {z_0}\sin \left( {{\theta _0}} \right) \sin \left( {{\psi _0}} \right) \cos \left( {{\psi _0}} \right) = 0; \end{aligned}$$

(15a)

$$\begin{aligned}&2iy'_0 + {y_0}\left\{ {1 - {{\cos }^2}\left( {{\theta _0}} \right) {{\sin }^2}\left( {{\psi _0}} \right) } \right\} \nonumber \\&\qquad -\, {x_0}\cos \left( {{\theta _0}} \right) \cos \left( {{\psi _0}} \right) \sin \left( {{\psi _0}} \right) \nonumber \\&\qquad -\, {z_0}\cos \left( {{\theta _0}} \right) \sin \left( {{\theta _0}} \right) {\sin ^2}\left( {{\psi _0}} \right) = 0; \end{aligned}$$

(15b)

$$\begin{aligned}&2iz'_0 + {z_0}\left\{ {1 - {{\sin }^2}\left( {{\psi _0}} \right) {{\sin }^2}\left( {{\theta _0}} \right) } \right\} \nonumber \\&\qquad -\, {x_0}\sin \left( {{\theta _0}} \right) \cos \left( {{\psi _0}} \right) \sin \left( {{\psi _0}} \right) \nonumber \\&\qquad -\, {y_0}\cos \left( {{\theta _0}} \right) \sin \left( {{\theta _0}} \right) {\sin ^2}\left( {{\psi _0}} \right) = 0; \end{aligned}$$

(15c)

$$\begin{aligned}&\sin \left( {{\psi _0}} \right) \theta '' _0 + \nu \sin \left( \psi \right) \theta ' _0 + 2\cos \left( {{\psi _0}} \right) \theta ' _0\psi ' _0 \nonumber \\&\qquad + \frac{1}{4}\sin \left( {{\psi _0}} \right) \sin \left( {2{\theta _0}} \right) \left\{ {{{\left| {{y_0}} \right| }^2} - {{\left| {{z_0}} \right| }^2}} \right\} \nonumber \\&\qquad + \frac{1}{4}\cos \left( {{\psi _0}} \right) \sin \left( {{\theta _0}} \right) \left\{ {{x_0}y_0^* + {y_0}x_0^*} \right\} \nonumber \\&\qquad - \frac{1}{4}\sin \left( {{\psi _0}} \right) \cos \left( {2{\theta _0}} \right) \left\{ {{y_0}z_0^* + {z_0}y_0^*} \right\} \nonumber \\&\qquad - \frac{1}{4}\cos \left( {{\psi _0}} \right) \cos \left( {{\theta _0}} \right) \left\{ {{z_0}x_0^* + {x_0}z_0^*} \right\} = 0; \end{aligned}$$

(15d)

$$\begin{aligned}&\psi '' _0 + \nu \psi ' _0 - \frac{1}{2}\sin \left( {2{\psi _0}} \right) {\left( {\theta ' _0} \right) ^2} + \frac{1}{4}\sin \left( {2{\psi _0}} \right) {\left| {{x_0}} \right| ^2}\nonumber \\&\qquad + \left\{ - \frac{1}{2}{{\sin }^2}\left( {{\theta _0}} \right) \cot \left( {{\psi _0}} \right) - \frac{5}{{16}}\cos \left( {2{\theta _0}} \right) \cot \left( {{\psi _0}} \right) \right. \nonumber \\&\qquad + \frac{1}{4}{{\cos }^2}\left( {{\psi _0}} \right) \cot \left( {{\psi _0}} \right) \nonumber \\&\qquad \left. + \frac{1}{{16}}\cos \left( {2{\theta _0}} \right) \cos \left( {3{\psi _0}} \right) \mathrm{{cosec}}\left( {{\psi _0}} \right) \right\} \nonumber \\&\qquad \times {\left| {{y_0}} \right| ^2} + \left\{ - \frac{1}{2}{{\cos }^2}\left( {{\theta _0}} \right) \cot \left( {{\psi _0}} \right) \right. \nonumber \\&\qquad \left. +\frac{5}{{16}}\cos \left( {2{\theta _0}} \right) \cot \left( {{\psi _0}} \right) + \frac{1}{4}{{\cos }^2}\left( {{\psi _0}} \right) \cot \left( {{\psi _0}} \right) \right. \nonumber \\&\qquad \left. - \frac{1}{{16}}\cos \left( {2{\theta _0}} \right) \cos \left( {3{\psi _0}} \right) \mathrm{cosec}\left( {{\psi _0}} \right) \right\} \nonumber \\&\qquad \times {\left| {{z_0}} \right| ^2} - \frac{1}{4}\cos \left( {2{\psi _0}} \right) \cos \left( {{\theta _0}} \right) \left\{ {{x_0}y_0^* + {y_0}x_0^*} \right\} \nonumber \\&\qquad \left. - \frac{1}{8}\sin \left( {2{\theta _0}} \right) \sin \left( {2{\psi _0}} \right) \left\{ {{y_0}z_0^* + {z_0}y_0^*} \right\} \right. \nonumber \\&\qquad - \frac{1}{4}\cos \left( {2{\psi _0}} \right) \sin \left( {{\theta _0}} \right) \left\{ {{z_0}x_0^* + {x_0}z_0^*} \right\} = 0 \end{aligned}$$

(15e)

where primes denote derivatives with respect to slow time-scale $\tau _1$. The original system (5) has a ten-dimensional phase space and so does the slow-flow model (15). Thus, despite partitioning the slow and fast dynamics of the system, the dimensionality of the system remains unchanged. In order to reduce the dimensionality of the system, we consider a spherical transformation for the translational coordinates of the external mass in the form

$$\begin{aligned} x_0 \left( {\tau _1 } \right)= & {} N\sin \left( {\xi \left( {\tau _1 } \right) } \right) \cos \left( {\eta \left( {\tau _1 } \right) } \right) e^{i\delta _1 \left( {\tau _1 } \right) }\nonumber \\ y_0 \left( {\tau _1 } \right)= & {} N\sin \left( {\xi \left( {\tau _1 } \right) } \right) \sin \left( {\eta \left( {\tau _1 } \right) } \right) e^{i\delta _2 \left( {\tau _1 } \right) }\nonumber \\ z_0 \left( {\tau _1 } \right)= & {} N\cos \left( {\xi \left( {\tau _1 } \right) } \right) e^{i\delta _3 \left( {\tau _1 } \right) } \end{aligned}$$

(16)

where $\xi \left( {\tau _1 } \right) , \eta \left( {\tau _1 } \right)$ denote the spherical angular coordinates modeling the slow evolving response of motion of the external mass along the three orthogonal directions. Here $\delta _i \left( {i=1,2,3} \right)$ are the corresponding slow time-varying phases of the response of the external mass in x-,y- and z- directions, respectively. The considered transformation inherently supports a conserved quantity (occupation number) given by,

$$\begin{aligned} \left| {x_0 } \right| ^{2}+\left| {y_0 } \right| ^{2}+\left| {z_0 } \right| ^{2}=N^{2} \end{aligned}$$

(17)

Interestingly, the slow-flow model (15) despite being dissipative does not preclude the existence of occupation number as a conserved quantity. This observation requires additional elaboration. It is true that, in general, one cannot expect for this (energy related) quantity to be conserved due to the presence of the dissipation in the considered model. However, we recall that the slow-flow model (15) is in essence the leading order approximation of the original system response (as it is clear from the multi-scale analysis). Therefore, the conserved quantity given in (17) holds true up to this order of approximation. However, the same quantity might evolve with respect to a slower (super-slow) time-scale ($\tau _2$). Apparently this decay is not described at this order of approximation.

In effect, the transformation (17) restricts the motion of the external mass on to the surface of a sphere of radius N. Introducing the transformation (16) in (15) and considering the relative phases $\delta _{12} =\delta _1 -\delta _2 , \delta _{23} =\delta _2 -\delta _3$, we reduce the dimensionality of the system to eight. The corresponding reduced slow-flow model takes the form,

$$\begin{aligned}&\xi ' = - \frac{1}{2}\left\{ {\left( {{A_2}\cos \left( \eta \right) + {B_2}\sin \left( \eta \right) } \right) \cos \left( \xi \right) - {C_2}\sin \left( \xi \right) } \right\} \nonumber \\ \end{aligned}$$

(18a)

$$\begin{aligned}&\eta ' = - \frac{1}{{2\sin \left( \xi \right) }}\left\{ {{B_2}\cos \left( \eta \right) - {A_2}\sin \left( \eta \right) } \right\} \end{aligned}$$

(18b)

$$\begin{aligned}&\delta _{12}^{\prime } =\frac{A_1 }{2\sin \left( \xi \right) \cos \left( \eta \right) }-\frac{B_1 }{2\sin \left( \xi \right) \sin \left( \eta \right) } \end{aligned}$$

(18c)

$$\begin{aligned}&\delta _{23}^{\prime } =\frac{B_1 }{2\sin \left( \xi \right) \sin \left( \eta \right) }-\frac{C_1 }{2\cos \left( \xi \right) }\end{aligned}$$

(18d)

$$\begin{aligned}&\qquad \quad \times \sin \left( {\psi _0 } \right) \theta _0^{{\prime }{\prime }} +\nu \sin \left( \psi \right) \theta _0^{\prime } +2\cos \left( {\psi _0 } \right) \theta _0^{\prime } \psi _0^{\prime } \nonumber \\&\qquad \quad +\frac{1}{4}N^{2}\sin \left( {\psi _0 } \right) \sin \left( {2\theta _0 } \right) \nonumber \\&\qquad \quad \times \left\{ {\cos ^{2}\left( \xi \right) -\sin ^{2}\left( \xi \right) \sin ^{2}\left( \eta \right) } \right\} \nonumber \\&\qquad \quad +\frac{1}{2}N^{2}\cos \left( {\psi _0 } \right) \nonumber \\&\qquad \quad \times \sin \left( {\theta _0 } \right) \left\{ {\sin ^{2}\left( \xi \right) \sin \left( \eta \right) \cos \left( \eta \right) \cos \left( {\delta _{12} } \right) } \right\} \nonumber \\&\qquad \quad -\frac{1}{2}N^{2}\sin \left( {\psi _0 } \right) \cos \left( {2\theta _0 } \right) \nonumber \\&\qquad \quad \times \left\{ {\sin \left( \xi \right) \cos \left( \xi \right) \sin \left( \eta \right) \cos \left( {\delta _{23} } \right) } \right\} \nonumber \\&\qquad \quad -\frac{1}{2}N^{2}\cos \left( {\psi _0 } \right) \cos \left( {\theta _0 } \right) \nonumber \\&\qquad \quad \times \left\{ {\sin \left( \xi \right) \cos \left( \xi \right) \cos \left( \eta \right) \cos \left( {\delta _{12} +\delta _{23} } \right) } \right\} =0\end{aligned}$$

(18e)

$$\begin{aligned}&\qquad \quad \times \psi _0^{{\prime }{\prime }} +\nu \psi _0^{\prime } -\frac{1}{2}\sin \left( {2\psi _0 } \right) \left( {\theta _0^{\prime } } \right) ^{2}\nonumber \\&\qquad \quad +\frac{1}{4}N^{2}\sin \left( {2\psi _0 } \right) \sin ^{2}\left( \xi \right) \cos ^{2}\left( \eta \right) \nonumber \\&\qquad \quad +N^{2}\left\{ -\frac{1}{2}\sin ^{2}\left( {\theta _0 } \right) \cot \left( {\psi _0 } \right) \right. \nonumber \\&\qquad \quad -\frac{5}{16}\cos \left( {2\theta _0 } \right) \cot \left( {\psi _0 } \right) +\frac{1}{4}\cos ^{2}\left( {\psi _0 } \right) \cot \left( {\psi _0 } \right) \nonumber \\&\qquad \quad \left. +\frac{1}{16}\cos \left( {2\theta _0 } \right) \cos \left( {3\psi _0 } \right) \hbox {cosec}\left( {\psi _0 } \right) \right\} \nonumber \\&\qquad \quad \times \sin ^{2}\left( \xi \right) \sin ^{2}\left( \eta \right) +N^{2}\left\{ -\frac{1}{2}\cos ^{2}\left( {\theta _0 } \right) \cot \left( {\psi _0 } \right) \right. \nonumber \\&\qquad \quad +\frac{5}{16}\cos \left( {2\theta _0 } \right) \cot \left( {\psi _0 } \right) +\frac{1}{4}\cos ^{2}\left( {\psi _0 } \right) \cot \left( {\psi _0 } \right) \nonumber \\&\qquad \quad \left. -\frac{1}{16}\cos \left( {2\theta _0 } \right) \cos \left( {3\psi _0 } \right) \hbox {cosec}\left( {\psi _0 } \right) \right\} \nonumber \\&\qquad \quad \times \cos ^{2}\left( \xi \right) -\frac{1}{2}N^{2}\cos \left( {2\psi _0 } \right) \cos \left( {\theta _0 } \right) \nonumber \\&\qquad \quad \times \left\{ {\sin ^{2}\left( \xi \right) \sin \left( \eta \right) \cos \left( \eta \right) \cos \left( {\delta _{12} } \right) } \right\} \nonumber \\&\qquad \quad -\frac{1}{4}N^{2}\sin \left( {2\theta _0 } \right) \sin \left( {2\psi _0 } \right) \nonumber \\&\qquad \quad \times \left\{ {\sin \left( \xi \right) \cos \left( \xi \right) \sin \left( \eta \right) \cos \left( {\delta _{23} } \right) } \right\} \nonumber \\&\quad \quad \quad -\frac{1}{2}N^{2}\cos \left( {2\psi _0 } \right) \sin \left( {\theta _0 } \right) \nonumber \\&\qquad \quad \times \left\{ {\sin \left( \xi \right) \cos \left( \xi \right) \cos \left( \eta \right) \cos \left( {\delta _{12} +\delta _{23} } \right) } \right\} =0 \nonumber \\ \end{aligned}$$

(18f)

where the coefficients $A_i ,B_i$ and $C_i$ ($i=1,2$) are defined in “Appendix 1.” Although, spherical coordinate transformation reduced the dimensionality of the system, the analysis of a system with eight-dimensional phase space still remains sufficiently complex. The considered reduced slow-flow system (18) is non-conservative, non-integrable, and therefore analytically intractable. But we consider conserved quantities of the corresponding conservative system which are slow time-varying quantities for the system considered herein and find analytical estimates for partial and complete unidirectional energy channeling.

4.2 Theoretical study

4.2.1 Stationary regimes associated with nonlinear normal modes (NNMs)

Before venturing into the analysis of non-stationary regimes of the reduced slow-flow model (18) corresponding to unidirectional energy channeling of the original system (5), we explore the rich family of equilibrium points of (18) and investigate their linear stability. The equilibrium points of the (18) would correspond to periodic motions of the system (5) and are thereby appropriately denoted as nonlinear normal modes (NNMs) [23]. In order to find the equilibrium points of the slow-flow system (18) we require the nullification of the slow time derivatives ($\xi ' = \eta '= \delta ' _{12} = \delta ' _{23} = \psi ' _0 = \psi '' _0 = \theta ' _0 = \theta '' _0 = 0$). In fact, the straightforward analysis of the system (18) seems difficult, given its complex structure. However, using some rather intuitive physical reasoning, the three distinct, continuous families of the equilibrium points of the slow-flow system (18) can be obtained. Thus, considering periodic oscillations of the outer mass in an arbitrary orientation in the three-dimensional space, one can accordingly adjust the orientation of the internal spherical rotator along the same direction as that of the oscillations of the external mass. These quite simple periodic motions constitute the trivial continuous family of NNMs which can be easily realized in the three-dimensional configuration under consideration. The three family of NNMs realized in this system is provided in the first part of the paper [20]. To ascertain the stability of the equilibrium points, we consider small perturbation about these equilibrium points in the form $\xi =\bar{\xi }\,+\,{\Delta }\xi ,\eta =\bar{\eta } \,+\,{\Delta }\eta , \delta _{12} =\bar{\delta } _{12} \,+\,{\Delta }\delta _{12} , \delta _{23} =\bar{\delta }_{23} +{\Delta }\delta _{23} ,\theta _0 =\bar{\theta }_0 +{\Delta }\theta _0 , \psi _0 =\bar{\psi }_0 +{\Delta }\psi _0$, where $\bar{(\cdot )}$ denotes the equilibrium point and ${\Delta }(\cdot )$ the corresponding perturbation. One can easily obtain a linear variational equation by introducing the considered perturbations in (18) and the eigenvalues of the corresponding Jacobian matrix govern the stability of the equilibrium point. However, it can be easily verified that the eigenvalues corresponding to all these families of equilibrium points have negative real parts and the realized equilibrium points are stable nodes/foci ($\nu >0$) since their conservative ($\nu =0$) counterparts are centers [20].

4.2.2 Non-stationary regimes of the unidirectional energy channeling

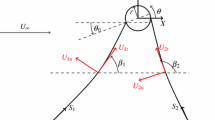
As shown in numerical simulations of Sect. 2, the unidirectional energy channeling discussed in this work corresponds to energy channeling from in-plane oscillations in $y-z$ plane to out-of-plane oscillations along x- direction. Furthermore, it is evident that the orientation plane of the rotator is stationary ($\theta _0^{\prime } =0$) all through the energy channeling process as schematically shown in Fig. 6. Accordingly, one can find the orientation angle of the rotator plane as

$$\begin{aligned} \tan \left( {\theta _0 } \right) =\frac{\cos \left( \xi \right) }{\sin \left( \xi \right) \sin \left( \eta \right) } \end{aligned}$$

(19)

Accordingly, in this section we attempt to analytically predict the regimes of partial and complete energy channeling in the framework wherein the orientation of the plane of rotation of the rotator is stationary.

Fig. 6

Schematic of out-of-plane energy exchange mechanism. a angular coordinates corresponding to external mass, b rotational angles corresponding to the internal rotator

In what follows we consider the balance of angular momenta in all the three directions. The averaged components (see “Appendix 2”) of the angular momenta are as follows,

$$\begin{aligned} L_x \left( {\tau _1 } \right)= & {} a_1 +a_2 \theta _0^{\prime } ; \end{aligned}$$

(20a)

$$\begin{aligned} L_y \left( {\tau _1 } \right)= & {} -b_1 -b_2 \theta _0^{\prime } -b_3 \psi _0^{\prime } ; \end{aligned}$$

(20b)

$$\begin{aligned} L_z \left( {\tau _1 } \right)= & {} c_1 -c_2 \theta _0^{\prime } +c_3 \psi _0^{\prime } \end{aligned}$$

(20c)

where the coefficients $a_i , b_j$ and $c_j$ ($i=1,2$ and $j=1,2,3$) are given in “Appendix 2.” Imposing the condition $\theta _0^{\prime } =0$, we have,

$$\begin{aligned} L_x \left( {\tau _1 } \right)= & {} a_1 ; \end{aligned}$$

(21a)

$$\begin{aligned} L_y \left( {\tau _1 } \right)= & {} -b_1 -b_3 \psi _0^{\prime } ; \end{aligned}$$

(21b)

$$\begin{aligned} L_z \left( {\tau _1 } \right)= & {} c_1 +c_3 \psi _0^{\prime } \end{aligned}$$

(21c)

Trivial analytical manipulation of (21) leads to

$$\begin{aligned} \psi _0^{\prime } =\left( {L_z -c_1 } \right) \cos \left( {\theta _0 } \right) -\left( {L_y +b_1 } \right) \sin \left( {\theta _0 } \right) \end{aligned}$$

(22)

Although we have assumed that the angular momenta are slowly varying with respect to time, (20) does not account for the damping. Considering the physical argument and invoking Newton’s second law, i.e., rate of change of angular momentum is equal to the total resisting torque which is generated due to the viscous damping at the hub. Accordingly, considering the components of rate of change of $L_x$, $L_y$, and $L_z$ about the $\psi$ axis, we have, (see “Appendix 2” for the details)

$$\begin{aligned} \frac{\partial L_z }{\partial \tau _1 }\cos \left( {\theta _0 } \right) -\frac{\partial L_y }{\partial \tau _1 }\sin \left( {\theta _0 } \right) =-\nu \psi _0^{\prime } \end{aligned}$$

(23)

Fig. 7

Response corresponding to unidirectional near complete energy channeling ($\xi =\pi /6,\eta =\pi /2, N=0.6$) for initial conditions $x\left( 0 \right) =0, y\left( 0 \right) =0.003, z\left( 0 \right) =0.0052,\theta \left( 0 \right) =\pi /3, \psi \left( 0 \right) =\pi /256, \nu =0.15$. a x displacement, b y displacement, c z displacement of external mass, d rotator angle $\theta$, e rotator angle $\psi$

Note that the variation of $L_x$ has no component about the $\psi$ axis. Integrating the above equation once by noting that $\theta _0^{\prime } =0$,

$$\begin{aligned} L_z \cos \left( {\theta _0 } \right) -L_y \sin \left( {\theta _0 } \right) =-\nu \psi _0 +Q \end{aligned}$$

(24a)

where Q is the constant of integration. It should however be noted that, in general, $\theta _0^{\prime }$ may not be equal to zero and the analysis considered herein is a specific case corresponding to $\theta _0^{\prime } =0$. Accordingly, the constant of integration is given by,

$$\begin{aligned} Q=L_z \left( 0 \right) \cos \left( {\theta _0 } \right) -L_y \left( 0 \right) \sin \left( {\theta _0 } \right) +\nu \psi _0 \left( 0 \right) \end{aligned}$$

(24b)

Inserting (24a) in (22), we have,

$$\begin{aligned} \psi _0^{\prime }= & {} \left\{ {L_z \left( 0 \right) -c_1 } \right\} \cos \left( {\theta _0 } \right) -\left\{ {L_y \left( 0 \right) +b_1 } \right\} \sin \left( {\theta _0 } \right) \nonumber \\&-\,\nu \left\{ {\psi _0 -\psi _0 \left( 0 \right) } \right\} \end{aligned}$$

(25)

Thus, the dimensionality can be further reduced and the slow-flow model takes the following form,

$$\begin{aligned} \xi '= & {} \frac{1}{2}\{ \left[ {{A_2}\cos \left( \eta \right) + {B_2}\sin \left( \eta \right) } \right] \cos \left( \xi \right) \nonumber \\&-\,{C_2}\sin \left( \xi \right) \} \end{aligned}$$

(26a)

$$\begin{aligned} \eta '= & {} \frac{1}{{2\sin \left( \xi \right) }}\left\{ {{B_2}\cos \left( \eta \right) - {A_2}\sin \left( \eta \right) } \right\} \end{aligned}$$

(26b)

$$\begin{aligned} \delta ' _{12}= & {} \frac{{{A_1}}}{{2\sin \left( \xi \right) \cos \left( \eta \right) }} - \frac{{{B_1}}}{{2\sin \left( \xi \right) \sin \left( \eta \right) }} \end{aligned}$$

(26c)

$$\begin{aligned} \delta ' _{23}= & {} \frac{{{B_1}}}{{2\sin \left( \xi \right) \sin \left( \eta \right) }} - \frac{{{C_1}}}{{2\cos \left( \xi \right) }} \end{aligned}$$

(26d)

$$\begin{aligned} \psi ' _0= & {} \left\{ {{L_z}\left( 0 \right) - {c_1}} \right\} \cos \left( {{\theta _0}} \right) - \left\{ {{L_y}\left( 0 \right) + {b_1}} \right\} \sin \left( {{\theta _0}} \right) \nonumber \\&- \nu \left\{ {{\psi _0} - {\psi _0}\left( 0 \right) } \right\} \end{aligned}$$

(26e)

We further restrict the analysis to $\delta _{23} =n\pi$ denoting in-phase or out-of-phase oscillations of the external mass along y and z directions. Equivalently, we have $\delta _{23}^{\prime } =0$. As presented in Sect. 2, the steady-state response of the system corresponds to an equilibrium point and equivalently represents a nonlinear normal mode (NNM). Accordingly, we represent the final state of the system as $\xi ^{F}, \eta ^{F}, \delta _{12}^F ,\delta _{23}^F ,\theta _0^F ,\psi _0^F$ and the corresponding initial state $\xi \left( 0 \right) =\xi ^{I},\eta \left( 0 \right) = \eta ^{I}, \delta _{12} \left( 0 \right) =\delta _{12}^I ,\delta _{23} \left( 0 \right) =\delta _{23}^I ,\theta _0 \left( 0 \right) =\theta _0^I ,\psi _0 \left( 0 \right) =\psi _0^I$. However, as described previously, $\theta _0^{\prime } =0$ and $\delta _{23}^{\prime } =0$ and accordingly we have $\theta _0^F =\theta _0^I$ and $\delta _{23}^F =\delta _{23}^I$. Thus, if one can choose the initial conditions of the external mass ($\xi ^{I}, \eta ^{I}, \delta _{12}^I ,\delta _{23}^I =n\pi$), the orientation plane of the rotator is determined as $\theta _0^I =\tan ^{-1}\left( {\frac{\cos \left( {\xi ^{I}} \right) }{\sin \left( {\xi ^{I}} \right) \sin \left( {\eta ^{I}} \right) }} \right)$. The only parameter governing the dynamics of the system is $\psi _0^I$ and thus complete/partial energy channeling depends on the initial position of the internal rotator. At steady state we have $\psi _0^{\prime } =0$, and thus the initial position of the internal rotator is given by (from 26e),

$$\begin{aligned} \psi _0^I= & {} \psi _0^F -\frac{\left\{ {L_z \left( 0 \right) -c_1 } \right\} \cos \left( {\theta _0^I } \right) }{\nu }\nonumber \\&+\frac{\left\{ {L_y \left( 0 \right) +b_1 } \right\} \sin \left( {\theta _0^I } \right) }{\nu } \end{aligned}$$

(27a)

In the absence of initial velocity of the internal rotator ($L_z \left( 0 \right) =L_y \left( 0 \right) =0)$, (20a) reduces to

$$\begin{aligned} \psi _0^I =\psi _0^F +\frac{c_1 \cos \left( {\theta _0^I } \right) }{\nu }+\frac{b_1 \sin \left( {\theta _0^I } \right) }{\nu } \end{aligned}$$

(27b)

Finally, the initial conditions of the external mass oscillating in the $y-z$ plane correspond to $\xi ^{I} \, \mathrm{is} \textit{ arbitrary}, \eta ^{I}=\left( {2q+1} \right) \pi /2, \delta _{12}^I \,\mathrm{is} \textit{ arbitrary},\delta _{23}^I =n\pi$, whereas those of the internal rotator are $\theta _0^I =\tan ^{-1}\left( {\frac{\cos \left( {\xi ^{I}} \right) }{\sin \left( {\xi ^{I}} \right) \sin \left( {\eta ^{I}} \right) }} \right)$ and $\psi _0^I \,\mathrm{is} \textit{ arbitrary}$. The corresponding final (steady) state of the system with external mass oscillating along x direction and the internal rotator oriented along the same direction is $\xi ^{F}=\frac{\pi }{2}, \eta ^{F}=0, \delta _{12}^F \,\mathrm{is}\, arbitrary,\delta _{23}^F =n\pi , \quad \theta _0^F =\tan ^{-1}\left( {\frac{\cos \left( {\xi ^{F}} \right) }{\sin \left( {\xi ^{F}} \right) \sin \left( {\eta ^{F}} \right) }} \right) =\theta _0^I$ and $\psi _0^F =0$. Accordingly, we have $c_1 =b_1 =0$ and $\psi _0^I =\psi _0^F =0$. This implies, for complete energy channeling, we need to have $\psi _0^I =\psi _0^F =0$. Interestingly, even for partial energy channeling one can deduce that $\psi _0^F \rightarrow \psi _0^I$ as $\tau _0 \rightarrow \infty$.

Fig. 8

Response corresponding to unidirectional partial energy channeling ($\xi =\pi /6,\eta =\pi /2, N=0.6$) for initial conditions $x\left( 0 \right) =0, y\left( 0 \right) =0.003, z\left( 0 \right) =0.0052,\theta \left( 0 \right) =\pi /3, \psi \left( 0 \right) =\pi /6,\nu =0.15$. a x displacement, b y displacement, c z displacement of external mass, d rotator angle $\theta$, e rotator angle $\psi$

The final part of this section is primarily devoted to the comparison of the responses of the original system (5) and the slow-flow model (18). The simplest system response corresponds to the simple time-periodic motion of the external mass. Such a response would correspond to an equilibrium point of the slow-flow model (18). The corresponding time histories of the response (related to the stable NNM) are illustrated in [20]. Since the stationarity of the internal rotator is a prerequisite for the realization of an equilibrium point, the equilibrium points corresponding to the underlying conservative system are supported by the dissipative system too. In fact the equilibrium points which were centers in the underlying conservative system are stable nodes/foci $(\nu >0)$ in the considered dissipative case.

The second set of numerical simulations corresponds to a system exhibiting complete unidirectional, out-of-plane energy exchange (initially localized in the $y-z$ plane). In Fig. 7 we present the response corresponding to energy localization in the $y-z$ plane with unidirectional energy exchange with the x- direction. As can be observed at steady state, the oscillations of the external mass in the $y-z$ plane are completely suppressed, whereas the energy is locked/entrapped in x- direction resulting in significant oscillations. This corresponds to near complete unidirectional energy channeling and the response of the slow-flow model matches sufficiently well with the numerical simulations of the original system (5). In Fig. 8 we present the response corresponding to partial unidirectional energy channeling. As can be observed, although there is sufficient energy transferred from the $y-z$ plane to the x- direction, the energy transfer is incomplete. In essence, at steady state, the external mass oscillates in all the three directions at the same frequency, but with varying amplitudes governed by the initial orientation of the internal rotator. In this case the response of the slow-flow model matches extremely well with the numerical simulations of the original system (5).

We conclude this section emphasizing that the described analysis can be extended further to any other scenario such as out-of-plane energy channeling from i) $x-y$ plane to z-direction and ii) $x-z$ plane to y-direction. The in-plane unidirectional energy channeling mechanism has been considered by Starosvetsky et al. [16], and a brief exposition has been provided here in “Appendix 3.” In fact the analysis of these scenarios would closely follow the analysis presented in this work owing to the inherent symmetry of the considered system.

5 Conclusions

In the present study we considered the low-energy, transient response regimes of locally resonant, three-dimensional linear oscillator comprising an external mass coupled with an internal spherical rotator. The external mass is mounted on three-dimensional, (perfectly symmetric) linear potential. Using the regular multi-time-scale analysis in the limit of low-energy regimes, we have derived the corresponding slow-flow model. Analysis of the derived slow-flow model reveals the peculiar regimes of transient irreversible energy channeling leading to complete three-dimensional reorientation of the vibrations of external mass. Using the symmetry of the problem under consideration, we derive the global analytical description of the formation and bifurcation of highly non-stationary regimes of complete (irreversible) unidirectional energy channeling from the initially in-plane to the out-of-plane vibrations of the external mass.

Unlike the bidirectional energy channeling mechanism, the unidirectional mechanism is manifested by permanent energy locking in the stationary vibrations being orthogonally oriented to the plane of initial excitation. The presented asymptotic model and the devised analytical methodology enables the extension of the analysis to a more complex study of wave propagation and redirection in a one- and two-dimensional lattice of unit-cells considered in this two-part series. Such material systems have applications in constructing seismic metamaterials and material systems for wave channeling.

Appendices

Appendix 1: Coefficients corresponding to the slow-flow equations of the three translational coordinates

The coefficients corresponding to equation (18) are given below

$$\begin{aligned} A_{1}= & {} -\cos \left( \delta _{12} \right) \cos \left( \theta _{0} \right) \cos \left( \psi _{0} \right) \sin \left( \psi _{0} \right) \sin \left( \xi \right) \sin \left( \eta \right) \nonumber \\&-\cos \left( \delta _{12}+\delta _{23} \right) \sin \left( \theta _{0} \right) \cos \left( \psi _{0} \right) \sin \left( \psi _{0} \right) \cos \left( \xi \right) \nonumber \\&+\sin \left( \xi \right) \cos \left( \eta \right) \sin ^{2}\left( \psi _{0} \right) \end{aligned}$$

(A1.1)

$$\begin{aligned} A_{2}= & {} \sin \left( \delta _{12} \right) \cos \left( \theta _{0} \right) \cos \left( \psi _{0} \right) \sin \left( \psi _{0} \right) \sin \left( \xi \right) \sin \left( \eta \right) \nonumber \\&+\sin \left( \delta _{12}+\delta _{23} \right) \sin \left( \theta _{0} \right) \cos \left( \psi _{0} \right) \sin \left( \psi _{0} \right) \cos \left( \xi \right) \nonumber \\ \end{aligned}$$

(A1.2)

$$\begin{aligned} B_{1}= & {} -\cos \left( \delta _{12} \right) \cos \left( \theta _{0} \right) \cos \left( \psi _{0} \right) \sin \left( \psi _{0} \right) \sin \left( \xi \right) \cos \left( \eta \right) \nonumber \\&-\cos \left( \delta _{23} \right) \cos \left( \theta _{0} \right) \sin \left( \theta _{0} \right) \sin ^{2}\left( \psi _{0} \right) \cos \left( \xi \right) \nonumber \\&+\left( 1-\cos ^{2}\left( \theta _{0} \right) \sin ^{2}\left( \psi _{0} \right) \right) \sin {\left( \xi \right) \sin \left( \eta \right) } \end{aligned}$$

(A1.3)

$$\begin{aligned} B_{2}= & {} -\sin \left( \delta _{12} \right) \cos \left( \theta _{0} \right) \cos \left( \psi _{0} \right) \sin \left( \psi _{0} \right) \sin \left( \xi \right) \cos \left( \eta \right) \nonumber \\&+\sin \left( \delta _{23} \right) \cos \left( \theta _{0} \right) \sin \left( \theta _{0} \right) \sin ^{2}\left( \psi _{0} \right) \cos \left( \xi \right) \end{aligned}$$

(A1.4)

$$\begin{aligned} C_{1}= & {} -\cos \left( \delta _{23} \right) \cos \left( \theta _{0} \right) \sin \left( \theta _{0} \right) \sin ^{2}{\left( \psi _{0} \right) \sin \left( \xi \right) \sin \left( \eta \right) }\nonumber \\&-\cos \left( \delta _{12}+\delta _{23} \right) \sin \left( \theta _{0} \right) \cos \left( \psi _{0} \right) \sin \left( \psi _{0} \right) \sin \left( \xi \right) \cos \left( \eta \right) \nonumber \\&-\sin ^{2}\left( \theta _{0} \right) \sin ^{2}\left( \psi _{0} \right) \cos \left( \xi \right) +\cos \left( \xi \right) \end{aligned}$$

(A1.5)

$$\begin{aligned} C_{2}= & {} -\sin \left( \delta _{23} \right) \cos \left( \theta _{0} \right) \sin \left( \theta _{0} \right) \sin ^{2}{\left( \psi _{0} \right) \sin \left( \xi \right) \sin \left( \eta \right) }\nonumber \\&-\sin \left( \delta _{12}+\delta _{23} \right) \sin \left( \theta _{0} \right) \cos \left( \psi _{0} \right) \sin \left( \psi _{0} \right) \sin \left( \xi \right) \cos \left( \eta \right) \nonumber \\ \end{aligned}$$

(A1.6)

Fig. 9

Schematic of in-plane energy exchange mechanism. a angular coordinates corresponding to external mass, b rotational angles corresponding to the internal rotator

Fig. 10

Response corresponding to unidirectional (near) complete energy channeling ($\eta =0, \xi =0, N=0.6$) for initial conditions $x\left( 0 \right) =0, y\left( 0 \right) =0, z\left( 0 \right) =0.006,\theta \left( 0 \right) =\pi /2, \psi \left( 0 \right) =\pi /256,\nu =0.15$. a x displacement, b y displacement, c z displacement of external mass, d rotator angle $\theta$, e rotator angle $\psi$

Appendix 2: Conservation of angular momentum

The presence of a conserved quantity (integral of motion) of a dynamical system effectively reduces the dimensionality of the system. Thus, finding an integral of motion is imperative when studying higher-dimensional systems, such as the one considered in this study. The underlying conservative system ($\nu =0$) corresponding to system (5 or 18) described in Sects. 2 and 4 has three more integrals of motion in addition to the first integral corresponding to energy. The three conserved quantities are the angular momenta ($L_{x}, L_{y},L_{z}$) along the three perpendicular directions. In order to find the integral of motion, we calculate the angular momentum in the original coordinates (corresponding to (5) with $\nu =0$), complexify the expressions and then average the expression with respect to the fast time scale corresponding to the slow-flow model (18). Accordingly (as per the notation in “Appendix 1”), we have

$$\begin{aligned} \dot{\tilde{x}}(\tau )= & {} \dot{x}(\tau )-\dot{\psi }\mathrm {cos}(\psi (\tau )) \end{aligned}$$

(A2.1)

$$\begin{aligned} \dot{\tilde{y}}(\tau )= & {} \dot{y}(\tau )+\dot{\psi }\cos \left( \theta \left( \tau \right) \right) \cos \left( \psi \left( \tau \right) \right) \nonumber \\&-\dot{\theta }\sin \left( \theta \left( \tau \right) \right) \cos \left( \psi \left( \tau \right) \right) \end{aligned}$$

(A2.2)

$$\begin{aligned} \dot{\tilde{z}}(\tau )= & {} \dot{z}(\tau )+\dot{\psi }{\sin \left( \theta \left( \tau \right) \right) \cos \left( \psi \left( \tau \right) \right) }\nonumber \\&+\dot{\theta }\cos \left( \theta \left( \tau \right) \right) \sin \left( \psi \left( \tau \right) \right) \end{aligned}$$

(A2.3)

The angular momentums about the three perpendicular directions are as follows

$$\begin{aligned} C_{x}= & {} \varepsilon \left\{ -\dot{\tilde{y}}\tilde{z}+\tilde{y}\dot{\tilde{z}} \right\} +\left( 1-\varepsilon \right) \left\{ -\dot{y}z+y\dot{z} \right\} \end{aligned}$$

(A2.4)

$$\begin{aligned} C_{y}= & {} \varepsilon \left\{ -\dot{\tilde{z}}\tilde{x}+\tilde{z}\dot{\tilde{x}} \right\} +\left( 1-\varepsilon \right) \left\{ -\dot{z}x+z\dot{x} \right\} \end{aligned}$$

(A2.5)

$$\begin{aligned} C_{z}= & {} \varepsilon \left\{ -\dot{\tilde{x}}\tilde{y}+\tilde{x}\dot{\tilde{y}} \right\} +\left( 1-\varepsilon \right) \left\{ -\dot{x}y+x\dot{y} \right\} \end{aligned}$$

(A2.6)

The averaged equation corresponding to the three angular momentums ($L_{x}, L_{y},L_{z}$) are

$$\begin{aligned} L_{x}= & {} \frac{1}{2i}\left\{ y_{0}z_{0}^{*}-y_{0}^{*}z_{0} \right\} +\sin ^{2}\left( \psi _{0} \right) \theta '_{0} \end{aligned}$$

(A2.7)

$$\begin{aligned} L_{y}= & {} \frac{1}{2i}\left\{ z_{0}x_{0}^{*}-z_{0}^{*}x_{0} \right\} \nonumber \\&-\frac{\cos \left( \theta _{0} \right) \sin \left( 2\psi _{0} \right) }{2}\theta _{0}^{'}-\sin \left( \theta _{0} \right) \psi ' _{0} \end{aligned}$$

(A2.8)

$$\begin{aligned} L_{z}= & {} \frac{1}{2i}\left\{ x_{0}y_{0}^{*}-x_{0}^{*}y_{0} \right\} \nonumber \\&-\frac{\sin \left( \theta _{0} \right) \sin \left( 2\psi _{0} \right) }{2}\theta '_{0}+\cos \left( \theta _{0} \right) \psi ' _{0} \end{aligned}$$

(A2.9)

Using the spherical coordinate transformation we have in the simplified notation

$$\begin{aligned} L_{x}= & {} a_{1}+a_{2}\theta '_{0} \end{aligned}$$

(A2.10)

$$\begin{aligned} L_{y}= & {} -b_{1}-b_{2}\theta '_{0}-b_{3}\psi '_{0} \end{aligned}$$

(A2.11)

$$\begin{aligned} L_{z}= & {} c_{1}-c_{2}\theta '_{0}+c_{3}\psi '_{0} \end{aligned}$$

(A2.12)

where the coefficients are defined as,

$$\begin{aligned} a_{1}= & {} \frac{1}{2}N^{2}\sin \left( \delta _{23} \right) \sin \left( \eta \right) \sin \left( 2\xi \right) \end{aligned}$$

(A2.13)

$$\begin{aligned} a_{2}= & {} \sin ^{2}\left( \psi _{0} \right) \end{aligned}$$

(A2.14)

$$\begin{aligned} b_{1}= & {} \frac{1}{2}N^{2}\sin \left( \delta _{12}+\delta _{23} \right) \cos \left( \eta \right) \sin \left( 2\xi \right) \end{aligned}$$

(A2.15)

$$\begin{aligned} b_{2}= & {} \frac{\cos \left( \theta _{0} \right) \sin \left( 2\psi _{0} \right) }{2}\end{aligned}$$

(A2.16)

$$\begin{aligned} b_{3}= & {} \sin \left( \theta _{0} \right) \end{aligned}$$

(A2.17)

$$\begin{aligned} c_{1}= & {} \frac{1}{2}N^{2}\sin \left( \delta _{12} \right) \sin \left( 2\eta \right) \sin ^{2}\left( \xi \right) \end{aligned}$$

(A2.18)

$$\begin{aligned} c_{2}= & {} \frac{\sin \left( \theta _{0} \right) \sin \left( 2\psi _{0} \right) }{2}\end{aligned}$$

(A2.19)

$$\begin{aligned} c_{3}= & {} \cos \left( \theta _{0} \right) \end{aligned}$$

(A2.20)

Appendix 3: In-plane unidirectional energy channeling across two orthogonal directions

As discussed toward the end of Sect. 4.2, the system under consideration can exhibit both in-plane and out-of-plane energy channeling regimes. The out-of-plane energy channeling mechanism has been quite extensively dealt with in Sect. 4.2. The in-plane energy channeling mechanism has been considered in [17] for a planar system. However, the system under consideration can exhibit such in-plane energy channeling in three orthogonal planes. For the sake of comprehensiveness and completeness, we describe all these three mechanisms. Similar to the analysis in Sect. 4.2, considering the reduced slow-flow model (26), we have,

• (1) For localization in $x-y$ plane we have $\xi =\pi / 2, \delta _{12}=\pi /2, \delta _{23}=0, \theta _{0}=0$ and the corresponding reduced order slow-flow equations take the form

  $$\begin{aligned} \begin{array}{cc} \xi '=0&{} \psi _{0}^{'}=\left\{ L_{z}(0)-c_{1} \right\} -\nu \left\{ \psi _{0}-\psi _{0}(0) \right\} \\ \eta '=\frac{1}{4}\sin \left( 2\psi _{0} \right) &{} \theta _{0}^{'}=0\\ \end{array}\nonumber \\ \end{aligned}$$

  (A3.1)

• (2) For localization in $x-z$ plane we have $\eta =0, \delta _{12}=\pi /2, \delta _{23}=0, \theta _{0}=\pi /2$ and the reduced order slow-flow equations take the form

  $$\begin{aligned} \begin{array}{cc} \xi '=-\frac{1}{4}\sin \left( 2\psi _{0} \right) &{}\quad \psi _{0}^{'}=-\left\{ L_{y}\left( 0 \right) +b_{1} \right\} -\nu \left\{ \psi _{0}-\psi _{0}(0) \right\} \\ \eta ^{'}=0&{} \theta _{0}^{'}=0\\ \end{array}\nonumber \\ \end{aligned}$$

  (A3.2)

• (3) For localization in $y-z$ plane we have $\eta =\pi / 2, \delta _{12}=0, \delta _{23}=\pi /2, \psi _{0}=\pi /2$ and the reduced order slow-flow equations take the form

  $$\begin{aligned} \begin{array}{cc} \xi '=-\frac{1}{4}\sin (2\theta _{0})&{} \psi _{0}^{'}=0\\ \eta '=0&{} a_{2}\theta _{0}^{'}=-\nu \left\{ \theta _{0}-\theta _{0}\left( 0 \right) \right\} +\left\{ L_{x}\left( 0 \right) -a_{1} \right\} \end{array}\nonumber \\ \end{aligned}$$

  (A3.3)

  It is interesting to note that the three cases described above are similar and therefore analyzing the dynamics corresponding to any one case is sufficient. The primary objective of the present section is to ascertain the initial orientation of the internal rotator resulting in unidirectional energy channeling. The in-plane energy channeling mechanism in $x-y$ plane has been previously explored in [18]. In the present section we consider the mechanism of in-plane energy channeling confined to the $x-z$ plane (ref. Fig. 9). Arguing exactly as in Sect. 4, incorporating $\theta _{0}=\pi /2$ in (A3.2), we have

  $$\begin{aligned} \psi _{0}^{'}=-\left\{ L_{y}\left( 0 \right) +b_{1} \right\} -\nu \left\{ \psi _{0}-\psi _{0}(0) \right\} \end{aligned}$$

  (A3.4)

The initial state of the system can be described as $\xi ^{I} \,\mathrm{is} \textit{ arbitrary}, \eta ^{I}=0, \delta _{12}^{I}+\delta _{23}^{I} \,\mathrm{is} \textit{ arbitrary}$, whereas those of the internal rotator are $\theta _{0}^{I}=\pi / 2$ and $\psi _{0}^{I} \,\mathrm{is} \textit{ arbitrary}$. The corresponding final state of the system with external mass oscillating along x direction and the internal rotator oriented along the same direction is $\xi ^{F}=\pi / 2, \eta ^{F}=0, \delta _{12}^{F}+\delta _{23}^{F}=n\pi , \quad \theta _{0}^{F}=\pi /2=\theta _{0}^{I}$ and $\psi _{0}^{F}=0$. Accordingly, we have $b_{1}=0$ and at steady state we have $\psi _{0}^{'}=0$ and $\psi _{0}^{I}=\psi _{0}^{F}=0$. In essence, for complete energy channeling we need to have $\psi _{0}^{I}=\psi _{0}^{F}=0$. Interestingly, even for partial energy channeling one can deduce that $\psi _{0}^{F}\rightarrow \psi _{0}^{I}$ as $\tau _{0}\rightarrow \infty$. The corresponding numerical simulation response of the original system and the slow-flow model is presented in Fig. 10. The response shows extremely good correspondence.