Adaptive and robust control of quadrotor aircrafts with input saturation

Abstract

This paper proposes a novel adaptive robust controller for the position and attitude tracking of quadrotor unmanned aerial vehicles subjected to additive disturbances and parameter uncertainties. The nonlinear dynamic equations of the quadrotor are obtained by using the Newton–Euler formalism. An emendatory tracking error is introduced to the modified controller to prevent the system and adaption law from degradation or even instability due to control input saturation caused by actuator constraints. The stability of the closed-loop aircraft system under the proposed control law is guaranteed via Lyapunov theory despite the sustained disturbances and actuator saturation. Simulation results are presented to demonstrate the effectiveness of the proposed control method, and the robustness against unknown nonlinear dynamics caused by parametric uncertainties.

1 Introduction

Quadrotor UAVs are versatile flying robots and are of importance for surveillance, building exploration, and information collection, primarily enabled by their autonomous flight, low-cost, vertical takeoff/landing ability [1, 2]. Therefore, autonomous control systems for quadrotor aircrafts have remained attractive in recent years.

In the last decade, many efforts have been made to investigate the automatic flight control of the quadrotor aircrafts. Classic feedback control including proportional–integral–derivative (PID) control and proportional–derivative (PD) control were presented by [3, 4] to achieve trajectory tracking of quadrotors. Advanced nonlinear control approaches such as backstepping control [5], output feedback control [6], model predictive control [7], sliding mode control [8], adaptive robust control [9], and nonlinear $H_{\infty }$ control [10] were proposed for quadrotors. However, from the practical point of view, the control input signals of four rotors’ velocity computed by the above-mentioned approaches cannot be implemented to real aircrafts due to the saturation nonlinearity caused by physical constraints on the rotors [11]. Furthermore, actuator saturation appears frequently in engineering systems and has immense effect on performance degradation as the control laws would act unexpectedly with saturation [12].

Significant amount of research has been done to address the control problem with input saturation, but very few methods are proposed to cope with actuator limitation problem in quadrotor systems where disturbances and uncertain dynamics exist simultaneously. In the works [13, 14], modified backstepping controllers with a static rescaling method and an inverse optimal approach were designed respectively to stabilize the quadrotors with actuator saturations. However, these kinds of control methods were very conservative when the model parameters cannot be exactly obtained. The global asymptotic stability of a quadrotor helicopter subject to actuator magnitude saturation was considered in [15], and the proposed nested-saturation-based nonlinear controller ensured the performance of the closed-loop system. However, this controller was based on a simplified model of the rotorcraft without considering the aerodynamic effects. Reference [16] investigated the formation control of quadrotors with bounded inputs and gained a quick state convergence from saturation zone to the linear zone in the case of separated saturations. Based on a priori input bound [17] employed the nested saturation approach and quaternion-based feedback control to generate a very simple controller suitable for attitude stabilization experiments. When the actuator fault occurred, reconfigurable fault-tolerant control synthesized a modified trajectory by using parameter-estimation-based unscented Kalman filter [18]. As shown in [19], a mixed robust feedback method based on linear $GH_{\infty }$ control was proposed and applied to a nonlinear quadrotor UAV in the presence of actuator constraints. Experiment results on tracking control of UAVs have been obtained by using LQR controller with an integrator anti-windup scheme to avoid actuator saturation in the real system [20].

In above-mentioned works, it was assumed that the systems of concern were linear, exactly known or without external disturbances. However, the real quadrotors have rich kinematics and dynamics, as well as input saturation and disturbances [11, 21]. They should be explicitly considered in controller design; otherwise, the affected control inputs possibly lead to degraded performance and even instability of the closed loop. Therefore it claims for a simple, anti-disturbance, robust and anti-saturation control law for path following problems of small quadrotor aircrafts. Adaptive robust control with input saturation has been investigated in the past decades. For example, in [22], an adaptive control method was proposed for time-variant plants subject to input constraints with a new tracking error introduced to the adaptation laws. To account for input saturation in nonlinear discrete-time systems, a nonlinear feedback controller with quick response and small overshoot was designed in [23]. Gao et al. [24] addressed a neural networks based adaptive robust method and [25] proposed an adaptive coordinated controller both for automatic train systems in the presence of input saturation and dynamic uncertainties. An adaptive nonlinear control was proposed in [26] with a novel additional term to prevent the trolley from running out of the permitted range.

This paper presents an adaptive and robust control design for quadrotor aircraft systems with input saturation nonlinearity. On the whole, the design process can be divided into two stages: First, an adaptive controller is designed for the dynamic uncertainties and external disturbances, to keep good tracking performance when the saturation does not occur. Then, an emendatory tracking error used in adaptation laws is introduced, which is the key preventing the adaptation law from being destroyed in the presence of saturation. Compared with the existing control algorithms in many publications, the main contributions of our proposed control algorithm are as follows: (i) a simple methodology is designed to assign the trajectory tracking problem of quadrotors by means of an adaptive robust control strategy, while tracking errors can decay to zero despite the general uncertainties and disturbances; (ii) when the saturation occurs, the emendatory tracking error can ensure the overall stabilization of the aircraft systems in the sense of Lyapunov and good tracking performance regardless of the unknown systematic parameters and control input saturation; (iii) this method has larger control domain than that of linear approaches, and continuous control signals promote the possibilities of this technique in real-time application.

The rest of this paper is organized as follows. In Sect. 2, the tracking control problem of quadrotor aircrafts modeled by Newton–Euler formalism is presented. Section 3 presents an adaptive control strategy for quadrotor systems without input saturation, where stability of the flight system is proved using Lyapunov stability theory. In Sect. 4, a novel adaptive and robust control scheme is proposed to cope with input saturation and parameter uncertainties. In Sect. 5, simulation results are provided to demonstrate the effectiveness and robustness of the proposed methods for systems with input saturation and sustained disturbances. Finally, the conclusions of this paper are drawn in Sect. 6.

2 Problem formulation

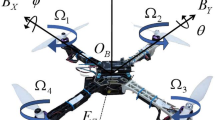
In this section, position coordinate is selected to describe the motion situations of the quadrotor model. This kind of aircraft system can be modeled by Euler formalism. As depicted in Fig. 1, a quadrotor is a cross rigid frame with four rotors to generate the driving forces, where $\varOmega _i$ denotes the angle velocity of the ith propeller. Based on the simplified rotor model, we can use rotational speed vector $\varOmega \in R ^4$ to obtain a mapped control inputs $u_T$, $u_\phi$, $u_\theta$ and $u_\psi$, defined as [27]

$$\begin{aligned} \left\{ \begin{array}{l} u_T=b\sum \limits _{i=1}^4 \varOmega _i^2\\ u_\phi =lb(\varOmega _1^2-\varOmega _3^2)\\ u_\theta =lb(\varOmega _2^2-\varOmega _4^2)\\ u_\psi =\kappa (-\varOmega _1^2+\varOmega _2^2-\varOmega _3^2+\varOmega _4^2), \end{array} \right. \end{aligned}$$

(1)

where $u_T\in R$ is thrust magnitude, $u_\phi$, $u_\theta$ and $u_\psi$ represent roll, pitch and yaw moments, l denotes the distance from the mass center to each rotor, $\kappa >0$ and $b>0$ are thrust and drag coefficients, respectively. Finally, the thrust magnitude $u_T$ and three rotational moments $u_\phi$, $u_\theta$ and $u_\psi$ are considered as the real control inputs to the dynamical system.

Fig. 1

Quadrotor aircraft concept

Let $B=[B_x,B_y,B_z]$ be the body fixed frame shown in Fig. 1, and denote $E=[E_x,E_y,E_z]$ an earth fixed inertial frame. Define the vector $[p,q,r]^\mathrm{T}$ to represent the quadrotor’s angular velocity in the body frame. A quadrotor system has six state variables, three translational motions $\xi =[x,y,z]^\mathrm{T}$ and three rotational motions $\eta =[\phi ,\theta ,\psi ]^\mathrm{T}$. The orientation of the quadrotor from the inertial frame to the body fixed frame can be obtained via three successive rotations about the three axes, and the transformation matrix from $[p,q,r]^\mathrm{T}$ to $[\phi ,\theta ,\psi ]^\mathrm{T}$ is given by [28]

$$\begin{aligned} \left[ {\begin{array}{*{20}c} {{\dot{\phi }}}\\ {{\dot{\theta }}}\\ {{\dot{\psi }}} \end{array}} \right] = \left[ {\begin{array}{*{20}c} {1}&{}{\mathrm{sin}\phi }{\mathrm{tan}\theta }&{}{\mathrm{cos}\phi }{tan\theta }\\ {0}&{}{\mathrm{cos}\phi }&{}{\mathrm{-sin}\phi }\\ {0}&{}{\mathrm{sin}\phi }{\mathrm{sec}\theta }&{}{\mathrm{cos}\phi }{\mathrm{sec}\theta } \end{array}} \right] \left[ {\begin{array}{*{20}c} {p}\\ {q}\\ {r} \end{array}} \right] . \end{aligned}$$

(2)

In view of the above discussion and [29,30,31], the dynamical model of the quadrotor can be described by the following equations:

$$\begin{aligned} \left\{ \begin{array}{l} m{\ddot{x}}=({\mathrm{cos}\phi }{\mathrm{sin}\theta }{\mathrm{cos}\psi }{+}{\mathrm{sin}\phi }{\mathrm{sin}\psi })u_T{-}{k_x}{\dot{x}}-A_x\\ m{\ddot{y}}=({\mathrm{cos}\phi }{\mathrm{sin}\theta }{\mathrm{sin}\psi }{-}{\mathrm{sin}\phi }{\mathrm{cos}\psi })u_T{-}{k_y}{\dot{y}}-A_y\\ m{\ddot{z}}=({\mathrm{cos}\phi }{\mathrm{cos}\theta })u_T-mg-{k_z}{\dot{z}}-A_z\\ {I_\phi }{\ddot{\phi }}={{{\dot{\theta }}}}{{{\dot{\psi }}}}(I_\theta -I_\psi )+lu_\phi -k_{\phi }l{{\dot{\phi }}}-A_\phi \\ {I_\theta }{\ddot{\theta }}={{{\dot{\psi }}}}{{{\dot{\phi }}}}(I_\psi -I_\phi )+lu_\theta -k_{\theta }l{{\dot{\theta }}}-A_\theta \\ {I_\psi }{\ddot{\psi }}={{{\dot{\phi }}}}{{{\dot{\theta }}}}(I_\phi -I_\theta )+u_\psi -k_{\psi }{{\dot{\psi }}}-A_\psi \end{array} \right. \end{aligned}$$

(3)

where $k_i$ is the drag coefficient and a positive constant, $I_\phi$, $I_\theta$ and $I_\psi$ represent the inertias of the aircrafts, m stands for the mass, g is the gravitational acceleration, and $A_i$ is the disturbance force or disturbance moment. This model is presented and is tested experimentally in [30].

Remark 1

It should be noted that the model (3) considers the parametric uncertainties of the quadrotor aircraft, and external disturbances on the six degrees of freedom as $A_i(i=x,y,z,\phi ,\theta ,\psi )$ when maintained winds disturb the whole system. In practice, the external disturbances like wind-gust for aircrafts are extremely difficult to obtain accurately, and thus we adopt the sustained disturbance signal model for quadrotor aircrafts which was presented in reference [10]. Therefore, following adaptive control will be designed to compensate disturbance influence by adaptively identifying this unknown sustained disturbance vector where its derivative is regarded as zero. Some recent literatures also handle the quadrotor aircraft disturbance in the same way where persistent light gusts of wind are considered as external disturbances on the aerodynamic forces and moments [32].

The overall control objective is to design a nonlinear adaptive controller for the quadrotor such that the UAVs are able to track a desired trajectory $\xi _r = [x_r, y_r, z_r]^\mathrm{T}$ and a desired yaw angle $\psi _r$. In translational subsystem, an adaptive controller is designed so as to obtain $u_T$, $\phi _r$ and $\theta _r$, which enables the aircraft to track the desired trajectory $\xi _r$. This adaptive law helps to compensate the uncertain system parameters as well as eliminate the effects caused by wind-gust disturbances. Based on the derived desired angles $\eta _r$, another adaptive controller is utilized in rotational subsystem to obtain proper rotor moment values $[u_\phi ,u_\theta ,u_\psi ]^\mathrm{T}$ to keep the aircraft tracking the desired attitude angles $\eta _r$. Finally, stability analysis is proved by using Lyapunov theory. To streamline the technical proof of the main results, the following lemma is needed, where Lemma 1 is brought from [33].

Lemma 1

For any uniformlly continuous function f(t), if $lim _{t\rightarrow \infty }\int _0^{t}f(\tau )d\tau$ exists and is finite, then $lim _{t\rightarrow \infty }f(t)=0$.

3 Adaptive control without input saturation

In this section, an attitude controller and a position controller are designed, respectively, based on the adaptive control approach. Then, a novel adaptive and robust controller is presented with an emendatory compensation introduced to attenuate the saturation influence involved in translational dynamics and rotational dynamics.

Translational dynamic equations of quadrotors can be obtained from (3). To begin, define new control inputs $u_x$, $u_y$ and $u_z$, satisfying

$$\begin{aligned} \left\{ \begin{array}{l} u_x(t)=(\mathrm{cos}{\phi }(t)\mathrm{sin}{\theta }(t)\mathrm{cos}{\psi }(t)\\ \quad +\,\mathrm{sin}{\phi }(t)\mathrm{sin}{\psi }(t))u_T\\ u_y(t)=(\mathrm{cos}{\phi }(t)\mathrm{sin}{\theta }(t)\mathrm{sin}{\psi }(t)\\ \quad -\,\mathrm{sin}{\phi }(t)\mathrm{cos}{\psi }(t))u_T\\ u_z(t)=(\mathrm{cos}{\phi }(t)\mathrm{cos}{\theta }(t))u_T. \end{array} \right. \end{aligned}$$

(4)

The translational and rotational tracking errors and velocity tracking errors can be defined as follows

$$\begin{aligned} e_{\xi {i}}= & {} \xi _{i}-\xi _{ir},\ {\dot{e}}_{\xi {i}}={{\dot{\xi }}}_{i}-{{{\dot{\xi }}}}_{ir},\quad i=x,y,z \end{aligned}$$

(5)

$$\begin{aligned} e_{\eta {i}}= & {} \eta _{i}-\eta _{ir},\ {\dot{e}}_{\eta {i}}={{\dot{\eta }}}_{i}-{{{\dot{\eta }}}}_{ir},\quad i=\phi ,\theta ,\psi \end{aligned}$$

(6)

where the $\xi _{ir}$ and ${{{\dot{\xi }}}}_{ir}$ are the desired translational trajectory and the corresponding velocity. The following auxiliary state error $\gamma _{{\xi }i}$ is introduced to facilitate the control formulation and stability analysis:

$$\begin{aligned} \gamma _{{\xi }i}= & {} {\dot{e}}_{{\xi }i}+\alpha _i{e_{{\xi }i}},\quad i={x,y,z} \end{aligned}$$

(7)

$$\begin{aligned} \gamma _{{\eta }i}= & {} {\dot{e}}_{{\eta }i}+\alpha _i{e_{{\eta }i}},\quad i={\phi ,\theta ,\psi } \end{aligned}$$

(8)

where $\alpha _i>0$ is an arbitrarily chosen constant to weigh the two terms.

For the translational subsystem, differentiating (5) with respect to time, one obtains

$$\begin{aligned} {{\dot{\gamma }}}_{{\xi }i}={\ddot{e}}_{{\xi }i}+\alpha _i{{\dot{e}}_{{\xi }i}}={{\ddot{\xi }}}_i-({{\ddot{\xi }}}_{ir}-\alpha _i{\dot{e}}_{\xi {i}}). \end{aligned}$$

(9)

Using (3) and (9), the height model in z direction can be considered as

$$\begin{aligned} m{{\dot{\gamma }}}_{{\xi }z}=u_z-mg-k_z{\dot{z}}-A_z-m({{\ddot{\xi }}}_{zr}-\alpha _z{\dot{e}}_{\xi {z}}). \end{aligned}$$

(10)

For technical simplicity, (10) can be written in the following compact form:

$$\begin{aligned} m{{\dot{\gamma }}}_{{\xi }z}=u_z-H_z\rho _z, \end{aligned}$$

(11)

with the known regression matrix $H_z\in {\mathfrak {R}^{1\times 3}}$ given by

$$\begin{aligned} H_z=[{\dot{z}},1,{{\ddot{\xi }}}_{zr}-\alpha _z{\dot{e}}_{\xi {z}}+g], \end{aligned}$$

(12)

and the unknown parameter vector $\rho _z\in \mathfrak {R}^{3\times 1}$ given by

$$\begin{aligned} \rho _z=[k_z,A_z,m]^\mathrm{T}. \end{aligned}$$

(13)

Similarly, according to (3) and (9), regression matrix and parameter vector for x and y channels are defined as

$$\begin{aligned} H_i= & {} [\dot{\xi _{i}},1,{{\ddot{\xi }}}_{ir}-\alpha _i{\dot{e}}_{\xi {i}}],\quad i={x,y} \end{aligned}$$

(14)

$$\begin{aligned} \rho _i= & {} [k_i,A_i,m]^\mathrm{T},\quad i={x,y} \end{aligned}$$

(15)

Therefore, the translational subsystem model with error signals can be described as follows

$$\begin{aligned} m{{\dot{\gamma }}}_{{\xi }i}=u_i-H_i\rho _i,\quad i={x,y,z} \end{aligned}$$

(16)

As for the rotational subsystem, substituting the derivative of (8) into (3) leads to

$$\begin{aligned} I_i{{\dot{\gamma }}}_{{\eta }i}= & {} f_i({{\dot{\phi }}},{{\dot{\theta }}},{{\dot{\psi }}}){\widetilde{I}}_i+l_i{u_i}-k_i{l_i}{{\dot{\eta }}}_i\nonumber \\&-A_i-I_i({{\ddot{\eta }}}_{ir}-\alpha _i{\dot{e}}_{\eta {i}}),\quad i={\phi ,\theta ,\psi } \end{aligned}$$

(17)

where $f_\phi ={{\dot{\theta }}}{{\dot{\psi }}},f_\theta ={{\dot{\psi }}}{{\dot{\phi }}},f_\psi ={{\dot{\phi }}}{{\dot{\theta }}}$, ${\widetilde{I}}_\phi =I_\theta -I_\psi ,{\widetilde{I}}_\theta =I_\psi -I_\phi ,{\widetilde{I}}_\psi =I_\phi -I_\theta$, $l_\phi =l,l_\theta =l,l_\psi =1$. For technical simplicity, (17) can also be written in the following compact form:

$$\begin{aligned} I_i{{\dot{\gamma }}}_{{\eta }i}=l_i{u_i}-H_i\rho _i,\quad i={\phi ,\theta ,\psi } \end{aligned}$$

(18)

where the regression matrix and corresponding unknown parameter vector are defined as

$$\begin{aligned} H_i= & {} [-f_i({{\dot{\phi }}},{{\dot{\theta }}},{{\dot{\psi }}}),{l_i}{{\dot{\eta }}}_i,1,{{\ddot{\eta }}}_{ir}-\alpha _i{\dot{e}}_{\eta {i}}],\, i={\phi ,\theta ,\psi }\nonumber \\ \end{aligned}$$

(19)

$$\begin{aligned} \rho _i= & {} [{\widetilde{I}}_i,k_i,A_i,I_i]^\mathrm{T},\quad i={\phi ,\theta ,\psi } \end{aligned}$$

(20)

Theorem 1

Consider the position subsystem in (16) and rotation subsystem in (18). If the adaptive control laws are defined by

$$\begin{aligned} u_i= & {} H_i{{\hat{\rho }}}_i\!-\!\mu _i\gamma _{\xi {i}},\ \dot{{{\hat{\rho }}}_i}\!=\!-\!\varGamma _i{H_i^T}\gamma _{\xi {i}},\quad i\!=\!{x,y,z} \end{aligned}$$

(21)

$$\begin{aligned} u_i= & {} (H_i{{\hat{\rho }}}_i\!-\!\mu _i\gamma _{\eta {i}})/l_i,\ \dot{{{\hat{\rho }}}_i}\!=\!-\!\varGamma _i{H_i^T}\gamma _{\eta {i}},\quad i\!=\!{\phi ,\theta ,\psi }\nonumber \\ \end{aligned}$$

(22)

where ${{\hat{\rho }}}_i$ represents the estimated value of the unknown parameter vector, then the position tracking error, attitude tracking error and their speed tracking error will decay to zero regardless of unknown system dynamics, and all closed-loop signals are bounded.

Proof

At first, consider the following Lyapunov candidate for position subsystem

$$\begin{aligned} V=\frac{1}{2}\gamma _{\xi {i}}m\gamma _{\xi {i}}+\frac{1}{2}{{{\widetilde{\rho }}}}_i^T\varGamma _i^{-1}{{{\widetilde{\rho }}}}_i,\quad i={x,y,z} \end{aligned}$$

(23)

where ${{{\widetilde{\rho }}}}_i=\rho _i-{{{\hat{\rho }}}}_i$ denotes the estimated error. As stated in Remark 1, the sustained disturbance is an unknown constant vector that needs to be estimated in an adaption process. In fact, even if it varies slightly with time, the disturbance term $A_i$ can still be regarded as a constant vector in a short time. And the tracking error bound regarding disturbance can be made arbitrarily small by selecting appropriate adaptive gains. Using this notation, the adaptation law in (21) yields

$$\begin{aligned} \dot{{{{\widetilde{\rho }}}}_i}=\varGamma _i{H_i^T}\gamma _{\xi {i}},\quad i={x,y,z} \end{aligned}$$

(24)

Then, substituting (21) and (24) into (16), one obtains

$$\begin{aligned} m{{\dot{\gamma }}}_{{\xi }i}=-H_i{{\widetilde{\rho }}}_i-\mu _i\gamma _{{\xi }i},\quad i={x,y,z} \end{aligned}$$

(25)

Differentiating (23) by using (24) and (25), the derivative of (23) is then obtained by

$$\begin{aligned} {\dot{V}}= & {} \gamma _{\xi {i}}(-H_i{{\widetilde{\rho }}}_i-\mu _i\gamma _{{\xi }i})+{{{\widetilde{\rho }}}}_i^T\varGamma _i^{-1}\varGamma _iH_i^T\gamma _{\xi {i}}\nonumber \\= & {} -\mu _i\gamma _{\xi {i}}^2,\quad i={x,y,z} \end{aligned}$$

(26)

Similarly, if the Lyapunov function adopted for rotation subsystem is given as follows

$$\begin{aligned} V=\frac{1}{2}\gamma _{\eta {i}}I_i\gamma _{\eta {i}}+\frac{1}{2}{{{\widetilde{\rho }}}}_i^T\varGamma _i^{-1}{{{\widetilde{\rho }}}}_i,\quad i={\phi ,\theta ,\psi } \end{aligned}$$

(27)

And considering ${{{\widetilde{\rho }}}}_i=\rho _i-{{{\hat{\rho }}}}_i$, (18) and (22), the differential form of (27) satisfies that

$$\begin{aligned} {\dot{V}}=-\mu _i\gamma _{\eta {i}}^2,\quad i={\phi ,\theta ,\psi } \end{aligned}$$

(28)

Since ${\dot{V}}$ is semi-negative definite, V has an upper bound V(0), which guarantees the boundedness of $\gamma _{\xi {i}}$, $\gamma _{\eta {i}}$, ${\widetilde{\rho }}_i$ and $u_i$. According to (7) and (8), one can obtain that e, ${\dot{e}}$, $\xi _i$, ${\dot{\xi }}_i$, $\eta _i$ and ${\dot{\eta }}_i$ are all bounded based on standard linear control arguments. Then, from (25) one can get that ${\dot{\gamma }}$ is bounded, which further ensures ${\ddot{V}}$ obtained by differentiating (26) and (28) to be bounded. Thus ${\dot{V}}$ is uniformly continuous. Overall, V is positive definite and bounded, and ${\dot{V}}$ is semi-negative definite and uniformly continuous, so Lemma 1 implies that

$$\begin{aligned} \lim \limits _{t\rightarrow \infty }{\dot{V}}(t)=0. \end{aligned}$$

(29)

In view of (26), (28) and (29), the limitation of $\gamma$ is

$$\begin{aligned} \lim \limits _{t\rightarrow \infty }\gamma (t)=0. \end{aligned}$$

(30)

Recall (7) and (8) and suppose that the initial error value is $e(0)=e_0$, and then the error can be solved as follows

$$\begin{aligned} e(t)=e(0)e^{-\alpha {t}}+\frac{\gamma (t)}{\alpha }(1-e^{-\alpha {t}}), \end{aligned}$$

(31)

which further implies that e(t) and ${\dot{e}}(t)$ will converge to zero as $t\rightarrow \infty$ based on (30) and (31). Therefore, the position tracking error, attitude tracking error, and their velocity errors of the quadrotor aircrafts will decay to zero even in the presence of the external disturbances and unknown dynamic parameters.$\square$

Remark 2

If the adaptive parameter $\varGamma _i$ is sufficiently large, one can conclude that ${{{\hat{\rho }}}}_i$ will approximate the unknown parameter vector $\rho _i$, and thereby the effects caused by the external disturbances and unknown dynamic parameters can be attenuated.

4 Adaptive robust control with input saturation

The control functions $u_z$, $u_\phi$, $u_\theta$ and $u_\psi$ cannot be put into use due to the rotational speed limitations in (1). In fact, four control inputs are influenced by the following saturation function

$$\begin{aligned} u_i=\mathrm{sat}(u_{iL},{\overline{u}}_i,u_{iU})= \left\{ \begin{array}{l} u_{iL}\quad {\overline{u}}_i\ \;<u_{iL}\\ {\overline{u}}_i\quad \ \;u_{iL}<{\overline{u}}_i\ <u_{iU}\\ u_{iU}\quad {\overline{u}}_i\ \;>u_{iU} \end{array} \right. \nonumber \\ \end{aligned}$$

(32)

where $u_{iL}$ and $u_{iU}(i=z,\phi ,\theta ,\psi )$ are the lower/uper limit bounds of the four control inputs respectively. Once the saturation occurs, the tracking errors of e and ${\dot{e}}$ will increase such that the filtered error signal $\gamma$ will be increased, which also leads to a oscillation in the adaptive laws. Thus the control performance under law (21) and (22) will be ruined. The basic idea underlying the anti-windup designs with input saturating actuators is to introduce modifications and compensations in order to reduce the influence of saturation nonlinearity.

In translational subsystem with actuator saturation $u_{zL}<u_z<u_{zU}$, define a new auxiliary error ${{\overline{\gamma }}}_{\xi {i}}=\gamma _{\xi {i}}-\chi _{\xi {i}}$ which satisfies

$$\begin{aligned} m{\dot{{{\overline{\gamma }}}}}_{\xi {i}}= & {} m{{\dot{\gamma }}}_{\xi {i}}-m{{\dot{\chi }}}_{\xi {i}}\nonumber \\= & {} u_i-H_i\rho _i-m{{\dot{\chi }}}_{\xi {i}},\quad i={x,y,z} \end{aligned}$$

(33)

with the regression matrix H and the unknown parameter vector $\rho$ defined as same as those in Sect. 3. And the newly introduced signal of $\chi _{\xi {i}}$ can change adaptively to attenuate the influence from actuator saturation, and its adaptive law will be discussed later.

When the saturation is considered, the adaptive control law given by (21) can be modified and the new control law is designed in the following form:

$$\begin{aligned} u_i= & {} \mathrm{sat}(u_{iL},{\overline{u}}_i,u_{iU}),\quad i={x,y,z} \end{aligned}$$

(34)

$$\begin{aligned} {\overline{u}}_i= & {} H_i{\hat{\rho _i}}-\mu _i{{\overline{\gamma }}}_{\xi {i}}{-}\beta _i\chi _{\xi {i}}{-}\delta _i\mathrm{sgn}({{\overline{\gamma }}}_{\xi {i}}), \quad i={x,y,z}\nonumber \\ \end{aligned}$$

(35)

with the unknown parameter vector and auxiliary error being updated as follows

$$\begin{aligned}&\dot{{\hat{\rho _i}}}=-\varGamma _i{H_i^T{{\overline{\gamma }}}_{\xi {i}}},\quad i={x,y,z} \end{aligned}$$

(36)

$$\begin{aligned}&{{\dot{\chi }}}_{\xi {i}}=-\frac{\beta _i}{{\hat{m}}}\chi _{\xi {i}}+\frac{u_i-{\overline{u}}_i}{{\hat{m}}},\quad i={x,y,z} \end{aligned}$$

(37)

where the function sat() is defined in (32), $\mu _i$ and $\beta _i$ represent freely chosen positive constants, and the robust signal term $\delta _i\mathrm{sgn}({{\overline{\gamma }}}_{\xi {i}})$ will be discussed later.

Consider that the precise physical parameters of quadrotor UAVs can not been obtained in practical environment, for example, the mass m and inertia moments $I_\phi$, $I_\theta$ and $I_\psi$. Based on the invariance of these parameters and bounds of the inputs, the following definitions are made.

Definition 1

The difference proportion $\epsilon _m$ of aircraft mass is defined as $m/{\hat{m}}=1+\epsilon _m$, and the known bound values $\epsilon _m^*$ guarantees $\epsilon _m^*>|\epsilon _m|=|m/{\hat{m}}-1|$. And according to (37), there exists bound $u_i^*$ such that $u_i^*>|\beta _i{\chi _{\xi {i}}}-u_i+{\overline{u}}_i|$ where $i={x,y,z}$. $\beta _i{\chi _{\xi {i}}}$ varies with the change of $u_i-{\overline{u}}_i$ until the adaptation error becomes zero, thus the upper bound of their subtraction will exist as $u_i^{*}$.

Following a similar procedure, the robust adaptive control function for attitude motion of the vehicle body under torque saturations of (32) can be designed as follows:

$$\begin{aligned}&{\overline{u}}_i=(H_i{\hat{\rho _i}}-\mu _i{{\overline{\gamma }}}_{\eta {i}}-\beta _i\chi _{\eta {i}}-\delta _i\mathrm{sgn}({{\overline{\gamma }}}_{\eta {i}}))/l_i,\nonumber \\&i={\phi ,\theta ,\psi } \end{aligned}$$

(38)

with the unknown parameter vector and auxiliary error being updated as follows

$$\begin{aligned}&\dot{{\hat{\rho _i}}}=-\varGamma _i{H_i^T{{\overline{\gamma }}}_{\eta {i}}},\quad i={\phi ,\theta ,\psi } \end{aligned}$$

(39)

$$\begin{aligned}&{{\dot{\chi }}}_{\eta {i}}=-\frac{\beta _i}{{\hat{I}}_i}\chi _{\eta {i}}+\frac{u_i-{\overline{u}}_i}{{\hat{I}}_i}, \quad i={\phi ,\theta ,\psi } \end{aligned}$$

(40)

To cope with the inertial parameter uncertainty in aircraft body and the input torque saturation, some definitions are expressed as follows.

Definition 2

The difference proportion of inertial values in three axis can be written as $\epsilon _i (i={\phi ,\theta ,\psi })$, which is further defined as $I_i/{\hat{I}}_i=1+\epsilon _i$, and the known bound value $\epsilon _i^*$ guarantees $\epsilon _i^*>|\epsilon _i|=|I_i/{\hat{I}}_i-1|$. And according to (40), there exists bound $u_i^*$ such that $u_i^*>|\beta {\chi _{\eta {i}}}-u_i+{\overline{u}}_i|$.

The following theorem will provide our main results on the adaptive robust control for quadrotor aircraft movements with input saturation.

Theorem 2

Consider the position subsystem with control signals in (16) and rotation subsystem in (18) both in the presence of finite-time saturation (32) under definition 1 and definition 2. If the modified control inputs are designed as (34–37) and (38–40) with the robust term satisfying $\delta _i\ge \epsilon _i^*u_i^*$, then the stability of the position tracking and attitude tracking can be guaranteed even in the presence of input saturation, and the control laws are robust to the parameter uncertainties including m and I. Also, all the signals in the closed-loop systems are bounded.

Proof

For position subsystem, select the quadratic Lyapunov function candidate as

$$\begin{aligned} V=\frac{1}{2}{{\overline{\gamma }}}_{\xi {i}}m{{\overline{\gamma }}}_{\xi {i}}+\frac{1}{2}{{{\widetilde{\rho }}}}_i^T\varGamma _i^{-1}{{{\widetilde{\rho }}}}_i,\quad i={x,y,z} \end{aligned}$$

(41)

Consider (33) and (36), the derivative of (41) can be rewritten as

$$\begin{aligned} {\dot{V}}= & {} {{\overline{\gamma }}}_{\xi {i}}m\dot{{{\overline{\gamma }}}}_{\xi {i}}+{{\widetilde{\rho }}}_i^T\varGamma _i^{-1}\dot{{{\widetilde{\rho }}}}_i^T\nonumber \\= & {} {{\overline{\gamma }}}_{\xi {i}}(u_i-H_i\rho _i-m{{\dot{\chi }}}_{\xi {i}})+{{\widetilde{\rho }}}_i^T\varGamma _i^{-1}\varGamma _iH_i^T{{\overline{\gamma }}}_{\xi {i}}\nonumber \\= & {} {{\overline{\gamma }}}_{\xi {i}}(u_i-H_i{\hat{\rho _i}}-m{{\dot{\chi }}}_{\xi {i}}). \end{aligned}$$

(42)

Arranging (37) and (35) together obtains the further derivative of (41) as follows

$$\begin{aligned} {\dot{V}}= & {} {{\overline{\gamma }}}_{\xi {i}}(u_i-H_i{\hat{\rho _i}}+\frac{m}{{\hat{m}}}(\beta _i\chi _{\xi {i}}-(u_i-{\overline{u}}_i)))\nonumber \\= & {} {{\overline{\gamma }}}_{\xi {i}}(u_i-H_i{\hat{\rho _i}}+(1+\epsilon _m)(\beta _i\chi _{\xi {i}}-(u_i-{\overline{u}}_i)))\nonumber \\= & {} {{\overline{\gamma }}}_{\xi {i}}({\overline{u}}_i-H_i{\hat{\rho _i}}+\beta _i\chi _{\xi {i}}+\epsilon _m(\beta _i\chi _{\xi {i}}-u_i+{\overline{u}}_i))\nonumber \\= & {} -\mu _i{{\overline{\gamma }}}_{\xi {i}}^2-{{\overline{\gamma }}}_{\xi {i}}\delta _i\mathrm{sgn}({{\overline{\gamma }}}_{\xi {i}})\nonumber \\&+{{\overline{\gamma }}}_{\xi {i}}\epsilon _m(\beta _i\chi _{\xi {i}}-u_i+{\overline{u}}_i))\nonumber \\\le & {} -\mu _i{{\overline{\gamma }}}_{\xi {i}}^2-|{{\overline{\gamma }}}_{\xi {i}}|\delta _i+|{{\overline{\gamma }}}_{\xi {i}}|\epsilon _m^*u_i^*\nonumber \\\le & {} -\mu _i{{\overline{\gamma }}}_{\xi {i}}^2 \le 0,\quad i={x,y,z} \end{aligned}$$

(43)

As for the rotational subsystem, define the following Lyapunov function:

$$\begin{aligned} V=\frac{1}{2}{{\overline{\gamma }}}_{\eta {i}}I_i{{\overline{\gamma }}}_{\eta {i}}+\frac{1}{2}{{{\widetilde{\rho }}}}_i^T\varGamma _i^{-1}{{{\widetilde{\rho }}}}_i,\quad i={\phi ,\theta ,\psi } \end{aligned}$$

(44)

Substituting (38–40) to the derivative of (44), the similar result can obtained as follows

$$\begin{aligned} {\dot{V}}\le & {} -\mu _i{{\overline{\gamma }}}_{\eta {i}}^2-|{{\overline{\gamma }}}_{\eta {i}}|\delta _i+|{{\overline{\gamma }}}_{\eta {i}}|\epsilon _i^*u_i^*\nonumber \\\le & {} 0,\quad i={\phi ,\theta ,\psi } \end{aligned}$$

(45)

Therefore, the proof of this theorem can be completed by using the same procedures in the proof of Theorem 1. $\square$

Remark 3

When the saturation occurs, the overall closed-loop quadrotor systems are stable in the sense of Lyapunov due to the modified adaptive robust controller. And the signal $\chi$ helps attenuate the windup influence caused by input saturation. Specifically, signal value $\chi$ will increase along with error $\gamma$ increasing, which in turn guarantees that there is no sudden rise in the modified tracking error ${{\overline{\gamma }}}$, and all the signals are bounded despite of the parametric uncertainties.

Remark 4

When no input saturation limits are exceeded, $u_i-{\overline{u}}_i$ will be zero such that the signal of $\chi$ will converge to zero and remain zero in view of Eqs. (37) and (40), where the control law is as same as that of Sect. 3. In this case, the control laws proposed in Sect. 4 will degenerate into those in Sect. 3 with same adaptive laws, and all the solutions in Sect. 3 still hold automatically here.

5 Simulation Results

In this section, several simulation examples are given to illustrate the effectiveness of the proposed control strategy for path following problem. The parameters of the quadrotor aircraft used in the simulations are given in Table 1, which are chosen from the test [10]. All simulations have been executed considering external disturbances on the six DOFs, and uncertain system parameters in order to indicate the robustness of the control method.

Table 1 Parameters of the quadrotor aircraft

The desired reference path used is a circle evolving in the $\mathrm{{R}}^3$ Cartesian space, where the yaw angle is required to be stabilized at zero. The circle is defined by $x_r=\frac{1}{2}\mathrm{cos}(\frac{\pi {t}}{20})\ \mathrm{m},\ y_r=\frac{1}{2}\mathrm{sin}(\frac{\pi {t}}{20})\ \mathrm{m}, z_r=3-2\mathrm{cos}(\frac{\pi {t}}{20})\ \mathrm{m},\ \psi _r=0\ \mathrm{{rad}}$. Suppose that the initial state values of the aircraft are $\xi _0=[0.45,0.05,0.45]^\mathrm{T}$ m, $\eta _0=[-0.02,0.05,0]^\mathrm{T}$ rad, and initial velocities are assumed as zeros. Here, in this simulation, it is assumed that the external disturbances on the aerodynamic forces and moments are given as: $A_x=1$ N at $t=5$ s; $A_y=1$ N at $t=15$ s; $A_z=1$ N at $t=25$ s; $A_\phi =1$ Nm at $t=10$ s; $A_\theta =1$ Nm at $t=20$ s and $A_\psi =1$ Nm at $t=30$ s.

In order to evaluate the flight characters with respect to actuator saturation of quadrotor aircrafts, the input limitations are taken into account. For example, in z direction, the control input ranges from 0 to 21 N, while torque inputs $u_2$ and $u_3$ range from $-10$–10 Nm. Based on the above assumed magnitude, the anti-windup performance can be validated in the following experiments. Alternatively, the sign function in robust term can be chosen as sigmoid function, and thus the control inputs avoid the chattering problem so that the obtained input control signals are acceptable and physically realizable.

Fig. 2

Adaptive path following without saturation

Fig. 3

Adaptive attitude tracking without saturation

Fig. 4

Adaptive position tracking error without saturation

Fig. 5

Adaptive attitude tracking error without saturation

Simulation results using adaptive control without actuator saturation are shown in Figs. 2, 3, 4 and 5, and performance is noticeable in these figures especially at the time when disturbances of forces and moments occur. Figures 2, 4 present position tracking responses in 3-D space and tracking errors, from which it can be seen how, starting from an initial position far from the reference, the proposed control strategy is able to make the vehicle follow the reference trajectory in a small delay. Besides, the adaptive law helps eliminate the effects caused by sustained disturbances, and three positions successfully track the desired position references with different phases simultaneously.

Figures 3, 5 show attitude angles tracking curves and the error results, respectively. It can be observed that the inner adaptive controller makes the vehicle track its rotational reference trajectory even when each degree of freedom is affected by the moment disturbances. And the estimated values of unknown system dynamics and disturbances are well tuned by the adaptive law. Furthermore, the desired attitude angles $\phi _r$ and $\theta _r$ calculated by the translational controller varies with time, but the adaptive controller achieves null steady-state error. From these figures, the designed controller succeeds in reaching the desired attitude trajectory while disturbances and model parameter uncertainty are well compensated.

Figures 6,  7 are plotted to show the tracking errors of the adaptive control under control laws (21) and (22) with input saturations. At $t=25s$, it is noticeable to see the position tracking error of z direction in Fig. 6 and control signal $u_T$ in Fig. 8 suffers from a drastic oscillation caused by the limitations of control input value, and it takes a longer time before convergence. From these figures, one can observe that windup phenomenon caused by actuator saturation leads to a delay in convergence time of the close-loop system control, which may cause physical accident to the real-time flight of quadrotor aircrafts.

Fig. 6

Adaptive position tracking error with saturation

Fig. 7

Adaptive attitude tracking error with saturation

Fig. 8

Control inputs of adaptive control with saturation

Fig. 9

Adaptive robust position tracking error with saturation

Fig. 10

Adaptive robust attitude tracking error with saturation

In contrast, simulation results using the proposed adaptive robust control (35) and (38) under the same saturation are presented in Figs. 9,  10, with Fig. 9 showing the position tracking errors and Fig. 10 showing the tracking errors of attitude angles, respectively. In these figures, it is worthy to mention that the proposed approach can obtain the less tracking errors compared with the saturated system under adaptive controller without introducing the anti-windup term, and our proposed controller reduces the convergence time in the presence of actuator saturation and disturbances. Figure 11 shows the corresponding control inputs, and it can be observed that the control signals return to normal states quickly after saturation vanishes especially in z direction, while those under adaptive control law face several oscillation. Moreover, the adaptive gain $\varGamma _i$ and robust gain $\beta _i$ decide the convergence rate of its robustness performance. Thus, the proposed law is able to cover many kinds of unknown system parameters and six degree sustained disturbances. This further confirms the highly robustness of the proposed adaptive robust anti-windup control approach.

Fig. 11

Control input of adaptive robust control with saturation

6 Concluding remarks

In this paper, an adaptive robust saturated control strategy has been proposed for a nonlinear uncertain quadrotor system with actuator saturation. After designing an adaptive controller for the quadrotor tracking problem with external disturbances acting on all degrees of freedom, an emendatory tracking error is proposed to adjust the control strategy and to reduce the control input influence on the system stability and tracking performance. Finally, simulations show that the proposed controller has achieved a good and smooth performance in tracking the desired trajectory, and all signals in the close-loop system are bounded. Besides, this controller is validated to be robust to unknown dynamic parameters and external disturbances. Compared to existing algorithms, the proposed scheme tends to be more practical since it obtains robust convergence, disturbance attenuation and anti-windup property simultaneously. Future research is to apply and validate this novel control method in real applications.