Routes to bursting in active control system with multiple time delays

Abstract

This paper investigates the generation of some novel bursting patterns in active control oscillator with multiple time delays. We present the bursting patterns, including symmetric codimension one and codimension two bursters with the slow variation of periodic excitation item. We calculate the bifurcation conditions of fast subsystem as well as its stability related to the time delay. We also identify some regimes of bursting depending on the magnitude of the delay itself and the strength of time delayed coupling in the model. Our results show that the dynamics of bursters in delayed system are quite different from those in systems without any delay. In particular, delay can be used as a tuning parameter to modulate dynamics of bursting corresponding to the different type. Furthermore, we use transformed phase space analysis to explore the evolution details of the delayed bursting behavior. Time delay can enhance the spiking performance and obtain the remarkable spiking dynamics even in a very simple model, which enriches the routes to bursting dynamics. Also some numerical simulations are included to illustrate the validity of our study.

1 Introduction

With the rapid development of active control of vibration, time delay feedback control has drawn much attention of researchers in modeling realistic neuronal networks, physics, mechanics and engineering systems and so on [1,2,3,4]. The existence of time delays may lead to oscillation, divergence, instability or chaos. Therefore, the subject of the analysis of dynamical systems with time delay is of both theory and practical value and has attracted considerable attention during the past two decades [5,6,7,8].

Fig. 1

Practical vibration device. a A mass-spring oscillator with delayed spring force related to Eq. (1). b An active delay control system related to Eq. (2)

In recent years, the studies of bursting (mixed-mode oscillations) have received great attentions [9,10,11], which are frequently involved in many dynamical systems. Bursting oscillations are waveforms that consist of alternating small and large amplitude excursions. Mathematically, the generation of bursting oscillations is often associated with fast and slow subsystems simultaneously [12, 13]. Then, bursting oscillations can be created by the system switching between the coexisting attractors of the fast subsystem corresponding to the slow current. Two important bifurcations associated with the bursting, i.e., the bifurcation of the quiescent (rest) process that leads to the repetitive spiking (firing) process and the bifurcation of the spiking (firing) process back to the quiescent (rest) process, can be observed [14,15,16].

Obviously, it is important to investigate the knowledge of both delay control and busting dynamic as typical dynamical behaviors in nonlinear dynamical phenomena. However, few publications are concerned with the effect of time delay on the bursting generation mechanism, and a variation of remarkable oscillations, due to the time delay, have not been effectively revealed especially in the system with multiple time delays. Moreover, the bifurcation analysis is a very important nonlinear research approach on various types of bursting oscillations, which is used to indicate a qualitative change under the variation of one or more parameters on which the considered system depends. It can be shown that the typical properties of different bursting behaviors are related to the bifurcations induced by delays.

Active control systems are used to control the response of structures to internal or external excitation [17,18,19]. Sun et al. [20] studied the bifurcation and chaotic motion in a Duffing oscillator subjected to an active control when delay is taken into account. Hu et al. [21] studied the controlled system with multiple time delays by singular perturbation method. We begin our work from the following classical one-degree-of-freedom system (Fig. 1a),

$$\begin{aligned} {\ddot{x}}(t)+{\dot{x}}(t)-x(t-\tau _1 )+ux^{3}(t-\tau _1 )=F\cos (\Omega t) \end{aligned}$$

(1)

Yutaka et al. [22] studied the resonance of Eq. (1) and examined the influence of initial conditions on the steady state solution by means of integral curves.

As shown in Fig. 1a, which has a positive mass, viscous damping and a restoring force expressed by the function of $f\left( x \right) =ux^{3}\left( {t-\tau _1 } \right) -x\left( {t-\tau _1 } \right)$, where u is the coefficient which represents a deviation from the linear restoring force, $\tau _{1}$ is the constant of nonlinear time delay and $x\left( t \right)$ is displacement and t is the time. System (1) is also excited by the external excitation item of $F\cos \left( {\Omega t} \right)$, where F is amplitude and $\Omega$ is the forcing frequency. The free vibration of Eq. (1) is investigated by using the method of center manifold reduction [23, 24].

In order to avoid divergence behavior related to the original delay system (1), a delayed state feedback $vx\left( {t-\tau _2 } \right)$ is introduced into Eq. (1), and the active controlled device can be illustrated in Fig. 1b, so that the closed loop can be described by the following multiple delay active control system (MDACS), which is written as

$$\begin{aligned}&{\ddot{x}}(t)+{\dot{x}}(t)-x(t-\tau _1 )+ux^{3}(t-\tau _1 )\nonumber \\&\quad +vx(t-\tau _2 )=F\cos (\Omega t) \end{aligned}$$

(2)

An essential feature of active control systems is that external power may affect the control action [25]. In our study, we assume $0<\Omega \ll 1$. For the external frequency, $\Omega$ deviates far from the frequency of self-excited vibration, i.e., two time scales evolve in the vector field, bursting oscillations may occur. The main goal of the paper is to investigate the bursting mechanism in this active control oscillator with time delay feedback, which can be analyzed by the local stability and divergence. Through bifurcation analysis, different types of bursting oscillations with the variation of parameters and effects of time delays on this bursting dynamic in active control system can be discussed in depth.

The rest part of this paper is organized as follows: In Sect. 2, an analysis of the bifurcations and dynamics is obtained as a function of the magnitude of time delay itself as well as its coupling values. In Sects. 3 and 4, bursting phenomena including some codimension one and codimension two bursters are presented, and the effects of some parameters including time delay on such bursting are discussed. Investigations of occurrence and mechanism of certain bursting dynamics are also presented. Finally, Sect. 5 concludes the paper.

2 Stability and bifurcation analysis

With the assumption that the excitation frequency $0<\Omega \ll 1$, which is far small comparing to the natural frequency, implying that the excitation term $F\cos \left( {\Omega t} \right)$ changes very slowly with the evolution of the time, we can regard $F\cos \left( {\Omega t} \right)$ as a generalized state variable $\rho =F\cos \left( {\Omega t} \right)$. The MDACS of Eq. (2) can be considered as the coupling of two subsystems, the fast subsystem of which can be presented as follow:

$$\begin{aligned} {\ddot{x}}(t)+{\dot{x}}(t)-x(t-\tau _1 )+ux^{3}(t-\tau _1 )+vx(t-\tau _2 )=\rho \end{aligned}$$

(3)

while the slow one can be written as $\rho =F\cos \left( {\Omega t} \right)$. It can be checked that $\dot{\rho }=-F\Omega \sin \left( {\Omega t} \right)$, which forms the slow subsystem for the far small value of $\Omega \ll 1$. The aim of this section is to find the practical criteria of delay-independent stability for the damped vibrating systems governed by Eq. (3), when two time delays appear in the state feedback. We start our study from the single delay active control system (SDACS), and then generalize t to the MDACS.

2.1 Bifurcation analysis of SDACS

Equation (3) can be reduced to the following SDACS, which is given by

$$\begin{aligned} {\ddot{x}}\left( t \right) +{\dot{x}}\left( t \right) -x\left( {t-\tau _1 } \right) +ux^{3}\left( {t-\tau _1 } \right) =\rho \end{aligned}$$

(4)

Putting ${\dot{x}}\left( t \right) =y\left( t \right)$ into Eq. (4), we can obtain the equilibrium coordinates of $\left( {x,0} \right)$, where x is decided by the following algebraic equation

$$\begin{aligned} ux^{3}-x-\rho =0 \end{aligned}$$

(5)

Fold bifurcation

From Eq. (5), it is easy to see the root discriminant is $\varDelta =81\left( {\rho /u} \right) ^{2}-12\left( {1/u} \right) ^{3}$, which implies that there is the unique equilibrium at $\varDelta >0$, there are three equilibriums at $\varDelta <0$, and there are two equilibriums at $\varDelta =0$. Simplify the discriminant, the critical condition for fold bifurcation can be expressed in the form of $u=4/27\rho ^{2}$.

Linear stability analysis

Fig. 2

Diagram for the stability and bifurcations in MDACS. a Cusp bifurcation in MDACS with respect to the parameters $\rho$ and v . b Bistable structure of two equilibrium attractors $E_\pm$ (focuses) separated by the saddle $E_0$

Next, we turn to the local stability and bifurcation of the stationary solution. Substituting solutions as the form of $x\left( t \right) =x_0 \mathrm{e}^{\lambda t}$, into the corresponding linearized form of Eq. (4), where $\lambda$ is the eigenvalue, $\lambda =\delta +\omega i$, $\delta$ is the growth or decay rate, $\omega$ is the frequency of oscillations and $x_0$ depends on the initial conditions, the characteristic equation is

$$\begin{aligned} \left( {\delta +\omega i} \right) ^{2}+\left( {\delta +\omega i} \right) -\mathrm{e}^{-\left( {\delta +\omega i} \right) \tau _1 }=0 \end{aligned}$$

(6)

Separating Eq. (5), the real and imaginary parts to yield the characteristic equations:

$$\begin{aligned}&\delta ^{2}-\omega ^{2}+\delta -\mathrm{e}^{-\delta \tau _1 }\cos \left( {\omega \tau _1 } \right) =0 \end{aligned}$$

(7)

$$\begin{aligned}&2\omega \delta +\omega +\mathrm{e}^{-\delta \tau _1 }\sin \left( {\omega \tau _1 } \right) =0 \end{aligned}$$

(8)

For a given time delay $\tau _1$, Eqs. (7) and (8) have infinitely many values of $\delta$ and $\omega$. The value $\delta =0$ can correspond to a bifurcation boundary separating stable from unstable trivial solution. If $\delta >0$, the system grows exponentially with time and is unstable; and if $\delta <0$, the system decays exponentially with time and is stable. To study the critical stability boundaries, we substitute $\delta =0$ and $\omega >0$ into Eq. (6), and yield:

$$\begin{aligned} -\omega ^{2}+\omega i-\mathrm{e}^{-\omega i\tau _1 }=0 \end{aligned}$$

(9)

Separating Eq. (9) into real and imaginary parts yields the following characteristic equations:

$$\begin{aligned}&\omega ^{2}+\cos \left( {\omega \tau _1 } \right) =0 \end{aligned}$$

(10)

$$\begin{aligned}&\omega +\sin \left( {\omega \tau _1 } \right) =0 \end{aligned}$$

(11)

The Hopf bifurcation can occur for two complex-conjugate eigenvalues transversely crossing the imaginary axis. Squaring both sides of Eqs. (10) and (11), adding to each other, then it can be written as:

$$\begin{aligned} F\left( \omega \right) =\omega ^{4}+\omega ^{2}-1=0 \end{aligned}$$

(12)

This equation has a pair of real roots. We are interested in the unique positive root, i.e., $\omega ^{*}=\sqrt{\left( {-1+\sqrt{5}} \right) /2}$, which can determine a series of critical time delays

$$\begin{aligned} \tau _k =\left[ {\arcsin \left( {-\omega ^{{*}}} \right) +2k\pi } \right] /\omega ^{{*}}, \quad k=1,2,\ldots \end{aligned}$$

(13)

The smallest positive critical time delay denoted by $\tau _1$ at $k=1$ is particularly interested. Denote this value by $\tau _1^{*} =\left( {\arcsin \left( {-\omega ^{*}} \right) +2\pi } \right) /\omega ^{*}$, and differentiate Eq. (12) with respect to $\omega$ for $\omega =\omega ^{*}$, we obtain

$$\begin{aligned} \frac{\mathrm{d}F}{\mathrm{d}\omega }\left| {_{\omega =\omega ^{*}} } \right. =4(\omega ^{*})^{3}+2\omega ^{*}>0 \end{aligned}$$

(14)

The condition for the inequality (14) indicates that each crossing of the real part of characteristic roots at $\tau _1^{*}$ must be from left to right. According to the criteria of stability switches, the characteristic Eq. (6) has at least a pair of conjugate purely imaginary roots with positive real parts for $\tau _1 <\tau _1^*$, and it has at least two pair of conjugate purely imaginary roots with positive real parts for $\tau _1 >\tau _1^*$. Therefore, the trivial equilibrium of SDACS is always unstable for any time delay $\tau _1 >0$, and the following results can be concluded.

Linear solution of SDACS:

• (i) The trivial equilibrium of SDACS is always unstable for any time delay $\tau _1 >0$.

• (ii) A fold bifurcation may occur at $u=4/27\rho ^{2}$.

2.2 Bifurcation analysis of MDACS

Now, we consider the stability and bifurcations of MDACS under the case of $v\ne 0$. Putting ${\dot{x}}\left( t \right) =y\left( t \right)$ into Eq. (3), we can obtain the equilibrium coordinates of $\left( {x,0} \right)$, where x is decided by the following algebraic equation

$$\begin{aligned} ux^{3}+\left( {v-1} \right) x-\rho =0 \end{aligned}$$

(15)

Cusp bifurcation

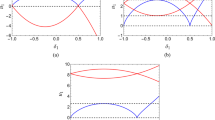
The numbers and bifurcations of these equilibriums are also determined by the coupling strength of two time delays. For the fixed coupling coefficient $u=1$, the equilibrium point curve on double-parameter bifurcation set of $\left( {v,\rho } \right)$ related to MDACS is computed and plotted in Fig. 2a, where $CP=\left( {1,0,0} \right)$ means the supercritical cusp bifurcation point, which implies the intersection of twofold bifurcation curves. Particularly taking $u=1$, $v=-1$, $\rho =0$, $\tau _1 =0.2$ and $\tau _2 =0.1$, three equilibriums are $E_0 =\left( {0,0} \right)$ and $E_\pm =\left( {\pm \sqrt{2},0} \right)$, while $E_0 =\left( {0,0} \right)$ is a saddle equilibrium and $E_\pm =\left( {\pm \sqrt{2},0} \right)$ are stable focuses, implying system is bistable.

To get a clear idea of the distribution of equilibrium points of Eq. (3), we plot the phase portraits in the space of $\left( {\rho ,x,y} \right)$ at $u=1$, $v=-1$, corresponding to these equilibriums in Fig. 2b. As $\rho$ increases (decreases) from the zero, the saddle $E_0$ becomes gradually far from the sink $E_\pm$ and approaches the other sink $E_\pm$. When $\rho$ increases (decreases) through the fold bifurcation points $F_{1,2}$, two untrivial equilibriums $E_\pm$ collide and disappear, leaving the only attractor of MDACS in the phase space and the system loses its bistability and becomes stable.

Linear stability analysis

The linearized equation of MDACS is

$$\begin{aligned} {\ddot{x}}+{\dot{x}}-x(t-\tau _1 )+vx(t-\tau _2 )=0 \end{aligned}$$

(16)

Substituting solutions as the form of $x\left( t \right) =x_0 \mathrm{e}^{\lambda t}$, into Eq. (16), where $\lambda$ is also the eigenvalue, $\lambda =\delta +\omega i$. The corresponding characteristic equation is

$$\begin{aligned} \left( {\delta +\omega i} \right) ^{2}+\left( {\delta +\omega i} \right) -\mathrm{e}^{-\left( {\delta +\omega i} \right) \tau _1 }+v\mathrm{e}^{-\left( {\delta +\omega i} \right) \tau _2 }=0 \end{aligned}$$

(17)

Obviously, Eq. (17) has zero root for the value of $v=1$; thus we can conclude the steady state bifurcation may occur at $v=1$, which is independent of the delay $\tau _2$. If $v<1$, it is easy to see that the trivial equilibrium of MDACS is always unstable. Therefore, $v>1$ is assumed to be true for the following discussion about trivial equilibrium point.

Substituting $\delta =0$ and $\omega >0$ into Eq. (17) and separating the real and imaginary parts to yield:

$$\begin{aligned} \omega ^{2}+\cos \left( {\omega \tau _1 } \right)= & {} v\cos \left( {\omega \tau _2 } \right) \end{aligned}$$

(18)

$$\begin{aligned} \omega +\sin \left( {\omega \tau _1 } \right)= & {} v\sin \left( {\omega \tau _2 } \right) \end{aligned}$$

(19)

Eliminating $\tau _1$ from Eqs. (18) and (19), gives

$$\begin{aligned}&F\left( \omega \right) =\left( {\omega ^{2}-v\cos \left( {\omega \tau _2 } \right) } \right) ^{2}\nonumber \\&\quad +\left( {\omega -v\sin \left( {\omega \tau _2 } \right) } \right) ^{2}-1=0 \end{aligned}$$

(20)

Equation (20) gives the frequencies $\omega$ of possible non-hyperbolic solutions. Due to the continuity of the characteristic exponents with respect to changes of parameters, the stability analysis can be performed for each domain described by Eqs. (18) and (19), while the corresponding stability and bifurcation boundaries are presented in delay parameter space of $\left( {\tau _1 ,\tau _2 } \right)$ for fixed $v=2$ by employing the numerical computations (see Fig. 3).

Fig. 3

Boundary interface of stability near stationary solution in MDACS on the delay parameter space $\left( {\tau _1 ,\tau _2 } \right)$ at $v=2$

Differentiating the characteristic Eq. (17) with respect to $\tau _1$ and $\tau _2$ at $\lambda =\omega i$, we have

$$\begin{aligned}&\left. {\frac{\mathrm{d}\left( {\text {Re}\lambda } \right) }{\mathrm{d}\tau _1 }} \right| _{\lambda =\omega i}\nonumber \\&\quad =\left. {\text {Re}\left( {\frac{-\lambda \mathrm{e}^{-\tau _1 \lambda }}{2\lambda +1+\tau _1 \mathrm{e}^{-\tau _1 \lambda }-\tau _2 ve^{-\tau _2 \lambda }}} \right) } \right| _{\lambda =\omega i} \ne 0\nonumber \\ \end{aligned}$$

(21)

$$\begin{aligned}&\left. {\frac{\mathrm{d}\left( {\text {Re}\lambda } \right) }{\mathrm{d}\tau _2 }} \right| _{\lambda =\omega i}\nonumber \\&\quad =\left. {\text {Re}\left( {\frac{\lambda \mathrm{e}^{-\tau _2 \lambda }}{2\lambda +1+\tau _1 \mathrm{e}^{-\tau _1 \lambda }-\tau _2 ve^{-\tau _2 \lambda }}} \right) } \right| _{\lambda =\omega i} \ne 0\nonumber \\ \end{aligned}$$

(22)

In Eqs. (21) and (22) imply the MDACS obeys the transversality conditions of Hopf bifurcation theorem and undergoes a sequence of Hopf bifurcation on the critical stability boundaries. Furthermore, in the stable range, the trivial equilibrium is a stable focus, while with the couple delays crossing the critical values defined by Eqs. (18) and (19) to unstable region, a pair of eigenvalues will cross the imaginary axis and the MDACS occurs Hopf bifurcation, i.e., a family of periodic solutions bifurcated from trivial equilibrium. Thus, we have the following results for MDACS.

Linear solution of MDACS

If v and $\tau _1$ satisfy the stability conditions, and all the roots related to Eqs. (17) and (18) are simple, then there exists exactly a critical time delay of $\tau _2^*\left( {v,\tau _1 } \right)$ in MDACS such that:

• (i) A cusp bifurcation may occur at $v=1$.

• (ii) The trivial equal equilibrium is asymptotically stable when $\tau _2 \le \tau _2^*\left( {v,\tau _1 } \right)$, and a Hopf bifurcation may occur at $\tau _2^{*} \left( {v,\tau _1 } \right)$, where $\tau _2^*\left( {v,\tau _1 } \right) \le \tau _1^{*}$.

Limit cycles bifurcated from nontrivial equilibriums Appearance of limit cycles bifurcated from nontrivial equilibriums can be discussed similarly. Take equilibrium points $E_\pm \left( {x_\pm ,0} \right)$ for example, where $x_\pm$ are non-zero solutions in Eq. (15). A transformation from $E_\pm$ to the origin, leads to the following equation.

$$\begin{aligned} \left\{ \! {\begin{array}{l} \dot{X}\left( t \right) =Y\left( t \right) \\ \dot{Y}\left( t \right) =-Y\left( t \right) +\left( {X\left( {t-\tau _1 } \right) +x_\pm } \right) \\ \!\!\quad -u\left( {X\left( {t-\tau _1 } \right) +x_\pm } \right) ^{3}-v\left( {X\left( {t-\tau _2 } \right) +x_\pm } \right) +\rho \\ \end{array}} \right. \end{aligned}$$

(23)

Denoting the equilibrium of Eq. (23) as $\left( {X_0 ,Y_0 } \right)$, and one can easily find out that $\left( {X_0 ,Y_0 } \right) =\left( {0,0} \right)$. The characteristic equation of Eq. (23) is

$$\begin{aligned} \hbox {det}\left( {{\begin{array}{cc} \lambda &{} {-1} \\ {-\mathrm{e}^{-\lambda \tau _1 }+v\mathrm{e}^{-\lambda \tau _2 }+3ux_\pm ^2 }&{} {\lambda +1} \\ \end{array} }} \right) =0 \end{aligned}$$

(24)

Thus, the corresponding characteristic equation can be described as

$$\begin{aligned} F\left( \lambda \right) =\lambda ^{2}+\lambda -\mathrm{e}^{-\lambda \tau _1 }+v\mathrm{e}^{-\lambda \tau _2 }+3ux_\pm ^2 =0 \end{aligned}$$

(25)

Letting $\lambda =\omega i$, where $\omega$ is real and positive, and separating (25) into real and imaginary parts, one can obtain

$$\begin{aligned}&-\omega ^{2}-\cos \left( {\omega \tau _1 } \right) +v\cos \left( {\omega \tau _2 } \right) +3ux_\pm ^2 =0,\hbox { and }\omega \\&\quad +\sin \left( {\omega \tau _1 } \right) -v\sin \left( {\omega \tau _2 } \right) =0. \end{aligned}$$

Using the square condition, adding the two equations and performing some simplification processes, the Hopf bifurcation can be illustrated in Fig. 4 for fixed couple delays $\left( {\tau _1 ,\tau _2 } \right)$ equal to $\left( {0.2,0.15} \right)$ and $\left( {0.25,0.1} \right)$, respectively. From Fig. 4, we can find that the two untrivial equilibriums $E_\pm$ will undergo Hopf bifurcations ($H_{1,2}$ or $H_{1,2}^{*}$ in Fig. 4) after $\rho$ increases (decreases) through fold bifurcations ($F_{1,2}$ in Fig. 4). When the couple delays are modulated, the critical values for the two symmetric Hopf bifurcations will have significant changes.

Fig. 4

Static Hopf bifurcations near two untrivial equilibriums $E_\pm$ in the parameter plane of $\left( {\rho ,x,y} \right)$ for fixed couple delays $\left( {\tau _1 ,\tau _2 } \right)$ equal to $\left( {0.2,0.15} \right)$ and $\left( {0.25,0.1} \right)$, where $u=1$ and $v=0.5$

Fig. 5

Diagrams related to MDACS for $u=1$, $v=0.5$, $F=2$, $\Omega =0.01$, $\tau _1 =0.2$ and $\tau _2 =0.15$. a Portrait phase on space $\left( {\rho ,x,y} \right)$, where $F_{1,2}$ are fold bifurcation points. b Time series of bursting trajectories

3 Bursting phenomena in MDACS

3.1 Burster related to codimension one bifurcation

In this subsection, we discuss the singularity in the fast system related to Eq. (2) and classify the bursting dynamic as codimension one periodic burster, namely that which occurs through codimension one bifurcation points in the fast subsystem. Spiking formation can be distinguished by analyzing bifurcation mechanism of steady state which transits from the quiescence process to the repetitive spiking process. For the fixed parameters $u=1$, $v=0.5$, $F=2$ and $\Omega =0.01$, we perform a detailed bifurcation analysis for codimension one burster and explore the properties of some crucial bifurcation points on such bursters, in which the appropriate time delay itself and the strength of time delayed coupling must be chosen based on the stability and bifurcation conditions we have discussed in Sect. 2.

3.1.1 Symmetric burster for fold bifurcation

When the delayed oscillator is subjected to slow parametric excitation, complex oscillation patterns can be obtained. Such oscillations are characterized by a cluster of large amplitude oscillations that alternates with the line-like small amplitude oscillations, which can be distinguished by analyzing bifurcation mechanisms of steady state that transits from the quiescent state to the repetitive spiking process. So the slow manifold and its bifurcation diagram can be superimposed to detect the generation mechanism of bursting oscillations.

At $\tau _1 =0.2$ and $\tau _2 =0.15$, the phase portrait as well as the time series are presented in Fig. 5, from which one may find the trajectories of the burster with symmetric structure oscillate between two parts associated with the two equilibrium points via fold bifurcations. The slow manifold and its bifurcation curve are also superimposed to detect the generation mechanism.

As shown in Fig. 5a, the transition behavior runs depending on the slow variable $\rho$, and the rate of convergence to the quiescent state is relatively weak. The trajectory in quiescent state disappears via fold bifurcations labeled by points $F_{1,2}$, while the repetitive spiking process also terminates by fold bifurcations. The specific mechanism of this codimension one burster can be explained as follows. In the bistable region, the system has three equilibria, two stable focuses and one unstable saddle. The current state of the system is the rest state. With the slow variation of $\rho$, the stable focus is approached to the unstable saddle, where the fold bifurcation occurs. Then the trajectory starts spiking and evolves to the other stable focus, which is the unique attractor in the system. Similar situation takes place to the initial stable branch of the attractor thereby completing the rest half of the bursting loop.

For the delayed oscillator does not have a limit cycle, we refer to such codimension one burster as “symmetric fold/fold bursting” of point–point type. We can remark such hysteresis loops oscillate around two coexisting stable focuses, i.e., the two stable branches of system may exhibit similar evolution behaviors.

Fig. 6

Diagrams related to MDACS for $u=1$, $v=0.5$, $F=2$, $\Omega =0.01$, $\tau _1 =0.25$ and $\tau _2 =0.1$. a Portrait phase in space of $\left( {\rho ,x,y} \right)$, where $F_{1,2}$ are fold bifurcation points, $H_{1,2}$ are supercritical Hopf bifurcation points. b Time series of bursting trajectories

3.1.2 Symmetric burster for fold and Hopf bifurcation

The variation of time delays will lead the oscillation interaction between the limit cycles bifurcated from the Hopf bifurcation near the two untrivial equilibriums, which makes the oscillator occurs another different type of bursting. At $\tau _1 =0.25$ and $\tau _2 =0.1$, the phase portrait as well as the time series are plotted in Fig. 6, from which one may find the trajectories of the burster with symmetric structure oscillate between two parts associated with the two equilibrium points via fold bifurcations and supercritical Hopf (supH) bifurcation, where codimension one bifurcation of interest here is the Hopf bifurcation.

As shown in Fig. 6a, system (2) runs depending on the slow variable $\rho$ which controls transitions of the oscillations. The trajectory in quiescent state disappears via fold bifurcations labeled by points $F_{1,2}$. Such dynamic behavior does not disappear until the two coexisting limit cycles are created by Hopf bifurcations labeled by points $H_{1,2}$, which lead to repetitive spiking process.

The specific mechanism of this codimension one burster can be explained as follows. In the bistable region, the system has three equilibriums, two stable focuses and one unstable saddle. The current state of the system is the resting state. With the slow variation of $\rho$, the stable focus is approached to the unstable saddle, where the fold bifurcation occurs. Then, the trajectory starts spiking and evolves to the other stable focus, which is the unique attractor in the system. With the further change of $\rho$, the amplitudes of oscillations increase gradually because of the influence of Hopf bifurcations at points of $H_{1,2}$, i.e., the trajectory starts to oscillate with large amplitude via supH bifurcation point caused by the time delay. Thereafter, the system terminates out of the spiking state and then decreases to settle down to the equilibrium curve, which forms the quiescent state. Similar situation takes place to the initial stable branch of the attractor thereby completing the rest half of the bursting loop.

The trajectory in quiescent state disappears via fold bifurcations, while the repetitive spiking process terminates by supH bifurcations. We can refer to such codimension one burster as “symmetric fold/supH bursting” of point-cycle type, since the spiking attractor is a limit cycle. This fold/supH bursting, also known as “tapered” bursting and “Type V” bursting, has been first observed in the electrical activity of pyramidal cells of the cat hippocampus or in models of the bursting electrical activity in pancreatic cells [26].

3.2 Burster related to codimension two bifurcation

The codimension two bifurcation points [27, 28] can be the source of more complicated dynamics such as multistability, quasi-periodicity and chaos. When the parameters and delays approach critical values of a Hopf–Hopf bifurcation, a Takes–Bogdanov bifurcation and a Hopf-fold bifurcation, the fast subsystem of Eq. (2) has the bursing types of codimension two. In this subsection, we analyze the bursting dynamics related to codimension two, which occur through some codimension two bifurcations in MDACS.

Fig. 7

Phase trajectories for Eq. (2) in the neighborhood of three types of codimension two bifurcation points at $\rho =0$. a near the Hopf-fold interaction for $u=1$, $v=-1$, $\tau _1 =0.3$ and $\tau _2 =0.28$; b near the Hopf–Hopf interaction for $u=1$, $v=2$, $\tau _1 =0.2$ and $\tau _2 =0.7$; c d near the Takes–Bogdanov interaction with two different initial conditions for $u=1$, $v=-2$, $\tau _1 =0.28$ and $\tau _2 =0.26$

In general, these codimension two bifurcation points cannot easily be solved in a closed form. However, they can be easily computed numerically. Therefore, the numerical experiments are given to demonstrate the behaviors of MDACS in the neighborhood of interaction points of the three types described above. For critical values of delay itself and delay coupling, a Hopf-fold bifurcation, a Hopf–Hopf bifurcation and a Takes–Bogdanov bifurcation can be illustrated for Eq. (2) at $\rho =0$ in Fig. 7. In Fig. 7a, two stable limit cycles, which surrounds the two nontrivial equilibriums, are observed near the Hopf-fold interaction at $u=1$, $v=-1$, $\tau _1 =0.3$ and $\tau _2 =0.28$. Figure 7b shows the existence of a stable 2-tour near the Hopf–Hopf interaction at $u=1$, $v=2$, $\tau _1 =0.2$ and $\tau _2 =0.7$. Near the Takes–Bogdanov interaction, solutions tend to the different nontrivial fixed points which are surrounded by a large amplitude unstable limit cycle as illustrated in Fig. 7c, d with two different initial conditions at $u=1$, $v=-2$, $\tau _1 =0.28$ and $\tau _2 =0.26$.

For the following discussion, we always fix the parameters of $u=1$, and the excited frequency is chosen to be $\Omega =0.05$, which is far smaller than the natural frequency in MDACS. We take suitable parameter values including the delays and the excitation item to perform a detailed bifurcation analysis for codimension two bursters and explore the properties of some crucial bifurcation points on such dynamics.

3.2.1 Symmetric burster for Hopf-fold bifurcation

Time delay magnitude will not affect the occurrence of fold bifurcations, but the delay coupling can dramatically affect the generation of the fold bursting. Moreover, we increase the delay across the critical value of Hopf bifurcation, and the two untrivial equilibrium will undergo a supercritical Hopf bifurcation, which leads to the occurrence of stable limit cycles, and then the fast manifold will intersects with the supercritical threshold near the Hopf-fold bifurcations, resulting into bursting attractor existing among a long parameter range.

Fig. 8

Diagrams related to MDACS for $u=1$,$v=-1$, $F=1.5$,$\Omega =0.05$, $\tau _1 =0.22$ and $\tau _2 =0.18$. a Portrait phase in space of $\left( {\rho ,x,y} \right)$, where $F_{1,2}$ are fold bifurcation points. b Time series of bursting trajectories

Fig. 9

Diagrams related to MDACS for $u=1$, $v=-2$, $F=0.70$, $\Omega =0.05$, $\tau _1 =0.18$ and $\tau _2 =0.05$. a Portrait phase in space of $\left( {\rho ,x,y} \right)$, where $Homo_{1,2}$ are the saddle homoclinic bifurcation points. b Time series of bursting trajectories

In order to further reveal the nature of the periodic bursting of this type, we take the following numerical case as an example, i.e., the case when we fix the parameters and delays at $v=-1$, $F=1.5$, $\tau _1 =0.22$ and $\tau _2 =0.18$. The corresponding phase portraits as well as the time series are presented in Fig. 8, where the slow manifold is superimposed to the phase diagram to get a clear idea about the dynamics. As shown in Fig. 8a, a supercritical saddle-node (fold) bifurcation is exhibited at $\rho =\pm 0.82$, which is also followed by two supercritical Hopf bifurcations, where the two nontrivial equilibrium points $E_\pm$ (bifurcated from fold bifurcations) lose their stabilities and two coexisting limit cycle attractors always exist. The trajectory in quiescent state disappears via Hopf bifurcations, where limit cycles are created by supHopf bifurcations, which lead to repetitive spiking process, while the repetitive spiking process also terminates by supHopf bifurcations.

The specific mechanism of this burster can be explained as follows. In the bistable region, the system has three equilibria, two stable untrivial equilibriums and one unstable saddle. Meanwhile, due to the interconnection of time delays, the trajectory starts to oscillate with large amplitude via supercritical Hopf bifurcations from two untrivial equilibriums induced by the time delays. With the slow variation of $\rho$, the stable limit cycle is approached to the unstable saddle, where the fold bifurcation occurs. Then the trajectory evolves to the other stable branch. Thereafter the system terminates out of the spiking state and decreases to settle down to the equilibrium curve also via Hopf bifurcation. Similar situation takes place to the initial stable branch of the attractor thereby completing the rest half of the bursting loop.

On the other hand, there are two bifurcations: one is the fold bifurcation that leads to the divergence from the stable branch $E_\pm$ and the other is the supercritical Hopf bifurcation that leads to the return to $E_\pm$. These two bifurcations from a hysteresis loop, which provides vital links between rest state and spiking attractor. Such spiking formations can be classified as the “symmetric supHopf/supHopf” bursting of cycle-cycle type via hysteresis loop, while the spiking attractors are limit cycles.

3.2.2 Symmetric burster for Takens–Bogdanov bifurcation

Basically, from the classification scheme for bursting behavior, the paths near the singularity of Takens–Bogdanov bifurcation may induce such different types of bursting oscillations as Circle/Circle, Circle/Homoclinic, Saddle-note/Circle, and Saddle-note/Homoclinic. In fact, in order to control the utmost possible, the magnitudes of time delay itself and its coupling value should be chosen near the codimension two bifurcation curve since the present work focuses on bursting generation mechanism induced by Takens–Bogdanov bifurcation, i.e., the existence of the saddle homoclinic orbit may cause the generation of another bursting dynamic.

We fix the parameters at $u=1$, $v=-2$, $F=0.70$, $\Omega =0.05$, $\tau _1 =0.18$ and $\tau _2 =0.05$. The corresponding phase portraits as well as the time series are presented in Fig. 9. With the variation of the slow excitation of $\rho$, the two nontrivial equilibrium points lose their stabilities and two coexisting limit cycle attractors appear. Further change of the parameter at $\rho =\pm 0.53$, leading to the occurrence of the saddle homoclinic bifurcation, causes the merge of the two types of oscillations to form large amplitude oscillations, which is the connection of the two groups of the cycles associated with $E_\pm$.

The specific mechanism of this burster can be explained as follows. In bistable region, the system has three equilibriums, two stable untrivial equilibriums and one unstable saddle. Meanwhile, due to the interconnection of time delays, the trajectory starts to oscillate with large amplitude via supercritical Hopf bifurcations from two untrivial equilibriums induced by the time delays.

With the slow variation of $\rho$, the stable limit cycle is approached to the unstable saddle, where the trajectory jumps from the original stable branch to the other branch of stable periodic orbits. The frequency of these periodic orbits decreases during the spiking process until the family of periodic orbits disappears in a saddle-loop connection (homoclinic orbit bifurcation). This saddle-loop connection, in turn, marks the end of the spiking state, since near it the trajectory will jump back to the original stable branch, where the system terminates out of the spiking state also via homoclinic bifurcation, which completing the rest half of the bursting loop.

Fig. 10

Time series in MDACS for three selected couple delays $\left( {\tau _1 ,\tau _2 } \right)$ of $\left( {0.2,0.1} \right)$, $\left( {0.3,0.2} \right)$ and $\left( {0.1,0.3} \right)$, where $u=1$, $v=0.5$, $F=2$ and $\Omega =0.01$

Fig. 11

Phase portraits for Eq. (2) with different initials for selected couple delays $\left( {\tau _1 ,\tau _2 } \right)$ of $\left( {0.1,0.06} \right)$, where $u=1$, $v=-2$, $F=1.5$ and $\Omega =0.01$. a limit cycle around untrivial equilibrium $E_{+}$. b limit cycle around untrivial equilibrium $E_{-}$

Such dynamic behavior is associated with two coexisting limit cycle interact with each other and form such periodic oscillations with large amplitudes as relaxation oscillation, which leads to repetitive complex spiking. We can refer to such spiking formation as the “symmetric homoclinic/homoclinic bifurcation” of cycle-cycle type, for the spiking process appears or terminates by homoclinic bifurcations.

4 Influence of time delay on bursting oscillations

The time delay is an important parameter of the delayed system, because it influences system dynamic bifurcations and its stability. Since bursting oscillations are created when slow control parameter $\rho$ passes through values of the local bifurcations, the delays will play an important role on the generation and evolution of bursting oscillations.

First, we investigate the effects of time delay on the amplitudes for fold bursting. Only if the forcing amplitude is greater than the fold bifurcation value, this bursting can appear. We can conclude the fold bursting occurs which is independent of time delays. This indicates that such dynamic will not lose its characters with the variation of delays and a considerable large range of delays could still stabilize the periodic bursting oscillation. Fix the parameters of $u=1$, $v=0.5$, $F=2$ and $\Omega =0.01$ in MDACS, time series for three selected different couple delays is presented in Fig. 10.

For comparison, it can be seen, even if the delays are selected as different sets of values, the bursting solution still has similar form of the fold bursting and nearly plots identical trajectories. We would like to point out that the time delay will not affect numbers of the spikes, but it can be used to regulate the vibration amplitudes of bursting oscillations.

Second, we turn to the effect of delays on bursting about Hopf and homoclinic bifurcations. We can identify the generation of Hopf bifurcation as well as the homoclinic orbit bifurcation bursting is closely related to the magnitude of time delay. If the delays cannot pass through such critical bifurcation values, trajectories will not go into the spiking state. To check what happens in the regions of delay variation, the numerical investigations are performed for the fixed parameters of $u=1$, $v=-2$, $F=1.5$ and $\Omega =0.01$ in MDACS (see in Figs. 11, 12, 13).

At the beginning, when $\left( {\tau _1 ,\tau _2 } \right) =\left( {0.1,0.06} \right)$, the periodic solution does not have obvious bursting trajectories and the system moves in the stationary process in Fig. 11. An influence of delays on bursting dynamics for the two bursting cases can be shown in Figs. 12 and 13. The first case when the couple delays vary to $\left( {\tau _1 ,\tau _2 } \right) =\left( {0.14,0.07} \right)$, the system oscillates in a spiking amplitude of vibrations significantly (see in Fig. 13). This type of motion arises from supH bifurcation and can be determined by the delays analytically. We can refer to such spiking formations as the “supHopf/ supHopf bifurcation” of point-cycle type. Both the quasi-stationary process and the repetitive spiking process terminate by supercritical Hopf bifurcations, where the trajectories switch between the untrivial equilibrium and a limit cycle.

Fig. 12

Phase portraits for Eq. (2) with different initials for selected couple delays $\left( {\tau _1 ,\tau _2 } \right)$ of $\left( {0.14,0.07} \right)$, where $u=1$, $v=-2$, $F=1.5$ and $\Omega =0.01$. a Spiking attractor around untrivial equilibrium $E_+$. b Spiking attractor around untrivial equilibrium $E_-$

Fig. 13

Phase portraits for Eq. (2) with selected couple delays $\left( {\tau _1 ,\tau _2 } \right)$ of $\left( {0.15,0.08} \right)$, where $u=1$, $v=-2$, $F=1.5$ and $\Omega =0.01$. a On the phase space of $\left( {x,y} \right)$. b On the phase space of $\left( {\rho ,x} \right)$

By an variation of delays to $\left( {\tau _1 ,\tau _2 } \right) =\left( {0.15,0.08} \right)$ from the second case, the irregular periodic bursting oscillations are obtained with the evolution of the limit cycle around the untrivial equilibrium $E_+$ (or $E_- )$ to homoclinic orbits. These novel spiking patterns are related to saddle-focus homoclinic orbit bifurcation, i.e., the repetitive spiking processes can be terminated by homoclinic orbits near two untrivial equilibriums and may interact with each other. We can refer to such delay-induced spiking formation as “symmetric homoclinic/homoclinic bifurcation” of focus-focus type. We would like to point out here that Fig. 13 exhibits the coexistence of two nontrivial stable equilibriums and symmetric homoclinic orbits, which coincides with a novel route to bursting dynamic.

5 Conclusions

We have investigated the generation of bursting in MDACS with the slowly varying external periodic excitation. The active control system with multiple time delays may exhibit different bursting oscillations for the order gap existing between the frequency of the excitation item and the natural frequency. The stability and bifurcation behaviors in this multiple time delayed oscillator are discussed, as well as some bifurcation conditions. By describing the external forcing as slow variable and combining this bifurcation analysis of the generalized autonomous system, we adopt bifurcation analytical approach to study the various routes to delay-induced bursting behaviors.

With the properly chosen delay and excitation, periodic delay-induced bursting behaviors may be created, and some remarkable wave forms to the repetitive spiking are revealed. Some types of bursters corresponding to codimension one or two bifurcations are obtained and their generation mechanisms are discussed. Time delay plays a key role to make simple system exhibit complex spiking modes corresponding to the different bifurcations.

The second-order non-autonomous differential equation discussed in this letter is considered to be one of the simplest dynamical systems, while it can produce so complicated spiking mode. Time delays could be used as a tuning parameter to generate bursting oscillations in a characteristic way, i.e., we conclude that the time delay can enhance the spiking performance and obtain the desired spiking dynamics even in a simple model. Applying a time delay may be one of the best approaches to control or regulate complicated bursting dynamical motions. It should be interesting to study such dynamics in systems with the velocity feedback delay, or larger number of delays, or delayed systems with two or more degrees, and we will discuss those in forthcoming papers.