1 Introduction

Traffic congestion usually emerges at bottlenecks, such as ramps, lane closures, intersections and sharp curves. To date, considerable traffic models have been developed to explain the mechanism underlying the phenomenon observed from the traffic congestion at bottlenecks, especially traffic jam at on-ramps. The empirical traffic patterns can mainly be summarized as moving local clusters (MLC), stop-and-go waves (SG), oscillating congested traffic (OCT), widening synchronized pattern (WSP), pinned localized cluster (PLC) and homogeneous congested traffic (HCT). The study on congested traffic pattern may provide a convenient way to master the nature of jam formation, and phase diagram is treated as a powerful approach to explore the intrinsic evolution mechanism. Diverse traffic models have been proposed to explain the inherent features of different instability diagrams found in actual traffic [1].

Fig. 1
figure 1

The schematic model of traffic flow on a two-lane highway

Full size image

Based on extensive experiment investigation, Kerner and Rehborn [1] referred two phase transitions (i.e., from free traffic flow to synchronized flow and from synchronized traffic flow to jam) as the first-order phase transitions. The synchronized flow can spread backward; for instance, it can turn into free flow after being self-maintained for several hours. Helbing and Treiber [2] proposed a macroscopic traffic model to interpret the synchronized flow along an on-ramp. In another work [3], they presented a phase diagram nearby on-ramp, and the analytical conditions for different type of congestion states are stated. By using an open boundary condition under on-ramp, Lee et al. [4] suggested a phase diagram to investigate the congested traffic states, in which various traffic patterns are reproduced. Gupta and Katiyar [5] studied the congestion patterns via a continuum traffic stream model under on-ramp. The numerical simulation reproduces a wide diversity of traffic patterns, and the congested patterns diagrams can be deemed as a nonlinear function of main road inflow flux and the on-ramp inflow flux. By adding the on-ramp system into speed gradient model, Tang et al. [6] compared the phase diagram of manual vehicles with adaptive cruise control (ACC) vehicles. Some congested traffic states disappear in phase ACC vehicles diagram since the traffic flow stability is enhanced by ACC vehicles. Tang et al. [7] presented a macrotraffic flow model with ramps. Numerical simulation results show that ramps usually have different effects on the main road traffic during the morning and evening rush hours. The traffic flow phases were carefully investigated in the recent literature [8]. They reproduced not only the congestion patterns (such as LC, SGW, OCT and HCT), but also the “widening synchronized patterns (WSP) and the widening moving clusters (WMC).”

Fig. 2
figure 2

Schematic illustration of the on-ramp system. a Deterministic on-ramp system, b stochastic on-ramp system

Full size image
Fig. 3
figure 3

The spatiotemporal evolutions of density and velocity for the homogeneous synchronized traffic (HST) with \(\rho _\mathrm{in}=0.10\), \(\rho _\mathrm{ramp}=0.10\)

Full size image
Fig. 4
figure 4

The spatiotemporal evolutions of density and velocity for the pinned localized clusters (PLC) with \(\rho _\mathrm{in}=0.21\), \(\rho _\mathrm{ramp}=0.07\)

Full size image
Fig. 5
figure 5

The spatiotemporal evolutions of density and velocity for the moving localized clusters (MLC) with \(\rho _\mathrm{in}=0.05\), \(\rho _\mathrm{ramp}=0.11\)

Full size image
Fig. 6
figure 6

The spatiotemporal evolutions of density and velocity for the triggered stop-and-go wave (TSG) with \(\rho _\mathrm{in}=0.05\), \(\rho _\mathrm{ramp}=0.12\)

Full size image
Fig. 7
figure 7

The spatiotemporal evolutions of density and velocity for the oscillating congested traffic (OCT) with \(\rho _\mathrm{in}=0.25\), \(\rho _\mathrm{ramp}=0.10\)

Full size image
Fig. 8
figure 8

The spatiotemporal evolutions of density and velocity for the homogeneous congested traffic (HCT) with \(\rho _\mathrm{in}=0.30\), \(\rho _\mathrm{ramp}=0.10\)

Full size image
Fig. 9
figure 9

The spatiotemporal evolutions of density and velocity for the combination of the triggered stop-and-go wave and the pinned localized clusters (\(\hbox {TSG} + \hbox {PLC}\)) with \(\rho _\mathrm{in}=0.06, \rho _\mathrm{ramp}=0.17\)

Full size image
Fig. 10
figure 10

The spatiotemporal evolutions of density and velocity for combination of the triggered stop-and-go wave and the homogeneous synchronized traffic with \(\rho _\mathrm{in}=0.09, \rho _\mathrm{ramp}=0.17\)

Full size image
Fig. 11
figure 11

The spatiotemporal evolutions of density and velocity for the combination of pinned localized clusters and the oscillating congested traffic with \(\rho _\mathrm{in}=0.12, \rho _\mathrm{ramp}=0.16\)

Full size image
Fig. 12
figure 12

The spatiotemporal evolutions of density and velocity for the pinned localized clusters with \(\rho _\mathrm{in}=0.14, \rho _\mathrm{ramp}=0.18\)

Full size image
Fig. 13
figure 13

The spatiotemporal evolutions of density and velocity for the oscillating congested traffic (OCT) with \(\rho _\mathrm{in}=0.18, \rho _\mathrm{ramp}=0.20\)

Full size image

The phase transition at on-ramp is also studied via the microscopic method. Using car-following model, Berg and Woods [9] investigated the solitary solution in detail. The traffic states were found to be qualitatively alike as they were in continuum model. Jiang et al. [10] studied the influence of main road on the on-ramp flow using the cellular automata traffic flow model. Treiber and Kesting [11] proposed a systematic method to determine the spatiotemporal dynamics in open systems with bottlenecks.

The lattice hydrodynamic model was initiated by Nagatani (for simplicity, we referred lattice hydrodynamic model as lattice model in remaining text) [12, 13]. Latter, the lattice model was used to analyze the characteristics of traffic stream on two-lane highway [14]. It is a simplified macroscopic hydrodynamic model, while still incorporates the microscopic concept described in the optimal velocity model. For this reason, the lattice hydrodynamic model has become quite popular in traffic modelling. In the context of the intelligent transportation system (ITS), various extended models emerged by considering different traffic conditions, such as physical delay [15, 16], passing [17,18,19,20], flux effect [21,22,23,24], driving behavior [25], control method [26, 27], stabilization effect [28,29,30,31] and road condition [32,33,34,35,36].

Currently, the traffic congestion patterns at on-ramp are investigated mainly by the continuum model, the car-following model and the cellular automata traffic flow model. Few studies investigate the congestion patterns by using a two-lane lattice model under the on-ramp system.

In this paper, the congestion traffic states regarding the on-ramp traffic system with a two-lane lattice hydrodynamic model are explored. Specifically, an improved two-lane lattice hydrodynamic traffic model is proposed first. Then, a new stochastic on-ramp system is designed. After that, numerical simulation is conducted to examine whether the lattice model can reproduce the empirical traffic phenomenon nearby on-ramp, as well as to test the validation of the new on-ramp system. Finally, the combinatorial congested patterns of PLC, TSG, HST and OCT under deterministic on-ramp are stated and analyzed.

The remaining text is organized as follows. Section 2 elaborates on the two-lane density difference lattice hydrodynamic model. The stochastic and deterministic on-ramp systems are designed in Sect. 3. Numerical analyses are performed in Sect. 4. Section 5 concludes the whole study.

2 Density difference lattice hydrodynamic model for two-lane traffic

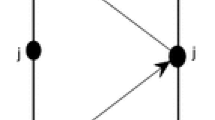
The single-lane traffic model is not able to capture the real traffic since the road networks are almost connected by two-lane or multi-lane roads. Based on the single-lane lattice model, Nagatani [14] proposed a two-lane lattice hydrodynamical model. Figure 1 illustrates the schematic diagram of the traffic flow on a two-lane highway. If the density of site \(j-1\) in the second lane is higher than that of site j in the first lane, cars will change from the second lane to the first one with a rate of \(\gamma \left| \rho _0^2V'(\rho _0)\right| (\rho _{2,j-1}(t)-\rho _{1,j}(t))\), where \(\gamma \) is a fixed dimensionless coefficient, \(\left| \rho _0^2V'(\rho _0)\right| \) is a scale parameter, \(\rho _0\) is the average density, \(\rho _{1,j}\) and \(\rho _{2,j}\) are the densities at site j in the first lane and second lane, respectively. Accordingly, the lane-change rate in the opposite case is \(\gamma \left| \rho _0^2V'(\rho _0)\right| (\rho _{1,j}(t)-\rho _{2,j+1}(t))\).

The lattice hydrodynamic model for two-lane traffic is governed by the following equation [14]. In our two-lane traffic model, the continuity equation and the evolution equation are independent. The continuity equation for the first lane is

$$\begin{aligned}&\partial _t\rho _{1,j}(t)+\rho _0(\rho _{1,j}(t)v_{1,j}(t)-\rho _{1,j-1}(t)v_{1,j-1}(t))\nonumber \\&\quad =S_{1,j}=S_{1,j}^\mathrm{in}-S_{1,j}^\mathrm{out}, \end{aligned}$$
(1)

Similarly, the continuity equation for the second lane is

$$\begin{aligned}&\partial _t\rho _{2,j}(t)+\rho _0(\rho _{2,j}(t)v_{2,j}(t)-\rho _{2,j-1}(t)v_{2,j-1}(t))\nonumber \\&\quad =S_{2,j}=S_{2,j}^\mathrm{in}-S_{2,j}^\mathrm{out}. \end{aligned}$$
(2)

\(S_{i,j}^\mathrm{in}(t)(i=1,2)\) is the inflow density of lattice j on lane i at time t. \(S_{i,j}^\mathrm{out}(t)\) is the outflow density from lattice j on lane i at time t. Note that t will be omitted in the following formulations for brevity. In Nagatani’s model, the lane-changing behavior is described as follows

$$\begin{aligned} S_{1,j}^\mathrm{in}= & {} \gamma \left| \rho _0^2V'(\rho _0)\right| (\rho _{2,j-1}-\rho _{1,j}), \end{aligned}$$
(3)
$$\begin{aligned} S_{1,j}^\mathrm{out}= & {} \gamma \left| \rho _0^2V'(\rho _0)\right| (\rho _{1,j}-\rho _{2,j+1}), \end{aligned}$$
(4)
$$\begin{aligned} S_{2,j}^{i\mathrm n}= & {} \gamma \left| \rho _0^2V'(\rho _0)\right| (\rho _{1,j-1}-\rho _{2,j}), \end{aligned}$$
(5)
$$\begin{aligned} S_{2,j}^\mathrm{out}= & {} \gamma \left| \rho _0^2V'(\rho _0)\right| (\rho _{2,j}-\rho _{1,j+1}). \end{aligned}$$
(6)

The original two-lane lattice model is an valuable work, but it had a flaw, i.e., the phenomenon of vehicle backward movement. Taking the inflow rate described in Eq. (3) as an example, when \(\rho _{2,j-1}<\rho _{1,j}\), the inflow density from lattice \(j-1\) on lane 2 to lattice j on lane 1 is negative, i.e., the density difference (\(\rho _{2,j-1}-\rho _{1,j})<0\). According to the lane-changing formula (3), \(S_{1,j}^\mathrm{in}<0\), which means that vehicles in lattice j on lane 1 move backward to lattice \(j-1\) on lane 2. This is unrealistic in actual traffic. An alternative to overcome this drawback is to let lane changing occur only when the density of inflow lattice is less than that of outflow lattice. For example, in formula (3), we add a constraint condition \(\rho _{2,j-1}>\rho _{1,j}\). Then, the new expressions of \(S_{i,j}^\mathrm{in}\) and \(S_{i,j}^\mathrm{out}\) are rewritten as follows:

$$\begin{aligned} S_{1,j}^\mathrm{in}= & {} \left\{ \begin{array}{ll} \gamma \left| \rho _0^2V'(\rho _0)\right| (\rho _{2,j-1}-\rho _{1,j}){:}&{}\qquad \rho _{2,j-1}>\rho _{1,j}\\ 0{:}&{} \qquad \hbox {other}\\ \end{array}\right. , \end{aligned}$$
(7)
$$\begin{aligned} S_{1,j}^\mathrm{out}= & {} \left\{ \begin{array}{ll} \gamma \left| \rho _0^2V'(\rho _0)\right| (\rho _{1,j}-\rho _{2,j+1}){:} &{}\qquad \rho _{1,j}>\rho _{2,j+1}\\ 0{:}&{}\qquad \hbox {other}\\ \end{array}\right. , \end{aligned}$$
(8)
$$\begin{aligned} S_{2,j}^\mathrm{in}= & {} \left\{ \begin{array}{ll} \gamma \left| \rho _0^2V'(\rho _0)\right| (\rho _{1,j-1}-\rho _{2,j}){:} &{}\qquad \rho _{1,j-1}>\rho _{2,j}\\ 0{:}&{}\qquad \hbox {other} \end{array}\right. , \end{aligned}$$
(9)
$$\begin{aligned} S_{2,j}^\mathrm{out}= & {} \left\{ \begin{array}{ll} \gamma \left| \rho _0^2V'(\rho _0)\right| (\rho _{2,j}-\rho _{1,j+1}){:} &{}\qquad \rho _{2,j}>\rho _{1,j+1}\\ 0{:}&{} \qquad \hbox {other} \end{array}\right. ,\nonumber \\ \end{aligned}$$
(10)

The evolution equation for two-lane traffic model is described below,

$$\begin{aligned} \partial _t(\rho _{1,j} v_{1,j})= & {} a\rho _0V_e(\rho _{1,j+1})-a\rho _{1,j} v_{1,j}. \end{aligned}$$
(11)
$$\begin{aligned} \partial _t(\rho _{2,j} v_{2,j})= & {} a\rho _0V_e(\rho _{2,j+1})-a\rho _{2,j} v_{2,j}. \end{aligned}$$
(12)

With the help of ITS, density difference can be incorporated into two-lane lattice model. Then, a new evolution equation is obtained:

$$\begin{aligned} \partial _t(\rho _{1,j} v_{1,j})= & {} a\rho _0V_e(\rho _{1,j+1})-a\rho _{1,j} v_{1,j}\nonumber \\&+\,\lambda (\rho _{1,j}-\rho _{1,j+1})/\rho _0, \end{aligned}$$
(13)
$$\begin{aligned} \partial _t(\rho _{2,j} v_{2,j})= & {} a\rho _0V_e(\rho _{2,j+1})-a\rho _{2,j} v_{2,j}\nonumber \\&+\,\lambda (\rho _{2,j}-\rho _{2,j+1})/\rho _0, \end{aligned}$$
(14)

where \(\lambda \) is the reaction coefficient of density difference between the current and leading vehicles.

Taken together, the present two-lane density difference lattice hydrodynamic model is described by Eqs. (1)–(4).

Eliminating velocity v in Eqs. (1), (13) and (2), (14) separately, we get an equation which is only related to density

$$\begin{aligned}&\partial ^2_t\rho _{1,j}+a\rho _0^2(V_e(\rho _{1,j+1})-V_e(\rho _{1,j})) -a\left( S_{1,j}^\mathrm{in}\right. \nonumber \\&\left. \quad -\,S_{1,j}^\mathrm{out}\right) +a\partial _t\rho _{1,j}-\lambda (\rho _{1,j+1}-2\rho _{1,j}+\rho _{1,j-1})\nonumber \\&\quad -\,\left( \partial _tS_{1,j}^\mathrm{in}-\partial _tS_{1,j}^\mathrm{out}\right) =0. \end{aligned}$$
(15)
$$\begin{aligned}&\partial ^2_t\rho _{2,j}+a\rho _0^2(V_e(\rho _{2,j+1})-V_e(\rho _{2,j}))-a\left( S_{2,j}^\mathrm{in}-S_{2,j}^\mathrm{out}\right) \nonumber \\&\quad +\,a\partial _t\rho _{2,j}-\lambda (\rho _{2,j+1}-2\rho _{2,j}+\rho _{2,j-1}) \nonumber \\&\quad -\,\left( \partial _tS_{2,j}^\mathrm{in}-\partial _tS_{2,j}^\mathrm{out}\right) =0. \end{aligned}$$
(16)

To facilitate simulation, below we give the difference form

$$\begin{aligned} \rho _{1,j}(t+2\tau )= & {} 2\rho _{1,j}(t+\tau )-\rho _{1,j}(t)-a\tau ^2\rho _0^2(V(\rho _{1,j+1})\nonumber \\&-\,V(\rho _{1,j}))-a\tau (\rho _{1,j}(t+\tau )-\rho _{1,j}(t))\nonumber \\&+\,\tau ^2a\left( S_{1,j}^\mathrm{in}-S_{1,j}^\mathrm{out}\right) -\lambda \tau ^2\left( 2\rho _{1,j}(t)\right. \nonumber \\&\left. -\,\rho _{1,j+1}(t)-\rho _{1,j-1}(t)\right) \nonumber \\&+\,\tau ^2\left( \partial _tS_{1,j}^\mathrm{in}-\partial _tS_{1,j}^\mathrm{out}\right) , \end{aligned}$$
(17)
$$\begin{aligned} \rho _{2,j}(t+2\tau )= & {} 2\rho _{2,j}(t+\tau )-\rho _{2,j}(t)-a\tau ^2\rho _0^2(V(\rho _{2,j+1})\nonumber \\&-\,V(\rho _{2,j}))-a\tau (\rho _{2,j}(t+\tau )-\rho _{2,j}(t))\nonumber \\&+\,\tau ^2a\left( S_{2,j}^\mathrm{in}-S_{2,j}^\mathrm{out}\right) -\lambda \tau ^2\left( 2\rho _{2,j}(t)\right. \nonumber \\&\left. -\,\rho _{2,j+1}(t)-\rho _{2,j-1}(t)\right) \nonumber \\&+\,\tau ^2\left( \partial _tS_{2,j}^\mathrm{in}-\partial _tS_{2,j}^\mathrm{out}\right) , \end{aligned}$$
(18)

where

$$\begin{aligned} \partial _tS_{1,j}^\mathrm{in}= & {} \frac{\gamma \left| \rho _0^2V'(\rho _0)\right| }{\tau }(\rho _{2,j-1}(t+\tau )\nonumber \\&-\,\rho _{2,j-1}(t)-\rho _{1,j}(t+\tau )+\rho _{1,j}(t)), \end{aligned}$$
(19)
$$\begin{aligned} \partial _tS_{1,j}^\mathrm{out}= & {} \frac{\gamma \left| \rho _0^2V'(\rho _0)\right| }{\tau }(\rho _{1,j}(t+\tau )\nonumber \\&-\,\rho _{1,j}(t)-\rho _{2,j+1}(t+\tau )+\rho _{2,j+1}(t)), \end{aligned}$$
(20)
$$\begin{aligned} \partial _tS_{2,j}^\mathrm{in}= & {} \frac{\gamma \left| \rho _0^2V'(\rho _0)\right| }{\tau }(\rho _{1,j-1}(t+\tau )\nonumber \\&-\,\rho _{1,j-1}(t)-\rho _{2,j}(t+\tau )+\rho _{2,j}(t)), \end{aligned}$$
(21)
$$\begin{aligned} \partial _tS_{2,j}^\mathrm{out}= & {} \frac{\gamma \left| \rho _0^2V'(\rho _0)\right| }{\tau }(\rho _{2,j}(t+\tau )\nonumber \\&-\rho _{2,j}(t)-\rho _{1,j+1}(t+\tau )+\rho _{1,j+1}(t)).\nonumber \\ \end{aligned}$$
(22)

In addition, we employ the following form of optimal velocity function:

$$\begin{aligned} V(\rho )=\tanh \left( \frac{2}{\rho _0}-\frac{\rho }{\rho _0^2} -\frac{1}{\rho _c}\right) +\tanh \left( \frac{1}{\rho _c}\right) . \end{aligned}$$
(23)

\(V(\cdot )\) is a monotonically decreasing function with upper bound. There is an inflection point at \(\rho =\rho _c\) when \(\rho _0=\rho _c\). In order to facilitate the analysis, \(V_e(\rho )\) is simplified as \(V(\rho )\) hereafter.

3 On-ramp

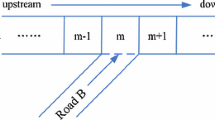
In this section, firstly, we design a stochastic and a deterministic on-ramp system. As is shown in Fig. 2, on-ramp is located at \(x_\mathrm{on}\), and the region \([x_\mathrm{on}, x_\mathrm{on}+L_\mathrm{ramp}]\) is the flux merging section from on-ramp, where \(L_\mathrm{ramp}\) is the length of the on-ramp. When the length of inserting area is set as \(L_\mathrm{ramp}=1\) (see Fig. 2a), i.e., at each time step, all the flux from on-ramp will enter the main road by one lattice. So, we named the system in Fig. 2a as “deterministic on-ramp.” When \(L_\mathrm{ramp}\ge 1\), as is shown in Fig. 3b, it is named as “stochastic on-ramp.” For the stochastic case, there is an accelerating section at the merging section between on-ramp and main road. Usually, the flux of on-ramp will distribute on the merging section randomly. Accordingly, the flux of on-ramp will enter the main road from accelerating section randomly. Then, we design a new on-ramp system to test whether the empirical spatiotemporal patterns can be well reproduced.

The density difference lattice model for two-lane traffic with on-ramp is described by a continuity equation and an evolution equation. The equations with respect to the left lane do not change, i.e., the governing equations are

$$\begin{aligned}&\partial _t\rho _{1,j}(t)+\rho _0(\rho _{1,j}(t)v_{1,j}(t)-\rho _{1,j-1}(t)v_{1,j-1}(t))\nonumber \\&\quad =S_{1,j}=S_{1,j}^\mathrm{in}-S_{1,j}^\mathrm{out}, \ \ \ \ \hbox {and} \end{aligned}$$
(24)
$$\begin{aligned} \partial _t(\rho _{1,j} v_{1,j})&=a\rho _0V_e(\rho _{1,j+1})-a\rho _{1,j} v_{1,j}\nonumber \\&\qquad +\,\lambda (\rho _{1,j}-\rho _{1,j+1})/\rho _0. \end{aligned}$$
(25)

While the equation on the right lane is related to the on-ramp, the density difference model for the right lane of two-lane traffic with on-ramp is described as follows:

The governing equation of lane 2 is

$$\begin{aligned}&\partial _t\rho _{2,j}(t)+\rho _0(\rho _{2,j}(t)v_{2,j}(t)-\rho _{2,j-1}(t)v_{2,j-1}(t))\nonumber \\&\quad =S_{2,j}=S_{2,j}^\mathrm{in}-S_{2,j}^\mathrm{out}+\rho _0\bar{Q_j}, \ \ \ \hbox {and} \end{aligned}$$
(26)
$$\begin{aligned} \partial _t(\rho _{2,j} v_{2,j})= & {} a\rho _0V_e(\rho _{2,j+1})-a\rho _{2,j} v_{2,j}\nonumber \\&+\,\lambda (\rho _{2,j}-\rho _{2,j+1})/\rho _0. \end{aligned}$$
(27)

The on-ramp flux \(\bar{Q_j}\) shown in Fig. 3b is described as

$$\begin{aligned} \bar{Q_j}=\left\{ \begin{array}{ll} Q_\mathrm{on}(t){:} &{}\quad j=s_i\\ 0{:} &{}\quad j\ne s_i \end{array}\right. , \end{aligned}$$
(28)

where \(s_i\) is lattice of the accelerating section. The on-ramp flux \(\bar{Q_j}\) shown in Fig. 3c is described as

$$\begin{aligned} \bar{Q_j}=\left\{ \begin{array}{ll} Q_\mathrm{on}(t)\times \frac{p_i}{\sum _{i=1}^{n} p_i}{:} &{}\quad j=s_i\\ 0{:} &{}\quad j\ne s_i \end{array}\right. . \end{aligned}$$
(29)

By eliminating the velocity term, the difference forms for lanes 1 and 2 are obtained.

$$\begin{aligned}&\rho _{1,j}(t+2\tau )\nonumber \\&\quad =2\rho _{1,j}(t+\tau )-\rho _{1,j}(t)-a\tau ^2\rho _0^2(V(\rho _{1,j+1})-V(\rho _{1,j}))\nonumber \\&\qquad -a\tau (\rho _{1,j}(t+\tau )-\rho _{1,j}(t))+\tau ^2a\left( S_{1,j}^\mathrm{in}-S_{1,j}^\mathrm{out}\right) \nonumber \\&\qquad -\,\lambda \tau ^2(2\rho _{1,j}(t)-\rho _{1,j+1}(t)-\rho _{1,j-1}(t))\nonumber \\&\qquad +\,\tau ^2\left( \partial _tS_{1,j}^\mathrm{in}-\partial _tS_{1,j}^\mathrm{out}\right) , \end{aligned}$$
(30)
$$\begin{aligned}&\rho _{2,j}(t+2\tau )\nonumber \\&\quad =2\rho _{2,j}(t+\tau )-\rho _{2,j}(t)-a\tau ^2\rho _0^2(V(\rho _{2,j+1})-V(\rho _{2,j}))\nonumber \\&\qquad -\,a\tau (\rho _{2,j}(t+\tau )-\rho _{2,j}(t))+\tau ^2a\left( S_{2,j}^\mathrm{in}-S_{2,j}^\mathrm{out}\right) \nonumber \\&\qquad -\,\lambda \tau ^2\left( 2\rho _{2,j}(t)-\rho _{2,j+1}(t)-\rho _{2,j-1}(t)\right) \nonumber \\&\qquad +\,\tau ^2\left( \partial _tS_{2,j}^\mathrm{in}-\partial _tS_{2,j}^\mathrm{out}\right) +a\tau ^2\rho _0\bar{Q_j}. \end{aligned}$$
(31)

4 Numerical simulation

In this section, we display the simulation results. To this end, the road is divided into N uniform lattices, and the on-ramp locates at \(x_\mathrm{on}=300\). The initial density \(\rho _h\) on main road is identical. The boundary condition is open, which can be described as:

$$\begin{aligned} \rho _{1,1}(t)= & {} \rho _{1,2}(t),\ \ \ \rho _{1,N-1}(t)=\rho _{1,N}(t),\ \ \hbox {and} \end{aligned}$$
(32)
$$\begin{aligned} \rho _{2,1}(t)= & {} \rho _{2,2}(t),\ \ \ \rho _{2,N-1}(t)=\rho _{2,N}(t), \end{aligned}$$
(33)

where \(\rho _{i,1}(i=1,2)\) is the density of the first lattice upstream, and \(\rho _N(t)\) is the density of the lattice located at the downstream boundary. The simulation parameters are \(a=0.5\) for \(\rho _{i,j}(i=1,2)\le 0.19\), and \(a=1\) for \(\rho _{i,j}(i=1,2)>0.19\). \(\gamma =0.1\), \(\lambda =0.1\), \(\tau =0.1\), \(\rho _0=0.25\), \(\rho _c=0.25\), \(v_{\max }=2\).

4.1 Stochastic on-ramp simulation

In this section, we simulate several open two-lane systems with different on-ramp bottlenecks. During the simulation, we change inflow \(Q_\mathrm{in}\) and on-ramp flow \(Q_\mathrm{ramp}\) to generate various congestion traffic patterns.

Firstly, we conduct simulation for the stochastic on-ramp and display the result in Fig. 2b. The five empirical congestion patterns are all reproduced under this type of on-ramp system. The initial density of main road is \(\rho =0.10\), and the density of on-ramp is \(\rho =0.10\). Given these parameters, traffic flow in the open system develops into slightly congested traffic states showed in Fig. 3. The congested traffic caused by the small bottleneck is moderate and homogeneous in the density space. The velocity for either the left lane or the right lane is not very low, and the density approximates to 0.2. Such a pattern is exactly the homogeneous synchronized traffic (HST). Since the densities in main road and on-ramp are relatively small, the traffic stream doesn’t grow into heavy traffic jam. The upstream density of on-ramp is almost the same as the free flow branch in fundamental diagram. The velocity tends to the synchronized state on different lanes. This is because every driver needs to reach a relatively high speed by lane change, and the driver has to adjust the leading vehicle’s speed due to significantly small passing probability in the same lane.

Figure 4 shows that traffic jams occur at the region upstream of on-ramp. The average density of the congestion region is obviously larger than that of the non-congestion region (see Fig. 4a, c). Accordingly, the average velocity of traffic in that region is much smaller than that in the rest (see Fig. 4b, d). The congested traffic stays at the on-ramp for a longer period. This is the pinned localized cluster (PLC). This congested pattern is featured when the downstream front of the PLC is fixed at the bottleneck and its upstream front does not propagate upstream over time.

Unlike the PLC illustrated in Fig. 4, the moving localized cluster (MLC) is an isolated single moving traffic waves propagating upstream with a determined speed (see Fig. 5). The single density (velocity) wave increases (decrease) with the growth of distance from on-ramp. Besides the single density (velocity) wave, the traffic stream is free flow with relative high density which corresponds to the end of free flow branch in the fundamental diagram.

Compared with MLC, TSG can be described as several moving localized clusters (see Fig. 6). As the density at the upstream inflow and on-ramp increases, the speed fluctuation frequency of vehicles also gradually rise up. When the density reaches a critical value, there is no free flow between the moving traffic waves. Then, the oscillatory congested traffic (OCT) formed (see Fig. 7).

The density and velocity profiles of two-lane in Fig. 8 are homogeneous over the space except the downstream boundary. It is the homogeneous congested state (HCT). Compared with HST, the density inside HCT is higher, and accordingly, the speed inside the HCT is lower. This traffic pattern can only be observed when there is an accident.

The above simulation results show that all the empirical congested patterns (MLC, HST, TSG, OCT and HCT) are reproduced. But there is a little difference in the congested traffic states between the left lane and the right lane. Traffic congestion of the left lane is not so intensive as that of the right lane. In subsequent subsection, we show some unobserved phenomena by simulating under the deterministic on-ramp system.

4.2 Deterministic simulation

In this section, we carry out the simulation by using the extended two-lane lattice model under deterministic on-ramp. However, these unknown traffic phenomena may exist in real traffic. The simulation parameters here are the same as those used in the stochastic case.

Firstly, let the density of inflow and on-ramp \(\rho _\mathrm{in}=0.06, \rho _\mathrm{ramp}=0.17\), respectively. The traffic states of density and velocity in the left lane and right lane are shown in Fig. 9, respectively. The traffic is HST pattern near the on-ramp. The TSG and OCT patterns appear successively at the upstream of the HST. After \(t=1650\), the OCT disappears, and the HST pattern arises in the whole road. This state can keep self-maintained for a very long time. Then, another TSG occurs at about \(t=1890\). This state is replaced by HST state again sooner. Finally, the TSG in which with PLCs occurs. We call this congestion pattern a combination of TSG and PLC.

Based on the combination mode of PLC and TSG, we increase the main road density to 0.09 and decrease the ramp density to 0.17. Then, TSG congestion pattern appears, but this blocking state emerges at about the 100th lattice of downstream and the duration only exists about 3000 time steps; then, the system develops into synchronized state (see Fig. 10). This phenomenon may attribute to the initial density of the main road is small and the on-ramp inflow is lower than that in Fig. 9. So, the TSG pattern is not quite heavy for a long time. The PLC pattern cannot emerge in this parameter combination since PLC mainly occurs in the case of smaller main road flow with larger ramp flow.

Using the same parameters in the TSG pattern, let \(\rho _\mathrm{in}=0.12\) and \(\rho _\mathrm{ramp}=0.16\). The TSG appears at about the 100th lattice downstream of the on-ramp. After a short synchronized flow pattern, the TSG pattern reappears, and the PLC pattern accompany with OCT style emerges. The wave shape of this special PCL pattern will change over time (see Fig. 11). This traffic congestion pattern is described as PLC and OCT combination pattern.

After further increasing the flow both on the main road upstream and on-ramp to 0.14 and 0.18, respectively, the unexpected congestion patterns are observed (see Fig. 12). As is shown in Fig. 12, the unit synchronized traffic flow emerges within 100 lattices upstream of on-ramp, while the intensive oscillate congestion traffic occurs from the 220th lattice. However, the fluctuations of this congestion pattern decrease along the direction of traffic wave propagation and final the fluctuation close to zero at the inflow boundary. We call this combination of congestion pattern as the PLC pattern associated with OCT.

When the densities of main road and on-ramp reach \(\rho _\mathrm{in}=0.18\) and \(\rho _\mathrm{ramp}=0.20\), respectively, the unreported traffic phenomena are observed (see Fig. 13). The traffic flow state within 100 lattices upstream of on-ramp is HST, which is similar to the above simulation results. Starting from the 200th lattice, the high frequency of OCT emerges quickly and propagates upstream.

In addition, we compare these simulation results with that in stochastic on-ramp. It is found that the reported congestion patterns can be reproduced by the two different models. However, the stochastic on-ramp model cannot obtain the complex combination of congested patters. Actually, these new congested states are not reported by scientist. So, we need empirical data to explore whether they exist in the real traffic.

5 Conclusions

This paper investigates the congested traffic flow by using a two-lane lattice hydrodynamic traffic flow model under on-ramps. We propose an improved lattice model on two-lane highway, which can avoid the unreasonable vehicle backward phenomenon. We design two types of on-ramps, i.e., the deterministic and stochastic on-ramps, to construct the on-ramp traffic flow model. The traffic model with stochastic on-ramp allows us to study the observed empirical congested patterns. It is found that all the observed empirical congested traffic pattern can be reproduced under the stochastic on-ramp. From the numerical experiments, some unobserved traffic phenomena are also found under the deterministic on-ramp.

This paper provides a methodology for management of the traffic. But the simulation results are not compared with the empirical data. Many works are worthy of exploring based on the current model; for example, the NGSIM trajectory data can be used to validate the model and to calibrate the parameters. In addition, the current model can be extended by considering the mixed manual and automated traffic, as well as more complex geometries.