1 Introduction

With the development of soliton theory, super-integrable systems and their super-Hamiltonian structures associated with Lie super algebras have been receiving growing attention. The super-integrable hierarchy is a significant model in nonlinear phenomena, such as super-Jaulent–Miodek hierarchy [1], super-NLS–MKdV hierarchy [2], super-Yang–Mills hierarchy [3], [4,5,6,7,8,9,10], which describe such situations more realistically than general integrable system in plasma physics, arterial mechanics and long-distance optical communications [11,12,13,14].

Supersymmetric extensions of the Schrödinger group and its Lie algebra have also been discussed in connection with various physical systems such as fermionic oscillator [15, 16], spinning particles [17], nonrelativistic Chern–Simons matter [18,19,20], Dirac monopole and magnetic vortex [19], many body quantum systems [21]. It introduces a \(Z_2\)-graded version of the nonlinear Schrödinger equation that includes one fermion and one boson at the same time, and the solution exhibits a super-version form of the classical Rosales solution in [22]. In [23], the nonrelativistic limits of the \(N=3\) Chern–Simons matter system in \(1+2\) dimensions are investigated; then, a family of super-Schrödinger-invariant field theories produced from the parent relativistic theory is presented.

Soliton equations are nonlinear partial differential equations (PDEs) described by infinite dimensional integrable systems and are important models describing nonlinear phenomena that occur in nature. Some methods have been proposed to solve the PDEs in Refs. [24,25,26], e.g., the Darboux transformation (DT) [27], inverse scattering transformation [28], B\({\ddot{a}}\)cklund transformation (BT) [29, 30], Painleve test [31], Hirota method [32] and Adomian decomposition method [33, 34]. In Ref. [35], Wazwaz et al. present an extended higher-order modified KdV equation and derive the one-soliton, two-soliton and three-soliton solutions by using simplified Hirota’s direct method. Three variants of nonlinear diffusion–reaction equations with derivative-type and algebraic-type nonlinearities, short-range and long-range diffusion terms are studied through the auxiliary equation method in [36]. Among those methods, the BT can also be used to obtain a nontrivial solution from a seed solution in Refs. [30, 31]). The DT is a powerful method to construct the soliton solution for the super-integrable equations. There are different methods to derive the DT, for instance, operator decomposition method [37], gauge transformation [27, 38], loop group method [39] and Riemann–Hilbert method [40]. The DT can be used for constructing multisoliton and localized coherent structure solutions of nonlinear integrable equations in both (\(1+1\)) and (\(2+1\)) dimensions [41,42,43,44]. The DT of the integrable coupling system composed by triangular system has been discussed [45].

The integrable nonlinear Schrödinger (NLS) equation is an important model for a variety of physical problems [46, 47]. It is used in nonlinear optics [46], condensed matter physics and in particular in modeling Bose–Einstein condensate (BEC) [47,48,49,50], and so on [51,52,53,54]. Bagnato et al. offer a general introduction to the theme of BEC and briefly discuss the evolution of a number of relevant research directions during the last two decades in [52]. Multidimensional solitons and their legacy in contemporary atomic, molecular and optical physics are reported in [53]. An overview of selected recent studies on the creation and the characterization of localized optical structures in nonlinear media is proved [54]. Optical solitons (bright and dark) in a fibers, which are created by a balance of group-velocity dispersion (GVD) and self-phase modulation (SPM), they are governed by the NLS equation under idealized conditions and are inherently stable. There are many works for the NLS equation with (time, space)-modulated potential and nonlinearity [49, 55]. For the two-component coupled system with both focusing cases, the coupled NLS equations admit bright–bright solitons and bright–dark, breather, rogue wave, bright–dark–breather and bright–dark–rogue wave solutions [56, 57].

In fact, the DT for the super-integrable hierarchy has an essential difference from the general cases. As we know, the super-integrable soliton equation hierarchies with four potentials are discussed. Consequently, in order to obtain the analytic soliton solutions of a super-NLS equation and a super-Dirac equation, we will employ the DT method, which is an effective computerization procedure and has been widely used to construct soliton-like solutions for a class of nonlinear evolution equations. In this paper, we construct explicit solutions and dark-bright solutions for two super-integrable equations.

This paper is organized as follows: In Sect. 2, we construct DT for super-AKNS soliton hierarchy and proof the procedure of DT, and some soliton solutions are obtained. In Sect. 3, we apply the DT for super-Dirac soliton hierarchy and obtain some soliton solutions. The evolutions of the intensity distribution of the soliton solutions are illustrated in figures.

2 Darboux transformation and exact solutions for super-Schrödinger equation

The Schrödinger symmetry can accommodate supersymmetries, in which case it enhanced a super-Schrödinger symmetry. Super-Schrödinger-invariant field theories would be important like superconformal field theories. The super-AKNS soliton hierarchy has already aroused widespread attention in physics and mathematical applications [58]. Ma presents the super-AKNS soliton hierarchy in [59], which includes not only even elements but also the odd elements.

2.1 Darboux transformation for super-Schrödinger equation

In this section, we introduce a graded formalism allowing us to deal with a classical field containing one bosonic and one fermionic component. And the super-Schrödinger equation can describe some particles according to their collective behavior in high or low temperature. Furthermore, the super-Schrödinger equation can describe the movement of microscopic particles, each microscopic system has a corresponding equation, and the specific form of wave function and the corresponding energy can be obtained by solving equations, so as to understand the nature of the microsystem. The super-Schrödinger equation can be reduced from the super-AKNS soliton hierarchy, which is as follows

$$\begin{aligned}&r_t=-\frac{1}{2}r_{xx}+r^2s+2r\alpha \beta -2\alpha \alpha _x, \nonumber \\&s_t=\frac{1}{2}s_{xx}-rs^2-2s\alpha \beta -2\beta \beta _x, \nonumber \\&\alpha _t=-\alpha _{xx}-r\beta _x-\frac{1}{2}r_x\beta +\frac{1}{2}rs\alpha , \nonumber \\&\beta _t=\beta _{xx}+s\alpha _x+\frac{1}{2}s_x\alpha -\frac{1}{2}rs\beta . \end{aligned}$$
(1)

We first consider the Lax pairs (or the linear isospectral problems) of Eq. (1) in the form

$$\begin{aligned} \varphi _x=U\varphi =\left( \begin{array}{lll} \lambda &{}{\quad }r&{}{\quad }\alpha \\ s&{}{\quad }-\lambda &{}{\quad }\beta \\ \beta &{}{\quad }-\alpha &{}{\quad }0\end{array}\right) {\varphi }, \end{aligned}$$
(2)

and

$$\begin{aligned} \varphi _t= & {} V\varphi \\= & {} \left( \begin{array}{lll} {\lambda }^2-\frac{1}{2}rs-\alpha \beta &{}{\quad }r\lambda +\frac{1}{2}r_{x}&{}{\quad }\alpha \lambda +\alpha _{x} \\ s\lambda -\frac{1}{2}s_{x}&{}{\quad }-{\lambda }^2+\frac{1}{2}rs+\alpha \beta &{}{\quad }\beta \lambda -\beta _x \\ \beta \lambda -\beta _{x}&{}{\quad }-\alpha \lambda -\alpha _x&{}{\quad }0 \end{array}\right) \varphi ,\nonumber \end{aligned}$$
(3)

here r(x, t), s(x, t), \(\alpha (x,t)\), \(\beta (x,t)\) are potentials, \(\lambda \) is a spectral parameter, \( \varphi =(\varphi _1 ,\varphi _2,\varphi _3)^\mathrm{T} \) is a column vector solution of Eqs. (2) and (3) associated with an eigenvalue \(\lambda \).

The aim of this section is to construct Darboux transformation for super-Schrödinger equations (2) and (3), which are satisfied with the \(3\times 3\) matrix transformation of \(\varphi \), \({\tilde{U}}\) and \({\tilde{V}}\). Now we recommend a gauge transformation T of the super-Schrödinger equations (2) and (3):

$$\begin{aligned} \widetilde{\varphi _{n}}=T\varphi _{n}, T=\left( \begin{array}{lll}T_{11} &{}{\quad }T_{12}&{}{\quad }T_{13} \\ T_{21}&{}{\quad }T_{22}&{}{\quad }T_{23} \\ T_{31}&{}{\quad }T_{32}&{}{\quad }T_{33}\end{array}\right) , \end{aligned}$$
(4)
$$\begin{aligned} \varphi _x={{\widetilde{U}}}\varphi ,{{\widetilde{U}}}=(T_x+TU)T^{-1}, \end{aligned}$$
(5)
$$\begin{aligned} \varphi _t={{\widetilde{V}}}\varphi ,{{\widetilde{V}}}=(T_t+TV)T^{-1}. \end{aligned}$$
(6)

If the \({{\widetilde{U}}}\), \({{\widetilde{V}}}\) and U, V have the same types, system(4) is called Darboux transformation of the super-Schrödinger equations.

Let \(\psi =(\psi _1,\psi _2,\psi _3)^\mathrm{T}\), \(\phi =(\phi _1,\phi _2,\phi _3)^\mathrm{T}\), \(X=(X_1,X_2,X_3)^\mathrm{T}\) are three basic solutions of systems (2) and (3), then we give the following linear algebraic systems:

$$\begin{aligned}&\sum _{i=0}^{N-1}\left( A_{11}^{(i)}+A_{12}^{(i)}M_j^{(1)}+A_{13}^{(i)}M_j^{(2)}\right) \lambda _j^{i}=-\lambda _j^{N}, \nonumber \\&\sum _{i=0}^{N-1}\left( A_{21}^{(i)}+A_{22}^{(i)}M_j^{(1)}+A_{23}^{(i)}M_j^{(2)}\right) \lambda _j^{i}=-M_j^{(1)}\lambda _j^{N}, \nonumber \\&\sum _{i=0}^{N-1}\left( A_{31}^{(i)}+A_{32}^{(i)}M_j^{(1)}+A_{33}^{(i)}M_j^{(2)}\right) \lambda _j^{i}=-M_j^{(2)}\lambda _j^{N},\nonumber \\ \end{aligned}$$
(7)

with

$$\begin{aligned} M_j^{(1)}= & {} \frac{\psi _2+\nu _j^{(1)}\phi _2+\nu _j^{(2)}X_2}{\psi _1+\nu _j^{(1)}\phi _1+\nu _j^{(2)}X_1}, \nonumber \\ M_j^{(2)}= & {} \frac{\psi _3+\nu _j^{(1)}\phi _3+\nu _j^{(2)}X_3}{\psi _1+\nu _j^{(1)}\phi _1+\nu _j^{(2)}X_1}, \quad 0\le j\le 3N, \end{aligned}$$
(8)

where \(\lambda _j\) and \(\nu _j^{(k)}\) (\(i\ne k\), \(\lambda _i \ne \lambda _j\), \(\nu _i^{(k)} \ne \nu _j^{(k)}\), \(k \ne 1,2\)) should choose appropriate parameters; thus, the determinants of coefficients for Eq. (7) are nonzero.

Defining a \(3\times 3\) matrix T, and T is of the form as following

$$\begin{aligned}&T_{11}=\lambda ^{N}+\sum _{i=0}^{N-1}A_{11}^{(i)}\lambda ^{i},{\quad } T_{12}=\sum _{i=0}^{N-1}A_{12}^{(i)}\lambda ^{i}, \nonumber \\&\quad T_{13}=\sum _{i=0}^{N-1}A_{13}^{(i)}\lambda ^{i}, \nonumber \\&T_{21}=\sum _{i=0}^{N-1}A_{21}^{(i)}\lambda ^{i},{\quad }T_{22}=\lambda ^{N}+ \sum _{i=0}^{N-1}A_{22}^{(i)}\lambda ^{i}, \nonumber \\&\quad T_{23}=\sum _{i=0}^{N-1}A_{23}^{(i)}\lambda ^{i}, \nonumber \\&T_{31}=\sum _{i=0}^{N-1}A_{31}^{(i)}\lambda ^{i},{\quad } T_{32}=\sum _{i=0}^{N-1}A_{32}^{(i)}\lambda ^{i}, \nonumber \\&\quad T_{33}=\lambda ^{N}+\sum _{i=0}^{N-1}A_{33}^{(i)}\lambda ^{i}, \end{aligned}$$
(9)

where N is a natural number, and the \(A_{mn}^{i}(m,n=1,2,3.\,m\ge 0)\) are the functions of x and t. Through calculations, we can obtain \(\Delta T\) as follows

$$\begin{aligned} \Delta T= \prod _{j=1}^{3N}(\lambda -\lambda _j) \end{aligned}$$
(10)

which proves that \(\lambda _j (j=1\le j\le 3N,)\) are 3N roots of \(\Delta T\). Based on these conditions, we will proof that the \({\widetilde{U}}\) and \( {\widetilde{V}}\) have the same forms with U and V, respectively.

Proposition 1

The matrix \({\widetilde{U}}\) defined by (5) has the same type as U, that is,

$$\begin{aligned} {\tilde{U}} = \left( \begin{array}{lll} \lambda &{}\quad {\widetilde{r}}&{}\quad {\widetilde{\alpha }} \\ {\widetilde{s}}&{}\quad -\lambda &{}\quad {\widetilde{\beta }} \\ {\widetilde{\beta }}&{}\quad -{\widetilde{\alpha }}&{}\quad 0 \end{array}\right) , \end{aligned}$$
(11)

in which the transformation formulas between old and new potentials are shown as follows

$$\begin{aligned}&{\widetilde{r}}=r-2A_{12}, \nonumber \\&{\widetilde{s}}= s+2A_{21}, \nonumber \\&{\widetilde{\alpha }}={\alpha }-A_{13}, \nonumber \\&{\widetilde{\beta }}=\beta +A_{31}. \end{aligned}$$
(12)

Transformations (12) are used to get a Darboux transformation of the spectral problem (5).

Proof

By assuming \(T^{-1}=\frac{T^*}{\Delta T}\) and

$$\begin{aligned} (T_x+TU)T^*=\left( \begin{array}{lll}B_{11}(\lambda ) &{}{\quad }B_{12}(\lambda )&{}{\quad }B_{13}(\lambda ) \\ B_{21}(\lambda )&{}{\quad }B_{22}(\lambda )&{}{\quad }B_{23}(\lambda ) \\ B_{31}(\lambda )&{}{\quad }B_{32}(\lambda )&{}{\quad }B_{33}(\lambda ) \end{array}\right) ,\nonumber \\ \end{aligned}$$
(13)

it is easy to verify that \(B_{sl} (1\le s,l\le 3)\) are 3N-order or \(3N+1\)-order polynomials in \(\lambda \).

Through some accurate calculations, \(\lambda _j (1\le j\le 3,)\) are the roots of \(B_{sl} (1\le s,l\le 3)\). Thus, Eq. (13) has the following structure

$$\begin{aligned} (T_x+TU)T^*=(\Delta T)C(\lambda ) \end{aligned}$$
(14)

where

$$\begin{aligned} C(\lambda )=\left( \begin{array}{lll}C_{11}^{(1)}\lambda +C_{11}^{(0)} &{}{\quad }C_{12}^{(0)}&{}{\quad }C_{13}^{(0)} \\ C_{21}^{(0)}&{}{\quad }C_{22}^{(1)}\lambda +C_{22}^{(0)}&{}{\quad }C_{23}^{(0)} \\ C_{31}^{(0)}&{}{\quad }C_{32}^{(0)}&{}{\quad }C_{33}^{(1)}\lambda +C_{33}^{(0)}\end{array}\right) ,\nonumber \\ \end{aligned}$$
(15)

and \(C_{mn}^{(k)} (m,n=1,2,k=0,1)\) satisfy the functions without \(\lambda \). Equation (14) is obtained as follows

$$\begin{aligned} (T_x+TU)=C(\lambda )T. \end{aligned}$$
(16)

Through comparing the coefficients of \(\lambda \) in Eq. (16), we can obtain

$$\begin{aligned}&C_{11}^{(1)}=1,C_{11}^{(0)}=0,\quad C_{12}^{(0)}=r-2A_{12}={\widetilde{r}}, \nonumber \\&\quad C_{13}^{(0)}=\alpha -A_{13}={\widetilde{\alpha }}, \nonumber \\&C_{21}^{(0)}=s+2A_{21}={\widetilde{s}},\quad C_{22}^{(1)}=-1,C_{22}^{(0)}=0, \nonumber \\&\quad C_{23}^{(0)}=\beta +A_{23}={\widetilde{\beta }}, \nonumber \\&C_{31}^{(0)}=\beta +A_{31}={\widetilde{\beta }},\quad C_{32}^{(0)}=-\alpha -A_{32}=-{\widetilde{\alpha }}, \nonumber \\&\quad C_{33}^{(1)}=0,C_{33}^{(0)}=0. \end{aligned}$$
(17)

In the following section, we assume that the new matrix \({\widetilde{U}}\) has the same type with U, which means that they have the same structures only \(r,s,\alpha ,\beta \) of U transformed into \({{\widetilde{r}}},{{\widetilde{s}}},{{\widehat{\alpha }}},{{\widetilde{\beta }}} \) of \({\widetilde{U}}\). After careful calculation, we compare the ranks of \(\lambda ^{N}\), and get the objective equations as following:

$$\begin{aligned}&{\widetilde{r}}=r-2A_{12}, \nonumber \\&{\widetilde{s}}= s+2A_{21}, \nonumber \\&{\widetilde{\alpha }}={\alpha }-A_{13}, \nonumber \\&{\widetilde{\beta }}=\beta +A_{31}. \end{aligned}$$
(18)

From Eqs. (11) and (12), we know that \(\widetilde{U}=C(\lambda )\). The proof is completed. \(\square \)

Proposition 2

Under transformation (18), the matrix \({\widetilde{V}}\) defined by (6) has the same form as V, that is,

$$\begin{aligned} {\widetilde{V}}=\left( \begin{array}{lll} {\lambda }^2-\frac{1}{2}{\widetilde{rs}}-\widetilde{\alpha \beta } &{}{\quad }{\widetilde{r}}\lambda +\frac{1}{2}\widetilde{r_{x}}&{}{\quad }{\widetilde{\alpha }}\lambda +\widetilde{\alpha _{x}} \\ {\widetilde{s}}\lambda -\frac{1}{2}\widetilde{s_{x}}&{}{\quad }-{\lambda }^2+\frac{1}{2}{\widetilde{rs}}+\widetilde{\alpha \beta }&{}{\quad }{\widetilde{\beta }}\lambda -\widetilde{\beta _x} \\ {\widetilde{\beta }}\lambda -\widetilde{\beta _{x}}&{}{\quad }-{\widetilde{\alpha }}\lambda -\widetilde{\alpha _x}&{}{\quad }0\end{array}\right) .\nonumber \\ \end{aligned}$$
(19)

Proof

We assume the new matrix \({\widetilde{V}}\) also has the same form with V. If we obtain the similar relations between \(r,s,\alpha ,\beta \) and \({{\widetilde{r}}},{{\widetilde{s}}},\widehat{\alpha },{{\widetilde{\beta }}}\) in Eq. (12), we can prove that the gauge transformations under T turn the Lax pairs U, V into new Lax pairs \({\widetilde{U}},{\widetilde{V}}\) with the same types.

By assuming \(T^{-1}=\frac{T^*}{\Delta T}\) and

$$\begin{aligned} (T_t+TV)T^*=\left( \begin{array}{lll}E_{11}(\lambda ) &{}{\quad }E_{12}(\lambda )&{}{\quad }E_{13}(\lambda ) \\ E_{21}(\lambda )&{}{\quad }E_{22}(\lambda )&{}{\quad }E_{23}(\lambda ) \\ E_{31}(\lambda )&{}{\quad }E_{32}(\lambda )&{}{\quad }E_{33}(\lambda )\end{array}\right) .\nonumber \\ \end{aligned}$$
(20)

It is easy to verify that \(E_{sl} (1\le s,l\le 3)\) are \(3N+1\)-order or \(3N+2\)-order polynomials in \(\lambda \).

Through some calculations, \(\lambda _j (j=1\le j\le 3,)\) are the roots of \(E_{sl} (s,l=1\le j\le 3)\). Thus, Eq. (20) has the following structure

$$\begin{aligned} (T_t+TV)T^*=(\Delta T)F(\lambda ), \end{aligned}$$
(21)

where

$$\begin{aligned} F(\lambda )=\left( \begin{array}{lll} F_{11}^{(2)}\lambda ^2+F_{11}^{(1)}\lambda +F_{11}^{(0)} &{}{\quad }F_{12}^{(1)}\lambda +F_{12}^{(0)}&{}{\quad }F_{13}^{(1)}\lambda +F_{13}^{(0)} \\ F_{21}^{(1)}\lambda +F_{21}^{(0)}&{}{\quad }F_{22}^{(2)}\lambda ^2+F_{22}^{(1)}\lambda +F_{22}^{(0)}&{}{\quad }F_{23}^{(1)}\lambda +F_{23}^{(0)} \\ F_{31}^{(1)}\lambda +F_{31}^{(0)}&{}{\quad }F_{32}^{(1)}\lambda +F_{32}^{(0)}&{}{\quad }F_{33}^{(2)}\lambda ^2+F_{33}^{(1)}\lambda +F_{33}^{(0)}\end{array}\right) ,\qquad \qquad \qquad \qquad \qquad \qquad \end{aligned}$$
(22)

and \(F_{mn}^{(k)} (m,n=1,2,k=0,1)\) satisfy the functions without \(\lambda \). According to Eq. (21), the following equation is obtained

$$\begin{aligned} (T_t+TV)=F(\lambda )T. \end{aligned}$$
(23)

Through comparing the coefficients of \(\lambda \) in Eq. (23), we get the objective equations as follows:

$$\begin{aligned}&F_{11}^{(2)}=0,F_{11}^{(1)}=0, \nonumber \\&F_{11}^{(0)}=-\frac{1}{2}rs-\alpha \beta +A_{12}s+A_{13} \beta -A_{21}{\widetilde{r}}-A_{31}{\widetilde{\alpha }} \nonumber \\&\quad \qquad =-\frac{1}{2}{\widetilde{r}}{\widetilde{s}}-{\widetilde{\alpha }}{\widetilde{\beta }}, \nonumber \\&F_{12}^{(1)}=r-2A_{12}={\widetilde{r}}, \nonumber \\&\quad F_{12}^{(0)}=\frac{1}{2}{r_{x}}+A_{11}r-A_{13}\alpha -A_{22}{\widetilde{r}}-A_{32}{\widetilde{\alpha }}=\frac{1}{2}\widetilde{r_{x}}, \nonumber \\&F_{13}^{(1)}=\alpha -A_{13}={\widetilde{\alpha }}, \nonumber \\&\quad F_{13}^{(0)}={\alpha _{x}}+A_{11}\alpha +A_{12}\beta -A_{23}{\widetilde{r}}-A_{33}{\widetilde{\alpha }}=\widetilde{\alpha _{x}}, \nonumber \\&F_{21}^{(1)}=s+2A_{21}={\widetilde{s}}, \nonumber \\&F_{21}^{(0)}=-\frac{1}{2}s_{x}+A_{22}s+A_{23}\beta -A_{11}{\widetilde{s}}-A_{31}{\widetilde{\beta }} \nonumber \\&\quad \qquad =-\frac{1}{2}\widetilde{s_{x}}, \nonumber \\&F_{22}^{(2)}=-1,\quad F_{22}^{(1)}=0, \nonumber \\&F_{22}^{(0)}=A_{21}r+\frac{1}{2}rs+\alpha \beta -A_{23}\alpha -A_{12}{\widetilde{s}}-A_{32}{\widetilde{\beta }} \nonumber \\&\quad \qquad =\frac{1}{2}{\widetilde{r}}{\widetilde{s}}+{\widetilde{\alpha }}{\widetilde{\beta }}, \nonumber \\&F_{23}^{(1)}=\beta +A_{23}={\widetilde{\beta }}, \nonumber \\&\quad F_{23}^{(0)}=A_{21}\alpha -\beta _x+A_{22}\beta -A_{33}{\widetilde{\beta }}-{\widetilde{s}}A_{13} =-\widetilde{\beta _{x}}, \nonumber \\&F_{31}^{(1)}=\beta +A_{13}={\widetilde{\beta }}, \nonumber \\&\quad F_{31}^{(0)}=A_{32}s-\beta _x+A_{33}\beta -A_{11}{\widetilde{\beta }}+A_{21}{\widetilde{\alpha }} =-\widetilde{\beta _{x}}, \nonumber \\&F_{32}^{(1)}=-\alpha -A_{32}=-{\widetilde{\alpha }}, \nonumber \\&\quad F_{32}^{(0)}=A_{31}r-\alpha _x-A_{33}\alpha -A_{12}{\widetilde{\beta }}+A_{22}{\widetilde{\alpha }} =-\widetilde{\alpha _x}, \nonumber \\&F_{33}^{(2)}=0,\quad F_{33}^{(1)}=0, F_{33}^{(0)}=0. \end{aligned}$$
(24)

In the above section, we assume the new matrix \({\widetilde{V}}\) has the same type with V, which means they have the same structures only \(r,s,\alpha ,\beta \) of V transformed into \({{\widetilde{r}}},{{\widetilde{s}}},{{\widehat{\alpha }}},{{\widetilde{\beta }}}\) of \({\widetilde{V}}\). From Eqs. (12) and (19), we know that \({{\widetilde{V}}}=F{(\lambda )}\). The proof is completed. \(\square \)

2.2 Explicit solutions for super-Schrödinger equation

Propositions 1 and 2 show that the transformations (4) and (12) are Darboux transformations connecting super-Schrödinger equation. In what follows, we can apply the above Darboux transformations (4) and (12) to construct exact solutions of super-Schrödinger equation. Firstly, we give a set of seed solutions \(r=s=\alpha =\beta =0\) and substitute the solutions into Eqs. (2) and (3), and we will get three basic solutions for these equations:

$$\begin{aligned} \psi _{(\lambda )}= & {} \left( \begin{array}{l}\hbox {e}^{\lambda x+\lambda ^2 t} \\ 0 \\ 0\end{array}\right) ,\quad \phi _{(\lambda )}=\left( \begin{array}{l}0 \\ \hbox {e}^{-\lambda x-\lambda ^2 t} \\ 0\end{array}\right) , \nonumber \\ X_{(\lambda )}= & {} \left( \begin{array}{l}0 \\ 0 \\ 1\end{array}\right) . \end{aligned}$$
(25)

Substituting Eq. (25) into Eq. (8), we obtain

$$\begin{aligned}&M_j^{(1)}=\frac{\nu _j^{(1)}\hbox {e}^{-\lambda x-\lambda ^2 t}}{\hbox {e}^{\lambda x+\lambda ^2 t}}=\hbox {e}^{-2\left( \lambda _j x+\lambda _j^2 t+F_j^{(1)}\right) }, \nonumber \\&M_j^{(2)}=\frac{\nu _j^{(2)}}{\hbox {e}^{\lambda x+\lambda ^2 t}}=\hbox {e}^{-\left( \lambda _j x+\lambda _j^2 t+F_j^{(2)}\right) }, \end{aligned}$$
(26)

with \(\nu _j^{(i)}=\hbox {e}^{\left( 3iF_j^{(i)}\right) }\,(1\le i\le 2, 1\le j\le 3N)\).

In order to calculate, we consider \(N=1\) in Eqs. (9) and (10), and obtain the matrix T

$$\begin{aligned} T=\left( \begin{array}{lll}\lambda +A_{11} &{}{\quad }A_{12}&{}{\quad }A_{13} \\ A_{21}&{}{\quad }\lambda +A_{22}&{}{\quad }A_{23} \\ A_{31}&{}{\quad }A_{32}&{}{\quad }\lambda +A_{33}\end{array}\right) , \end{aligned}$$
(27)

and

$$\begin{aligned}&\lambda _j+A_{11}+M_{j}^{(1)}A_{12}+M_{j}^{(2)}A_{13}=0, \nonumber \\&A_{21}+M_{j}^{(1)}(\lambda _j+A_{22})+M_{j}^{(2)}A_{23}=0, \nonumber \\&A_{31}+M_{j}^{(1)}(\lambda _j+A_{32})+M_{j}^{(2)}(\lambda _j+A_{33})=0.\nonumber \\ \end{aligned}$$
(28)

According to Eq. (28), we get

$$\begin{aligned} \Delta= & {} \left| \begin{array}{lll}1 &{}{\quad }\hbox {e}^{-2\left( \lambda _1 x+\lambda _1^2 t+F_1^{(1)}\right) }&{}{\quad }\hbox {e}^{-\left( \lambda _1 x+\lambda _1^2 t+F_1^{(2)}\right) }\\ 1&{}{\quad }\hbox {e}^{-2\left( \lambda _2 x+\lambda _2^2 t+F_2^{(1)}\right) }&{}{\quad }\hbox {e}^{-\left( \lambda _2 x+\lambda _2^2 t+F_2^{(2)}\right) }\\ 1 &{}{\quad }\hbox {e}^{-2\left( \lambda _3 x+\lambda _3^2 t+F_3^{(1)}\right) }&{}{\quad }\hbox {e}^{-\left( \lambda _3 x+\lambda _3^2 t+F_3^{(2)}\right) } \end{array}\right| , \nonumber \\ \Delta _{13}= & {} \left| \begin{array}{lll}1 &{}{\quad }\hbox {e}^{-2\left( \lambda _1 x+\lambda _1^2 t+F_1^{(1)}\right) }&{}{\quad }-\lambda _1\\ 1&{}{\quad }\hbox {e}^{-2\left( \lambda _2 x+\lambda _2^2 t+F_2^{(1)}\right) }&{}{\quad }-\lambda _2\\ 1 &{}{\quad }\hbox {e}^{-2\left( \lambda _3 x+\lambda _3^2 t+F_3^{(1)}\right) }&{}{\quad }-\lambda _3 \end{array}\right| , \nonumber \\ \Delta _{12}= & {} \left| \begin{array}{lll} 1 &{}{\quad }-\lambda _1&{}{\quad }\hbox {e}^{-\left( \lambda _1 x+\lambda _1^2 t+F_1^{(2)}\right) }\\ 1&{}{\quad }-\lambda _2&{}{\quad }\hbox {e}^{-\left( \lambda _2 x+\lambda _2^2 t+F_2^{(2)}\right) }\\ 1 &{}{\quad }-\lambda _3&{}{\quad }\hbox {e}^{-\left( \lambda _3 x+\lambda _3^2 t+F_3^{(2)}\right) } \end{array}\right| , \nonumber \\ \Delta _{21}= & {} \left| \begin{array}{lll} -\lambda _1\hbox {e}^{-2\left( \lambda _1 x+\lambda _1^2 t+F_1^{(1)}\right) } &{}{\quad }\hbox {e}^{-2\left( \lambda _1 x+\lambda _1^2 t+F_1^{(1)}\right) }&{}{\quad }\hbox {e}^{-\left( \lambda _1 x+\lambda _1^2 t+F_1^{(2)}\right) }\\ -\lambda _2\hbox {e}^{-2\left( \lambda _2 x+\lambda _2^2 t+F_2^{(1)}\right) }&{}{\quad }\hbox {e}^{-2\left( \lambda _2 x+\lambda _2^2 t+F_2^{(1)}\right) }&{}{\quad }\hbox {e}^{-\left( \lambda _2 x+\lambda _2^2 t+F_2^{(2)}\right) }\\ -\lambda _3\hbox {e}^{-2\left( \lambda _3 x+\lambda _3^2 t+F_3^{(1)}\right) } &{}{\quad }\hbox {e}^{-2\left( \lambda _3 x+\lambda _3^2 t+F_3^{(1)}\right) }&{}{\quad }\hbox {e}^{-\left( \lambda _3 x+\lambda _3^2 t+F_3^{(2)}\right) } \end{array}\right| , \nonumber \\ \Delta _{31}= & {} \left| \begin{array}{lll} -\lambda _1\hbox {e}^{-\left( \lambda _1 x+\lambda _1^2 t+F_1^{(2)}\right) } &{}{\quad }\hbox {e}^{-2\left( \lambda _1 x+\lambda _1^2 t+F_1^{(1)}\right) }&{}{\quad }\hbox {e}^{-\left( \lambda _1 x+\lambda _1^2 t+F_1^{(2)}\right) }\\ -\lambda _2\hbox {e}^{-\left( \lambda _2 x+\lambda _2^2 t+F_2^{(2)}\right) }&{}{\quad }\hbox {e}^{-2\left( \lambda _2 x+\lambda _2^2 t+F_2^{(1)}\right) }&{}{\quad }\hbox {e}^{-\left( \lambda _2 x+\lambda _2^2 t+F_2^{(2)}\right) }\\ -\lambda _3\hbox {e}^{-\left( \lambda _3 x+\lambda _3^2 t+F_3^{(2)}\right) } &{}{\quad }\hbox {e}^{-2\left( \lambda _3 x+\lambda _3^2 t+F_3^{(1)}\right) }&{}\hbox {e}^{-\left( \lambda _3 x+\lambda _3^2 t+F_3^{(2)}\right) } \end{array}\right| .\nonumber \\ \end{aligned}$$
(29)

Based on Eqs. (8) and (32), we can obtain the following systems

$$\begin{aligned}&A_{12}=\frac{\Delta _{12}}{\Delta },{\quad }A_{13}=\frac{\Delta _{13}}{\Delta },{\quad }\nonumber \\&A_{21}=\frac{\Delta _{21}}{\Delta },{\quad }A_{31}=\frac{\Delta _{31}}{\Delta }; \end{aligned}$$
(30)

the analytic soliton solutions of super-Schrödinger equation are obtained by the DT method as follows

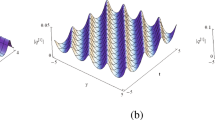
$$\begin{aligned}&{\widetilde{r}}=-2\frac{\Delta _{12}}{\Delta }, \nonumber \\&{\widetilde{s}}= 2\frac{\Delta _{21}}{\Delta }, \nonumber \\&{\widetilde{\alpha }}=-\frac{\Delta _{13}}{\Delta }, \nonumber \\&{\widetilde{\beta }}=\frac{\Delta _{31}}{\Delta }. \end{aligned}$$
(31)

To illustrate the wave propagations of the obtained soliton solutions (31), we can choose these free parameters in the forms \(\lambda _1, \lambda _2,\lambda _3\), \(F_{m}^{(k)} (m=1,2,3,k=1,2,3)\) and the intensity distributions for the soliton solutions given by Eq. (31) are illustrated in Figs. 1 and 2.

Fig. 1
figure 1

(Color online) Profiles of a the intensity distribution \(|{\tilde{r}}|\) of Eq. (31); b the intensity distribution \(|{\tilde{s}}|\) of Eq. (31) with \(\lambda _1=0.1\hbox {i}\), \(\lambda _2=0.4\hbox {i}\), \(\lambda _3=0.3\hbox {i}\), \(F_1^{(1)}=0.3\hbox {i}\), \(F_2^{(2)}=0.2\hbox {i}\), \(F_3^{(3)}=0.1\hbox {i}\), \(F_1^{(2)}=0.2\hbox {i}\), \(F_1^{(3)}=0\), \(F_2^{(1)}=0.5\hbox {i}\), \(F_2^{(3)}=0\), \(F_3^{(1)}=0.4\hbox {i}\), \(F_3^{(2)}=0\), c the intensity distribution \(|{\tilde{\alpha }}|\) of Eq. (31); d the intensity distribution \(|{\tilde{\beta }}|\) of Eq. (31) with \(\lambda _1=2\hbox {i}\), \(\lambda _2=3\hbox {i}\), \(\lambda _3=5\hbox {i}\), \(F_1^{(1)}=i\), \(F_2^{(2)}=2\hbox {i}\), \(F_3^{(3)}=4\hbox {i}\), \(F_1^{(2)}=3\hbox {i}\), \(F_1^{(3)}=0\), \(F_2^{(1)}=3\hbox {i}\), \(F_2^{(3)}=0\), \(F_3^{(1)}=7\hbox {i}\), \(F_3^{(2)}=0\)

Full size image
Fig. 2
figure 2

(Color online) Profiles of a the intensity distribution \(|{\tilde{r}}|\) of Eq. (31); b the intensity distribution \(|{\tilde{s}}|\) of Eq. (31) with \(\lambda _1=0.2+0.1\hbox {i}\), \(\lambda _2=0.3+0.2\hbox {i}\), \(\lambda _3=0.5+0.4\hbox {i}\), \(F_1^{(1)}=0.1+0.1\hbox {i}\), \(F_2^{(2)}=0.2+0.1\hbox {i}\), \(F_3^{(3)}=0.4+0.3\hbox {i}\), \(F_1^{(2)}=0.3+0.3\hbox {i}\), \(F_1^{(3)}=0\), \(F_2^{(1)}=0.3+0.1\hbox {i}\), \(F_2^{(3)}=0\), \(F_3^{(1)}=0.7+0.4\hbox {i}\), \(F_3^{(2)}=0\), c the intensity distribution \(|{\tilde{\alpha }}|\) of Eq. (31); d the intensity distribution \(|{\tilde{\beta }}|\) of Eq. (31) with \(\lambda _1=0.1\), \(\lambda _2=0.4\), \(\lambda _3=0.2\), \(F_1^{(1)}=0.3\), \(F_2^{(2)}=0.2\), \(F_3^{(3)}=0.4\), \(F_1^{(2)}=0.6\), \(F_1^{(3)}=0.5\), \(F_2^{(1)}=0\), \(F_2^{(3)}=0.4\), \(F_3^{(1)}=0\), \(F_3^{(2)}=0\)

Full size image

It is shown that solitary waves in nonautonomous nonlinear and dispersive systems can propagate in the form of so-called nonautonomous solitons or soliton-like similaritons. From the single soliton, we can find that the amplitude of the bright-dark soliton grows and decays with time depending on the parameters \(\lambda _1, \lambda _2,\lambda _3\), \(F_{m}^{(k)} (m=1,2,3,k=1,2,3) \). We can also see that the soliton velocity is related to all the parameters presented in the equation. For illustration, the propagations and evolutions of \(|{\tilde{r}}|, |{\tilde{s}}|,|{\tilde{\alpha }}|, |{\tilde{\beta }}|\) are shown in Figs. 1 and 2.

In Fig. 1, the soliton is central symmetric around the peak point. The width experiences the process of decreasing–increasing with time, while the amplitude experiences increasing–decreasing with time. In Fig. 2, the amplitude of the bright soliton also grows and decays with time. But the velocities before and after the peak time are different, which can be observed clearly from the nonsymmetric contour plot. The collapsing process after the largest amplitude is quicker, and it vanishes rapidly.

3 Darboux transformation and exact solution for super-Dirac soliton hierarchy

Super-Dirac soliton hierarchy has already aroused widespread attention in physics and mathematical applications [60]. Ma had presented the super-Dirac soliton hierarchy in the theory of super-integrable systems, which include not only even elements but also the odd elements [59, 61,62,63].

3.1 Darboux transformation for super-Dirac soliton hierarchy

We note that the super-Dirac equation is decomposed into two equations in the nonrelativistic limit. We can replace the first component of the nonrelativistic spinor; then, the nonrelativistic equation for the second component of the fermion is given by the Pauli equation. In the same way, the Dirac equation can be given by [20]. The super-Dirac equations can reduced from the super-Dirac soliton hierarchy, which are as follows

$$\begin{aligned}&r_t=\frac{1}{2}s_{xx}-(r^2+s^2)s-2s\alpha \beta +\alpha \alpha _x-\beta \beta _x, \nonumber \\&s_t=-\frac{1}{2}r_{xx}+r(s^2+r^2)+2r\alpha \beta _x-\beta _x\beta , \nonumber \\&\alpha _t=\beta _{xx}-r\beta _x+s\alpha _x-\frac{1}{2}r_x\beta \nonumber \\&\qquad \quad +\frac{1}{2}s_x\alpha -\frac{1}{2}(r^2+s^2)\beta , \nonumber \\&\beta _t=-\alpha _{xx}-r\alpha _x-s\beta _x- \frac{1}{2}q_x\alpha \nonumber \\&\qquad \quad -\frac{1}{2}s_x\beta +\frac{1}{2}(r^2+s^2)\alpha . \end{aligned}$$
(32)

Considering the isospectral problem of super-Dirac hierarchy, the Lax pairs of the system are given as follows

$$\begin{aligned} \varphi _x=U\varphi =\left( \begin{array}{lll}r &{}{\quad }\lambda +s&{}{\quad }\alpha \\ -\lambda +s&{}{\quad }-r&{}{\quad }\beta \\ \beta &{}{\quad }-\alpha &{}{\quad }0\end{array}\right) {\varphi }, \end{aligned}$$
(33)
$$\begin{aligned} \varphi _t= & {} V\varphi \nonumber \\= & {} \left( \begin{array}{lll} r\lambda -\frac{1}{2}s_{x}&{}{\quad }{\lambda }^2+s\lambda +\frac{1}{2}r_x+\frac{1}{2}(r^2+s^2)+\alpha \beta &{}{\quad }\alpha \lambda -\beta _{x} \\ -{\lambda }^2+s\lambda +\frac{1}{2}r_x-\frac{1}{2}(r^2+s^2)-\alpha \beta &{}{\quad }-r\lambda +\frac{1}{2}s_{x}&{}{\quad }\beta \lambda +\alpha _x\\ \beta \lambda +\alpha _{x}&{}{\quad }-\alpha \lambda +\beta _x&{}{\quad }0\end{array}\right) \varphi , \end{aligned}$$
(34)

here r(x, t), s(x, t), \(\alpha (x,t)\), \(\beta (x,t)\) are potentials, \(\lambda \) is a spectral parameter, \( \varphi =(\varphi _1 ,\varphi _2,\varphi _3)^\mathrm{T} \) is a column vector solution of Eqs. (33) and (34) associated with an eigenvalue \(\lambda \).

The aim of this section is to construct Darboux transformation for the super-Dirac hierarchy with Eqs. (33) and (34), which is satisfied with the \(3\times 3\) matrix transformation on \(\varphi \), \({\tilde{U}}\) and \({\tilde{V}}\). Now we recommend a gauge transformation T of the super-Dirac hierarchy(33) and (34):

$$\begin{aligned} \widetilde{\varphi _{n}}=T\varphi _{n}, T=\left( \begin{array}{lll}T_{11} &{}\quad T_{12}&{}{\quad }T_{13} \\ T_{21}&{}{\quad }T_{22}&{}{\quad }T_{23} \\ T_{31}&{}{\quad }T_{32}&{}{\quad }T_{33}\end{array}\right) , \end{aligned}$$
(35)
$$\begin{aligned} \varphi _x={{\widetilde{U}}}\varphi ,\quad {{\widetilde{U}}}=(T_x+TU)T^{-1}, \end{aligned}$$
(36)
$$\begin{aligned} \varphi _t={{\widetilde{V}}}\varphi ,\quad {{\widetilde{V}}}=(T_t+TV)T^{-1}. \end{aligned}$$
(37)

If the \({{\widetilde{U}}}\), \({{\widetilde{V}}}\) and U, V have the same types, system(35) is called Darboux transformation of super-Dirac hierarchy.

Let \(\psi =(\psi _1,\psi _2,\psi _3)^\mathrm{T}\), \(\phi =(\phi _1,\phi _2,\phi _3)^\mathrm{T}\), \(X=(X_1,X_2,X_3)^\mathrm{T}\) are three basic solutions of the super-Dirac hierarchy (33) and (34); thus, we give the following linear algebraic system:

$$\begin{aligned}&\sum _{i=0}^{N-1}\left( A_{11}^{(i)}+A_{12}^{(i)}M_j^{(1)}+A_{13}^{(i)}M_j^{(2)}\right) \lambda _j^{i}=-\lambda _j^{N}, \nonumber \\&\sum _{i=0}^{N-1}\left( A_{21}^{(i)}+A_{22}^{(i)}M_j^{(1)}+A_{23}^{(i)}M_j^{(2)}\right) \lambda _j^{i}=-M_j^{(1)}\lambda _j^{N}, \nonumber \\&\sum _{i=0}^{N-1}\left( A_{31}^{(i)}+A_{32}^{(i)}M_j^{(1)}+A_{33}^{(i)}M_j^{(2)}\right) \lambda _j^{i}=-M_j^{(2)}\lambda _j^{N},\nonumber \\ \end{aligned}$$
(38)

with

$$\begin{aligned} M_j^{(1)}= & {} \frac{\psi _2+\nu _j^{(1)}\phi _2+\nu _j^{(2)}X_2}{\psi _1+\nu _j^{(1)}\phi _1+\nu _j^{(2)}X_1}, \nonumber \\ M_j^{(2)}= & {} \frac{\psi _3+\nu _j^{(1)}\phi _3+\nu _j^{(2)}X_3}{\psi _1+\nu _j^{(1)}\phi _1+\nu _j^{(2)}X_1},\quad 0\le j\le 3N, \end{aligned}$$
(39)

where \(\lambda _j\) and \(\nu _j^{(k)}\) (\(i\ne k\), \(\lambda _i \ne \lambda _j\), \(\nu _i^{(k)} \ne \nu _j^{(k)}\), \(k \ne 1,2\)) should choose some appropriate parameters, so that the determinants of coefficients for Eq. (38) are nonzero.

Defining a \(3\times 3\) matrix T, and the T is of the form as following

$$\begin{aligned}&T_{11}=\lambda ^{N}+\sum _{i=0}^{N-1}A_{11}^{(i)}\lambda ^{i},{\quad }T_{12}=\sum _{i=0}^{N-1}A_{12}^{(i)}\lambda ^{i}, \nonumber \\&\quad T_{13}=\sum _{i=0}^{N-1}A_{13}^{(i)}\lambda ^{i}, \nonumber \\&T_{21}=\sum _{i=0}^{N-1}A_{21}^{(i)}\lambda ^{i},{\quad }T_{22}=\lambda ^{N}+\sum _{i=0}^{N-1}A_{22}^{(i)}\lambda ^{i}, \nonumber \\&\quad T_{23}=\sum _{i=0}^{N-1}A_{23}^{(i)}\lambda ^{i}, \nonumber \\&T_{31}=\sum _{i=0}^{N-1}A_{31}^{(i)}\lambda ^{i},{\quad }T_{32}=\sum _{i=0}^{N-1}A_{32}^{(i)}\lambda ^{i}, \nonumber \\&\quad T_{33}=\lambda ^{N}+\sum _{i=0}^{N-1}A_{33}^{(i)}\lambda ^{i}, \end{aligned}$$
(40)

where N is a natural number, and the \(A_{mn}^{i}(m,n=1,2,3.m\ge 0)\) are the functions of x and t. Through calculations, we find

$$\begin{aligned} \Delta T= \prod _{j=1}^{3N}(\lambda -\lambda _j) \end{aligned}$$
(41)

which proves that \(\lambda _j (j=1\le j\le 3N)\) are 3N roots of \(\Delta T\). Based on these conditions, we will proof that the \({\widetilde{U}}\) and \( {\widetilde{V}}\) have the same forms with U and V, respectively.

Proposition 3

The matrix \({\widetilde{U}}\) defined by (36) has the same type as U, that is,

$$\begin{aligned} {\tilde{U}} = \left( \begin{array}{lll} {{\widetilde{r}}} &{}{\quad }\lambda +{{\widetilde{s}}}&{}{\quad }{\widetilde{\alpha }} \\ -\lambda +{{\widetilde{s}}}&{}{\quad }-{{\widetilde{r}}}&{}{\quad }{\widetilde{\beta }} \\ {\widetilde{\beta }}&{}{\quad }-{\widetilde{\alpha }}&{}{\quad }0 \end{array}\right) , \end{aligned}$$
(42)

in which the transformation formulas between old and new potentials are shown

$$\begin{aligned}&{\widetilde{r}}=r-A_{12}-A_{21}, \nonumber \\&{\widetilde{s}}= s+A_{11}-A_{22}, \nonumber \\&{\widetilde{\alpha }}={\alpha }-A_{23}, \nonumber \\&{\widetilde{\beta }}=\beta +A_{13}. \end{aligned}$$
(43)

Transformation (43) is used to get a Darboux transformation of spectral problem (36).

Proof

By assuming \(T^{-1}=\frac{T^*}{detT}\) and

$$\begin{aligned} (T_x+TU)T^*=\left( \begin{array}{lll} B_{11}(\lambda ) &{}{\quad }B_{12}(\lambda )&{}{\quad }B_{13}(\lambda ) \\ B_{21}(\lambda )&{}{\quad }B_{22}(\lambda )&{}{\quad }B_{23}(\lambda ) \\ B_{31}(\lambda )&{}{\quad }B_{32}(\lambda )&{}{\quad }B_{33}(\lambda )\end{array}\right) .\nonumber \\ \end{aligned}$$
(44)

It is easy to verify that \(B_{sl} (1\le s,l\le 3)\) are 3N-order or \(3N+1\)-order polynomials in \(\lambda \).

Through some accurate calculations, \(\lambda _j (1\le j\le 3)\) are the roots of \(B_{sl} (1\le s,l\le 3)\). Then, Eq. (44) has the following structure

$$\begin{aligned} (T_x+TU)T^*=(\hbox {det} T)C(\lambda ) \end{aligned}$$
(45)

where

$$\begin{aligned} C(\lambda )=\left( \begin{array}{lll} C_{11}^{(0)} &{}{\quad }C_{12}^{(1)}\lambda +C_{12}^{(0)}&{}{\quad }C_{13}^{(0)} \\ C_{21}^{(1)}\lambda +C_{21}^{(0)}&{}{\quad }C_{22}^{(0)}&{}{\quad }C_{23}^{(0)} \\ C_{31}^{(0)}&{}{\quad }C_{32}^{(0)}&{}{\quad }0\end{array}\right) ,\nonumber \\ \end{aligned}$$
(46)

and \(C_{mn}^{(k)} (m,n=1,2,k=0,1)\) satisfy the functions without \(\lambda \). So the following equation is obtained

$$\begin{aligned} (T_x+TU)=C(\lambda )T. \end{aligned}$$
(47)

Through comparing the coefficients of \(\lambda \) in Eq. (47), we see

$$\begin{aligned}&C_{11}^{(0)}=r-A_{12}-A_{21}={\widetilde{r}},C_{12}^{(1)}=1, \nonumber \\&C_{12}^{(0)}=s-A_{22}+A_{11}={\widetilde{s}},C_{13}^{(0)}=\alpha -A_{23}={\widetilde{\alpha }}, \nonumber \\&C_{21}^{(1)}=-1,C_{21}^{(0)}=s+A_{11}-A_{22}={\widetilde{s}}, \nonumber \\&C_{22}^{(0)}=-r+A_{12}+A_{21}=-{\widetilde{r}}, \nonumber \\&C_{23}^{(0)}=\beta +A_{13}={\widetilde{\beta }}, \nonumber \\&C_{31}^{(0)}=\beta -A_{32}={\widetilde{\beta }},\quad C_{32}^{(0)}=-\alpha -A_{31}=-{\widetilde{\alpha }}.\nonumber \\ \end{aligned}$$
(48)

In the following section, we assume the new matrix \({\widetilde{U}}\) has the same type with U, which means that they have the same structures only \(r,s,\alpha ,\beta \) of U transformed into \({{\widetilde{r}}},{{\widetilde{s}}},{{\widehat{\alpha }}},{{\widetilde{\beta }}} \) of \({\widetilde{U}}\). After careful calculation, we compare the ranks of \(\lambda ^{N}\) and get the objective equations as follows:

$$\begin{aligned}&{\widetilde{r}}=r-A_{12}-A_{21}, \nonumber \\&{\widetilde{s}}= s+A_{11}-A_{22}, \nonumber \\&{\widetilde{\alpha }}={\alpha }-A_{23}, \nonumber \\&{\widetilde{\beta }}=\beta +A_{13}. \end{aligned}$$
(49)

From Eqs. (42) and (43), we know that \(\widetilde{U}=C(\lambda )\). The proof is completed. \(\square \)

Proposition 4

Under transformation (49), the matrix \({\widetilde{V}}\) defined by (37) has the same form as V, that is,

$$\begin{aligned} {\widetilde{V}}=\left( \begin{array}{lll} {{\widetilde{r}}}\lambda -\frac{1}{2}{{\widetilde{s}}}_{x}&{}{\quad }{\lambda }^2+{\tilde{s}}\lambda +\frac{1}{2}{\tilde{r}}_x+\frac{1}{2} ({{{\widetilde{r}}}}^2+{{{\widetilde{s}}}}^2) +{{\widetilde{\alpha }}} {{\widetilde{\beta }}} &{}{\quad }{{\widetilde{\alpha }}}\lambda -{{\widetilde{\beta }}}_{x} \\ -{\lambda }^2+{\tilde{s}}\lambda +\frac{1}{2}r_x-\frac{1}{2} ({{{\widetilde{r}}}}^2+{{{\widetilde{s}}}}^2)-{{\widetilde{\alpha }}}\widetilde{\beta }&{}{\quad }-{{\widetilde{r}}}\lambda +\frac{1}{2}{{\widetilde{s}}}_{x}&{}{\quad }\widetilde{\beta }\lambda +{{\widetilde{\alpha }}}_x \\ {{\widetilde{\beta }}}\lambda +{{\widetilde{\alpha }}}_{x}&{}{\quad }-{{\widetilde{\alpha }}}\lambda +{{\widetilde{\beta }}}_x&{}{\quad }0\end{array}\right) . \end{aligned}$$
(50)

Proof

We assume the new matrix \({\widetilde{V}}\) also has the same form with V. If we obtain the similar relations between \(r,s,\alpha ,\beta \) of V and \({{\widetilde{r}}},{{\widetilde{s}}},\widehat{\alpha },{{\widetilde{\beta }}}\) of \({\widetilde{V}}\) in Eq. (43), we can prove the gauge transformation under T turns the Lax pairs U, V into new Lax pairs \({\widetilde{U}},{\widetilde{V}}\) with the same types.

By assuming \(T^{-1}=\frac{T^*}{\Delta T}\), and we can obtain the following equation

$$\begin{aligned} (T_t+TV)T^*=\left( \begin{array}{lll} E_{11}(\lambda ) &{}{\quad }E_{12}(\lambda )&{}{\quad }E_{13}(\lambda ) \\ E_{21}(\lambda )&{}{\quad }E_{22}(\lambda )&{}{\quad }E_{23}(\lambda ) \\ E_{31}(\lambda )&{}{\quad }E_{32}(\lambda )&{}{\quad }E_{33}(\lambda )\end{array}\right) .\nonumber \\ \end{aligned}$$
(51)

It is easy to verify that \(E_{sl} (1\le s,l\le 3)\) are \(3N+1\)-order or \(3N+2\)-order polynomials in \(\lambda \).

Through an accurate calculation, \(\lambda _j (j=1\le j\le 3,)\) are the roots of \(E_{sl} (s,l=1\le j\le 3)\). Then, Eq. (51) has the following structure

$$\begin{aligned} (T_t+TV)T^*=(detT)F(\lambda ), \end{aligned}$$
(52)

where

$$\begin{aligned} F(\lambda )=\left( \begin{array}{lll} F_{11}^{(1)}\lambda +F_{11}^{(0)} &{}{\quad }F_{12}^{(2)}\lambda ^2+F_{12}^{(1)}\lambda +F_{12}^{(0)}&{}{\quad }F_{13}^{(1)}\lambda +F_{13}^{(0)} \\ F_{21}^{(2)}\lambda ^2+F_{21}^{(1)}\lambda +F_{21}^{(0)}&{}{\quad }F_{22}^{(1)}\lambda +F_{22}^{(0)}&{}{\quad }F_{23}^{(1)}\lambda +F_{23}^{(0)} \\ F_{31}^{(1)}\lambda +F_{31}^{(0)}&{}{\quad }F_{32}^{(1)}\lambda +F_{32}^{(0)}&{}{\quad }0\end{array}\right) , \end{aligned}$$
(53)

and \(F_{mn}^{(k)} (m,n=1,2,k=0,1)\) satisfy the functions without \(\lambda \). So the following equation is obtained

$$\begin{aligned} (T_t+TV)=F(\lambda )T. \end{aligned}$$
(54)

Through comparing the coefficients of \(\lambda \) in Eq. (54), we get the objective equations as follows:

$$\begin{aligned}&F_{11}^{(1)}=r-A_{12}-A_{21}={\widetilde{r}}, \nonumber \\&F_{11}^{(0)}=-\frac{1}{2}s_x+A_{11}r+A_{12}s+A_{13}\beta -A_{11}{\widetilde{r}} \nonumber \\&\qquad \quad -A_{21}{\widetilde{s}}-A_{31}{\widetilde{\alpha }} =-\frac{1}{2}\widetilde{s_x}, \nonumber \\&F_{12}^{(2)}=1,F_{12}^{(1)}=s+A_{11}-A_{22}={\widetilde{s}}, \nonumber \\&F_{12}^{(0)}=\frac{1}{2}{r_{x}}+\frac{1}{2}(r^2+s^2)+\alpha \beta +A_{11}s \nonumber \\&\qquad \quad -A_{12}r-A_{13}\alpha -A_{12}{\widetilde{r}} -A_{22}{\widetilde{s}}-A_{32}{\widetilde{\alpha }} \nonumber \\ \end{aligned}$$
$$\begin{aligned}&\qquad =\frac{1}{2}\widetilde{r_{x}}+\frac{1}{2}({\widetilde{r}}^2+{{{\widetilde{s}}}}^2)+{{\widetilde{\alpha }}} {{\widetilde{\beta }}}, \nonumber \\&F_{13}^{(1)}=\alpha -A_{23}={\widetilde{\alpha }}, \nonumber \\&F_{13}^{(0)}={-\beta _{x}}+A_{11}\alpha +A_{12}\beta -A_{13}{\widetilde{r}} \nonumber \\&\qquad \quad -A_{23}{\widetilde{s}}-A_{33}{\widetilde{\alpha }}=-\widetilde{\beta _{x}}, \nonumber \\&F_{21}^{(2)}=-1,F_{21}^{(1)}=s-A_{22}+A_{11}={\widetilde{s}}, \nonumber \\&F_{21}^{(0)}=A_{21}r+\frac{1}{2}r_{x}-\frac{1}{2}(r^2+s^2)-\alpha \beta \nonumber \\&\quad +A_{22}s+A_{23}\beta -A_{11}{\widetilde{s}} +A_{21}{\widetilde{r}}-A_{31}{\widetilde{\beta }} \nonumber \\&=\frac{1}{2}\widetilde{r_{x}}-\frac{1}{2}({\widetilde{r}}^2+{{{\widetilde{s}}}}^2)-{{\widetilde{\alpha }}}{{\widetilde{\beta }}}, \nonumber \\&F_{22}^{(1)}=A_{21}-r+A_{12}=-{\widetilde{r}}, \nonumber \\&F_{22}^{(0)}=A_{21}s+\frac{1}{2}s_x-A_{22}r-A_{23}\alpha -A_{12}{\widetilde{s}} \nonumber \\&\qquad \quad +A_{22}{\widetilde{r}}-A_{32}{\widetilde{\beta }} =\frac{1}{2}\widetilde{s_x}, \nonumber \\ \end{aligned}$$
$$\begin{aligned}&F_{23}^{(1)}=\beta +A_{13}={\widetilde{\beta }}, \nonumber \\&F_{23}^{(0)}=A_{21}\alpha -\alpha _x+A_{22}\beta -A_{13}{\widetilde{s}} \nonumber \\&\qquad \quad +A_{23}{\widetilde{r}}-{\widetilde{\beta }}A_{33} =\widetilde{\alpha _{x}}, \nonumber \\&F_{31}^{(1)}=\beta -A_{32}={\widetilde{\beta }}, \nonumber \\&\quad F_{31}^{(0)}=A_{31}r+A_{32}s-\alpha _x+A_{33}\beta \nonumber \\&\qquad \quad -A_{11}{\widetilde{\beta }}-A_{21}{\widetilde{\beta }} =\widetilde{\alpha _{x}}, \nonumber \\&F_{32}^{(1)}=-\alpha +A_{31}=-{\widetilde{\alpha }}, \nonumber \\&F_{32}^{(0)}=A_{31}s-A_{32}r+\beta _x-A_{33}\alpha \nonumber \\&\qquad \quad -A_{12}{\widetilde{\beta }}+A_{22}{\widetilde{\alpha }} =\widetilde{\beta _x}, \nonumber \\&A_{11}= -A_{22},\quad A_{12}= -A_{21},\quad A_{31}= A_{23}, \nonumber \\&A_{13}= -A_{32}, \nonumber \\&2A_{12}^2-2rA_{12}+\alpha A_{13}-A_{23} A_{13} \nonumber \\&\quad -A_{23}\beta +2 A_{11}^2+2s A_{11}=0. \end{aligned}$$
(55)

In the following section, we assume the new matrix \({\widetilde{V}}\) has the same type with V, which means they have the same structures about \(r,s,\alpha ,\beta \) of V transformed into \({{\widetilde{r}}},{{\widetilde{s}}},{{\widehat{\alpha }}},{{\widetilde{\beta }}}\) of \({\widetilde{V}}\). From Eqs. (43) and (50), we know that \({{\widetilde{V}}}=F{(\lambda )}\). The proof is completed. \(\square \)

3.2 Exact solution for super-Dirac equation

Propositions 3 and 4 show that the transformations (35) and (43) are Darboux transformation connecting super-Dirac hierarchy. In what follows, we can apply the above Darboux transformation (35) and (43) to construct some exact solutions of super-Dirac equation. Firstly, we give a set of seed solutions \(r=s=\alpha =\beta =0\) and substitute the solutions into Eqs. (33) and (34), and we will get three basic solutions for these equations:

$$\begin{aligned} \psi _{(\lambda )}= & {} \left( \begin{array}{l} 0 \\ \hbox {e}^{\lambda x+\lambda ^2 t} \\ 0\end{array}\right) ,\quad \phi _{(\lambda )}=\left( \begin{array}{l} \hbox {e}^{-\lambda x-\lambda ^2 t} \\ 0 \\ 0\end{array}\right) , \nonumber \\ X_{(\lambda )}= & {} \left( \begin{array}{l} 0 \\ 0 \\ 1\end{array}\right) . \end{aligned}$$
(56)

Taking (56) into (39), we obtain

$$\begin{aligned}&M_j^{(1)}=\frac{\nu _j^{(1)}\hbox {e}^{-\lambda x-\lambda ^2 t}}{\hbox {e}^{\lambda x+\lambda ^2 t}}=\hbox {e}^{2\left( \lambda _j x+\lambda _j^2 t+F_j^{(1)}\right) }, \nonumber \\&M_j^{(2)}=\frac{\nu _j^{(2)}}{\hbox {e}^{\lambda x+\lambda ^2 t}}=\hbox {e}^{\left( \lambda _j x+\lambda _j^2 t+F_j^{(2)}\right) }, \end{aligned}$$
(57)

with \(\nu _j^{(i)}=\hbox {e}^{(3iF_j^{(i)})} (1\le i\le 2, 1\le j\le 3N)\).

In order to calculate, we consider \(N=1\) in Eqs. (40) and (41), and obtain the T as follows

$$\begin{aligned} T=\left( \begin{array}{lll} \lambda +A_{11} &{}{\quad } A_{12}&{}{\quad }A_{13} \\ A_{21}&{}{\quad }\lambda +A_{22}&{}{\quad }A_{23} \\ A_{31}&{}{\quad }A_{32}&{}{\quad }\lambda +A_{33}\end{array}\right) , \end{aligned}$$
(58)

and

$$\begin{aligned}&\lambda _j+A_{11}+M_{j}^{(1)}A_{12}+M_{j}^{(2)}A_{13}=0, \nonumber \\&A_{21}+M_{j}^{(1)}(\lambda _j+A_{22})+M_{j}^{(2)}A_{23}=0,\nonumber \\&A_{31}+M_{j}^{(1)}(\lambda _j+A_{32})+M_{j}^{(2)}(\lambda _j+A_{33})=0. \end{aligned}$$
(59)
Fig. 3
figure 3

(Color online) Profiles of a the intensity distribution \(|{\tilde{r}}|\) of Eq. (62); b the intensity distribution \(|{\tilde{s}}|\) of Eq. (62); c the intensity distribution \(|{\tilde{\alpha }}|\) of Eq. (62); d the intensity distribution \(|{\tilde{\beta }}|\) of Eq. (62) with \(\lambda _1=0.2\hbox {i}\), \(\lambda _2=0.3\hbox {i}\), \(\lambda _3=0.8\hbox {i}\), \(F_1^{(1)}=0.1\hbox {i}\), \(F_2^{(2)}=0.2\hbox {i}\), \(F_3^{(3)}=0.4\hbox {i}\), \(F_1^{(2)}=0.3\hbox {i}\), \(F_1^{(3)}=0.2\hbox {i}\), \(F_2^{(1)}=0.3\hbox {i}\), \(F_2^{(3)}=0\), \(F_3^{(1)}=0.7\hbox {i}\), \(F_3^{(2)}=0\)

Full size image
Fig. 4
figure 4

(Color online) Profiles of a the intensity distribution \(|{\tilde{r}}|\) of Eq. (62); b the intensity distribution \(|{\tilde{s}}|\) of Eq. (62) with \(\lambda _1=0.2+0.1\hbox {i}\), \(\lambda _2=0.3+0.2\hbox {i}\), \(\lambda _3=0.5+0.4\hbox {i}\), \(F_1^{(1)}=0.1+0.1\hbox {i}\), \(F_2^{(2)}=0.2+0.1\hbox {i}\), \(F_3^{(3)}=0.4+0.3\hbox {i}\), \(F_1^{(2)}=0.3+0.3\hbox {i}\), \(F_1^{(3)}=0\), \(F_2^{(1)}=0.3+0.1\hbox {i}\), \(F_2^{(3)}=0\), \(F_3^{(1)}=0.7+0.4\hbox {i}\), \(F_3^{(2)}=0\), c the intensity distribution \(|{\tilde{\alpha }}|\) of Eq. (62); d the intensity distribution \(|{\tilde{\beta }}|\) of Eq. (62) with \(\lambda _1=0.2\), \(\lambda _2=0.3\), \(\lambda _3=0.7\), \(F_1^{(1)}=0.1\), \(F_2^{(2)}=0.2\), \(F_3^{(3)}=0.4\), \(F_1^{(2)}=0.3\), \(F_1^{(3)}=0.4\), \(F_2^{(1)}=0.3\), \(F_2^{(3)}=0.6\), \(F_3^{(1)}=0.7\), \(F_3^{(2)}=0.9\)

Full size image

According to Eq. (59), we get

$$\begin{aligned} \Delta= & {} \left| \begin{array}{lll} 1 &{}{\quad }\hbox {e}^{2\left( \lambda _1 x+\lambda _1^2 t+F_1^{(1)}\right) }&{}{\quad }\hbox {e}^{\left( \lambda _1 x+\lambda _1^2 t+F_1^{(2)}\right) }\\ 1&{}{\quad }\hbox {e}^{2\left( \lambda _2 x+\lambda _2^2 t+F_2^{(1)}\right) }&{}{\quad }\hbox {e}^{\left( \lambda _2 x+\lambda _2^2 t+F_2^{(2)}\right) }\\ 1 &{}{\quad }\hbox {e}^{2\left( \lambda _3 x+\lambda _3^2 t+F_3^{(1)}\right) }&{}{\quad }\hbox {e}^{\left( \lambda _3 x+\lambda _3^2 t+F_3^{(2)}\right) } \end{array}\right| , \nonumber \\ \Delta _{11}= & {} \left| \begin{array}{lll} -\lambda _1 &{}{\quad }\hbox {e}^{2\left( \lambda _1 x+\lambda _1^2 t+F_1^{(1)}\right) }&{}{\quad }\hbox {e}^{\left( \lambda _1 x+\lambda _1^2 t+F_1^{(2)}\right) }\\ -\lambda _2&{}{\quad }\hbox {e}^{2\left( \lambda _2 x+\lambda _2^2 t+F_2^{(1)}\right) }&{}{\quad }\hbox {e}^{\left( \lambda _2 x+\lambda _2^2 t+F_2^{(2)}\right) }\\ -\lambda _3 &{}{\quad }\hbox {e}^{2\left( \lambda _3 x+\lambda _3^2 t+F_3^{(1)}\right) }&{}{\quad }\hbox {e}^{\left( \lambda _3 x+\lambda _3^2 t+F_3^{(2)}\right) } \end{array}\right| ,\nonumber \\ \Delta _{22}= & {} \left| \begin{array}{lll}1 &{}{\quad }-\lambda _1 \hbox {e}^{2\left( \lambda _1 x+\lambda _1^2 t+F_1^{(1)}\right) }&{}{\quad }\hbox {e}^{\left( \lambda _1 x+\lambda _1^2 t+F_1^{(2)}\right) }\\ 1&{}{\quad }-\lambda _2 \hbox {e}^{2\left( \lambda _2 x+\lambda _2^2 t+F_2^{(1)}\right) }&{}{\quad }\hbox {e}^{\left( \lambda _2 x+\lambda _2^2 t+F_2^{(2)}\right) }\\ 1 &{}{\quad }-\lambda _3 \hbox {e}^{2\left( \lambda _3 x+\lambda _3^2 t+F_3^{(1)}\right) }&{}{\quad }\hbox {e}^{\left( \lambda _3 x+\lambda _3^2 t+F_3^{(2)}\right) } \end{array}\right| . \nonumber \\ \Delta _{13}= & {} \left| \begin{array}{lll}1 &{}{\quad }\hbox {e}^{2\left( \lambda _1 x+\lambda _1^2 t+F_1^{(1)}\right) }&{}{\quad }-\lambda _1\\ 1&{}{\quad }\hbox {e}^{2\left( \lambda _2 x+\lambda _2^2 t+F_2^{(1)}\right) }&{}{\quad }-\lambda _2\\ 1 &{}{\quad }\hbox {e}^{2\left( \lambda _3 x+\lambda _3^2 t+F_3^{(1)}\right) }&{}{\quad }-\lambda _3 \end{array}\right| , \nonumber \\ \Delta _{12}= & {} \left| \begin{array}{lll}1 &{}{\quad }-\lambda _1&{}{\quad }\hbox {e}^{\left( \lambda _1 x+\lambda _1^2 t+F_1^{(2)}\right) }\\ 1&{}{\quad }-\lambda _2&{}{\quad }\hbox {e}^{\left( \lambda _2 x+\lambda _2^2 t+F_2^{(2)}\right) }\\ 1 &{}{\quad }-\lambda _3&{}{\quad }\hbox {e}^{\left( \lambda _3 x+\lambda _3^2 t+F_3^{(2)}\right) } \end{array}\right| , \nonumber \\ \Delta _{21}= & {} \left| \begin{array}{lll}-\lambda _1\hbox {e}^{2\left( \lambda _1 x+\lambda _1^2 t+F_1^{(1)}\right) } &{}{\quad }\hbox {e}^{2\left( \lambda _1 x+\lambda _1^2 t+F_1^{(1)}\right) }&{}{\quad }\hbox {e}^{\left( \lambda _1 x+\lambda _1^2 t+F_1^{(2)}\right) }\\ -\lambda _2\hbox {e}^{2\left( \lambda _2 x+\lambda _2^2 t+F_2^{(1)}\right) }&{}{\quad }\hbox {e}^{2\left( \lambda _2 x+\lambda _2^2 t+F_2^{(1)}\right) }&{}{\quad }\hbox {e}^{\left( \lambda _2 x+\lambda _2^2 t+F_2^{(2)}\right) }\\ -\lambda _3\hbox {e}^{2\left( \lambda _3 x+\lambda _3^2 t+F_3^{(1)}\right) } &{}{\quad }\hbox {e}^{2\left( \lambda _3 x+\lambda _3^2 t+F_3^{(1)}\right) }&{}{\quad }\hbox {e}^{\left( \lambda _3 x+\lambda _3^2 t+F_3^{(2)}\right) } \end{array}\right| , \nonumber \\ \Delta _{31}= & {} \left| \begin{array}{lll}-\lambda _1\hbox {e}^{\left( \lambda _1 x+\lambda _1^2 t+F_1^{(2)}\right) } &{}{\quad }\hbox {e}^{2\left( \lambda _1 x+\lambda _1^2 t+F_1^{(1)}\right) }&{}{\quad }\hbox {e}^{\left( \lambda _1 x+\lambda _1^2 t+F_1^{(2)}\right) }\\ -\lambda _2\hbox {e}^{\left( \lambda _2 x+\lambda _2^2 t+F_2^{(2)}\right) }&{}{\quad }\hbox {e}^{2\left( \lambda _2 x+\lambda _2^2 t+F_2^{(1)}\right) }&{}{\quad }\hbox {e}^{\left( \lambda _2 x+\lambda _2^2 t+F_2^{(2)}\right) }\\ -\lambda _3\hbox {e}^{\left( \lambda _3 x+\lambda _3^2 t+F_3^{(2)}\right) } &{}{\quad }\hbox {e}^{2\left( \lambda _3 x+\lambda _3^2 t+F_3^{(1)}\right) }&{}{\quad }\hbox {e}^{\left( \lambda _3 x+\lambda _3^2 t+F_3^{(2)}\right) } \end{array}\right| .\nonumber \\ \end{aligned}$$
(60)

Depending on Eqs. (38) and (39), we can obtain that

$$\begin{aligned} A_{11}= & {} \frac{\Delta _{11}}{\Delta },A_{22}=\frac{\Delta _{22}}{\Delta }, A_{12}=\frac{\Delta _{12}}{\Delta }, \nonumber \\ A_{13}= & {} \frac{\Delta _{13}}{\Delta }, A_{21}=\frac{\Delta _{21}}{\Delta },A_{31}=\frac{\Delta _{31}}{\Delta }; \end{aligned}$$
(61)

the analytic soliton solutions of super-Dirac hierarchy are obtained by the DT method as follows

$$\begin{aligned}&{\widetilde{r}}=-\frac{\Delta _{12}}{\Delta }-\frac{\Delta _{21}}{\Delta }, \nonumber \\&{\widetilde{s}}= \frac{\Delta _{11}}{\Delta }-\frac{\Delta _{22}}{\Delta }, \nonumber \\&{\widetilde{\alpha }}=-\frac{\Delta _{23}}{\Delta }, \nonumber \\&{\widetilde{\beta }}=\frac{\Delta _{13}}{\Delta }. \end{aligned}$$
(62)

To illustrate the wave propagations of the obtained soliton solutions (62), we can choose these free parameters \(\lambda _1, \lambda _2,\lambda _3\), \(F_{m}^{(k)} (m=1,2,3,k=1,2,3)\) and the evolutions of the intensity distribution for the soliton solutions given by Eq. (62) are illustrated in Figs. 3 and 4.

The DT of Eq. (32) gives the required solution, and the explicit soliton solutions under different cases are portrayed in Figs. 3 and 4. Some special soliton solutions are localized both in space and time in Fig. 3. They exhibit the similar features of the so-called rogue waves, but they are based on zero background rather than a plane wave background. Figure 4 exhibits the similar features of the so-called breather waves; this figure indicates a sharp compression and strong amplification of the nonautonomous soliton under the action of inhomogeneity.

4 Conclusions

In this paper, we have constructed DT for super-AKNS hierarchy and super-Dirac hierarchy which have four commuting variables, such that some soliton solutions are found. The wave profiles of those solutions have been discussed in detailed for distinct parameters, which possess the bright and dark soliton structures. Moreover, we also study the dynamical behaviors of these solutions. These results might be helpful for understanding physical phenomena described by Eqs. (1) and (32) and finding possible applications of solitons. The method is also appropriate for more nonlinear soliton equations in physics and mathematics.