The Boubaker polynomials and their application to solve fractional optimal control problems

Abstract

In this paper, we focus on Boubaker polynomials in fractional calculus area and obtain the operational matrix of Caputo fractional derivative and the operational matrix of the Riemann–Liouville fractional integration for the first time. Also, a general formulation for the operational matrix of multiplication of these polynomials has been achieved to solve the nonlinear problems. Then, these matrices are applied to solve fractional optimal control problems directly. In fact, the functions of the problem are approximated by Boubaker polynomials with unknown coefficients in the constraint equations, performance index and conditions. Thus, a fractional optimal control problem converts to an optimization problem, which can then be solved easily. Convergence of the algorithm is proved. Numerical results are given for several test examples to demonstrate the applicability and efficiency of the method.

1 Introduction

Polynomial expansion methods are applied in many mathematical and engineering problems to obtain good results. Among the most frequently used polynomials, the Boubaker polynomials are one of the non-orthogonal polynomial sequences established by Boubaker in 2007 [1]. In [2, 3], the authors presented temperature profiling theoretical investigations in cylindrical coordinates and solved the related problems using Boubaker polynomials. Kumar solved the Love’s equation via the Boubaker polynomials expansion scheme [4], and the Boltzmann diffusion equation was solved using these polynomials in [5]. In [6], the authors used these polynomials to solve the optimal control problems that have a long history, and this paper motivated us to use these polynomials for solving the fractional order optimal control problems (FOCPs) that involve at least one fractional derivative, and they are a very new field in mathematics. Optimality conditions for FOCPs with Riemann–Liouville derivative were achieved by Agrawal in [7]. Since analytical solution of Hamiltonian system is very complicated, some researchers have presented several numerical methods to solve this system; for example in [8] the author approximated fractional dynamic systems using the Grunwald–Letnikov definition and then applied numerical method for solving the obtained algebraic equations, and in [9] Agrawal introduced Hamiltonian equations for a class of FOCPs with Caputo derivative and then presented an approach based on the equivalence of the Euler–Lagrange and the Volterra integral equations. In [10], a central difference numerical scheme was used to solve these equations. In [11], the authors used rational approximation to solve fractional order optimal control problems. In [12], the Legendre multiwavelet collocation method was introduced, and in [13] another numerical method was applied to solve a class of FOCPs by the authors. [14] presented a quadratic numerical scheme, and in [15] Legendre spectral collocation method was used to solve some type of fractional optimal control problems. A discrete method was used to solve fractional optimal control problem in [16]. Recently, the fractional optimal control problems have been solved directly without using Hamiltonian equation by some authors [17, 18]; in fact, in these papers the authors have converted fractional optimal control problems to a system of algebraic equations, which should be solved by some methods similar to the methods presented in [19,20,21,22] for solving nonlinear system. The organization of this paper is as follows. Section 2 contains three subsections that present some preliminaries needed later. In Sects. 3 and 4, the Boubaker operational matrices of the Caputo fractional derivative and Riemann–Liouville fractional integration are presented. In Sect. 5, we introduce the operational matrix of multiplication. Section 6 contains problem statement by using the obtained operational matrices. In Sect. 7, the convergence analysis is discussed, and Sect. 8 presents several numerical examples to show validity of our method. Finally, conclusion is presented in Sect. 9.

2 Preliminaries and notations

In this section, we will recall some basic definitions and auxiliary results that will be needed later in our discussion. Here we give the standard definitions of left and right Riemann–Liouville fractional integrals and Caputo fractional derivatives.

2.1 The fractional integral and derivative

Definition 1

Let $x:[a,b] \rightarrow {\mathbb {R}}$ be a function, $\alpha > 0$ a real number and $n=\left\lceil { \alpha }\right\rceil$, where $\left\lceil { \alpha }\right\rceil$ denotes the smallest integer greater than or equal to $\alpha$, the left and right Riemann–Liouville fractional integrals are defined by [23]:

$$\begin{aligned} I_t^\alpha x(t)= & {} \frac{1}{\varGamma (\alpha )} \int _a^t (t-\tau )^{\alpha -1}x(\tau )\mathrm{d}\tau ,\\ I_b^\alpha x(t)= & {} \frac{1}{\varGamma (\alpha )}\int _t^b (\tau -t)^{\alpha -1}x(\tau )\mathrm{d}\tau . \end{aligned}$$

For the Riemann–Liouville fractional integrals, we have:

$$\begin{aligned} I_t^\alpha t^n=\frac{\varGamma (n+1)}{\varGamma (n+1+\alpha )}t^{n+\alpha },\quad n>-1. \end{aligned}$$

(1)

Moreover, the left and right Caputo fractional derivatives are defined by means of:

$$\begin{aligned} D_t^\alpha x(t)= & {} \frac{1}{\varGamma (n-\alpha )}\int _a^t (t-\tau )^{n-\alpha -1}x^{(n)}(\tau )\mathrm{d}\tau ,\nonumber \\ D_b^\alpha x(t)= & {} \frac{(-1)^n}{\varGamma (n-\alpha )} \int _t^b (\tau -t)^{n-\alpha -1}x^{(n)}(\tau )\mathrm{d}\tau . \end{aligned}$$

(2)

The left Caputo fractional derivative has the property,

$$\begin{aligned} D_t^\alpha t^n=\left\{ \begin{array}{ll} 0, &{}\quad n\in N_0\quad \textit{and} \quad n<\lceil \alpha \rceil ,\\ \frac{\varGamma (n+1)}{\varGamma (n+1-\alpha )}t^{n-\alpha },&{}\quad n\in N_0\quad \textit{and}\quad n\ge \lceil \alpha \rceil ,\\ \end{array}\right. \end{aligned}$$

where $N_0=\lbrace 0,1,2,\ldots \rbrace$, and $D_t^\alpha C = 0$, holds for constant C.

2.2 Boubaker polynomials

In this section, Boubaker polynomials, which are used in the next sections, are reviewed briefly. The Boubaker polynomials were established for the first time by Boubaker et al. to solve heat equation inside a physical model. The first monomial definition of the Boubaker polynomials on interval $t \in [0,1]$ was introduced by [1]:

$$\begin{aligned} B_i(t)=\sum \limits _{r= 0}^{\lfloor i/2\rfloor }(-1)^r\left( \begin{array}{c}i-r\\ r \end{array}\right) \frac{i-4r}{i-r}t^{i-2r}, \quad i\ge 2 \end{aligned}$$

where $\lfloor \cdot \rfloor$ is the floor function. The Boubaker polynomials have also a recursive relation:

$$\begin{aligned} B_m(t)=tB_{m-1}(t)-B_{m-2}(t) \quad m>2, \end{aligned}$$

and the first few Boubaker polynomials are

$$\begin{aligned} B_0 (t)= & {} 1,~~~~B_1 (t) = t,~~~~\\ B_2 (t)= & {} t^2 +2,~~~~B_3 (t) = t^3 +t,\,\,\ldots . \end{aligned}$$

2.3 Function approximation

It is clear that

$$\begin{aligned} Y=span\{B_0(t),B_1(t),\ldots ,B_m(t)\} , \end{aligned}$$

is a finite dimensional and closed subspace of the Hilbert space $H=L^2[0,1]$, and therefore, Y is a complete subspace and there is a unique best approximation out of Y such as ${\tilde{f}}\in Y$ for each $f \in H$, that is

$$\begin{aligned} \forall y\in Y,~~ \parallel f-{\tilde{f}} \parallel \le \parallel f-y \parallel . \end{aligned}$$

Since ${\tilde{f}} \in Y,$ there exist unique coefficients $c_0,c_1,\ldots ,c_m$, such that [24]

$$\begin{aligned} f(t)\simeq {\tilde{f}}(t) = \sum \limits _{j=0}^{m} c_jB_j(t)=C^\mathrm{T} \varPsi (t), \end{aligned}$$

where T shows transposition, C and $\varPsi (t)$ are the following vectors:

$$\begin{aligned}&C = [c_0,c_1,\ldots ,c_m]^\mathrm{T},\nonumber \\&\varPsi (t)= [B_0(t),B_1(t),\ldots ,B_m(t)]^\mathrm{T}. \end{aligned}$$

(3)

We let

$$\begin{aligned} f_{j} = \langle f, B_j \rangle = \int _{0}^{1}f(t) B_j(t) \mathrm{d}t, \end{aligned}$$

where $\langle , \rangle$ denotes inner product, and then, we have

$$\begin{aligned}&f_{j} \simeq \sum \nolimits _{i = 0}^{m}c_{i}\int _{0}^{1}B_i(t) B_j(t) \mathrm{d}t = \sum \nolimits _{i = 0}^{m} c_{i}d_{ij},\\&\quad j = 0, 1, \ldots , m, \end{aligned}$$

with

$$\begin{aligned} d_{ij}= \int _{0}^{1}B_i(t) B_j(t) \mathrm{d}t ,\quad i , j = 0, 1, \ldots , m. \end{aligned}$$

Now we suppose that

$$\begin{aligned} F =\langle f, \varPsi \rangle =\left[ \begin{array}{c} f_{0} \\ f_{1} \\ \vdots \\ f_{m} \end{array}\right] , \quad \hbox {and} \quad D = [d_{ij}], \end{aligned}$$

where

$$\begin{aligned} f _{j} = C^\mathrm{T} [ d_{0j}, d_{1j}, \ldots , d_{m,j}]^\mathrm{T}, \end{aligned}$$

so we can write

$$\begin{aligned} F^{ T} = C^\mathrm{T} D, \end{aligned}$$

and C can be calculated as

$$\begin{aligned} C=D^{-1}\langle f, \varPsi \rangle , \end{aligned}$$

(4)

where D is the following $(m+1) \times (m+1)$ matrix

$$\begin{aligned} D = \langle \varPsi (t) , \varPsi (t) \rangle = \int _{0}^{1} \varPsi (t) (\varPsi (t))^\mathrm{T} \mathrm{d}t. \end{aligned}$$

3 Boubaker operational matrix of the Caputo fractional derivative

The Caputo fractional derivative of vector $\varPsi (t)$ mentioned in Eq. (3) can be expressed by:

$$\begin{aligned} D^{\alpha }\varPsi (t)=D_\alpha \varPsi (t), \end{aligned}$$

(5)

where $D_\alpha$ is the $(m+1)\times (m+1)$ Caputo fractional operational matrix of derivative that will be constructed in this section. The Boubaker polynomials basis can be considered as:

$$\begin{aligned} \varPsi (t)=\varLambda T_m(t), \end{aligned}$$

(6)

where $T_m(t) = [1,t,\ldots ,t^m]^\mathrm{T},$ and $\varLambda =(\varUpsilon _{i,j})_{i,j=0}^m,$ is an $(m+1)\times (m+1)$ matrix.

Considering the following terms

$$\begin{aligned} B_i(t)=\sum \limits _{r= 0}^{\lfloor i/2\rfloor }(-1)^r\left( \begin{array}{c}i-r\\ r \end{array}\right) \frac{i-4r}{i-r}t^{i-2r}{=}\sum \limits _{j= 0}^{m}\varUpsilon _{i,j} t^j, \end{aligned}$$

or

$$\begin{aligned} B_i(t)= & {} \sum \limits _{j= i-2\lfloor i/2\rfloor }^{i}(-1)^{\frac{i-j}{2}}\left( \begin{array}{c}\frac{i+j}{2}\\ \frac{i-j}{2} \end{array}\right) \frac{2j-i}{\frac{i+j}{2}}t^j\\= & {} \sum \limits _{j= 0}^{m}\varUpsilon _{i,j} t^j, \end{aligned}$$

we can obtain the entries of the matrix $\varLambda$ for $i\ge 2, j= i-2\lfloor i/2\rfloor ,\ldots ,i,$ as:

$$\begin{aligned} \varUpsilon _{i,j}=\left\{ \begin{array}{ll} 0, &{}\quad \text { if}\,\, (i-j) \text { is odd},\\ (-1)^{\frac{i-j}{2}}\left( \begin{array}{c}\frac{i+j}{2}\\ \frac{i-j}{2} \end{array}\right) \frac{2j-i}{\frac{i+j}{2}}, &{}\quad \textit{ if} \,\,(i-j) \text { is even}.\\ \end{array}\right. \end{aligned}$$

And based on the definition $B_0(t)$ and $B_1(t)$, this formula is valid for $i=1,$, and for $i=0,$ we have

$$\begin{aligned} \varUpsilon _{0,0}=1 \quad \quad \varUpsilon _{0,j}=0, \quad j=1,\ldots ,m. \end{aligned}$$

By using Eqs. (5) and (6), we set

$$\begin{aligned} D^{\alpha }\varPsi (t)=\varLambda D^{\alpha } T_m(t). \end{aligned}$$

Giving consideration to the following property of the Caputo fractional derivative,

$$\begin{aligned} D_t^\alpha t^j=\left\{ \begin{array}{ll} 0, &{}\quad j=0,1,\ldots ,\lceil \alpha \rceil -1,\\ \frac{\varGamma (j+1)}{\varGamma (j+1-\alpha )}t^{j-\alpha },&{}\quad j=\lceil \alpha \rceil ,\ldots ,m,\\ \end{array}\right. \end{aligned}$$

define:

$$\begin{aligned} D^{\alpha } T_m(t)={\tilde{\varSigma }} {\tilde{T}}, \end{aligned}$$

(7)

where ${\tilde{\varSigma }} =({\tilde{\varSigma }}_{i+1,j+1})$ is a diagonal $(m+1)\times (m+1)$ matrix with entries

$$\begin{aligned} {\tilde{\varSigma }}_{i+1,j+1} =\left\{ \begin{array}{ll} \frac{\varGamma (j+1)}{\varGamma (j+1-\alpha )}, &{}\quad i=j=\lceil \alpha \rceil ,\ldots ,m,\\ 0,&{}\quad \textit{otherwise,}\\ \end{array}\right. \end{aligned}$$

and ${\tilde{T}}=({\tilde{T}} _{i+1})_{(m+1)\times 1},$ with

$$\begin{aligned} {\tilde{T}} _{i+1} =\left\{ \begin{array}{ll} 0, &{}\quad i=0,1,\ldots ,\lceil \alpha \rceil -1,\\ t^{i-\alpha }, &{}\quad i=\lceil \alpha \rceil ,\ldots , m.\\ \end{array}\right. \end{aligned}$$

Now, ${\tilde{T}}$ is expanded in terms of Boubaker polynomials as

$$\begin{aligned} {\tilde{T}}\simeq P^\mathrm{T}\varPsi (t), \end{aligned}$$

(8)

where

$$\begin{aligned} P= & {} [P_0,P_1,\ldots ,P_m], \quad \quad P_i=D^{-1}\hat{P_i},\\ {\hat{P}}_i= & {} [{\hat{P}}_{i,0},{\hat{P}}_{i,1},\ldots ,{\hat{P}}_{i,m}]^\mathrm{T}. \end{aligned}$$

The entries of the vector ${\hat{P}}_i$ can be calculated as

$$\begin{aligned} {\hat{P}}_{i,j}=\int _{0}^{1} t^{i-\alpha }B_j(t)\mathrm{d}t, \end{aligned}$$

then we have

$$\begin{aligned} D_t^\alpha \varPsi (t)\simeq D_\alpha \varPsi (t), \quad \quad D_\alpha =\varLambda {\tilde{\varSigma }} P^\mathrm{T}. \end{aligned}$$

(9)

In Eq. (9), $D_\alpha$ is the operational matrix of Caputo derivative.

4 Boubaker operational matrix of the Riemann–Liouville fractional integration

In this section, we derive the $(m+1)\times (m+1)$ Riemann–Liouville fractional operational matrix of integration $F^{(\alpha )}$ expressed by:

$$\begin{aligned} I^{\alpha }\varPsi (t)=F^{(\alpha )}\varPsi (t). \end{aligned}$$

(10)

By using Eq. (1) and linearity of Riemann–Liouville fractional integral, for $i\ge 2,$ we have

$$\begin{aligned}&I^{\alpha } B_i(t)=\sum \limits _{r= 0}^{\lfloor i/2\rfloor }(-1)^r\left( \begin{array}{c}i-r\\ r \end{array}\right) \frac{i-4r}{i-r} I^{\alpha }t^{i-2r}\nonumber \\&\quad =\sum \limits _{r= 0}^{\lfloor i/2\rfloor } b_{i,r}t^{i-2r+\alpha }, \end{aligned}$$

(11)

where

$$\begin{aligned} b_{i,r}=(-1)^r\frac{(i-r-1)!(i-4r)}{r!\varGamma (i-2r+\alpha +1)}. \end{aligned}$$

Now we can expand $t^{i-2r+\alpha }$ in terms of Boubaker polynomials as

$$\begin{aligned} t^{i-2r+\alpha }=\sum \limits _{j= 0}^{m} c_{r,j} B_j(t) , \end{aligned}$$

with

$$\begin{aligned} c_{r,j}=\frac{\langle t^{i-2r+\alpha },B_j(t)\rangle }{\langle B_j(t),B_j(t)\rangle }, \end{aligned}$$

and substitution in Eq. (11) we get

$$\begin{aligned} I^{\alpha } B_i(t)\simeq & {} \sum \limits _{r= 0}^{\lfloor i/2\rfloor } b_{i,r}\sum \limits _{j= 0}^{m}c_{r,j} B_j(t)\nonumber \\= & {} \sum \limits _{j= 0}^{m} \left( \sum \limits _{r= 0}^{\lfloor i/2\rfloor }b_{i,r}c_{r,j}\right) B_j(t). \end{aligned}$$

(12)

Now let

$$\begin{aligned} \theta _{i,j,r}=b_{i,r}c_{r,j}, \end{aligned}$$

and rewrite Eq. (12) for $i=2,\ldots ,m,$ as

$$\begin{aligned}&I^{\alpha } B_i(t){\simeq }\left[ \sum \limits _{r= 0}^{\lfloor i/2\rfloor }\theta _{i,0,r},\sum \limits _{r= 0}^{\lfloor i/2\rfloor }\theta _{i,1,r},\ldots ,\sum \limits _{r= 0}^{\lfloor i/2\rfloor }\theta _{i,m,r}\right] \\&\quad \varPsi (t). \end{aligned}$$

For $i=0,1$, we have

$$\begin{aligned} I^{\alpha } B_0(t)= & {} \frac{1}{\varGamma (\alpha +1)} t^{\alpha },\\ I^{\alpha } B_1(t)= & {} \frac{1}{\varGamma (\alpha +2)} t^{\alpha +1}, \end{aligned}$$

so like the previous process $t^{\alpha }$ and $t^{\alpha +1}$ are expanded with respect to Boubaker polynomials as

$$\begin{aligned}&t^{\alpha } \simeq \sum \limits _{j= 0}^{m} \vartheta _{0,j} B_j(t),\\&t^{\alpha +1} \simeq \sum \limits _{j= 0}^{m}\vartheta _{1,j} B_j(t). \end{aligned}$$

Hence, we have

$$\begin{aligned} F^{(\alpha )}=\left[ {\begin{array}{cccc} \frac{1}{\varGamma (\alpha +1)} \vartheta _{0,0} &{}\frac{1}{\varGamma (\alpha +1)} \vartheta _{0,1} &{} \ldots &{}\frac{1}{\varGamma (\alpha +1)}\vartheta _{0,m} \\ \frac{1}{\varGamma (\alpha +2)} \vartheta _{1,0} &{}\frac{1}{\varGamma (\alpha +2)}\vartheta _{1,1} &{} \ldots &{} \frac{1}{\varGamma (\alpha +2)}\vartheta _{1,m} \\ \sum \limits _{r= 0}^{1}\theta _{2,0,r} &{} \sum \limits _{r= 0}^{1}\theta _{2,1,r}&{} \ldots &{}\sum \limits _{r= 0}^{1}\theta _{2,m,r}\\ \vdots &{} \vdots &{} \ddots &{}\vdots \\ \sum \limits _{r= 0}^{\lfloor m/2\rfloor }\theta _{m,0,r} &{}\sum \limits _{r= 0}^{\lfloor m/2\rfloor }\theta _{m,1,r} &{}\ldots &{}\sum \limits _{r= 0}^{\lfloor m/2\rfloor }\theta _{m,m,r}\\ \end{array}} \right] . \end{aligned}$$

5 The operational matrix of multiplication

The product of two Boubaker function vectors satisfies in the following equation

$$\begin{aligned} A^\mathrm{T}\varPsi (t)\varPsi (t)^\mathrm{T}\simeq \varPsi (t)^\mathrm{T}{\tilde{A}}^\mathrm{T}, \end{aligned}$$

where A is the any arbitrary vector and ${\tilde{A}}$ is a $(m+1)\times (m+1)$ matrix. To calculate the entries of this matrix, we notice that $A^\mathrm{T}\varPsi (t)\varPsi (t)^\mathrm{T}$ can be approximated by $\varPsi (t)$ as following

$$\begin{aligned}&A^\mathrm{T}\varPsi (t)\varPsi (t)^\mathrm{T} =[a_0(t),\ldots ,a_m(t)],\nonumber \\&a_i(t)\simeq \sum \limits _{j= 0}^{m}\tilde{a_{i,j}}B_j(t)=\tilde{A_i^\mathrm{T}}\varPsi (t), \end{aligned}$$

(13)

where

$$\begin{aligned} \tilde{A_i}=[\tilde{a_{i,0}},\tilde{a_{i,1}},\ldots ,\tilde{a_{i,m}}]^\mathrm{T}. \end{aligned}$$

Using Eq. (13), we obtain

$$\begin{aligned} a_i^k= \left\langle \sum \limits _{j= 0}^{m}\tilde{a_{i,j}}B_j,B_k \right\rangle =\sum \limits _{j= 0}^{m}\tilde{a_{i,j}}d_{j,k},\quad j,k=0,1,\ldots ,m. \end{aligned}$$

where $a_i^k=\langle a_i,B_k\rangle ,d_{j,k}=\langle B_j,B_k\rangle$. So by considering $A_i=[a_i^0,a_i^1,\ldots ,a_i^m]^\mathrm{T},$ we have

$$\begin{aligned} A_i^\mathrm{T}=\tilde{A_i}^\mathrm{T} D, \end{aligned}$$

or

$$\begin{aligned} \tilde{A_i}^\mathrm{T}=A_i^\mathrm{T} D^{-1}, \end{aligned}$$

therefore the operational matrix of multiplication is obtained.

6 Problem statement

In this section, we consider the following FOCPs,

$$\begin{aligned}&\min \quad J(x,u)=\int _{0}^{1} (u^\mathrm{T}(t)A(t)u(t)+x^\mathrm{T}(t)B(t)x(t)\\&\quad +x^\mathrm{T}(t)C(t)u(t)) \mathrm{d}t \end{aligned}$$

where

$$\begin{aligned} x(t)= & {} [ x_{1}(t), x_{2}(t), \ldots , x_{l}(t)]^\mathrm{T},\\ u(t)= & {} [u_{1}(t), u_{2}(t), \ldots , u_{q}(t) ]^\mathrm{T}, \end{aligned}$$

are state and control vectors and also A(t), B(t) and C(t) are matrices of appropriate dimensions with B(t) a symmetric positive-semi definite matrix and A(t) a symmetric positive-definite matrix. Subject to dynamical system

$$\begin{aligned}&\sum \limits _{i= 1}^{n}M_i x^{(i)}(t)+\sum \limits _{j= 1}^{m} N_j D_t^{\alpha _{j}}x(t)\\&\quad =P(t)x(t)+Q(t)u(t)+F(t),\\&\quad n-1<\alpha _m\le n,\\&\quad 0\le \alpha _1\le \alpha _2\le \cdots \le \alpha _m, \end{aligned}$$

and conditions

$$\begin{aligned} x(0)=x_0,\quad x'(0)=x_1,\ldots ,x^{(n-1)}(0)=x_{n-1}, \end{aligned}$$

where $M_i,\quad i=1,\ldots ,n,$ and $N_j,\quad j=1,\ldots ,m,$ are real numbers and at least one of them should be nonzero. P(t), Q(t), F(t) are continuous matrix functions of time as follows

$$\begin{aligned} P(t)= & {} \left[ {\begin{array}{cccc} p_{11}(t) &{}p_{12}(t) &{} \ldots &{}p_{1l}(t) \\ p_{21}(t) &{}p_{22}(t) &{} \ldots &{} p_{2l}(t) \\ \vdots &{} \vdots &{} \ddots &{}\vdots \\ p_{l1}(t) &{}p_{l2}(t)&{}\ldots &{}p_{ll}(t)\\ \end{array}} \right] ,\\ Q(t)= & {} \left[ {\begin{array}{cccc} q_{11}(t) &{}q_{12}(t) &{} \ldots &{}q_{1q}(t) \\ q_{21}(t) &{}q_{22}(t) &{} \ldots &{} q_{2q}(t) \\ \vdots &{} \vdots &{} \ddots &{}\vdots \\ q_{l1}(t) &{}q_{l2}(t)&{}\ldots &{}q_{lq}(t)\\ \end{array}} \right] . \end{aligned}$$

and

$$\begin{aligned} F(t)=[f_1(t),f_2(t),\ldots ,f_l(t)]^\mathrm{T}, \end{aligned}$$

and $x_k, k=0,\ldots ,n-1,$ are specified constant vectors. The resolution process by using the operational matrices is discussed in the following subsections.

6.1 Application of operational matrix of derivative

We expand the state and control variables with respect to the Boubaker polynomials as:

$$\begin{aligned}&x_i(t)\simeq X_i^\mathrm{T}\varPsi (t),\quad \quad u_j(t)\simeq U_j^\mathrm{T}\varPsi (t),\nonumber \\&\quad i=1,\ldots ,l, \quad \quad \quad \quad j=1,\ldots ,q, \end{aligned}$$

(14)

where $X_i$ and $U_j$ are the following unknown coefficients vectors

$$\begin{aligned} X_i=[x_{i0},x_{i1},\ldots ,x_{im}]^\mathrm{T},\quad U_j=[u_{j0},u_{j1},\ldots ,u_{jm}]^\mathrm{T}, \end{aligned}$$

so we derive

$$\begin{aligned} D_t^\alpha x_i(t)\simeq D_\alpha X_i^\mathrm{T}\varPsi (t). \end{aligned}$$

(15)

Suppose that ${\hat{\varPsi }}(t)$ and ${\hat{\varPsi }}^{*}(t)$ are the following $l(m+1)\times l$ and $q(m+1) \times q$ matrices, respectively

$$\begin{aligned} {\hat{\varPsi }}(t) = I_{l} \otimes \varPsi (t), \quad {\hat{\varPsi }}^{*}(t) = I_{q} \otimes \varPsi (t), \end{aligned}$$

(16)

where $I_{l}$ and $I_{q}$ are $l \times l$ and $q\times q$ identity matrices, respectively, and $\otimes$ denotes the Kronecker product [25]. So we can write

$$\begin{aligned}&u(t)\simeq U^\mathrm{T}{\hat{\varPsi }}^{*}(t),\quad x(t)\simeq X^\mathrm{T}{\hat{\varPsi }}(t),\quad \\&D_t^\alpha x(t)\simeq \hat{D_\alpha } X^\mathrm{T}{\hat{\varPsi }}(t). \end{aligned}$$

where X, U are vectors of order $l(m+1) \times 1$ and $q(m+1) \times 1$, respectively, given by

$$\begin{aligned} X = [X_{1}, X_{2}, \ldots , X_{l}]^\mathrm{T},\quad U= [U_{1}, U_{2}, \ldots , U_{l}]^\mathrm{T}, \nonumber \\ \end{aligned}$$

(17)

and

$$\begin{aligned} \hat{D_\alpha }= I_{l} \otimes D_\alpha . \end{aligned}$$

Also, we expand other functions of t in the problem with respect to Boubaker polynomials as

$$\begin{aligned}&f_i(t)\simeq F_i^\mathrm{T}\varPsi (t),\quad p_{ij}(t)\simeq P_{ij}^\mathrm{T}\varPsi (t),\\&q_{ij}(t)\simeq Q_{ij}^\mathrm{T}\varPsi (t), \end{aligned}$$

where the vectors

$$\begin{aligned}&F_i=[f_{i0},f_{i1},\ldots ,f_{im}]^\mathrm{T},\\&P_{ij}=[p^{ij}_0,p^{ij}_1,\ldots ,p^{ij}_m]^\mathrm{T},\\&Q_{ij}=[q^{ij}_0,q^{ij}_1,\ldots ,q^{ij}_m]^\mathrm{T}, \end{aligned}$$

can be achieved using Eq. (4).

Then, one can expands $x_i^{(k)}(t)$ as

$$\begin{aligned} x_i^{(k)}(t)\simeq & {} X_i^\mathrm{T} \varPsi ^{(k)}(t)\simeq X_i^\mathrm{T} D^k \varPsi (t),\\&i=1,\ldots ,l,\quad k=1,\ldots ,n, \end{aligned}$$

where $D^1$ is the $(m+1)\times (m+1)$ operational matrix of derivative of order 1 and can be obtained easily by choosing $\alpha =1,$ in $D_\alpha$.

Now, if these approximations are applied in the problem, we have:

$$\begin{aligned}&J\simeq \int _{0}^{1} [(U^\mathrm{T}{\hat{\varPsi }}^{*}(t))^\mathrm{T}A(t)U^\mathrm{T}{\hat{\varPsi }}^{*}(t)\\&\quad +\,(X^\mathrm{T}{\hat{\varPsi }}(t))^\mathrm{T}B(t)X^\mathrm{T}{\hat{\varPsi }}(t)\\&\quad +\,(X^\mathrm{T}{\hat{\varPsi }}(t))^\mathrm{T}C(t)U^\mathrm{T}{\hat{\varPsi }}^{*}(t)]\mathrm{d}t, \end{aligned}$$

that can be solved numerically by Gauss–Legendre integration method.

Subject to the system

$$\begin{aligned}&\sum \limits _{i= 1}^{n}M_i x_k^{(i)}(t)+\sum \limits _{j= 1}^{m} N_j D_t^{\alpha _{j}} x_k(t)=\sum \limits _{r= 1}^{l}p_{kr}(t)x_r(t)\\&\quad + \sum \limits _{h= 1}^{q}q_{kh}(t)u_h(t)+f_k(t),\quad k=1,\ldots ,l. \end{aligned}$$

Or

$$\begin{aligned}&\sum \limits _{i= 1}^{n}M_iX_k^\mathrm{T} D^i \varPsi (t) +\sum \limits _{j= 1}^{m}N_j X_k^\mathrm{T}D_{\alpha _{j}}\varPsi (t)\\&\quad - \sum \limits _{r= 1}^{l}P_{kr}^\mathrm{T}(t)\varPsi (t)\varPsi (t)^\mathrm{T} X_r-\sum \limits _{h= 1}^{q}Q_{kh}^\mathrm{T}\varPsi (t)\varPsi (t)^\mathrm{T} U_h\\&\quad -F_k^\mathrm{T}\varPsi (t)=0. \end{aligned}$$

Now using

$$\begin{aligned}&P_{kr}^\mathrm{T}\varPsi (t)\varPsi (t)^\mathrm{T}\simeq \varPsi (t){\tilde{P}}_{kr}^\mathrm{T}, \quad \\&Q_{kh}^\mathrm{T}\varPsi (t)\varPsi (t)^\mathrm{T}\simeq \varPsi (t){\tilde{Q}}_{kh}^\mathrm{T}, \end{aligned}$$

we obtain the following system of algebraic equations

$$\begin{aligned} G_k= & {} \sum \limits _{i= 1}^{n}M_iX_k^\mathrm{T} D^i +\sum \limits _{j= 1}^{m}N_j X_k^\mathrm{T}D_{\alpha _{j}}-\sum \limits _{r= 1}^{l}X_r^\mathrm{T}{\tilde{P}}_{kr}\\&-\sum \limits _{h= 1}^{q}U_h^\mathrm{T}{\tilde{Q}}_{kh}-F_k^\mathrm{T}=0, \quad k=1,\ldots ,l. \end{aligned}$$

Also, we need to write the initial conditions

$$\begin{aligned} x^{(i)}(0)=x_i,\quad \quad i=0,\ldots ,n-1, \end{aligned}$$

in terms of the Boubaker basis as

$$\begin{aligned} x^{(i)}(0)=X^\mathrm{T}{{\hat{D}}}^i{\hat{\varPsi }}(0). \end{aligned}$$

To solve mentioned optimization problem, let

$$\begin{aligned} J^\star =J+\sum \limits _{k= 1}^{l}\lambda _k(G_k)+\sum \limits _{i= 0}^{n-1}\mu _i(x_i-X^\mathrm{T}{{\hat{D}}}^i{\hat{\varPsi }}(0)),\nonumber \\ \end{aligned}$$

(18)

where $\mu _i ,$ and $\lambda _k=[\lambda _{k0},\lambda _{k1},\ldots ,\lambda _{km}]^\mathrm{T}$ are unknown Lagrange multipliers solved by Newton’s iterative method. The necessary conditions for $(X,U,\lambda _k,\mu _i)$ to be the extreme of $J^\star$ are

$$\begin{aligned} \frac{\partial J^\star }{\partial X_i}= & {} 0,\; i=1,\ldots ,l,\quad \frac{\partial J^\star }{\partial U_j}=0, \quad j=1,\ldots ,q,\\ \frac{\partial J^\star }{\partial \lambda _k}= & {} 0,\; k=1,\ldots ,l,\; \frac{\partial J^\star }{\partial \mu _i}=0, \; i=0 ,\ldots ,n-1. \end{aligned}$$

As a result, by replacing the values obtained from (18) in Eq. (14), u(t) and x(t) can be calculated.

6.2 Application of operational matrix of integration

In this section, the operational matrix of integration is applied to solve the mentioned FOCP. For this purpose, we approximate

$$\begin{aligned} x_k^{(n)}(t)=D^n x_k(t)\simeq X_k^\mathrm{T}\varPsi (t),\quad k=1,\ldots ,l, \end{aligned}$$

therefore we have

$$\begin{aligned} x_k(t)=I_t^{n}D_t^n x_k(t)+\sum \limits _{i= 0}^{n-1}x_k^{(i)}(0) \frac{t^i}{i!}. \end{aligned}$$

Now we write

$$\begin{aligned} \sum \limits _{i= 0}^{n-1}x_k^{(i)}(0) \frac{t^i}{i!} \simeq d_k^\mathrm{T}\varPsi (t), \end{aligned}$$

and we have

$$\begin{aligned} x_k(t)= & {} (X_k^\mathrm{T} F^{(n)}+d_k^\mathrm{T})\varPsi (t),\quad k=1,\ldots ,l,\nonumber \\&u_k(t)\simeq U_k^\mathrm{T}\varPsi (t),\quad k=1,\ldots ,q, \end{aligned}$$

(19)

also for $j=1,\ldots ,n-1,$ and $k=1,\ldots ,l,$ we have

$$\begin{aligned} x_k^{(j)}(t)= & {} X_k^\mathrm{T} F^{(n-j)}\varPsi (t)+\sum \limits _{i= j+1}^{n-1}x_k^{(i)}(0) \frac{t^{i-j}}{(i-j)!}\\\simeq & {} (X_k^\mathrm{T} F^{(n-j)}+d_{k,j}^\mathrm{T})\varPsi (t), \end{aligned}$$

and for $j=1,\ldots ,m,$ and $k=1,\ldots ,l,$ we have

$$\begin{aligned}&D_t^{\alpha _j} x_k(t)=X_k^\mathrm{T} F^{(n-\alpha _j)}\varPsi (t)\\&\quad +\sum \limits _{i= \lceil j \rceil }^{n-1}x_k^{(i)}(0) \frac{t^{i-\alpha _j}}{\varGamma (i+1-\alpha _j)}\\&\quad \simeq (X_k^\mathrm{T} F^{(n-\alpha _j)}+{\tilde{d}}_{k,j}^\mathrm{T})\varPsi (t), \end{aligned}$$

by replacing the approximation of x(t) and u(t) in the performance index J,  this functional can be calculated numerically like previous subsection, and also by using the mentioned approximations in this subsection, the system

$$\begin{aligned}&\sum \limits _{i= 1}^{n}M_i x_k^{(i)}(t)+\sum \limits _{j= 1}^{m} N_j D_t^{\alpha _{j}} x_k(t)=\sum \limits _{r= 1}^{l}p_{kr}(t)x_r(t)\\&\quad + \sum \limits _{h= 1}^{q}q_{kh}(t)u_h(t)+f_k(t),\quad k=1,\ldots ,l, \end{aligned}$$

can be writen as

$$\begin{aligned}&M_n X_k^\mathrm{T}\varPsi (t)+\sum \limits _{i= 1}^{n-1}M_i(X_k^\mathrm{T} F^{(n-i)}+d_{k,i}^\mathrm{T})\varPsi (t)\\&\quad + \sum \limits _{j= 1}^{m}N_j(X_k^\mathrm{T} F^{(n-\alpha _j)}+{\tilde{d}}_{k,j}^\mathrm{T})\varPsi (t)\\&\quad -\sum \limits _{r= 1}^{l}P_{kr}^\mathrm{T}(t)\varPsi (t)\varPsi (t)^\mathrm{T} X_r\\&\quad -\sum \limits _{h= 1}^{q}Q_{kh}^\mathrm{T}\varPsi (t)\varPsi (t)^\mathrm{T} U_h-F_k^\mathrm{T}\varPsi (t)=0. \end{aligned}$$

Now using

$$\begin{aligned} P_{kr}^\mathrm{T}\varPsi (t)\varPsi (t)^\mathrm{T}\simeq \varPsi (t){\tilde{P}}_{kr}^\mathrm{T}, \quad Q_{kh}^\mathrm{T}\varPsi (t)\varPsi (t)^\mathrm{T}\simeq \varPsi (t){\tilde{Q}}_{kh}^\mathrm{T}, \end{aligned}$$

we obtain the following linear system of algebraic equations

$$\begin{aligned}&H_k=M_n X_k^\mathrm{T}+\sum \limits _{i= 1}^{n-1}M_i(X_k^\mathrm{T} F^{(n-i)}+d_{k,i}^\mathrm{T})\\&\quad + \sum \limits _{j= 1}^{m}N_j(X_k^\mathrm{T} F^{(n-\alpha _j)}+{\tilde{d}}_{k,j}^\mathrm{T})-\sum \limits _{r= 1}^{l}X_r^\mathrm{T}{\tilde{P}}_{kr}\\&\quad -\sum \limits _{h= 1}^{q}U_h^\mathrm{T}{\tilde{Q}}_{kh}-F_k^\mathrm{T}=0, \quad k=1,\ldots ,l. \end{aligned}$$

To solve mentioned optimization problem, let

$$\begin{aligned} J^\star =J+\sum \limits _{k= 1}^{l}\lambda _k(H_k). \end{aligned}$$

(20)

where $\lambda _k=[\lambda _{k0},\lambda _{k1},\ldots ,\lambda _{km}]^\mathrm{T}$ are unknown Lagrange multipliers solved by iterative method. The necessary conditions for $(X,U,\lambda _k)$ to be the extreme of $J^\star$ are

$$\begin{aligned}&\frac{\partial J^\star }{\partial X_i}=0, \quad i=1,\ldots ,l,\quad \frac{\partial J^\star }{\partial U_j}=0, \quad j=1,\ldots ,q,\\&\quad \frac{\partial J^\star }{\partial \lambda _k}=0,\quad k=1,\ldots ,l. \end{aligned}$$

As a result, by replacing the values obtained from (20) using Newton’s iterative method in Eq. (19), u(t) and x(t) can be calculated.

7 Convergence analysis

In this section, we focus on the convergence of the method, first we consider the operational matrix of derivative and show that $X_k^\mathrm{T}D_\alpha \varPsi (t)$ tends to $D_t^\alpha x_k(t)$ as m tends to infinity in Eq. (15) for $k=1,\ldots ,l$. For this purpose, we notice that we have,

$$\begin{aligned}&\lim _{j \rightarrow \infty }\sum _{j=0}^m x_{kj}B_j(t)=x_k(t),\nonumber \\&\lim _{j \rightarrow \infty }\sum _{j=0}^m x_{kj}B_j^{(n)}(t)=x_k^{(n)}(t). \end{aligned}$$

(21)

Since $B_j^{(n)}(t)$ is a continuous function, we have:

$$\begin{aligned}&\lim _{m \rightarrow \infty }\int _{0}^{t}\frac{\sum _{j=0}^m x_{kj}B_j^{(n)}(t)}{(t-\tau )^{n-\alpha -1}}\mathrm{d}\tau \\&\quad =\lim _{m \rightarrow \infty }\sum _{j=0}^m x_{kj}\int _{0}^{t}\frac{B_j^{(n)}(t)}{(t-\tau )^{n-\alpha -1}}\mathrm{d}\tau . \end{aligned}$$

We can write the above equation as

$$\begin{aligned}&\int _{0}^{t}\frac{\lim _{m \rightarrow \infty }\sum _{j=0}^m x_{kj}B_j^{(n)}(t)}{(t-\tau )^{n-\alpha -1}}\mathrm{d}\tau \nonumber \\&\quad = \lim _{m \rightarrow \infty }\sum _{j=0}^m x_{kj}\int _{0}^{t}\frac{B_j^{(n)}(t)}{(t-\tau )^{n-\alpha -1}}\mathrm{d}\tau , \end{aligned}$$

(22)

by Eqs. (2), (21) and (22), for $n-1<\alpha \le n$, we obtain

$$\begin{aligned} \int _{0}^{t}\frac{x_k^{(n)}(t)}{(t-\tau )^{n-\alpha -1}}\mathrm{d}\tau =\varGamma (n-\alpha )\lim _{m \rightarrow \infty }\sum _{j=0}^m x_{kj}D_t^\alpha B_j(t), \end{aligned}$$

or

$$\begin{aligned} D_t^\alpha x_k(t)=\lim _{m \rightarrow \infty }\sum \limits _{j=0}^{m} x_{kj}D_t^\alpha B_j(t). \end{aligned}$$

(23)

Now we recall Eq. (9) that $D_\alpha =\varLambda {\tilde{\varSigma }} P^\mathrm{T},$ where ith column of $P^\mathrm{T}$ is the coefficients vector of Boubaker approximation of $t^{i-\alpha }$ for $i=1,\ldots ,m.$

By the Weierstrass approximation theorem, we know that Boubaker approximation of every continuous function converges uniformly to that function, so considering Eq. (8) we have

$$\begin{aligned} \lim _{n \rightarrow \infty }\sum _{j=0}^n P_{j,i} B_j(t)=t^{i-\alpha }, \quad i=1,\ldots ,m. \end{aligned}$$

or

$$\begin{aligned} \lim _{n \rightarrow \infty }P^\mathrm{T} \varPsi _n(t)=\lim _{n \rightarrow \infty }\left[ {\begin{array}{c} \sum \limits _{j=0}^{n} P_{j,0} B_j(t)\\ \sum \limits _{j=0}^{n} P_{j,1} B_j(t) \\ \vdots \\ \sum \limits _{j=0}^{n} P_{j,m} B_j(t)\\ \end{array}} \right] ={\tilde{T}}, \end{aligned}$$

where $\varPsi _n(t)=[B_0(t),B_1(t),\ldots ,B_n(t)]^\mathrm{T},$ so we can write,

$$\begin{aligned} \lim _{n \rightarrow \infty }\varLambda {\tilde{\varSigma }} P^\mathrm{T}\varPsi _n(t)=\varLambda {\tilde{\varSigma }}\lim _{n \rightarrow \infty }P^\mathrm{T}\varPsi _n(t)=\varLambda {\tilde{\varSigma }}{\tilde{T}}. \end{aligned}$$

Now we use Eqs. (6) and (7) and insert the following term in the above equation,

$$\begin{aligned}{\tilde{\varSigma }}{\tilde{T}}=D_t^\alpha T_m=D_t^\alpha \varLambda ^{-1}\varPsi (t), \end{aligned}$$

and obtain

$$\begin{aligned} \lim _{n \rightarrow \infty }D_\alpha \varPsi _n(t)=D_t^\alpha \varPsi (t). \end{aligned}$$

(24)

Then, the following result can be achieved from Eqs. (23) and (24)

$$\begin{aligned} D_t^\alpha x_k(t)=\lim _{m \rightarrow \infty } X_k^\mathrm{T}\lim _{n \rightarrow \infty }D_\alpha \varPsi _n(t). \end{aligned}$$

Finally, this proof is complete by $n\ge m$. It should be noticed that this result is valid for any arbitrary $\alpha _j$ and can be expanded for general form of dynamical system presented in this article.

Now the operational matrix of integration is considered to find an upper bound for the error of operational matrix of the fractional integration $F^{(\alpha )}$ and to show that by increasing the number of Boubaker polynomials $F^{(\alpha )}\varPsi (t)$ tends to $I_t^{\alpha }\varPsi (t)$. To obtain this result, we recall the following lemma and theorems.

Lemma 1

Suppose $f\in C^{m+1}[0,1]$ and

$$\begin{aligned} Y=span\{B_0(t),B_1(t),\ldots ,B_m(t)\}. \end{aligned}$$

Let $y_0$ be the best approximation for f out of Y then

$$\begin{aligned} \Vert f-y_0\Vert _{L^2[0,1]}\le \frac{K}{(m+1)!\sqrt{2m+3}}, \end{aligned}$$

where $K=Max_{t\in [0,1]}\vert f^{(m+1)}(t)\vert .$

Proof

The set $\lbrace 1, t,\ldots , t^m\rbrace ,$ is a basis for polynomials space of degree m. We define

$$\begin{aligned} y_1(t)=f(0)+tf'(0)+\frac{t^2}{2!}f^{(2)}(0)+\cdots +\frac{t^m}{m!}f^{(m)}(0) \end{aligned}$$

From Taylor expansion, we have

$$\begin{aligned} \vert f(t)-y_1(t)\vert =\frac{f^{(m+1)}(\tau )t^{m+1}}{(m+1)!}, \end{aligned}$$

where $\tau \in (0,1)$. Since $y_0$ is the best approximation f(t) out of $S_m, y_1(t)\in S_m,$ and from above equation, we have

$$\begin{aligned}&\Vert f-y_0\Vert _{L^2[0,1]}^2\le \Vert f-y_1\Vert _{L^2[0,1]}^2\\&\quad = \int _{0}^{1} \vert f-y_1\vert ^2\mathrm{d}t=\frac{K^2}{(m+1)!^2(2m+3)} \end{aligned}$$

Then by taking square roots, the proof is complete. $\square$

Theorem 1

Suppose that H is a Hilbert space, Y is a finite dimensional and closed subspace of H and $\lbrace y_1,y_2,\ldots ,y_n\rbrace ,$ is a basis for Y. Let x be an arbitrary element in H and $y_0$ be the unique best approximation to x out of Y. Then [24]

$$\begin{aligned} \Vert x-y_0\Vert _2^2=\frac{G(x,y_1,y_2,\ldots ,y_n)}{G(y_1,y_2,\ldots ,y_n)}, \end{aligned}$$

where G is Gramian matrix.

Theorem 2

Suppose that $f\in L^2[0,1]$ and f(t) is approximated by $\sum _{i=0}^{m}c_i B_i(t)$, then we have [24]

$$\begin{aligned} \lim _{m \rightarrow \infty }\Vert f(t)-\sum _{i=0}^{m}c_i B_i(t)\Vert _{L^2[0,1]}=0. \end{aligned}$$

Now by using these theorems, we show that $(F^{(\alpha )}B_i(t)-I_t^{\alpha }B_i(t))$ tends to zero for $i=0,1,\ldots ,m,$ as follow: for $i=0,$

$$\begin{aligned}&\Vert I_t^{\alpha }B_0(t)-\sum _{j=0}^{m}\frac{\vartheta _{0,j}}{\varGamma (\alpha +1)}B_j(t)\Vert \nonumber \\&\quad \le \quad \frac{1}{\varGamma (\alpha +1)}\Vert t^{\alpha }-\sum _{j=0}^{m}\vartheta _{0,j}B_j(t)\Vert \nonumber \\&\quad \le \frac{1}{\varGamma (\alpha +1)}\left( \frac{G(t^\alpha ,B_0,B_1,\ldots ,B_m)}{G(B_0,B_1,\ldots ,B_m)}\right) ^{1/2}. \end{aligned}$$

(25)

For $i=1$

$$\begin{aligned}&\Vert I_t^{\alpha }B_1(t)-\sum _{j=0}^{m}\frac{\vartheta _{1,j}}{\varGamma (\alpha +2)}B_j(t)\Vert \nonumber \\&\quad \le \frac{1}{\varGamma (\alpha +2)}\Vert t^{\alpha +1} -\sum _{j=0}^{m}\vartheta _{1,j}B_j(t)\Vert \nonumber \\&\quad \le \frac{1}{\varGamma (\alpha +2)}(\frac{G(t^{\alpha +1},B_0,B_1,\ldots ,B_m)}{G(B_0,B_1,\ldots ,B_m)})^{1/2}, \end{aligned}$$

(26)

and for $i\ge 2$

$$\begin{aligned}&\Vert I_t^{\alpha }B_i(t)-\sum \limits _{j= 0}^{m} \left( \sum \limits _{r= 0}^{\lfloor i/2\rfloor }b_{i,r}c_{r,j}\right) B_j(t)\Vert \nonumber \\&\quad \le \Vert \sum \limits _{r= 0}^{\lfloor i/2\rfloor } (-1)^r\frac{(i-r-1)!(i-4r)}{r!\varGamma (i-2r+\alpha )}t^{i-2r+\alpha }-\nonumber \\&\quad \sum \limits _{j= 0}^{m} \left( \sum \limits _{r= 0}^{\lfloor i/2\rfloor }b_{i,r}c_{r,j}\right) B_j(t)\Vert \nonumber \\&\quad \le \sum \limits _{r= 0}^{\lfloor i/2\rfloor }b_{i,r}\Vert t^{i-2r+\alpha }-\sum \limits _{j= 0}^{m} B_j(t)\Vert \nonumber \\&\quad \le \sum \limits _{r= 0}^{\lfloor i/2\rfloor }b_{i,r} \left( \frac{G(t^{i-2r+\alpha },B_0,B_1,\ldots ,B_m)}{G(B_0,B_1,\ldots ,B_m)}\right) ^{1/2}. \end{aligned}$$

(27)

Now we can conclude by Theorem 2 and Eqs. (25), (26) and (27) that the difference of $F^{(\alpha )}\varPsi (t)$ and $I_t^{\alpha }\varPsi (t)$ tends to zero when the number of Boubaker basis functions tends to infinity so this approximation could be used for each elements of state vector.

8 Numerical examples

Now we present some examples of optimal control problems and use the mentioned algorithms for solving them.

Example 1

Assume that we wish to minimize the functional

$$\begin{aligned}&J(x,u)=\int _{0}^{1} (0.625 x^2(t)+0.5x(t)u(t)\\&\quad +\,0.5u^2(t)) \mathrm{d}t , \end{aligned}$$

subject to dynamical system

$$\begin{aligned} D_t^{\alpha }x(t)=0.5x(t)+u(t), \quad t\in [0,1],\quad 0<\alpha \le 1, \end{aligned}$$

and the condition

$$\begin{aligned} x(0)=1, \end{aligned}$$

that its exact optimal cost for $\alpha =1$, is $J=0.3807971,$ and the exact value of control variable is [26]

$$\begin{aligned} u(t)=\frac{-(\tanh (1-t)+0.5)\cosh (1-t)}{\cosh (1)}. \end{aligned}$$

Here we solve this problem by using the Boubaker integration operational matrix for $m=5$, as follows:

$$\begin{aligned} D_t^{\alpha }x(t)=X^\mathrm{T}\varPsi (t),\quad u(t)=U^\mathrm{T}\varPsi (t). \end{aligned}$$

where

$$\begin{aligned} X=[x_0,x_1\ldots ,x_5]^\mathrm{T},\quad U=[u_0,u_1\ldots ,u_5]^\mathrm{T}. \end{aligned}$$

So we have

$$\begin{aligned} x(t)=X^\mathrm{T}F^{(\alpha )}\psi (t)+1=(X^\mathrm{T}F^{(\alpha )}+d^\mathrm{T}), \end{aligned}$$

with $d=[1,0,0,0,0,0]^\mathrm{T}$. Substituting these into problem, we get

$$\begin{aligned} J= & {} 0.625(X^\mathrm{T}F^{(\alpha )}+d^\mathrm{T})D(X^\mathrm{T}F^{(\alpha )}+d^\mathrm{T})^\mathrm{T}\\&+\,0.5(X^\mathrm{T}F^{(\alpha )}+d^\mathrm{T})DU+0.5U^\mathrm{T}DU, \end{aligned}$$

D is introduced in Eq. (4).

$$\begin{aligned} J^\star = J+(X^\mathrm{T}-0.5(X^\mathrm{T}F^{(\alpha )}+d^\mathrm{T})-U^\mathrm{T})\lambda _1, \end{aligned}$$

where $\lambda _1$ is

$$\begin{aligned} \lambda _1=[\lambda _{10},\lambda _{11},\ldots ,\lambda _{15}]. \end{aligned}$$

Now we solve the following system using Newton’s iterative method

$$\begin{aligned}&\frac{\partial J^\star }{\partial x_i}= 0,\quad i=0,1,\ldots ,5,\\&\frac{\partial J^\star }{\partial u_j}=0,\quad j=0,1,\ldots ,5,\\&\frac{\partial J^\star }{\partial \lambda _{1k}}= 0,\quad k=0,\ldots ,5, \end{aligned}$$

and for example for $\alpha =1,$ we obtain

$$\begin{aligned} X = \left[ \begin{array}{c} 0.0767781\\ -0.642253\\ 0.499522\\ -0.127832\\ 0.0379117\\ -0.00284627 \end{array}\right] , \quad U =\left[ \begin{array}{c} -0.0981257\\ 1.16778\\ -0.630319\\ 0.23572\\ -0.0485852\\ 0.00758233 \end{array}\right] , \end{aligned}$$

and

$$\begin{aligned} x(t)= & {} 0.999999 - 0.761547 t + 0.499522 t^2 - 0.124986 t^3\\&+\, 0.0379117 t^4 - 0.00284627 t^5,\\ u(t)= & {} -1.26159 + 1.38075 t - 0.630319 t^2 + 0.228138 t^3\\&-\, 0.0485852 t^4 + 0.00758233 t^5. \end{aligned}$$

We present the results for different values of $\alpha$ in Table 1 and see that as $\alpha$ approaches to 1, the numerical values of J converge to the objective value of $\alpha =1$.

Table 1 Values of J for different values of $\alpha$, for Example 1

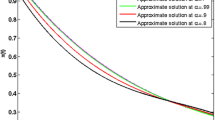
Also, Fig. 1 shows the curves for exact values of control variable and numerical values of u(t) and x(t) for $\alpha =0.5, 0.8, 0.9, 1$.

Fig. 1

Curves for $\alpha =0.5, 0.8, 0.9,1$, Example 1. a Numerical and exact values of x(t). b Numerical and exact values of u(t)

This problem is solved in [26] for $\alpha =1,$ with Chebyshev finite difference method and the result for $m=7,$ is as accurate as our values for $m=5$.

Example 2

We consider the FOCPs:

$$\begin{aligned}&J(x,u)=\frac{1}{2}\int _{0}^{1} (x_1(t)^2+x_2(t)^2+u^2(t)) \mathrm{d}t , \end{aligned}$$

subject to

$$\begin{aligned}&D_t^{\alpha }x_1(t)=-x_1(t)+x_2(t)+u(t),\\&D_t^{\alpha }x_2(t)=-2x_2(t),\\&x_1(0)=1,\quad \quad x_2(0)=1, \end{aligned}$$

with the following exact solution in the case of $\alpha =1,$

$$\begin{aligned}&x_1(t)=\frac{-3}{2}\mathrm{e}^{-2t}+2.48164 \mathrm{e}^{-\sqrt{2}t}+0.018352 \mathrm{e}^{\sqrt{2}t},\\&x_2(t)= \mathrm{e}^{-2t},\\&u(t)=\frac{1}{2}\mathrm{e}^{-2t}-1.02793 \mathrm{e}^{-\sqrt{2}t}+0.0443056 \mathrm{e}^{\sqrt{2}t},\\&J=0.43198. \end{aligned}$$

The absolute errors of $x_1(t), x_2(t)$ and u(t) for different values of m and $\alpha =1$ are given in [12] by the use of Legendre multiwavelet collocation method. We also give these results using operational matrix of integration in Tables 2, 3 and 4 to show that our results for $x_2(t)$ are better, for $x_1(t)$ are as accurate as the results obtained by Legendre multiwavelet and for u(t) are more accurate almost everywhere. It should be noted that the numbers of basis polynomials are equal to $m+1$, in our method while it is obtained as multiplication of $m+1$ in the numbers of subintervals via multiwavelet.

Table 2 Absolute errors of $x_1(t)$ for $\alpha =1$, Example 2

Table 3 Absolute errors of $x_2(t)$ for $\alpha =1$, Example 2

Table 4 Absolute errors of u(t) for $\alpha =1$, Example 2

Considering Tables 2, 3 and 4, it is shown that if the number of Boubaker basis functions is increased the absolute errors are decreased, and therefore, the numerical values of parameters converge to exact solution. In Fig. 2, we show the curves of unknown functions of this example for different values of $\alpha$ to show convergence of fractional order to integer one.

Fig. 2

Curves for $\alpha =0.5, 0.8, 0.9,1$, Example 2. a Numerical and exact values of $x_1(t)$. b Numerical and exact values of $x_2(t)$. c Numerical and exact values of u(t)

Also, Table 5 shows the convergence between the values of J for different $\alpha$ as $\alpha$ approaches to 1.

Table 5 Values of J for different values of $\alpha$, for Example 2

Example 3

The next example under consideration is as follows [27]:

$$\begin{aligned} \quad J(x,u)=\frac{1}{2}\int _{0}^{1} (3x(t)^2+u(t)^2)\mathrm{d}t, \end{aligned}$$

subject to dynamical system

$$\begin{aligned} D_t^{\alpha }x(t)=-x(t)+u(t),\quad t \in [0,1], \quad 0<\alpha \le 1, \end{aligned}$$

and the conditions

$$\begin{aligned} x(0)=0 ,\quad \quad x(1)=2, \end{aligned}$$

with the exact solution

$$\begin{aligned} x(t)= & {} \frac{2}{\sinh (2)}\sinh (2t),\\ u(t)= & {} \frac{2}{\sinh (2)}(\sinh (2t)+2\cosh (2t)), \end{aligned}$$

for $\alpha =1,$ and in this case $J=6.149258$.

We have used the operational matrix of fractional derivative and achieved $J=6.149258977,$ for $m=5,$ as follows, however, the best result obtained in [27] is $J=6.149061,$ with 32 nodes.

$$\begin{aligned} x(t)=X^\mathrm{T}\varPsi (t),\quad u(t)=U^\mathrm{T}\varPsi (t), \end{aligned}$$

where

$$\begin{aligned} X=[x_0,x_1\ldots ,x_5]^\mathrm{T},\quad U=[u_0,u_1\ldots ,u_5]^\mathrm{T}. \end{aligned}$$

So we have

$$\begin{aligned} D_t^{\alpha }x(t)=X^\mathrm{T}D_\alpha \psi (t), \end{aligned}$$

substituting these into problem we get

$$\begin{aligned} J=\frac{3}{2} X^\mathrm{T}DX+\frac{1}{2}U^\mathrm{T}DU. \end{aligned}$$

D is introduced in Eq. (4).

$$\begin{aligned} J^\star= & {} J+(X^\mathrm{T}D_{\alpha }+X^\mathrm{T}-U^\mathrm{T})\lambda _1+(X^\mathrm{T}\psi (0)-0)\lambda _2\\&+ (X^\mathrm{T}\psi (1)-2)\lambda _3, \end{aligned}$$

where $\lambda _2,\lambda _3$ are real numbers and $\lambda _1$ is

$$\begin{aligned} \lambda _1=[\lambda _{10},\lambda _{11},\ldots ,\lambda _{15}]. \end{aligned}$$

Now we solve the following system

$$\begin{aligned}&\frac{\partial J^\star }{\partial x_i}=0, i=0,1,\ldots ,5,\quad \frac{\partial J^\star }{\partial u_j}=0, j=0,1,\ldots ,5,\\&\quad \frac{\partial J^\star }{\partial \lambda _{1k}}=0, k=0,\ldots ,5, \quad \frac{\partial J^\star }{\partial \lambda _2}=0,\quad \frac{\partial J^\star }{\partial \lambda _3}=0, \end{aligned}$$

and for $\alpha =1,$ we obtain

$$\begin{aligned} X = \left[ \begin{array}{c} -0.237723\\ 0.765405\\ -0.018142\\ 1.05099\\ -0.137003\\ 0.23741 \end{array}\right] , \quad U =\left[ \begin{array}{c} -1.64091\\ 1.27713\\ 2.42258\\ 0.502972\\ 1.05005\\ 0.23741 \end{array}\right] , \end{aligned}$$

and

$$\begin{aligned} x(t)= & {} -3.48776\times 10^{-10 }+ 1.10416 t - 0.018142 t^2 \\&+ 0.813575 t^3 - 0.137003 t^4 + 0.23741 t^5,\\ u(t)= & {} 1.10416 + 1.06788 t + 2.42258 t^2 + 0.265561 t^3\\&+ 1.05005 t^4 + 0.23741 t^5. \end{aligned}$$

In Fig. 3, the exact and numerical values of state and control functions are shown.

Fig. 3

Curves for $\alpha =0.5, 0.8, 0.9, 1$, Example 3. a Numerical and exact values of x(t). b Numerical and exact values of u(t)

Example 4

Now consider the following time varying problem [18]

$$\begin{aligned} \min \quad J(x,u)=\frac{1}{2}\int _{0}^{1} (x(t)^2+u(t)^2)\mathrm{d}t, \end{aligned}$$

subject to

$$\begin{aligned} D_t^{\alpha }x(t)=tx(t)+u(t), \quad x(0)=1. \end{aligned}$$

Table 6 compares the values of J, obtained via Boubaker operational matrix of fractional derivative and the results reported in [18]. The number of our basis and calculation is less than [18]. In addition, the more values of J for different $\alpha$ in our method show the better convergence.

Table 6 Values of J for different values of $\alpha$, for Example 4

Figure 4 demonstrates the values of state and control functions for different values of $\alpha$.

Fig. 4

Curves for $\alpha =0.5, 0.8, 0.9,1$, Example 4. a Numerical and exact values of x(t). b Numerical and exact values of u(t)

9 Conclusion

In this paper, we have presented the Boubaker operational matrices of Caputo fractional derivative and Riemann–Liouville fractional integration for the first time. Then, a general formulation for operational matrix of multiplication is achieved, and these matrices have been used to approximate numerical solution of fractional optimal control problems. In fact, the problem is solved by the direct use of the functional without solving fractional Hamiltonian equations, and by using these matrices the mentioned fractional optimal control problem is reduced to systems of algebraic equations. Some numerical examples, solved by Wolfram Mathematica 10, show the validity of the method. Also, it is shown that if the number of Boubaker basis functions is increased this method is convergent.