The distinct stochastic and deterministic dynamics between period-adding and period-doubling bifurcations of neural bursting patterns

Abstract

Period-adding bifurcations and period-doubling bifurcations of neural firing patterns, which were both observed in the biological experiment on a neural pacemaker and simulated in a theoretical model (Chay model), manifested different stochastic dynamics near the bifurcation points. For period-adding bifurcations, a noise-induced stochastic bursting, whose behavior is stochastic transition between period-k and period-($k+1$) bursts, lying between period-k and period-($k+1$) burstings ($k=1,2,3$). For period-doubling bifurcations, period-1 bursting is changed to period-2 bursting firstly and then to period-4 bursting. No stochastic firing patterns similar to those lying in the period-adding bifurcation were detected. Using the method of the fast–slow variables dissection, the deterministic burstings in both period-adding bifurcation and period-doubling bifurcation are classified into “fold/homoclinic” bursting with a saddle-node point and a saddle-homoclinic point, which behaves as a critical phase sensitive to noisy disturbance. For the bursting pattern near the period-doubling bifurcation point, the trajectory of burstings is far from the saddle-homoclinic point. Near the period-adding bifurcation points from period-k to period-($k+1$) burstings, the trajectories of the bursting patterns pass through the neighborhood of the saddle-homoclinic point and exhibit a platform. The platform appears after the k-th spike for the period-k bursting and between the k-th spike and the ($k+1$)-th spike for the period-($k+1$) bursting. For some bursts of period-k bursting, noise can induce a novel spike near the platform to form a burst with $k+1$ spikes, and for some bursts of period-($k+1$) bursting, the last spike can be terminated by noise to form a burst with k spikes. It is the cause that the stochastic bursting whose behavior is stochastic transition between period-k burst and period-($k+1$) burst is induced by noise, and the stochastic transition happens within or near the platform, i.e., the neighborhood of the saddle-homoclinic point. More detailed transition dynamics can be explained by the stable/unstable manifold of the saddle point. The underlying deterministic dynamics between period-adding and period-doubling bifurcation points that can lead to distinct stochastic dynamics are identified, which are helpful for understanding the roles of noise and provide critical phase to apply control strategy to modulate the firing patterns.

1 Introduction

In the nervous system, information is encoded into various firing patterns including bursting or spiking patterns. The nonlinear dynamics of different firing patterns and transition regularities between different firing patterns are of fundamental importance to the understanding of the neural coding [1,2,3,4]. In the last three decades, the transition processes of neural firing patterns have been identified with the help of the bifurcation theory. Many bifurcation scenarios of neural firing patterns have been simulated in the theoretical models and observed in the biological experiments [5,6,7,8,9,10,11,12,13,14,15,16,17]. These bifurcation scenarios include transitions from period-1 bursting to period-1 spiking with simple or complex processes, period-adding bifurcations of bursting patterns, and period-doubling bifurcations of firing patterns. Based on these bifurcation processes, the framework of relationships between periodic and chaotic firing patterns in the parameter space is provided [3, 18,19,20,21].

Period-adding bifurcation and period-doubling bifurcation, both as the representatives of the neural firing pattern transition process, exhibit different stochastic dynamics near bifurcation points [22,23,24,25,26,27,28]. When noise is introduced, period-adding bifurcation from period-k bursting to period-($k+1$) bursting ($k=1,2,3$) directly in the deterministic Chay model is changed into period-adding bifurcation with stochastic bursting in the stochastic Chay model [25]. The noise-induced stochastic bursting lies between period-k bursting and period-($k+1$) bursting, and the behavior of the stochastic bursting exhibits stochastic transitions between period-k burst and period-($k+1$) burst ($k=1,2,3$). The intervals between continuous period-k or period-($k+1$) bursts exhibit multimode characteristics ($k=1,2,3$) similar to those of the interspike interval (ISI) of the integer multiple bursting caused by coherence resonance (CR) [25]. In the stochastic Chay model, the processes of period-doubling bifurcation remain unchanged and are still from period-1 bursting, to period-2 bursting, and to period-4 bursting, except that the ISIs of period-1, 2, and 4 burstings are disturbed by noise. Period-adding bifurcation and period-doubling bifurcation processes observed in the biological experiments on a neural pacemaker closely matched those simulated in the stochastic Chay model.

What’s the cause that can induce distinct stochastic dynamics between the period-adding bifurcation and period-doubling bifurcation processes? The answer is helpful to further identify the dynamics of the firing patterns lying in the period-adding bifurcation and the difference between firing patterns near period-adding and doubling bifurcation points. This paper will answer this question using the dissection of the fast and slow variables to the bursting patterns. The dynamical system of neuronal model with bursting patterns can always be divided into a fast subsystem and a slow subsystem. The three-dimensional neuronal system such as the Chay model and the HR model is the representative systems with bursting patterns [8, 12, 19, 20, 23, 24, 29,30,31,32,33,34]. There exist only two behaviors in the fast subsystem being of a two-dimensional system, resting state and spiking, when one-dimensional slow variable is chosen as the bifurcation parameter. The firing patterns of the dynamical system can be classified into bursting or spiking pattern by the bifurcation structures of the fast subsystem combined with the trajectory of the firing patterns. The firing pattern is suggested as spiking pattern if the trajectory does not pass through the resting state of the fast subsystem and only circles around the trajectory of spiking of the fast subsystem, or is thought to be bursting pattern if the trajectory transits between the resting state and spiking of the fast subsystem. According to two bifurcations within the bursting pattern, one from the resting state to spiking of the fast subsystem, and the other from the spiking to the resting state, bursting patterns can be classified into different kinds, as proposed by Rinzel or Izhikevich [7, 10, 35]. For example, type I bursting proposed by Rinzel et al. is named as “fold/homoclinic” bursting by Izhikevich. The transition from the resting state to spiking is via a fold bifurcation of the equilibrium points, and the transition from spiking behavior to resting state is via a saddle-homoclinic (abbreviated as SH) orbit of the fast subsystem.

In the present study, the bursting patterns lying in the period-adding bifurcation processes and period-doubling bifurcation processes in the deterministic Chay model are identified to be “fold/homoclinic” bursting. Near the period-adding bifurcation point, the trajectory of the bursting passes through a critical point of the fast subsystem, a SH point. The SH point is a critical point near which a suitable perturbation can induce two behaviors, either resting state or a spike. For the period-k bursting, some period-k bursts can change to period-($k+1$) bursts due to that suitable noisy disturbance near the critical phase can induce a spike ($k=1,2,3$). For the period-($k+1$) bursting, some period-($k+1$) bursts can change to period-k bursts due to that suitable noisy disturbance near the critical phase ($k=1,2,3$) can terminate the last spike. More detailed transition dynamics can be explained by the stable/unstable manifold of the saddle point of the fast subsystem. It is the cause that the appearance of the stochastic bursting whose behavior is stochastic transition between period-k burst and period-($k+1$) burst ($k=1,2,3$). Near the period-doubling bifurcation point, the trajectory of bursting does not pass through the SH point. No novel noise-induced firing patterns can be detected near the period-doubling bifurcation points.

The rest of paper is organized as follows. Section 2 is the experimental model and results. Section 3 presents the theoretical model, and simulation results of the period-adding bifurcation and period-doubling bifurcation processes. Section 4 is the identification of dynamics of deterministic bursting patterns with fast–slow dissection method. Section 5 presents the dynamics of stochastic bursting patterns near period-adding bifurcation points and the distinction to the period-doubling bifurcations. Section 6 is discussion and conclusion.

2 Experimental model and results

2.1 Experimental model

Experimental pacemaker is formed at the injured site of rat sciatic nerve subjected to chronic ligature and has been widely used to investigate the spontaneous pain and nonlinear dynamics—such as the bifurcations and chaos—of the neural firing patterns. Male Sprague-Dawley rats (200–300 g) were used and treated in strict accord with institutional protocols. All experiments were approved by the university biomedical research ethics committee. Surgical operation to produce the pacemaker was performed at anesthetized state with pentobarbital sodium (40 mg/kg, i.p.; supplemented as necessary) [36]. After a survival time of 8–12 days, the previously injured site was exposed and perfused continuously with $34\,^{\circ }\hbox {C}$ Kreb’s solution. The spontaneous spike trains of individual fibers ending at the injured site were recorded with a PowerLab system (Australia) with a sampling frequency being 10.0 kHz. Meanwhile, the spike trains were monitored with the PowerLab system during the experiment to make sure that the recording is of a single unit. The time intervals between the maximal values of the successive spikes were calculated as ISI series. The experimental protocol was described in detailed in our previous studies [11, 21].

2.2 Experimental results

Both period-adding bifurcations and period-doubling bifurcations were observed in the neural pacemakers, as extra-cellular calcium concentration $([\hbox {Ca}^{2+}]_\mathrm{o})$ of the perfusion fluid was gradually decreased from 1.2 to 0 mmol.

2.2.1 Difference between period-adding bifurcation and period-doubling bifurcation from period-1 bursting to period-2 bursting

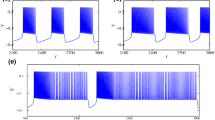
The process of a period-adding bifurcation scenario with stochastic bursting was from period-1 bursting, to stochastic bursting, to period-2 bursting, as shown in Fig. 1(a1), while a process of the period-doubling bifurcation scenario was from period-1 bursting to period-2 bursting directly, as shown in Fig. 1(a2). The spike trains of the period-1 bursting, the stochastic bursting lying between period-1 bursting and period-2 bursting, and period-2 bursting lying in the bifurcation process shown in Fig. 1(a1) are depicted in Fig. 1(b1)–(d1), respectively. The spike trains of the period-1 bursting, period-2 bursting near period-1 bursting, and period-2 bursting far from period-1 bursting lying in the bifurcation process depicted in Fig. 1(a2) are illustrated in Fig. 1(b2)–(d2), respectively.

Fig. 1

Bifurcations and firing patterns observed in the experimental neural pacemakers when $[\hbox {Ca}^{2+}]_\mathrm{o}$ was decreased. Bifurcations: (a1) period-adding bifurcation with stochastic bursting; (a2) period-doubling bifurcation; spike trains: (b1) period-1 bursting of panel (a1); (b2) period-1 bursting of panel (a2); (c1) stochastic firing patterns lying between period-1 bursting and period-2 bursting of panel (a1); (c2) period 2-bursting near period-1 bursting of panel (a2); (d1) period-2 bursting of panel (a1); (d2) period 2-bursting far from period-1 bursting of panel (a2)

2.2.2 Period-adding bifurcation

The transition from period-1 bursting to period-2 bursting shown in Fig. 1(a1) lay in a period-adding bifurcation scenario with a process from period-1 bursting, to stochastic bursting, to period-2 bursting, to stochastic bursting, to period-3 bursting, to stochastic bursting, and to period-4 bursting, as shown in Fig. 2a. Figure 1(a1) is a part of Fig. 2a. The spike trains of the stochastic bursting lying between period-2 bursting and period-3 bursting, period-3 bursting, the stochastic bursting lying between period-3 bursting and period-4 bursting, and period-4 bursting were depicted in Fig. 2b–e, respectively.

Fig. 2

a Period-adding bifurcation with stochastic bursting observed in an experimental neural pacemaker as $[\hbox {Ca}^{2+}]_\mathrm{o}$ was decreased from 1.2 to 0 mmol. Spike trains; b stochastic firing patterns lying between period-2 bursting and period-3 bursting; c period-3 bursting; d stochastic firing patterns lying between period-3 bursting and period-4 bursting; e period-4 bursting

2.2.3 Period-doubling bifurcation

Period-doubling bifurcation, which is from period-1 bursting to period-2 bursting shown in Fig. 1(a2), lay within a period-doubling bifurcation scenario to chaos, as shown in Fig. 3a. The process was from period-1 bursting, to period-2 bursting, to period-4 bursting, and to chaotic bursting. The spike trains of the period-4 bursting are depicted in Fig. 3b.

Fig. 3

a Period-doubling bifurcation observed in an experimental neural pacemaker as $[\hbox {Ca}^{2+}]_\mathrm{o}$ was decreased; b spike trains of period-4 bursting

In the present study, the dynamics of the period-adding and period-doubling bifurcation points from period-1 bursting to period-2 bursting and the firing patterns lying between period-1 bursting and period-2 bursting were studied particularly.

3 Theoretical model and simulation results

3.1 Chay model

Chay model [8, 9, 37] contains the ionic channel dynamics based on Hodgkin–Huxley model and is verified to be closely relevant to the experimental neural pacemaker [11, 25]. It contains the following three simultaneous differential equations given as follows:

$$\begin{aligned} \frac{\hbox {d}V}{\hbox {d}t}= & {} g_{I}{m^3_{\infty }}{h_{\infty }}(v_I-V)+g_{kv}{n^4}(v_k-V)\nonumber \\&+\,g_{kc}\frac{C}{1+C}(v_k-V)+g_{l}(v_l-V) \end{aligned}$$

(1)

$$\begin{aligned} \frac{\hbox {d}n}{\hbox {d}t}= & {} \frac{n_{\infty }-n}{{\lambda _{n}}({\alpha _{n}+\beta _{n}})} \end{aligned}$$

(2)

$$\begin{aligned} \frac{\hbox {d}C}{\hbox {d}t}= & {} \rho ({m^3_{\infty }}{h_{\infty }}(v_c-V)-k_{c}{C}) \end{aligned}$$

(3)

Here, t is the time (the independent variable). The dependent variables are V (the membrane potential), C (the dimensionless intracellular concentration of calcium ion), and n (the probability of potassium channel activation). $v_k, v_I, v_l$, and $v_c$ are the reversal potentials for $\hbox {K}^{+}$, mixed $\hbox {Na}^{+}$–$\hbox {Ca}^{2+}$, leakage ions, and $\hbox {Ca}^{2+}$ respectively; $g_I$, $g_{kv}$, $g_{kc}$, and $g_l$ are, respectively, the maximal conductance divided by the membrane capacitance; $k_c$ is the rate constant for the efflux of intracellular $\hbox {Ca}^{2+}$ ions. $\tau _n$ is the relaxation time of the voltage-gated $\hbox {K}^{+}$ channel; and $\rho$ is a time constant which determines how fast C changes with respect to time. $n_{\infty }$ is the steady-state value of n; $h_{\infty }$ and $m_{\infty }$ are the probabilities of activation and inactivation of the mixed channel. The explicit expressions for $m_{\infty }$, $h_{\infty }$, $n_{\infty }$, and $\tau _n$ are given in the previous description [8, 9, 37].

When a stochastic factor, a Gaussian white noise, $\xi (t)$, reflecting the fluctuation in the real nervous system, is directly added to the right hand of Eq. (1) with other two equations unchanged, the stochastic Chay model is then formed. The stochastic factor possesses the statistical properties as ${<}\xi (t){>}=0$ and ${<}\xi (t)\xi (t^{\prime }){>}=2D\delta (t-t^{\prime })$, where D is the noise intensity, reflecting the degree of noise fluctuation. $\delta (\cdot )$ is the Dirac $\delta$-function. The simulation results of the dynamics of stochastic firing patterns are qualitatively similar if noise is added to Eqs. (1) or (3) (not shown here).

In the present paper, the parameter values are $v_I= 100\,\hbox {mV}$, $v_k=-75\,\hbox {mV}$, $v_l=-40\,\hbox {mV}$, $g_l=7\,\hbox {mS}$, $g_I=1800\,\hbox {mS}$, $k_c=3.3/18$, $\rho =0.27$. The deterministic and stochastic Chay models are solved by Mannella numerical integrate method [38] with integration time step being $10^{-4}\,\hbox {s}$. Upstrokes of the voltage reached the amplitude $-25.0\,\hbox {mV}$ are counted as spikes.

3.2 Period-adding bifurcation simulated in the Chay model

In the present paper, the period-adding bifurcation process is simulated when $\lambda _{n}=\frac{1}{\tau _{n}}=215$, $g_{kv}=1400\,\hbox {mS}$, and $g_{kc}=27\,\hbox {mS}$.

In the deterministic Chay model, when $v_c$ is changed from 108 to 20 mV, the behavior of the firing patterns is changed from period-1 bursting, to period-2 bursting, to period-3 bursting, and to period-4 bursting directly, as shown in Fig. 4a. No firing patterns are simulated lying between two neighboring periodic bursting patterns.

Fig. 4

a Period-adding bifurcation simulated in the deterministic Chay model; b period-adding bifurcation with stochastic bursting simulated in the stochastic Chay model ($D=0.01$); c period-adding bifurcation from period-1 bursting to period-2 bursting directly in the deterministic Chay model; d period-adding bifurcation from period-1 bursting, to stochastic bursting, and to period-2 bursting in the stochastic Chay model ($D=0.01$)

In the stochastic Chay model, a noise-induced firing pattern lies between two neighboring periodic firing patterns. For example, when $D=0.01$, the bifurcation process is from period-1 bursting, to stochastic bursting, to period-2 bursting, to stochastic bursting, to period-3 bursting, to stochastic bursting, and to period-4 bursting, as shown in Fig. 4b. When D is between $10^{-6}{-}10^{-1}$, the bifurcation processes are similar.

The period-adding bifurcation from period-1 bursting to period-2 bursting in the deterministic Chay model and stochastic Chay model with $D=0.01$ is shown in Fig. 4c, d, respectively. A novel stochastic bursting lies between period-1 firing and period-2 firing patterns.

The trajectory of (C, V) of the period-1 bursting in the deterministic Chay ($v_c=85.2\,\hbox {mV}$), of the stochastic bursting in the stochastic Chay model ($v_c=85.2\,\hbox {mV}$), of the period-2 bursting in the deterministic Chay ($v_c=85.0\,\hbox {mV}$), and of the stochastic bursting in the stochastic Chay model ($v_c=85.0\,\hbox {mV}$) are shown in Fig. 5(a1)–(a4), respectively. Figure 5(b1)–(b4) are the trajectory of (C, V) of bursting patterns corresponding to Fig. 5(a1)–(a4), respectively. Compared these trajectories of (C, V), a critical phase can be identified locate near a platform appearing after the first spike of the period-1 bursting or between the first and second spikes of the period-2 bursting. Near the critical phase, for period-1 bursting, a novel spike can be induced by suitable noisy disturbance and some period-1 bursts change to period-2 bursts, and for period-2 bursting, the second spike of period-2 bursting can be terminated by suitable noisy disturbance to form period-1 spike. This is the cause that the stochastic bursting whose behavior is stochastic transition between period-1 and period-2 bursts is induced by noise.

Fig. 5

Spike trains and trajectory of the firing patterns simulated in the Chay model. Spike trains: (a1) period-1 bursting in the deterministic model when $v_c=85.2\,\hbox {mV}$; (a2) stochastic bursting when $v_c=85.2\,\hbox {mV}$ and $D=0.01$; (a3) period-2 bursting in the deterministic Chay model when $v_c=85.0\,\hbox {mV}$; (a4) stochastic bursting when $v_c=85.0\,\hbox {mV}$ and $D=0.01$. Trajectory: (b1), (b2), (b3) and (b4) corresponding to (a1)–(a4), respectively

3.3 Period-doubling bifurcation simulated in the Chay model

The period-doubling bifurcation is simulated in the deterministic Chay model when $\lambda _{n}=\frac{1}{\tau _{n}}= 221$, $g_{kv} = 1700\,\hbox {mS}$, and $g_{kc}= 17\,\hbox {mS}$. As $v_c$ is changed from 120 to 63 mV, period-1 bursting is changed to period-2 bursting, and to period-4 bursting, as shown in Fig. 6a.

Fig. 6

Period-doubling bifurcation: a deterministic Chay model; b stochastic Chay model ($D=0.001$); period-1 bursting to period-2 bursting: c deterministic Chay model; d stochastic Chay model ($D=0.001$)

In the stochastic Chay model, the process of the period-doubling bifurcation remains unchanged. For example, when $D=0.001$, the process of the period-doubling bifurcation is still from period-1 bursting, to period-2 bursting, and to period-4 bursting, as shown in Fig. 6b. When D is between $10^{-6}{-}10^{-3}$, the bifurcation processes are similar.

The period-doubling bifurcation from period-1 bursting to period-2 bursting in the deterministic Chay model and stochastic Chay model with $D=0.001$ are shown in Fig. 6c, d, respectively. No a novel stochastic bursting is detected lies between period-1 and period-2 bursting patterns.

The trajectories of (C, V) of the period-1 bursting in the deterministic Chay ($v_c= 102.0\,\hbox {mV}$), of the stochastic bursting in the stochastic Chay model ($v_c=102.0\,\hbox {mV}$), of the period-2 bursting deterministic Chay ($v_c=101.4\,\hbox {mV}$), and of the stochastic bursting in the stochastic Chay model ($v_c=101.4\,\hbox {mV}$) are shown in Fig. 7(a1)–(a4), respectively. Figure 7(b1)–(b4) are the trajectories of (C, V) of the bursting patterns corresponding to Fig. 7(a1)–(a4), respectively. No a stochastic bursting similar to that lies in the period-adding bifurcation is detected near the period-doubling bifurcation point. Compared these trajectories of (C, V), no a critical phase resembling that of the stochastic bursting pattern lying in period-adding bifurcations can be identified.

Fig. 7

Spike trains and the trajectory of the firing patterns simulated in the Chay model. Spike trains of period-1 bursting when $v_c=102.0\,\hbox {mV}$: (a1) deterministic Chay model; (a2) stochastic Chay model with $D=0.01$. Spike trains of period-2 bursting when $v_c=101.4\,\hbox {mV}$: (a3) deterministic Chay model; (a4) stochastic Chay model with $D=0.01$. (b1), (b2), (b3), and (b4) are the trajectory of bursting patterns corresponding to (a1)–(a4), respectively

4 Identification of dynamics of bursting patterns with fast–slow dissection method

The period-1 bursting and period-2 bursting near both period-adding bifurcation point and period-doubling bifurcation point are studied as representative in this section.

4.1 The bifurcations of equilibrium points of the fast subsystem

The Chay model composed of Eqs. (1)–(3) is called full system in the present paper. According to the fact that $\rho$ is usually a small quantity, the slow variability C is considered as a parameter of the fast subsystem. The fast subsystem of the Chay model is the first two equations shown as follows:

$$\begin{aligned} \frac{\hbox {d}V}{\hbox {d}t}= & {} g_{I}{m^3_{\infty }}{h_{\infty }}(v_I-V)+g_{kv}{n^4}(v_k-V)\nonumber \\&+\,g_{kc}\frac{C}{1+C}(v_k-V)+g_{l}(v_l-V) \end{aligned}$$

(4)

$$\begin{aligned} \frac{\hbox {d}n}{\hbox {d}t}= & {} \frac{n_{\infty }-n}{{\lambda _{n}}({\alpha _{n}+\beta _{n}})} \end{aligned}$$

(5)

Here, C is chosen as the bifurcation parameter.

4.1.1 Bursting lying in the period-adding bifurcation

For the bursting lying in the period-adding bifurcation, as C is changed, the equilibrium points of the fast subsystem of Chay model form a Z-shaped bifurcation curve, as shown in Fig. 8(a1). Lower branch of the Z-shaped curve is a stable node (thin solid line) and C is between [$0.14664,\,+{\infty }$). Middle branch of the Z-shaped curve is a saddle (dashed line) and C is within (0.14664, 0.51156). The intersection of the left knee of the Z-shaped curve is a saddle-node bifurcation point of equilibrium point, also named as a fold bifurcation point ($C\approx 0.14664$). Upper branch of the Z-shaped curve is a focus and C is within ($-{\infty }$, 0.51156]. There exists a supercritical Hopf bifurcation point in the upper branch when $\hbox {C}\approx -0.07615$. The focus is stable (middle solid line) when C is within ($-{\infty }$, $-0.07615$] and becomes unstable (dotted line) when C within ($-0.07615$, 0.51156). Related to the supercritical Hopf bifurcation point locating at the upper branch, a limited cycle appears when $C\>-0.07615$ and disappears when the limited cycle comes into contact with the middle branch (the saddle) to form a SH orbit bifurcation at $C \approx 0.16002$. The upper gray and lower black bold solid lines, respectively, represent the minimal and maximal values of V of the limited cycle. The saddle locating at the limited cycle, which is a homoclinical orbit, is a SH point. Figure 8(b1) is the enlargement around SH point of Fig. 8(a1).

Fig. 8

Bifurcation of equilibrium points and limited cycles of the fast subsystem of the Chay model with period-adding bifurcation or period-doubling bifurcation when C is taken as the bifurcation parameter. (a1) Period-adding bifurcation; (a2) period-doubling bifurcation; (b1) and (b2): a part of panel (a1) and (a2), respectively. The V-C trajectory of the bursting patterns and bifurcation structures of the fast subsystem of the Chay model with period-adding bifurcation or period-doubling bifurcation plotted in one figure. (c1) Period-1 bursting ($v_c=85.2\,\hbox {mV}$, blue line) and period-2 bursting ($v_c= 85.0\,\hbox {mV}$, green line) for period-adding bifurcation and bifurcation structure; (c2) Period-1 bursting ($v_c=102.0\,\hbox {mV}$, blue line) and period-2 bursting ($v_c = 101.4\,\hbox {mV}$, green) for period-doubling bifurcation and bifurcation structure; (d1) and (d2): a part of panel (c1) and (c2), respectively. (Color figure online)

4.1.2 Bursting lying in period-doubling bifurcation

For the bursting lying in the period-doubling bifurcation, the equilibrium points of the fast subsystem of Chay model is also composed of three branches of a Z-shaped curve similar to Fig. 8(a1). The saddle-node (fold) bifurcation point corresponding to the left knee of the Z-shaped curve appears at $C \approx 0.25136$. The intersection of the right knee of the Z-shaped curve is at $C \approx 0.84346$. There exists a supercritical Hopf bifurcation point in upper branch at $C \approx -0.31000$ and a SH orbit bifurcation in the middle branch at $C \approx 0.25609$. Figure 8(b2) is the enlargement around SH point of Fig. 8(a2).

4.2 Dynamics of the bursting patterns identified by the method of the fast–slow variables dissection

For both period-adding bifurcation and period-doubling bifurcation, the behaviors of the deterministic period-1 bursting (blue) and period-2 bursting (green) are the transition between the limited cycle around the upper branch and the stable node corresponding to the lower branch, as shown in Fig. 8(c1), (c2), respectively. The transition from stable node to the stable limited cycle is caused by the fold bifurcation of equilibrium points and the transition from the stable limited cycle to the stable node is caused by the SH bifurcation. Both period-1 and period-2 bursting patterns can be classified into “fold/homoclinic” bursting according to Izhikevich’s scheme or is called type I bursting according to Rinzel’s scheme.

For period-adding bifurcation, Fig. 8(c1), (d1) shows the critical phase between period-1 bursting and period-2 bursting, which is identified appear near the SH point of the fast subsystem. For period-doubling bifurcation, no a critical phase can be detected, as shown in Fig. 8(c2), (d2), respectively.

4.3 The dynamics in cross section (n, V) of the fast subsystem near the SH point

Because the bifurcation structures and trajectories of bursting patterns in the three-dimensional phase space (V, C, n) is difficult to be visualized, dynamics in two-dimensional cross section (n, V) at three fixed C values near SH point are investigated.

4.3.1 The period-adding bifurcation

There are three equilibriums, stable node, saddle, and unstable focus, in each of the planes of (n, V) at fixed C values, as shown by bold cycle point, half-bold cycle point, and hollow circle in Fig. 9(a1)–(e1). The stable manifold (the line with smaller slope) and the unstable manifold (the line with larger slope) of the saddle shown in Fig. 9 are represented by bold black solid line and bold gray solid line, respectively. When $C=0.15950$, a stable limit cycle around the focus and up-right to the saddle appears, as shown in Fig. 9(a1). Figure 9(b1) is the enlargement of Fig. 9(a1). When $C=0.16002$ (corresponding to value of the SH point, the vertical red line shown in Fig. 8(b1)), the saddle hits the limited cycle to form a SH orbit (red line), as depicted in Fig. 9(c1). Figure 9(d1) is the enlargement of Fig. 9(c1). When $C=0.16070$, the limit cycle disappears, as illustrated in Fig. 9(e1).

Fig. 9

Dynamics in the cross section (n, V) at different C values of the bifurcation structures of the fast subsystem. Period-adding bifurcation: (a1) $C=0.15950$; (b1) a part of panel (a1); (c1) $C=0.16002$; (d1) a part of panel (c1); (e1) $C = 0.16070$. Period-doubling bifurcation: (a2) $C= 0.25500$; (b2) a part of panel (a2); (c2) $C =0.25609$; (d2) a part of panel (c2); (e2) $C=0.25700$. Circle, half-bold cycle point, and bold cycle point represents unstable focus, saddle, and stable node, respectively. Bold black solid line, bold gray solid line, and thin solid red line represents stable manifold of the saddle, unstable manifold of the saddle, and a saddle-homoclinic orbit, respectively. (Color figure online)

4.3.2 The period-doubling bifurcation

As performed in the period-adding bifurcation, the dynamics in two-dimensional (n, V) planes at $C = 0.25500$, 0.25609, and 0.25700, which locate left to, approximately at, and right to the SH point, and correspond to red vertical bold lines shown in Fig. 8(b2), were identified. The results resemble those of the period-adding bifurcation, as shown in Fig. 9(a2)–(e2).

4.4 The dynamics of deterministic and stochastic bursting patterns near the SH point

4.4.1 Deterministic bursting patterns lying in the period-adding bifurcation

Three (n, V) planes corresponding to Fig. 9(a1)–(e1) are adopted. The trajectories of both period-1 bursting ($v_c=85.2\,\hbox {mV}$) and period-2 bursting ($v_c=85.0\,\hbox {mV}$) across each of the three (n, V) planes two times, and two points appear in the corresponding (n, V) plane, as shown in Fig. 10. Figure 10(b1), (b2), (d1), (d2) are the enlargement of a part of Fig. 10(a1), (a2), (c1), (c2), respectively. One point is labeled with “outward orbit” and the other “inward orbit”. The “outward orbit” corresponds to the trajectory passing through the cross section from right to left, i.e., from a larger C value to a lower C value. The “inward orbit” corresponds to the trajectory passing through the cross section from left to right, i.e., from a lower C value to a larger C value. The “outward orbit” point in three (n, V) planes is close to the stable node for both period-1 and period-2 bursting, as shown in Fig. 10.

Fig. 10

Dynamics of period-1 ($v_c=85.2\,\hbox {mV}$) and period-2 bursting ($v_c=85.0\,\hbox {mV}$) patterns lying in period-adding bifurcation near SH point at (n, V) cross section with different values. (a1) Period-1 bursting when $C=0.16002$; (a2) period-2 bursting when $C=0.16002$; (b1) and (b2) are the enlargement of (a1) and (a2), respectively; (c1) period-1 bursting when $C=0.16070$; (c2) period-2 bursting when $C=0.16070$; (d1) and (d2) are the enlargement of (c1) and (c2), respectively

Fig. 11

Dynamics of original bursting pattern (solid line) lying in period-adding bifurcation scenarios and the response after a suitable disturbance (dashed line). Period-1 bursting when $v_c = 85.2\,\hbox {mV}$: a $V-t$; b the trajectory in the (C, V) plane and the bifurcations of the fast subsystem; period 2 bursting when $v_c= 85.0\,\hbox {mV}$: c $V-t$; d the trajectory in the (C, V) plane and the bifurcations of the fast subsystem

Although the “inward orbit” in (n, V) planes is close to the saddle, the detailed relationships between the saddle and the “inward orbit” for the period-1 bursting ($v_c=85.2\,\hbox {mV}$) and period-2 bursting ($v_c=85.0\,\hbox {mV}$) are shown in Fig. 10(b1), (d1), (b2), (d2). When $C=0.16002$ (the vertical red line shown in Fig. 8(b1)), for both period-1 bursting and period-2 bursting, the “inward orbit” point locates above the stable manifold of the saddle, on the upper branch of the unstable manifold of the saddle, and near the saddle point, i.e., the SH point, as shown in Fig. 10(b1), (b2). No distinction can be identified between period-1 and period-2 bursting. For the cross section with $C=0.16070$, it can be found distinction between period-1 bursting (Fig. 10(d1)) and period-2 bursting (Fig. 10(d2)). For period-1 bursting, the “inward orbit” point locates below the stable manifold of the saddle, on the lower branch of unstable manifold of the saddle point, and near the saddle. For the period-2 bursting, the “inward orbit” point locates above the stable manifold of the saddle, on the upper branch of unstable manifold of the saddle point, and near the saddle.

These indicate that the both trajectory of period-1 bursting and period-2 bursting pass through the neighborhood of the SH point. For the period-1 bursting, the trajectory passes through the stable manifold of the SH point from upper to lower and along the lower branch of the unstable manifold of the saddle, and turns to the stable node to terminate the spike. However, for period-2 bursting, the trajectory locates above the stable manifold of the SH point and and passes through the neighborhood of the SH point along the upper branch of the unstable manifold of the saddle and becomes far from the SH point to form the second spike. The minimum distance between the “inward orbit” point and SH point is 0.00030 for the period-1 bursting and 0.00067 for the period-2 bursting.

4.4.2 Responses of bursting lying in period-adding bifurcation to disturbance near the SH point

A platform appears after the first spike of the period-1 bursting ($v_c=85.2\,\hbox {mV}$) and near the critical phase corresponding to the neighborhood of the SH point. When a suitable positive disturbance is introduced into the platform, a novel spike is induced to form a period-2 burst instead of the original period-1 burst, as shown in Fig. 11a, b.

The deterministic period-2 bursting ($v_c=85.0\,\hbox {mV}$) manifests period-2 burst in each period without any disturbance. When a suitable negative disturbance is introduced into the trough or platform before the second spike, i.e., the critical phase near the SH point, the original second spike can be terminated to form a period-1 burst instead of the original period-2 burst, as shown in Fig. 11c, d.

Fig. 12

Dynamics of stochastic bursting pattern ($D=0.01$) lying in period-adding bifurcation near SH point at (n, V) cross section with different C values. The stochastic bursting: (a1) $v_c=85.2\,\hbox {mV}$; (a2) $v_c=85.0\,\hbox {mV}$; the (n, V) cross section for different values: (b1) the stochastic bursting when $v_c= 85.2\,\hbox {mV}$ and $C=0.16002$; (b2) the stochastic bursting when $v_c=85.0\,\hbox {mV}$ and $C=0.16002$; (c1) and (c2) are the enlargement of (b1) and (b2), respectively; (d1) the stochastic bursting when $v_c=85.2\,\hbox {mV}$ and $C=0.16070$; (d2) the stochastic bursting when $v_c= 85.0\,\hbox {mV}$ and $C=0.16070$; (e1) and (e2) are the enlargement of (d1) and (d2), respectively

The dynamics of the response of the bursting to suitable disturbance can be used to the understanding of the generation of stochastic bursting in the stochastic Chay model. When noise intensity is suitable, some disturbances induced by noise near the critical phase can terminate the second spike of the period-2 burst and lead to a period-1 burst, and others cannot terminate the second spike, and the period-2 burst pattern remained unchanged. It indicates that the trajectory of period-2 burst near the saddle passes through the stable manifold of the SH point and form a period-1 burst when noise intensity is suitable. It is the cause that a stochastic bursting whose behavior is stochastic transition between period-1 burst and period-2 burst instead of period-2 bursting is induced. Similarly, the disturbance induced by noise near the critical phase can evoke an extra spike followed the period-1 burst to form a period-2 burst. It indicates that the trajectory of period-1 burst near the saddle can transit into the neighborhood above the stable manifold of the SH point and form a new spike (period-2 bursting) when noise intensity is suitable. It is the cause that the stochastic bursting instead of the period-1 bursting is induced in the stochastic Chay model.

4.4.3 The dynamics of the stochastic bursting patterns lying in the period-adding bifurcation near the SH point

The dynamics of the stochastic bursting ($D=0.01$) changed from period-1 bursting ($v_c=85.2\,\hbox {mV}$) and from period-2 bursting ($v_c=85.0\,\hbox {mV}$) are shown in Fig. 12. For the stochastic burstings, the stochastic transitions between period-1 burst and period-2 burst happen near the critical phase, i.e., the neighborhood of the SH point, as shown in Fig. 12(a1), (a2). The dynamics of the stochastic bursting patterns in the (n, V)-cross section are illustrated in Fig. 12(b1)–(e2). Compared with the deterministic situation (Fig. 10), the “outward orbit” points (blue points) still appear near the stable node; however, the dynamics of the “inward orbit” points changed.

For both stochastic bursting patterns ($v_c=85.2\,\hbox {mV}$, and $v_c=85.0\,\hbox {mV}$) and both values ($C=0.16002$, and $C=0.16070$), the “inward orbit” point in the (n, V)-cross section appears on not only the upper branch but also the lower branch of the unstable manifold of the saddle, as shown in Fig. 12(c1), (c2), (e1), (e2). Figure 12(c1), (c2), (e1), (e2) are the enlargement of Fig. 12(b1), (b2), (d1), (d2), respectively. For both stochastic bursting patterns, the “inward orbit” points corresponding to period-1 burst locates below the stable manifold of the saddle and the “inward orbit” points corresponding to period-2 burst above the stable manifold. The stochastic transitions between period-1 burst and period-2 burst are the transitions across the stable manifold of the saddle.

4.4.4 The deterministic bursting patterns lying in the period-doubling bifurcation

As performed in the bursting patterns lying in period-adding bifurcation scenario (Fig. 10), the dynamics of the period-1 bursting ($v_c=102.0\,\hbox {mV}$) and period-2 bursting ($v_c=101.4\,\hbox {mV}$) lying in period-doubling bifurcation are shown in Fig. 13. Two (n, V) planes at $C=0.25609$ and $C=0.25700$ are adopted. Compared with Fig. 10 to show the dynamics of bursting patterns lying in period-adding bifurcations, distinction is found from Fig. 13.

Fig. 13

Dynamics of period-1 ($v_c=102.0\,\hbox {mV}$) and period-2 bursting ($v_c=101.4\,\hbox {mV}$) patterns lying in period-doubling bifurcation near SH point at (n, V) cross section with different C values. (a1) Period-1 bursting when $C=0.25609$; (a2) period-2 bursting when $C=0.25609$; (b1) and (b2) are the enlargement of (a1) and (a2), respectively; (c1) period-1 bursting when $C=0.25700$; (c2) period-2 bursting when $C=0.25700$; (d1) and (d2) are the enlargement of (c1) and (c2), respectively

For the period-1 bursting, there exist an “outward orbit” point and an “inward orbit” point. For the period-2 bursting patterns, there exist two “outward orbit” points and two “inward orbit” points. For both bursting patterns and both (n, V) planes, the “outward orbit” points still locate below the stable manifold of the saddle but the distance between the “outward orbit” points and the stable node becomes longer, compared with those of the period-adding bifurcations. It is the most important distinction that the “inward orbit” points locate far from the saddle, as shown in Fig. 13. When $C=0.25609$ (the cross section corresponding to the SH point, the vertical red line shown in Fig. 8(b2)), the “inward orbit” points locate on the limit cycle. The minimal distance between the “outward orbit” point and SH point is 0.75958 for the period-1 bursting and 0.42346 for the period-2 bursting. The minimal distance between the “inward orbit” point and SH point is 20.45344 for the period-1 bursting and 23.97828 for the period-2 bursting. The distances are much longer than those of the period-adding bifurcation scenarios. It is the cause that no a critical phase is detected within the bursting pattern lying in period-doubling bifurcations.

4.4.5 The dynamics of the bursting patterns lying in the period-doubling bifurcation in the stochastic Chay model

As performed in the deterministic bursting patterns (Fig. 13), the dynamics of bursting when $v_c= 102.0\,\hbox {mV}$ ($D=0.01$) and when $v_c=101.4\,\hbox {mV}$ ($D=0.01$) are shown in Fig. 14. For both period-1 bursting and period-2 bursting, no novel spike can be induced by noise, as shown in Fig. 14(a1), (a2).

Fig. 14

Dynamics of stochastic bursting pattern ($D=0.01$) lying in period-doubling bifurcation near SH point at (n, V) cross section with different C values. The stochastic bursting: (a1) $v_c=102.0\,\hbox {mV}$; (a2) $v_c=101.4\,\hbox {mV}$. The (n, V) cross section for different values: (b1) the stochastic bursting when $v_c=102.0\,\hbox {mV}$ and $C=0.25609$; (b2) the stochastic bursting when $v_c= 101.4\,\hbox {mV}$ and $C=0.25609$; (c1) and (c2) are the enlargement of (b1) and (b2), respectively

The dynamics of the stochastic bursting patterns in the (n, V)-cross section are shown in Fig. 14(b1)–(c2). For both bursting patterns ($v_c= 102.0\,\hbox {mV}$, and $v_c=101.4\,\hbox {mV}$) and C value ($C=0.25609$), the “inward orbit” points in the (n, V)-cross section locate far from the saddle, which is different from that of the period-adding bifurcation, as shown in Fig. 14(b1)–(c2). Figure 14(c1), (c2) are the enlargement of Fig. 14(b1), (b2), respectively. The similar results are obtained when $C=0.25700$. However, the locations of “outward orbit” and “inward orbit” points are different from those of the period-adding bifurcation. The “outward orbit” points locate below the stable manifold of the saddle, and the “inward orbit” points locate above the stable manifold of the saddle. Noise cannot induce transitions across the stable manifold of the saddle for the period-doubling bifurcation. No novel spike can be induced by noise for period-1 bursting and period-2 bursting.

5 Firing patterns near other bifurcation points

As shown in Eqs. (4) and (5), the fast subsystem does not contain the bifurcation parameter $v_c$. It shows that the bifurcation structures of the equilibrium points and the limited cycle of the fast subsystem are independent of $v_c$.

5.1 Dynamics near other period-adding bifurcation points

The period-k bursting and period-($k+1$) bursting ($k=2,3$) near period-adding bifurcation point from period-k bursting to period-($k+1$) bursting manifest dynamics similar to those of the period-1 bursting and period-2 bursting near the bifurcation point from period-1 bursting to period-2 bursting. To avoid repetition, we do not address the detailed results of the period-k bursting and period-($k+1$) bursting ($k=2,3$) near period-adding bifurcation point from period-k bursting to period-($k+1$) bursting. For example, the period-2 bursting when $v_c=47.9\,\hbox {mV}$ (blue line) and the period-3 bursting when $v_c=47.8\,\hbox {mV}$ (green line) in the deterministic Chay model are shown in Fig. 15a, b. The minimal distance between the “inward orbit” point and SH point is 0.00721 for the period-2 bursting and 0.00056 for the period-3 bursting. The period-3 bursting when $v_c=30.6\,\hbox {mV}$ (blue line) and the period-4 bursting when $v_c=30.4\,\hbox {mV}$ (green line) in the deterministic Chay model are shown in Fig. 15c, d. The minimum distance between the “inward orbit” point and SH point is 0.00697 for the period-3 bursting and 0.00091 for the period-4 bursting. The minimum distance between SH point and the trajectory of the bursting near the period-adding bifurcation point is shorter than 0.01. The trajectory of the bursting near the period-adding bifurcation point passes through the neighborhood of the SH point. The SH point is a critical point near which a suitable perturbation can induce transition between two behaviors, quiescent state or a spike.

Fig. 15

Trajectory of (C, V) of bursting and bifurcation structures of the fast subsystem of the Chay model plotted in one figure. a Period-2 bursting when $v_c=47.9\,\hbox {mV}$ (blue line) and period-3 bursting (green line) when $v_c = 47.8\,\hbox {mV}$; b a part of panel (a); c period-3 bursting when $v_c=30.6\,\hbox {mV}$ (blue line) and period-4 bursting (green line) when $v_c= 30.4\,\hbox {mV}$; d a part of panel (c). (Color figure online)

Fig. 16

a The trajectory of (C, V) of period-2 bursting ($v_c=66.0\,\hbox {mV}$, blue line) and period-4 bursting ($v_c=65.5\,\hbox {mV}$, green line) and bifurcation structures of the fast subsystem of the Chay model plotted in one figure; b a part of panel (a)

5.2 Dynamics near period-doubling bifurcation point from period-2 to period-4 bursting patterns

When the trajectory of (C, V) of the bursting and the bifurcation structures of the fast subsystem of the Chay model are plotted in one figure, it can be found that period-2 bursting ($v_c=66\,\hbox {mV}$) and period-4 ($v_c=65.5\,\hbox {mV}$) bursting are far from the SH point of the fast subsystem, as shown in Fig. 16. The minimal distance between the “outward orbit” point and SH point is 0.75513 for the period-2 bursting and 0.49078 for the period-4 bursting. The minimal distance between the “inward orbit” point and SH point is 24.35367 for the period-2 bursting and 26.63235 for the period-4 bursting. The minimal distance between SH point and the trajectory of the bursting near the period-doubling bifurcation point is great than 0.4. The trajectory of bursting near the period-doubling bifurcation point does far from the SH point. No noise-induced firing patterns can be detected near the period-doubling bifurcation points.

6 Discussion and conclusion

Period-adding bifurcation scenario with stochastic bursting patterns and period-doubling bifurcation of neural firing pattern were the important transition regularities observed in the experiments and simulated in theoretical models [11, 12, 27, 28]. No stochastic firing patterns like those within period-adding bifurcation scenario were detected lies in the period-doubling bifurcation. In the present paper, using the fast–slow variables dissection method, the deterministic burstings lying in both period-adding bifurcation and period-doubling bifurcation are classified into “fold/homoclinic” bursting with a SH point. The trajectory is far from the SH point for the bursting patterns near period-doubling bifurcation points, and passes through the neighborhood of the SH point for the bursting patterns near the period-adding bifurcation points. The SH point behaves as a critical point near which a suitable perturbation can induce two behaviors, either resting state or a spike. Near the critical phase, some period-k bursts can change to period-($k+1$) bursts due to suitable noisy disturbance can induce a novel spike for the period-k bursting, and some period-($k+1$) bursts can change to period-k bursts due to suitable noisy disturbance can terminate the last spike to form quiescent state for the period-($k+1$) bursting ($k=1,2,3$). It is the cause that the stochastic bursting whose behavior is stochastic transition between period-k burst and period-($k+1$) burst lies not in the period-doubling bifurcation but in the period-adding bifurcation scenarios. The critical point also provides suitable phase to apply control signal to modulate the firing patterns.

The stochastic transition and coherence resonance of the stochastic bursting patterns lying in the period-adding bifurcation, and the distinction to the chaotic bursting have been investigated [21, 25, 26, 39]. In the present paper, the underlying dynamics to induce the stochastic bursting, i.e., the dynamics near the SH point, are identified with bifurcation analysis and fast–slow variables dissection method. The fast subsystem exhibits a stable node, a saddle, and a stable limited cycle. The dynamics near the SH point, including the trajectory of the bursting and the dynamics of the saddle, play important roles in the generation of the stochastic bursting. The trajectory of bursting lying in period-adding bifurcation passes through the neighborhood of the SH point, and the behavior of the stochastic bursting pattern across the (n, V) plane runs along the unstable manifold of the saddle.

Noise has been identified play important roles near the bifurcation points [2, 21, 40,41,42,43]. In the nervous system, stochastic resonance or coherence resonance has been observed near the bifurcation points of equilibrium points, such as the supercritical and subcritical Hopf bifurcation points, saddle-node bifurcation point, bifurcation point of saddle-node bifurcation on an invariant cycle [40, 41, 44]. The stochastic firing patterns are dependent on the types of the bifurcation points. The roles of the threshold effect near the equilibrium bifurcation points in the stochastic resonance or coherence resonance have been widely investigated [2, 21, 40, 45, 46]. In the present paper, the stochastic bursting patterns does not appear near the period-doubling bifurcation points but the period-adding bifurcation points, which are also dependent on the types of the bifurcations. The stable manifold of the saddle forms a threshold across which the period-k burst and period-($k+1$) burst can be changed each other. The trajectory of the period-k burst across the (n, V) plane runs along lower branch of the unstable manifold of the saddle and of the period-($k+1$) burst run along the upper branch of the unstable manifold of the saddle. The upper and lower branches of the unstable manifold of the saddle locate above and below the stable manifold of the saddle, respectively. The detailed transition dynamics of the stochastic bursting patterns can well be explained by the stable/unstable manifold of the saddle point.